1975年,Kau[1]提出了一种利用地面线型地标进行导航的方法。通过采用人工选取地标的方法,进行交互式地标导航工作[2-4],需要做大量的重复性工作,并不适用于对大数据量导航图像进行实时自动处理的遥感卫星[5]。同时,人工选取地标的方法涉及大量的人工操作,缺乏一致性标准,工作人员的主观性会影响地标选取的质量,直接导致导航精度大幅度下降。另外,地标匹配误差对全局的遥感应用产生严重的影响[6-7],因此自动的地标生成和识别是必要的[8]。
国内外科学家对自动地标生成技术进行了大量的研究。Emery等[9]于2003年提出了基于最大相关系数(Maximum Correlation Coefficient,MCC)的自动地标导航方法,由于该方法具有易于实现、计算速度快、精度高的优点,其已成为目前为止应用范围最为广泛的地标建立方法。郭强等[10]优化了最大相关系数法的计算流程,降低了算法的复杂度。但是与人工地标导航类似,基于最大相关系数的自动地标导航方法仍然需要依据大量历史遥感资料,人工制定不同季节、不同光照条件的模板,同样依赖于地标选取人员的经验。美国空间科学与工程中心(Space Science and Engineering Center,SSEC)对静止轨道GOES卫星设计了自动地标导航系统[11],认为当匹配模板的细节信息量不够时,Emery等[9]的最大相关系数法不适用。卢耀秋[12]、赵礼铮和白光弼[13]分别在静止气象卫星和极轨气象卫星上使用了地标导航方法,但仍然是人工交互式的方法。杨磊等[8, 14]研究了基于最大相关系数法的自动地标导航方法,提出了将地面图像建立控制点并自动生成地标的方法,但其地标选取的范围也局限于海岸线和河流地标。
针对以上地标导航中地标建立的局限性问题,本文提出了一种基于全局地标信息的选取原则及导航方法,即将地标遥感图像的边界和粗糙纹理作为生成地标图像的基准,通过筛选全球模板建立地标库,利用建立的地标库进行自动地标匹配,进而有效地提高了自主地标导航的精度。
1 地标导航原理 图 1为基于地标的卫星自主导航原理图。其工作过程是:将飞行器上预先装订的标准地标库中的模板与卫星实时拍摄图像进行地标匹配,使用最大相关系数法得到若干个已标定的地标在遥感图像上的位置坐标。Rosborough等[15]认为要实现准确的地标导航需要至少匹配得到2个地标。将地标在遥感图像上的坐标转化为视线矢量,结合轨道动力学模型进行导航解算,获得位置、速度等导航信息。
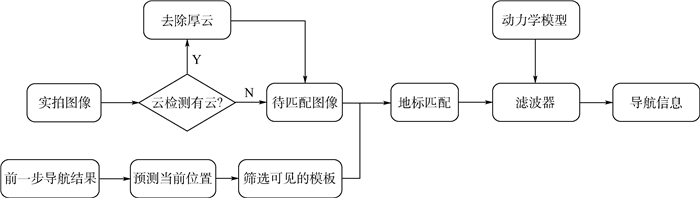 |
| 图 1 地标导航原理图 Fig. 1 Schematic of landmark navigation |
| 图选项 |
该导航方法使用的前提是在获取遥感卫星数据时,要求卫星姿态的预报或测量是准确的,否则卫星姿态的误差将会影响到位置误差及速度误差的测量。同时,遥感图像中存在大量不确定形状的云层,严重影响地标匹配,因此,在地标匹配之前需要对拍摄图像进行严格的云检测。
2 全局地标库的建立与匹配算法 2.1 地标的选取原则 在基于地标的自主导航方案中,地标库的生成将直接影响到导航精度。全局地标库需要建立不同光照条件下的地标模板,而对于每一个地标,需要建立至少8个模板(白昼、黑夜,春、夏、秋、冬)[9]。这些地标图像需要具备以下2个特征:①地标图像具有清晰的结构特征;②地标图像与待匹配的卫星遥感图像具有相同的投影方式。
具体做法如下:
1) 地标库主要由湖泊、河流、海岸线、岛屿组成,由于水域和陆地的灰度值差异很大,可以容易地获取水陆边界的结构特征作为地标。
2) 为了减少误匹配的概率,选取水陆边界地标的结构特征必须是独特的,由于不确定卫星拍摄图像相对于模板的角度,所以不能使用水陆边界斜率作为特征。
3) 使用边界中高曲率和拐点区域作为生成水陆地标的基础。使用世界数据银行(World Data Bank)和世界海岸线矢量库(World Vector Shoreline)中的数据[8],自动计算地标轮廓拐点,“T”型连接点作为控制点,用于扩展成地标,如图 2[8]所示。
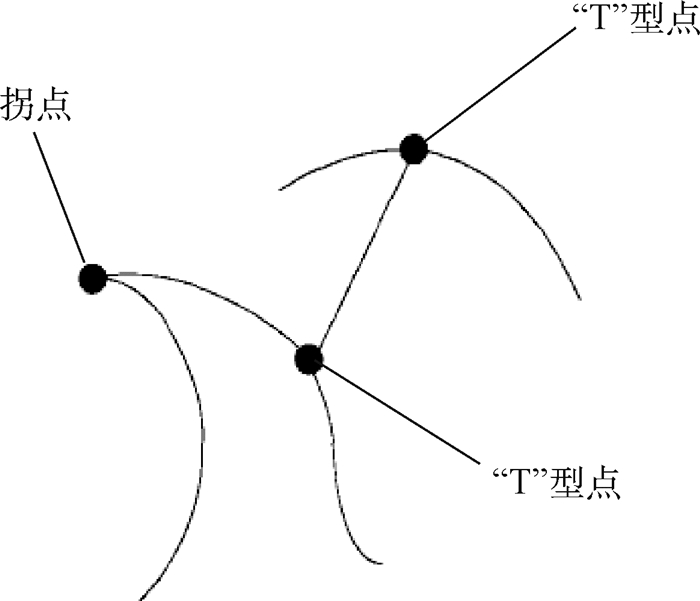 |
| 图 2 地面控制点的定义[8] Fig. 2 Definition of control point on earth surface[8] |
| 图选项 |
4) 在非水陆地标区域,存在大量不规则灰度剧烈变化区域,无法筛选出高曲率点,但其中有大量的不规则天然粗纹理可以提供唯一的辨识特征[16],可以作为这一区域的主要结构特征,很好地补充海陆地标。
2.2 全局地面控制区的建立 将拥有足够多粗糙纹理的区域定义为控制区,并作为形成地标块的基础。在选取控制区的过程中,没有考虑地面纹理的具体特征,地形的粗糙程度体现的纹理已足以提供导航信息[17]。因此,无需使用计算量大的灰度共生矩阵来描述图像纹理特性。设大小为M×N的图像f(x, y),选取m×n的计算局部窗口,用以下灰度场特征参数描述地面粗糙程度。
1) 灰度标准差。描述灰度值偏离平均值的程度,可以宏观反映特征值整体的起伏程度。
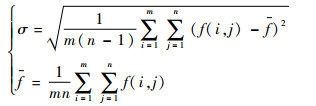 | (1) |
2) 灰度粗糙度。描述灰度值变化的剧烈程度,粗糙度越大,局部的灰度起伏约剧烈。x轴和y轴方向的粗糙度分别为
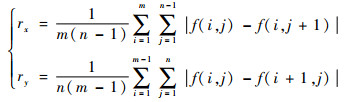 | (2) |
3) 局部灰度相关系数。描述局部的灰度相关度,如果地标本身相关性很大,将大大影响地标匹配的准确度。x轴和y轴方向的局部灰度相关系数分别为
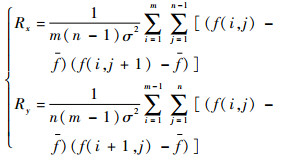 | (3) |
实际上,在表达地形的局部变化情况时,灰度粗糙度和局部灰度相关系数是一致的[17]。
图 3为中哈边境天山山脉附近的遥感图像,是典型的具有大量混合地貌的遥感图像,除了通常可作为地标的水陆边界地貌之外,还包括了雪山、草原、森林、荒漠、河流等多种地貌,是全球具有代表性的模板图像。
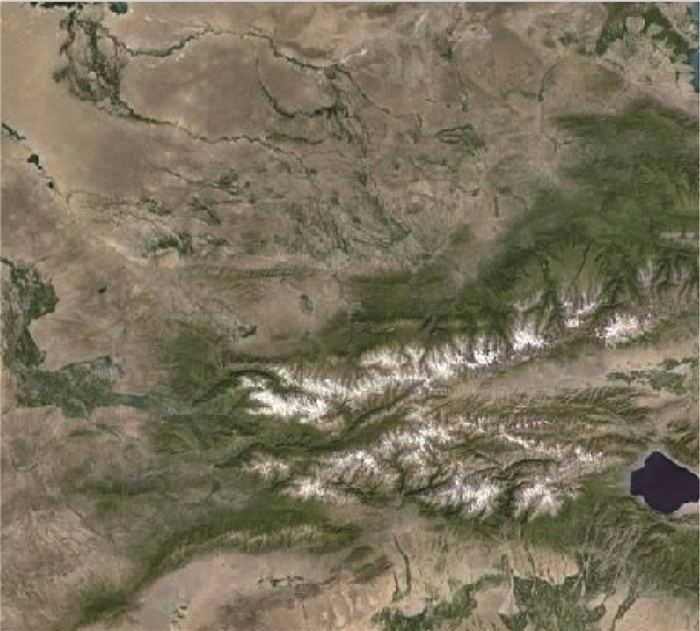 |
| 图 3 混合地貌遥感图像 Fig. 3 Remote sensing image of mixed landscape |
| 图选项 |
根据2.1节中的选取地标原则,将图 3灰度化,结果如图 4所示。
 |
| 图 4 混合地貌遥感图像的灰度化结果 Fig. 4 Grayscale results of remote sensing image of mixed landscape |
| 图选项 |
以图 4为基础,根据本节内容,取m、n的值为5,计算图像的地形标准差和地形粗糙度,得到的标准差和粗糙度如图 5~图 6所示。
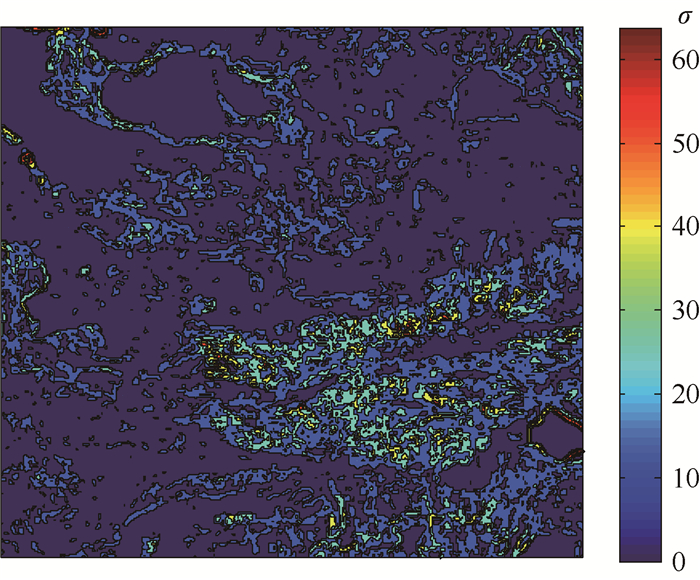 |
| 图 5 灰度标准差 Fig. 5 Standard deviation of grayscale |
| 图选项 |
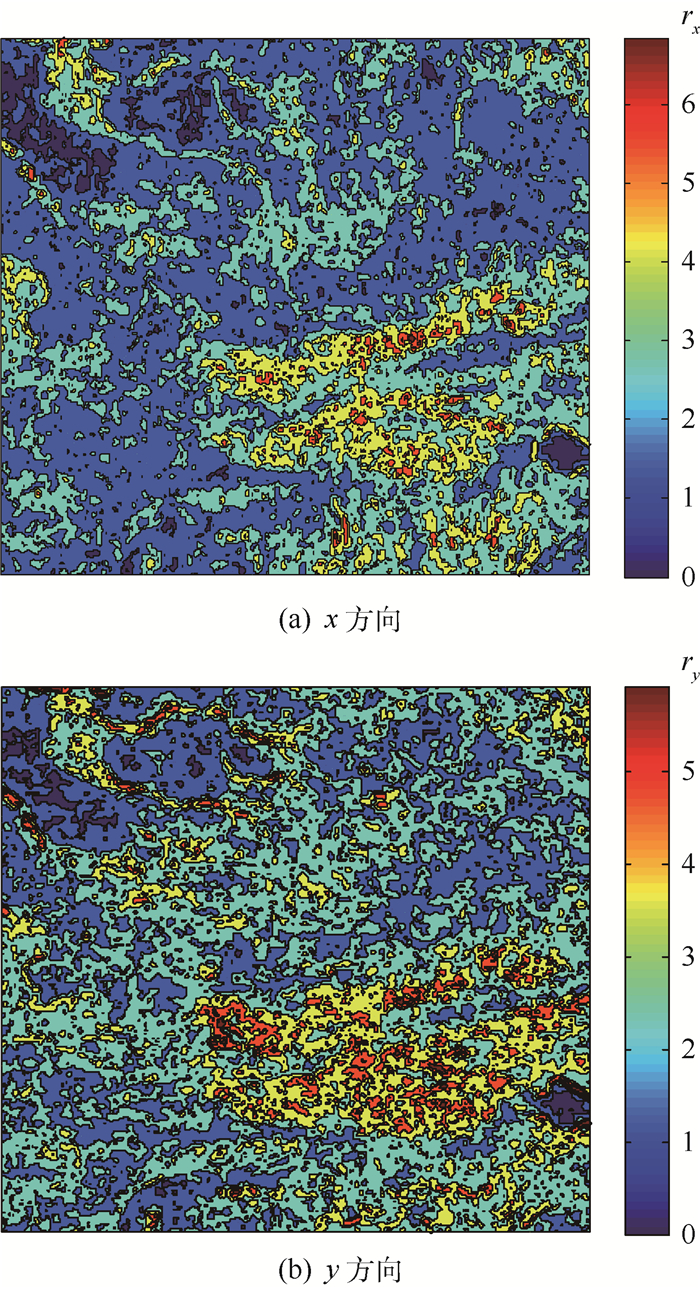 |
| 图 6 灰度粗糙度 Fig. 6 Roughness of grayscale |
| 图选项 |
将灰度标准差作为衡量局部地形的特征数量指标,并参考灰度粗糙度建立控制区域。若某一区域的灰度标准差和灰度粗糙度2个参数都大于某个阈值,则可以将这一区域作为候选控制区域。
具体在建立全球地标模板库时,选取灰度标准差阈值为30,灰度粗糙度阈值为6,可以得到图 7所示的候选控制区域(白色高亮)。
 |
| 图 7 候选控制区域 Fig. 7 Selected ground control area |
| 图选项 |
由图 7看出,使用灰度差作为特征参数选取的控制区域内包含了大量的水陆边界地标,此类地标需要计算控制点后扩展为可用地标。
依据以上方法挑选出的控制区域主要包含以下3类:
1) 2种易于区分的地形或地貌的边界地区,如海岸线、岛屿、沙漠边界等,如图 8所示。
 |
| 图 8 典型地貌边界地标 Fig. 8 Typical landmarks of topographic boundary |
| 图选项 |
2) 较为均匀地貌中出现较为明显变化的区域,如河流、湖泊、山脉等,如图 9所示。
 |
| 图 9 典型地貌变化地标 Fig. 9 Typical landmarks of topographic diversification |
| 图选项 |
3) 有较为明显的粗纹理地区,如戈壁、森林、丘陵等,如图 10所示。
 |
| 图 10 典型纹理地标 Fig. 10 Typical texture landmarks |
| 图选项 |
综上所述,首先计算控制区域并筛选出可用于生成地标的控制区域,再以这些控制区域为基础,扩展成为用于匹配的全局地标图像库(地标块大小为30×30)。使用这一方法获得的地标库的地标数据量比单纯的水陆边界地标库增加了43.97%。
2.3 地标匹配算法 地标匹配算法采用灰度相关系数法,其具有运算速度快、准确率高的特点。
设大小为M×N的卫星图像f(x, y)和大小为J×K的模板图像w(x, y),如图 11所示。在图像f(x, y)中寻找与模板w(x, y)相匹配的区域,即将模板作为一个空间滤波器在卫星图像f(x, y)中求取每个位置上的相关系数R(x, y)。使用归一化最大互相关(normalized maximum cross correlation)系数表达二者的相关性,具体表示为
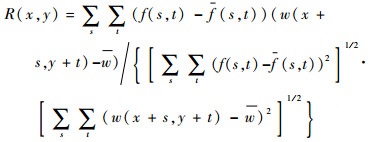 | (4) |
 |
| 图 11 地标模板在卫星图像上的匹配 Fig. 11 Matching of landmark template on satellite image |
| 图选项 |
R(x, y)值越接近1,表示图像的相似度越高,匹配精度越高。同时应用t检验:当显著水平小于0.05为误匹配,此时相关系数R(x, y)的阈值为0.72;当相关系数R(x, y)取到最大值Rm(xm, ym)且超过0.72的位置,就是卫星图像与地标模板图像相匹配的位置[8]。
对全球模板进行匹配的计算量极大,需要在匹配之前对卫星拍摄图像进行处理,地标匹配的具体步骤如下:
1) 对拍摄图像进行严格的云检测,剔除厚云的部分。
2) 将剩余部分依照式(1)和式(2)计算灰度标准差和灰度粗糙度,本文选取标准差阈值为15,粗糙度阈值为1.2,剔除图像中标准差和粗糙度同时小于阈值的部分。
3) 在地标库中选择对应光照条件(白昼、黑夜,春、夏、秋、冬)部分的地标,依据卫星图像幅宽,选取坐标处于卫星星下点附近幅宽范围内的地标。
4) 将选出的地标与拍摄图像中剩余部分的每一个可能的位置进行相关系数计算,相关系数取到最大值且超过阈值0.72的位置就是地标匹配的位置。
3 地标导航 3.1 地标导航观测方程 对于给定的时刻,通过对地观测设备得到实时的拍摄图像,在与地标库中的地标进行匹配后,能得到若干个已知具体地理位置的地标在实时拍摄图像上的位置坐标。假设Pi为实时拍摄图像上匹配后得到的第i个地标的中心,在实时拍摄图像上的坐标为(xi, yi),如图 12所示。
 |
| 图 12 相机成像的几何关系 Fig. 12 Geometry of camera imaging |
| 图选项 |
为推导计算方便,假定相机坐标系和卫星本体坐标系重合,即相机安装矩阵为单位矩阵,则地标在卫星本体坐标系中的单位地标视线矢量为地标中心在相机像平面上的坐标加上相机焦距,表示为
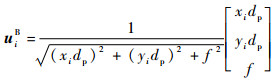 | (5) |
式中:f为CCD相机焦距;dp为CCD器件像元尺寸。转换到惯性坐标系为
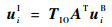 | (6) |
式中:A为卫星的姿态矩阵;TIO为质心轨道坐标系到惯性坐标系的变换矩阵。
卫星除去在大面积的海洋上空运行外,都可以在实时拍摄图像中匹配得到多个地标,卫星和地标的空间关系图如13所示。
图 13中,RV为卫星位置,Ri为匹配得到的第i个地标的位置,与单位地标视线矢量之间的关系可以表示为
 | (7) |
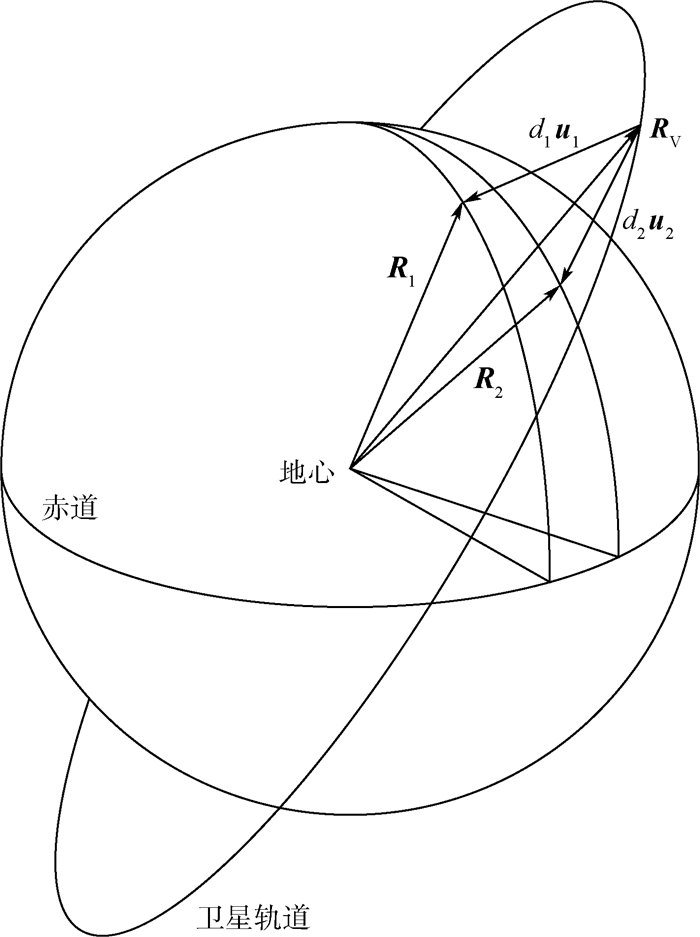 |
| 图 13 地标导航的相关矢量关系 Fig. 13 Related vector relation in landmark navigation |
| 图选项 |
式中:地标位置矢量Ri由地标库已知。同时,地标视线矢量的长度d与单位地标视线矢量ui以及地标位置矢量Ri满足余弦定理,如下:
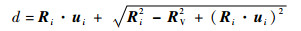 | (8) |
式中:卫星位置RV可根据动力学一步估计获得。
取相机坐标系下的地标单位视线矢量ui作为量测量,由式(7)和式(8)推得量测方程为
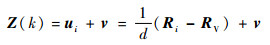 | (9) |
式中:v为量测噪声。
3.2 卫星状态模型 选取历元(J2000.0)地心赤道惯性坐标系。只考虑引力场摄动二阶带谐项,其他摄动如日月引力摄动、太阳光压摄动、大气阻力摄动均为高阶小量。系统的状态方程为
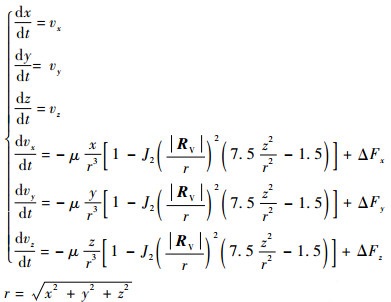 | (10) |
式中:x、y、z分别为卫星三轴的位置;vx、vy、vz分别为卫星三轴的速度;μ为引力常数;J2为摄动系数;ΔFx、ΔFy、ΔFz分别为除引力场摄动二阶带谐项外其他摄动因素影响之和在三轴的分量。
4 导航仿真 仿真条件为:轨道高度为1 000 km;卫星参数如表 1所示。表中:a为轨道半长轴;e为偏心率;i为轨道倾角;ω为近地点幅角;M0为平近点角。
表 1 样例轨道的轨道要素 Table 1 Orbital elements of sample orbit
| 参数 | a/m | e | i/(°) | ω/(°) | M0/(°) |
| 数值 | 7 478 137.0 | 0 | 45.0 | 0 | 0 |
表选项
卫星保持三轴稳定、对地定向。拍摄得到的图像参考风云系列卫星,即星下点分辨率为1 100 m,图像幅宽为2 900 km。假设卫星每30 s能获得一幅可用的图像,并且拍摄时刻均为当地时间的日间,考虑到仿真中匹配计算的时间,匹配所用的拍摄图像使用了拍摄图像中心500像素×500像素的部分。导航地标库采用2.2节建立的地标库中的春季白天部分,使用文献[10]中经过优化的匹配算法,平均每0.899 7 s可以完成一次匹配。
导航计算中,滤波计算周期设为5 s,并假设每步滤波最多使用3个匹配到的图像信息进行导航。
图 14为系统在5个周期内的仿真结果。其平均位置误差为125.827 4 m(3σ),平均速度误差为0.104 9 m/s(3σ)。
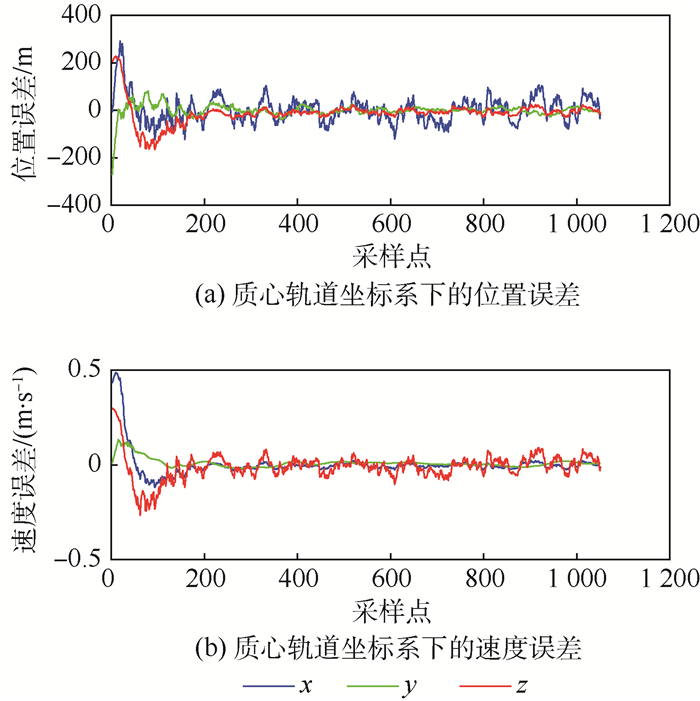 |
| 图 14 使用本文地标库进行导航的导航误差 Fig. 14 Navigation error of navigation with landmark library in the text |
| 图选项 |
将轨道高度从500~2 000 km取不同值进行仿真,仿真结果如表 2所示。
表 2 不同轨道高度仿真结果对比 Table 2 Comparison of simulation results of different orbital heights
| 轨道高度/ km | 平均位置误差 (3σ)/m | 平均速度误差 (3σ)/(m·s-1) |
| 500 | 62.713 4 | 0.058 2 |
| 800 | 87.832 8 | 0.080 3 |
| 1 100 | 99.125 5 | 0.086 9 |
| 1 400 | 123.505 0 | 0.109 4 |
| 1 700 | 165.607 7 | 0.130 0 |
| 2 000 | 192.363 7 | 0.141 5 |
表选项
仿真中,地标视线矢量是根据地标位置和模拟轨道中卫星的位置预先计算好的。从表 2中数据看出,在地标导航中,轨道下降会使位置和速度误差明显减弱,这是因为轨道高度下降会使拍摄图像的分辨率提高,因而导航精度提高。
在上述仿真中,导航均限制使用3个地标信息,而实际对于幅宽为2 900 km的遥感图像而言,在仿真的5个周期内均有超过70%的图像可以获得至少4个导航地标信息。地标信息数量对导航精度有一定影响,如表 3所示。
表 3 不同地标信息数量仿真结果对比 Table 3 Comparison of simulation results of different number of landmarks information
| 地标信息数量 | 平均位置误差 (3σ)/m | 平均速度误差 (3σ)/(m·s-1) |
| 2 | 99.917 7 | 0.088 2 |
| 3 | 99.125 5 | 0.086 9 |
| 4 | 98.898 4 | 0.085 2 |
表选项
由表 3看出,在导航中使用更多个地标信息数量并不能有效提高导航精度,但至少需要2个地标才能进行导航[15],而更多的地标信息却可以加快数据的收敛,见图 15中3组仿真的均方根误差RMSE曲线。因此,当飞行器运行在容易获得地标的区域时,应以选择质量较高的地标为前提,适当控制数量以提高匹配速度;反之,即在难以获取地标信息的区域,一旦获取地标信息应当尽可能多的使用地标信息,使导航快速收敛。
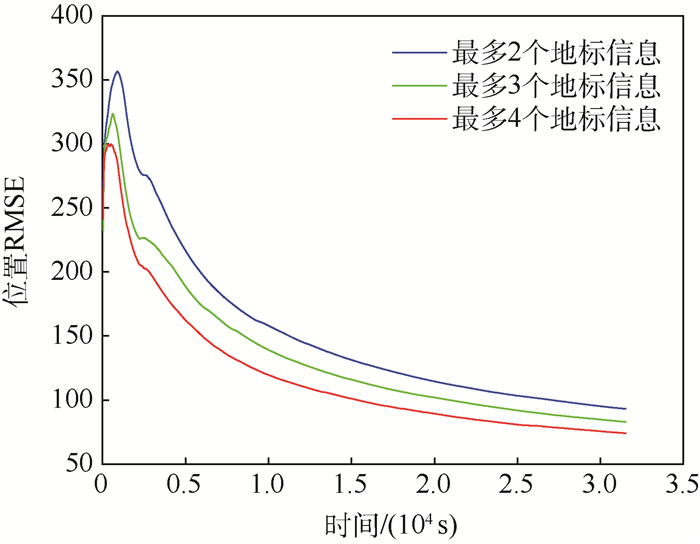 |
| 图 15 不同地标信息数量的位置RMSE对比 Fig. 15 Comparison of position RMSE for different number of landmark information |
| 图选项 |
图 15为只用水陆地标导航解算结果,在相同的仿真条件下,由于缺少了大量的非水陆地标,即非全局地标,导致导航精度明显下降,平均位置误差为144.638 8 m(3σ),平均速度误差为0.128 2 m/s(3σ),仿真结果如图 16所示。与使用本文全局地标库导航算法相比,导航位置精度和速度精度降低了10%和11%。
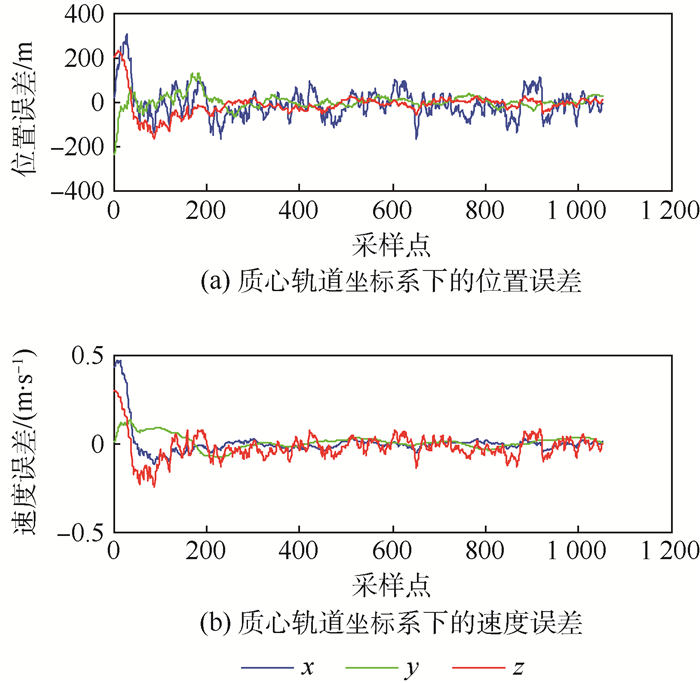 |
| 图 16 使用传统地标库进行导航的导航误差 Fig. 16 Navigation error of navigation with traditional landmark library |
| 图选项 |
同时,从2次仿真的RMSE曲线(见图 17)可见,收敛速度也受到了影响。
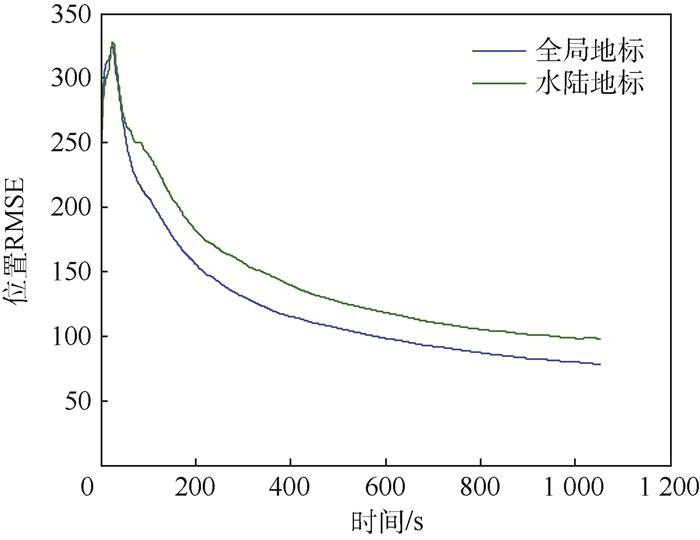 |
| 图 17 不同地标库的位置RMSE对比 Fig. 17 Comparison of position RMSE for different landmark libraries |
| 图选项 |
5 结论 本文针对利用地标的卫星自主导航方案中的瓶颈问题,即地标库的建立和匹配方法,提出了一种新的全局地标选取原则及匹配算法,具体工作如下:
1) 全局地标选取范围包括水陆边界以及扩展到有灰度差为特征参数的地貌区域,由此建立的地标库的数据量比单纯的水陆边界地标库增加了43.97%。由于受季节影响较大,需要准备不同季节的地标模板,并且需要时常更新。
2) 采用拥有足够多粗糙纹理的区域的控制区域作为地标块的基础,不用考虑地面纹理的具体特征,因此可以大大减少描述图像纹理特性的灰度共生矩阵来描述图像纹理特性。
3) 使用全局地标库进行导航解算,相比于已有只用水陆边界的地标库,导航精度提高了10%,相应速度也提高了11%。
参考文献
| [1] | KAU S P. Autonomous satellite orbital navigation using known and unknown earth landmarks[C]//Guidance and Control Conference. Reston: AIAA, 1975: 1-12. |
| [2] | BACHMANN M, BENDIX J. An improved algorithm for NOAA-AVHRR image referencing[J].International Journal of Remote Sensing, 1992, 13(16): 3205–3215.DOI:10.1080/01431169208904111 |
| [3] | HO D, ASEM A. NOAA AVHRR image referencing[J].International Journal of Remote Sensing, 1986, 7(6): 895–904. |
| [4] | ILLERA P, DELGADO J A, CALLE A. A navigation algorithm for satellite images[J].International Journal of Remote Sensing, 1996, 17(3): 577–588.DOI:10.1080/01431169608949028 |
| [5] | MOIGNE J L, CAMPBELL W J, CROMP R F, et al. An automated parallel image registration technique based on the correlation of wavelet features[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1849–1864.DOI:10.1109/TGRS.2002.802501 |
| [6] | TOWNSHEND J R, JUSTICE C O, GURNEY C E, et al. The impact of misregistration on change detection[J].IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 1054–1060.DOI:10.1109/36.175340 |
| [7] | DAI X, KHORRAM S. The effects of image misregistration on the accuracy of remotely sensed change detection[J].IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1566–1577.DOI:10.1109/36.718860 |
| [8] | 杨磊, 杨忠东. 极轨气象卫星自动地标导航方法[J].应用气象学报, 2009, 20(3): 329–336. YANG L, YANG Z D. The automated landmark navigation of the polar meteorological satellite[J].Journal of Applied Meteorological Science, 2009, 20(3): 329–336.(in Chinese) |
| [9] | EMERY W J, BALDWIN D, MATTHEWS D. Maximum cross correlation automatic satellite image navigation and attitude corrections for open-ocean image navigation[J].IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 33–42.DOI:10.1109/TGRS.2002.808061 |
| [10] | 郭强, 杨磊, 赵现纲, 等. 气象卫星图像导航的地标匹配算法研究与优化[J].计算机工程与应用, 2013, 49(24): 152–156. GUO Q, YANG L, ZHAO X G, et al. Research and optimization of landmark matching algorithm for meteorological satellite image navigation[J].Computer Engineering and Applications, 2013, 49(24): 152–156.DOI:10.3778/j.issn.1002-8331.1305-0212(in Chinese) |
| [11] | KIM T, LEE T, CHOI H. Landmark extraction, matching and processing for automated image navigation of geostationary weather satellites[J].Proceedings of SPIE, 2005, 5657(1): 30–37. |
| [12] | 卢耀秋. 静止气象卫星的地标导航计算方法[J].计算物理, 1992, 9(4): 775–777. LU Y Q. Landmark navigation method of geostationary meteorological satellite[J].Chinese Journal of Computational Physics, 1992, 9(4): 775–777.(in Chinese) |
| [13] | 赵礼铮, 白光弼. 极轨气象卫星局部数据集的精地标导航[J].气象, 1992, 18(11): 44–46. ZHAO L Z, BAI G B. Navigation of precise landmarks in polar-orbit meteorological satellite local data[J].Meteorological Monthly, 1992, 18(11): 44–46.(in Chinese) |
| [14] | 杨磊, 冯小虎, 郭强, 等. 风云二号气象卫星图像自动几何精校正[J].计算机工程与应用, 2011, 47(3): 202–206. YANG L, FENG X H, GUO Q, et al. Automatic geometric precision correction of Fengyun-2 meteorological satellite imagery[J].Computer Engineering and Applications, 2011, 47(3): 202–206.(in Chinese) |
| [15] | ROSBOROUGH G W, BALDWIN D G, EMERY W J, et al. Precise AVHRR image navigation[J].IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(3): 644–657.DOI:10.1109/36.297982 |
| [16] | 蒋春华. 浅析纹理防伪技术[J].中国防伪报道, 2012(11): 47–50. JIANG C H. Analysis of texture anti-counterfeiting technology[J].China Anti-Counterfeiting Report, 2012(11): 47–50.(in Chinese) |
| [17] | 郑彤, 蔡龙飞, 王志刚, 等. 地形匹配辅助导航中匹配区域的选择[J].中国惯性技术学报, 2009, 17(2): 191–196. ZHENG T, CAI L F, WANG Z G, et al. Selection of matching area in terrain match aided navigation[J].Journal of Chinese Inertial Technology, 2009, 17(2): 191–196.(in Chinese) |
