频率步进信号通过多脉冲相参合成处理获得距离维高分辨成像能力，信号瞬时带宽小。不仅大大降低了对系统采样率的要求及工程实现难度，而且可以在一定程度上提高雷达的抗干扰能力，因此被广泛应用于雷达目标检测、成像等领域^[1-6]。
利用频率步进信号成像主要存在2个问题：一是频率步进信号对运动目标比较敏感。频率步进信号要求序贯脉冲之间保持严格的相位关系，雷达与目标之间的相对径向运动会造成目标距离像的偏移和成像质量的退化，为得到运动目标的正确成像结果，通常在脉冲综合前需要首先完成速度测量与补偿。文献[7-12]对上述问题已经进行了较为详细的研究，相关问题已得到较好的解决。二是频率步进信号受信号参数设计的理论制约，存在距离向最大无模糊测绘带宽度的限制问题，严重制约了该信号在高分辨-宽测绘带SAR成像探测领域的应用。为解决该问题，文献[13-14]分别提出利用参差重频和脉冲波形分集技术实现距离向解模糊处理，但是，由于需要改变雷达的系统参数，增加了系统实现的复杂度。文献[15]利用仰角维自由度，提出了一种解距离模糊的三维空时自适应处理(Space Time Adaptive Processing, STAP)算法，但是算法复杂，难以实际应用。文献[16]基于频率分集阵列雷达的天线方向图，提出了一种改善距离模糊的STAP算法。文献[17]利用频率分集阵列雷达在距离向的空变自由度，实现了距离模糊杂波抑制和运动目标距离解模糊，算法简单有效，无需改变系统参数。实质上，频率步进信号可以看成是一种频率分集信号，在“走-停”模型假设下，可以将频率步进合成孔径雷达(SAR)的各组脉冲串等效为沿航迹分布的虚拟线性阵列信号。于是，基于频率分集阵列雷达解距离模糊的思想，通过将频率步进SAR等效为虚拟频率分集阵列雷达并进行相应的成像处理，可解决频率步进SAR距离向无模糊测绘带宽度有限的问题。
本文首先给出了频率步进SAR虚拟阵列模型及其高分辨距离像合成方法；然后，为实现目标的精确二维成像，给出了适用于虚拟阵列模型的改进后向投影方法，解决了经典方法距离向无模糊测绘带宽度受限的问题；最后，通过实验和结果分析验证了本文方法的有效性。
1 虚拟阵列模型的频率步进SAR高分辨距离像合成方法 图 1给出了基于虚拟阵列模型的频率步进SAR成像空间几何示意图，其中频率步进脉冲串被等效为虚拟的天线阵列信号。以场景中心点O为原点建立直角坐标系O-xyz，雷达沿航线y′以速度v匀速运动(y′轴与y轴平行)，发射信号的子脉冲时间间隔为T_r，宽度为T_p，则相邻子脉冲之间的距离为d=|v|T_r。雷达在合成孔径时间内共发射N_a组N_p个子脉冲的频率步进脉冲串。以脉冲串的第1个子脉冲为参考，记其对应的雷达位置为O′，发射信号载频为f₀，则第n个子脉冲发射信号载频为f_n，有f_n=f₀+nΔf，n=0, 1, …, N_p-1，其中Δf为频率步进间隔。O′到场景中心点O的距离矢量为r₀，其擦地角与方位角分别记为φ_η0和θ_η0，大小与场景中心点O和方位慢时间η有关；O′到目标p的距离矢量为r_p0，第n个子脉冲到目标p的距离矢量为r_np，其中r_p0的擦地角与方位角分别记为φ_ηp和θ_ηp，其大小与目标p和方位慢时间η有关。

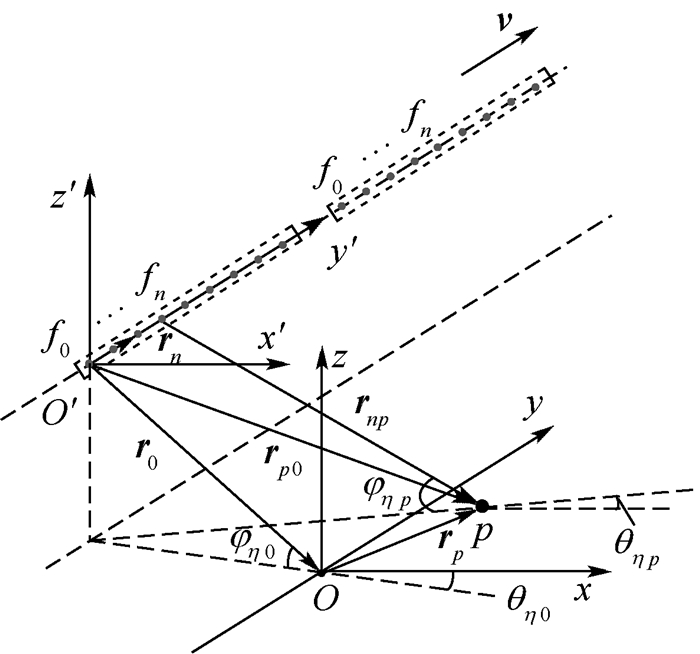图 1 虚拟阵列模型的频率步进SAR成像空间几何示意图 Fig. 1 Spatial geometry of frequency-stepped SAR imaging of virtual array model

图选项

假设雷达发射信号为

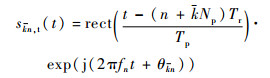(1)

式中：t为全时间，-T_p/2+(n+kN_p)T_r≤t≤(n+kN_p)T_r+T_p/2；k=0, 1, …, N_a-1为脉冲串序号；n=0, 1, …, N_p-1为脉冲串的子脉冲序号；θ_kn为每个发射脉冲的初始相位。
假设理想点目标p的散射系数为σ_p，则频率步进SAR的接收信号可表示为

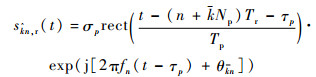(2)

式中：τ_p为目标p与雷达之间的双程时延; -T_p/2+(n+kN_p)T_r≤t-τ_p≤(n+kN_p)T_r+T_p/2，方位慢时间η=kN_pT_r，k=0, 1, …, N_a-1。
在“走-停”模型下，频率步进SAR的一组脉冲串可等效为一个沿航迹分布的虚拟天线阵列信号。为方便表述，本节在推导频率步进SAR虚拟阵列回波模型时，仅以一组脉冲串为例，其余脉冲串的信号表达式可类推获得。假设频率步进SAR脉冲串信号的第n个子脉冲的发射信号为

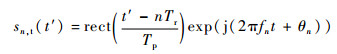(3)

式中：t′为快时间，-T_p/2+nT_r≤t′≤nT_r+T_p/2；θ_n为信号的初始相位；全时间t=t′+η。由已知条件可知，第n个子脉冲到目标p的距离矢量

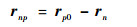(4)

式中：r_n为第1个子脉冲到第n个子脉冲位置的距离矢量。故第n个子脉冲对应的目标回波为

(5)

式中：k_np=k_n·为距离矢量r_np对应的波数，k_n=2πf_n/c，为r_np的单位向量，c为光速；-T_p/2+nT_r+2|r_np|/c≤t′≤nT_r+2|r_np|/c+T_p/2。远场条件下，≈，为r_p0的单位向量。因此，波数k_np=k_n·≈k_n·，k_n=2πf_n/c。忽略信号包络项，将k_np=k_n·和r_np=r_p0-r_n代入式(5)，则第n个子脉冲的回波信号可表示为

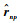
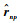
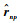
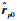
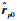
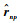
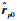
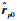
(6)

式(6)中最后一个相位随着子脉冲发生改变，反映了子脉冲位置与目标之间的相对几何关系以及子脉冲发射信号载频对回波相位的影响。由图 1可知，=和r_n可分别表示为

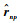
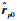
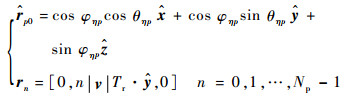(7)

式中：、?和?分别对应x轴、y轴和z轴的单位向量。将式(7)代入式(6)，同时对N_p个子脉冲回波进行叠加，有

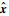
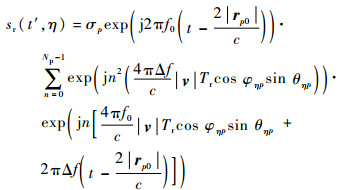(8)

当式(8)中二次相位项小于π/4时，可忽略其对成像质量的影响。令最后一个相位项为exp(jnΦ₁)，其中Φ₁为

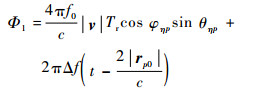(9)

将的结果代入式(8)，并利用参考信号s_ref(t)=exp(j2πf₀t)对回波信号进行解调，有

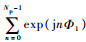
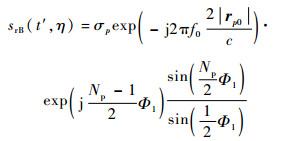(10)

当Φ₁=2κπ(κ=0, ±1, ±2, …)时，|s_rB(t′, η)|取得极大值，此时有

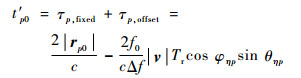(11)

式中：τ_{p, fixed}=2|r_p0|/c为参考脉冲位置与目标之间的双程距离回波延时；τ_{p, offset}=-2f₀|v|T_r·cos φ_ηpsin θ_ηp/(cΔf)为目标回波的额外延时，它与雷达平台速度|v|、子脉冲发射时间间隔T_r、参考子脉冲位置以及目标p之间的空间几何关系、参考子脉冲发射信号载频f₀和频率步进间隔Δf有关。
由式(10)可知，s_rB(t′, η)具有周期性，其峰值两边第1零点之间的时间间隔反映了距离向分辨率。由于第1零点t_p±1满足条件N_pΦ₁/2=±π，于是有

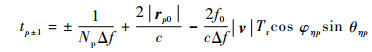(12)

因此，距离分辨率ρ_r可表示为

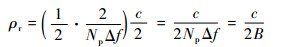(13)

式中：系数1/2为半功率峰值处的时间间隔；B为频率步进信号带宽。上述结果与频率步进信号距离向分辨率的理论值一致。
可见，通过将频率步进SAR的各组脉冲串等效为沿航迹排列的虚拟阵列信号，并对同一组脉冲串内的所有子脉冲回波进行累加，可实现频率步进SAR信号的距离像合成。相比经典成像方法，基于虚拟阵列模型的频率步进SAR高分辨距离像合成方法在得到目标正确的距离向成像结果基础上，进一步简化了信号处理的流程。
2 方位能量累积 2.1 后向投影原理 因目标对应的额外延时τ_{p, offset}具有空变性，不便于统一进行距离校正，因此，后向投影方法成为方位成像的首选。通过逐方位向对目标的回波能量进行累积，后向投影方法可获得任意成像几何条件下的目标二维高分辨成像结果。设最终成像结果I的网格点数为K×L(距离向×方位向)，各网格点相对于场景中心点O的位置矢量为r_kl, 其中k=1, 2, …, K, l=1, 2, …, L。根据后向投影方法原理，网格点kl处对应的二维成像结果可表示为

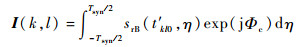(14)

式中：t′_kl0=τ_{kl, fixed}+τ_{kl, offset}，τ_kl，offset为网络点kl对应的时间空变偏移量，τ_{kl, fixed}为网格点kl与参考子脉冲位置O′之间对应的回波双程时延, 它可表示为

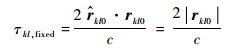(15)

其中：为参考子脉冲位置O′到网格点的单位距离矢量。与r_kl0对应的相位补偿因子exp(jΦ_c)为

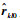
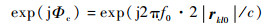(16)

由式(15)和式(16)可知，网格点kl对应的回波真实传播时延τ_{kl, fixed}和相位补偿因子exp(jΦ_c)，与原始后向投影方法目标的脉冲压缩峰值点时刻和相位补偿项相等。
2.2 距离偏移校正 由式(14)中t′_kl0=τ_{kl, fixed}+τ_{kl, offset}可知，相比原始后向投影方法，基于虚拟阵列模型的频率步进SAR距离像中还引入了一个额外时间偏移量τ_{kl, offset}，其表达式为

(17)

式中：φ_ηkl和θ_ηkl分别为r_kl0的擦地角和方位角，其随方位慢时间η变化；τ_{kl, offset}导致空变距离偏移量ΔR=-(f₀|v|T_rcos φ_ηklsin θ_ηkl)/Δf。为获得正确的成像结果，必须在后向投影成像时对其进行补偿。由式(17)可知，τ_{kl, offset}与每个图像网格点kl有关，可在反投影过程中同时实现。
2.3 二次相位补偿 当式(8)中二次相位项的取值大于π/4时，必须对该项进行补偿，否则图像将散焦。当成像场景较小时，由于远场条件下≈(和分别为距离矢量r_p0和r₀的单位向量)。此时，可利用场景中心点O处对应的二次相位对整个场景进行统一补偿，有

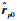
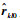
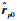
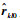
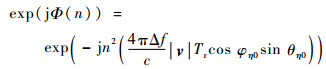(18)

式中：n=0, 1, …, N_p-1；因子φ_η0和θ_η0与η、参考子脉冲位置O′与场景中心点O的相对空间几何关系有关。
3 仿真实验 为验证本文方法正确性，现进行3组成像实验，实验仿真参数见表 1。
表 1 仿真参数 Table 1 Simulation parameters

参数	数值
参考载频/GHz	10
子脉冲数目	1 025
天线波束宽度/(°)	1.30
平台高度/km	8.00
总信号带宽/MHz	700
脉冲串重复频率/Hz	333.14
场景大小(距离向×方位向)/(m×m)	200×200
频率步进量/MHz	0.683
子脉冲宽度/μs	1.46
平台速度/(m·s-1)	58.50
参考斜距/km	11.31
占空比	0.50
子脉冲重复频率/kHz	341.46
地距分辨率(距离向×方位向)/(m×m)	0.30×0.36

表选项






3.1 高分辨距离像合成 假定场景中存在3个位于无模糊距离范围内不同距离单元的点目标，分别利用经典方法和本文方法进行距离像合成，图 2给出了2种方法对应的距离像对比。

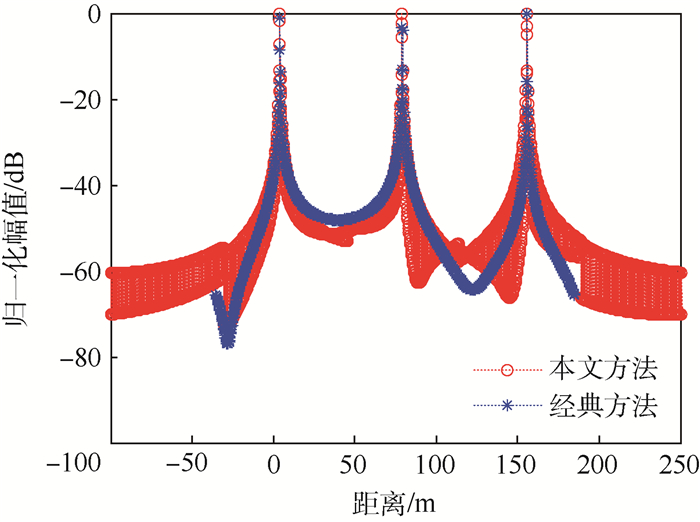图 2 经典方法与本文方法目标距离像对比 Fig. 2 Comparison of target range profile between classic method and proposed method

图选项

由图 2可见，2种方法均能得到目标的正确距离像，但是经典方法成像结果仅表示无模糊距离cT_p/2内目标的相对距离，而本文方法距离向成像结果表示的是整个回波信号时间长度内目标的绝对距离。由于设定目标均位于无模糊距离范围内，2种方法成像结果一致。需要说明的是，实验为得到所有方位时刻完整的目标回波，总的回波时间长度为实际场景延迟前后各增加T_p/2的时间长度，故图中有距离为负的部分。
3.2 频率步进SAR虚拟阵列模型方法成像 为验证本文方法成像性能，在3.1节实验3个点目标的基础上，方位向上再各自增加3个点目标，组成一个3×3的点目标阵，其位置分别为(-80, -80, 0)m、(-80, 0, 0)m、(-80, 80, 0)m、(0, -80, 0)m、(0, 0, 0)m、(0, 80, 0)m、(80, -80, 0)m、(80, 0, 0)m和(80, 80, 0)m。
图 3给出了本文方法的目标成像结果，9个点目标聚焦良好。为进一步分析成像性能，表 2给出了图 3中所有目标对应的点散布函数统计结果，表 3给出了所有目标经典方法对应的点散布函数统计结果。其中，PSLR为峰值旁瓣比，ISLR为积分旁瓣比。对比表 2和表 3的结果可知，本文方法目标点散布函数性能的取值与经典方法非常接近，验证了本文方法的有效性。

图 3 本文方法成像结果 Fig. 3 Imaging result of proposed method

图选项

表 2 本文方法目标点散布函数结果 Table 2 Target point spread function results of proposed method

目标 序号	距离向			方位向
	PSLR/dB	ISLR/dB		PSLR/dB	ISLR/dB
1	-13.382 0	-9.857 6		-13.277 6	-10.225 8
2	-13.383 5	-9.848 7		-13.303 5	-10.209 2
3	-13.382 0	-9.857 6		-13.277 6	-10.225 8
4	-13.462 5	-9.895 5		-13.283 4	-10.225 7
5	-13.470 1	-9.885 1		-13.326 2	-10.228 3
6	-13.462 5	-9.895 5		-13.283 4	-10.225 7
7	-13.619 6	-9.960 1		-13.292 1	-10.221 3
8	-13.624 9	-9.952 2		-13.306 4	-10.216 5
9	-13.619 6	-9.960 1		-13.292 1	-10.221 3

表选项






表 3 经典方法目标点散布函数结果 Table 3 Target point spread function results of classic method

目标 序号	距离向			方位向
	PSLR/dB	ISLR/dB		PSLR/dB	ISLR/dB
1	-13.310 3	-9.957 4		-13.203 1	-10.218 2
2	-13.312 9	-9.840 0		-13.203 5	-10.218 9
3	-13.314 0	-9.771 2		-13.274 3	-10.221 5
4	-13.300 3	-9.895 5		-13.213 0	-10.217 2
5	-13.387 6	-9.966 4		-13.221 2	-10.220 8
6	-13.320 0	-10.009 0		-13.230 3	-10.217 5
7	-13.310 3	-9.961 9		-13.213 4	-10.221 3
8	-13.390 3	-9.856 9		-13.202 1	-10.220 6
9	-13.319 6	-9.985 4		-13.198 4	-10.219 1

表选项






3.3 抗距离模糊及宽测绘带成像效果 当场景距离向宽度超过频率步进信号的最大无模糊距离范围时，经典成像方法的频率步进SAR成像结果将出现距离向模糊。为对比经典方法与本文方法抗距离模糊的成像效果，对场景距离范围为3倍频率步进信号无模糊距离的17个点目标进行成像实验。实验中，在3.2节仿真实验9个点目标的基础上，增加了8个位于无模糊距离范围之外的点目标，新增加的8个点目标位置分别为(-296, -296, 0)m、(-296, 0, 0)m、(-296, 296, 0)m、(0, -296, 0)m、(0, 296, 0)m、(296, -296, 0)m、(296, 0, 0)m和(296, 296, 0)m。图 4(a)、(b)给出了经典方法与本文方法的成像结果。

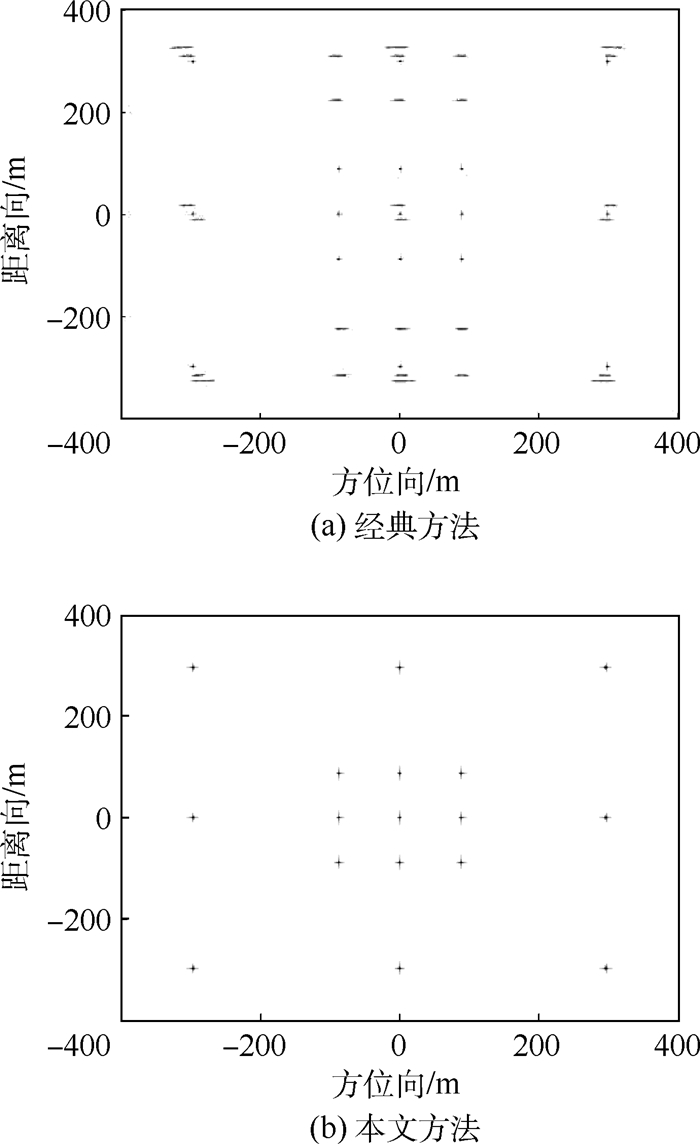图 4 经典方法和本文方法后向投影成像结果对比 Fig. 4 Comparison of back-projection imaging results between classic method and proposed method

图选项

对比图 4(a)和(b)可知，当场景大小超过频率步进信号参数决定的无模糊成像范围时，采用频率步进SAR经典成像方法的成像结果中存在严重的距离向模糊问题，有些模糊能量甚至遮盖了正确的目标成像结果；而采用本文方法的成像结果中不存在距离向模糊，精确地实现了对17个点目标的正确成像。实验结果证明，本文方法可以有效克服经典成像方法测绘带宽度受距离向最大无模糊距离限制的问题，这对于频率步进SAR在高分辨-宽测绘带领域的应用具有重大的现实意义。
4 结论 1) 频率步进SAR虚拟阵列模型成像方法可解决经典方法距离向无模糊测绘带宽度受限的问题，克服频率步进SAR在宽测绘带成像时面临的距离模糊问题，有利于频率步进技术在高分辨-宽测绘带SAR成像领域的推广应用。
2) 虚拟阵列模型高分辨距离像合成方法通过对各子脉冲回波进行相位补偿和累加，实现对频率步进信号的距离向能量累积，简化了成像处理流程，易于工程实现。
3) 频率步进SAR虚拟阵列模型成像方法可实现对目标的二维精确成像，方法复杂度与原始后向投影方法处于同一量级。
后续工作中，将进一步研究方法的快速实现问题, 考虑运动误差对方法成像性能的影响并研究相应的运动补偿方法。

参考文献

[1]	颜志升. 步进频波形优化设计及处理技术[J].现代雷达, 2015, 37(9): 40–43. YAN Z S. Optimized design of the stepped-frequency signal waveform and its processing technology[J].Modern Radar, 2015, 37(9): 40–43.(in Chinese)
[2]	彭岁阳, 张军, 沈振康. 随机频率步进雷达成像分析[J].国防科技大学学报, 2011, 33(1): 59–64. PENG S Y, ZHANG J, SHEN Z K. Imaging analysis of random step frequency radar[J].Journal of National University of Defense Technology, 2011, 33(1): 59–64.(in Chinese)
[3]	顾福飞, 张群, 娄昊, 等. 一种孔径和频率二维稀疏的步进频SAR成像方法[J].航空学报, 2015, 36(4): 1221–1229. GU F F, ZHANG Q, LOU H, et al. A SAR imaging method with 2D sparse aperture and frequency using stepped-frequency waveform[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1221–1229.(in Chinese)
[4]	吕明久, 李少东, 杨军, 等. 频率步进信号距离-方位联合超分辨成像方法[J].电波科学学报, 2016, 31(3): 537–545. LYU M J, LI S D, YANG J, et al. Range-azimuth joint ISAR super-resolution imaging method based on frequency-stepped signal[J].Chinese Journal of Radio Science, 2016, 31(3): 537–545.(in Chinese)
[5]	李俊慧, 王洪, 汪学刚, 等. 步进频、脉冲和连续波SAR的对比研究[J].雷达科学与技术, 2016, 14(1): 45–53. LI J H, WANG H, WANG X G, et al. Comparative study on stepped frequency, pulsed and continuous wave SARs[J].Radar Science and Technology, 2016, 14(1): 45–53.(in Chinese)
[6]	陈一畅, 张群, 陈校平, 等. 多重测量矢量模型下的稀疏步进频率SAR成像算法[J].电子与信息学报, 2014, 36(12): 2986–2993. CHEN Y C, ZHANG Q, CHEN X P, et al. An imaging algorithm of sparse stepped frequency SAR based on multiple measurement vectors model[J].Journal of Electronics & Information Technology, 2014, 36(12): 2986–2993.(in Chinese)
[7]	李海英, 杨汝良. 频率步进信号的合成孔径雷达处理[J].电子学报, 2003, 31(3): 349–352. LI H Y, YANG R L. Stepped-frequency synthetic aperture radar imaging[J].Acta Electronica Sinica, 2003, 31(3): 349–352.(in Chinese)
[8]	吕明久, 李少东, 杨军, 等. 基于全局最小熵的随机稀疏调频步进信号运动补偿方法[J].系统工程与电子技术, 2016, 38(8): 1744–1751. LYU M J, LI S D, YANG J, et al. Motion-compensation method based on global minimum entropy for random sparse stepped-frequency chirp signal[J].Systems Engineering and Electronics, 2016, 38(8): 1744–1751.(in Chinese)
[9]	梁福来. 低空无人机载UWB SAR增强成像技术研究[D]. 长沙: 国防科学技术大学, 2013: 27-35. LIANG F L. Research on enhanced imaging techniques of low-altitude UAV-mounted UWB SAR[D]. Changsha: National University of Defense Technology, 2013: 27-35(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-1015959086.htm
[10]	牛涛, 陈卫东. 脉冲步进频率雷达的一种运动补偿新方法[J].中国科学技术大学学报, 2005, 35(2): 161–166. NIU T, CHEN W D. A new method of motion compensation for pulse stepped-frequency radars[J].Journal of University of Science and Technology of China, 2005, 35(2): 161–166.(in Chinese)
[11]	李俊慧, 王洪, 汪学刚, 等. 步进频SAR的波数域成像算法研究[J].现代雷达, 2016, 38(7): 25–31. LI J H, WANG H, WANG X G, et al. Stepped frequency SAR imaging using wavenumber domain algorithm[J].Modern Radar, 2016, 38(7): 25–31.(in Chinese)
[12]	周芳. 高分辨SAR/ISAR成像信号补偿新技术研究[D]. 西安: 西安电子科技大学, 2014: 18-26. ZHOU F. New signal compensation techniques for high resolution SAR/ISAR imaging[D]. Xi'an: Xidian University, 2014: 18-26(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10701-1015437824.htm
[13]	VILLANO M, KRIEGER G, MOREIRA A. A novel processing strategy for staggered SAR[J].IEEE Geoscience and Remote Sensing Letters, 2014, 11(11): 1891–1895.DOI:10.1109/LGRS.2014.2313138
[14]	SCHOLNIK D P. Range-ambiguous clutter suppression with pulse-diverse waveforms[C]//2011 IEEE Radar Conference. Piscataway, NJ: IEEE Press, 2011: 336-341.
[15]	HALE T B, TEMPLE M A, RAQUET J F, et al. Localized three-dimensional adaptive spatial-temporal processing for airborne radar[J].IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(1): 18–22.DOI:10.1049/ip-rsn:20030075
[16]	BAIZERT P, HALE T B, TEMPLE M A, et al. Forward-looking radar GMTI benefits using a linear frequency diverse array[J].Electronics Letters, 2006, 42(22): 1311–1312.DOI:10.1049/el:20062791
[17]	王伟伟, 吴孙勇, 徐京伟, 等. 基于频率分集阵列的机载雷达距离模糊杂波抑制方法[J].电子与信息学报, 2015, 37(10): 2321–2327. WANG W W, WU S Y, XU J W, et al. Range ambiguity clutter suppression for airborne radar based on frequency diverse array[J].Journal of Electronics & Information Technology, 2015, 37(10): 2321–2327.(in Chinese)