泡沫金属材料内部结构受力后的变形演化复杂,常规试验研究手段存在诸多的困难,因此基于精细化分析模型的数值模拟成为有效的研究手段。Gibson和Ashby基于对泡沫金属实际结构的高度抽象,提出了用立方体单胞元模型来近似泡沫铝细观结构的思想[1]。以此为基础,研究人员对单元形状不断改进,先后发展了改进的立方体模型[6-7]、十四面体(Kelvin模型)[8-9]及八面体模型[10-11]等。这些单胞元模型能为材料的力学性能分析提供一种简便的方法,但其简单的单元形状与规则排列的特点过于理想化,和实际结构相差甚远。考虑胞孔的位置和大小在一定范围内随机分布的特点,Voronoi拓扑算法被很多****用来构建泡沫金属的细观随机模型。Zhang[12]、Zheng[13]和Li[14]等先后应用该方法建立细观模型,并开展了泡沫金属材料的动静态力学性能和损伤破坏模式的研究。但该模型基于等壁厚单元的假设与实际情况不符。为此,三维随机椭球体模型[15]和三维随机多面体模型[16-17]先后被提出来,并克服了单胞元模型规则排列的缺点和胞孔等壁厚的问题,但这些算法仍存在所建模型受随机因子影响大以及算法稳定性不高的问题,实际应用尚不十分令人满意。
近年来,一些****尝试利用计算机层析成像(Computed Tomography,CT)扫描技术对泡沫金属材料进行研究[18-20],能够将材料的细观结构形态逐层以灰度图像直观、无损地展示出来,并可进一步利用图像重建技术得到材料的三维细观结构模型[21],最大程度地还原了泡沫金属材料的胞孔形态和拓扑结构特征,具有其他方法无法比拟的真实性。目前,基于CT的建模方法复杂,中间处理步骤繁多,往往需要借助于大型商用软件来实施,限制了其广泛的应用性。
本文基于CT扫描图像,利用Fortran语言编写了材料属性判别程序,基于映射网格思想建立了闭孔泡沫铝的细观有限元分析模型。建模过程无需生成点、线、面、体等几何元素,而是直接生成节点和单元,避免了图像重建过程中网格剖分质量控制的难题。所建立的闭孔泡沫铝三维细观分析模型,更加接近实际材料的细观结构特征,分析结果与试验结果吻合良好,为泡沫铝材料的细观结构分析提供一种新的途径。
1 CT试验 CT技术在不破坏被扫描物体结构的前提下,根据材料内部不同密度的成分对X射线衰减值不同的原理,由多角度收集X射线穿过物体衰减后的投影数据,再通过数学方法处理得到物体中不同点的X射线衰减值信息,并逐层转化为灰度图像以进行观察。该技术经医学领域拓展到工业、农业、工程、安全检测等方面,能够真实还原出物体内部复杂的细观结构形态和拓扑结构特征。
1.1 试件制作 本文闭孔泡沫铝试件利用粉末冶金技术制备,基体材料为Al-7%Si(7%为质量分数)合金,孔径主要分布在1~3mm,通过称重法得到孔隙率为85.52%。
依据Jeon和Asahina[22]实验研究,只要泡沫铝的胞孔不存在大的缺陷,如局部的胞孔相连、缺失、坍塌等,小尺寸泡沫铝试件的力学特性就能有效地表征整个材料的力学特性。同时对于尺寸大小固定的CT探测器,试件越小扫描的放大倍数越大,得到的扫描结果精度也更高。鉴于此,本文立方体试件和圆柱体试件分别按10mm×10mm×10mm和?30mm×20mm的尺寸加工,如图 1所示。
 |
| 图 1 闭孔泡沫铝试件 Fig. 1 Closed-cell aluminum foam specimens |
| 图选项 |
1.2 CT扫描 CT扫描采用丹东奥龙射线有限责任公司研制的ICT-3400型工业CT检测系统,该CT系统的空间分辨率为25LP/cm,密度分辨率为0.25%,扫描模式为锥束连续扫描,为兼顾扫描效果和后期数据的处理,选用的扫描精度为33μm,通过360°旋转扫描共得到720个不同角度的扫描数据。对这些数据进行滤波、校正等处理,10mm×10mm×10mm试件经由FDK算法[23]计算得到292个截面的切片数据。本文基于这些数据进行三维细观分析模型的重建。
上述切片数据可以用灰度图像进行显示,如图 2所示。由于铝和空气对X射线的衰减系数相差较大,在灰度图像中能明显的区分出铝基体材料和空气,清晰地展示了泡沫铝内部的细观结构。从图中可以看出,泡沫铝内部结构非常复杂,不同截面切片结构的形态大不相同,胞孔的大小分布毫无规律,胞孔形状复杂多变,孔壁厚度变化互不相同,许多胞壁内存在数量不等的细微孔洞,造成胞壁的局部肿大或缺陷。可见,高精度的CT扫描能够很好地还原材料内部的微缺陷等细观结构特征,可基于此建立复杂真实的细观结构模型来精细地研究泡沫铝的力学性能及破坏形态。
 |
| 图 2 CT扫描得到的泡沫铝灰度图像 Fig. 2 Gray images of aluminum foam by CT scanning |
| 图选项 |
2 分析模型的重建 CT扫描得到的灰度图像能清晰地识别出材料的内部结构特征。本文以10 mm×10 mm×10 mm试件为例,基于扫描得到的图像,进行三维细观模型的重建,为有限元计算打下基础,其步骤见2.1节~2.4节。
2.1 映射网格的生成 试件扫描后的切片图像大小为292像素×292像素,共292层。将这些图像逐层叠放,得到292×292×292的点云矩阵,称为衰减值矩阵,矩阵中每一个数值代表该区域的X射线衰减值。对切片数据的处理,通常是先进行二值化转化,即针对衰减值矩阵取定一个阈值,将高于该阈值的区域重新赋予数值1并判定为胞壁,低于该阈值的将重新赋予数值0并判定为胞孔,从而将灰度图像转化为具有明显对比度的黑白图像。要对泡沫铝进行细观模型重建,通常生成包含点、线、面、体等大量的中间过渡数据,并对重建的几何模型划分网格以进行有限元分析[20-21]。然而,由于泡沫铝内部结构的复杂性,即使用二值化的图像进行几何模型重建也是很困难的,并且很难划出高质量的有限元分析网格。
为避免上述重建过程的困难,本文直接利用三维衰减值矩阵生成有限元模型。首先,对扫描图像进行二值化处理,判定图像中的各点属性为胞壁或胞孔,建立新的点云矩阵;然后,取矩阵中第1个点,以其为中心生成一个正方体单元和相应的8个节点,如果该点在二值化过程中判定为胞壁,则确定此单元的属性为胞壁,否则确定为胞孔(空气)。以此方式逐行、逐列、逐层推进,就在整个点云矩阵中生成了规则有序、均匀划分的有限元模型。显然,这是一种映射化的网格模型,其中包含了胞壁(基体铝)和胞孔(空气)2种成分。
图 3给出了典型切面的二值化图像与有限元模型的对比情况,可以看到有限元模型很好地还原了CT扫描图像中的结构细节特征。
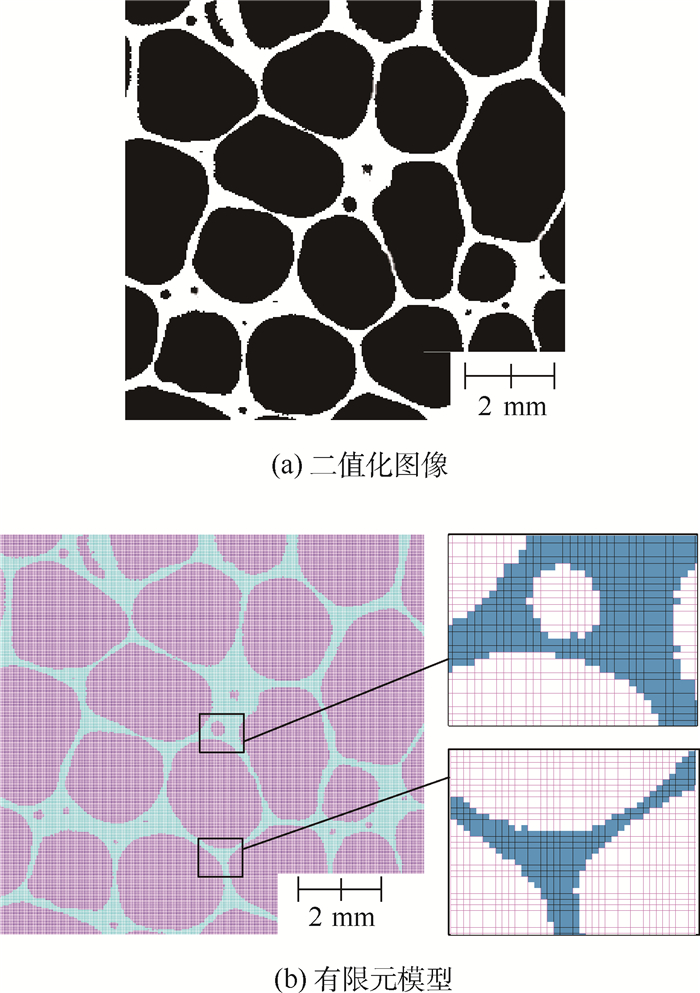 |
| 图 3 二值化图像与有限元模型的对比 Fig. 3 Comparison between binary image and finite element model |
| 图选项 |
2.2 材料阈值的判定 泡沫铝是铝基体胞壁和空气胞孔组成的两相材料,尽管二者的X射线衰减值有明显差别,但要从原始灰度图像中区分出空气与胞孔的界面,就存在一个灰度阈值的选取问题(如图 2所示)。如果阈值取得过高,则会有一部分铝基体被误判为空气;如果阈值取得过低,则一部分过多的空气误判为铝基体。为便于计算机处理,利用CT数据进行三维细观模型重建时,先将切片图像进行了二值化处理,为此必须选取合适的灰度阈值。
泡沫铝是一种组分鲜明的材料,扫描后的图像对比度好,对于这种前景与背景具有明显差别的,图像判别中的阈值可采用Otsu算法[24]进行估计。该算法假定某一个阈值将数据分成两组,当2组数据类间方差最大时则认为二值化效果最佳。也就是对于所选定的阈值,在判定图像上某点是属于目标还是背景时出错的概率最小。Otsu是数字图像处理中的常用算法,在MATLAB软件中通过Multithresh函数直接调用。
本文CT扫描得到的X射线衰减值最大为0.016,最小为0,基体材料衰减值主要处于10-3量级,空气衰减值主要处于10-4量级,通过MATLAB计算得到区分基体材料和空气的阈值为0.0022。此时,对应的孔隙率为80.16%,比称重法测得的孔隙率小5.36%。误差产生的主要原因是,泡沫铝在制备过程中除生成胞孔外,还在基体材料中产生大量微细孔洞[25]。尺寸小于扫描精度的微细孔洞在图像处理中均判定为基体,从而降低了计算的孔隙率。Mcdonald等[25]研究表明,当泡沫铝压缩到达屈服应力及孔壁出现坍塌时,相对大的胞孔优先发生破坏,而微细孔洞对材料的力学性能影响非常小。这表明,上述误差难以消除但可接受。
2.3 单元尺寸选择 上述建模过程中,单元的边长即搜索步长需人为给定。若按照CT系统原始扫描精度构造空间立方体单元,单元尺寸为0.033mm,整个试件包含的单元数目将超过2000万个,这对于目前的计算机求解能力来说是很困难的。对扫描图像的分析表明,本文泡沫铝试件的壁厚主要分布在0.1~0.3mm之间。综合考虑计算效率和精度的要求,重建中对原始衰减值矩阵进行间隔取点,在行列层方向上每隔3个点取一个点,来表征闭孔征泡沫铝的主要结构形态,即使得单元的最小尺寸变为0.132mm。这样,在保留胞孔主要结构形态的基础上大大减少了单元的数量。
根据以上方法,编制了Fortran程序,生成的分析模型用ANSYS软件的APDL语言描述,其中包括节点数据、单元数据和材料属性数据,可以直接读入ANSYS进行分析。典型试件的三维细观有限元模型如图 4所示,单元总数量为389017,其中基体材料单元为77185,空气单元为311832。
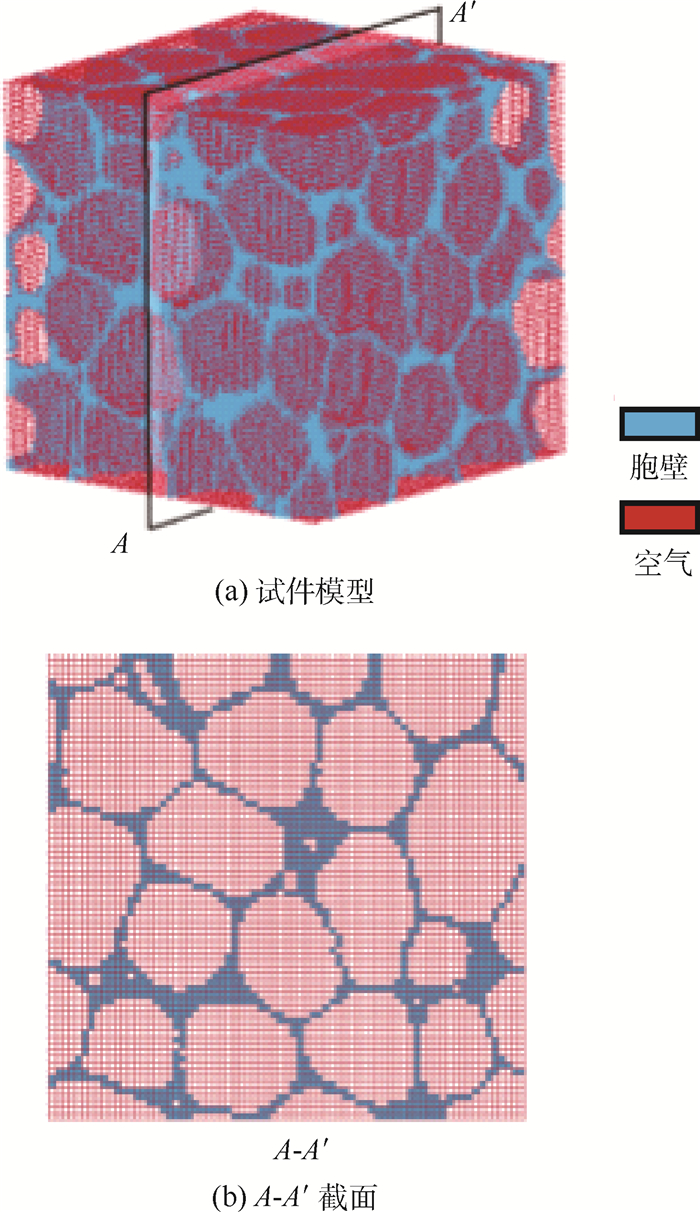 |
| 图 4 闭孔泡沫铝三维细观有限元模型 Fig. 4 Three-dimensional mesoscopic finite element model of closed-cell aluminum foam |
| 图选项 |
2.4 方法的验证 在所建立三维细观模型中等距离截取9个切片S1~S9,分别统计各切片上基体材料单元和空气单元个数,计算每个切片的孔隙率ρ,并与相应灰度图像计算的孔隙率进行对比,同时计算得到两者之间的误差,结果如图 5所示。从图中可以看出,模型中不同切片的孔隙率与灰度图像吻合良好,最大相差0.57%,说明所建立的模型能准确地表达泡沫铝的细观结构特征,本文方法的重建结果可靠。
 |
| 图 5 有限元模型不同截面和灰度图像对比 Fig. 5 Comparison of different section and gray images of finite element model |
| 图选项 |
3 泡沫铝静、动态特性 3.1 静态力学特性 采用长春试验机研究所生产的CSS-44200电子万能试验机对10mm×10mm×10mm试件进行准静态压缩试验。加载用位移控制,速度为0.6mm/min,名义应变率为0.001s-1。
同时,利用ANSYS/LS-DYNA对重建后的模型进行有限元分析。其中基体材料的模型取为*MAT_PLASTIC_KINEMATIC[26],材料密度为2680kg/m3,弹性模量为70GPa,泊松比为0.31,屈服强度取70MPa,切线模量取80 MPa。采用侵蚀算法模拟材料断裂,破坏准则取为最大主应变准则,破坏应变为0.4。数值分析模型如图 6所示,刚性加载板与试件之间设置接触,摩擦系数取0.1。
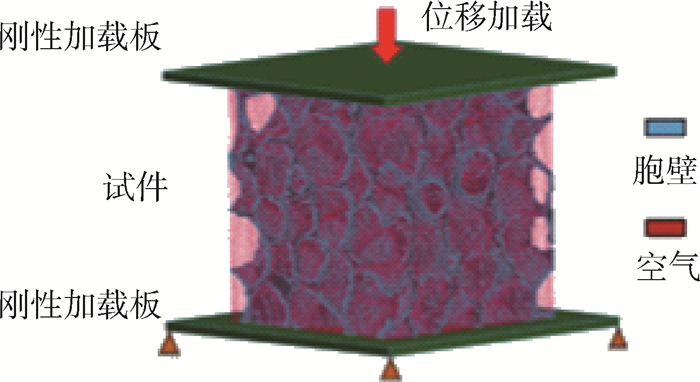 |
| 图 6 泡沫铝准静态压缩数值分析模型 Fig. 6 Numerical analysis model of aluminum foam under quasi-static compression |
| 图选项 |
图 7给出了试验与数值模拟得到的名义应力-应变曲线。可以看出,两者总体吻合良好,都分为3个阶段:在应变小于0.03的初始加载阶段,应力水平较小,试件主要处于弹性加载状态,名义应力-应变成线性关系;随着进一步加载,泡沫铝的局部孔壁达到屈服强度,产生塑性变形,名义应变从0.03增加0.51时,名义应力的增加幅度变化很小,呈现为稳定的应力平台;当名义应变到达0.51之后,基体材料基本被压密实,此时随应变增加名义应力急剧上升。
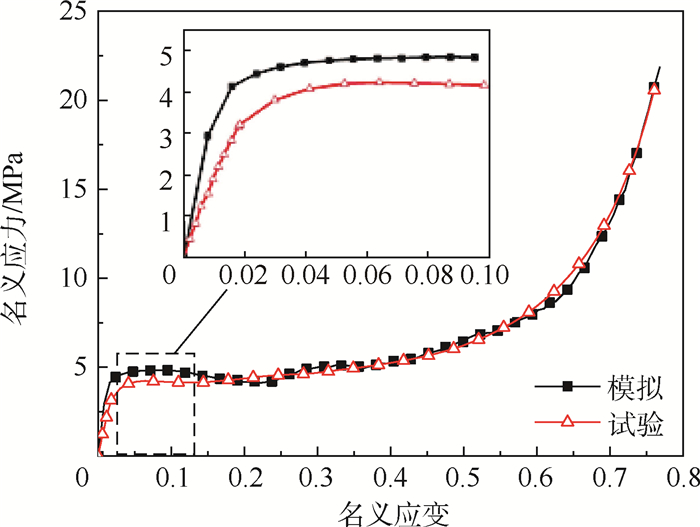 |
| 图 7 准静态压缩试验与模拟的名义应力-应变曲线 Fig. 7 Nominal stress-strain curves of test and simulation under quasi-static compression |
| 图选项 |
将图 7中名义应变0~0.1之间的部分放大观察发现,模拟所得曲线在名义应变小于0.03时的弹性模量大于试验值,这主要是由于实际材料中基体的力学曲线表现出非线性[27],而本文为了简化计算采用线性模型。尽管如此,二者对应的材料吸能效果只相差1%左右。图中还发现,在名义应变0.03~0.2之间时数值模拟得到的名义应力值略高于试验值。这可能是由于建模过程中忽略了胞壁中的微细孔洞,导致孔壁的强度增大所致。虽然如此,这一区间内的名义应力相差在5%以内,说明本文模型能够描述泡沫铝在静态荷载压缩下的基本力学性能特征。
为进一步观察泡沫铝压缩过程中内部变形破坏情况,选取3个纵向截面进行对比分析,如图 8所示。其中x为截面距端面的距离,ε为试件的名义应变。可以看到,试件在压缩的各个阶段,各部分同时产生变形,但各纵向截面都存在局部的不均匀变形,且不均匀变形出现的位置各不相同,破坏形态也有所区别,出现了随机的压溃带或剪切破坏带,这与文献[28]较为吻合。同时可明显看出,各纵向截面中的较大塑性变形并非首先出现在截面中最薄位置,而是存在一定的随机性,这表明泡沫铝胞壁发生变形直至坍塌破坏与整个试件的三维结构密切相关。
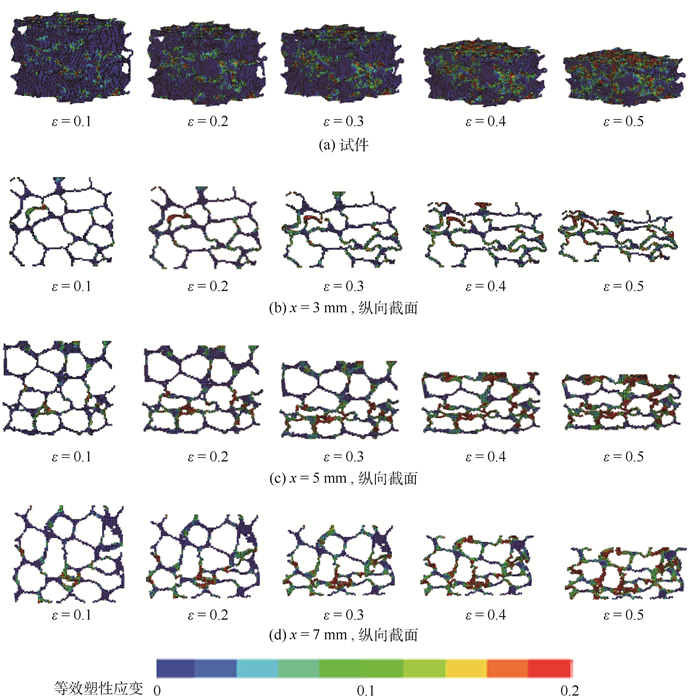 |
| 图 8 准静态加载下试件及胞壁的变形形态 Fig. 8 Deformation morphology of specimen and cell-wall under quasi-static loading |
| 图选项 |
3.2 动态冲击特性 采用直径37.5mm的霍普金森压杆(SHPB)设备进行动态冲击试验。子弹长度为600mm,入射杆和透射杆长度均为2000mm,材料为LC4铝合金。圆柱体试件直径30mm,高20mm,子弹的冲击速度为10.61m/s。入射杆采用电阻应变片,透射杆采用半导体应变片进行测量,入射杆和透射杆中的应力-时间曲线如图 9所示。试验前对泡沫铝试件进行CT扫描,利用第2节方法建立了试件的三维细观有限元模型,模型中同时包含了与试验尺寸相同的入射杆和透射杆,材料参数、破坏准则以及接触定义均与准静态加载条件下相同。利用所建立的模型进行模拟分析,结果示于图 9中。可以看到,试验与数值模拟得到的入射波、反射波和透射波总体吻合良好,说明本文模型能有效地模拟泡沫铝试件的动态冲击过程。
 |
| 图 9 动态冲击试验与模拟的应力-时间曲线 Fig. 9 Comparison between test and simulation results under impact loading |
| 图选项 |
图 10给出了模拟得到的动态冲击加载作用下泡沫铝试件的截面应力状态和变形过程。可以看出,冲击荷载作用下泡沫铝的内部变形与准静态加载下有显著区别,变形首先发生在冲击端附近,并随着冲击过程逐层推进,表现出明显的局部效应。这与文献[28]中等加载速度下的变形与破坏形态相一致。图中胞壁的破坏变形呈多样化,有屈曲变形、剪切破坏、扭转变形等,表明了该种材料变形破坏过程的复杂性。
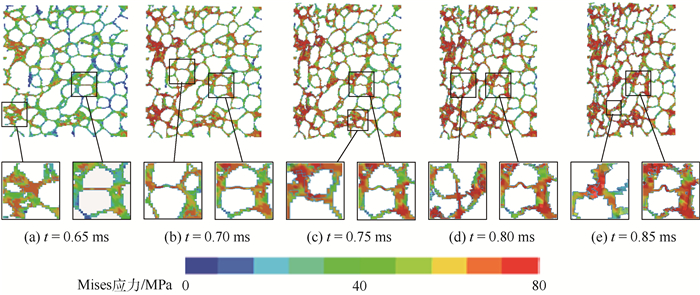 |
| 图 10 动态冲击加载下试件内部的Mises应力分布 Fig. 10 Mises stress distribution inside specimen under dynamic impact loading |
| 图选项 |
图 11为试件两端的平均应力-时程关系曲线。结合图 10、图 11发现,应力波在试件内的传播速度很快,大约0.015ms就传到整个试件,表现为图 11中试件两端平均应力-时程曲线中初始阶段的快速上升。图 11表明,试件冲击端平均应力增长更快,首先达到材料的屈服强度,胞孔孔壁开始发生塑性变形。随后,试件两端的平均应力都呈现出平台阶段,孔壁开始大范围地发生变形,直至最终压溃。另外,整个冲击过程中试件冲击端的平均应力始终高于支撑端,导致这一现象的可能原因:一是冲击过程中存在宏观惯性效应;二是冲击端局部压密的材料具有更高的屈服应力。
 |
| 图 11 试件冲击端、支撑端的平均应力-时程曲线 Fig. 11 Average stress-time history curves at loading and supporting ends of specimen |
| 图选项 |
4 结论 本文提出了一种基于CT的泡沫铝材料三维有限元分析模型重建新方法,基于此模型分析了泡沫铝试件在准静态压缩和动态冲击作用下的受力与变形特性,并与试验进行了对比。主要结论如下:
1) 本文方法很大程度上简化了CT扫描图像转化为有限元模型的过程,重建过程中直接生成节点和单元,不存在冗余的点、线、面、体等数据;所采用的灰度阈值判定算法和映射网格技术,使得基体材料和空气单元能有效区分,生成的单元大小相同、形状统一,真实地还原出了泡沫铝的细观结构特性,并有利于有限元计算。
2) 利用所建立的三维细观模型对泡沫铝试件在准静态压缩和动态冲击作用下的模拟分析与试验结果吻合良好,说明利用本文方法具有很高的可靠性和实用性。
3) 准静态压缩作用下泡沫铝的变形在试件内部随机出现,且破坏的位置与材料的三维结构密切相关;在中等速度冲击作用下泡沫铝试件的破坏形态完全异于准静态加载作用,首先在冲击端附近开始压缩,并逐层压溃,表现出明显的变形局部化效应。
4) 本文方法可用于其他具有细观结构特征材料的三维细观模型建模与研究。
参考文献
| [1] | GIBSON L J, ASHBY M F. Cellular solids:Structure and properties[M].Cambridge: Cambridge University Press, 1999: 6-11. |
| [2] | BANHART J. Manufacture characterization and application of cellular metals and metal foams[J].Progress in Materials Science, 2001, 46(6): 559–632.DOI:10.1016/S0079-6425(00)00002-5 |
| [3] | MAGNUCKA B E, MAGNUCKI K. Effective design of a sandwich beam with a metal foam core[J].Thin-Walled Structures, 2007, 45(4): 432–438.DOI:10.1016/j.tws.2007.03.005 |
| [4] | YUJ L, LI J R, HU S S. Strain-rate effect and micro-structural optimization of cellular metals[J].Mechanics of Materials, 2006, 38(1): 160–170. |
| [5] | DESHPANDE V S, FLECK N A. High strain rate compressive behavior of aluminum alloy foams[J].International Journal of Impact Engineering, 2000, 24(3): 277–298.DOI:10.1016/S0734-743X(99)00153-0 |
| [6] | MEGUID S A, CHEON S S, EI-ABBASI N. FE modelling of deformation localization in metallic foams[J].Finite Elements in Analysis and Design, 2002, 38(7): 631–643.DOI:10.1016/S0168-874X(01)00096-8 |
| [7] | NAMMI S K, MYLER P, EDWARDS G. Finite element analysis of closed-cell aluminum foam under quasi-static loading[J].Materials & Design, 2010, 31(2): 712–722. |
| [8] | ZHU H X, KNOTT J F, MILLS N J. Analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells[J].Journal of the Mechanics and Physics of Solids, 1997, 45(3): 319–343.DOI:10.1016/S0022-5096(96)00090-7 |
| [9] | DE GIORGI M, CAROFALO A, DATTOMA V, et al. Aluminum foams structural modelling[J].Computers & Structures, 2010, 88(1): 25–35. |
| [10] | 刘培生. 关于多孔材料的新模型[J].材料研究学报, 2009, 20(1): 64–68. LIU P S. A new model for porous materials[J].Chinese Journal of Materials Research, 2009, 20(1): 64–68.(in Chinese) |
| [11] | 刘培生, 夏凤金, 罗军. 多孔材料模型分析[J].材料工程, 2009(7): 83–87. LIU P S, XIA F J, LUO J. Analyses of the classical model for porous materials[J].Journal of Material Engineering, 2009(7): 83–87.(in Chinese) |
| [12] | ZHANG C Y, TANG L Q, YANG B, et al. Meso-mechanical study of collapse and fracture behaviors of closed-cell metallic foams[J].Computational Materials Science, 2013, 79: 45–51.DOI:10.1016/j.commatsci.2013.05.046 |
| [13] | ZHENG Z J, WANG C, YU J L, et al. Dynamic stress-strain states for metal foams using a 3D cellular model[J].Journal of the Mechanics and Physics of Solids, 2014, 72: 93–114.DOI:10.1016/j.jmps.2014.07.013 |
| [14] | LI Z, ZHANG J, FAN J, et al. On crushing response of the three-dimensional closed-cell foam based on Voronoi model[J].Mechanics of Materials, 2014, 68: 85–94.DOI:10.1016/j.mechmat.2013.08.009 |
| [15] | CAROFALO A, DE GIORGI M, MORABITO A, et al. Geometric modelling of metallic foams[J].Engineering Computations, 2013, 30(7): 924–935.DOI:10.1108/EC-06-2011-0070 |
| [16] | FANG Q, ZHANG J H, LIU J C, et al. Mesoscopic investigation of closed-cell aluminum foams on energy absorption capability under impact[J].Composite Structures, 2015, 124: 409–420.DOI:10.1016/j.compstruct.2015.01.001 |
| [17] | FANG Q, ZHANG J H, ZHANG Y D, et al. A 3D mesoscopic model for the closed-cell metallic foams subjected to static and dynamic loadings[J].International Journal of Impact Engineering, 2015, 82: 103–112.DOI:10.1016/j.ijimpeng.2014.10.009 |
| [18] | MAIRE E, FAZEKAS A, SALVO L, et al. X-ray tomography applied to the characterization of cellular materials related finite element modeling problems[J].Composites Science and Technology, 2003, 63(16): 2431–2443.DOI:10.1016/S0266-3538(03)00276-8 |
| [19] | MCDONALD S A, MMMMERY P M, JOHNSON G, et al. Characterization of the three-dimensional structure of a metallic foam during compressive deformation[J].Journal of Microscopy, 2006, 223(2): 150–158.DOI:10.1111/jmi.2006.223.issue-2 |
| [20] | JEON I, ASAHINA T, KANG K J, et al. Finite element simulation of the plastic collapse of closed-cell aluminum foams with X-ray computed tomography[J].Mechanics of Materials, 2010, 42(3): 227–236.DOI:10.1016/j.mechmat.2010.01.003 |
| [21] | SUN Y L, LI Q M, LOWE T, et al. Investigation of strain-rate effect on the compressive behavior of closed-cell aluminum foam by 3D image-based modelling[J].Materials & Design, 2016, 89: 215–224. |
| [22] | JEON I, ASAHINA T. The effect of structural defects on the compressive behavior of closed-cell Al foam[J].Acta Materialia, 2005, 53(12): 3415–3423.DOI:10.1016/j.actamat.2005.04.010 |
| [23] | TURBELL H.Cone-beam reconstruction using filtered back projection[D].Linkping:Linkping University, 2001. |
| [24] | 韩思奇, 王蕾. 图像分割的阈值法综述[J].系统工程与电子技术, 2002, 24(6): 91–94. HAN S Q, WANG L. A survey of thresholding methods for image segmentation[J].Systems Engineering and Electronics, 2002, 24(6): 91–94.(in Chinese) |
| [25] | MCDONALD S A, MMMMERY P M, JOHNSON G, et al. Characterization of the three-dimensional structure of a metallic foam during compressive deformation[J].Journal of Microscopy, 2006, 223(Pt 2): 150–158. |
| [26] | HALLQUISTJ O.LS-DYNA keyword user's manual[Z].Livermore:Livermore Software Technology Corporation, 2015. |
| [27] | JEON I, KATOU K, SONODA T, et al. Cell wall mechanical properties of closed-cell Al foam[J].Mechanics of Materials, 2009, 41(1): 60–73.DOI:10.1016/j.mechmat.2008.08.002 |
| [28] | 李妍妍, 郑志军, 虞吉林, 等. 闭孔泡沫金属变形模式的有限元分析[J].爆炸与冲击, 2014, 34(4): 464–470. LI Y Y, ZHENG Z J, YU J L, et al. Finite element analysis on deformation modes of closed-cell metallic foam[J].Explosion and Shock Waves, 2014, 34(4): 464–470.DOI:10.11883/1001-1455(2014)04-0464-07(in Chinese) |
