传统信号采样过程需要遵循Nyquist采样定理才能精确得到信号，即采样速率需达到信号带宽2倍以上。高采样速率的要求使得硬件成本高昂，随着信号所占带宽的急剧增加，将导致硬件系统面临巨大压力，而且这种高速采样再压缩的方式容易造成计算和存储资源的大量浪费，甚至导致信号恢复错误。
2004年，Donoho^[1]提出压缩感知(Compressed Sensing，CS)理论，该理论指出，若信号在某一变换域是稀疏的，那么可选取与稀疏基不相关的矩阵对信号进行低维投影，经过凸优化方法或者匹配追踪方法可以较高精度地还原出信号。
与传统的信号获取和处理过程相比较，压缩感知将采样过程和压缩过程合并进行，利用信号的稀疏特性，可以突破Nyquist采样定理，采集高分辨信号^[2-3]，这使其在信号处理领域有着广阔的应用前景，已经被广泛应用于信源编码、机器学习等领域。
重构是指从低维观测信号中恢复出原始信号的过程，是压缩感知中最为关键的部分。重构算法的优劣将直接影响重构效果。
稀疏重构算法主要分为凸优化算法和迭代贪婪算法2种^[4]。凸优化算法是针对L₁范数最小化提出的，如基追踪(BP)法、内点法等，该类算法的重构精度较高，但其计算复杂度也很高，如基追踪法的复杂度为O(N³)(N为信号长度)，不适合应用于大规模问题。迭代贪婪算法是针对L₀范数最小化提出的，具备重构复杂度低、重构速率快等优点，在实际中应用广泛。Mallat和Zhang^[5]首次提出匹配追踪(MP)，即每次迭代获得支撑集的一个原子，但是不能保证残差值与该原子正交。正交匹配追踪(OMP)算法弥补了上述算法的不足，不会重复选择相同的原子，但是该算法在每次迭代中仅选取一个原子，使得重构速率较慢^[6]。为了在一次迭代过程中可以选取多个原子，****们提出了采用阈值原则的分段正交匹配追踪(StOMP)算法和采用正则化思想的正则化正交匹配追踪(ROMP)算法^[7-8]。这些算法的时间复杂度约为O(KMN)(K为信号稀疏度，M为观测值长度)，远低于基追踪算法，但需观测值较大时才能获得较好的重构效果^[9]。因此，有****引入了具有回溯思想的压缩采样匹配追踪(CoSaMP)算法和子空间追踪(SP)算法，该类算法最大的创新是对选取的支撑集原子进行回溯以剔除错误的原子，达到更高的重构精度^[10-11]。以上算法均需建立在对稀疏度K具备先验信息的基础上，但在实际应用中K通常是未知的。因此，有****提出了稀疏度自适应匹配追踪(SAMP)算法^[12]，该算法不依赖于信号稀疏度，通过倍增固定步长S逐步逼近信号真实稀疏度进行重构，如果步长S远小于稀疏度K，则需要大量迭代过程，如果S较大，将导致稀疏度估计值与实际值相差较大，重构误差较大^[13-14]。此外，由于在每次迭代中初始选取原子时没有进行二次筛选，容易导致选取出错误的原子，降低重构精度。
本文在研究现有压缩感知重构算法的基础上提出了一种新的迭代贪婪算法——正则化稀疏度变步长自适应匹配追踪(Regularized Sparsity Variable step-size Adaptive Matching Pursuit，RSVss-AMP)算法，可在对信号稀疏度无先验知识的情况下，结合正则化和步长自适应变化思想，通过可变步长及新旧残差值比较来控制重构精度和重构次数，实现对信号快速精确的重构。
1 压缩感知理论 1.1 信号的稀疏表示 假设采样信号x(x∈R^N)，长度为N，ψ∈R^N×N为正交矩阵，称为稀疏基，x在该变换域下可稀疏表示。基向量为ψ_i(i=1, 2, …, N)，x可以表示为

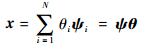(1)

式中：θ为信号x在ψ域的表示，若θ中非零元素个数为K(K?N)，则信号是K-稀疏的。选取信号的最佳稀疏域是压缩感知技术的基础。常用的稀疏基包括离散余弦基、傅里叶变换基等。
1.2 信号的低维观测 选取与稀疏基不相关的观测矩阵φ∈R^M×N(M＜N)信号进行低维投影，得到观测值y。y是M维向量，观测过程可表示为

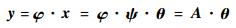(2)

式中：A∈R^M×N为传感矩阵，满足M≥Klg(N/K)。由于信号稀疏，若式(2) 中的A满足有限等距性质(RIP)，即对于任意K-稀疏信号x和常数δ_k∈(0, 1)，满足：

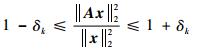(3)

则稀疏信号中K个系数能够通过测量值y精确获得。观测矩阵直接影响信号的压缩，同时也影响信号能否被精确重构。常用的观测矩阵主要包括高斯矩阵、伯努利矩阵等。
1.3 信号的重构 得到观测值y之后，根据稀疏重构关系，通过合适的重构算法可以实现信号x的重构。通过求解L₀范数下最优化问题，从观测值y中恢复稀疏系数θ，从而得到未知信号的精确估计。

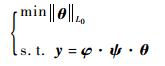(4)

L₀范数最小使得结果尽可能得稀疏，但是求解L₀范数最小是一个NP-Hard问题。有文献表明，在一定条件下，L₁与L₀范数问题可以互相转换。于是，式(4) 可转化为L₁范数下的凸优化问题求解，有

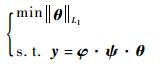(5)

重构算法在引言已经进行了详细的描述。当前，重构算法的研究主要集中在如何构造稳定的、适用于信号稀疏度未知、计算复杂度较低的算法来精确恢复信号。本文提出的RSVssAMP算法是一种在稀疏度无先验知识情况下，通过步长自适应变化及新旧残差值比较来控制重构精度和重构次数的迭代贪婪算法，与现有重构算法相比，可以达到更高的重构精度和重构速率。
2 算法描述及其应用 迭代贪婪算法是重构算法中比较重要的研究方向，其基本思想是：在每一次迭代过程中，从传感矩阵里选取一组与信号最为匹配的原子组成支撑集，重构得到信号，并计算出相应残差值，根据残差值对支撑集进行更新。通过多次迭代过程，可以实现信号的精确重构。
根据信号稀疏度是否已知，迭代贪婪算法可以分为2类：第1类以OMP算法为代表，需将稀疏度作为先验信息来控制算法的迭代次数；第2类算法则不需要稀疏度先验信息，通过调整步长估计出真实稀疏度来重构。
实际中，信号稀疏度通常是未知的，因此第2类算法应用更加广泛，SAMP算法是其中最具代表性的。该算法将重构过程分为多个阶段，在每个阶段中，重构所需支撑集F的长度W不发生改变并进行多次迭代，当该支撑集不能满足重构要求时，则增加步长S以进入下一个阶段，随着W不断增大，可以在未知稀疏度下逐步逼近K。其中，步长S需要根据信号特点进行合理选取。但是该算法也有一些明显的缺点。SAMP算法在形成支撑集时没有对原子进行二次筛选，这在一定程度上会限制信号重构精度。此外，由于信号稀疏度K未知，重构过程中采用固定步长策略将带来一些问题，如当步长S取较小的值时是稳妥的，但这使得重构阶段次数增加；当步长S取较大值时，可能出现重构误差较大的问题。为了更加精确地重构信号，同时保证较高的重构速率，本文采取改变步长的思想以自适应地逐步逼近稀疏度K进行重构。而且为了保证在每次迭代的支撑集剔除错误原子，使得选取的原子更加准确，获得更高的重构精度，对选取原子进行正则化处理^[15-17]。
本文将正则化思想与稀疏度变步长自适应思想相结合，提出RSVssAMP算法。
正则化：选取传感矩阵各列向量与残差内积绝对值的最大值不能比最小值大2倍以上且能量最大的一组原子。正则化实现了对原子的二次筛选，使得选取原子的准确率得到极大的提高，重构误差明显降低。
稀疏度变步长自适应：变步长思想可以弥补固定步长的不足。在初始重构阶段，由于估计稀疏度与真实值相差较大，可以用大步长快速接近；当精度达到一定时，调整为小步长进行精确逼近。应用变步长进行处理，可以用较少的迭代次数获得更高的重构精度。自适应体现在对于小步长设定上，可以根据信号特点对其进行自适应调整。
RSVssAMP算法即是在每次重构过程中先通过正则化选取部分原子添加到支撑集中，再比较相邻重构过程获得的残差值大小，设定相对阈值调整步长，通过大步长快速接近、小步长精确逼近的思想，实现信号快速并精确的重构。根据新旧残差值的比较设计了判别条件。当相邻阶段新旧残差值之比大于相对阈值时，增加整数倍步长，算法通过大步长快速重构信号，减少重构时间；当相邻阶段新旧残差值之比小于相对阈值时，减小步长增加量，算法通过小步长逐步逼近重构信号，提高重构精度。
2.1 算法描述 假设y(M×1) 为观测向量，x(N×1，有M ?N)为原信号，压缩感知观测过程如式(2) 所示。
定义r_t表示残差，t表示迭代次数，?表示空集，∧_t表示t次迭代的索引(列序号)集合(元素个数为L，L等于步长S的整数倍)，a_j表示矩阵A的第j列，A_t={a_j}表示按照索引集合选出的矩阵A的列所组成的矩阵(设列数为L_t)，θ_t为L_t×1的列向量。算法步骤描述如下：
步骤1??初始化r₀=y，∧₀=?，L=S，t=1。
步骤2??计算u=abs[A^Tr_t-1] (即计算〈r_t-1，a_j〉，1≤j≤N)，选择u中L个最大值进行正则化，将这些值对应A的列序号j构成集合S_k(列序号集合)。
步骤3??令C_k=∧_t-1∪S_k，A_t={a_j} (下标j∈C_k)。
步骤4??求y=A_tθ_t的最小二乘解：

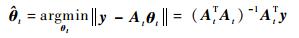步骤5??从中选出绝对值最大的L项记为，对应的A_t中的L列记为A_tL，对应的A的列序号记为∧_tL，记集合F=∧_tL。
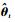
步骤6??更新残差r_new=y－A_tL(A_tL^TA_tL)^－1·A_tL^Ty。
步骤7??若||r_new||₂＜||r_t－1||₂，如果残差r_new=0或||r_new||₂≤alpha (alpha是一个很小的值)，则停止迭代，进入步骤9；如果||r_new||₂＞alpha，则∧_t=F，r_t= r_new，t=t+1，当t=M时，停止迭代，进入步骤9。
步骤8??若||r_new||₂≥r_t－1||₂，如果||r_new||₂/||r_t－1||₂≥beta，更新步长：L=L+S，t=t+1，返回步骤2，当t=M时，停止迭代，进入步骤9；如果beta＞||r_new||₂/r_t－1||₂≥1，更新步长：L=L+aS，t=t+1，返回步骤2，其中自适应参数a∈(0, 1)，当t=M时，停止迭代，进入步骤9。
步骤9??重构所得在∧_tM处有非零项，其值分别为最后一次迭代所得。
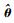
2.2 算法流程 根据2.1节算法步骤，可以得到RSVssAMP算法的流程，如图 1所示。

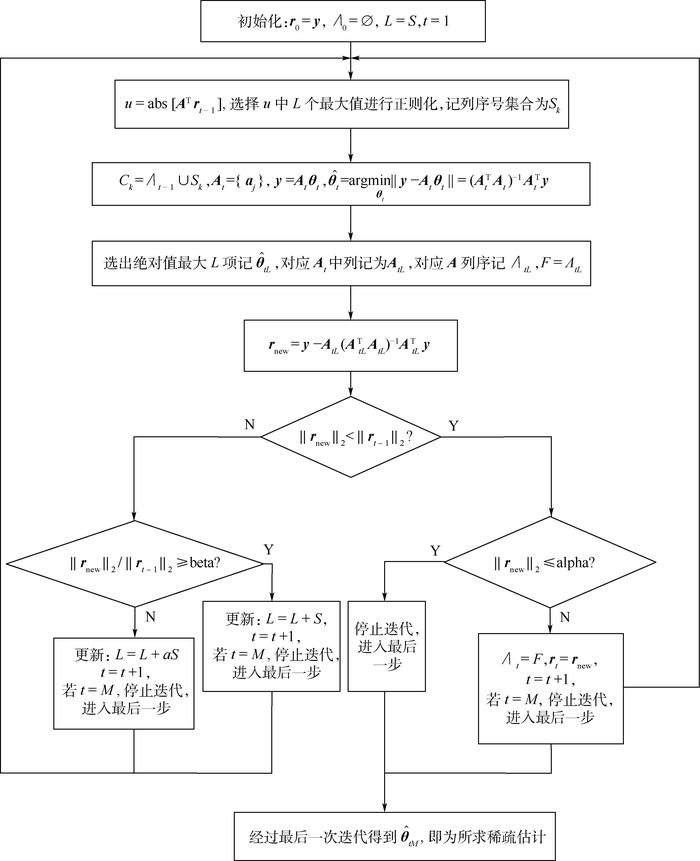图 1 正则化稀疏度变步长自适应匹配追踪算法流程图 Fig. 1 Flowchart of regularized sparsity variable step-size adaptive matching pursuit algorithm

图选项

在重构过程中一共存在4个参数，分别是步长S、迭代停止条件参数alpha、步长变换条件参数beta、步长自适应参数a。这些参数值的设定将直接影响重构精度和重构迭代次数。步长S在仿真初始阶段设定，可以适当选取较大值，实现大步长快速逼近；alpha应用于判断迭代过程是否停止，通常取10^－6；beta应用于比较新旧残差值，以进行步长变换；自适应参数a可以根据信号特征进行步长的调整，实现小步长精确逼近。
2.3 算法应用 RSVssAMP算法具有非常重要的应用价值，特别适用于对重构精度和重构效率要求较高的场景，如应用于卫星遥测数据实时监控过程中。
卫星遥测数据反映了卫星有效载荷的状态和卫星运行情况。由于遥测参数种类众多，对信号的采集又是一个持续而长期的过程，因此，大量数据需要采集和存储。可采用压缩感知技术，在信号采集端对其进行有效地采样和压缩。随着卫星运行状态实时分析和监控概念的提出，压缩后的遥测数据通过无线电通信实时地传输给地面中心进行重构和信息交互，这对于重构精度和重构效率的要求非常高。因此，非常有必要应用RSV-ssAMP算法进行数据重构，在保证较高重构精度的条件下，使得所需重构时间尽可能少。
3 仿真与讨论 3.1 压缩感知重构算法评价指数 压缩感知重构算法的评价指数主要包括2类：重构效率和重构成功率。
重构效率包括迭代重构次数和迭代效率，可以通过重构时间来衡量。对于不同算法，可以通过比较相同条件下重构所需平均时间T来比较重构效率。所需重构时间越少，说明重构效率越高。
重构相对误差代表重构信号保真度信息，记离散采样信号为s，为重构信号，s_i和表示对应信号的第i维幅值，信号长度为N，则均方根相对误差PRD定义如下：

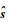
(6)

重构成功率指一次实验重构均方根相对误差在既定阈值γ内的概率。重构成功率越高，说明算法越精确。
需要说明的是，本文仿真是在Dell Optiplex 9020 (i7-4790，6GB DDR3内存)和MATLAB 2010环境下进行。
3.2 不同稀疏度下的重构算法性能比较 对于目标信号，由于不同信号段的真实稀疏度可能不同，优秀的重构算法应当保证对于不同信号稀疏度均可以获得较好的重构效果，因此，有必要考察和比较在不同稀疏度下算法的重构性能。
在本次实验中，选取典型的时域稀疏信号——高斯稀疏信号和离散稀疏信号作为目标信号，比较重构算法在不同稀疏度下的重构效果。
在目标高斯稀疏信号中，非零元素呈高斯分布，选取信号段长度N=256，观测信号长度M=128；在目标离散稀疏信号中，非零元素具有随机性，选取的信号段长度和观测信号长度与上述一致。

3.2.1 不同稀疏度下重构成功率比较 本次实验将RSVssAMP算法与OMP、ROMP、StOMP、SP、CoSaMP、SAMP算法在不同稀疏度下的重构成功率进行比较。对于稀疏度K的每一个值，均进行1 000次实验，既定阈值γ取值为10^－6。通过大量实验仿真，设定RSVssAMP算法中的自适应参数a=0.5，步长S=5，迭代停止条件参数alpha=10^－6，步长变换条件参数beta=1.2。
图 2为不同稀疏度K下高斯稀疏信号和离散稀疏信号的重构成功率。

图 2 不同稀疏度下重构成功率比较 Fig. 2 Comparison of reconstruction success rate under different sparsity

图选项

可以看出，对于迭代贪婪算法，当信号长度和观测值保持不变时，随着稀疏度增大，重构成功率降低，这是由于原始信号不确定性越来越高，但是能获取的信息非常有限导致的。而且，无论对高斯稀疏信号，还是离散稀疏信号，RSVssAMP算法重构效果明显优于OMP、ROMP、StOMP、SP、CoSaMP等第1类贪婪迭代算法；与SAMP算法相比，重构成功率仍有一定提高。

3.2.2 不同稀疏度下重构时间比较 考察RSVssAMP算法和SAMP算法的重构时间。图 3为高斯稀疏信号和离散稀疏信号的重构时间，选取若干稀疏度值K进行比较。图中纵轴重构时间取为1 000次实验的平均重构时间。实验中，为了保证一定的重构精度，SAMP算法步长设置为5，RSVssAMP算法步长设置为10。

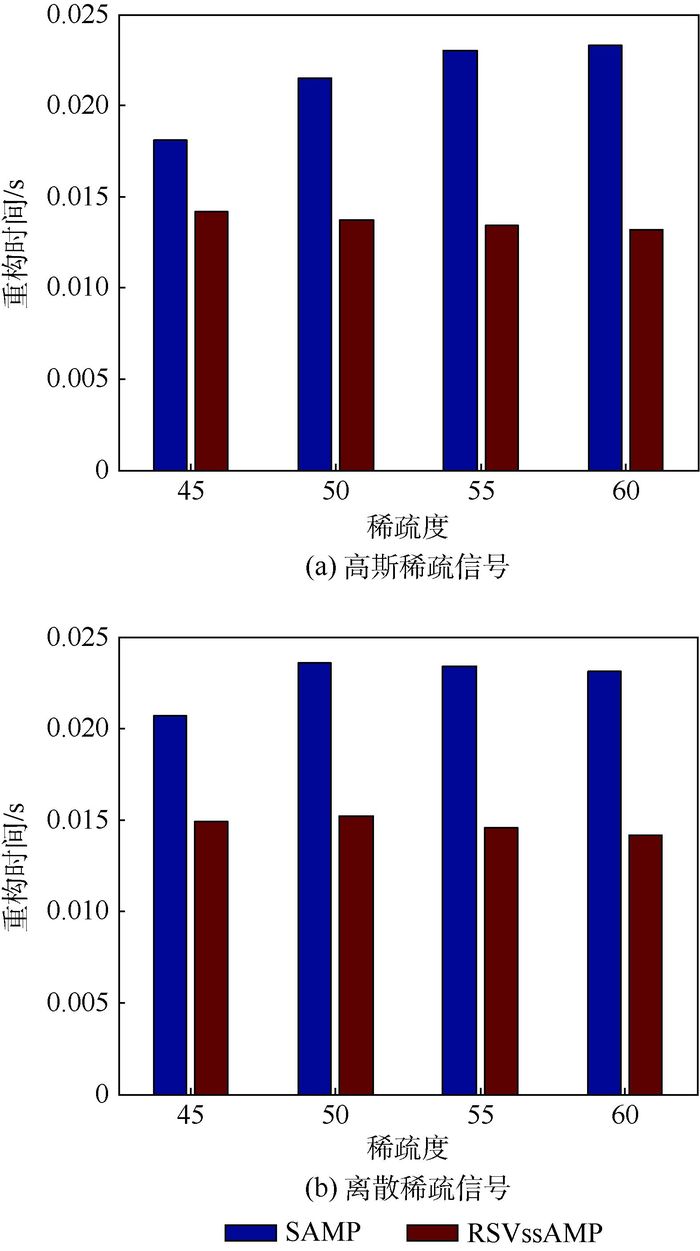图 3 不同稀疏度下重构时间比较 Fig. 3 Comparison of reconstruction time under different sparsity

图选项

从图 3可以看出，对于高斯稀疏信号和离散稀疏信号，RSVssAMP算法平均重构时间比SAMP算法所需重构时间少，说明对于不同信号稀疏度情况，RSVssAMP算法效率更高。
3.3 不同观测值下的重构算法性能比较 对于目标信号，由于传感器数量和信道容量有限，应用压缩感知进行低维投影得到的观测信号长度将受到限制。即使对于同一目标信号段，在不同条件下的观测信号长度可能不同，优秀的重构算法应当保证对于不同观测值均可以获得较好的重构效果，因此，有必要考察和比较在不同观测信号长度下算法的重构性能。
在本次实验中，同样选取高斯稀疏信号和离散稀疏信号作为目标信号，比较重构算法在不同观测值下的重构效果。选取目标信号段长度N=1 024，稀疏度K=20。

3.3.1 不同观测值下重构成功率比较 考察不同重构算法在不同观测值下的重构成功率。对于观测值M的每一个值，均进行1 000次实验。RSVssAMP算法中步长取为8，其他参数设置同3.2.1节。
图 4为不同观测值M下高斯稀疏信号和离散稀疏信号的重构成功率。对于不同信号，不同观测值下重构成功率差别较大，为了更好地比较重构性能，对高斯稀疏信号观测值范围取为[75, 120]，对于离散稀疏信号观测值范围取为[90, 140]。

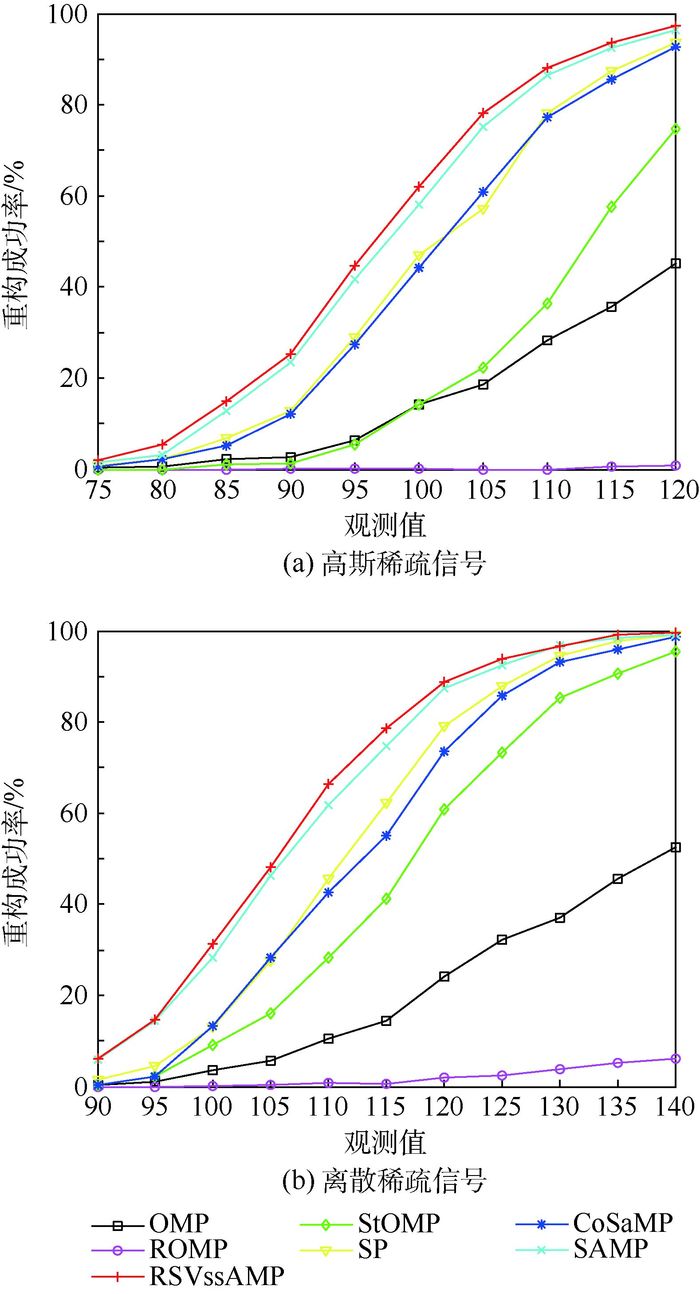图 4 不同观测值下重构成功率比较 Fig. 4 Comparison of reconstruction success rate under different observed values

图选项

从图 4可以看出，对于迭代贪婪算法，当信号长度和稀疏度保持不变时，随着观测值数量增大，重构成功率增大，这是因为获取原始信号的信息越来越多，估计出的稀疏信号也越加精确。对高斯稀疏信号和离散稀疏信号，RSVssAMP算法和SAMP算法重构效果明显优于OMP、ROMP、StOMP、SP、CoSaMP等第1类迭代贪婪算法；并且RSVssAMP算法重构效果稍优于SAMP算法。

3.3.2 不同观测值下重构时间比较 考察RSVssAMP算法和SAMP算法的重构时间。图 5为高斯稀疏信号和离散稀疏信号的重构时间。图中纵轴重构时间取为1 000次实验的平均重构时间。在实验中，为了保证一定的重构精度，SAMP算法步长设置为4，RSVssAMP算法步长设置为8。

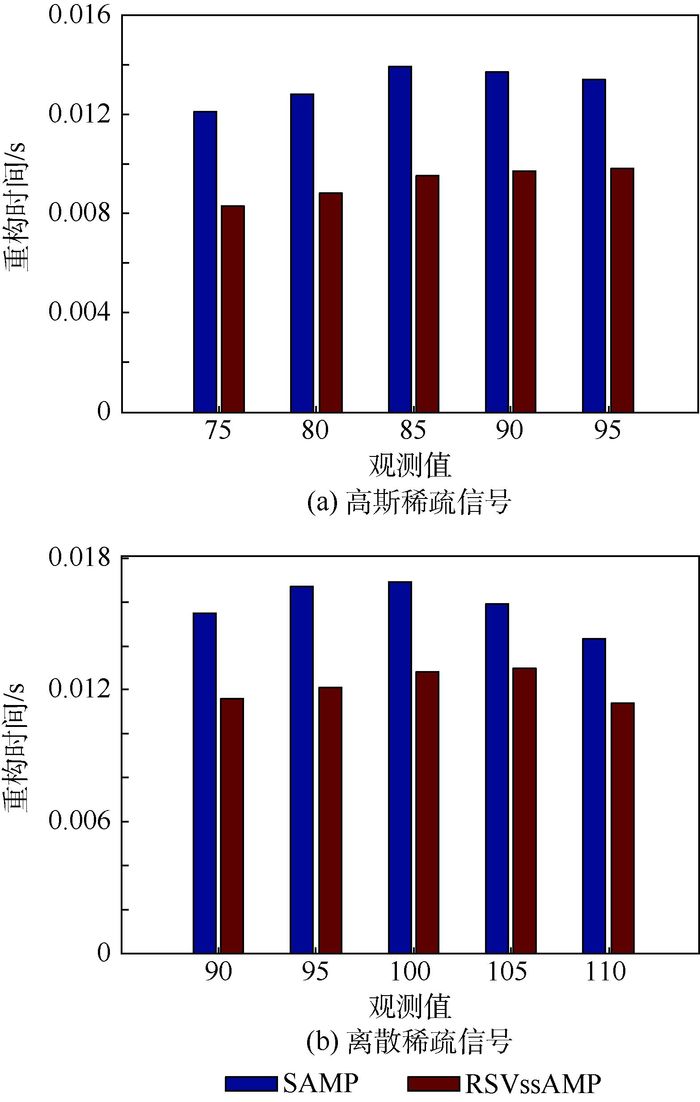图 5 不同观测值下重构时间比较 Fig. 5 Comparison of reconstruction time under different observed values

图选项

从图 5可以看出，RSVssAMP算法平均重构时间比SAMP算法所需重构时间更少，说明对于不同观测值情况，RSVssAMP算法效率更高。

3.3.3 不同步长情况下重构性能比较 考察RSVssAMP算法和SAMP算法在不同步长情况下的重构性能，主要比较步长S为2和8的情况。图 6为高斯稀疏信号和离散稀疏信号在不同步长时的重构成功率。

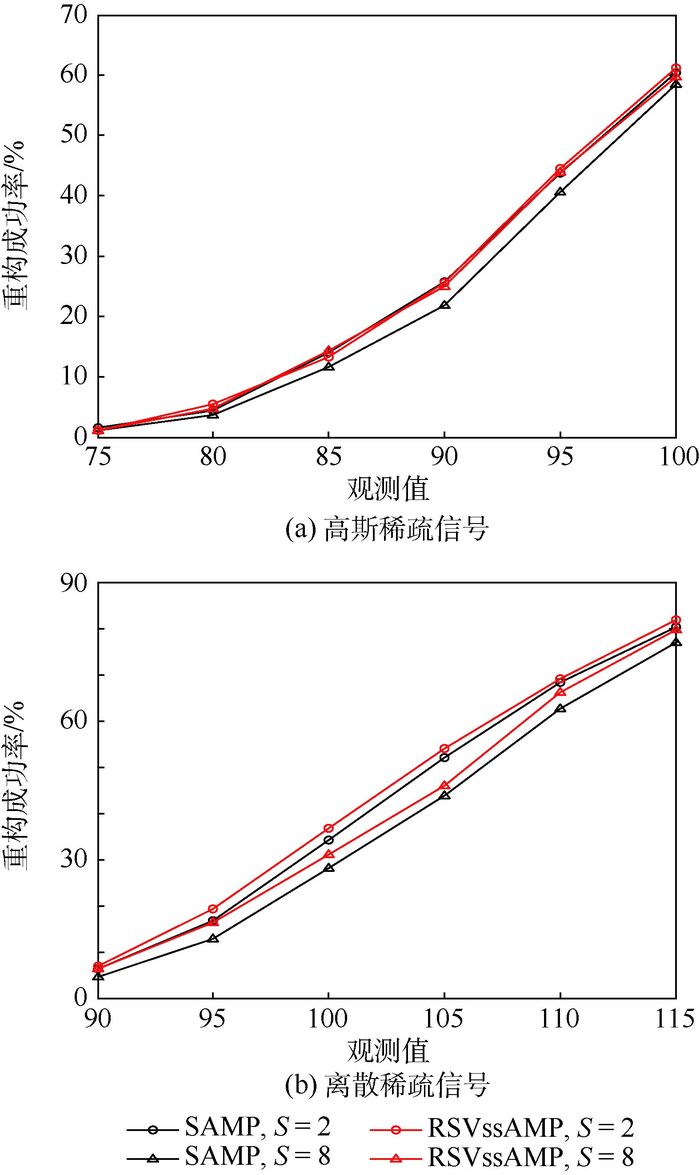图 6 不同步长下重构成功率比较 Fig. 6 Comparison of reconstruction success rate under different step-sizes

图选项

从图 6可以看出，步长减小，重构成功率具有增大的趋势，这是因为步长越小越容易逼近真实稀疏度。在相同步长情况下，RSVssAMP算法和SAMP算法重构成功率很接近，当步长为2时，前者稍微优于后者；而当步长为8时，RSVssAMP算法具有更明显的优势。
4 结论 本文针对当前迭代贪婪算法对数据稀疏度依赖较大以及重构所需时间较长的问题，将正则化和步长自适应变化思想相结合，提出一种改进的迭代贪婪算法——正则化稀疏度变步长自适应匹配追踪(RSVssAMP)算法。
1) 与稀疏度自适应匹配追踪(SAMP)算法相比，本文算法应用正则化对原子进行二次筛选，确保选取支撑集的正确性以提高重构精度。
2) 应用双重阈值实现步长的自适应变化，以达到大步长快速接近、小步长精确逼近的思想，不仅提高重构速率，而且使得估计出的信号稀疏度与真实值更加接近，达到更高的重构精度。
3) 仿真结果表明，本文算法在不同观测值、不同信号稀疏度情况下，重构性能均明显优于OMP等第1类迭代贪婪算法；相比第2类迭代贪婪算法，如SAMP算法，本文算法获得重构成功率略高，所需重构时间降低。并且当步长减小时，本文算法重构成功率具有增大的趋势。
4) 本文算法中，步长参数、步长变换条件参数、步长自适应参数等将直接影响到重构性能，如何针对信号特点进行科学地设定是下一步需要研究的方向。

参考文献

[1]	DONOHO D L. Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306.DOI:10.1109/TIT.2006.871582
[2]	WANG X, ZHAO Z, ZHAO N, et al.On the application of compressed sensing in communication networks[C]//20105th International ICST Conference on Communications and Networking.Piscataway, NJ:IEEE Press, 2010:1-7.
[3]	WEI T C, WANG H Y.Research on application of compressed sensing based on signal decomposition[C]//Communication Problem-Solving(ICCP).Piscataway, NJ:IEEE Press, 2014:326-331.
[4]	李博. 压缩感知理论的重构算法研究[D]. 长春: 吉林大学, 2013. LI B.Study on the reconstruction algorithms of the compressed sensing[D].Changchun:Jilin University, 2013(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193495.htm
[5]	MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415.DOI:10.1109/78.258082
[6]	TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666.DOI:10.1109/TIT.2007.909108
[7]	DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].IEEE Transactions on Information Theory, 2012, 58(2): 1094–1121.DOI:10.1109/TIT.2011.2173241
[8]	NEEDELL D, VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 310–316.DOI:10.1109/JSTSP.2010.2042412
[9]	杨真真, 杨震, 孙林慧. 信号压缩重构的正交匹配追踪类算法综述[J].信号处理, 2013, 29(4): 486–496. YANG Z Z, YANG Z, SUN L H. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction[J].Journal of Signal Processing, 2013, 29(4): 486–496.(in Chinese)
[10]	NEEDELL D, TROPP J A. CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Applied & Computational Harmonic Analysis, 2008, 26(3): 301–321.
[11]	WEI D, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory, 2009, 55(5): 2230–2249.DOI:10.1109/TIT.2009.2016006
[12]	DO T T, GAN L, NGUYEN N, et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Conference on Signals.Piscataway, NJ:IEEE Press, 2008:581-587.
[13]	高睿, 赵瑞珍, 胡绍海. 基于压缩感知的变步长自适应匹配追踪重建算法[J].光学学报, 2010, 30(6): 1639–1644. GAO R, ZHAO R Z, HU S H. Variable step size adaptive matching pursuit algorithm for image reconstruction based on compressive sensing[J].Acta Optica Sinica, 2010, 30(6): 1639–1644.(in Chinese)
[14]	SUN H, NI L.Compressed sensing data reconstruction using adaptive generalized orthogonal matching pursuit algorithm[C]//Computer Science and Network Technology (ICCSNT), 20133rd International Conference.Piscataway, NJ:IEEE Press, 2014:1102-1106.
[15]	HUANG W Q, ZHAO J L, LV Z Q, et al.Sparsity and step-size adaptive regularized matching pursuit algorithm for compressed sensing[C]//Information Technology and Artificial Intelligence Conference.Piscataway, NJ:IEEE Press, 2014:536-540.
[16]	YU Z.Variable step-size compressed sensing-based sparsity adaptive matching pursuit algorithm for speech reconstruction[C]//Chinese Control Conference.Piscataway, NJ:IEEE Press, 2014:7344-7349.
[17]	LI J, WU Z, FENG H, et al.Greedy orthogonal matching pursuit algorithm for sparse signal recovery in compressive sensing[C]//Instrumentation and Measurement Technology Conference(I2MTC)Proceedings.Piscataway, NJ:IEEE Press, 2014:1355-1358.