目前,关于体系的研究已经成为热点,国内外****在体系及体系工程方面开展了大量的研究,建立了许多专门进行体系研究的机构[3],并完成了体系设计、分析和集成等体系工程的各项研究工作,其中涉及到多个领域,如武器装备[4]、交通运输[5]和太空开发[6]等。由于体系不同于一般系统的集成,它具有复杂的体系结构、独立组成系统和动态演化性,并且在遭受内部或外部干扰时具有相应的恢复能力,因此其具备一般系统所不具备的功能,用传统的方法分析、设计和评价体系具有一定的局限性[7]。体系的设计需要在研究组成系统间关系的基础上描述并构建体系结构,而体系结构的弹性是体系研究的一个重要组成部分,也是表征体系抗干扰能力和恢复能力的特性之一[8]。虽然现有体系研究已经逐渐成熟,但是体系结构弹性的研究尚处于发展阶段。目前关于弹性的研究主要集中在复杂系统方面,认为弹性由组件或系统故障后进行修复,其性能恢复的程度和速度所决定的;同时,系统或组件的恢复策略也被认为是影响弹性的关键[9-10]。也就是说,体系或系统弹性研究需要关注以下2点:① 干扰对体系或系统造成的负面影响,可以用目标系统被破坏前后性能水平的变化来衡量;② 恢复策略,恢复被破坏的系统或组件所消耗资源的数量。此外,还有很多研究也与弹性相关,这些文献往往更加关注弹性模型构建[11-12]或弹性指标确定[13-14]。这也为后续体系结构弹性的研究奠定了基础,但关于体系结构弹性的物理含义,以及如何定量评价其弹性还需要进一步深入探讨。
本文首先分析了体系结构的弹性及体系性能变化的过程;然后建立了量化体系结构弹性的数学模型,并通过体系结构组件重要度分析(CIMs),为选择和改进体系的构建方案提供借鉴,从而为体系性能恢复策略优化指明方向;最后通过应用案例分析验证该评价方法与模型的适用性。
1 体系结构的弹性 体系结构是一个体系的基本组织,包括体系的组成单元、组成单元之间的关系和组成单元与环境之间的关系,以及指导设计和扩展的原则[2]。从上述定义可以看出,体系结构涵盖了系统、系统之间的交互关系、约束、行为以及系统的设计、演化原则等方面的内容。因此,体系结构的优劣,以及其在受到干扰时对体系性能的影响直接影响了体系的可靠性和脆弱性。
本文对体系的研究从体系结构入手,为了表征体系遭受破坏或者干扰后的恢复能力,将复杂系统研究中弹性一词引入到体系中。现有研究中对于复杂系统的弹性存在大量的讨论[15-16],但它们都是从系统角度进行考虑的,而体系不同于一般的系统的集成,其组件的广泛分布性以及结构演化性要求体系结构的弹性研究能够适应更灵活多样的体系使命,并具有非常强的抗干扰能力和恢复能力。本文根据复杂系统的弹性定义以及体系结构的特性,给出体系结构弹性的具体含义:在不确定的体系使命环境中,体系的一个组成系统或组件在干扰事件发生后(如遭受敌对势力或外部环境的干扰和攻击),其状态遭到破坏,进而导致整个体系的性能降级或体系崩溃;而体系结构的弹性衡量的是在不同的恢复策略下体系的性能恢复能力。在体系遭受干扰事件而性能下降时,通常存在2种不同的恢复策略:① 系统或组件的维修和修复;② 体系结构的任务重组[17]。本文主要讨论体系中系统或组件的修复对整个体系性能恢复的影响。由于体系结构是体系中组成系统或组件之间关系的一种描述,因此本文认为:弹性是体系结构的一种特性,可以用来衡量体系恢复到初始状态的能力。
在体系运行过程中,其受到外部干扰时,体系的性能变化过程以及体系可靠性、脆弱性和恢复性之间的关系如图 1所示。因此,体系结构的弹性可以描述为一个与时间相关的函数。
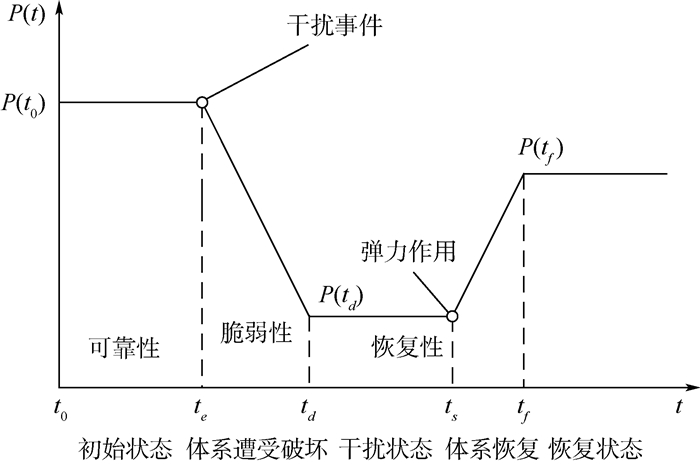 |
| 图 1 干扰事件发生后体系性能变化示意图 Fig. 1 Schematic of SoS performance transition under occurrence of disruption event |
| 图选项 |
图 1中,P(t)指的是体系的性能。体系从t0时刻到te时刻,在一定的可靠性水平下正常工作,在te时刻,体系遭受干扰事件ej的影响,在脆弱性(健壮性)作用下,体系性能开始下降,直到td时刻,体系的性能保持不变(没有发生体系崩溃);然后由于体系结构的弹性,体系具有一定的抗干扰能力和恢复能力,在开始实施体系性能恢复策略后,体系恢复性发挥作用,体系的性能在经过td-tf段时间后开始恢复,直到tf时刻性能恢复到一定水平后稳定(恢复到原来程度或降级状态)。
根据以上体系性能变化过程,可以定义体系结构弹性为体系性能的恢复与损耗的比值[18]:
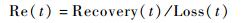 | (1) |
式中:Re(t)为体系结构的弹性;Recovery(t)和Loss(t)分别为体系性能恢复和损耗值。
也就是说,体系结构的弹性取决于不同时刻体系性能的变化程度,即
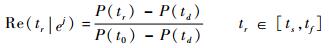 | (2) |
式中:Re(tr|ej)为体系遭受干扰后在tr时刻的弹性;P(t0)、P(td)和P(tr)分别为不同时刻体系的性能。
根据上述分析可知,当体系处于干扰状态时,其弹性Re(td)=0;同时,因为不确定恢复策略能否使体系性能恢复到初始状态,因此体系的弹性Re(tf)=1也是不确定的。
2 基于弹性的体系组件重要度分析 2.1 体系结构的网络描述 在对体系和体系结构进行研究时,针对体系结构网络化的特点,往往将其看作网络进行分析,可以表示为G=(V, E),V为体系所包含的系统或组件,也就是网络中的节点,E为体系中系统或组件的连接关系,也就是网络中的边。体系中每个组件的性能变化都会影响整个体系的性能,当体系遭受干扰事件时,体系中所有组件的性能可用向量表示为
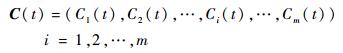 | (3) |
式中:Ci(t)为第i个组件的性能。
体系的性能并非体系中各个组件性能的简单加和,因此可以将体系的性能表示为P(C(t))。
2.2 体系性能变化过程 在不确定的环境中,体系的一个系统或组件遭受干扰事件ej时(如遭受敌对势力或外部环境的干扰和攻击),其状态受到破坏,此时该组件不能正常运作或发生故障,其性能也会受到一定的影响,而它的性能下降则会直接导致整个体系性能下降。考虑到实际情况,由于干扰事件的不确定性,体系中第i个组件性能的下降也是随机事件,则第i个组件性能下降的程度在区间[a, b]∈[0, 1]上的概率可以表示为
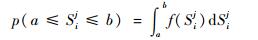 | (4) |
式中:Sij为干扰事件ej导致第i个组件的性能下降的程度,当Sij=1时则说明该组件完全崩溃;f(Sij)为组件性能下降程度的概率密度函数。
此时,第i个组件的性能为
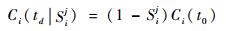 | (5) |
式中:Ci(t0)为第i个组件的初始性能;Ci(td|Sij)为第i个组件遭受干扰事件后td时刻的性能。
对于体系性能恢复过程,体系的一个系统或组件遭受干扰事件后,在恢复策略的作用下,其性能会慢慢恢复,而性能的恢复则会使整个体系性能恢复甚至达到初始状态。体系的恢复策略影响体系性能恢复的幅度和速度。体系中组件的恢复时间同样是一个随机变量,则第i个组件的性能在时刻tr∈[ts, tf]恢复的概率为
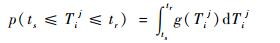 | (6) |
式中:Tij为弹性作用下第i个组件的恢复时间;g(Tij)为组件恢复时间的概率密度函数。
2.3 组件重要度分析建模 传统的基于可靠性的重要度分析研究的是系统中部件的故障对整个系统可靠性的影响,而当考虑体系中组件故障对体系弹性的影响时,其重要度分析则需要重点强调2个因素[9]:① 该组件的故障对整个体系性能的影响程度;② 在组件发生故障时其性能的恢复时间。因此,对于体系弹性来说,其组件重要度可以从体系性能恢复时间角度出发[18],表示为
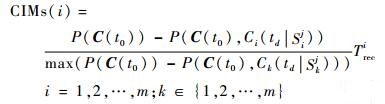 | (7) |
式中:P(C(t0))为体系未遭受干扰事件前的初始性能;P(C(t0), Ci(td|Sij))为第i个组件遭受干扰后体系的性能;max(P(C(t0))-P(C(t0), Ck(td|Skj)))为干扰事件发生时m个组件中故障对体系性能影响的最大值;Tirec为第i个组件恢复从而使整个体系性能恢复到恢复状态所需要的时间。
在式(7) 中,体系性能变化的比值可以理解为第i个组件性能变化对于整个体系性能恢复时间的加权贡献,反映了第i个组件性能对体系性能变化影响占最大可能影响的比例,它与体系性能的恢复时间的乘积即表示了从弹性角度来衡量的组件重要度。
2.4 组件重要度排序 由上述体系性能变化过程与重要度模型可知,组件性能下降的程度Sij和恢复时间Tij都是随机变量,因此,计算出的组件重要度也是服从一定概率分布的随机变量,这与传统的组件重要度分析方法(如故障树分析方法)中以故障概率来衡量组件的重要度有所区别,传统方法对于解决体系中的不确定性问题具有一定的局限性,因此需要从概率统计角度对体系中系统或组件进行重要度排序,以便直观找出对体系结构弹性或者体系性能恢复影响最大的组件,并对体系的恢复提供更准确的决策。
对于体系中组件重要度的不确定问题,本文采用科普兰评分法对其进行排序[9]。基于科普兰评分法的重要度排序是一种单参数排序方法,它不要求任何有关决策者偏好的信息,只需要两两比较体系中不同组件重要度的累积概率分布曲线,然后统计每个组件击败其他组件的次数,即可得到准确的组件重要度顺序。
在进行重要度排序时,首先检查体系中所有组件的重要度累积概率分布曲线,根据给定的百分比间隔Δq确定参数Ω=(1+Δq)/Δq,然后两两比较所有组件的重要度累积概率分布曲线,依次增加给定的百分比,在此基础上统计体系中各个组件的得分,即
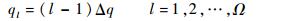 | (8) |
式中:ql为第l次比较时的百分比。
基于科普兰评分法的体系组件重要度排序模型可表示为
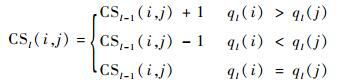 | (9) |
式中:CSl(i, j)为百分比ql时组件i对组件j的科普兰得分,且CS0(i, j)=0;ql(i)和ql(j)分别为百分比ql时对应的第i和第j个组件的重要度。
因此,体系中第i个组件的总科普兰得分为
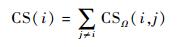 | (10) |
3 体系的恢复策略优化 优化体系结构弹性的关键就在于设计和选择合适的体系恢复策略以使体系性能得到恢复。一般情况下,干扰事件往往会影响体系的多个组件,在多组件故障的情况下,体系的恢复策略则取决于体系中故障组件的修复顺序。因此,在研究体系恢复策略时需要重点分析多个组件失效后不同的组件修复顺序对于体系性能恢复的影响。
假设干扰事件ej使体系的m个组件中n个组件发生故障,恢复策略从td时刻依次修复故障组件,直到tf时刻所有组件修复完成。在组件修复的过程中,考虑到组件修复顺序的多种组合,体系的恢复策略可表示为不同组件修复顺序的集合:
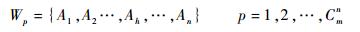 | (11) |
式中:Ah为修复顺序为h的故障组件。
在体系性能恢复过程中,恢复策略决定了体系性能恢复的速度和幅度。因此,为了度量不同恢复策略对体系性能恢复的影响,引入体系恢复效率这一指标:
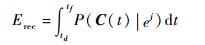 | (12) |
式中:P(C(t)|ej)为体系在任意时刻的性能。
体系恢复的效率衡量了体系恢复过程中,多个组件或系统成组修复给体系整体带来的规模效益,该指标既反映了体系性能恢复的时间,也综合体现了体系性能恢复的程度。选择体系恢复效率作为体系结构弹性的优化指标,其目的是找到合适的体系恢复策略,即体系受到干扰事件影响时,体系中故障组件的最优修复顺序,从而使体系的性能以最高的效率进行恢复,即求:
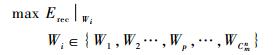 | (13) |
在体系性能恢复过程中,体系恢复策略的优化就是基于体系组件重要度分析的结果,对比不同恢复策略下体系的恢复效率,从而改进和优化体系结构弹性的过程。通过不同体系恢复策略的比较,可以选择出最优的恢复方案,从而使体系在遭受干扰事件时能够快速和有效的恢复性能。
4 案例应用 随着近年来面向服务架构的兴起,原来由一个系统就可以完成的业务流程,现在则要通过多系统的交互来实现,因此,系统之间的数据传输也成为衡量体系性能的一个重要的标准。本文以图 2所示拓扑结构的体系[18]中的数据传输为例来说明上述方法的应用。该体系包含2个端系统、5个中间件和12条数据传输的介质,12条数据传输介质都有各自的组件编号以及带宽(最大数据流速),考虑到端系统和中间件的容量足够大以至于并不影响数据传输,因此认为影响体系性能的组件只有12条数据传输的介质,体系的性能度量指标为单位时间的最大数据流通量,即体系网络单位时间的最大流。体系未遭遇干扰事件时单位时间的最大数据流量(即体系的性能)P=14。
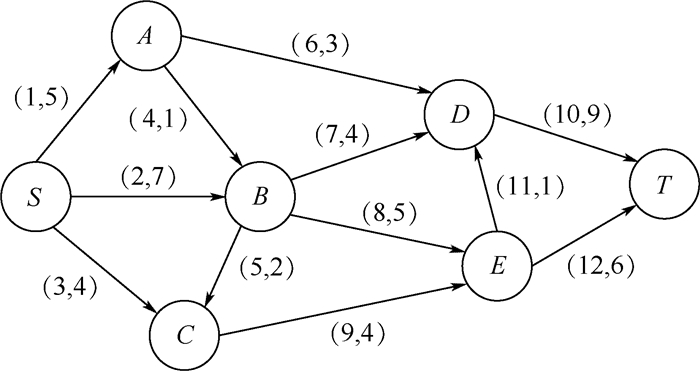 |
| 图 2 体系结构的拓扑[18] Fig. 2 Topology of SoS architecture[18] |
| 图选项 |
4.1 组件重要度计算 假设某时刻干扰事件e1使该体系中任意一个组件性能下降,其性能下降的程度和恢复时间都服从U(0, 1) 分布,通过仿真1 000次,即可得到1 000个该组件的组件重要度,统计组件重要度的范围并将其均匀分为20段,再统计不同分段内组件重要度的频率,从而可以绘制出各组件的组件重要度累积概率分布曲线,如图 3所示。
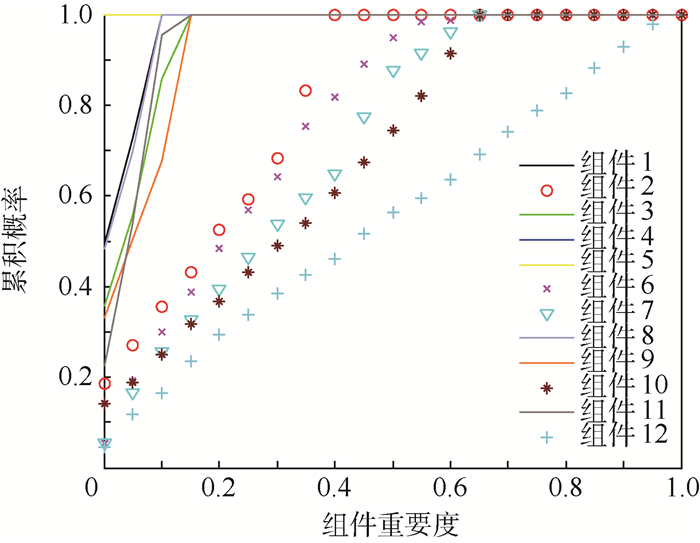 |
| 图 3 各组件的组件重要度累积概率分布曲线 Fig. 3 Cumulative probability distribution curves of component importance for each component |
| 图选项 |
图 3反映了体系中12个组件的重要度累积概率分布曲线,横轴为体系中的组件重要度,通过统计可得到不同重要度对应的概率值,纵轴为统计后的累积概率值。从图中可以看到,除组件2、12、10、7、6等5个组件外,其余7个组件的重要度曲线都集中在区间[0, 0.2]中,也就是说,这7个组件对体系的性能影响很小,其中,组件4、5这2个组件对体系的性能几乎无影响。再比较组件2、12、10、7、6等5个组件,组件2对体系单位时间最大数据流通量的影响最大,组件12次之,而组件10和组件7的重要度并不能准确判断。
因此,通过基于科普兰评分法的组件重要度排序方法可以得到图 4所示的12个组件的科普兰评分,为了结果的精确性,在仿真过程中,取Δq=0.01参与科普兰得分的计算。如图 4所示,组件7比组件10稍微重要一些,即组件7、10、6这3个组件的重要度依次降低,因此可以得出体系中组件的重要度顺序为2>12>7>10>6>11>9>3>1>8>4>5;又从图 2可知,组件2、7、10这3个组件分别连接2个端系统(收发数据,其重要性不做参考)和B、D这2个中间件,这也间接说明B、D这2个中间件的重要性。
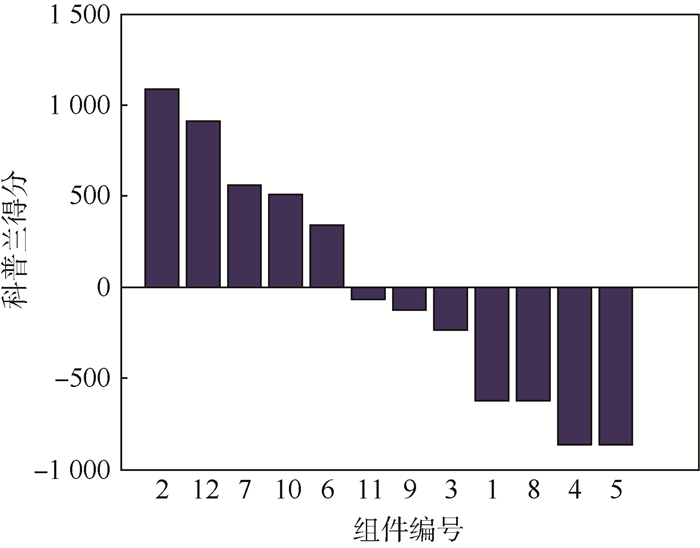 |
| 图 4 各组件的科普兰评分 Fig. 4 Copeland score for each component |
| 图选项 |
4.2 恢复策略的优化分析 在进行优化分析时,假设干扰事件使该体系任意5个组件故障,故障后立刻依次修复故障的组件,且修复所需的时间相同。
优化体系结构弹性的目的是找到故障组件的最优修复顺序,也就是最优的组件重要度排序。由于12个组件有12!种修复顺序,5个组件故障也有C125种可能的故障情况,因此,为了减少仿真的数据量,根据4.1节组件重要度分析将12个组件分为3级,分别为L1={2, 12, 7, 10, 6},L2={11, 9, 3, 1, 8},L3={4, 5},通过改变每一级中组件的修复顺序来计算最大的体系性能恢复效率;同时,在每次修复完成后,统计一次体系单位时间最大数据流通量的概率分布,并求其期望。
由于第3级2个组件对体系性能恢复基本没有影响,因此在仿真实现过程中不作分析。仿真共产生240组数据,对应的第1级和第2级分别有120组修复顺序,对其分别进行编号,将仿真结果与优化前的重要度排序结果进行对比,得出最终结论。
图 5为改变第1级和第2级组件的修复顺序体系性能恢复的曲线。其中,编号109是按照优化前的组件修复顺序进行修复。图 5(a)中,相比于按照优化前的组件修复顺序进行修复,按照编号99、45、111、96的修复顺序,体系性能恢复的能力都更强,其中采用编号99和45的修复顺序其体系恢复曲线基本相同,编号111和96也很接近,但次于编号99和45,编号109最差;而图 5(b)中,按照编号25、27、33、31的修复顺序,体系性能恢复的效率明显高于按照优化前的组件修复顺序进行修复,这4种修复顺序的体系性能恢复曲线也基本相同。
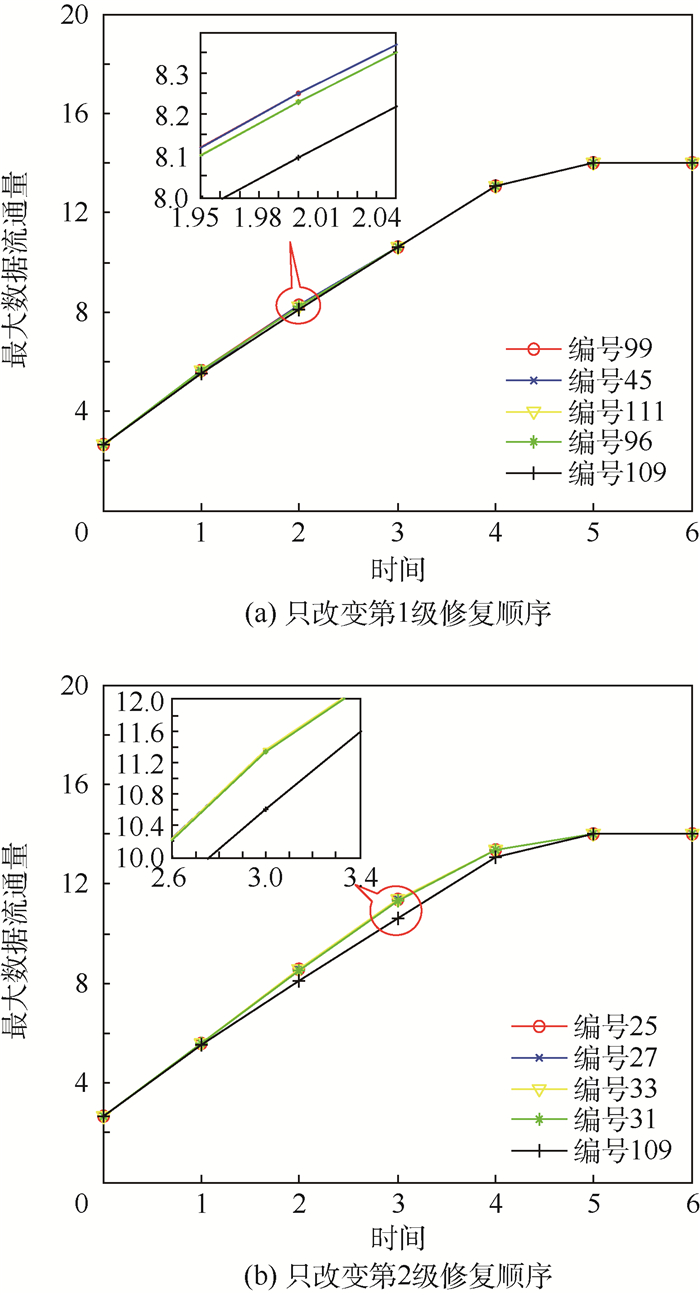 |
| 图 5 体系性能恢复曲线 Fig. 5 Performance recovery curves of SoS |
| 图选项 |
表 1和表 2分别为在改变第1级修复顺序和第2级修复顺序的情况下,体系性能恢复的具体细节。从表 1中可以明显看出,编号99的体系恢复效率高于45,编号111高于编号96,也就是说,对于第1级5个组件,最佳的修复顺序是编号99,即其重要度顺序为2>10>12>7>6。
表 1 体系性能恢复详情(改变第1级修复顺序) Table 1 Performance recovery details of SoS (Change the priority of repair at the first level)
| 编号 | 重要度排序/修复顺序 | 体系恢复效率 | 优化的比率/% |
| 99 | 2>10>12>7>6 | 1.350 3 | 1.95 |
| 45 | 10>2>12>7>6 | 1.348 8 | 1.83 |
| 111 | 2>12>10>7>6 | 1.348 6 | 1.82 |
| 96 | 12>2>10>7>6 | 1.347 7 | 1.75 |
| 109 | 2>12>7>10>6 | 1.324 5 |
表选项
表 2 体系性能恢复详情(改变第2级修复顺序) Table 2 Performance recovery details of SoS (Change the priority of repair at the second level)
| 编号 | 重要度排序/修复顺序 | 体系恢复效率 | 优化的比率/% |
| 25 | 1>8>3>9>11 | 1.488 8 | 12.40 |
| 27 | 1>8>9>3>11 | 1.488 8 | 12.40 |
| 33 | 1>3>9>8>11 | 1.486 6 | 12.24 |
| 31 | 1>3>8>9>11 | 1.481 6 | 11.86 |
| 109 | 11>9>3>1>8 | 1.324 5 |
表选项
表 2中,编号25和编号27的体系恢复效率相同,编号33高于编号31,则对第2级5个组件来说,最佳的修复顺序是编号25和编号27,其组件重要度顺序为1>8>3>9>11和1>8>9>3>11。综合第1级和第2级的最佳修复顺序可知,优化后的组件重要度排序为2>10>12>7>6>1>8>3>9>11>4>5或>2>10>12>7>6>1>8>9>3>11>4>5。
为了验证上述分析,本文最后对比3种不同恢复策略下体系性能恢复曲线,从而得出结论。恢复策略1为按照科普兰得分的组件重要度排序进行修复;恢复策略2为按照体系恢复效率最大的组件修复顺序进行修复;恢复策略3为按照组件编号进行修复。
图 6给出了按照不同恢复策略对组件进行修复时体系性能恢复曲线对比。根据对比结果可以看出,在体系性能恢复的任意时刻,无论是按照优化前还是优化后的恢复策略进行组件修复,体系结构的弹性都高于按照组件编号进行修复的体系结构的弹性,恢复策略优化后体系结构的弹性也大于优化前;按照组件编号修复故障组件时,体系性能恢复的效率为0.550 8,按照优化前组件重要度修复故障组件时,体系性能恢复效率为1.324 5,而优化后体系性能恢复效率为1.518 4,比优化前提高了14.64%;此外,优化后的组件重要度顺序与优化前的组件重要度顺序相差较大,说明优化前的组件重要度分析方法对于重要度高的组件,其分析准确性较高,重要度低的则效果相对较差;同时,也能看出维修顺序对体系恢复效率和体系弹性有很大影响,从而说明恢复策略对体系结构弹性和组件重要度分析的重要性。
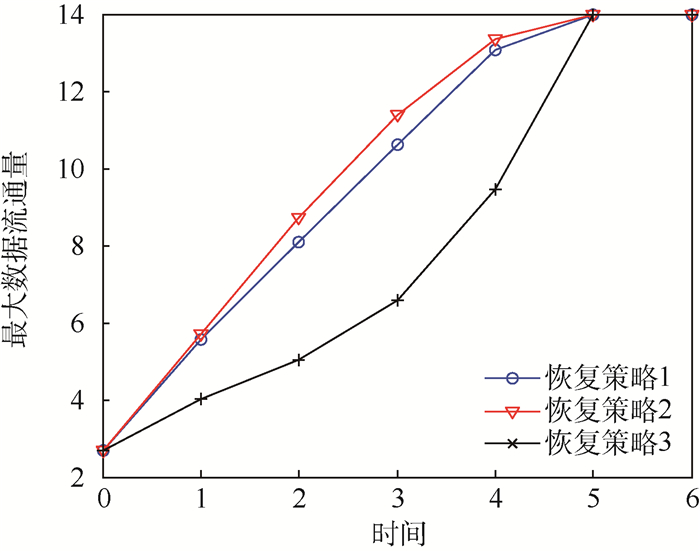 |
| 图 6 体系性能恢复曲线对比 Fig. 6 Comparison of performance recovery curves of SoS |
| 图选项 |
5 结论 体系结构的弹性分析是一个新的研究领域,本文在综合分析体系及弹性理论的基础上,提出一种基于弹性的体系结构评价方法,并对其进行优化。
1) 体系结构弹性概念的提出更为全面地考虑了体系性能损耗与恢复过程,为分析和评价不同类型的体系提供了新的思路。
2) 体系结构弹性建模与仿真工作,定量地分析了单个组成系统对于体系整体的影响,有助于体系的保障和维护。
3) 弹性优化指标和修复策略的改进,提高了系统或组件重要度分析的准确性,优化了体系结构弹性及体系性能恢复的能力。
不过,本文方法仍然有不足之处。在进行恢复策略研究时只是从体系拓扑结构的角度出发,因此适用性较为局限,下一步将从体系任务流程的角度出发,考虑任务重组对于体系弹性的影响。
参考文献
| [1] | 游光荣, 初军田, 吕少卿, 等. 关于武器装备体系研究[J].军事运筹与系统工程, 2010, 24(24): 15–22. YOU G R, CHU J T, LV S Q, et al. Study on weapon equipment system-of-systems[J].Military Operations Research and Systems Engineering, 2010, 24(24): 15–22.(in Chinese) |
| [2] | 潘星, 黄元星, 尹宝石. 基于功能和联接的装备体系结构[J].系统工程与电子技术, 2012, 34(10): 2054–2057. PAN X, HUANG Y X, YIN B S. Equipment system-of-systems architecture based on functionality and connectivity[J].Systems Engineering and Electronics, 2012, 34(10): 2054–2057.(in Chinese) |
| [3] | LIU H, TIAN Y L, GAO Y, et al. System of systems oriented flight vehicle conceptual design:Perspectives and progresses[J].Chinese Journal of Aeronautics, 2015, 28(3): 617–635.DOI:10.1016/j.cja.2015.04.017 |
| [4] | 王华, 赵英俊, 钟季龙. 装备体系结构的复杂网络混合模型建模[J].火力与指挥控制, 2015, 40(8): 70–73. WANG H, ZHAO Y J, ZHONG J L. Hybrid model of complex networks of equipment system-of-systems[J].Fire Control and Command Control, 2015, 40(8): 70–73.(in Chinese) |
| [5] | DELAURENTIES D.Understanding transportation as a system-of-systems design problem[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2005:1-14. |
| [6] | DAN D L, CALLAWAY R K. A system-of-systems perspective for future public policy decisions[J].Review of Policy Research, 2004, 21(6): 829–837.DOI:10.1111/ropr.2004.21.issue-6 |
| [7] | NAHAVANDI S, CREIGHTON D, LE V T, et al.Future integrated factories:A system of systems engineering perspective[M]//FATHI M. Integrated systems:Innovations and applications. Berlin:Springer, 2015:147-161. |
| [8] | UDAY P, MARAIS K B. Resilience-based system importance measures for system-of-systems[J].Procedia Computer Science, 2014, 28: 257–264.DOI:10.1016/j.procs.2014.03.033 |
| [9] | FANG Y P, PEDRONI N, ZIO E. Resilience-based component importance measures for critical infrastructure network systems[J].IEEE Transactions on Reliability, 2016, 65(2): 502–512.DOI:10.1109/TR.2016.2521761 |
| [10] | DESSAVRE D G, RAMIREZ-MARQUEZ J E, BARKER K. Multidimensional approach to complex system resilience analysis[J].Reliability Engineering and System Safety, 2015, 149: 34–43. |
| [11] | ZOBEL C W, KHANSA L. Characterizing multi-event disaster resilience[J].Computers and Operations Research, 2014, 42: 83–94.DOI:10.1016/j.cor.2011.09.024 |
| [12] | FATURECHI R, LEVENBERG E, MILLER-HOOKS E. Evaluating and optimizing resilience of airport pavement networks[J].Computers and Operations Research, 2014, 43: 335–348.DOI:10.1016/j.cor.2013.10.009 |
| [13] | OMER M, MOSTASHARI A, LINDEMANN U. Resilience analysis of soft infrastructure systems[J].Procedia Computer Science, 2014, 28: 873–882.DOI:10.1016/j.procs.2014.03.104 |
| [14] | JANIC M. Modelling the resilience, friability and costs of an air transport network affected by a large-scale disruptive event[J].Transportation Research Part A:Policy & Practice, 2015, 71: 1–16. |
| [15] | YOUN B D, HU C, WANG P, et al. Resilience-driven system design of complex engineered systems[J].Journal of Mechanical Design, 2011, 133(10): 1179–1188. |
| [16] | CARDOSO S R, BARBOSA-POVOAS A P F D, RELVAS S, et al. Resilience assessment of supply chains under different types of disruption[J].Computer Aided Chemical Engineering, 2014, 34: 759–764.DOI:10.1016/B978-0-444-63433-7.50111-5 |
| [17] | UDAY P, MARAIS K. Exploiting stand-in redundancy to improve resilience in a system-of-systems (SoS)[J].Procedia Computer Science, 2013, 16(4): 532–541. |
| [18] | BARKER K, RAMIREZ-MARQUEZ J E, ROCCO C M. Resilience-based network component importance measures[J].Reliability Engineering and System Safety, 2013, 117(2): 89–97. |
