目前,研究者们对于单质的溅射研究比较透彻,做了很多实验和理论研究。Sigmund[1]对大量的实验数据作了总结,并在Linhard和Thompson等的研究基础上,根据迁移理论给出了用分析法处理溅射现象的理论描述。同时,通过解线性化的Boltzmann传输方程分析得到了计算单质的溅射率公式,适用于不同入射离子在不同能量下轰击各种单质靶材的溅射率计算。目前,基于解Boltzmann传输方程的Sigmund溅射理论已经是实验研究的参考标准,被广泛地使用。
但是,Sigmund溅射理论无法直接应用于航天器的羽流溅射污染。第一,Sigmund溅射理论只能用于单元素靶材的溅射率计算,对于化合物的溅射并未涉及;第二,理论中的模型仅仅适用于keV以上的入射离子能量范围,对于低能离子的溅射计算值与实验偏差较大。而航天器上有很多十分重要的化合物材料,比如SiO2,作为太阳能帆板和相机视窗的材料之一,对于航天任务至关重要。而且,目前在轨的电推力器羽流中仍有大量低能离子溅射现象的存在。
相对单质溅射来说,对于化合物的溅射研究发展较晚,其理论研究也较少[2]。目前关于化合物溅射的理论模型大多都是研究者根据Sigmund溅射理论推导出的一些半经验性质的理论模型。Boyd和Falk[3]分析总结了2种关于低能离子轰击SiO2的理论模型,Seah和Nunney[4]也提出了二元化合物的溅射模型。本文主要根据这些溅射模型对低能离子轰击SiO2的溅射率进行研究,并利用等效原子法对Seah模型进行了改进。根据已有的Ar+和Xe+轰击SiO2的实验数据,对所有模型进行对比分析,得出不同模型的拟合精度,从而为Ar+和Xe+轰击SiO2的溅射率计算提供更为精确的理论依据。
1 溅射模型 1.1 溅射率 目前的溅射机理研究认为固体靶材表面的溅射其实是入射离子和靶材表面的原子发生一系列的级联碰撞导致的。一个入射离子通过弹性碰撞将能量转移给靶材表面的原子核,倘若转移的这部分能量高于原子的晶格束缚能,靶原子就会发生反冲,形成具有较高能量的初级反冲原子,初级反冲原子再与其他靶材原子发生级联碰撞将能量转移给其他靶材原子。如果转移给表面层靶原子的能量使表面层的靶原子具有指向靶材表面法向外的动量,并且靶原子的能量高于靶材的表面束缚能,那么表面层的靶原子就会被溅射出去。
可以发现,溅射过程与入射离子的能量,角度和离子种类等都有很大的关系。为了对溅射过程进行定量描述,研究者们定义了溅射率,即每个入射离子使靶材表面溅射出原子的平均数,其表达式为
 |
式中:Y为溅射率,单位为atoms/ion。在实验和理论研究的过程中,研究者也都是围绕溅射率,对影响溅射的不同因素展开研究的。
1.2 Pencil模型 Bohdansky等[5]在研究单质元素的溅射率过程中,搜集了大量的实验数据,发现若将法向溅射率表达成入射离子能量的函数,绘制成图,并将横纵坐标都按照对数形式分布,则不同离子对不同单质元素的法向溅射率分布具有相似的形式。若将这些曲线归一化,那么在低能区域(大约2 keV以内),这些曲线基本重合。同时,Kelly和Lam[6]对于多种氧化物的溅射率进行了研究,并给出了部分元素以及对应氧化物的溅射率比值。
由于Pencil等[7]在研究SiO2的溅射率时并没有对应的Xe对SiO2的低能溅射率实验数据,于是,Pencil结合了上述研究者的成果,先通过实验数据给出单原子硅的溅射率拟合公式,再乘以相应系数,得出了Xe对SiO2的离子法向轰击单质的溅射率的半经验公式:
 | (1) |
式中:E为入射离子能量,eV;a为SiO2与单原子硅的溅射率比值;S0和S1为通过单原子硅的溅射数据得到的拟合系数。
根据Yamamura和Tawara[8]采集到的大量离子法向轰击单元素硅靶材的溅射数据,以及Rosenberg和Wehner[9]通过实验得到的Xe+的溅射率数据,Pencil给出了式(1) 中的拟合系数如下:a=0.57,S0=0.183 97,S1=92.125。其中,S1的物理意义可以理解为溅射阈值,即当能量低于S1不发生溅射,从式(1) 中也可以看出,当E < S1时,公式无实数解。对于不同材料的化合物,拟合参数需要根据对应的大量实验数据给出。
1.3 Bach模型 Bach[10]提供了一种法向轰击SiO2的计算模型,在Bach模型中,Y为
 | (2) |
式中:K=4.2 nm-2;ci为原子分数;αi为与入射离子和靶材元素相关的系数;Sni为核阻止截面,计算公式由式(3) 给出;Ua为原子化能;Z为分子的原子数目。
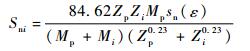 | (3) |
其中:Zp为入射离子的原子序数;Zi为靶材元素i的原子序数;Mp为入射离子的摩尔质量;Mi为靶材元素i的摩尔质量;sn(ε)为核阻止截面的中间系数。文献[10]给出了αi和sn(ε)的计算公式。对于SiO2来说,Ua=18.8 eV,Z=3。
在Bach模型中,并未考虑溅射阈值的存在,所以,在低能离子轰击时,无法判断模型的有效范围,即没有给出当入射离子能量低于何值时,计算值应当舍去,而取溅射率为零。
1.4 Seah模型 Seah和Nunney[4]在已有的单质溅射率公式基础上进一步研究,结合化合物溅射实验数据,给出了化合物溅射的相关模型。
首先,根据Sigmund溅射理论得到离子法向轰击单质的溅射率Y的公式为
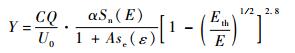 | (4) |
式中:C=4.2 nm-2;U0为原子的表面键能,等于原子的升华能[11];A=0.35U0;Eth为溅射阈值;Sn(E)为核阻止截面,eV·(0.1 nm)/atom,表达式如式(5) 所示;se(ε)为电子阻止截面,如式(6) 所示。
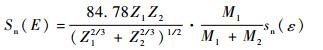 | (5) |
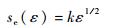 | (6) |
其中:Z1和M1分别为入射离子的原子序数和摩尔质量;Z2和M2分别为靶材元素的原子序数和摩尔质量;k、ε和sn(ε)的具体表达形式可以查阅文献[4]。
Seah和Nunney[4]参考了Matsunami等[12]关于α和Eth的计算方法,给出如下表达式:
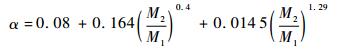 | (7) |
 | (8) |
Seah[13]同时对于Q也提出了相应的计算公式,如下:
 | (9) |
式中:r为平均原子间距,即原子半径,可以通过式(10) 计算得出,单位为nm;系数a、b、c、d、e、f的计算方法可以查阅文献[13]。对于Ar+和Xe+,式(9) 中的相关系数参见表 1。
表 1 Seah模型中计算Q的相关系数 Table 1 Correlation coefficients for calculation of Q in Seah model
| 离子 | a | b | c | d | e | f |
| Ar+ | 0.020 6 | 15.483 | 19.83 | 0.022 1 | 16 | 50 |
| Xe+ | 0.029 6 | 9.729 | 29.52 | 0.018 8 | 30 | 50 |
表选项
 | (10) |
其中:ρ为溅射靶材的密度,kg/m3;Na为阿伏伽德罗常数。
在此理论基础上,Seah和Nunney[4]研究发现化合物的溅射率可以由不同组分元素的溅射率线性组合得到。对于上述模型中的主要参数,先利用化合物的组分元素分别单独求出,再利用化合物中组分元素的原子分数对这些参数进行线性叠加,最后代入式(4) 中,求出化合物的溅射率。
以二元化合物为例,假设化合物的组分为A和B的2种元素,XA和XB分别是化合物中组分A和B的原子分数,ZA和ZB分别是A和B的原子序数,MA和MB分别是A和B的原子质量,rA和rB分别是A和B的原子半径。
首先,将式(5)~式(8) 中的Z2、M2、r,分别用A和B 2种元素对应的参数代替,得出主要参数,这些参数包括α、Sn(E)、ε、Eth。然后,利用XA和XB分别与A和B对应参数相乘求和,得出化合物的溅射参数。最后,代入式(4) 中即可求出对应化合物的溅射率。
以参数α为例,用MA和MB分别代替式(7) 中的M2,可得αA和αB,继续求解α=XAαA+XBαB,最后代入式(4) 即可。
但是,在上述模型的溅射参数中,化合物的平均原子间距r仍需要根据化合物的密度计算求得,不是通过线性叠加。关于参数Q的计算,则是通过将式(9) 中的M2替换成MA和MB,得到QArA3和QBrB3,再利用Qr3=XA(QArA3)+XB(QBrB3),代入实际化合物的r计算得出。
此外,Seah和Nunney[4]对于U0的计算方法也做出了修正。由于化合物形成不是单纯的原子组合,考虑到化合反应中放热,因此加入了混合热HAB,来计算U0,公式如下:
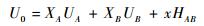 | (11) |
式中:UA和UB分别为组分A和B的升华能,即硅(Si)和氧(O)的升华能;HAB为化合物的混合热;x为更好地拟合数据而增加的系数,0≤x≤1。
对于SiO2来说,UA=4.7,UB=2,HAB=3.12,单位均为eV/atom。
由于上述参数x的存在,实际上根据Seah模型计算出来的不同能量下的溅射率是一个区间,对于x的选择只能通过拟合数据与实验值的比对确定。当x从0到1变化时,溅射率的计算值相应地越来越小,以Ar+轰击SiO2为例,代入相关参数,分别取x=0,0.25,0.5,1,得出溅射率变化如图 1所示,选取Xe+轰击SiO2也具有相同的趋势。
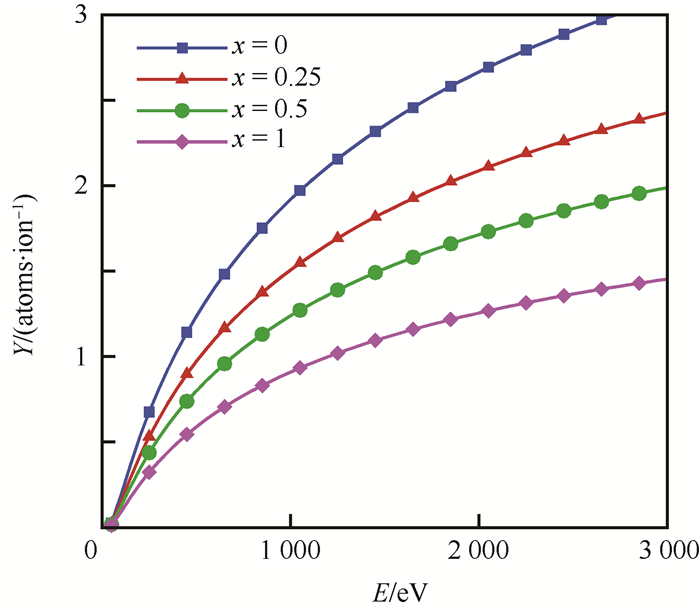 |
| 图 1 Seah模型中当x=0, 0.25, 0.5, 1时溅射率变化 Fig. 1 Variation of sputtering yields when x=0, 0.25, 0.5, 1 in Seah model |
| 图选项 |
1.5 对Seah模型的改进 本文关于Seah模型的改进,仍然以Sigmund的单质溅射模型为基础,在对化合物溅射的应用过程中,采用新的方法计算化合物的溅射参数。
首先,关于Eth的计算方法,本文拟采用Yamamura[14]提出的计算公式:
 | (12) |
 | (13) |
其次,对于模型中其他溅射参数将不采用组分元素的线性叠加的方式,而是参考Malherbe[15]提出的等效原子法进行计算。等效原子法就是不再将化合物看成不同组分的组合,而是将其当作一种新的单组分物质,新组分的原子序数Z2和摩尔质量M2根据式(14) 进行等效计算:
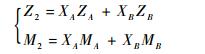 | (14) |
将等效之后的Z2和M2代入式(4)~式(10),即可求得SiO2的溅射率。
由于采用等效原子法,式(4) 中的U0将不再利用式(11) 进行计算,而是直接采用Si—O的键能,为4.73 eV。这样做的另一个好处就是同时规避了Seah模型中的不确定变量x,使模型预测值更加确定唯一。
需要说明的是,在之前3个模型中,得到的溅射率Y的计算单位都是units/ion。对于SiO2来说可以理解为molecules/ion,一个SiO2分子有3个原子,所以换算成定义单位atoms/ion的话,应将计算值乘以3倍。而本文改进的模型中,由于采用等效原子,所以,units/ion和atoms/ion的单位是等效的。
2 SiO2溅射模型的对比及分析 在早期实验中,研究者都会根据材料的质量、密度等性质将溅射量转化为原子数,从而与模型单位统一,进行对比。但是,在后来的实验中,研究者发现对于多元素组成的化合物来说,存在择优溅射的现象,即每种元素的溅射量并不同,这会导致表面成分会发生变化。以SiO2为例,溅射出来的粒子可能是Si、O或者SixOy,这样无法确定溅射出来的总原子数,用atoms/ion表示并不适宜。因此,采用新的溅射率单位mm3/C,即每库仑的入射离子溅射出的靶材体积。
为了将模型与实验数据进行对比,本文将单位进行统一。因此,需将atoms/ion转换成mm3/C,转换关系可以通过式(15) 得到:
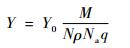 | (15) |
式中:Y的单位为mm3/C;Y0的单位为atoms/ion;M为摩尔质量;q为电子的电荷量;N为单个分子的原子数目。
Davidse[16]、Jorgenson[17]、Cantagrel[18]和Tu[19]等通过实验得到不同能量Ar+法向轰击SiO2的溅射率,文献[16-19]中的单位多为atoms/ion或者molecules/ion,需要通过式(15) 转换单位来进行比较;Seah[4]、Mogi[20]、Tartz[21]、Yalin[22-23]和Tondu[24]等通过实验得到Xe+法向轰击SiO2的溅射率,文献[4, 20-24]中的单位均为mm3/C。由于不同研究者采用的测量方法不同,造成实验数据也具有一定的离散性。
本文通过上述4种溅射模型同时计算得出Ar+和Xe+法向轰击SiO2的溅射数据,并与实验数据进行对比,如图 2和图 3中所示,分别展示了在垂直入射的条件下,不同能量的Ar+和Xe+轰击SiO2的溅射率的实验值和计算值对比。
 |
| 图 2 不同能量Ar+法向轰击SiO2的溅射率 Fig. 2 Energy dependence of sputtering yields of SiO2 for bombardment at normal incidence with Ar+ |
| 图选项 |
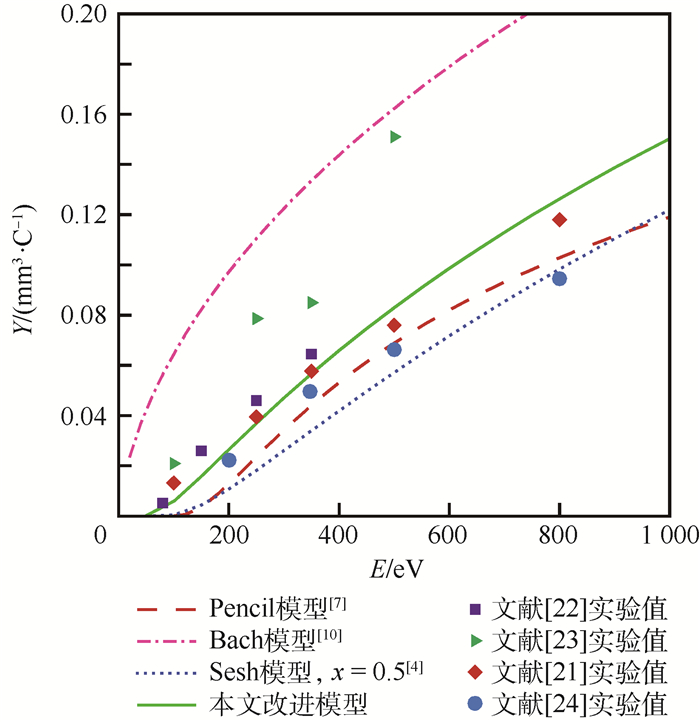 |
| 图 3 不同能量Xe+法向轰击SiO2的溅射率 Fig. 3 Energy dependence of sputtering yields of SiO2 for bombardment at normal incidence with Xe+ |
| 图选项 |
由图 2可以看出,在Ar+法向轰击SiO2的条件下,Bach模型的计算值要明显高于实验数据,另外,由于其模型中并未提及溅射阈值,模型仍有不足之处,有待改进。在其他3个模型中,可以发现3条曲线都十分接近。其中,Seah和Nunney[4]在利用模型计算后与实验值进行对比,发现当x取0的时候计算值比实验值偏高,需要整体乘以一个系数,或者改变x的取值,这里为了与Seah的实验数据吻合,x选取0.5,得出图 2中曲线。
为进一步比较分析,利用3种模型对实验数据进行拟合,分别得出均方根误差(RMSE)和拟合优度(R),如表 2所示。
表 2 不同模型对于Ar+法向轰击SiO2实验数据的拟合 Table 2 Fitting of experimental data of SiO2 bombarded at normal incidence by Ar+ using different models
| 拟合结果 | Pencil模型 | Seah模型 | 本文改进模型 |
| RMSE | 0.040 0 | 0.037 3 | 0.036 9 |
| R | 0.764 3 | 0.798 7 | 0.803 7 |
表选项
从表 2可以看出,本文改进模型的均方根误差最小,拟合优度最高。因此,本文的改进模型仍然稍优于其他2种模型。
在图 3中Xe+法向轰击SiO2的数据中,可以很明显看出Bach模型的计算值依然全部偏高于实验值,而Pencil模型的计算值则比大多数实验数据要低。对于Seah模型来说,由于在文献[4]中并未对Xe+法向轰击SiO2的实验数据进行分析,为考察其模型的通用性,仍取x的值为0.5,从图中可以发现此时Seah模型的计算值要明显偏低。
同样,利用3种模型对实验数据进行拟合,得出的回归参数如表 3所示。
表 3 不同模型对于Xe+法向轰击SiO2实验数据的拟合 Table 3 Fitting of experimental data of SiO2 bombarded at normal incidence by Xe+ using different models
| 拟合结果 | Pencil模型 | Seah模型 | 本文改进模型 |
| RMSE | 0.029 1 | 0.034 3 | 0.023 2 |
| R | 0.635 5 | 0.410 9 | 0.788 2 |
表选项
从表 3可以看出,本文改进模型无论是从均方根误差还是拟合优度来说,都优于其他模型,尤其是与Seah模型对比,拟合优度高出接近一倍。从Ar+和Xe+2组不同数据对比可以看出,Seah模型中x的取值对实验数据的依赖性较强。
由于在Ar+实验数据中,x选取了合适的值,使Seah模型与本文改进模型几乎一致,所以,本文同样探究在Xe+实验数据中是否也存在这样一个取值,为此,在Seah模型中选取不同的x取值,与本文改进模型对比,结果如图 4所示。
 |
| 图 4 不同x取值下的Seah模型与本文改进模型对比 Fig. 4 Contrast of advanced model and Seah model at different values of x |
| 图选项 |
从图 4中可以看出,无论x取值如何,Seah模型的计算值整体都偏低,尤其是在低能阶段。即使在x已经取为零,Seah模型处于最大值时,低于400 eV能量下的计算值仍低于改进模型,而此处实验数据基本都更接近改进后的模型。因此,对于Xe+法向轰击SiO2来说,本文的改进模型明显更优。
通过上述2组数据对比可以看出,已有模型对于不同离子法向入射SiO2溅射率的拟合程度具有差异性,而本文模型对于不同离子都可以与实验数据很好地吻合,而且对不同离子的拟合都优于已有3种模型。
3 结论 本文通过等效原子法改进了Seah模型,并结合已有实验数据,将其与Pencil[7]、Bach[10]和Seah[4]等提出的低能离子法向轰击SiO2的理论模型相比较。结果表明:
1) Pencil模型对不同离子轰击SiO2的实验值拟合程度较好,对于不同离子的适用性也不错,但是整体效果相比本文改进模型稍差一些。同时,由于Pencil模型为纯经验模型,其中的拟合参数随着不同溅射对象的不同而改变,对于其他化合物的溅射率计算需要大量对应的实验数据进行参数拟合。
2) Bach模型相对于Ar+和Xe+的实验数据都偏高,而且其模型溅射阈值为0,与实际溅射不符,说明Bach模型还存在问题,需要进一步完善。
3) Seah模型的计算值落在一个范围内,针对不同的实验数据,选取合适的变量值,可以获得较好的溅射率预测值,但是对于实验数据依赖性较大,针对不同离子轰击的适应性较差。
4) 本文针对Seah模型改进后得到的模型计算值与实验数据吻合得很好,且对于不同的离子轰击,计算结果相比于其他模型都是最优。采用等效原子法,消除了Seah模型中的变量,使计算结果确定,针对不同离子的适用性更强。因此,本文通过等效原子法改进的Seah模型可以更精确地计算Ar+和Xe+法向轰击SiO2的溅射率。
参考文献
| [1] | SIGMUND P. Theory of sputtering.I:Sputtering yield of amorphous and polycrystalline targets[J].Physical Review, 1969, 184(2): 383–416.DOI:10.1103/PhysRev.184.383 |
| [2] | 计京津. 稀薄等离子体羽流的溅射效应研究[D]. 上海: 上海交通大学, 2011: 3-9. JI J J.Study of rarefied plasma plume sputtering effect[D].Shanghai:Shanghai Jiao Tong University, 2011:3-9(in Chinese).https://wuxizazhi.cnki.net/lunwen-1011268095.html |
| [3] | BOYD I D, FALK M L.A review of spacecraft material sputtering by Hall thruster plumes:AIAA-2001-3353[R].Reston:AIAA, 2001. |
| [4] | SEAH M P, NUNNEY T S. Sputtering yields of compounds using argon ions[J].Journal of Physics D:Applied Physics, 2010, 43(25): 253001.DOI:10.1088/0022-3727/43/25/253001 |
| [5] | BOHDANSKY J, ROTH J, BAY H L. An analytical formula and important parameters for low-energy ion sputtering[J].Journal of Applied Physics, 1980, 51(5): 2861–2865.DOI:10.1063/1.327954 |
| [6] | KELLY R, LAM N Q. The sputtering of oxides.Part I:A survey of the experimental results[J].Radiation Effects, 1973, 19(1): 39–48.DOI:10.1080/00337577308232213 |
| [7] | PENCIL E J, RANDOLPH T, MANZELLA D H.End-of-life stationary plasma thruster far-field plume characterization:AIAA-1996-2709[R].Reston:AIAA, 1996. |
| [8] | YAMAMURA Y, TAWARA H. Energy dependence of ion-induced sputtering yields from monatomic solids at normal incidence[J].Atomic Data and Nuclear Data Tables, 1996, 62(2): 149–253.DOI:10.1006/adnd.1996.0005 |
| [9] | ROSENBERG D, WEHNER G K. Sputtering yields for low energy He+, Kr+, and Xe+ ion bombardment[J].Journal of Applied Physics, 1962, 33(5): 1842–1845.DOI:10.1063/1.1728843 |
| [10] | BACH H. Ion beam sputtering of silicate glasses and oxides[J].Journal of Non-Crystalline Solids, 1988, 102(1): 36–42. |
| [11] | SEAH M P, CLIFFORD C A, GREEN F M, et al. An accurate semi-empirical equation for sputtering yields.I:For argon ions[J].Surface and Interface Analysis, 2005, 37(5): 444–458.DOI:10.1002/(ISSN)1096-9918 |
| [12] | MATSUNAMI N, YAMAMURA Y, ITIKAWA Y, et al. Energy dependence of the ion-induced sputtering yields of monatomic solids[J].Atomic Data and Nuclear Data Tables, 1984, 31(1): 1–80.DOI:10.1016/0092-640X(84)90016-0 |
| [13] | SEAH M P. An accurate semi-empirical equation for sputtering yields.Ⅱ:For neon, argon and xenon ions[J].Nuclear Instruments and Methods in Physics Research Section B:Beam Interactions with Materials and Atoms, 2005, 229(3): 348–358. |
| [14] | YAMAMURA Y. Contribution of anisotropic velocity distribution of recoil atoms to sputtering yields and angular distributions of sputtered atoms[J].Radiation Effects, 1981, 55(1-2): 49–55.DOI:10.1080/00337578108225465 |
| [15] | MALHERBE J B. Sputtering of compound semiconductor surfaces.I.Ion-solid interactions and sputtering yields[J].Critical Reviews in Solid State and Material Sciences, 1994, 19(2): 55–127.DOI:10.1080/10408439408244588 |
| [16] | DAVIDSE P D, MAISSEL L I. Equivalent dc sputtering yields of insulators[J].Journal of Vacuum Science and Technology, 1967, 4(1): 33–36.DOI:10.1116/1.1492514 |
| [17] | JORGENSON G V, WEHNER G K. Sputtering studies of insulators by means of Langmuir probes[J].Journal of Applied Physics, 1965, 36(9): 2672–2674.DOI:10.1063/1.1714558 |
| [18] | CANTAGREL M, MARCHAL M. Argon ion etching in a reactive gas[J].Journal of Materials Science, 1973, 8(12): 1711–1716.DOI:10.1007/BF02403521 |
| [19] | TU Y Y, CHUANG T J, WINTERS H F. Chemical sputtering of fluorinated silicon[J].Physical Review B, 1981, 23(2): 823–835.DOI:10.1103/PhysRevB.23.823 |
| [20] | MOGI K, OGIWARA T, SUZUKI M. Sputter etching rate ratio of Si to SiO2 using Mesh-Replica method[J].Journal of Surface Analysis, 2002, 9(4): 514–523.DOI:10.1384/jsa.9.514 |
| [21] | TARTZ M, HEYN T, BUNDESMANN C, et al.Measuring sputter yields of ceramic materials[C]//Proceedings of the 31st International Electric Propulsion Conference.Fairview Park:ERPS, 2009:IEPC-2009-240. |
| [22] | YALIN A P, SURLA V, FARNELL C, et al.Sputtering studies of multi-component materials by weight loss and cavity ring-down spectroscopy:AIAA-2006-4338[R].Reston:AIAA, 2006.http://www.engr.colostate.edu/lpdl/publications.html |
| [23] | YALIN A P, RUBIN B, DOMINGUE S R, et al. Differential sputter yields of boron nitride, quartz, and kapton due to low energy Xe bombardment:AIAA-2007-5314[J].Reston:AIAA, 2007. |
| [24] | TONDU T, CHARDON J P, ZURBACH S.Sputtering yield of potential ceramics for Hall effect thruster discharge channel[C]//Proceedings of the 32nd International Electric Propulsion Conference.Fairview Park:ERPS, 2011:IEPC-2011-106. |
