目前,随机不确定性灵敏度分析方法已经发展得相对成熟,如非参数方法的指标[3-4]、基于方差的全局灵敏度指标[5-6]、矩独立的全局灵敏度指标[7-8],但同时考虑模糊和随机不确定性的灵敏度分析则相对研究较少。文献[9]通过将模糊变量在其每个隶属水平下近似处理为均匀分布的随机变量,建立了模糊随机混合不确定性灵敏度指标来分别度量模糊输入变量和随机输入变量对输出响应概率密度函数的影响程度。由于本质上并不能确定模糊变量在某个隶属水平下的取值规律,因此这种近似处理方式不甚合理。在同时包含随机不确定性和模糊不确定性结构系统中,模型输出将具有模糊性和随机性,Li等[10]通过有条件和无条件地输出响应的一阶、二阶概率矩的差异,建立了基于输出一阶、二阶概率矩的模糊输入变量和随机输入变量的灵敏度指标。但其仅考虑了模糊变量固定在其最大似然值处对输出响应的影响,并未对模糊变量在其整个可能取值范围内进行全局考虑。Greegar和Manohar[11]固定模糊变量于其名义值点处,然后通过求解有条件和无条件的输出特征之间的差异,建立混合输入不确定性全局灵敏度指标,同样对模糊变量没有进行考虑其全局的取值规律。在客观输入变量具有主观分布参数的全局灵敏度分析过程中,Li[12]和陈超[13]等通过固定模糊变量的隶属水平,从不同角度建立了主观分布参数的灵敏度指标。从直观上讲,这种固定方式反映了模糊变量的隶属水平对输出响应特征的影响,并不能完全代表该模糊变量整个取值特征对输出响应特征的重要性。
针对目前混合不确定性灵敏度研究存在的一些问题,本文结合模糊集合理论,从输出的可能性矩的角度出发,提出了混合输入不确定作用下的全局灵敏度新指标。不同于以往的模糊变量的固定方式,本文依据模糊变量的全局取值规律来固定模糊变量本身。因此,由于固定某个模糊输入变量而造成的有条件输出响应特征和无条件输出响应特征的之间的差异应该为该模糊输入变量的函数,进而输出响应特征之间的差异本质上为一个模糊变量,对该模糊变量求可能性均值即可从全局角度考虑条件模糊输入变量对输出响应特征的重要性。本文还讨论了所提指标的一些数学性质并介绍了指标的求解步骤。为了减少计算成本,采用Kriging代理模型来提高计算效率。最后通过算例验证了本文所提方法的准确性和高效性。
1 模糊数可能性矩的定义 对于一个模糊数A,在某一隶属水平γ下,其取值范围为一个固定区间[a1(γ), a2(γ)],Christer和Robert[14]定义了模糊数的可能性期望与可能性方差,其形式分别为
 | (1) |
对于一个模糊数A,Saeidifar和Pasha[15]进一步定义模糊数高阶可能性中心矩为
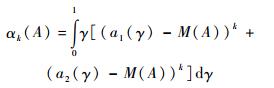 | (2) |
式中:k为可能性矩的阶次。类似于随机数,模糊数2阶中心矩即为可能性方差,3阶、4阶中心矩分别可以用来计算可能性偏度和可能性峰度。
2 混合输入对输出影响的定性分析 当结构系统的功能响应函数Y=g(XR)中只含有随机变量XR时,系统输出响应量Y只具有随机性,此时输出响应量的各阶概率矩均为确定的值。当结构系统的功能响应函数Y=g(XF)中只含有模糊变量XF时,系统输出响应量Y只具有模糊性,此时输出响应量的各阶可能性矩同样为确定的值。
而当结构或系统的输入变量X中同时含有随机变量和模糊变量时:假设结构中有n(n=nR+nF)个基本变量X=(X1, X2, …, Xn),其中前nR个变量XR=(X1, X2, …, XnR)为相互独立的随机变量,其概率密度函数(PDF)分别为fXRi(xRi)(i=1, 2, …, nR);后nF个变量XF=(XnR+1, XnR+2, …, Xn)为相互独立的模糊性变量,其隶属函数分别为μXFj(xFj)(j=nR+1, nR+2, …, nR+nF)。由于结构的响应量函数g(XR, XF)为模糊变量XF和随机变量XR的函数,此时输出响应量Y将同时具有模糊性和随机性。
对于模型Y=g(XR, XF),输出响应量的概率矩可表示为
 | (3) |
式中:f(XR)(xR)为XR的联合概率密度函数;αkY为Y的k(k>2) 阶中心距,则此时输出响应量的各阶概率矩均为由隶属函数表示的模糊变量。
对于模型Y=g(XR, XF),当随机向量XR任取某一实现值xR*时,输出响应为其余nF个模糊变量的函数,此时输出响应为一模糊变量,可得输出响应的可能性矩为一确定的值。因此,输出响应Y的可能性矩为XR的函数,即输出响应量的各阶可能性矩为由概率密度函数描述的随机变量。
从上述分析可以看出,对于模糊随机混合不确定性灵敏度分析,可以从输出响应的概率矩和可能性矩两方面来考虑。本文从输出响应的可能性矩角度,以输出响应的可能性期望为例,讨论模糊和随机输入变量对输出响应量可能性矩的影响。
3 混合不确定性下的灵敏度指标 3.1 随机输入变量灵敏度指标 对于模型Y=g(XR, XF),关于输出响应求可能性期望M=M(Y),则所得响应的可能性期望值为一个随机变量,其PDF记为fM(m),可能性期望的随机性是由模型中随机输入变量引起的。当固定某个随机输入变量XRi时,输出响应的随机性会发生变化,由于模型中模糊变量和随机变量的相互作用,输出响应的模糊性同时也会变化。因此,输出响应的可能性期望的PDF会发生变化。此时输出响应可能性期望的条件PDF记为fM|XRi(m)。fM|XRi(m)与fM(m)之间的面积差异大小可以衡量变量XRi对输出响应可能性期望PDF的影响。
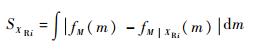 | (4) |
此时SXRi为XRi的函数,为一个随机变量。对SXRi求平均,并进行归一化处理,可得到随机输入变量XRi的灵敏度指标δXRi为
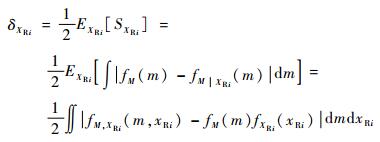 | (5) |
δXRi进一步可写为Copula函数的形式,来表达输出响应Y的可能性期望与XRi的相关性大小。
 | (6) |
式中:c(u, vi)为(M, XRi)的Copula密度函数。
根据上述单个随机输入变量灵敏度指标δXRi的定义可给出一组随机输入变量(XRi1, XRi2, …, XRim)(1≤im≤nR m>1, ij(j=1, 2, …, m)∈(1, 2, …, nR))的灵敏度指标δXRi1, XRi2, …, XRim:
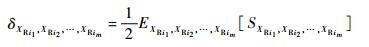 | (7) |
式中:
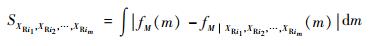 |
3.2 模糊输入变量灵敏度指标 对于模型Y=g(XR, XF),响应的可能性期望为一个随机变量,其PDF记为fM(m)。固定某个模糊变量XFi时,输出响应的模糊性会发生变化,同时由于模型中模糊变量和随机变量的相互作用,输出响应的随机性因此也会变化。所以,固定某个模糊变量XFi后,有条件输出响应可能性期望的PDF与无条件输出响应可能性期望的PDF会有差异,输出响应的条件PDF记为fM|XFi(m)。fM|XFi(m)与fM(m)之间的面积差异大小SXFi可以衡量变量XFi对输出响应可能性期望的PDF的影响。
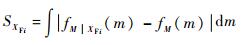 | (8) |
由于XFi为模糊变量,此时SXFi为XFi的函数,所以SXFi为一个模糊变量。关于SXFi求可能性期望,并进行归一化处理,则可得模糊输入变量XFi的灵敏度指标δXFi为
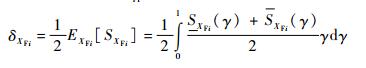 | (9) |
式中:SXFi(γ)和SXFi(γ)分别表示在隶属水平γ下SXFi的和上界和下界。
根据上述单个模糊输入变量灵敏度指标δXFi的定义可给出一组模糊输入变量(XFi1, XFi2, …, XFim)(1≤im≤nF, m>1, ij(j=1, 2, …, m)∈(1, 2, …, nF))的灵敏度指标δXFi1, XFi2, …, XFim:
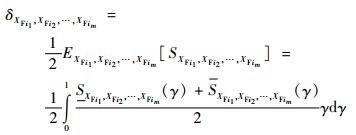 | (10) |
上述指标体系还可以根据需要扩展到输入变量对响应量可能性方差或更高阶可能性矩的影响上,进而满足不同的工程实际要求。
3.3 灵敏度指标的数学性质 以上所提灵敏度指标具有下列数学性质:
性质1????0≤δi<1。
证明????类似于Borgonovo[1]提出的矩独立指标,可知

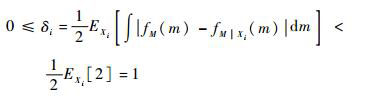 | (11) |
证毕
性质2????如果输入变量Xi独立于输出响应的可能性期望,则δi=0。
证明????如果输入变量独立于输出响应的可能性期望,则有条件和无条件的输出响应可能性期望的PDF重合,所以δi=0。????????????????????????????证毕
性质3????若δij=δi,则输入变量Xj独立于输出响应的可能性期望。
证明????若输出响应的可能性期望依赖于变量Xi,但独立于变量Xj,则fM|Xi, Xj(m)=fM|Xi(m)。所以:
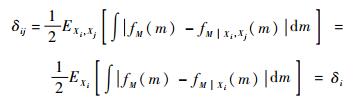 | (12) |
证毕
4 灵敏度指标的求解方法 4.1 灵敏度指标一般求解方法
4.1.1 随机输入变量灵敏度指标的求解方法 由上述分析可知,求解随机输入变量灵敏度指标步骤如下:
1) 将随机输入变量在其整个分布范围内抽样,通过不确定性传递和优化算法得到输出响应量隶属函数,求得输出响应的可能性期望,进而估计响应量可能性期望的无条件概率密度函数fM(m)。
2) 根据XRi的概率密度函数抽取其样本,将XRi固定在其中一个样本点(记为xRi*)处,其余的输入变量仍在整个分布范围内变化抽样,通过不确定性传递和优化算法得到此时响应量可能性期望的条件概率密度函数fM|XRi(m)。此时,便可以得到fM|XRi(m)和fM(m)在XRi=xRi*处的差异面积SXRi*。
3) 重复这个过程,最终得到SXRi的均值,进而得到δXRi的估计值。
4.1.2 模糊输入变量灵敏度指标的求解方法 由上述分析可知,求解模糊输入变量灵敏度指标步骤如下:
1) 将随机输入变量在其整个分布范围内抽样,通过不确定性传递和优化算法得到输出响应量的可能性期望,进而估计响应量可能性期望的无条件概率密度函数fM(m)。
2) 同样将随机输入变量在其整个分布范围内变化抽样。固定某个模糊输入变量XFi的隶属水平γ,根据XFi的隶属函数可得此时XFi∈[XFi(γ), XFi(γ)],XFi在区间[XFi(γ), XFi(γ)]内任取一实现值xFi*,可通过不确定性传递和优化算法求得输出响应的可能性期望的有条件概率密度函数fM|xFi*(m)。此时,便可以得到fM|XFi(m)和fM(m)在XFi=xFi*处的面积差异SXFi*,当XFi遍历区间[XFi(γ), XFi(γ)]时,便可得到SXFi的一个区间[SXFi(γ), SXFi(γ)]。
3) 遍历XFi的隶属水平,即可相应地得到SXFi的隶属函数,进而得到SXFi的可能性期望值和δXFi的估计值。
由上述分析可知,求解随机输入变量灵敏度指标时,需要双重循环抽样以及单层优化求解SXRi的均值。求解模糊输入变量的灵敏度指标时,需要单层抽样,但是需要双重优化来求解SXFi的均值。求解所提指标的一般方法计算量较大。为了提高计算效率,本文采用Kriging代理模型法来近似代理原功能函数,模型代理以后所有的计算过程不变,但可以大大减少计算成本,Kriging代理模型法详细步骤见4.2节。
4.2 Kriging代理模型法 Kriging代理模型法是一种具有很强全局近似能力的逼近技术,它借助某一点周围的已知信息的加权线性组合来估计该点的未知信息[16]。Kriging代理模型法可以用来逼近模型。
4.2.1 Kriging法中的抽样阶段 Kriging法对试验点的预测需要知道一系列观测点X(k)={X1(k),X2(k), …, Xn(k)}(k=1, 2, …, Nt,Nt为训练点的个数)(称为训练点(TP))的信息,其预测能力取决于训练点所携带的信息量。若所携带的信息量足够反映整个参数空间,那么预测结果将会较为准确。但达到足够的信息量需要大量的样本,这导致计算成本的大幅度增加。因此,训练点的选取对Kriging法的预测能力有至关重要的影响。
相比较于传统的蒙特卡罗随机抽样,拉丁超立方抽样[17]是一种多维分层抽样方法,它对样本数量较为节省,尤其是当输出结果能用一个线性函数很好地逼近的情况下。应用拉丁超立方抽样得到一组输入变量样本X(k)(k=1, 2, …, Nt)。根据函数关系Y=g(X)可计算得到训练点处的输出响应值:
 | (13) |
式中:YTP为训练点向量对应的输出响应值。
根据训练点和与之对应的输出响应的信息,Kriging代理模型法可以构造出g(X)近似模型。
4.2.2 Kriging法的基本理论 通常情况下,Kriging模型由线性回归部分和非参数随机部分组成[18-19]。描述如下:
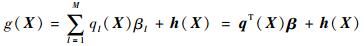 | (14) |
式中:β=[β1, β2, …, βM]T为回归系数;q(X)=[q1(X), q2(X), …, qM(X)]T为回归模型基函数;h(X)为高斯随机部分,服从N(0, σ2),且(Xi, Xj)的方差可定义如下:
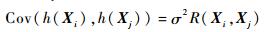 | (15) |
其中:R(Xi, Xj)为相关方程,对近似精确程度起决定性作用。Koehler和Owen[20]提供了若干可供选择的相关方程,其中高斯相关方程最为通用。
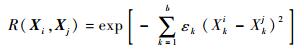 | (16) |
式中:εk为相关性参数;Xki和Xkj分别为向量Xi和Xj的第k个分量。相关方程反映了参数空间中2个点的相似程度。若点Xki和Xkj之间的距离很小,那么这2个点携带的信息就很相似,这表征了2个点的高相似度。因此,相关方程能更为有效地被用来收集试验点周围训练点的信息。
由于未知参数β和σ2依赖于相关性参数εk,根据最大似然估计理论[20],易得
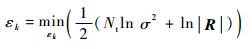 | (17) |
根据文献[20-21],未知参数β和σ2可估计如下:
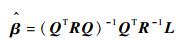 | (18) |
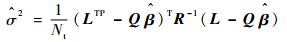 | (19) |
式中:
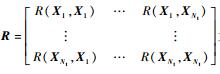
故对于试验点X,g(X)模型的最佳无偏估计为
 | (20) |
式中:r(X)=[R(X, X1), R(X, X2), …, R(X, XNt)]T为试验点与训练点之间的相关性向量。
式(20) 中的第2项是第1项的插值残留项,因此,输出响应统计特征能被精准地估计。尽管构建Kriging模型非常复杂,但其得到了广泛的应用,同时发展了DACE工具箱[21]。本文指标的求解就是基于此工具箱。
由上述分析可知,采用Kriging代理模型法需要Nt个训练点,因此,上述方法调用原始模型次数为Nt次。采用Kriging代理模型法可大大提高指标计算效率。
5 算例 本节通过一个数值算例和2个工程算例,分别通过一般方法和Kriging代理模型法计算上文所提指标,验证了所提方法的准确性和高效性。
算例1????考虑线性模型g(x)=2x1-3x2+x3+2x4,其中x1和x2为相互独立的正态随机变量,均值向量μ=(3, 4), 标准差向量σ=(1, 1)。x3和x4均为模糊变量,隶属函数分别为μX3(x3)=exp[-(x3-62)/2]和μX4(x4)=exp[-(x3-3)2/2]。
分别用一般方法和Kriging代理模型法计算关于输出响应的可能性期望的灵敏度指标,计算结果如表 1所示。
表 1 算例1各输入变量的灵敏度指标值 Table 1 Sensitivity index values of input variables in Example 1
| 随机变量 | 灵敏度指标值 | |
| 一般方法 | Kriging法 | |
| x1 | 0.211 3 | 0.211 3 |
| x2 | 0.408 7 | 0.408 7 |
| x3 | 0.048 2 | 0.048 2 |
| x4 | 0.094 7 | 0.094 8 |
表选项
从表 1计算结果可以看出,随机变量对输出可能性期望影响排序为x2>x1,模糊变量对输出可能性期望影响排序为x4>x3。应用Kriging代理模型计算结果与一般方法计算结果一致。一般方法计算量为108次,而应用Kriging代理模型计算量仅为100次,采用Kriging代理模型法极大地提高了计算效率。
算例2????如图 1所示的流体管道,根据管道的蓄水能力建立极限状态方程为[22]
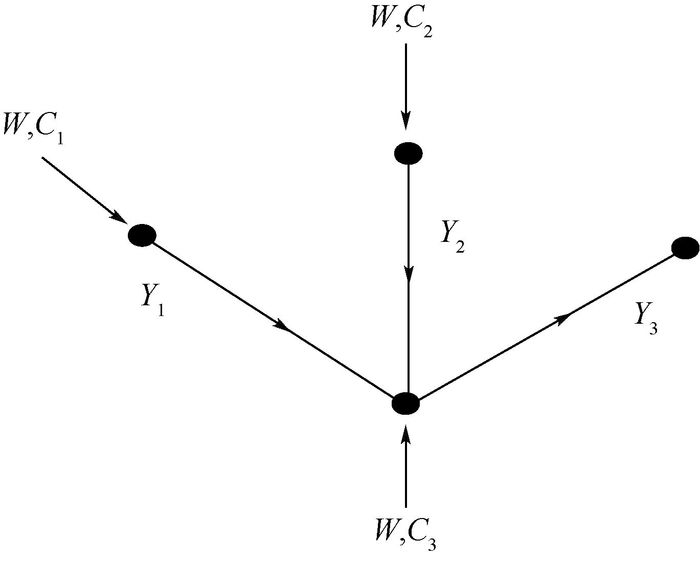 |
| 图 1 流体管道系统示意图 Fig. 1 Schematic diagram of a sewer pipe system |
| 图选项 |
 |
其中:各变量是描述管道性能的参数, 其中K=0.9。假设C1、C2和C3为模糊变量,隶属函数为μXi(xi)=exp[-(xi-c)2/2σ2],隶属函数的参数如表 2所示;Y(Y1,Y2,Y3)为与摩擦因子负相关的参数,W为与沉淀率正相关的参数,均值向量μ=(8.59, 7.01),标准差向量σ=(2, 0.862)。
表 2 算例2各模糊变量参数值 Table 2 Parameter values of fuzzy variables in Example 2
| 随机变量 | 模糊变量 | c | σ |
| x1 | C1 | 0.825 | 0.070 |
| x2 | C2 | 0.825 | 0.070 |
| x3 | C3 | 0.900 | 0.050 |
表选项
分别用一般方法和Kriging代理模型法计算关于输出的可能性期望的灵敏度指标,可得计算结果如表 3所示。
表 3 算例2各输入变量的灵敏度指标值 Table 3 Sensitivity index values of input variables in Example 2
| 参数 | 灵敏度指标值 | |
| 一般方法 | Kriging法 | |
| C1 | 0.004 9 | 0.004 9 |
| C2 | 0.004 9 | 0.004 9 |
| C3 | 0.004 3 | 0.004 3 |
| Y | 0.764 2 | 0.764 2 |
| W | 0.053 7 | 0.053 7 |
表选项
从表 3计算结果可以看出,随机变量对输出可能性期望影响排序为Y>W,模糊变量对输出可能性期望影响排序为C3>C1=C2。应用Kriging代理模型计算结果与一般方法计算结果一致。一般方法计算量为108次,而应用Kriging代理模型计算量仅为200次,采用Kriging代理模型法极大地提高了计算效率。
算例3????如图 2所示的屋架,屋架的上弦杆和其他压杆采用钢筋混凝土杆,下弦杆和其他拉杆采用钢杆。设屋架承受均布载荷q作用,将均布载荷q化成节点载荷后有P=ql/4。结构力学分析可得C点沿垂直地面方向的位移为ΔC=
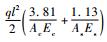
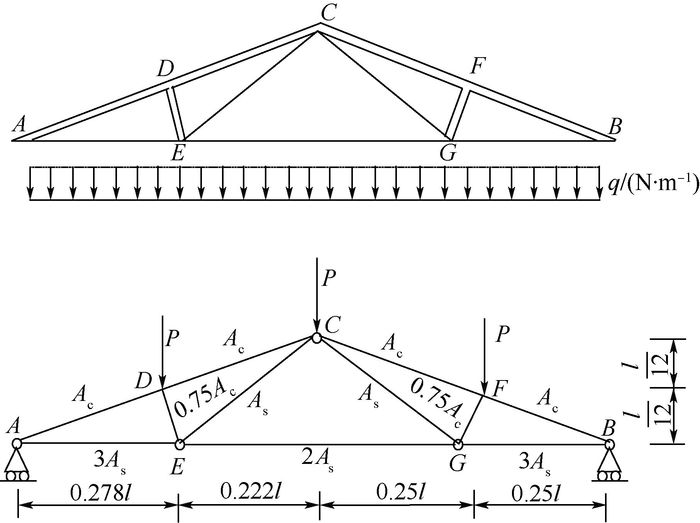 |
| 图 2 屋架结构的简单示意图 Fig. 2 Schematic diagram of a roof truss structure |
| 图选项 |
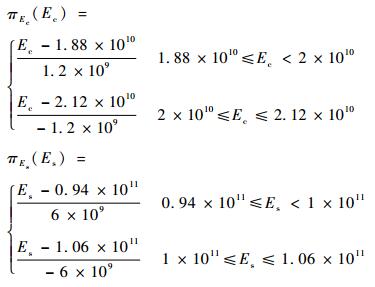 |
Ac、As、q、l为随机变量,分布参数参见表 4。
表 4 屋架结构随机变量的数值特征 Table 4 Numerical characteristics of random variables in roof truss structure
| 随机变量 | 分布类型 | 均值 | 标准差 |
| q/(N·m-1) | 正态 | 20 000 | 1 400 |
| l/m | 正态 | 12 | 0.12 |
| As/m2 | 正态 | 9.82×10-4 | 5.982×10-5 |
| Ac/ m2 | 正态 | 0.04 | 0.004 8 |
表选项
分别用一般方法和Kriging代理模型法计算关于输出的可能性期望的灵敏度指标,可得计算结果如表 5所示。
表 5 算例3各输入变量基于输出可能性期望的灵敏度指标值 Table 5 Sensitivity index values of input variables based on output possibilistic expectation in Example 3
| 参数 | 灵敏度指标值 | |
| 一般方法 | Kriging法 | |
| q | 0.339 4 | 0.339 1 |
| l | 0.673 9 | 0.673 6 |
| Ac | 0.144 4 | 0.144 3 |
| Ec | 0.012 0 | 0.011 9 |
| As | 0.158 5 | 0.158 4 |
| Es | 0.029 1 | 0.029 0 |
表选项
从表 5的计算结果可以看到,随机输入变量对输出响应可能性期望的重要性排序为:δl>δq>δAs>δAc,模糊输入变量对输出响应可能性期望的重要性排序为:δEs>δEc。采用Kriging代理模型计算结果与一般方法的重要性排序一致,指标值非常接近。一般方法计算量为108次,而应用Kriging代理模型计算量仅为200次,采用Kriging代理模型法极大地提高了计算效率。
6 结论 1) 通过分析混合不确定性下输出响应的特征,指出混合不确定性作用下响应输出的概率矩为一个模糊变量,而可能性矩为一个随机变量。
2) 基于模糊变量可能性矩的定义,以输出响应的一阶可能性中心距为例,比较输出响应有条件和无条件可能性期望的概率密度函数的平均差异,分别建立了随机输入变量和模糊输入变量关于输出响应的可能性期望的灵敏度指标。类似地可以将所提指标扩展来衡量输入变量对输出响应的高阶可能性矩的影响。
3) 为了高效求解所提指标,本文采用了Kriging代理模型法,该方法只需对原始模型进行一次代理即可较精确求解所提指标,因此大大较少了计算量。
参考文献
| [1] | BORGONOVO E. Measuring uncertainty importance:Investigation and comparison of alternative approaches[J].Risk Analysis, 2006, 26(5): 1349–1361.DOI:10.1111/risk.2006.26.issue-5 |
| [2] | HAMBY D M. A review of techniques for parameter sensitivity analysis of environmental models[J].Environmental Monitoring and Assessment, 1994, 32(2): 135–154.DOI:10.1007/BF00547132 |
| [3] | SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J].Reliability Engineering & System Safety, 1990, 28(2): 229–253. |
| [4] | STORLIE C B, SWILER L P, HELTON J C, et al. Implementation and evaluation of nonparametric regression procedures for sensitivity analysis of computationally demanding models[J].Reliability Engineering & System Safety, 2009, 94(11): 1735–1763. |
| [5] | SOBOL I M. Sensitivity estimates for nonlinear mathematical models[J].Mathematical Modeling and Computational Experiment, 1993, 1(4): 407–414. |
| [6] | SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics and Computers in Simulation, 2001, 55(1): 271–280. |
| [7] | BORGONOVO E. A new uncertainty importance measure[J].Reliability Engineering & System Safety, 2007, 92(6): 771–784. |
| [8] | LIU Q, HOMMA T. A new computational method of a moment-independent uncertainty importance measure[J].Reliability Engineering & System Safety, 2009, 94(7): 1205–1211. |
| [9] | SONG S F, LU Z Z, CUI L J. A generalized Borgonovo's importance measure for fuzzy input uncertainty[J].Fuzzy Sets & Systems, 2012, 189(1): 53–62. |
| [10] | LI L Y, LU Z Z, LI W. Importance measure system of fuzzy and random input variables and its solution by point estimates[J].Science China Technological Sciences, 2011, 54(8): 2167–2179.DOI:10.1007/s11431-011-4402-4 |
| [11] | GREEGAR G, MANOHAR C. Global response sensitivity analysis of uncertain structures[J].Structural Safety, 2016, 58(10): 94–104. |
| [12] | LI L Y, LU Z Z. Importance analysis for model with mixed uncertainties[J].Fuzzy Sets & Systems, 2017, 310(6): 90–107. |
| [13] | 陈超, 吕震宙. 模糊分布参数的全局灵敏度分析新方法[J].工程力学, 2016, 2(3): 25–33. CHEN C, LV Z Z. A new method for global sensitivity analysis of fuzzy distribution parameters[J].Engineering Mechanics, 2016, 2(3): 25–33.(in Chinese) |
| [14] | CHRISTER C, ROBERT F. On possibilistic mean value and variance of fuzzy numbers[J].Fuzzy Sets & Systems, 2012, 122(2): 315–326. |
| [15] | SAEIDIFAR A, PASHA E. The possibilistic moments of fuzzy numbers and their applications[J].Journal of Computational & Applied Mathematics, 2009, 223(2): 1028–1042. |
| [16] | KAYMAZ I. Application of Kriging method to structural reliability problems[J].Structural Safety, 2005, 27(2): 133–151.DOI:10.1016/j.strusafe.2004.09.001 |
| [17] | OLSSON A, SANDBERG G, DAHLBLOM O. On Latin hypercube sampling for structural reliability analysis[J].Structural Safety, 2003, 25(2): 47–68. |
| [18] | LV Z Y, LU Z Z, WANG P. A new learning function for Kriging and its applications to solve reliability problems in engineering[J].Computers & Mathematics with Applications, 2015, 70(5): 1182–1197. |
| [19] | PIERRIC K, BRUNO S, NADèGE V, et al. A new surrogate modeling technique combining Kriging and polynomial chaos expansions -Application to uncertainty analysis in computational dosimetry[J].Journal of Computational Physics, 2015, 286(10): 103–117. |
| [20] | KOEHLER J R, OWEN A B. 9 computer experiments[J].Handbook of Statistics, 1996, 13(2): 261–308. |
| [21] | ZHANG L G, LU Z Z, WANG P. Efficient structural reliability analysis method based on advanced Kriging model[J].Applied Mathematical Modelling, 2015, 39(2): 781–793.DOI:10.1016/j.apm.2014.07.008 |
| [22] | ROBERT H S, MARK A C. System reliability and sensitivityfactors via the MPPSS method[J].Probabilistic Engineering Mechanics, 2005, 20(2): 148–157.DOI:10.1016/j.probengmech.2005.02.001 |
