1995年,****Vollertsen等[7]在研究直接激光弯曲成形的屈曲机理时提出了先对板料进行悬臂弯曲再使用激光扫描以实现成形的模型,这是该工艺最早的成形模型。此后,陆续有****对该工艺展开研究,研究涉及工程应用的可行性分析、工艺参数对成形的影响研究以及成形件的力学性能分析等。工艺参数对成形的影响研究占了这些研究的绝大部分,相对直接激光弯曲成形而言,该工艺中加入了预载荷这一因素,所以****们在研究工艺参数对成形的影响时把重点放在了讨论预载荷对成形的影响上[3, 8-10]。其中,Guan[3]和Liu[8]等选取了悬臂弯曲作为预加载方式,通过使用有限元软件MSC.Marc分析了预载荷大小对最终板料成形效果的影响规律。研究表明,板料弯曲角度随预载荷的增大呈现指数增大,通过控制预载荷的方向和大小便可以控制板料弯曲方向。Yao等[9]使用有限元软件ANSYS分析了不同形式预载荷带来的不同悬臂弯曲效果下,板料在经过激光扫描及冷却卸载后的成形情况。Roohi等[10]结合有限元法和试验法,对比了板料直接激光弯曲成形和预悬臂弯曲下激光弯曲成形的成形效果,得到了加入预载荷这一因素对成形效果的影响大小。
引入预载荷这一因素后,实际上板料在激光扫描过程其内部热力耦合效应会更加显著,进而造成激光工艺参数对成形的影响与直接激光弯曲成形时也会有所不同,不过目前这块的研究还开展较少。2011年,****彭青等[11]开展了一些相关研究,他们通过单因素试验法分析了由激光工艺参数组合而成的3个无量纲量[12]对成形效果的影响,获得了一些有用结论。
以上研究都有重要意义,然而,这些研究基本是定性研究,且大部分涉及的工艺参数较少。各工艺参数及它们之间可能存在的交互作用对成形的影响还未被系统探讨过。为此,本文开展如下研究:建立成形过程的有限元模型并进行试验验证,在此基础上,采用均匀设计法对模型进行变工艺参数仿真试验设计,利用试验结果构建各工艺参数与变形量间的回归模型,并进一步系统分析工艺参数对变形量的影响及其内在原因。
1 有限元模型及验证 使用软件ABAQUS进行了有限元建模,模型如图 1所示。模型中试件选用尺寸为300 mm×100 mm×4 mm的2219-T6铝合金板料。成形时,先对板料进行弹性范围内的三点弯曲加载,其中左右支撑的相对表面间距为260 mm,加载后板料中心被顶高20 mm。随后激光束对板料上表面弹性应变能集中的中间区域进行1道次扫描,激光功率为1 000 W,扫描速度为20 mm/s,光斑直径为5.5 mm。待扫描结束板料冷却至室温后对板料进行卸载,最终得到成形效果。
 |
| 1—左支撑;2—右支撑;3—顶头;4—板料。 图 1 成形过程的有限元模型 Fig. 1 Finite element model of forming processes |
| 图选项 |
考虑到左右支撑以及顶头与板料之间的接触均是线接触,进而忽略它们与板料间的接触传热作用,并将它们定义为解析刚体,以提高运算速率。在整个成形过程中,考虑板料与周围环境间的对流换热和热辐射这2个热边界条件。
建模过程中,其他一些重要的技术环节如下所述。
实际成形时,板料内的温度场和位移场相互影响,故模型采用了温度-位移耦合有限元模型。
由于材料的热物性参数(热传导率、比热、热膨胀系数)以及力学性能参数(屈服强度、弹性模量)均与温度相关,故必须采用随温度变化的材料参数。模型中材料参数取自文献[13]。
模型中激光束采用基模高斯光束[14],通过使用DFLUX用户子程序将激光束以面热流密度的形式加载到板料表面。热流密度分布式为
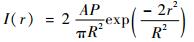 | (1) |
式中:r为距光斑中心的距离;R为照射到板料表面的光斑半径;P为激光功率;A为材料对激光的吸收率。
板料表面激光作用区在实际试验时要涂抹碳黑以提高对激光的吸收率,根据实际处理情况,模型中吸收率取0.56。
网格划分时,为了较精确表征激光光斑内功率密度分布、激光的连续移动以及板料厚度方向上的温度梯度,并兼顾运算速率,激光直接作用区域采用了0.5 mm×0.5 mm×0.8 mm的小网格,其他区域则采用了1 mm×0.5 mm×0.8 mm的网格。其中,厚度方向共有5层网格。
对有限元模型进行计算,得到了如图 2所示仿真结果。图 2(a)为预三点弯曲后的板料等效应力场,最大等效应力299.9 MPa小于材料在常温下的屈服强度值303 MPa,属于弹性范围内加载。从该图还可以推断板料弹性能集中在中间区域。图 2(b)为激光扫描过程的温度场,所取时刻板料上最高温度为322 ℃。图 2(c)为激光扫描过程的等效塑性应变场,该时刻激光扫描到板料的中部,在扫描区域内及周边出现了塑性应变。图 2(d)为卸载后板料的位移场,可看出板料实现了变形。
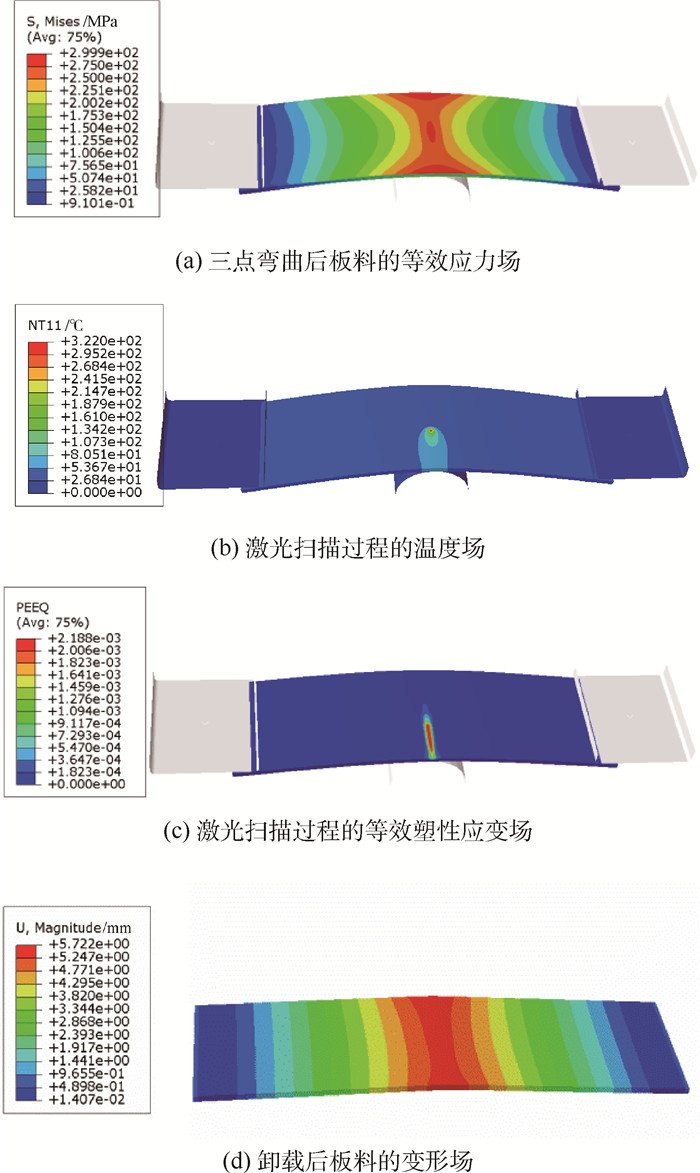 |
| 图 2 有限元仿真结果 Fig. 2 Finite element simulation results |
| 图选项 |
为了验证该模型的可靠性,开展了相应的成形试验,对仿真得到的顶头的力-位移曲线及成形件的弦高进行了试验验证。试验装置和试验得到的成形件如图 3所示。试验中,顶头上的力通过力传感器实时测量。试验和仿真分别得到的顶头的力-位移曲线如图 4所示。图 4表明试验和仿真曲线基本吻合,成形件弦高的仿真结果(5.7 mm)与试验结果(6.5 mm)较为接近。由于力传感器测得的力是顶头对板料所施加力的反作用力,而顶头对板料施加的力乘以其位移代表它对板料做的功,这个功与板料内弹性应变能总量始终是相等的,所以图 4可以反映出试验和仿真得到的成形过程中板料内弹性应变能总量变化情况基本一致,这说明有限元模型可靠。
 |
| 图 3 成形试验装置及成形件 Fig. 3 Forming test devices and formed plate |
| 图选项 |
 |
| 图 4 试验和仿真的力-位移曲线对比 Fig. 4 Comparison of force-displacement curves between test and simulation |
| 图选项 |
2 仿真试验设计及结果 利用已建好的有限元模型,采用变参数仿真试验法开展对工艺参数的试验研究,以获得工艺参数与变形量之间的关系。有限元模型中涉及的工艺参数包括预载荷大小F、激光功率P、光斑直径Φ以及扫描速度V。变形量用成形后板料的弦高值H表征。
由于所建有限元模型网格尺寸较小,且涉及复杂的热力耦合计算以及几何非线性、材料非线性等多种非线性问题,所以计算速率很低。为了在精度不受太大影响前提下,尽量减少试验量以提高试验效率,选取了均匀设计法[15]设计试验。
试验中使用的工艺参数取值范围在既满足能够产生明显成形效果,又不致使板料材料性能发生明显变化这两大前提下进行选取。最终确定各工艺参数的取值区间如下:预载荷830~1 050 N;激光功率1 000~1 500 W;光斑直径4~6.5 mm;扫描速度10~35 mm/s。将各工艺参数在其取值区间内等分成6水平,选取均匀设计表[15]U12(1210)安排试验,依照其使用表的规则,得到了如表 1所示的试验方案和相应的试验结果。
表 1 试验方案和结果 Table 1 Test scheme and results
| 试验号 | F/N | P/W | Φ/mm | V/(mm·s-1) | H/mm |
| 1 | 830 | 1 200 | 5.5 | 30 | 2.61 |
| 2 | 830 | 1 500 | 4.5 | 25 | 3.49 |
| 3 | 874 | 1 200 | 6.5 | 15 | 3.85 |
| 4 | 874 | 1 500 | 5.0 | 10 | 6.02 |
| 5 | 918 | 1 100 | 4.0 | 35 | 4.17 |
| 6 | 918 | 1 400 | 6.0 | 25 | 2.94 |
| 7 | 962 | 1 100 | 4.5 | 20 | 4.82 |
| 8 | 962 | 1 400 | 6.5 | 10 | 6.82 |
| 9 | 1 006 | 1 000 | 5.5 | 35 | 4.67 |
| 10 | 1 006 | 1 300 | 4.0 | 30 | 5.53 |
| 11 | 1 050 | 1 000 | 6.0 | 20 | 5.85 |
| 12 | 1 050 | 1 300 | 5.0 | 15 | 7.48 |
表选项
3 工艺参数研究 3.1 回归模型的建立 在得到试验结果后,采用回归分析法处理试验数据,建立工艺参数与变形量间的回归模型。各工艺参数与变形量之间是多元非线性关系,只考虑各工艺参数间一级交互作用的情况下,最终选取二次多项式逐步回归法进行分析[16]。回归方程中只保留对Y有显著影响的变量,得到的回归模型方程式为
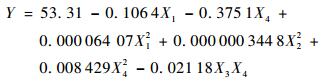 | (2) |
式中:Y为成形后板料的弦高值;X1、X2、X3和X4分别为预载荷、激光功率、光斑直径和扫描速度的值。采用F检验对上述回归方程进行显著性检验。结果表明,式(2) 达到了0.01的高度显著水平,置信度为99%。
3.2 工艺参数对变形量的影响显著性分析 对式(2) 右侧除常数项外各项的回归系数进行显著性检验[17],以判定它们对Y的影响显著性。回归系数的显著性检验采用t检验,具体做法是:计算各回归系数的t值,并将这些t值的绝对值与tn-m-1(α)进行比较,n为试验次数,m为回归方程中变量的个数,α为显著性水平。若t>tn-m-1(0.01) 表示高度显著;若tn-m-1(0.01)>t>tn-m-1(0.05) 表示显著;若t < tn-m-1(0.05) 表示不显著。表 2为各回归系数的t值计算结果。
表 2 各回归系数的t值 Table 2 t values of regression coefficients
| 回归系数 | X1 | X4 | X12 | X22 | X42 | X3X4 |
| t值 | -5.33 | -9.47 | 6.04 | 2.25 | 10.30 | -7.76 |
表选项
代入n=12及m=6,并通过查询t分布表[17]得到t5(0.05)=2.02,t5(0.01)=3.37。t检验结果表明,X22对Y的影响是显著,其余项对Y的影响都是高度显著。将各项对Y的影响显著性从大到小排序,有:X42>X4>X3X4>X12>X1>X22。
从回归系数的显著性检验结果看,4个工艺参数都是对变形量有显著或高度显著影响的。其中,扫描速度对变形量影响最大,激光功率对变形量的影响最小。光斑直径与扫描速度之间存在对变形量有高度显著影响的负交互作用。
3.3 工艺参数对变形量的影响规律分析 基于回归方程式(2),使方程右侧1个变量在其取值区间内连续变化,同时保持其他3个变量不变,分析单个工艺参数变化对变形量的影响规律及其内在原因。
图 5为预载荷F对变形量H的影响曲线。从图 5可以看出,随着预载荷的增大,变形量越来越大,两者近似呈指数关系。对板料的预加载是在弹性范围内,预载荷越大则板料内部的弹性应变能总量就越大。板料成形时内部的弹性应变能转化率由板料在激光扫描阶段获得的温度场决定,温度越高,屈服强度下降越大,弹性应变能转化率越高[11]。激光参量不变时板料在激光扫描阶段获得的温度场不变,进而弹性应变能的转化率不变。这种情况下,预载荷越大时,弹性应变能总量越大,转化产生的塑性应变能总量也会越大,使得变形量增大。另外,预载荷与变形量间近似呈指数关系说明,在弹性范围内增大预载荷大小,变形量的增大效果会越来越明显。
 |
| 图 5 预载荷对变形量的影响 Fig. 5 Influence of preload on deformation amount |
| 图选项 |
图 6为激光功率P对变形量H的影响曲线。图 6显示激光功率越大则变形量越大,且两者之间近似呈线性关系。在激光扫描过程中,被板料吸收的激光能量E与激光功率P和扫描时间T成正比。在板料尺寸不变的情况下,扫描时间T又与扫描速度V成反比,所以有
 |
| 图 6 激光功率对变形量的影响 Fig. 6 Influence of laser power on deformation amount |
| 图选项 |
 | (3) |
根据式(3),保持其他工艺参数不变,增大激光功率会使板料内各点吸收的激光能量增多,进而造成各点的温度更高,板料整体的弹性应变能转化率更大,变形量更大。
图 7为光斑直径Φ对变形量H的影响曲线。由图 7知,变形量随着光斑直径增大而减小,且两者之间是线性关系。当然,这种绝对的线性关系是由回归方程得到,只是近似关系。在其他参数不变,光斑直径增大的情况下,一方面光斑直接作用的板料区域增大了,一些之前不能发生塑性变形的区域可能会出现塑性变形。另一方面,光斑内的功率密度将下降,这会造成板料上光斑圆心附近区域的温度升高量下降,由于这些区域是弹性应变能主要集中的区域,所以板料整体弹性应变能转化量是下降的,进而使变形量减小。
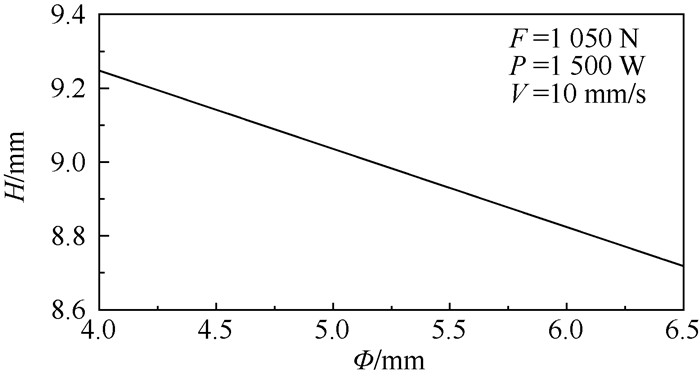 |
| 图 7 光斑直径对变形量的影响 Fig. 7 Influence of laser spot diameter on deformation amount |
| 图选项 |
图 8为扫描速度V对变形量H的影响曲线。图 8显示,随着扫描速度的增大,变形量先减小后增大。根据式(3),增大扫描速度使板料吸收的激光能量减小,板料上各点的温度升高量也将减小,致使板料整体弹性应变能转化率变低,变形量下降。这一规律在扫描速度处于10~27 mm/s时是成立的。但当速度处于27~35 mm/s时,出现了变形量随扫描速度增大而增大的反常现象。这里进行如下解释。当速度为27 mm/s时,板料的整体弹性应变能转化率已经比较低了,随着这个原本占主导地位的弹性应变能转化机制弱化,另一个温度梯度机制开始显著。激光扫描使板料整体温度升高,且在上下表面之间形成温度梯度。这种温度梯度会给板料内部带来一定热应力。当扫描速度较低时,板材受激光照射的时间较长,加之铝合金的热传导率大,板材上下表面温度梯度较小,这种热应力较小,由这种热应力带来的塑性变形很少。随着扫描速度不断增大,温度梯度将逐渐显著,这种热应力将增大,由此带来的塑性变形也会增大,温度梯度机制的作用会变得显著。但是,当扫描速度大于某一阈值时,由于板料上表面吸收到的激光能量太少,上下表面的温度梯度又会开始减小,热应力带来的塑性变形也将下降。分析知,35 mm/s是小于这个阈值的。在27~35 mm/s范围内,随着扫描速度的增大,弹性应变能转化机制带来的塑性变形下降,而温度梯度机制带来的塑性变形增大,且后者带来塑性变形的增大量大于前者带来塑性变形的减少量,这导致了板料变形量的增大。
 |
| 图 8 扫描速度对变形量的影响 Fig. 8 Influence of scanning speed on deformation amount |
| 图选项 |
4 结论 1) 各工艺参数中,扫描速度是对变形量影响最大的因素,而激光功率的影响作用最小。
2) 光斑直径与扫描速度间存在对变形量有高度显著影响的负交互作用。
3) 变形量随预载荷的增大近似呈指数增大,随激光功率的增大近似呈线性增大,随光斑直径的增大近似呈线性下降。
4) 当扫描速度处于10~27 mm/s时,弹性应变能转化机制是产生塑性变形的主导机制,变形量随扫描速度的增大而减小,而扫描速度处于27~35 mm/s时,出现了变形量随扫描速度增大而增大的反常现象,这可能是由于温度梯度机制开始变得显著造成的。
参考文献
| [1] | 陈光南, 王秀凤, 罗耕星, 等. 压弯激光复合成形方法: 200710062910.2[P].2008-03-12. CHEN G N, WANG X F, LUO G X, et al.A forming methodology including bending and laser heating:200710062910.2[P].2008-03-12(in Chinese). |
| [2] | YIBAS B S, AKHTAR S, SHUJA S Z. Laser forming and welding processes[M].Heidelberg: Springer International Publishing, 2013: 1-4. |
| [3] | GUAN Y J, SUN S, ZHAO G Q, et al. Finite element modeling of laser bending of pre-loaded sheet metals[J].Journal of Materials Processing Technology, 2003, 142(2): 400–407.DOI:10.1016/S0924-0136(03)00603-4 |
| [4] | XU L, LI W D, WAN M, et al.Laser bending process of preloaded sheet metal[C]//Proceedings of the 4th International Conference on New Forming Technology.Glasgow:EDP Sciences, 2015, 4:1-7. |
| [5] | 彭青, 陈光南, 吴臣武, 等. 整体壁板激光辅助预应力成形[J].航空学报, 2009, 30(8): 1544–1548. PENG Q, CHEN G N, WU C W, et al. Laser-assisted pre-stress forming for integral panels[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1544–1548.(in Chinese) |
| [6] | WANG X F, LIU D X, LI W D, et al. Study of laser bending of a preloaded titanium alloy sheet[J].Manufacturing Review, 2014, 1: 1–6.DOI:10.1051/mfreview/2013001 |
| [7] | VOLLERTSEN F, KOMEL I, KALS R. Laser bending of steel foils for micro parts by the buckling mechanism-A model[J].Modelling & Simulation in Materials Science & Engineering, 1995, 3(1): 107–119. |
| [8] | LIU J, SUN S, GUAN Y J. Numerical investigation on the laser bending of stainless steel foil with pre-stresses[J].Journal of Materials Processing Technology, 2009, 209(3): 1580–1587.DOI:10.1016/j.jmatprotec.2008.04.006 |
| [9] | YAO Z Q, SHEN H, SHI Y J. Numerical study on laser forming of metal plates with pre-loads[J].Computational Materials Science, 2007, 40(1): 27–32.DOI:10.1016/j.commatsci.2006.10.024 |
| [10] | ROOHI A H, GOLLO M H, NAEINI H M. External force-assisted laser forming process for gaining high bending angles[J].Journal of Manufacturing Processes, 2012, 14(3): 269–276.DOI:10.1016/j.jmapro.2012.07.004 |
| [11] | 彭青, 陈光南, 王明星, 等. 工艺参数对激光辅助预应力成形效率的影响[J].中国激光, 2011, 38(10): 73–77. PENG Q, CHEN G N, WANG M X, et al. Finite element modeling of laser bending of pre-loaded sheet metals[J].Chinese Journal of Lasers, 2011, 38(10): 73–77.(in Chinese) |
| [12] | 彭青, 陈光南, 王秀凤. 激光辅助预应力成形的相似性问题[J].中国激光, 2009, 36(5): 1261–1266. PENG Q, CHEN G N, WANG X F. Similarity criterion of laser-assisted pre-stress forming[J].Chinese Journal of Lasers, 2009, 36(5): 1261–1266.(in Chinese) |
| [13] | National Technical Information Service.Metallic materials properties development and standardization-01:DOT/FAA/AR-MMPDS-01[S].Washington, D.C.:Department of Transportation, 2003:166-181. |
| [14] | XI Y, ZHAN H Y, RASHID R A, et al. Numerical modeling of laser assisted machining of a beta titanium alloy[J].Computational Materials Science, 2014, 92(5): 149–156. |
| [15] | 方开泰. 均匀设计与均匀设计表[M].北京: 科学出版社, 1994: 14-18. FANG K T. Uniform design and uniform design tables[M].Beijing: Science Press, 1994: 14-18.(in Chinese) |
| [16] | 唐启义. DPS数据处理系统[M].北京: 科学出版社, 2013: 474-477. TANG Q Y. DPS data processing system[M].Beijing: Science Press, 2013: 474-477.(in Chinese) |
| [17] | 王黎明. 应用回归分析[M].上海: 复旦大学出版社, 2008: 64-65. WANG L M. Applied regression analysis[M].Shanghai: Fudan University Press, 2008: 64-65.(in Chinese) |
