副翼效率静弹分析的难点主要集中在跨声速区域,在此速度区域,副翼表面常会出现局部激波及激波附面层干扰等强非线性现象,同时激波位置和强度会随着舵面弹性变形而改变,气动和结构之间表现出非线性强耦合特征,给静弹分析带来很大困难。
目前,针对上述问题,工程设计上一般还沿用基于面元法和结构耦合的线化分析方法,分析精度难以令人满意,分析结果用于飞控设计后可导致地面仿真结果和实际飞行结果出现较大偏差。
近年来,基于计算流体力学 (CFD)/计算结构动力学 (CSD) 耦合的高精度静弹分析方法快速发展。在网格变形方面,从20世纪90年代以来,已经发展出了多种方法,并不同程度地得到了应用。张伟伟[5]、张来平[6]等总结了网格变形技术的研究进展,并对超限插值法、弹簧法、Delaunay背景网格插值法、径向基函数插值法等给出了详细的介绍及比较。在应用方面,Prananta和Meijer[7]将CFD/CSD耦合方法用于F-16飞机的全机跨声速静弹分析。
由上述分析可见,基于CFD/CSD耦合的高精度静弹分析方法理论上可以较好解决跨声速副翼效率的静弹问题,但从工程适用角度及目前的应用情况看,主要还存在以下问题:①舵面偏转后局部网格变形鲁棒性问题。由于用于网格变形的函数一般都是多阶连续的 (如径向基函数),用于连续变形问题效果较好,但舵面的存在经常导致局部变形出现间断,从而导致网格变形失败,尤其是用于附面层网格时。②分析结果缺乏有效验证。CFD/CSD耦合方法目前用于整体翼面类问题的分析较多,用于舵面效率的分析相对较少,分析结果更是缺乏试验或试飞的有效验证,用于实际复杂工程问题的能力亟待检验。
针对上述问题,本文提出了基于虚拟网格及虚拟位移的网格变形方法,对于迭代中出现的非物理振荡、非一致收敛问题,在迭代策略、收敛判据方面也进行了改进设计,并将上述方法用于某型战斗机跨声速副翼效率的静弹分析,为验证分析结果,开展了静弹试飞辨识,两者吻合良好,表明本文所提方法可以满足跨声速副翼效率高精度静弹分析的需求,对于提高静弹工程设计能力具有重要意义。
1 计算模型及网格 本文计算模型为某型战斗机,包括机身、机翼及尾翼等全部部件,机翼上的舵面包括前缘襟翼、后缘襟翼以及副翼。
气动网格采用非结构混合网格,全机网格总数约为450万,其中用于模拟附面层流动的三棱柱网格数约为220万,第1层三棱柱网格距离壁面10-4 m,所有舵面均单独分区生成网格,机翼表面网格及剖面空间网格如图 1所示。
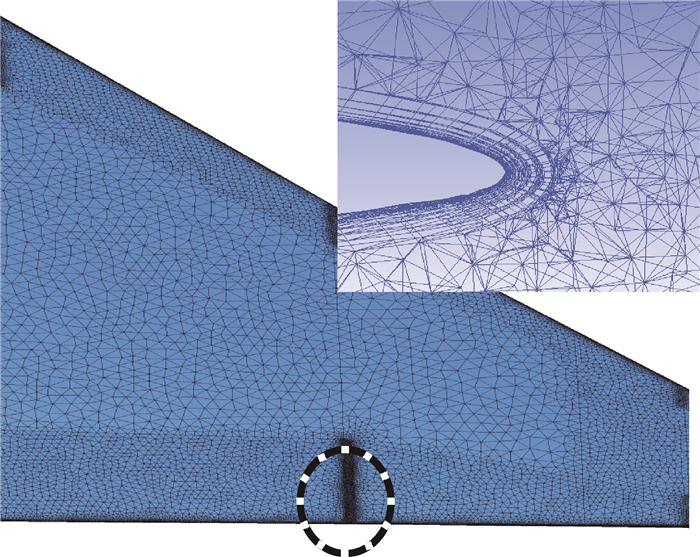 |
| 图 1 机翼非结构混合气动网格 Fig. 1 Non-structural hybrid aerodynamic mesh of wing |
| 图选项 |
结构有限元模型采用经地面振动试验 (GVT) 修正后的全机动力学有限元模型,翼面部分模型如图 2所示。
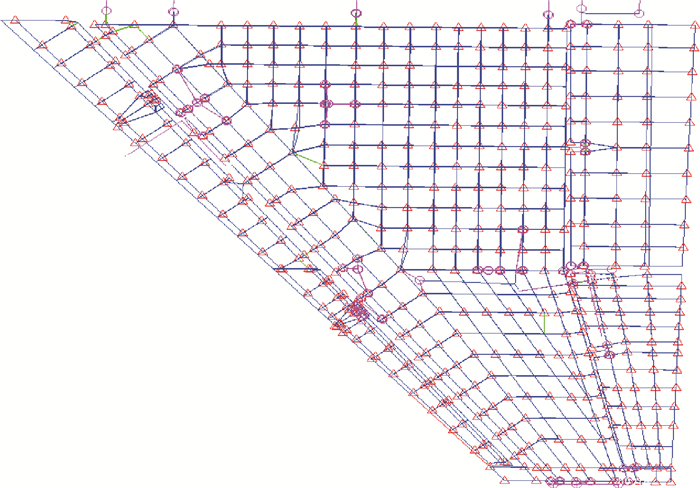 |
| 图 2 机翼动力学有限元模型 Fig. 2 Dynamic finite element model of wing |
| 图选项 |
2 计算方法 为进行高精度的静弹分析,本文发展了基于Navier-Stokes方程求解器及Nastran有限元分析软件的流固耦合计算方法,为了提高计算的精度和鲁棒性,本文重点在空间网格变形、松弛迭代、收敛判据方面进行了优化改进。
2.1 空间网格变形 本文空间网格变形采用基于径向基函数的插值方法[8-11],该方法实质上是一种散乱数据的插值方法,因此对网格类型适应性很强,适合本文混合网格的变形插值。具体插值方法如下:
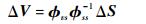 | (1) |
式中:ΔV和ΔS分别为空间网格和表面网格的位移;?ss为表面网格点之间的基函数矩阵;?vs为空间网格点和表面网格点之间的基函数矩阵。对于给定的网格,?ss和?vs均为已知量。因此,当表面网格位移确定后,根据式 (1) 即可得到空间网格的位移。
为降低插值矩阵计算量,提高变形效率,在应用该插值方法的过程中,采用了贪心算法、函数空间子集逐级逼近等算法[12-15]。
应用上述方法进行混合网格变形的难点集中在附面层网格上,因为其尺度非常小,如果变形连续,则问题不大,但在分析舵面问题时,由于舵面变形和主翼面变形一般并不连续,常会发生网格交叉,导致计算崩溃,为此,本文提出了基于虚拟网格和虚拟位移的变形方法。
根据式 (1),空间网格点的位移由网格点的相对位置及表面网格位移决定,然而对于确定的流固耦合问题,这些已无法改变。网格产生交叉主要是因为用于插值的径向基函数是高阶连续函数,不能很好适应间断变形问题的处理,通过在间断变形处设置虚拟点和该点的虚拟位移,相当于在间断边界处强制增加了约束条件,可有效解决间断变形问题。在理论上表现为在式 (1) 中增加辅助项,假设局部存在虚拟表面网格,其虚拟位移为ΔS0,则空间网格位移可写为
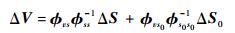 | (2) |
根据径向基函数的性质,虚拟表面网格对临近空间网格将有显著影响,随着距离的增加,其影响量将急剧衰减,最终起到改善局部空间网格质量的作用。
在实际应用中,只需要增加几个网格点即可,对于本文静弹分析中出现的网格间断变形情况 (见图 3), 其虚拟点设置如图 4所示 (共4个)。虚拟位移一般设为和其流向最近网格点的位移相等或在此基础上适当增减。采用该方法前后的网格变形对比如图 5所示 (图 3中B剖面),可见,虚拟点的存在明显缓解了间断变形处的网格挤压,负体积网格消失,达到了虚拟点的设置目的。
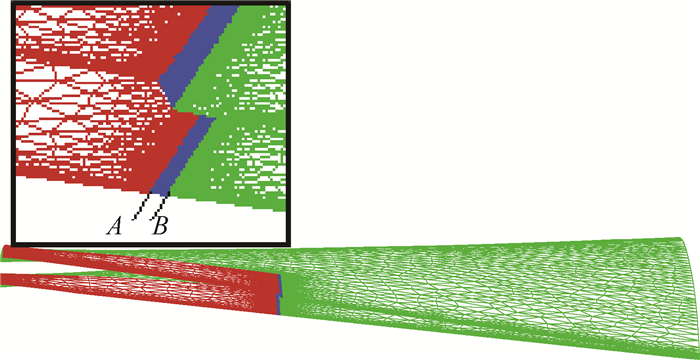 |
| 图 3 机翼表面网格变形情况 Fig. 3 Deformation of wing surface mesh |
| 图选项 |
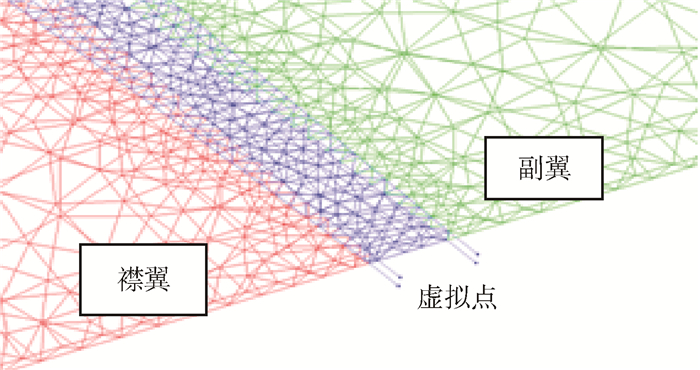 |
| 图 4 虚拟点的设置 Fig. 4 Dummy grids setting |
| 图选项 |
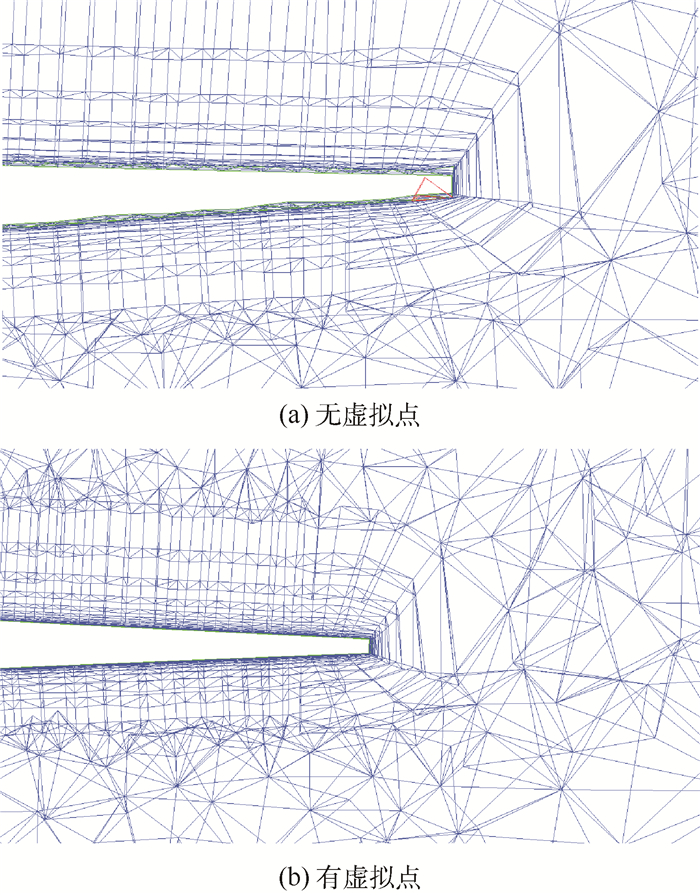 |
| 图 5 虚拟点对空间网格变形的影响 Fig. 5 Influence of dummy grids on space mesh deformation |
| 图选项 |
2.2 松弛迭代 常规的流固耦合迭代以本次结构变形作为下一次流体计算的外形,但本文在副翼效率的静弹分析中发现,由于存在局部激波,激波位置以及强度随静弹变形而改变后对机翼外段气动载荷影响显著,导致常规迭代方法产生非物理振荡。为解决此问题,本文采用了一种改进的迭代方法——松弛迭代,具体操作方法如下:
1) 迭代步数N=1时,采用常规迭代方法,并记下该步结构位移X1。
2) 迭代步数N=2时, 结构位移X2=(X1+X′2)/2,X′2为第2步的直接计算位移,X2为最终使用的松弛位移 (下同)。
3) 迭代步数N≥3时,XN=(XN-2+XN-1+X′N)/3。
计算实践表明,采用上述方法后,可有效避免流固耦合出现非物理振荡并加速收敛。
2.3 收敛判据 流固耦合计算一般以翼尖最大位移作为收敛标准,但本文研究表明,在带舵面构型下,舵面和主机翼变形并不完全同步,翼尖位移收敛时,舵面上的变形并未收敛。因此,为提高计算精度,本文采用部件载荷作为收敛标准。
某部件第N步的第i分量残差定义如下:
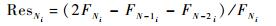 | (3) |
式中:FNi为第N步第i分量载荷。
该部件第N步的第6分量综合残差为
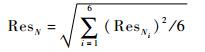 | (4) |
当所有部件的综合残差均低于某一设定标准时,则认为迭代收敛。图 6给出了典型计算状态下副翼载荷与翼尖最大位移残差的收敛历程对比,可见以部件载荷作为收敛标准更准确。
 |
| 图 6 不同收敛判据比较 Fig. 6 Comparison of different convergent criterions |
| 图选项 |
3 试飞辨识 在副翼效率的试飞辨识中,飞机主要进行滚转机动飞行,滚转方向的单自由度动力学方程可以描述为
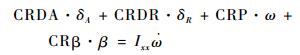 | (5) |
式中:CRDA、CRDR、CRP和CRβ分别为副翼、方向舵、滚转角速度以及侧滑角的滚转效率;δA、δR、ω、β和Ixx分别为副翼偏度、方向舵偏度、滚转速率、侧滑角和飞机绕滚转轴的转动惯量。式 (5) 右侧是已知惯性项,方程左侧的各项中,飞行参数都是已知的,各导数项均是待辨识的未知量。
式 (5) 可以抽象为如下形式:
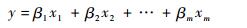 | (6) |
式中:(β1, β2, …, βn) 为CRDA、CRDR等未知参数;(x1, x2, …, xn) 和y为可以从飞参记录仪读取的已知量。
每个试飞机动动作均有几十个甚至几百个时间步,对任意一个时间步,均可以写出上述方程。当有n个时间步时,可以形成方程组,用矩阵形式表达为
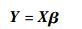 | (7) |
一般来说,观测点数量n很大 (n

 | (8) |
式中:ε为回归的误差。
定义误差函数如下:
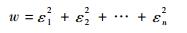 | (9) |
如果一组b=(β1, β2, …, βn) 使得误差函数取得最小值,则称这一组b=(β1, β2, …, βn) 为矛盾方程组的最小二乘解,由此获得各参数的辨识结果。
4 计算结果及试飞验证 本文将第2节和第3节的方法用于某型战斗机跨声速副翼效率的静弹分析,选择Ma=0.95作为研究状态点,高度分别取H=3,6,9 km,副翼偏度δA±5°,下面给出详细的计算结果以及试飞验证情况。
4.1 刚性气动力验证 为保证静弹分析精度,本文首先进行了刚性气动力计算精度的验证。图 7给出了Ma=0.95时,全机升力系数CL、俯仰力矩系数Cm、机翼剖面 (副翼展向中部) 压力系数Cp分布和风洞试验结果对比。图中:α为迎角。可见,采用本文的计算网格及气动力计算方法可以获得满意的跨声速计算效果。
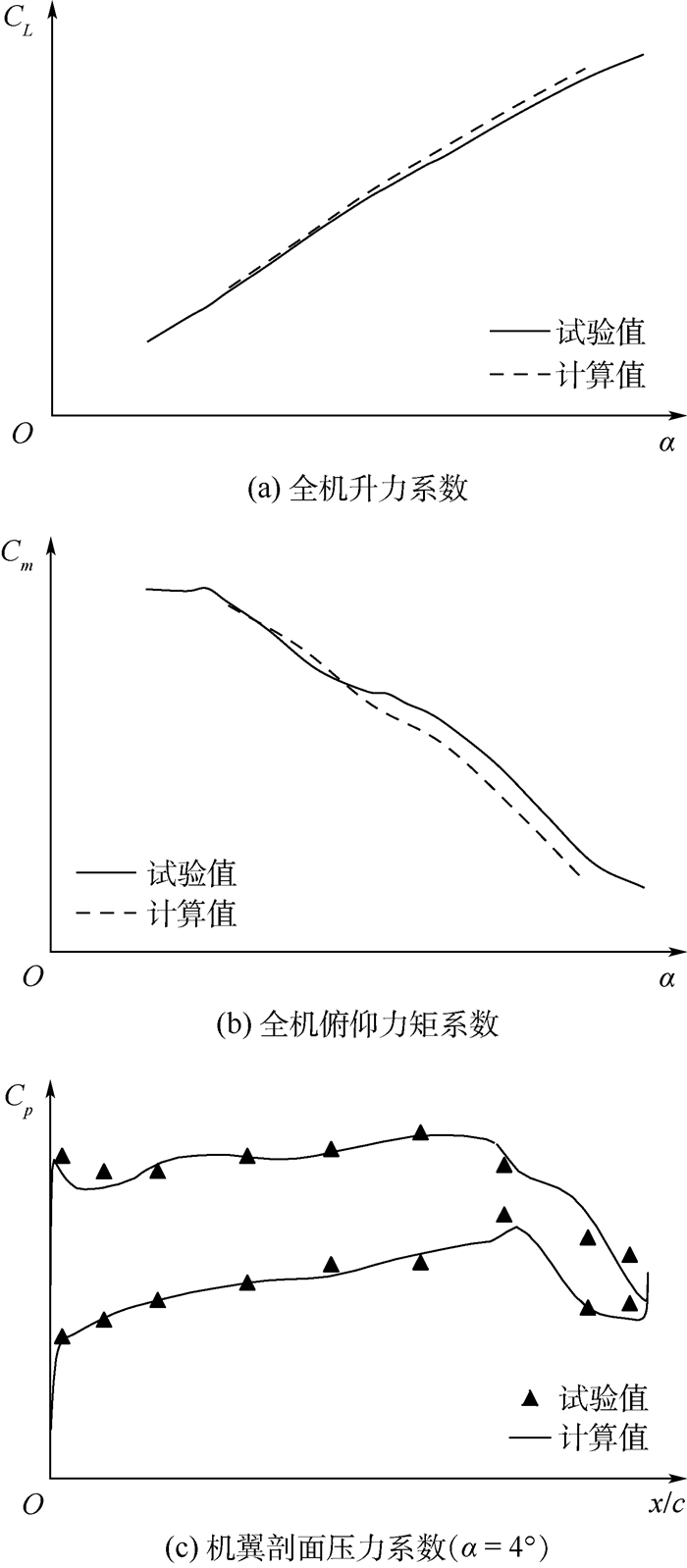 |
| 图 7 刚性气动力计算值与试验值的比较 Fig. 7 Comparision of rigid aerodynamics between calculation and test values |
| 图选项 |
4.2 静弹计算结果 图 8给出了Ma=0.95、α=4°、δA=5°、H=0 km状态下机翼变形情况。可见,机翼此时有明显的向上翘曲变形。
 |
| 图 8 机翼气动网格变形 Fig. 8 Aerodynamic mesh deformation of wing |
| 图选项 |
机翼的变形对翼面压力分布产生了明显的影响。图 9和图 10给出了机翼上表面变形前后的压力分布云图以及副翼展向中间位置 (图 9中横线示位置) 剖面压力系数的比较。可见,变形前,副翼上表面存在明显的局部激波,变形后,由于后掠机翼的弯扭耦合效应以及副翼本身的弹性上偏变形导致激波位置显著前移,激波强度也明显减弱,表现出典型的跨声速静弹特征。
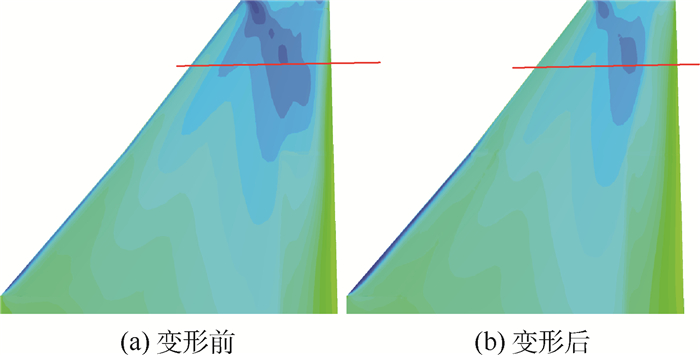 |
| 图 9 机翼上表面变形前后压力分布比较 (δA=5°) Fig. 9 Comparison of pressure contour of wing's upper surface before and after deformation (δA=5°) |
| 图选项 |
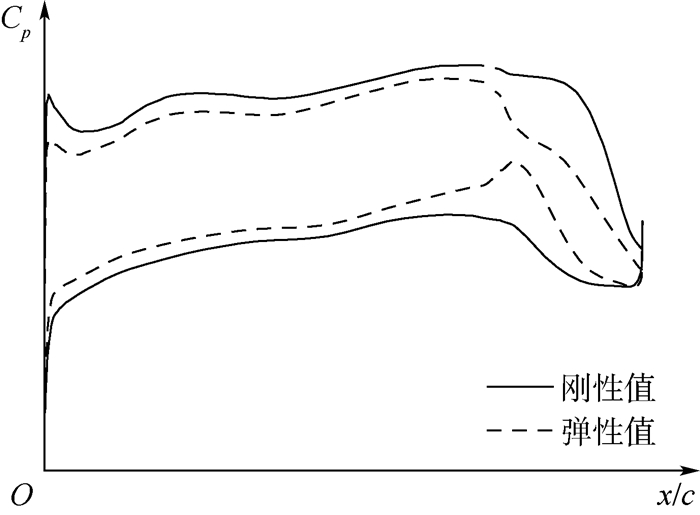 |
| 图 10 副翼剖面压力系数分布比较 (δA=5°) Fig. 10 Comparison of aileron's section pressure coefficient distribution (δA=5°) |
| 图选项 |
图 11和图 12给出了Ma=0.95、α=4°、δA=-5°、H=0 km状态下的机翼上表面变形前后的压力分布云图以及副翼展向中间位置 (图 9中横线位置) 剖面压力系数的比较。可见,在副翼上偏时,激波主要出现在主翼面上,但副翼的气动特性变得更为复杂,出现了近似力偶现象,该力偶使得副翼有继续上偏的趋势,导致弹性变形后,主翼面和副翼之间的激波强度稍加强,副翼上近似力偶的载荷分布也有所改变,总体上变化不大,表现出与副翼下偏时截然不同的静弹特征。
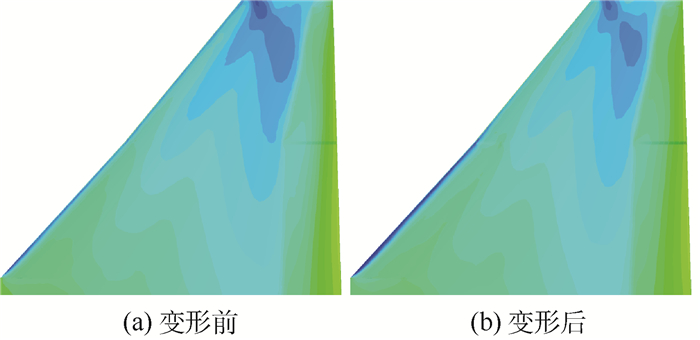 |
| 图 11 机翼上表面变形前后压力分布比较 (δA=-5°) Fig. 11 Comparison of pressure contour of wing's upper surface before and after deformation (δA=-5°) |
| 图选项 |
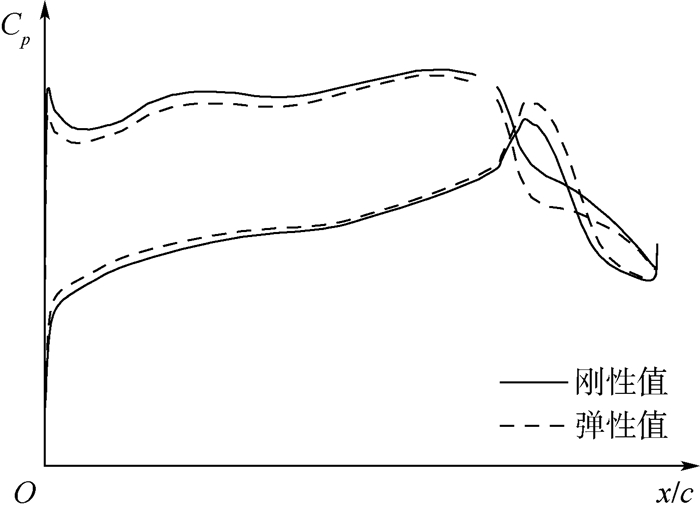 |
| 图 12 副翼剖面压力系数分布比较 (δA=-5°) Fig. 12 Comparison of aileron's section pressure coefficient distribution (δA=-5°) |
| 图选项 |
4.3 试飞验证 本文所研究的某型战斗机在试飞期间针对跨声速副翼效率问题开展了广泛的静弹辨识试飞研究,试飞机动包括不同高度下的脉冲副翼操纵、横向扫频、稳定滚转等,根据第3节静弹试飞辨识方法,获得了不同高度下的副翼效率参数。
图 13给出了Ma=0.95时不同高度下副翼静弹修正系数K试飞结果与本文计算结果的比较。可见,在低高度时 (大动压),两者的修正系数吻合良好,随着高度的增加 (动压减小),差别略增大,这主要由飞行迎角增大后气动力计算精度下降所致 (见图 7(a)和图 7(b))。试飞参数表明,H=9 km时的飞行迎角比H=3 km时一般大约3°。
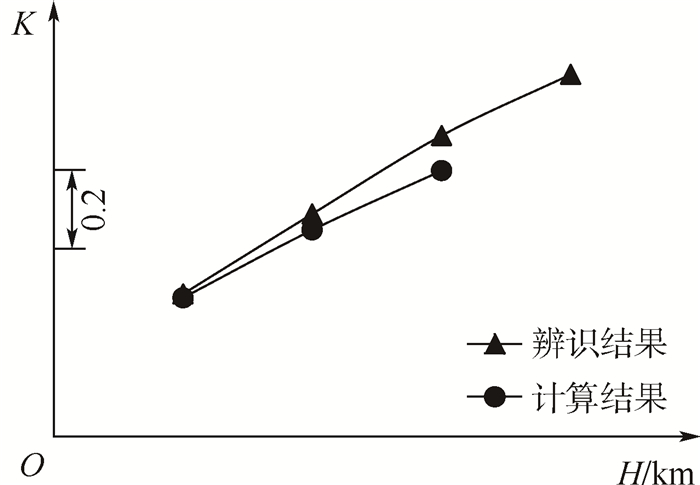 |
| 图 13 副翼效率静弹修正系数与试飞辨识结果的比较 Fig. 13 Comparison between static aeroelastic correction coefficient of aileron efficiency and test flight identification results |
| 图选项 |
总体看来,本文计算结果和试飞辨识结果具有良好的一致性,验证了本文发展的高精度静弹计算方法的可靠性。
5 结论 针对CFD/CSD耦合方法在跨声速舵面效率分析方面存在的问题,提出了基于虚拟网格和虚拟位移的网格变形方法,在迭代策略、收敛判据等方面也做了诸多针对性改进设计,并将之用于某型战斗机跨声速副翼效率的静弹分析,为验证分析结果,开展了静弹试飞辨识研究,结果表明:
1) 跨声速区域,副翼表面出现局部激波等复杂气动现象且和弹性变形强烈耦合。
2) 副翼效率弹性修正系数和试飞辨识结果吻合良好。
上述结果表明,本文所提方法可以满足现代战斗机对跨声速副翼效率高精度静弹分析的需求,对于提高静弹工程设计能力具有重要意义。
参考文献
| [1] | BOEHM B, FLICK P, SANDERS B, et al.Static aeroelastic response predictions of the active aeroelastic wing (AAW) flight research vehicle:AIAA-2001-1372[R].Reston:AIAA, 2001. |
| [2] | HEEG J, SPAIN C V, FLORANCE J R, et al.Experimental results from the active aeroelastic wing wind tunnel test program:AIAA-2005-2234[R].Reston:AIAA, 2005. |
| [3] | WISEMAN C D, SILVA W A, SPAIN C V, et al.Transonic-small-disturbance and linear analyses for the active aeroelastic wing program:AIAA-2005-1995[R].Reston:AIAA, 2005. |
| [4] | LEE D H, BALDELLI D H, LINDSLEY N J, et al.Static aeroelastic and open-loop aeroservoelastic analyses for the F/A-18 AAW aircraft:AIAA-2007-2135[R].Reston:AIAA, 2007. |
| [5] | 张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展[J].航空学报, 2014, 35(2): 303–319.ZHANG W W, GAO C Q, YE Z Y. Research progress on mesh deformation method in computational aeroelasticity[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 303–319.(in Chinese) |
| [6] | 张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J].力学进展, 2010, 40(4): 424–447.ZHANG L P, DENG X G, ZHANG H X. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J].Advances in Mechanics, 2010, 40(4): 424–447.(in Chinese) |
| [7] | PRANANTA B B, MEIJER J J.Transonic static aeroelastic simulations of fighter aircraft:NLR-TP-2003-187[R].Toronto:[s.n.], 2003. |
| [8] | FRANK R. Scattered data interpolation:Tests of some methods[J].Mathematics of Computation, 1982, 38(175): 181–200. |
| [9] | 林言中, 陈兵, 徐旭. 径向基函数插值方法在动网格技术中的应用[J].计算物理, 2012, 29(2): 191–197.LIN Y Z, CHEN B, XU X. Radial basis function interpolation in moving mesh technique[J].Chinese Journal of Computational Physics, 2012, 29(2): 191–197.(in Chinese) |
| [10] | 贾欢, 孙秦. 基于径向基函数的动网格技术应用研究[J].机械科学与技术, 2013, 32(4): 510–513.JIA H, SUN Q. Analyzing dynamic grid based on radial basis function[J].Mechanical Science and Technology for Aerospace Engineering, 2013, 32(4): 510–513.(in Chinese) |
| [11] | ALLEN C B, RENDALL T C S.Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions:AIAA-2007-3804[R].Reston:AIAA, 2007. |
| [12] | SHENG C H, ALLEN C B. Efficient mesh deformation using radial basis functions on unstructured meshes[J].AIAA Journal, 2013, 51(3): 707–720.DOI:10.2514/1.J052126 |
| [13] | RENDALL T C S, ALLEN C B.An efficient fluid-structure interpolation and mesh motion scheme for large aeroelastic simulations:AIAA-2008-6235[R].Reston:AIAA, 2008. |
| [14] | 王刚, 雷博琪, 叶正寅. 一种基于径向基函数的非结构混合网格变形技术[J].西北工业大学学报, 2011, 29(5): 784–788.WANG G, LEI B Q, YE Z Y. An efficient deformation technique for hybrid unstructured grid using radial basis functions[J].Journal of Northwestern Polytechnical University, 2011, 29(5): 784–788.(in Chinese) |
| [15] | 谢亮, 徐敏, 张斌, 等. 基于径向基函数的高效网格变形算法研究[J].振动与冲击, 2013, 32(10): 141–145.XIE L, XU M, ZHANG B, et al. Space points reduction in grid deforming method based on radial basis functions[J].Journal of Vibration and Shock, 2013, 32(10): 141–145.(in Chinese) |
