在纯方位目标跟踪问题中,所能获得的测量信息只有目标的方位角。由于测量与被估计量之间是强非线性映射 (反正切函数),只利用角度信息对目标进行被动跟踪定位是一个非线性状态估计问题。而针对非线性滤波问题,主要分为基于统计噪声假设的滤波算法和基于未知但有界 (Unknown-But-Bounded,UBB) 噪声假设的滤波算法。对于通常的机动目标跟踪问题,常把系统模型和量测方程所受到的噪声扰动视为随机变量,用一定的概率参数来对其进行描述,例如高斯噪声或有色噪声[8-10]。在统计噪声假设下,递推跟踪算法得到迅速发展。Aidala[11]分析了扩展Kalman滤波 (Extended Kalman Filter,EKF) 在纯方位目标跟踪中的性能,由于EKF的线性化的误差较大,其性能不稳定。鹿传国等[12]提出基于距离参数化的均方根容积卡尔曼滤波 (Cubature Kalman Filter,CKF) 算法;Leong等[13]提出了一种高斯和CKF纯方位跟踪算法;方君等[14]提出了一种强跟踪平方根CKF算法。以上基于CKF的跟踪算法计算时间都在秒级,而基于粒子滤波的纯方位跟踪滤波算法,计算时间也都在秒级[15-17]。
以上机动目标跟踪算法都是基于统计噪声假设,但是当噪声的统计假设不成立时,将会影响跟踪算法的性能。而对于在线的实时跟踪测量系统,当仅能获得较少的传感器测量数据时,很难确定测量数据的噪声概率分布函数。与统计噪声假设的估计算法不同,基于未知但有界噪声假设的集员估计 (Set-Membership Estimation,SME) 算法只要求噪声有界,且噪声界已知,而不需要对噪声在界内的统计特性做任何假设[18]。集员估计所求出的是系统状态的一个可行集,可行集内的每个元素都可作为对系统状态的有效估计,可行集的中心可作为对状态的一个点估计,可行集的测度可作为衡量集员估计有效性的标准。通常选用凸集对可行集进行近似描述,如外定界椭球、多胞形、凸多面体等。由于其数学描述上的直观性和可在线快速递推计算的特点,已用于导航[19-20]、移动机器人定位[21]等领域,本文选择外定界椭球集员估计 (Ellipsoidal Outer-Bounding Set-Membership Estimation,EOB-SME) 算法用于目标跟踪。
EOB-SME与Kalman滤波类似,也分为时间更新和量测更新2个递推阶段,且在每个递推更新阶段分别有一个最优参数,通过不同的优化准则,来获得不同的最优椭球。Maksarov和Norton[22]给出包含2个椭球和或交的最小容积和最小迹的线性系统EOB-SME算法,但在求解椭球交时的计算较复杂。Scholte和Campbell[23]利用区间估计技术建立了非线性系统的扩展EOB-SME算法,但未得到最优的椭球结果。周波等[24]将UD分解方法运用到非线性系统的扩展EOB-SME中,改进了算法的数值稳定性和实时性。通过最小化估计误差的Lyapunov函数上界来求取量测更新的最优参数,笔者提出了一种针对线性系统的EOB-SME算法[25]。
关于集员算法在机动目标跟踪中的应用,Fletcher等[26]在单基站情况下将最小体积椭球集合估计算法运用到纯方位目标跟踪系统,获得估计结果的精度低于Kalman滤波。Rahmati等[27]基于非最优椭球集员估计算法建立了一种机动目标跟踪算法。笔者针对随机和未知但有界双重噪声影响下的机动目标跟踪问题,给出了一个性能优于EKF的椭球集合滤波器[28]。
为了将集员估计算法用于实时机动目标跟踪的非线性状态估计,本文提出了一种适用于纯方位目标跟踪的EOB-SME算法,该算法通过最小化估计误差Lyapunov函数的上界来求取量测更新的最优参数;利用区间分析技术估计非线性系统线性化后所产生的误差,将其用椭球进行外包后与量测方程噪声椭球组成新的量测噪声椭球。仿真结果表明:EOB-SME算法每次递推更新所得到的椭球集合均包含了目标真实的位置,提高了估计精度,同时计算耗时为毫秒级,从而验证了本文所提算法的可行性。
1 问题描述 定义1??定义椭球集合为
 | (1) |
式中:a∈Rn为椭球集合的中心;对称正定矩阵σ2P∈Rn×n为椭球的形状矩阵,变量σ2∈R+为标量。
假设在二维平面直角坐标系中,机动目标运动模型可由一个线性状态方程和一个非线性观测方程描述。采用匀加速运动来描述目标的时间状态方程:
 | (2) |
式中:
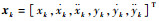
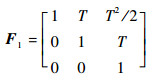 | (3) |
其中:T为采样间隔。
虽然匀加速模型是用来模拟目标进行匀加速运动时的运动模型,即

量测方程为
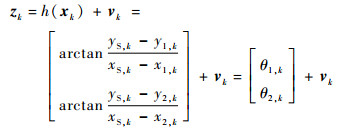 | (4) |
式中:θi,k (i=1, 2) 为双基阵的方位角;xi,k和yi,k (i=1, 2) 为双基阵传感器的位置坐标;xS,k和yS,k为目标的位置坐标;vk为量测噪声;h (xk) 为观测向量。
假设过程噪声wk和量测噪声vk分别位于以下椭球集合内:
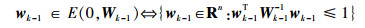 | (5) |
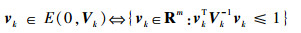 | (6) |
式中:Wk-1和Vk为已知的对称正定矩阵。
如图 1所示,点T表示机动目标,S1和S2表示双基阵传感器,假设基阵S1位于坐标系原点,已知S1和S2的距离为D。当每个基阵的传感器测量到对目标的方位角后,由于传感器的量测噪声未知但有界,因此2个基阵传感器的测量范围将确定一个目标所位于的几何区域,即由传感器测量误差构成的可行集。用一个外定界椭球将其包围,即构成了包含目标的椭球集合,使目标椭球集合随着递推更新逐渐缩小,从而能够更有效地确定目标的位置。
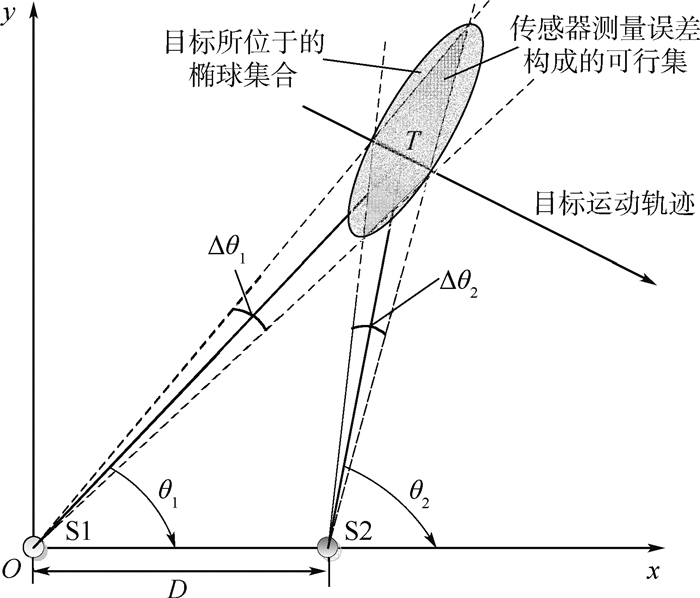 |
| 图 1 未知但有界噪声下双基阵纯方位机动目标跟踪 Fig. 1 Bearing-only maneuvering target tracking with two sensors under unknown-but-bounded noises |
| 图选项 |
2 外定界椭球集员估计 2.1 外定界椭球集员估计基本算法 考虑机动目标运动模型式 (2) 和式 (4),线性化量测方程式 (4) 可得
 | (7) |
式中:?h (xk)/?x为量测函数h (·) 的梯度;O (xk2) 为高阶项,即线性化误差。
先从几何角度概述EOB-SME的两步递推更新,再给出各个步骤的递推方程。假设在k-1时刻,状态向量xk-1包含在椭球

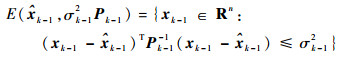 | (8) |
由系统状态方程和有界过程噪声假设可知,一步预测状态
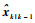
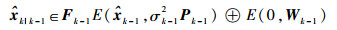 | (9) |
式中:
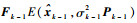
通常,2个椭球的矢量和是1个凸集但并不是1个椭球,需要构造1个椭球来包含矢量和的凸集,即
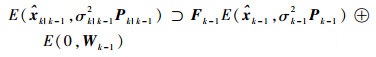 | (10) |
式中:
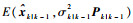
定义量测椭球集合为
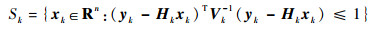 | (11) |
式中:Hk为量测矩阵。
在k时刻获得量测椭球集合Sk后,状态xk应位于时间更新椭球
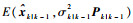
 | (12) |
同样,量测椭球集合与时间更新椭球的交集通常不是一个椭球,需要构造量测更新椭球

 | (13) |
结合双基阵目标跟踪,EOB-SME的量测更新过程如图 2所示。在时刻k,假设已知时间更新椭球,根据双基站传感器的测量误差,当获得量测集合后,用量测更新椭球来外包时间更新椭球与量测集合的交集。
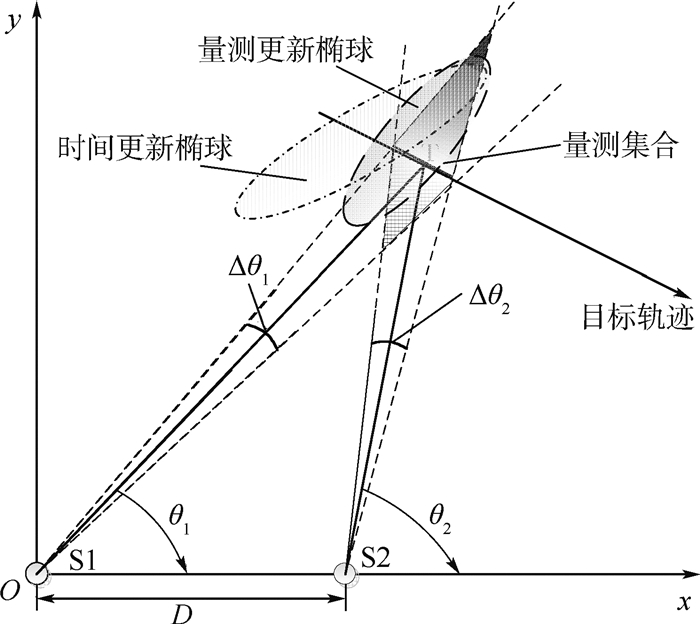 |
| 图 2 双基阵纯方位测量下的量测更新过程 Fig. 2 Observation update process under bearing-only measurement with two sensors |
| 图选项 |
定义2??闭凸集Ω的支撑函数s (η) 为
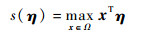 | (14) |
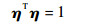 | (15) |
定理1??EOB-SME的时间更新和量测更新递推方程如下:
1) 时间更新。若已知状态xk-1位于椭球

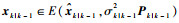
 | (16) |
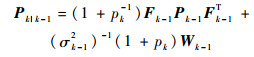 | (17) |
 | (18) |
式中:参数pk∈(0, 1);σk|k-12 > 0。
2) 量测更新。若已知量测椭球集合Sk和时间更新椭球
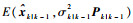
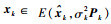
 | (19) |
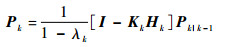 | (20) |
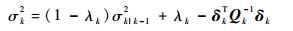 | (21) |
 | (22) |
 | (23) |
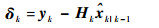 | (24) |
式中:参数λk∈(0, 1);σk2 > 0。
证明
1) 证明时间更新递推方程。假设时间更新椭球具有如下形式:
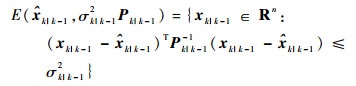 | (25) |
根据椭球支撑函数应有以下关系成立:
 | (26) |
即
 | (27) |
因为
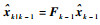
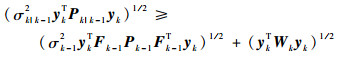 | (28) |
若令
 | (29) |
由不等式 (1-p-1) b12+(1+p) b22≥(b1+b2)2 可得
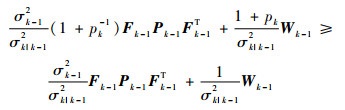 | (30) |
令σk|k-12=σk-12,可得
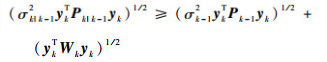 | (31) |
则按照式 (25) 构造的椭球可包含2个椭球的矢量和,时间更新递推方程证明完毕。
2) 证明量测更新递推方程。当可获得量测椭球集合Sk时,假设量测更新椭球为
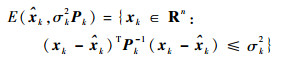 | (32) |
则包含量测椭球集合与时间更新椭球集合交集的椭球为
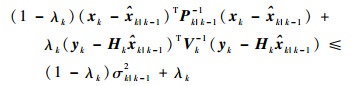 | (33) |
令

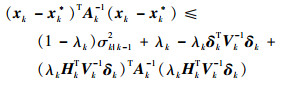 | (34) |
式中:
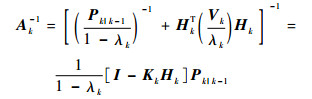 | (35) |
根据式 (22) 和式 (23) 有
 | (36) |
令

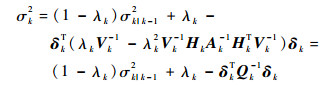 | (37) |
则按式 (32) 构造的椭球可以包含2个椭球的交集,量测更新递推方程证明完毕。
从定理1的时间更新和量测更新递推方程可以看出,尽管EOB-SME与Kalman滤波有着同样的预测-校正结构,但是它们之间有着根本不同的意义:Kalman滤波的估计结果是一个点,而EOB-SME的结果是一个椭球可行集。椭球可行集的大小可作为评估估计精度的指标。可认为椭球可行集的中心是一个最小-最大估计,即最小化估计值与真值之间的最大误差。
Kalman滤波中,估计误差的协方差矩阵表示点估计结果在随机噪声假设下的不确定度;而EOB-SME中的σ2P表示椭球可行集估计结果在有界噪声假设下的不确定度。根据所要最小化椭球尺寸的准则不同,将得到不同的最优参数。
2.2 最优参数的选择 通常情况下,采用最小化椭球的体积det (σ2P) 或椭球的迹tr (σ2P) 来求得时间更新或量测更新的最优参数pk和λk。通常选择最小迹准则来求取时间更新最优参数pk:
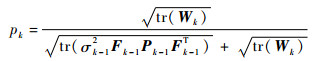 | (38) |
由于求解包含量测椭球集合与时间更新椭球集合交集的椭球较为复杂,所以对于求解量测更新参数λk,采用最小化椭球体积或迹准则都比较复杂。由于σk2可视为状态估计误差的Lyapunov函数的上界,即
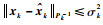
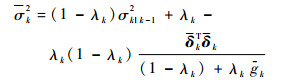 | (39) |
式中:
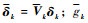
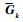

定理2[28]??假设初始参数为σ0|02≤1,
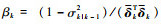

 | (40) |
式中:λk∈(0, 1)。
由定理2可知,当
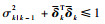
3 外定界椭球集员估计跟踪算法 为了提高EOB-SME跟踪算法对双基阵目标状态估计的精度,首先将量测方程在状态的一步预测估计点处进行一阶泰勒展开,用区间分析技术构造一个椭球来外包线性化后所产生的高阶项误差;再将该椭球与量测噪声椭球进行直和,得到新的量测噪声椭球。
定义区间变量


 | (41) |
式中:Pk|k-1i,i的上标i表示矩阵的第 (i, i) 个元素。
线性化误差的区间为
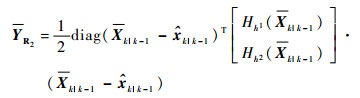 | (42) |
再用椭球来包含线性化误差的区间,即
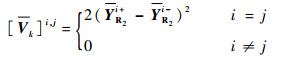 | (43) |
式中:上标+和-表示区间变量

最终得到新的量测噪声椭球为
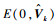
 | (44) |
 | (45) |
基于EOB-SME跟踪算法如下:
1) 在初始时刻设置初始参数

2) 在时刻k,根据定理1中的时间更新式 (16)~式 (18) 进行目标状态的一步预测估计,时间更新最优参数采用式 (38) 进行计算。
3) 先根据式 (7) 对量测方程进行一阶线性化展开。当获得量测集合后,根据定理2进行选择量测更新判断,若
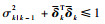
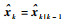

4) 继续更新直到跟踪过程结束。
4 仿真试验 仿真初始条件设置如下:2个基阵之间的距离D=1000 m,目标初始状态为x0=(2000 m, 3.42 m/s, 0, 10000 m, -9.39 m/s, 0)T,P0=[100, 50, 10, 100, 50, 10],σ0=1。过程椭球噪声的矩阵为W=diag (10, 10, 10,10, 10, 10),量测椭球噪声的矩阵为V=diag (0.1°, 0.1°)。采样周期为0.1 s,仿真时间为200 s。在以上仿真条件下,通过50次Monte Carlo仿真,对比EKF算法、CKF算法和本文提出的EOB-SME算法在双基阵情况下的跟踪效果。将椭球集合的中心作为点估计结果。定义均方根误差为
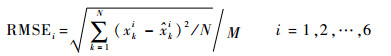 |
图 3所示为未知但有界的量测噪声,所有噪声均位于椭球内部。图 4给出了机动目标的实际速度和加速度变化曲线。
 |
| 图 3 未知但有界的量测噪声 Fig. 3 Unknown-but-bounded measurement noises |
| 图选项 |
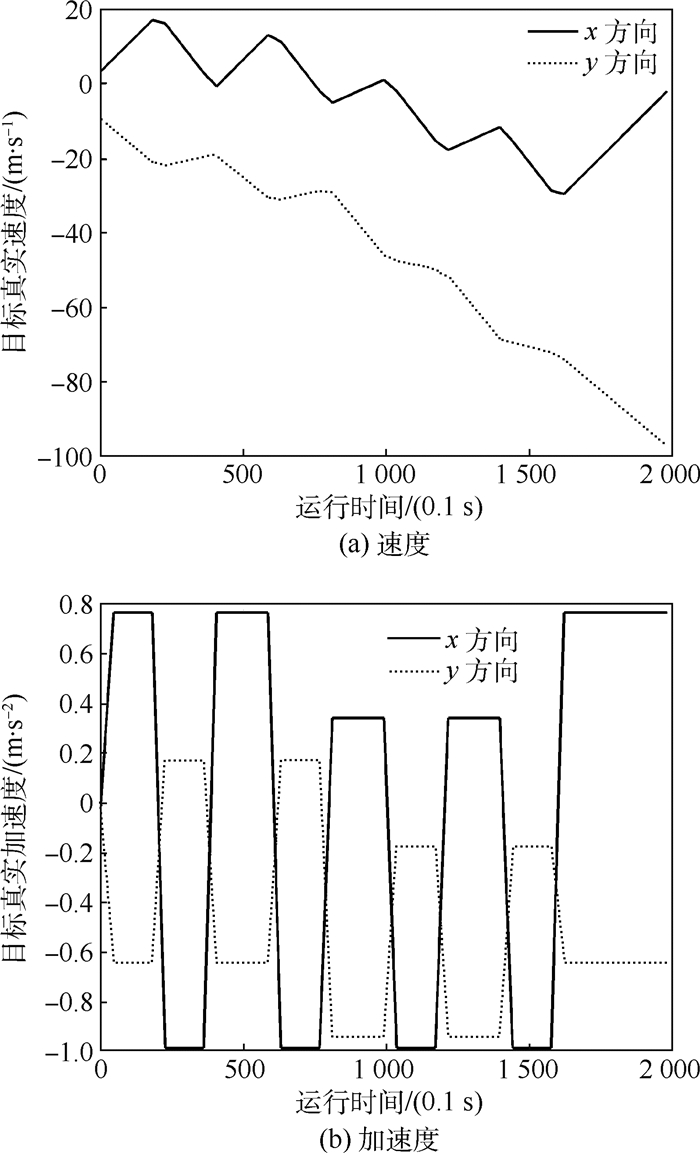 |
| 图 4 机动目标的速度和加速度曲线 Fig. 4 Maneuvering target velocity and acceleration curves |
| 图选项 |
图 5为不同算法对目标在x方向上的位置、速度和加速度均方根误差曲线。对于目标x方向上的位置估计,EOB-SME算法在跟踪阶段开始时,误差较大,随着跟踪过程的递推更新,逐渐减小。在跟踪后期,EOB-SME算法的x方向位置误差最小。而对于x方向上的速度和加速度估计,EKF算法的估计误差最大,CKF算法与EOB-SME算法在x方向速度的估计上误差比较接近,但CKF算法对于x方向加速度的估计在初期误差较大,随着跟踪递推的更新,在跟踪后期的误差逐渐与EOB-SME算法接近。
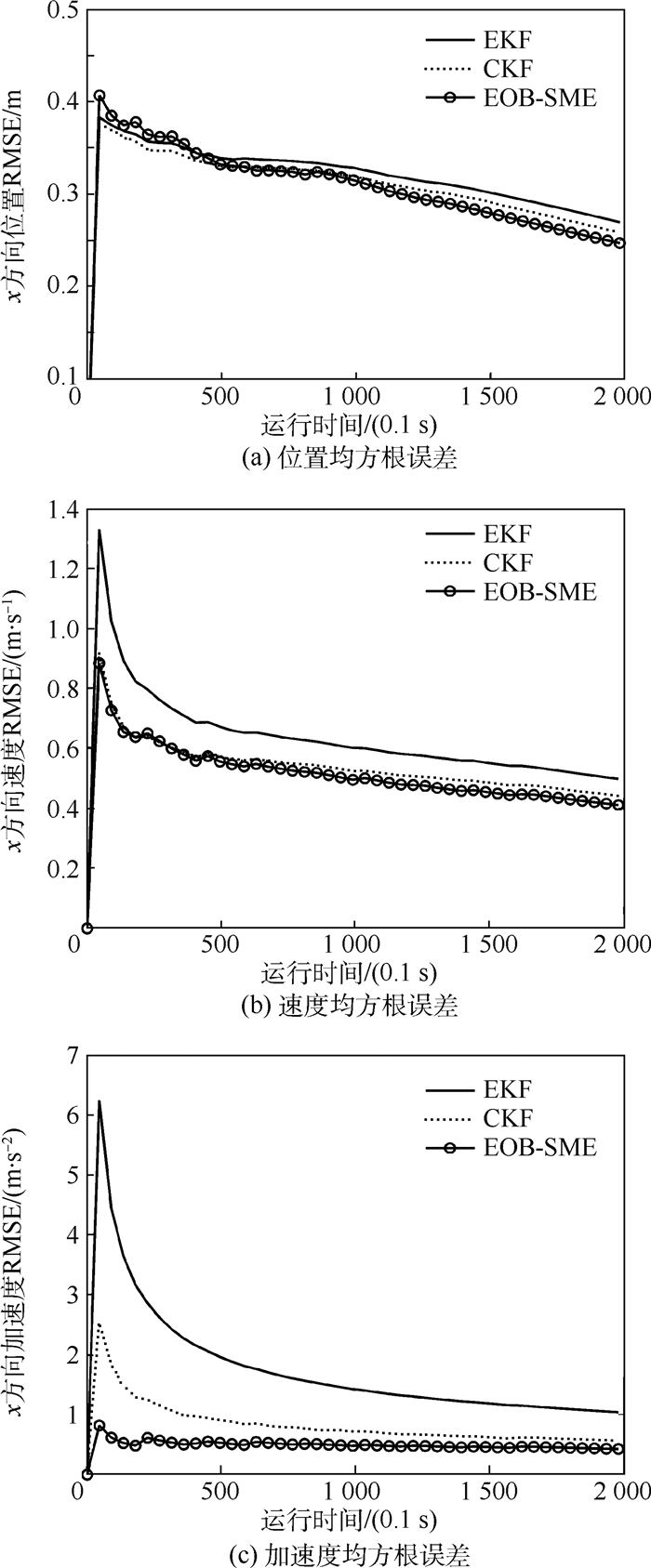 |
| 图 5 不同算法对目标在x方向上的位置、速度和加速度均方根误差曲线 Fig. 5 Position, velocity and acceleration root mean square error curves of target in the x direction for different algorithms |
| 图选项 |
图 6为不同算法对目标在y方向上的位置、速度和加速度均方根误差曲线。可以看出,由于目标在y方向上做较大的机动,EKF算法对位置、速度和加速度3个状态分量的均方根误差都较大。而CKF算法对目标的速度和加速度在跟踪初期均方根误差较大。随着跟踪的递推更新,CKF算法的均方根误差与EOB-SME算法的均方根误差曲线逐渐接近。
 |
| 图 6 不同算法对目标在y方向上的位置、速度和加速度均方根误差曲线 Fig. 6 Position, velocity and acceleration root mean square error curves of target in the y direction for different algorithms |
| 图选项 |
图 7为机动目标的运动轨迹。可以看出,EOB-SME算法的估计结果是一个椭球集合,机动目标的真实位置始终被椭球集合所包围。在目标转弯的时刻,目标的速度和加速度变化较剧烈,同时椭球的体积也会增大,表明此刻对目标状态估计结果的不确定性增大。到跟踪后期,由于目标不再进行机动,椭球体积逐渐缩小。
 |
| 图 7 机动目标的位置和椭球可行集 Fig. 7 Position of maneuvering target and ellipsoid feasible set |
| 图选项 |
表 1为EKF算法、CKF算法和EOB-SME算法对目标位置、速度和加速度估计的平均均方根误差。可以看出,CKF算法对目标x方向位置的均方根误差最小,EOB-SME算法对目标x方向的速度和加速度的均方根误差最小。而在对目标y方向各状态的估计中,EOB-SME算法的均方根误差最小。
表 1 目标状态估计的平均均方根误差 Table 1 Average RMSE of target state estimation
| 算法 | 位置/m | 速度/(m·s-1) | 加速度/(m·s-2) | |||
| x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | |
| EKF | 0.334 | 0.267 | 0.752 | 0.370 | 2.983 | 0.415 |
| CKF | 0.324 | 0.141 | 0.610 | 0.374 | 0.999 | 0.314 |
| EOB-SME | 0.329 | 0.121 | 0.567 | 0.272 | 0.550 | 0.284 |
表选项
表 2列出了EKF算法、CKF算法和EOB-SME算法的单次递推运行时间。由于CKF算法的计算量较大,所以其耗时最多,超过了1 ms。而EOB-SME算法的计算时间在1 ms以内,适合于在线实时的机动目标跟踪中应用。
表 2 每次递推更新的算法平均运行时间 Table 2 Average run time at each recursive update step for different algorithmsms
| ms | |||
| 算法 | EKF | CKF | EOB-SME |
| 运行时间 | 0.207 | 2.343 | 0.791 |
表选项
5 结论 本文针对在未知但有界噪声假设下的双基阵纯方位机动目标跟踪问题,提出了一种基于EOB-SME算法, 该算法通过最小化估计误差的Lyapunov函数上界来求取量测最优参数,降低了计算量;同时,通过用椭球对量测方程线性化后所产生的误差进行外包,与量测噪声椭球组成新的量测噪声椭球。在未知但有界噪声假设下,该算法对纯方位机动目标状态估计的精度优于EKF算法和CKF算法,并且计算时间为毫秒级。
在双基阵纯方位目标跟踪问题中,基站之间基线测量的精度和基阵之间的相对空间位置将会影响跟踪的效果。如何优化双基站的空间布局,在有基线偏差的情况下如何提高跟踪系统的性能,是值得进一步研究的课题。
参考文献
| [1] | 刘忠, 周丰, 石章松, 等. 纯方位目标运动分析[M].北京: 国防工业出版社, 2009: 4.LIU Z, ZHOU F, SHI Z S, et al. Bearing-only target motion analysis[M].Beijng: National Defense Industry Press, 2009: 4.(in Chinese) |
| [2] | BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with application to tracking and navigation[M].New York: John Wiley & Sons, Inc, 2001: 9. |
| [3] | 胡科强, 袁志勇, 周浩. 双基阵纯方位被动定位跟踪方法[J].舰船科学技术, 2012, 34(5): 83–86.HU K Q, YUAN Z Y, ZHOU H. Methods on the performance of bearing-only target tracking based two arrays[J].Ship Science and Technolgy, 2012, 34(5): 83–86.(in Chinese) |
| [4] | 徐本连. 双 (多) 基纯方位目标定位跟踪算法研究[D]. 南京: 南京理工大学, 2006: 1-4.XU B L.The algorithm study on bearings-only target localization and tracking using two or more observer[D].Nanjing:Nanjing University of Science and Technology, 2006:1-4(in Chinese). |
| [5] | XU B L, CHEN Q L, WU Z Y, et al. Analysis and approximation of performance bound for two-observer bearings-only tracking[J].Information Sciences, 2008, 178(8): 2059–2078.DOI:10.1016/j.ins.2007.12.004 |
| [6] | 吴卫华, 江晶, 范雄华, 等. WGS-84坐标系下双机纯角度无源定位及性能分析[J].红外与激光工程, 2015, 44(2): 654–661.WU W H, JIANG J, FAN X H, et al. Performance analysis of passive location by two airborne platforms with angle-only measurements in WGS-84[J].Infrared and Laser Engineering, 2015, 44(2): 654–661.(in Chinese) |
| [7] | 冉华明, 周锐, 吴江, 等. 双机协同无源目标跟踪轨迹优化[J].北京航空航天大学学报, 2015, 41(1): 160–166.RAN H M, ZHOU R, WU J, et al. Trajectory optimization of two air crafts in collaborative passive target tracking[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 160–166.(in Chinese) |
| [8] | 任波, 闫向远. 纯角度跟踪非线性预测滤波算法研究[J].弹箭与制导学报, 2014, 34(2): 6–8.REN B, YAN X Y. Bearing-only tracking nonlinear prediction filter algorithm research[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(2): 6–8.(in Chinese) |
| [9] | 许兆鹏, 韩树平. 一种双基阵纯方位机动目标被动跟踪方法[J].舰船科学技术, 2012, 34(11): 100–103.XU Z P, HAN S P. Research on an algorithm for passive tracking of maneuvering target based on two arrays bearings[J].Ship Science and Technolgy, 2012, 34(11): 100–103.(in Chinese) |
| [10] | JAUFFRET C, PILLON D, PIGNOL A C. Bearings-only maneuvering target motion analysis from a nonmaneuvering platform[J].IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1934–1949.DOI:10.1109/TAES.2010.5595605 |
| [11] | AIDALA V J. Kalman filter behavior in bearings-only tracking application[J].IEEE Transactions on Aerospace and Electronic Systems, 1979, 15(1): 29–39. |
| [12] | 鹿传国, 冯新喜, 张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J].系统工程与电子技术, 2012, 34(1): 28–33.LU C G, FENG X X, ZHANG D. Pure bearing tracking based on improved cubature Kalman filter[J].Systems Engineering and Electronics, 2012, 34(1): 28–33.(in Chinese) |
| [13] | LEONG P H, ARULAMPALAM S, LAMAHEWA T A, et al. A Gaussian-sum based cubature Kalman filter for bearing-only[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1161–1176.DOI:10.1109/TAES.2013.6494405 |
| [14] | 方君, 戴邵武, 许文明, 等. 基于ST-SRCKF的超高速强机动目标跟踪算法[J].北京航空航天大学学报, 2016, 42(8): 1698–1708.FANG J, DAI S W, XU W M, et al. Highly maneuvering hypervelocity-target tracking algorithm based on ST-SRCKF[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1698–1708.(in Chinese) |
| [15] | 陈辉, 韩崇昭. 纯方位距离参数化概率假设密度和势概率假设密度滤波器[J].控制理论与应用, 2015, 32(5): 579–590.CHEN H, HAN C Z. Bearings-only range-parameterized probability hypothesis density and cardinalized probability hypothesis density filter[J].Control Theory and Applications, 2015, 32(5): 579–590.(in Chinese) |
| [16] | 孔云波, 冯新喜, 鹿传国, 等. 改进高斯混合粒子滤波的纯方位目标跟踪算法[J].宇航学报, 2012, 33(7): 971–977.KONG Y B, FENG X X, LU C G, et al. An improved Gaussian mixture particle filter based targets tracking algorithm for bearing-only tracking system[J].Journal of Astronautics, 2012, 33(7): 971–977.(in Chinese) |
| [17] | 李银伢, 谭维茜, 盛安冬. 改进型粒子滤波算法在多站纯方位被动跟踪中的应用[J].控制理论与应用, 2011, 28(8): 1081–1086.LI Y Y, TAN W Q, SHENG A D. Application of improved particle filter algorithm to bearings-only passive tracking in multiple stations[J].Control Theory and Applications, 2011, 28(8): 1081–1086.(in Chinese) |
| [18] | SCHWEPPE F C. Recursive state estimation unknown but bounded errors and system inputs[J].IEEE Transactions on Automatic Control, 1968, 13(1): 22–28.DOI:10.1109/TAC.1968.1098790 |
| [19] | 孙先仿, 王世纪, 张海. 扩展集员滤波在捷联惯导大方位失准角初始对准中的应用[J].中国惯性技术学报, 2008, 16(5): 505–508.SUN X F, WANG S J, ZHANG H. Application of extended set-membership filter in SINS initial alignment of large azimuth misalignment[J].Journal of Chinese Inertial Technology, 2008, 16(5): 505–508.(in Chinese) |
| [20] | 江涛, 钱富才. 基于ESMF算法的GPS信号多普勒频率估计[J].控制与决策, 2016, 31(2): 378–384.JIANG T, QIAN F C. Estimated Doppler frequency of GPS signal based on ESMF[J].Control and Decision, 2016, 31(2): 378–384.(in Chinese) |
| [21] | 宋大雷, 吴冲, 齐俊桐, 等. 基于MIT规则的自适应扩展集员估计方法[J].自动化学报, 2012, 38(11): 1847–1860.SONG D L, WU C, QI J T, et al. A MIT-based nonlinear adaptive set-membership filter for ellipsoidal estimation[J].Acta Automatica Sinica, 2012, 38(11): 1847–1860.DOI:10.3724/SP.J.1004.2012.01847(in Chinese) |
| [22] | MAKSAROV D G, NORTON J P. State bounding with ellipsoidal set description of the uncertainty[J].International Journal of Control, 1996, 65(5): 847–866.DOI:10.1080/00207179608921725 |
| [23] | SCHOLTE E, CAMPBELL M E. A nonlinear set-membership filter for on-line applications[J].International Journal of Robust and Nonlinear Control, 2003, 13(15): 1337–1358.DOI:10.1002/(ISSN)1099-1239 |
| [24] | ZHOU B, HAN J D, LIU G J. A UD factorization-based nonlinear adaptive set-membership filter for ellipsoidal estimation[J].International Journal of Robust and Nonlinear Control, 2008, 18(16): 1513–1531.DOI:10.1002/rnc.v18:16 |
| [25] | LIU Y S, ZHAO Y, WU F L. Ellipsoidal state-bounding-based set-membership estimation for linear system with unknown-but-bounded disturbances[J].IET Control Theory and Applications, 2016, 10(4): 431–442.DOI:10.1049/iet-cta.2015.0654 |
| [26] | FLETCHER K F, ARULAMPALAM S M, EVANS J R, et al. Ellipsoidal set based tracking with nonlinear measurements[J].IEE Proceeding-Radar, Sonar and Navigation, 2005, 152(5): 335–344.DOI:10.1049/ip-rsn:20045108 |
| [27] | RAHMATI H, KHALOOZADEH H, AYATI M.Maneuvering target tracking method based on unknown but bounded uncertainties[C]//18th IFAC World Congress.Milano:IFAC Press, 2011:4290-4295. |
| [28] | LIU Y S, ZHAO Y.Ellipsoidal set filter combined set-membership and statistics uncertainties for bearing-only maneuvering target tracking[C]//IEEE/ION Position Lacation and Navigation Symposium.Piscataway, NJ:IEEE Press, 2014:753-759. |
