文献[2]提出的基于随机集理论的概率假设密度滤波器 (PHD) 和势概率假设密度滤波器 (CPHD),突破了传统算法所使用的数据关联理论,在保证精度的同时,提高了实时性,对于线性系统具有较高的实用价值。但在实际应用中,多目标跟踪系统大部分属于非线性系统。针对这一问题,专家们提出了如高斯和概率假设密度滤波器 (GSPHD)[3]、序贯蒙特卡罗概率假设密度滤波器 (SMC-PHD)[4]、扩展卡尔曼概率假设密度滤波器 (EK-PHD)、无迹卡尔曼概率假设密度滤波器 (UK-PHD)[5]、高斯混合粒子概率假设密度滤波器 (GMP-PHD)[6]和中心差分卡尔曼概率假设密度滤波器 (CDKF-PHD)[7]等多种滤波方法。
近年来,为了增加多目标跟踪的可靠性,提高目标观测效率,国内外研究****通过引入幅值信息来判断量测的有效性。文献[8]提出一种基于幅值信息的概率数据关联算法,算法在粒子滤波的基础上,将概率数据关联算法中的关联似然函数与幅值似然比相结合,实现对多目标进行跟踪。文献[9]将幅值信息与交互式多模型概率数据关联算法相结合,有效地改善了对多机动目标的跟踪。文献[10]针对基于幅值信息的多目标跟踪中信杂比非先验,提出了一种信噪比 (SNR) 估计的多目标跟踪算法。文献[11-12]将目标幅值信息与PHD、CPHD算法相结合, 对于线性模型系统中的多目标跟踪获得了较好的效果。目前,基于幅值信息的多目标跟踪算法中,大多背景杂波幅值服从高斯或者瑞利分布[8-12],文献[13]中实验证明,这些假设并不适用于实际应用过程,因此,杂波幅值服从重尾分布的多目标跟踪问题更应该被考虑到。
本文在文献[7]的基础上,提出了一种基于极大似然 (ML) 背景参数估计的中心差分卡尔曼-势概率假设密度滤波 (BE-CDKF-CPHD) 算法。算法首先运用韦布尔分布对背景杂波的幅值信息进行建模,之后采用ML法估计背景信杂比,计算检测概率和虚警概率,通过极大相然性虚警 (ML-CFAR) 算法提取有效量测,利用中心插值理论对非线性函数做多项式逼近,将幅值似然函数与CPHD中的位置似然函数、杂波强度函数相结合对多目标后验均值进行估计,实现非线性系统下的多目标的跟踪。该算法对目标状态跟踪的同时考虑了幅值信息的影响,增强了算法的鲁棒性,提高了跟踪精度。
1 CPHD滤波器 由于PHD滤波器仅是对多目标概率假设密度的一阶近似,丢失高阶信息,导致低信杂比环境下目标数目的错误估计。Mahler[2]提出了递推强度函数与目标个数完整统计信息的CPHD滤波器,其递推过程与PHD滤波器一致,主要包含预测与更新2个过程。
在CPHD滤波器的预测过程中,运用k-1时刻的后验势分布函数pk-1与后验强度函数Dk-1分别对k时刻势分布函数与强度函数进行预测。CPHD预测方程与势分布预测方程分别为
 | (1) |
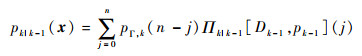 | (2) |
式中:
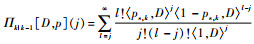
fk|k-1 (·∣ζ) 为k时刻状态转移密度函数;ps,k (ζ) 为k时刻目标存活概率;pΓ,k (·) 为k时刻新生目标势分布; γk (·) 为k时刻新生目标强度函数。
假定k时刻传感器接收到的量测集为Zk,预测强度函数与势分布函数如式 (1) 和式 (2) 所示,则CPHD对于强度函数和势分布函数的更新过程可以表示为
 | (3) |
 | (4) |
式中:
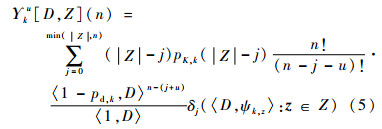 | (5) |
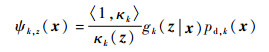 | (6) |
式中:〈·, ·〉为2个函数的内积;gk (·∣x) 为k时刻目标似然函数;δj为初等对称函数;pd,k (x) 为目标检测概率;κk (z) 为杂波量测强度函数;pK,k (·) 为杂波势分布。目标数目
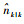
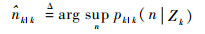 | (7) |
相比于PHD的期望后验估计,CPHD可得到更为准确和稳定的目标数目估计。
2 背景参数估计 2.1 杂波模型 在对杂波幅值信息进行建模的过程中,高斯分布与瑞利分布并不能很好地模拟杂波真实分布状态。虽然传统的复合高斯分布可用来对杂波幅值进行建模,但是复合高斯分布形式较为复杂, 导致直接求解其概率密度困难。根据文献[14],本文运用韦布尔分布对目标幅值信息进行建模。
令幅值a为符合包络检测条件的匹配滤波器输出,若不考虑信号损失,则杂波幅值信息的概率密度函数为
 | (8) |
式中:ν和b分别为韦布尔分布的形状参数与尺度参数。
因目标幅值信息受雷达功率强度、目标距离范围等多方面影响,具有波动性。对时变信号强度的估计较为困难。本文采用目标幅值为Swelling Ⅰ条件下具有瑞利分布的窄频信号模型[15]。假设目标平均幅值为δt,目标信杂比 (SCR) 计算如式 (9) 所示:
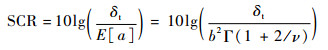 | (9) |
式中:E[a]为韦布尔分布下的杂波幅值强度的一阶矩;Γ () 为伽马函数。含有目标幅值信息的概率密度函数如式 (10) 所示:
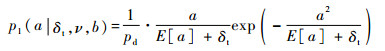 | (10) |
式中:pd为目标检测概率。
2.2 ML背景参数估计 传统多目标跟踪构架中,将经过匹配滤波器得到的原始信号进行恒虚警处理,获得量测,并将其作为滤波器的输入,以此循环递推达到跟踪目的。在杂波幅值服从重尾分布的环境中,原始信号经过恒虚警处理后依旧有大量数据存在,大大增加系统计算负担。针对这一问题,提出一种ML背景估计器,运用ML估计理论[16]对杂波模型参数进行估计,并计算检测概率与虚警概率,之后采用ML-CFAR算法有效消除背景杂波,提高检测能力。
设k时刻匹配滤波器输出M个采样的数据信息为 (ak1,ak2, …, akM),且每一个参考单元相互独立,则k时刻韦布尔分布联合概率密度函数为
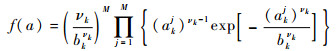 | (11) |
对式 (11) 求导可得k时刻韦布尔分布尺度参数

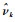
 | (12) |
 | (13) |
式 (13) 可运用Newton-Raphson法进行递归求解。对于韦布尔分布中的信号检测,固定门限CFAR与平均CFAR效果并不明显[17]。本文采用ML-CFAR[18]对信号进行处理。当信杂比大于1时,可运用ML-CFAR计算检测概率与虚警概率:
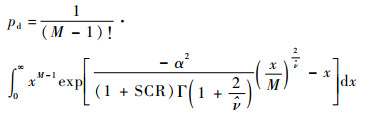 | (14) |
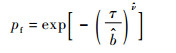 | (15) |
式中:α为采样点数M和虚警概率pf的函数,α=[M (pf-1/M-1)]1/ν。
将式 (9)、式 (12) 和式 (13) 分别代入式 (14)、式 (15),即可求得检测概率pd与虚警概率pf。
3 基于ML背景参数估计的CDKF-CPHD滤波器 3.1 CDKF-CPHD滤波器 CDKF-CPHD滤波器是以非线性最优滤波器为基本理论框架,运用Stirling插值公式对状态向量进行非线性变换,采用CPHD滤波器中概率假设密度计算的思想,递推估计系统状态的后验均值以及协方差,实现对多个非线性目标的目标数目估计与状态跟踪。
Stirling插值运用多项式近似方法实现非线性函数的线性变换问题。假设随机向量x, x∈Rn, y=f (x)。采用多维插值公式对函数进行二次截断可得
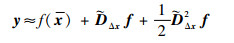 | (16) |
式中:
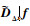
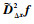
根据Striling插值公式以及中心差分逼近,对CPHD滤波器中Dk|k-1 (x) 和Dk (x) 中的非高斯成分进行近似,并运用卡尔曼滤波器的思想计算均值、协方差和互协方差,就可得到CDKF-CPHD滤波器。
考虑非线性状态空间模型xk+1=f (xk, vk),yk=g (xk, wk)。假设vk、wk为独立同分布的高斯白噪声,vk~N (vk, Qk),wk~N (wk, Rk)。量测zk由量测位置信息yk与幅值信息ak组成,即zk=[ykak]T。
设k-1时刻CPHD滤波器后验强度函数Dk-1中高斯项中的权值、均值和协方差分别为ωk-1(i)、mk-1(i)和Pk-1(i),则存活目标的预测概率假设密度中高斯项的权值、均值、协方差分别为
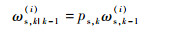 | (17) |
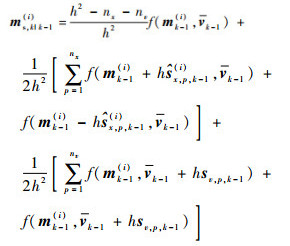 | (18) |
 | (19) |
式中:
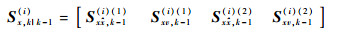 |
其中:
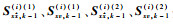
在CDKF-CPHD滤波器中预测势分布的计算公式与传统CPHD滤波器的计算一致,如式 (2) 所示。
假设预测概率假设密度滤波Dk|k-1中高斯项中的权值、均值和协方差分别为ωk|k-1(i)、mk|k-1(i)和Pk|k-1(i),杂波的概率假设密度为κk (y), CDKF-CPHD滤波器更新后概率假设密度滤波中高斯项的权值、均值、协方差分别为
 | (20) |
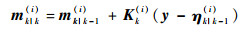 | (21) |
 | (22) |
式中:
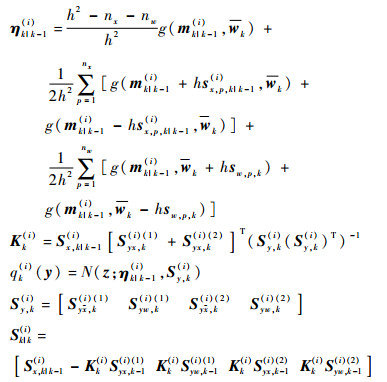 |
nx、nv和nw分别为状态向量、过程噪声向量和量测噪声向量维数;h为区间长度;sv,p,k、sw,p,k为Sv、Sw的第p列;Syx,k(i)(1)、Syx,k(i)(2)、Syw,k(i)(1)、Syw,k(i)(2)分别为中心差分卡尔曼滤波中的一阶、二阶差分算子,其具体形式参见文献[19]。
3.2 BE-CDKF-CPHD滤波算法高斯混合实现 在算法实现阶段,前一时刻的后验强度函数与当前时刻的新生目标强度函数均采用高斯混合模型进行逼近。虽然高斯混合模型可以对任意密度函数进行逼近,但是在实际场景中,新生目标可能出现在场景的任意位置,这是等概率事件,应服从均匀分布。故CDKF-CPHD滤波器的新生目标采用部分均匀模型[20]。其中新生目标的先验分布与量测似然函数分别为
 | (23) |
 | (24) |
式中:θ和φ分别为状态y中可观测与不可观测部分;U (θ, B) 为θ在区域B中的均匀分布;φ和σφ2分别为不可观测状态先验均值与方差;ζb,k为k时刻期望新生目标数目;σθ2为高斯分布的先验方差。BE-CDKF-CPHD滤波器高斯实现过程如下。
1) 初始化
在k=0时刻,选择一个初始先验概率假设密度D0|0 (θ, φ),初始势分布p0|0。
2) 背景估计
k时刻将经过匹配滤波器输出得到的原始信号通过ML估计获得韦布尔分布参数νk、bk, 并在ML-CFAR中计算检测概率与虚警概率pd,k、pf, 将检测到的信号作为k时刻所得量测值Zk。
3) 预测步骤
令k-1时刻混合高斯项的参数为{ωk-1(i), mk-1(i), Pk-1(i)}i=1Jk-1,假设新生目标总能被检测,新生目标所产生的预测概率密度假设参数为
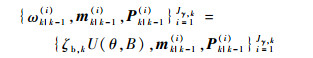 |
存活目标的预测概率假设密度参数计算如式 (17)~式 (19) 所示,则高斯分量数目和为Jk|k-1=Js,k|k-1+ζb,k。
4) 更新步骤
对k-1时刻预测得到的混合高斯项分别进行更新,预测高斯概率假设密度Dk|k-1的参数为{ωk|k-1(i), mk|k-1(i), Pk|k-1(i)}i=1Jk|k-1。首先运用式 (8)、式 (10) 和式 (15) 计算杂波幅值信息似然函数与含有目标幅值信息的似然函数κa (a) 和ga (a|δt)
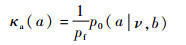 | (25) |
 | (26) |
假设幅值信息与量测相互独立,量测似然函数与杂波强度函数可以改为
 | (27) |
 | (28) |
将式 (27) 和式 (28) 代入式 (6) 得到
 | (29) |
将式 (29) 代入式 (5) 中计算内积,并利用式 (20)~式 (22) 计算高斯项中的权值、均值、协方差。为了简化计算,令
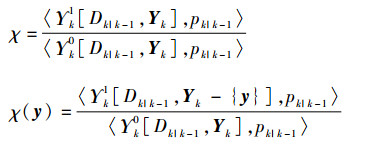 |
计算未检测目标的假设概率密度高斯项参数为
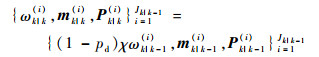 |
已检测到存活目标的假设概率密度高斯项参数为
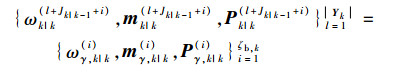 |
式中:
 |
已检测到新生目标的假设概率密度高斯项参数为
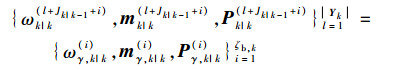 |
其中:
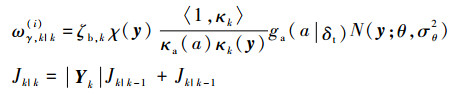 |
势分布状态更新与传统CPHD更新一致计算方法参考式 (4)。
4 仿真分析 本文通过模拟二维空间内3个机动目标的运动情况来验证本文算法的有效性能。目标运动模型主要由匀速直线模型与转弯模型组成。假设目标i在k时刻的飞行状态为

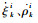
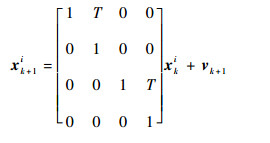 | (30) |
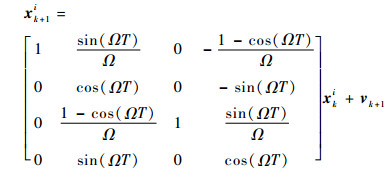 | (31) |
式中:Ω为转弯角速度;T为采样时间间隔; 过程噪声vk+1~N (0, Q), Q=diag (σv2G, σv2G)。
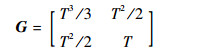 |
量测状态方程如式 (32) 所示:
 | (32) |
量测噪声wk+1~N (0, diag (σξ2, σρ2)), 采样时间T=1 s σv2=0.2 m, σξ2=σρ2=0.5 m。目标跟踪场景中每个目标的存活概率为ps,k=0.98。目标运动参数如表 1所示,目标运动轨迹如图 1所示。
表 1 目标运动参数 Table 1 Target motion parameters
| 目标 | 初始 (结束) 时刻/s | 初始位置/m | 初始速度/(m·s-1) |
| 1 | 2(40) | (61, 30) | (-1, 1) |
| 2 | 12(40) | (64, 27) | (-1.5, -1.5) |
| 3 | 12(50) | (64, 30) | (1, 1.5) |
表选项
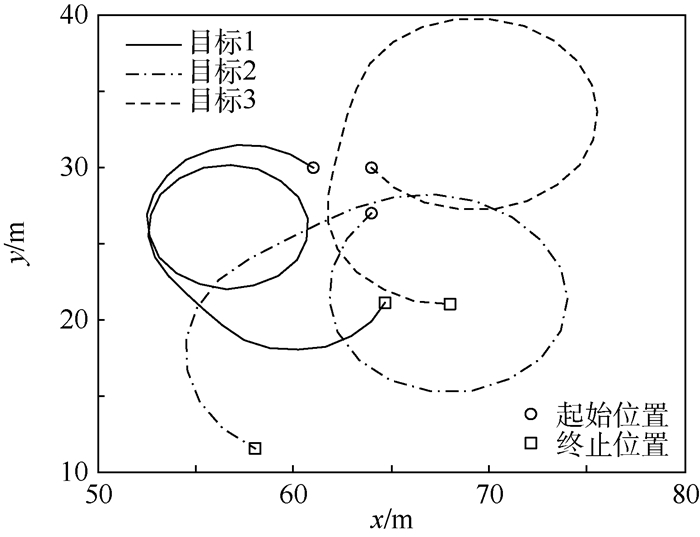 |
| 图 1 目标运动轨迹 Fig. 1 Target motion trajectories |
| 图选项 |
BE-CDKF-CPHD滤波器初始高斯参数{ω0, m0, P0}i=1J0的参数为
 |
新生目标的概率假设密度γk (θ, φ) 中的新生目标数目ζb,k=4, 检测区域面积B=100 m×100 m, 新生目标速度信息满足均值为0、方差为5的高斯分布。中心差分区间长度h=5。
为了评估所提滤波器性能,本文运用最优子模式分配 (OSPA) 距离[21]进行分析。OSPA距离能够同时兼顾有限集的势间差异和有限集的元素间差异。OSPA距离公式为
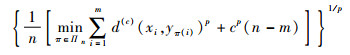 | (33) |
式中:X={x1, x2, …, xm}和Y={y1, y2,…,yn}分别为目标状态的真实有限集合与目标状态的估计有限集合,m、n分别为集合X、Y元素数;p为序列参数,用来调节OSPA距离对于异常值的敏感度;c为截断系数,用来调节误差误分配权值。
在3种不同情况下对BE-CDKF-CPHD进行100次蒙特卡罗仿真,仿真环境如表 2所示。
表 2 仿真环境 Table 2 Simulation environment
| 情况 | ν | b | δt | SCR/dB |
| 1 | 2 | 0.5 | 2.5 | 10 |
| 2 | 2 | 0.1 | 1 | 20 |
| 3 | 1 | 0.1 | 20 | 30 |
表选项
从图 2中可以看出,当信杂比相对较高时,系统对于多机动目标的OSPA距离越小。
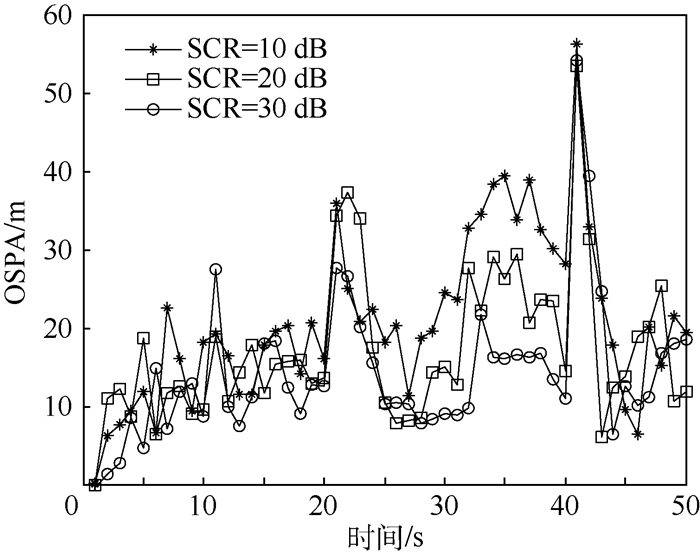 |
| 图 2 不同信杂比下的OSPA距离比较 Fig. 2 Comparison of OSPA distance under different signal-to-clutter ratios |
| 图选项 |
本文在表 2中SCR=10 dB仿真环境下,对CPHD滤波器、CDKF-PHD滤波以及BE-CDKF-CPHD滤波器分别进行100次蒙特卡罗仿真。设定c=70,p=2。OSPA距离仿真结果与目标数目估计结果分别如图 3和图 4所示。
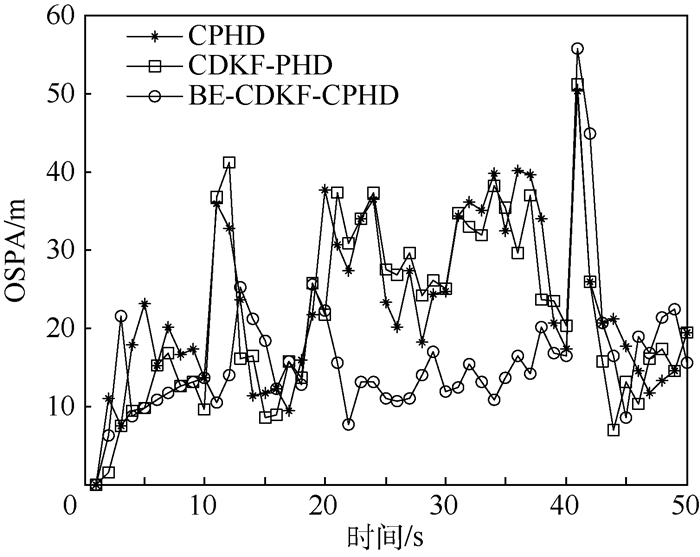 |
| 图 3 3种算法的OSPA距离比较 Fig. 3 Comparison of OSPA distance for three algorithms |
| 图选项 |
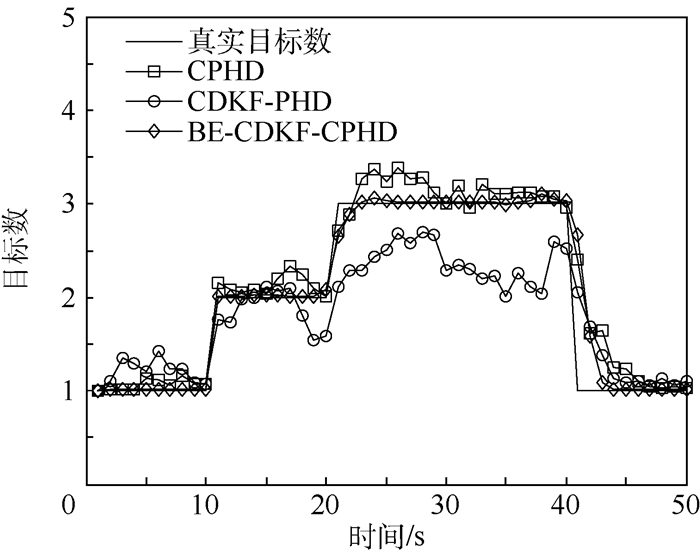 |
| 图 4 3种算法的目标数估计与真实目标数的比较 Fig. 4 Comparison of true and estimated target numbers for three algorithms |
| 图选项 |
从图 3可以看出t < 40 s时,相比于CPHD滤波器与CDKF-PHD滤波器,BE-CDKF-CPHD滤波器的OSPA距离小于以上两者。当t > 40 s, 由于目标1、目标2均消失, 目标数目产生较大变化, 3种算法的OSPA基本相同。在图 4中BE-CDKF-CPHD滤波器的目标数目估计与真实目标数目基本一致,CDKF-PHD滤波器的估计效果相比于CPHD滤波器具有较大的振荡。
5 结论 为了解决多个非线性目标在重尾杂波下的跟踪问题。本文提出一种基于ML-CFAR背景参数估计的CDKF-CPHD多目标跟踪算法。仿真实验表明:
1) 本文所提的BE-CDKF-CPHD多目标跟踪算法可以实现对多个机动目标在重尾分布杂波下的准确跟踪。相比于CDKF-PHD滤波器,CPHD滤波器,其OSPA距离较低。
2) 随着信杂比的增大,BE-CDKF-CPHD多目标跟踪算法的OSPA距离也逐步变小。
3) 本文所提出的BE-CDKF-CPHD多目标跟踪算法能够在目标数目产生较大变化时,仍可准确估计目标的数目。
BE-CDKF-CPHD多目标跟踪算法的滤波精度仍需提高,下一步研究在重尾杂波分布下具有更高精度的多目标跟踪算法。
参考文献
| [1] | STONE L D, STREIT R L, CORWIN T L, et al. Bayesian multiple target tracking[M].2nd edLondon: Artech House, 2013: 1-5. |
| [2] | MAHLER R P S. Statistical multisource-multitarget information fusion[M].London: Artech House, 2007: 5-13. |
| [3] | YIN J J, ZHANG J Q, ZHUANG Z S. Gaussian sum PHD filtering algorithm for nonlinear non-Gaussian models[J].Chinese Journal of Aeronautics, 2008, 21(4): 341–351.DOI:10.1016/S1000-9361(08)60045-X |
| [4] | VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224–1245.DOI:10.1109/TAES.2005.1561884 |
| [5] | VO B N, MA W K. The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104.DOI:10.1109/TSP.2006.881190 |
| [6] | CLARK D, VO B T, VO B N.Gaussian particle implementations of probability hypothesis density filters[C]//Proceedings of IEEE Aerospace Conference.Piscataway, NJ:IEEE Press, 2007:1-11. |
| [7] | 陈里铭, 陈喆, 殷福亮. 基于中心差分卡尔曼-概率假设密度滤波的多目标跟踪方法[J].控制与决策, 2013, 28(1): 36–42.CHEN L M, CHEN Z, YIN F L. Central difference Kalman-probability hypothesis density filter for multi-target tracking[J].Control and Decision, 2013, 28(1): 36–42.(in Chinese) |
| [8] | 章飞, 周杏鹏, 陈小惠. 基于幅值信息的联合概率数据关联粒子滤波算法[J].系统工程与电子技术, 2011, 33(2): 453–457.ZHANG F, ZHOU X P, CHEN X H. Joint probabilistic data association particle filter algorithm based on amplitude information title[J].Systems Engineering and Electronics, 2011, 33(2): 453–457.(in Chinese) |
| [9] | LERRO D, BAR-SHALOM Y. Interacting multiple model tracking with target amplitude feature[J].IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(2): 494–509.DOI:10.1109/7.210086 |
| [10] | BAE S H, KIM D Y, YOON J H, et al. Automated multi-target tracking with kinematic and non-kinematic information[J].IET Radar Sonar Navigation, 2012, 6(4): 272–281.DOI:10.1049/iet-rsn.2011.0154 |
| [11] | CLARK D, RISTIC B, VO B N.PHD filtering with target amplitude feature[C]//Proceedings of the 11th International Conference on Information Fusion, FUSION 2008.Piscataway, NJ:IEEE Press, 2008:1-7. |
| [12] | QIU C, ZHANG Z, LU H, et al. Amplitude-aided CPHD filter for multitarget tracking in infrared images[J].Progress in Electromagnetics Research B, 2014, 61(1): 211–224. |
| [13] | ABRAHAM D.Choosing a non-Rayleigh reverberation model[C]//Proceedings of the OCEANS '99 MTS/IEEE-Riding the Crest into the 21st Century.Piscataway, NJ:IEEE Press, 1999, 1:284-288. |
| [14] | WARD K D, WATTS S, TOUGH R J A. Sea clutter:Scattering, the K distribution and radar performance[M].2nd edLondon: IET, 2013: 375-389. |
| [15] | BREKKE E, HALLINGSTAD O, GLATTETRE J. Tracking small targets in heavy-tailed clutter using amplitude information[J].IEEE Journal of Oceanic Engineering, 2010, 35(2): 314–329.DOI:10.1109/JOE.2010.2044670 |
| [16] | 杨谋存, 聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J].南京航空航天大学学报, 2007, 39(1): 22–25.YANG M C, NIE H. Advanced algorithm for maximum likelihood estimation of three parameter Weibull distribution[J].Journal of Nanjing University of Aeronautics and Astronautics, 2007, 39(1): 22–25.(in Chinese) |
| [17] | RICHARDS M A. Fundamentals of radar signal processing[M].New York: Tata McGraw-Hill Education, 2005: 347-382. |
| [18] | RAVID R, LEVANON N. Maximum-likelihood CFAR for Weibull background[J].IEE Proceedings, Part F:Radar and Signal Processing, 1992, 139(3): 256–264.DOI:10.1049/ip-f-2.1992.0033 |
| [19] | N?RGAARD M, POULSEN N K, RAVN O. New developments in state estimation for nonlinear systems[J].Automatica, 2000, 36(11): 1627–1638.DOI:10.1016/S0005-1098(00)00089-3 |
| [20] | BEARD M, VO B T, VO B N, et al.Gaussian mixture PHD and CPHD filtering with partially uniform target birth[C]//International Conference on Information Fusion.Piscataway, NJ:IEEE Press, 2012:535-541. |
| [21] | SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing, 2008, 56(8): 3447–3457.DOI:10.1109/TSP.2008.920469 |
