一般而言,瞬时可用度都用特定模型来研究,如基于马尔可夫过程的马氏模型[13-14],运用更新理论的更新模型[15]以及离散概率模型[16]。由于在故障时间和修复时间服从指数分布下的两状态更新模型中,瞬时可用度不具有波动性。对于相关随机变量服从指数分布的三状态更新模型中,是否还有类似的结论成为本文研究的重点。
三状态 (工作、修理延迟、修理) 基本更新模型中为了避免修理延迟,可以通过改变维修方式来弥补。一般维修方式分为故障小修、预防性维修和事后维修[17-18]。维修策略也主要分为使总成本最低和使系统稳态可用度最大2种[19-21]。本文首先提出带有故障小修的三状态更新模型,可以使稳态可用度提升。同时使用一套波动判定理论分析了在此模型下瞬时可用度产生波动的条件,结论说明了在某些条件下带有故障小修的三状态更新模型中瞬时可用度是存在波动的。最后给出了一个抑制波动的方法。通过控制平均修理时间小于平均工作时间的1/4,则瞬时可用度将不存在波动。
1 预备知识 本节首先引入三状态的基本更新模型并给出其相应的性质作为后面分析的理论基础。
1.1 模型引入 按照文献[11],瞬时可用度是基于单部件三状态可修系统的更新模型,是由随机变量故障时间X、修理延迟时间W和修理时间Y构成的更新过程。模型中瞬时可用度满足如下更新方程:
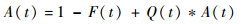 | (1) |
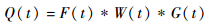 | (2) |
式中:“*”表示卷积;A(t) 为瞬时可用度;F(t)、W(t) 和G(t) 分别为相关随机变量服从的分布函数;Q(t) 为周期T的分布函数。
图 1为由三状态形成更新过程建模的示意图。
 |
| 图 1 单部件三状态的更新模型 Fig. 1 A renewal process for one unit with three states |
| 图选项 |
1.2 模型变化 三状态的基本模型中,存在修理延迟,无疑导致部件停止工作的时间延长。一般部件发生故障分为暂时性故障和永久性故障。所以针对暂时性故障只要采取故障小修 (应急小修) 即可恢复使用。本文通过用故障小修替代修理延迟,构成了新的三状态模型。
其中假设:
1) 部件发生永久性故障之前,有且仅有一次暂时性故障。
2) 故障小修所用时间不计。
3) 故障小修后部件恢复,但故障率不发生改变。
4) 永久性故障修理后,部件如新。
变化后模型中瞬时可用度满足如下更新方程:
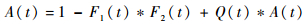 | (3) |
 | (4) |
其中:随机变量首次故障时间X, 二次故障间隔时间ΔX, 修理时间Y为如下分布函数:
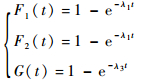 | (5) |
式中:λ为相关指数分布的参数,λ1≠λ3。
ΔX的分布函数为
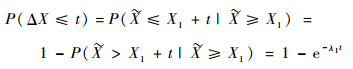 |
其中:X为部件的寿命与X1同为指数分布 (由于假设3) 和指数分布的无记忆性)。
图 2为由三状态形成更新过程建模的示意图。
 |
| 图 2 带有故障小修的单部件三状态更新过程 Fig. 2 A renewal process for one unit with three states under minor repair |
| 图选项 |
1.3 模型性质 在本节证明一些式 (3) 解的性质。首先稳态可用度的计算方法由下面引理给出。
引理1??稳态可用度表达如式 (6) 所示。
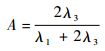 | (6) |
证明??因为A=limt→∞ A(t),使用文献[22]中对两状态模型稳态可用度的计算方法,通过拉氏变换式 (6) 容易得到。证毕
推论1??相比于模型 (1),模型 (3) 中的稳态可用度得到提升。
证明??模型 (1) 的稳态可用度为
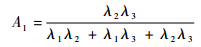 |
由式 (6),可以得到
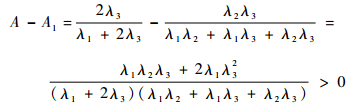 |
证毕
式 (3) 解的可微性由下一个引理给出。
引理2??如果随机变量X、ΔX、Y服从指数分布,如式 (5),则A(t) 具有任意可微性。
证明??按照文献[15],式 (3) 的解可以表示为
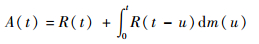 | (7) |
式中:
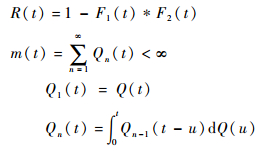 |
由式 (4),可以得到Q(t) 的表达式为
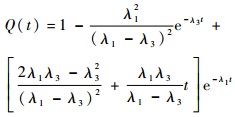 | (8) |
显然Q(t) 任意次可微,即m(t) 任意次可微,从而A(t) 任意次可微。 证毕
最后,给出式 (3) 解的等价形式。
引理3??如果随机变量X、ΔX、Y服从指数分布如式 (5),则A(t) 为常微分方程式 (9) 的解。
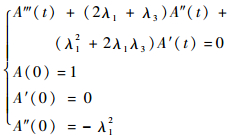 | (9) |
证明??由引理2和式 (8),对式 (3) 两边微分,可以得到如下方程:
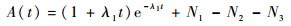 | (10) |
 | (11) |
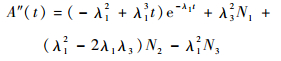 | (12) |
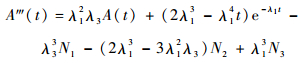 | (13) |
式中:
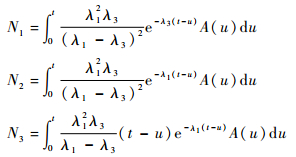 |
消去式 (10)~式 (12) 中Ni(i=1, 2, 3) 并代入式 (13),可以得到常微分方程式 (9)。证毕
2 波动分析 本节分析基于故障小修的三状态模型下,瞬时可用度的波动性。首先引入连续函数的相关波动理论[23]。
定义1[23]??若一个连续函数A(t) 定义域内存在三点t0、t1、t2且t0 < t1 < t2,满足 (A(t0)-A(t1))·(A(t1)-A(t2)) < 0,则称此连续函数A(t) 具有波动性。
引理4[23]??若连续函数A(t) 存在极小值点,则此连续函数具有波动性。
引理5[23]??若连续函数A(t) 为单调函数,则此连续函数没有波动性。
结合上述波动理论,下面定理给出了瞬时可用度产生波动的充分条件。
定理1??如果随机变量X、ΔX、Y服从指数分布如式 (5),则
1) 若Δ≥0,则A(t) 没有波动性。
2) 若Δ < 0,则A(t) 有波动性。
其中:Δ=λ32-4λ1λ3。
证明??由引理3,式 (3) 中A(t) 是常微分方程式 (9) 的解。
常微分方程特征方程式 (9) 的判别式为Δ=λ32-4λ1λ3。
1) Δ=0
式 (3) 中解可以表示为
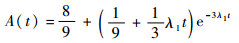 | (14) |
通过对式 (14) 求导,易知A′(t) < 0,由引理5可得A(t) 没有波动性。
2) Δ>0
式 (3) 中解可以表示为
 | (15) |
式中:
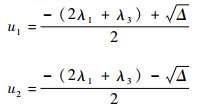 |
通过对式 (15) 求导,易知A′(t) < 0,由引理5可得A(t) 没有波动性。
3) Δ < 0
式 (3) 中解可以表示为
 | (16) |
式中:

显然正弦函数具有波动性,所以A(t) 具有波动性。 证毕
下面通过不同情形下的图例来说明定理1的有效性。
图 3给出了3种情形下瞬时可用度曲线,分别显示其是否存在波性。所以定理1说明指数分布下,带有故障小修的三状态更新模型具有存在波动的可能。这与两状态更新模型的结论不同。
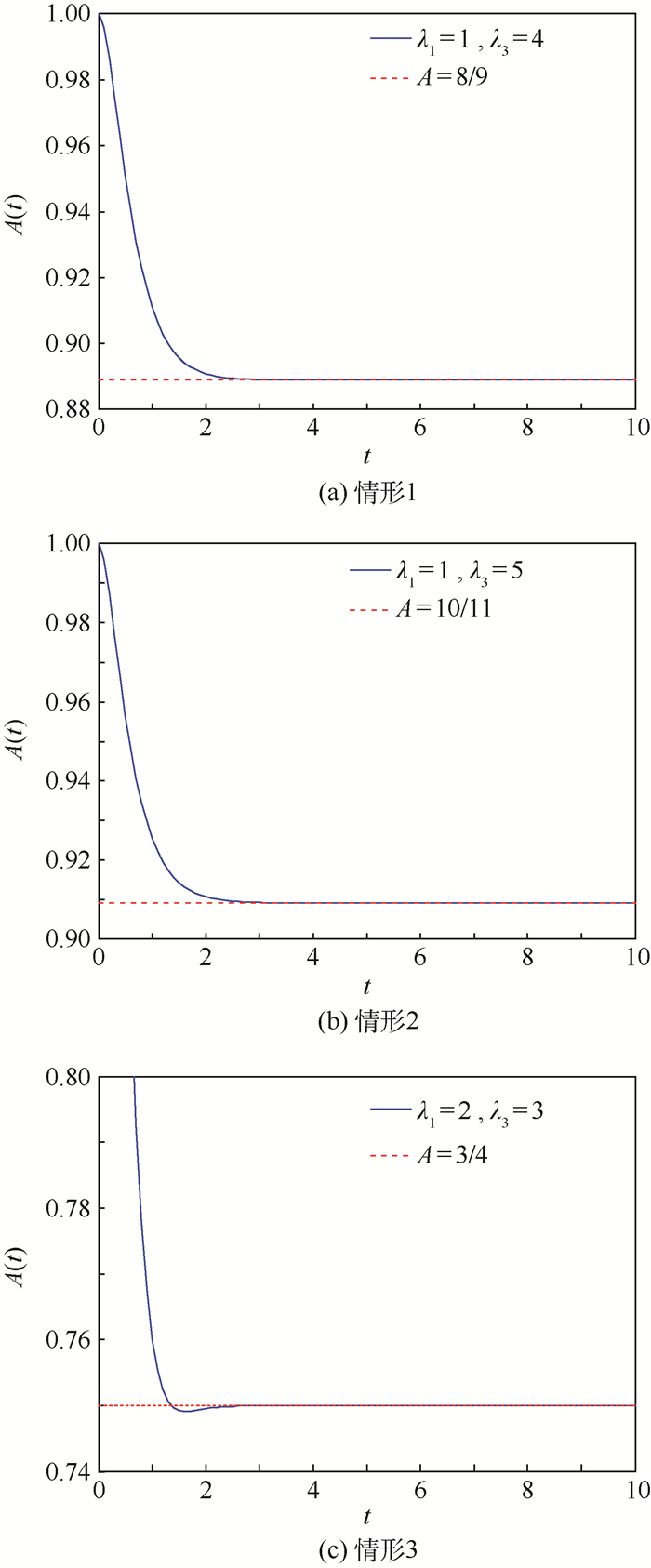 |
| 图 3 3种情形下瞬时可用度曲线 Fig. 3 Curves of instantaneous availability in three cases |
| 图选项 |
3 波动抑制 由第2节知,对于带有故障小修的三状态更新模型,瞬时可用度的波动产生与判别式Δ=λ32-4λ1λ3有关。如果需要抑制波动可以调节故障率λ1和修复率λ3,使得Δ≥0。由于故障率λ1大多由部件的设计和生产所决定,属于部件的固有属性。所以调节修复率λ3是抑制波动的一种方法。
图 4显示修复率λ3对瞬时可用度波动的影响。图中显示当修复率λ3变大,则瞬时可用度的极值点消失,由引理4说明其没有波动性。与定理1中Δ=λ3(λ3-4λ1)≥0时不存在波动的结论一致。
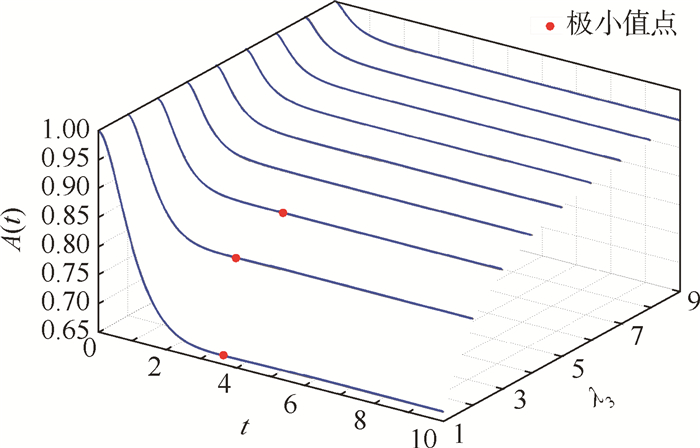 |
| 图 4 修复率对瞬时可用度波动的影响 Fig. 4 Influence of repair rate on fluctuation of instantaneous availability |
| 图选项 |
定理1的实际意义在于采用故障小修的三状态模型中,控制平均修理时间1/λ3小于等于平均工作时间1/λ1的1/4,那么瞬时可用度将不存在波动。
4 结论 1) 用故障小修替代修理延迟得到的新模型仍然为更新模型。新模型适用更新模型的基本性质以及波动理论。
2) 故障小修模型具有简化瞬时可用度波动的存在条件,以及提升稳态可用度的优势。
3) 对于故障小修模型的波动抑制,可以采用调整修复率λ3或平均修理时间1/λ3的方法。
然而,对于一般分布而言,瞬时可用度的波动分析将进入另一领域,也将是继续努力的课题。
参考文献
| [1] | 康锐, 王自立. 可靠性系统工程的理论与技术框架[J].航空学报, 2005, 26(5): 633–636.KANG R, WANG Z L. Framework of theory and technique on reliability system engineering[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(5): 633–636.(in Chinese) |
| [2] | BESNARD F, FISCHER K, BERTLING L.Reliability-centred asset maintenance-A step towards enhanced reliability, availability, and profitability of wind power plants[C]//Proceedings of Innovative Smart Grid Technologies Conference Europe.Piscataway, NJ:IEEE Press, 2010:1-8. |
| [3] | JACKSON D S, KUNZINGER F F. Calculation of system availability using traffic statistics[J].Bell Labs Technical Journal, 2003, 7(3): 139–150.DOI:10.1002/bltj.10024 |
| [4] | DVORSKA J, PODIVIN L, LIPP A, et al.GBAS GAST D availability analysis for business aircraft[C]//Proceedings of IEEE Aerospace Conference.Piscataway, NJ:IEEE Press, 2013:1-15. |
| [5] | TU M H, XIAO L L, XU D X.Maximizing the availability of replicated services in widely distributed systems considering network availability[C]//Proceedings of 7th International Conference on Software Security and Reliability.Piscataway, NJ:IEEE Press, 2013:178-187. |
| [6] | AMIRI M, PRENOSIL V.General solution for MTTF and steady-state availability of NMR system[C]//Proceedings of 9th International Symposium on Reconfigurable and Communication-Centric Systems-on-Chip.Piscataway, NJ:IEEE Press, 2014:1-4. |
| [7] | SMITH D T.Calculating the system steady-state availability as a function of subsystem steady-state availability[C]//Proceedings of IEEE Southeastcon.Piscataway, NJ:IEEE Press, 2014:1-3. |
| [8] | PHAM H. Commentary:Steady-state series-system availability[J].IEEE Transactions on Reliability, 2003, 52(2): 146–147.DOI:10.1109/TR.2003.811164 |
| [9] | HUANG K, MI J. Properties and computation of interval availability of system[J].Statistics and Probability Letters, 2013, 83(5): 1388–1396.DOI:10.1016/j.spl.2013.01.018 |
| [10] | MACIEJEWSKI H, CABAN D. Estimation of repairable system availability within fixed time horizon[J].Reliability Engineering and System Safety, 2008, 93(1): 100–106.DOI:10.1016/j.ress.2006.10.016 |
| [11] | 杨懿. 一般概率分布下系统瞬时可用度离散时间建模分析与应用[D]. 南京: 南京理工大学, 2008: 20-47.YANG Y.The instantaneous availability of the systems under discrete time modeling analysis and application in general probability distribution[D].Nanjing:Nanjing University of Science and Technology, 2008:20-47(in Chinese). |
| [12] | 杨懿, 任思超, 于永利. 均匀分布下系统瞬时可用度理论分析[J].北京航空航天大学学报, 2016, 42(1): 28–34.YANG Y, REN S C, YU Y L. Theory analysis of system instantaneous availability under uniform distribution[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 28–34.(in Chinese) |
| [13] | 温艳清, 崔利荣, 刘宝亮. 修理工带休假的n部件冷贮备可修系统[J].北京航空航天大学学报, 2016, 42(3): 569–575.WEN Y Q, CUI L R, LIU B L. Cold standby n-component repairable system with repairman vacation[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(3): 569–575.(in Chinese) |
| [14] | XUE A C, JING Q, LUO L, et al.Instantaneous availability for the protection devices based on non-homogeneous Markov model and a case study[C]//Proceedings of 33rd Chinese Control Conference.Piscataway, NJ:IEEE Press, 2014:6524-6527. |
| [15] | 林元烈. 应用随机过程[M].北京: 清华大学出版社, 2002: 58-71.LIN Y L. Applied stochastic processes[M].Beijing: Tsinghua University Press, 2002: 58-71.(in Chinese) |
| [16] | NEIL M, MARQUEZ D. Availability modelling of repairable systems using Bayesian networks[J].Engineering Applications of Artificial Intelligence, 2012, 25(4): 698–704.DOI:10.1016/j.engappai.2010.06.003 |
| [17] | 张庆. 带有故障小修的单部件可修系统的预防维修策略[D]. 成都: 西南交通大学, 2012: 19-37.ZHANG Q.Preventive maintenance strategy of one-unit repairable system with minor repair[D].Chengdu:Southwest Jiaotong University, 2012:19-37(in Chinese). |
| [18] | YIN M L, ANGUS J E, TRIVEDI K S. Optimal preventive maintenance rate for best availability with hypo-exponential failure distribution[J].IEEE Transactions on Reliability, 2013, 62(2): 351–361.DOI:10.1109/TR.2013.2256672 |
| [19] | DERSIN P, PERONNE A, ARROUM C.Selecting test and maintenance strategies to achieve availability target with lowest life-cycle cost[C]//Proceedings of Reliability and Maintainability Symposium.Piscataway, NJ:IEEE Press, 2008:301-306. |
| [20] | 程志军, 郭波. 机会维修策略下的系统可用度分析[J].数学的实践与认识, 2006, 36(10): 137–140.CHENG Z J, GUO B. Analysis of system availability under opportunity maintenance steategy[J].Journal of Mathematics in Practice and Theory, 2006, 36(10): 137–140.(in Chinese) |
| [21] | 徐文静. 不完全维修条件下的可用度与维修策略分析[D]. 长沙: 国防科学技术大学, 2008: 26-63.XU W J.Analysis of maintenance strategy and availability under imperfect repair[D].Changsha:National University of Defense Technology, 2008:26-63(in Chinese). |
| [22] | 曹晋华, 程侃. 可靠性数学引论[M].2版北京: 高等教育出版社, 2012: 182-261.CAO J H, CHENG K. A mathematical introduction to reliability[M].2nd edBeijing: Higher Education Press, 2012: 182-261.(in Chinese) |
| [23] | REN S C, YANG Y, XU H L.Fluctuation analysis of instantaneous availability under delay-repair[C]//Proceedings of the 35th Chinese Control Conference.Piscataway, NJ:IEEE Press, 2016:6746-6750. |
