插值边界处的插值精度是保证子网格流场计算准确的基础之一。为了提高非守恒型插值精度,科研人员从两方面开展了大量工作:一方面,从改善插值区网格尺寸匹配度着手,如L?hner等[4]以物面距离和网格单元体积的组合量建立了准则参数,确保插值单元与其宿主单元尺度匹配,Noack[5]区分对待物面和远场网格,将插值区域推离物面至合适的位置, 蔡晋生等[6]基于隐式切割准则确定优化插值边界;另一方面,发展了多种插值方式,如Togashi和Ito[7]把非四面体插值单元剖分为四面体,针对四面体特点设计了一种插值策略,田书玲[8]将单元标准化,并结合拉格朗日基函数发展了一种适合高阶格式的插值方法,许和勇等[9]根据单元几何特征,采用面积加权法获得了四面体网格上的插值格式。
实际运用中发现,即使优化重叠边界有时也难以保证插值区网格尺寸的匹配度,为了改善插值区网格尺寸匹配度较差时的插值精度,本文基于文献[10]中的方法,发展了一种适用于任意单元类型混合重叠网格的插值方法。通过引入二阶精度插值方法,提高插值精度,传递流动变量,再结合加权的最小二乘法获得新的插值单元梯度信息。本文方法只需一层插值网格,既继承了文献[10]中方法对各单元类型的透明特性和实现简单特性,又提高了在插值区单元尺寸匹配度较差时的插值精度。算例结果表明,相比文献[10]中方法,本文方法计算出的等值线过渡更为光滑,与试验值符合更好,证明其准确可靠。
1 原插值方法 文献[10]中基于线性重构思想,发展了一种格心到格心、适用于任意网格单元类型的插值策略。该方法依赖插值单元格心处流场变量W、单元梯度?W和限制器函数Φ计算完成。由式(1)可获得从宿主单元B的格心到插值单元A的格心的变量、限制器及变量梯度的插值策略:
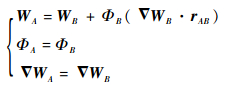 | (1) |
式中:下标A、B表示单元A、B格心处变量;rAB为单元A、B格心间的距离矢量。
上述方法包含宿主单元的梯度和限制器函数,这实际上是利用了宿主单元相邻单元的信息,因为梯度和限制器函数都是根据相邻单元信息构造得到的。从式(1)可见,原则上该方法只需一层插值单元,而且对各单元类型统一。该方法另一个特点是对插值边界可以像对其他边界一样透明处理,无需区别对待。
从上述方法的实际运用过程中发现,当插值区网格尺寸匹配度较好时,上述方法与线性重构有相同的精度,但是该方法的插值精度严重依赖于插值区网格尺寸匹配度。当运动物体处于背景网格或母网格稀疏处时,插值区网格尺寸的匹配度差。当网格尺度差异较大时,一方面会出现插值精度损失,如图 1所示,网格2中宿主单元123难以覆盖网格1中单元p1p2p3,传值引起明显误差;另一方面,即便网格1中多个单元的中心都落在网格2单元p1p2p3内部,单元p1p2p3却只取一个网格1中单元的值,显然浪费了计算模板。
 |
| 图 1 重叠区域网格尺寸不匹配 Fig. 1 Mismatch of grid scale at overset area |
| 图选项 |
2 混合重叠网格插值方法的改进 为了减小插值误差,一方面可以在流场重构时使用足够多的模板涵盖当地流动特征,另一方面还可以提高插值的精度。为了经济地提高模板数,适应插值边界情况,合理地插值流动变量和梯度信息,提高插值精度,本文对原插值方法做出如下改进。
2.1 二阶精度的插值方法 由式(1)可知,插值策略首先要考虑变量的插值,提高变量插值精度是减小插值误差的关键之一。考虑到非结构/混合网格单元的无序性,大多采用单元内部分段线性重构方法进行插值,此方法依赖于单元插值基函数,在非均匀网格上只有一阶精度。
为了使插值精度提高到二阶,需要对线性插值结果进行误差修正,Baker[11]利用一阶的插值基函数,提出如下修正方式:
 | (2) |
式中:W(x)为x处的二阶精度变量插值;W1(x)为对x处的一阶精度的线性插值结果;f(x)为二阶值和一阶值间的误差估计。
一阶线性插值可以用插值基函数的线性组合表示,即
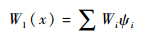 | (3) |
式中:Wi为取值点i处变量值;ψi为i点处的基函数。
如图 2所示,以平面三角形单元中p点为例,插值基函数定义在点1、2、3上,对于该二维情况,插值基函数满足:
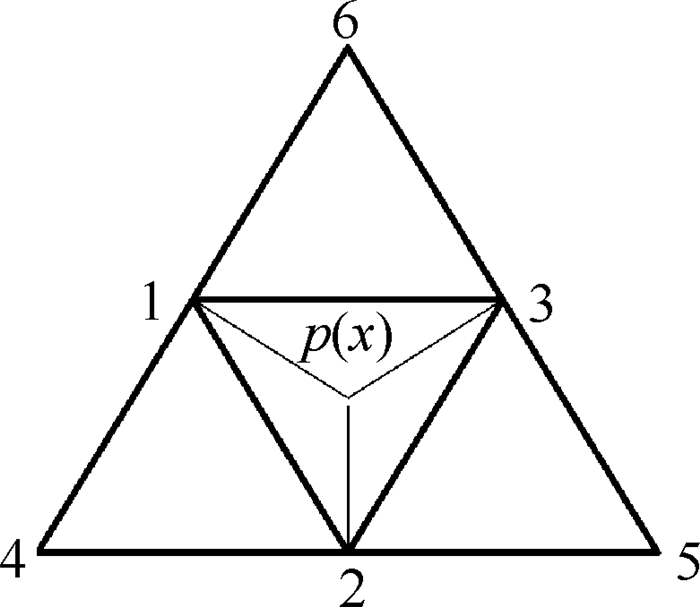 |
| 图 2 二阶插值示意图 Fig. 2 Illustration of 2nd order interpolation |
| 图选项 |
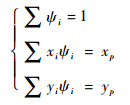 | (4) |
求解式(4)可获得插值基函数在各点上的值。
二阶插值误差修正函数的确定是使插值精度达到二阶的关键。根据Baker[11]的理论,式(2)中x处的二阶误差修正函数为
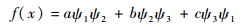 | (5) |
式中:a、b和c为待定系数。为了获得待定系数的值,利用相邻4、5、6点上的变量值,待定系数满足:
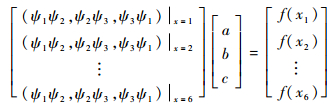 | (6) |
其中:左端矩阵中下标x=1, 2, …, 6表示插值基函数取值点;f(xi)(i=1, 2, …, 6)为一阶插值结果同节点已有值的误差,定义为
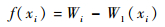 | (7) |
采用最小二乘法求解式(6),即可确定待定系数。确定待定系数后,就可利用式(5)对一阶线性插值进行修正。
只要确定单元的插值基函数,其他单元类型的二阶插值误差修正函数计算方法类似。以三维四面体单元为例,其插值基函数为ψi(i=1, 2, 3, 4),用式(4)求解基函数在各顶点上的值,其相应的二阶误差修正函数为
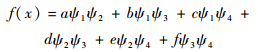 | (8) |
式(8)在相邻点上满足式(6),通过最小二乘法,可求得待定系数a, b, c, d, e, f。其他单元类型误差修正函数计算方法类似。
2.2 插值单元同宿主单元的关系分类 确定插值单元同宿主单元间的联系是实现插值的前提条件。有多种算法可以获得插值单元中心在其他网格的宿主单元信息。本文选择相邻单元搜索算法实现该过程,该算法在混合网格上鲁棒性和效率较好,已得到广泛应用[12-13]。
原始方法中没有考虑单元相对大小等情况,插值单元和宿主单元的关系总是一对一的,在插值单元和宿主单元尺度差异较大时可导致非物理流动。本文按照单元尺寸,将插值情况分为3类,并建立相应的一对多、多对一的数据结构,以图 3中三角形单元为例。
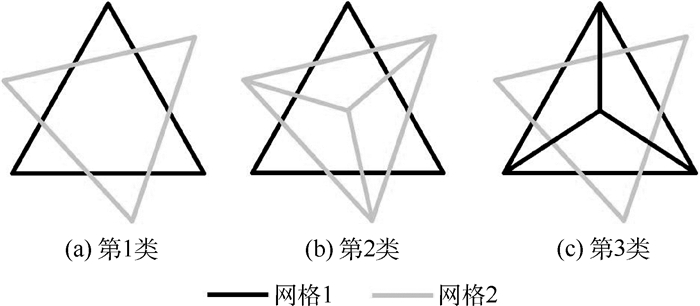 |
| 图 3 3类插值单元和宿主单元重叠情况示意图 Fig. 3 Three types of relationship of interpolation and donor cells at overset area |
| 图选项 |
第1类为只有一个插值单元的中心落在宿主单元内部,且只有该宿主单元的中心落在该插值单元内部,如图 3(a)所示,此时插值单元尺寸同宿主单元尺寸相当。在设计重叠挖洞或生成网格时,经验性的原则是尽量使重叠区域的网格重叠属于该类。
第2类为有多个插值单元的中心落在同一个宿主单元内部,如图 3(b)所示,此时插值单元尺寸小于宿主单元。
第3类为有多个宿主单元的中心落在同一个插值单元内部,如图 3(c)所示,此时宿主单元尺寸小于插值单元,宿主单元格心表征的是插值单元内的变量分布点。
上述3类情况可推广到三维任意单元类型。其中,第2类和第3类引起的插值误差最大,往往出现在子网格运动到远场附近时,是本文重点考虑的情况。对于第1类情况,经验表明直接采用式(1)进行插值不会带来太大误差。
2.3 流动变量插值策略 本节给出流动变量的插值策略,这里流动变量可以包括流动的原始变量、湍流黏性系数等。
2.3.1 第2类情况策略 首先考虑第2类插值情况,即多个插值单元中心落于一个宿主单元内的流动变量插值。为了有效地扩大插值模板,在流动变量插值时,本文策略如下:
1) 扩展插值模板。采用Frink[14]加权重构方法,利用宿主相邻单元的格心值进行线性距离导数加权插值,在宿主网格上(见图 4(a)中网格1),将宿主单元附近的正常单元格心变量插值到宿主单元的格点上,如图 4(a)所示。加权公式为
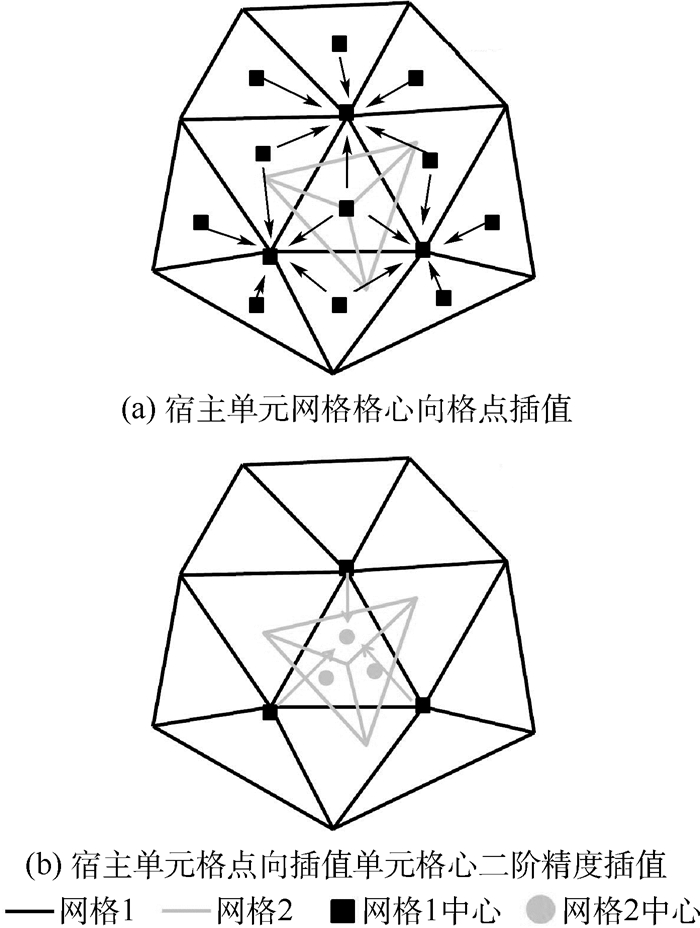 |
| 图 4 第2类情况插值示意图 Fig. 4 Illustration of second interpolation type |
| 图选项 |
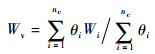 | (9) |
式中:Wv为单元顶点值;Wi表示单元中心值;θi为各单元中心到其顶点的加权系数,定义为单元中心到顶点距离的倒数;nc为相邻单元个数。
由于在求解器中采用Green Gauss法计算变量梯度时,同样需要采用式(9)将单元格心变量插值到格点上,因此上述过程可直接利用当前步的梯度计算中的结果,无需另外花费计算时间。
2) 利用宿主单元(见图 4(b)中网格1)上格点变量,依次对插值网格(见图 4(b)中网格2)单元中心采用式(2)、式(5)和式(6)进行二阶精度插值,获得插值单元格心处变量。
2.3.2 第3类情况策略 如图 5所示,第3类情况下,存在多个宿主单元中心落于一个插值单元内部,此时宿主单元格心表征的是插值单元内的变量分布点。满足二阶空间离散的网格单元内变量可认为是线性分布的,因此,一个简单的思路是采用网格1的中心变量值对插值单元网格2中心进行线性拟合,获得网格2中心变量值。
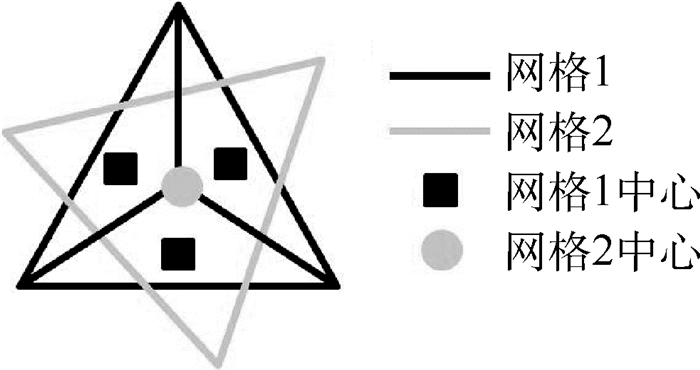 |
| 图 5 第3类情况插值示意图 Fig. 5 Illustration of third interpolation type |
| 图选项 |
利用网格1和网格2中心坐标,利用式(9),即可获得网格2中心的变量。此时式(9)中右端Wi表示网格1各单元中心值,θi可取为网格1各单元的体积。
2.4 梯度和限制器函数的计算 二阶格式的实现需要梯度和限制器函数。对于第1类和第2类重叠情况,采用第2.3节中方法确定插值单元格心流动变量后,利用插值获得的格心变量和周围正常单元格心变量,在插值单元的网格上调用求解器中方法对插值单元重新计算梯度。对于第3类重叠情况,基于图 5中网格2中心处插值获得的变量,以及网格1中网格中心处的变量,可获得网格2中心处的变量梯度值,梯度满足:
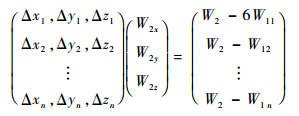 | (10) |
式中:Δxi、Δyi和Δzi(i=1,2, …,n)为图 5中网格1各单元中心到网格2单元中心的距离;W2x、W2y和W2z为网格2单元中心处待求的变量在3个坐标方向上的梯度;右端项W2-W1i(i=1, 2,…,n)为网格2单元中心变量同网格1各单元中心变量的差。式(10)可以采用最小二乘法求解[15]。
获得插值网格单元中心变量和梯度后,即可将插值单元看做正常单元,利用相邻单元信息,调用求解器中流程计算当地的限制器函数值。
3 控制方程及数值方法 本文采用格心型有限体积法,求解三维非定常可压缩Navier-Stokes方程,该方程的守恒型积分形式为
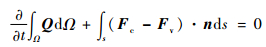 | (11) |
式中:Q为守恒变量;Ω、s和n分别为控制体、控制面和面外法矢量;Fc和Fv分别为对流通量和黏性通量。各项具体形式参见文献[16]。
无黏通量采用带熵修正的Roe格式计算,控制面两侧变量采用Barth[15]提出的分段线性重构获得,采用Green Gauss法计算单元中心梯度。当流动出现强间断时,利用Venkatakrishnan限制器抑制振荡,该限制器有较好的收敛特性。上述方法在规则网格上可以达到二阶精度。黏性通量采用中心格式离散获得,湍流黏性采用一方程Spalart Allmaras湍流模型计算,湍流方程与平均方程解耦求解,时间推进采用LU-SGS隐式格式,并采用基于共享内存的OpenMP并行技术提高计算效率。
4 算例及计算结果 根据第2节和第3节描述,编写了具有混合重叠网格功能的求解器,并将插值方法模块化处理。在生成初始网格、给定来流参数、设定边界条件等信息后,本文求解器即可实现各单元类型的混合重叠网格计算和重叠,无需人工干预,并具有背景网格重叠、体网格重叠等多种混合网格重叠功能。
4.1 RAE2822超临界翼型 对RAE2822超临界翼型[17]进行模拟,计算来流条件为:Ma=0.73,Re=6.5×106,攻角α=2.31°,采用SA湍流模型模拟湍流黏性。本算例为准二维算例,由于求解器是三维的,因此将网格在展向方向拉伸一层网格,两侧设为对称面。网格分为翼型网格和背景网格两部分。翼型网格在壁面处采用六面体网格以较好地捕捉壁面附近的黏性,远离壁面处采用三棱柱网格;背景网格全部采用三棱柱网格。两部分网格重叠效果如图 6所示。可以注意到,由于人为地将背景网格分布得较为稀疏,因此在重叠区网格的尺度差异较大,这样可以在本网格上对比本文方法和原插值方法的区别,并验证本文方法的可行性、正确性和对收敛性的影响。
 |
| 图 6 RAE2822翼型重叠网格 Fig. 6 Overset grid of RAE2822 wing figure |
| 图选项 |
图 7为采用原插值方法和本文插值方法计算得到的马赫数分布。可见,在翼型上部有激波穿过插值区域。由于本算例人为地将插值区网格尺寸匹配度调整得较大,当激波这种流动间断穿过插值区域时,马赫数云图过渡光滑性更好。图 8为翼面压力系数Cp分布对比。可见,由于本文插值方法在翼型上表面重叠区域处将激波位置捕捉得更好,激波在翼型表面处产生的压力突变位置更加接近试验值。
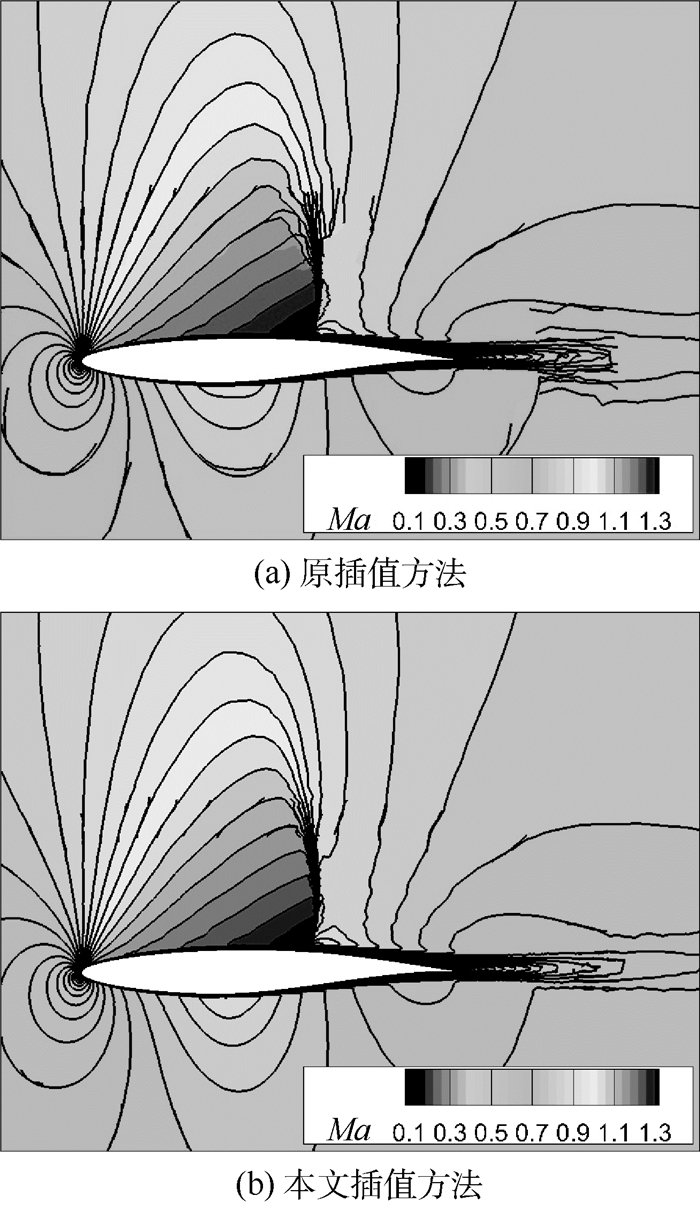 |
| 图 7 2种插值方法的马赫数分布比较 Fig. 7 Mach number contour distribution comparison of two interpolation methods |
| 图选项 |
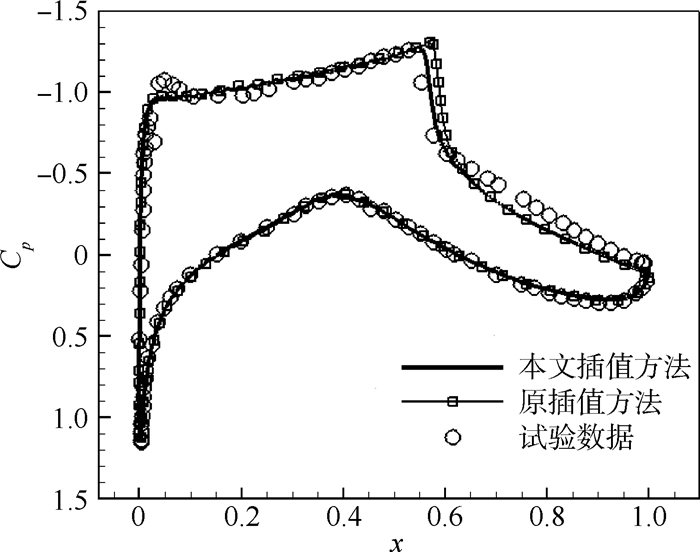 |
| 图 8 翼面压力系数分布 Fig. 8 Pressure coefficient distribution on wing surface |
| 图选项 |
图 9为采用原插值方法和本文插值方法计算得到的翼型尾部拖出的尾涡无量纲涡黏性分布。图中:tur为无量纲涡黏性系数。尾涡主要在翼壁面附近产生,涡黏性随着流动向后逐渐耗散掉。由图 9可见,采用本文插值方法,在插值界面过渡光滑,经过插值区域后尾部涡黏性系数保持情况有所改善,表明本文插值方法在插值区域产生的数值误差更小。
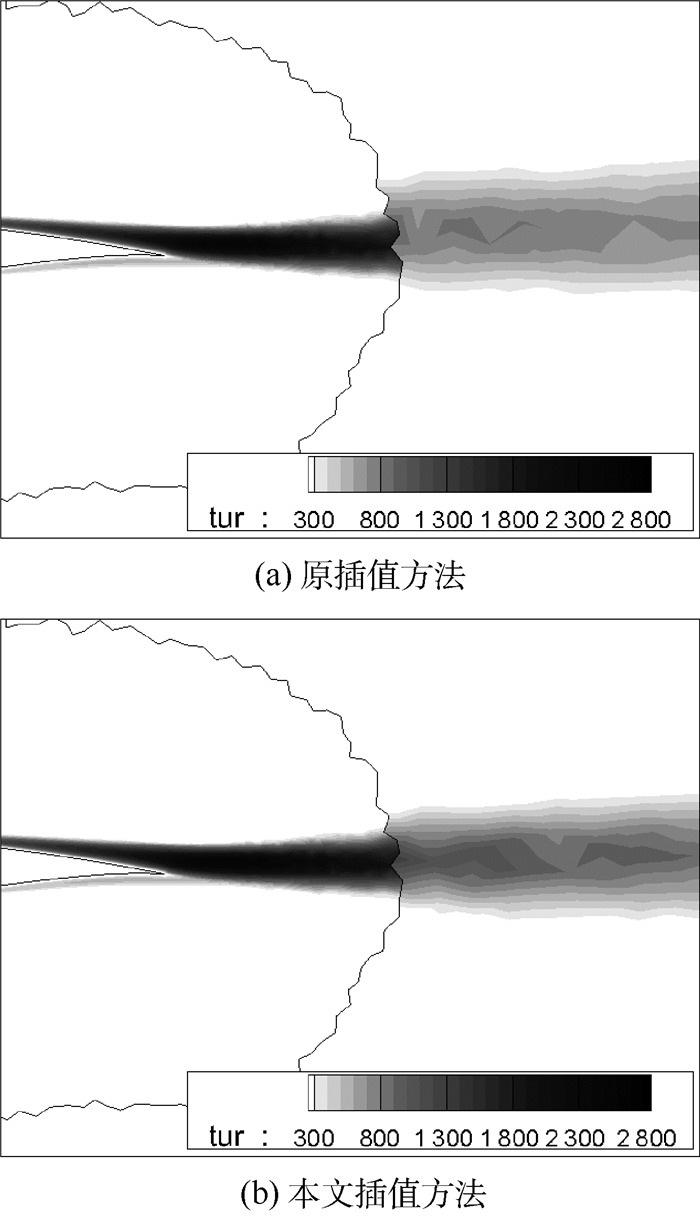 |
| 图 9 2种插值方法的尾涡无量纲涡黏性分布对比 Fig. 9 Rear eddy nondimensional viscosity contour distribution comparison of two interpolation methods |
| 图选项 |
由于重叠网格在重叠区域会引入误差,使流场偏离正确解,因此减小插值误差是提高收敛速度、加快流动收敛的一个途径。图 10为采用原插值方法和本文插值方法计算残差收敛曲线对比。可见,采用本文插值方法对本算例流动残差减小有所促进。
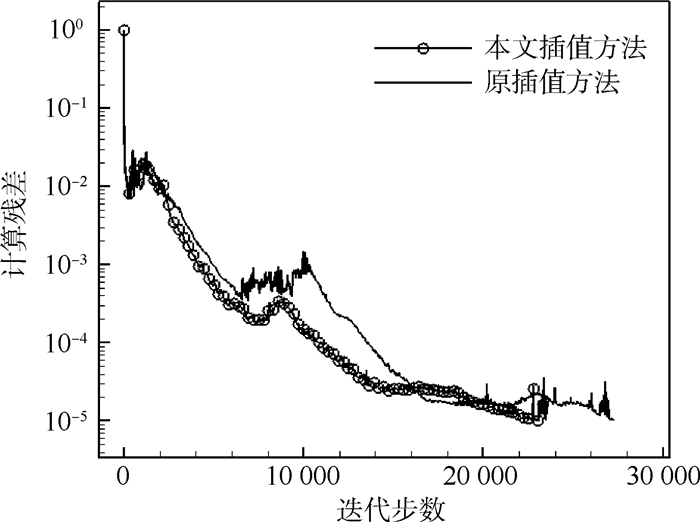 |
| 图 10 2种插值方法的残差收敛情况对比 Fig. 10 Comparison of residual error convergence history of two interpolation methods |
| 图选项 |
4.2 三维机翼抛弹分离 三维机翼抛弹模拟有较多的试验数据和计算结果[18],可以用于验证重叠网格计算在多体运动模拟中的正确性。计算网格如图 11所示,网格包含3部分:外挂子物网格、机翼及挂件网格和背景网格。网格共计170万,其中机翼壁面附近采用三棱柱模拟黏性。同样地,为了检验本文插值方法,人为将背景网格布置得较粗。
 |
| 图 11 三维机翼挂架重叠网格 Fig. 11 3D overset grid of wing/pylon/store |
| 图选项 |
计算来流条件为:Ma=0.9,采用高度8 km的大气参数,攻角α=0°。外挂物质心初速度和初角速度都为0。在释放外挂物时,施加一定弹射力以便顺利分离。模型质心、弹射力等具体参数设置参见文献[18]。
图 12为0.3 s时刻的对称面和物面压力p分布云图,可见计算流场结构清晰。图 13为外挂物释放时刻物体的5°和185°子母线上的压力系数Cp分布同试验值对比,可见重叠网格计算结果同试验结果接近。图 14(a)和图 14(b)分别为外挂物质心和姿态角随时间的变化曲线与试验数据对比。计算获得的质心位置和姿态角同试验值之间吻合较好,证明本文插值方法在处理混合网格的重叠问题时准确有效。
 |
| 图 12 0.3 s时刻对称面和物面压力分布 Fig. 12 Surface and symmetry pressure contour at 0.3 s |
| 图选项 |
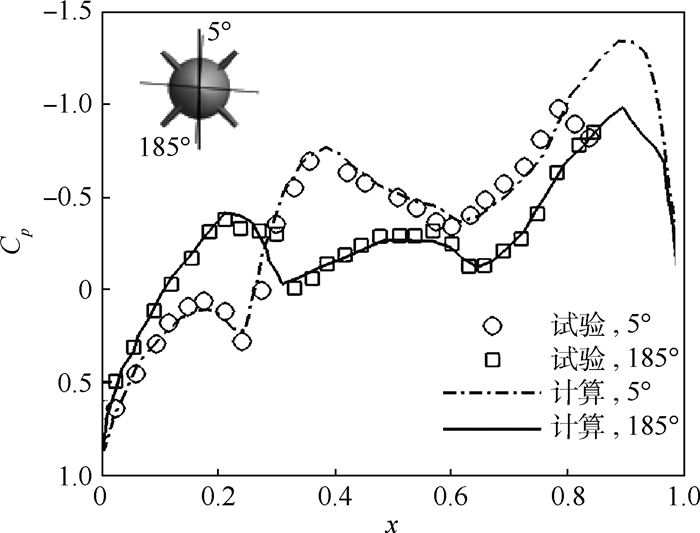 |
| 图 13 初始时刻5°和185°子母线压力系数分布 Fig. 13 Pressure coefficient distribution on circumferential location 5° and 185° at initial time |
| 图选项 |
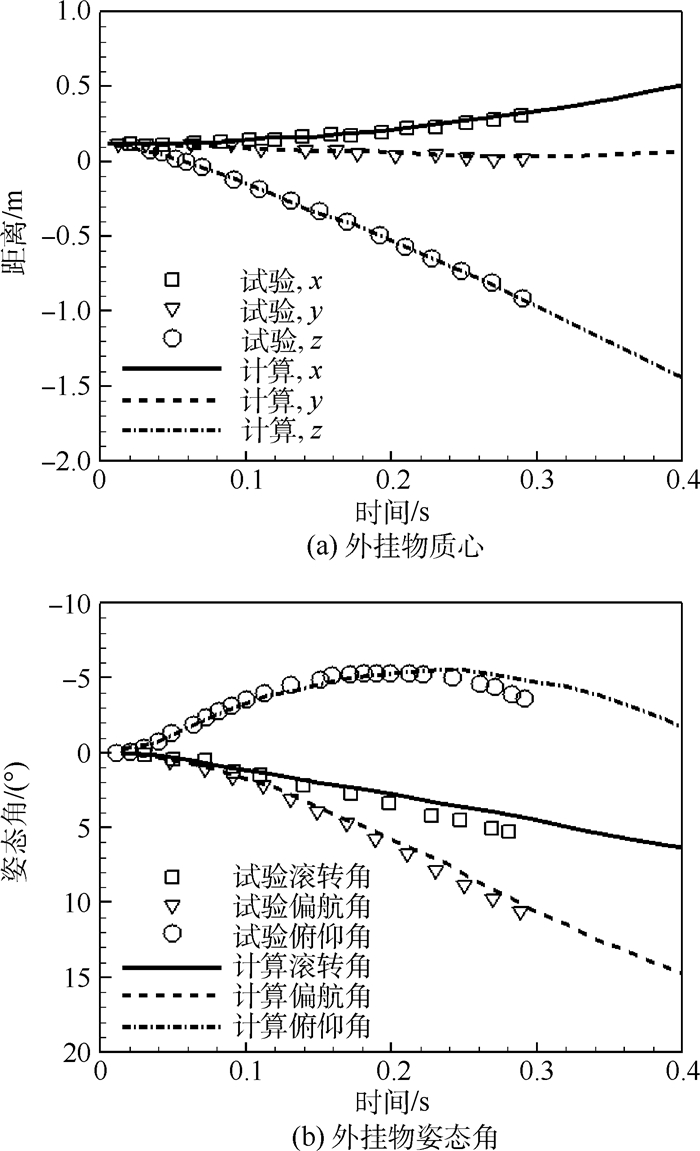 |
| 图 14 外挂物质心和姿态角随时间变化 Fig. 14 Variation of store movement and attitude angle with time |
| 图选项 |
5 结 论 本文针对混合重叠网格,引入二阶插值精度,通过区分重叠区域网格匹配程度扩充模板,发展了一套插值策略,研究结果表明:
1) 本文插值策略适用于各种类型网格单元,且对各类单元处理过程类似,能保证混合重叠网格计算中流场变量传递的合理性和正确性。
2) 引入二阶精度插值方法,降低了重叠区插值引起的误差,在插值区网格尺寸匹配度较差时,流场变量经过插值区后保持得更好,耗散更低。
3) 进行插值误差修正时,直接使用当前时间步获得的梯度计算中获得了加权节点值,减小了额外计算量。
4) 本文插值策略根据插值区网格尺寸匹配度情况选择不同的方法,仅对尺寸匹配度较差时采用本文方法,可以有效地减低插值计算的时间,并对二维和三维情况均有较好的适用性。
参考文献
| [1] | ?NAKAHASHI K,TOGASHI F,SHAROV D.An intergrid boundary definition method for overset unstructured grid approach:AIAA-1999-3304[R].Reston:AIAA,1999. |
| [2] | TOGASHI F, ITO Y, NAKAHASHI K, et al. Extensions of overset unstructured grids to multiple bodies in contact[J].Journal of Aircraft, 2006, 43(1): 52–57.DOI:10.2514/1.540 |
| [3] | TAKAHASHI S,MONJUGAWA I,NAKAHASHI K.Unsteady flow computation around moving multiple bodies using overset unstructured grids:AIAA-2006-2839[R].Reston:AIAA,2006. |
| [4] | L?HNER R,SHAROV D,LUO H,et al.Overlapping unstructured grids:AIAA-2001-0439[R].Reston:AIAA,2001. |
| [5] | NOACK R W.Resolution appropriate overset grid assembly for structured and unstructured grids:AIAA-2003-4123[R].Reston:AIAA,2003. |
| [6] | 徐嘉, 刘秋洪, 蔡晋生, 等. 基于隐式嵌套重叠网格技术的阻力预测[J].航空学报, 2013, 34(2): 208–217.XU J, LIU Q H, CAI J S, et al. Drag prediction based on overset grids with implicit hole cutting technique[J].Acta Aeronautic et Astronautic Sinica, 2013, 34(2): 208–217.(in Chinese) |
| [7] | TOGASHI F,ITO Y.Overset unstructured grids method for viscous flow computations:AIAA-2003-3405[R].Reston:AIAA,2003. |
| [8] | 田书玲.基于非结构网格方法的重叠网格算法研究[D].南京:南京航空航天大学,2008.TIAN S L.Investigation of overset unstructured grids algorithm[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2008(in Chinese). |
| [9] | 许和勇, 叶正寅, 王刚, 等. 基于非结构嵌套网格的旋翼前飞流场计算[J].西北工业大学学报, 2006, 24(6): 763–767.XU H Y, YE Z Y, WANG G, et al. Improving numerical simulation of rotor forward flight flow field with unstructured dynamic overset grids[J].Journal of Northwestern Polytechnical University, 2006, 24(6): 763–767.(in Chinese) |
| [10] | KANG Z L, YAN H, YU J, et al. A fast and reliable overset unstructured grids approach[J].Acta Mechanica Sinica, 2013, 29(2): 149–157.DOI:10.1007/s10409-013-0021-6 |
| [11] | BAKER T J.Interpolation from a cloud of points[C]//Proceedings of the 12th International Meshing Roundtable,Santa Fe,2003:55-63. |
| [12] | L?HNER R. Robust,vectorized search algorithms for interpolation on unstructured grids[J].Journal of Computational Physics, 1995, 118(2): 380–387.DOI:10.1006/jcph.1995.1107 |
| [13] | 田书玲, 伍贻兆, 夏健. 用动态非结构重叠网格法模拟三维多体相对运动绕流[J].航空学报, 2007, 28(1): 46–51.TIAN S L, WU Y Z, XIA J. Simulation of flows past multi body in relative motion with dynamic unstructured overset grid method[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 46–51.(in Chinese) |
| [14] | FRINK N T.Recent progress toward a three-dimensional unstructured Navier-Stokes flow solver:AIAA-1994-0061[R].Reston:AIAA,1994. |
| [15] | BARTH T J.A 3-D upwind Euler solver for unstructured meshes:AIAA-1991-1548[R].Reston:AIAA,1991. |
| [16] | 阎超. 计算流体力学方法及应用[M].北京: 北京航空航天大学出版社, 2006: 18-25.YAN C. Computational fluid dynamics methods and applications[M].Beijing: Beihang University Press, 2006: 18-25.(in Chinese) |
| [17] | ANDERSON W K, BONHAUS D L. An implicit upwind algorithm for computing turbulent flows on unstructured grids[J].Computers Fluid, 1994, 23(1): 1–21.DOI:10.1016/0045-7930(94)90023-X |
| [18] | HALL L H,PARTHASARATHY V.Validation of an automated Chimera/6-DOF methodology for multiple moving body problems:AIAA-1998-0767[R].Reston:AIAA,1998. |
