经典的数据驱动模型有线性回归、自回归滑动平均(Auto Regressive Moving Average,ARMA) 等。线性回归模型假定系统的输出与输入成线性关系,即输出为输入的线性组合,并使用最小二乘方法计算线性模型中各个系数,完成模型的建立。线性模型简洁便利,在医学研究[2]、大气物理[3]、金属分析[4]、故障预测等方面有着重要应用。ARMA模型最初被用于分析时间序列,该模型认为当前输出等于该时间序列前p个输入与前q个随机噪声之和。ARMA模型比现行回归模型更加复杂,也更加有效,在生态学中取得了良好的应用。
然而,无论是现行回归模型还是ARMA模型,都只是将输入进行线性处理后得到输出,泛化能力很弱,不适用于复杂非线性系统。针对该问题,著名****Vapnik等[5]提出了支持向量机(Support Vector Machine,SVM)。相对于传统数据驱动模型,支持向量机使用支持向量的概念动态地调整模型的结构,与使用固定结构的线性回归方法相比适应性更加广泛。其次,支持向量机在模型计算上摆脱了传统方法经常使用的最小二乘法(使用最小二乘法需要计算逆矩阵,而在某些场合,无法精确计算奇异矩阵的逆矩阵,这给模型的计算带来了巨大的困难),将计算问题转换为优化问题,即使在海量数据的应用场景中,支持向量机依然有着优异的效率。支持向量机通过核函数将低维度非线性在高维度空间中转换为线性问题,弥补了传统线性模型不能够处理非线性数据的缺陷。
一经提出,支持向量机便受到了强烈关注,并取得了令人瞩目的研究成果。然而,目前的研究一般都局限于对支持向量机核函数的选择、参数优化以及与其他方法进行简单结合。尽管这些优化与改进在很大程度上提高了原始支持向量机的性能,但仍有很多问题未被解决,其中之一便是多模式系统。
多模式系统具备更加复杂的行为:模式与行为相互耦合,不同模式下系统具备不同的行为,同时各个模式下系统的行为又会影响系统模式切换。使用单个支持向量机对多模式系统进行建模显然是不适宜的。针对该问题,本文提出了一种名为经验概率混合自动机(Empirical Probabilistic Hybrid Automata,EPHA) 的模型,在该模型中,定性符号被用来描述系统模式之间的转移关系。随后本文提出了针对EPHA模型的基于支持向量回归(SVR) 的定性定量混合建模方法,实现了通过历史数据对原系统建立混合模型。
1 理论基础 本文所提出的方法以支持向量回归为核心,结合D-Markov回归与基于小波的奇异点识别对多模式系统建立混合模型。本节主要介绍各个基础方法。
1.1 支持向量回归 支持向量回归以支持向量机为基础,同支持向量机类似,使用核函数将非线性问题转化为线性问题解决,将回归问题转换为优化问题计算。典型回归问题可以表述如下,已知训练样本集为:(x1, y1),(x2, y2),…,(xN, yN)。其中:xi∈Rn,为n维向量;yi∈R。回归分析即通过已知训练样本集拟合变量与自变量之间的函数关系y=f(x)。
在正式介绍支持向量回归之前,首先需要介绍ε-不敏感函数。ε-不敏感函数用于评价拟合函数y=f(x) 的准确性。ε-不敏感函数由ε区间和误差累积函数组成。典型的绝对值误差函数为
 | (1) |
其含义为:当拟合误差在ε之内时,可以认为是0,否则误差函数的值等于真实误差减去ε。
根据分类间隔最大化的思想,模型求解问题被转化为如下二次凸规划问题:
 | (2) |
式中: W为支持向量回归系数矩阵; b为截距。
因为噪声的存在,实际应用中不可能全部落入ε中,支持向量机通过引入ε-不敏感函数,使松弛变量ζi弥补超出的偏差。此时转换为一个新的规划问题:
 | (3) |
式中:ζi和ζi*分别对应样本点在最优超平面上方和下方2种情况;C为实现确定的惩罚系数。最终得到的最优超平面解析表达式为(非支持向量xi对应的系数为0)
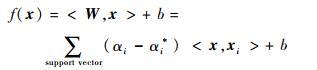 | (4) |
将其中的内积符号<·, ·>换成核函数K(·, ·),支持向量回归便能够对(单模式) 非线性系统进行建模。在本文所提出的混合建模方法中,支持向量回归对单个模式下的系统连续行为进行建模。
1.2 基于小波的奇异点分析 奇异点即2条曲线相切换的点,具体可以分为3类:断点、尖点与变点。断点即不连续点;尖点即2条曲线相交,但很尖锐(过渡不平滑) 的点;变点即2条曲线光滑过渡的点。实际应用中,通常探测到的是断点与尖点。在假定有限长曲线f(x)(不失一般性,将长度设为1) 仅包含有限个奇异点的前提下,该曲线可使用式(5) 表示:
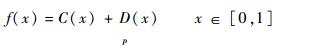 | (5) |
式中:
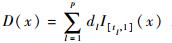
尖点的定义[6]为
 | (6) |
式中:0 < αi < α < 1, i=1, 2, …, q; q、si、αi和Ki是未知的,但α是已知的。进一步,假定C(x) 在[0,1]区间上除了si之外的点都可微。
对小波ψ(x), x∈(-∞, +∞),可以构造相应的区间小波
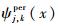
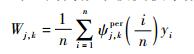 | (7) |
那么Wj, k根据连续、阶跃与噪声可以被分解为
 | (8) |
当ψ(x) 满足一定条件时[7],有区间小波奇异点定理:如果j=jn满足j=jn→∞(n→∞) 且

1) 对于所有的k∈I(tl, 2-jn)
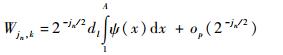 | (9) |
其中op(·) 是对k一致收敛的, l=1, 2, …, p。
2) 对于所有

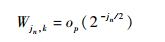 | (10) |
3)k∈I(sl, 2-jn) 时,则存在一个与k、n无关常数C0>0,使得
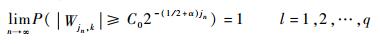 | (11) |
4)

 | (12) |
这里vn=op(bn) 表示随即变量bn-1vn随着n趋向于无穷时依概率收敛于零。
式(9) 与式(10) 表明,采样的区间离散小波变换在断点处的幅值是其附近的dl倍,由于dl存在下限d,因此断点处的幅值较大。式(11) 与式(12) 表明,尖点处的幅值是其他处的C0倍。总的来说,奇异点所对应的区间离散小波系数的幅值更高,因此所对应的细节也有着更高的幅值。经验表明,对大多数小波,细节尺度在奇异点处均有着更高的幅值。利用该特性,即可有效识别系统奇异点。
1.3 D-Markov重构 Pennsylvania州立大学机械系的Ray等[8-10]提出一种基于D-Markov机的模型重构方法,在该方法中,他将系统在“慢时间尺度”和“快时间尺度”上分析, 见图 1。对应于混合系统中模式间切换与模式内部行为。在快慢尺度上的分析能够有效地挖掘动态系统的特征[11]。
 |
| 图 1 慢时间尺度与快时间尺度 Fig. 1 Slow time scale and fast time scale |
| 图选项 |
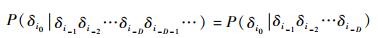 | (13) |
该方法首先将原始数据离散化、符号化,之后对该符号序列进行分析。当式(13) 满足,即序列中,下一个符号的概率分布仅由前D的符号所决定时,称该稳态符号序列是D-Markov的。对于一个复杂的系统来说,D的取值会非常大,甚至不存在这样的整数,再加上时间序列符号化过程中所丢失的信息,严格地讲,不可能通过序列化和提取D-Markov特性来完整地描述一个系统的特性。但随着序列化过程中符号集合容量的增加,随着D取值的增加,提取出的Markov特性会无限逼近系统的统计特性,当符号集合的容量和D取到合适的值时,将能够描述系统的绝大部分统计特性。
假设某系统的历史数据,经符号化之后得到的符号序列满足D阶马尔可夫特性,那么可以根据该符号序列构造出相应的马尔可夫机,称之为D-Markov机。本质上来说,D-Markov机与概率有限状态自动机没有区别。
当某符号序列具备D-Markov特性时,知道了前面D个符号序列,便能得知下一个符号的分布概率。前面D个符号最多有∑ D种排布可能(∑为符号集合的容量),在特定的序列中,由于有些序列从不出现,所以有可能出现比∑D少的情况。一种排布可以认为是D-Markov机中的一种状态,那么该D-Markov机最多有∑D种状态。
设某一符号序列中D个符号共有N种排布,那么相应的D-Markov机拥有N种状态。定义其转移概率
 | (14) |
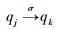 | (15) |
式(14) 与式(15) 表明当D-Markov机的状态由qj转移至qk时,出现符号σ的概率。所有的πjk组成的矩阵∏[πjk]即为D-Markov机的转移矩阵。式(14) 和式(15) 表征的是概率,由于只是得到了部分时间序列,因此只能通过频率来逼近概率,计算式为
 | (16) |
由蒙特卡罗思想可知,当时间序列足够长的时候,频率一定能够在给定的精度内逼近概率,由此便重构了D-Markov机。
阶次D实际上表示系统当前状态受之前输入输出的影响范围。确定方法一般有2种:第1种方法是将数据分为重构集合与测试集合,使D由0开始逐步增大,依次重构,并使用测试验证,当误差在预期范围之内时,即终止;第2种方法是计算原始数据的自相关函数,根据设置的阈值确定强自相关区间,D即该区间长度。经验表明,对大多数数据,D取3~5较为合适。
2 定性定量混合建模 2.1 混合建模方法 正如引言中所述,多模式系统与单模式系统最大的区别就在于,多模式系统的模式切换与其各个模式下的行为相互耦合,既有定性的模式切换行为(多个模式之间进行切换),也有定量的演化(单个模式下系统连续状态在不断演化)。
支持向量回归能够给出系统输入、输出之间的量化关系,属于定量模型。D-Markov机将原始数据符号化,并根据长度为D的字符串构造有限的系统模式,属于定性模型。使用它们对混合系统建模时,以支持向量回归为代表的定量模型精确度很差,以D-Markov机为代表的定性模型则需要很大的D值。为准确描述混合系统的行为,需要既能够描述定性又能够描述定量动态行为的混合模型。
目前,基于系统结构、原理的混合模型有混合键合图(Hybrid Bond Graph, HBG)[12-13]与概率混合自动机(Probabilistic Hybrid Automata, PHA)[14-16]等。仍然缺乏基于历史数据的混合模型。本文参考PHA,结合D-Markov机与支持向量回归模型,定义了能够描述系统定性、定量行为的经验概率混合自动机,并给出了定性定量混合建模方法。
定义??经验概率混合自动机由元组 < M, S, T>定义,其中:M={mi}为离散模式集合;S={si}为系统连续行为集合;T={ti}为模式转移集合,ti={siD, pi, miori, mides}, siD为长度为D的马尔可夫序列,pi为转移概率,miori和mides分别为系统初始模式以及目标模式。
经验概率混合自动机使用M表示系统不同的工作模式,使用S表示在各个模式下的连续行为,并使用T表示系统在各个模式之间的转移关系。为根据系统历史数据建立系统的经验概率自动机,本文做出以下假设。
假设1 ??系统行为是稳态的,即系统离散模式是有限的,各个模式下的行为是稳定的,且系统模式之间的转移条件是稳定的。
假设2 ??系统模式的切换将导致系统的输入、输出出现奇异点。
假设3 ??系统模式切换仅仅与系统当前模式及输入、输出值有关。
假设1是通过数据重构模型的基础,假设2是使用奇异点探测技术识别模式切换点的保证,假设3是使用D-Markov重构系统模型的前提。
本文提出的经验概率混合自动机建模框架如图 2所示。
 |
| 图 2 混合建模框图 Fig. 2 Block diagram of hybrid modeling |
| 图选项 |
原始数据首先经过奇异点检测,被分割为分段数据,每一段数据代表系统一种可能的模式;随后对每一段数据使用SVR建立定量模型;接着对各个SVR模型分配符号,当2个SVR模型的输出一致时,对其分配同一个符号。与此同时,将切换点附近的输入、输出数据符号化,与模式符号一起组成多维有序符号集合。再使用D-Markov重构符号序列,得到D-Markov机。D-Markov机与单模式下定量模型共同构成EPHA模型。
EPHA重构算法如下:
EPHA-Re-Construct
输入:混合系统历史数据data,马尔可夫长度D
输出:EPHA模型model
//使用奇异点识别技术,探测历史数据中模式切
换点
switching_points
SwitchingPointsDetection (data)
//根据模式切换点得到分段数据
data_section=SplitData (data, switching_points)
//分段拟合
 |
//归类与符号映射
 |
//当svri与映射表中对应的svr输出结果一致时,认为已经为svri分配了符号
if AssignedSymbol (svri, map_set)
//已经分配了符号时,什么都不用做
else
//否则为svri分配新的符号,并将映射关系添加到map_set中
 |
//符号化切换点附近的数据
sym_set=Symbol (data, D, switching_points)
//将模式符号与数据符号有序排列
sym_seq=Sequence (symbol in map_set+sym_set)
//D-Markov重构
markov_machine=MarkovReConstruction (D, sym_seq)
//得到EPHA模型
EPHA=map_set+markov_machine
2.2 方法分析 系统对外输出的数据中在一定程度上包含了系统的信息与特征,使用其历史数据,能够在一定程度上重构系统。模型重构的最终目标是完全恢复系统的行为模型,但是在没有其他信息的情况下,数据中仅包含部分信息,因此不可能完全恢复系统,因此只能够使用数据近似重构原系统。
本文所提出的EPHA模型重构方法基于3点假设:
假设1 ??是所有基于数据的模型重构方法的基础。当系统呈现非稳态特性时,是不可能根据数据恢复系统行为的。
假设2 ??并不适用于所有混合系统的情况。但当系统切换并未引起输入、输出出现奇异点时,说明切换前后模式行为十分接近,此时使用传统的定量建模方法也能够得到比较精确的模型。即使最终EPHA模型中所包含的模式数目与系统真实模式数目不相同,EPHA模型仍然能够给出系统准确的行为,是符合建模要求的。
假设3 ??同样不是所有混合系统都能够满足。然而假设3对大多数系统而言是合理的。并且对某些特殊的系统,当由其他渠道得到模式切换影响因素时,可以很容易地将该因子符号化,扩展目前的重构方法,从而构建新的D-Markov机。
综上所述,本文所提出的建模方法是一种具备良好适应性与扩展性模型重构算法。
3 实验验证 为验证本文所提出建模方法的有效性,使用式(17) 所描述的混合系统系统为建模对象,使用该的历史数据重构系统模型。
 | (17) |
由式(17) 可知,该系统包含3个工作模式,每个工作模式持续1 s。
1) 对该系统按0.01 s等间隔采样,前4 s的系统行为如图 3所示。其中信噪比为10 dB。
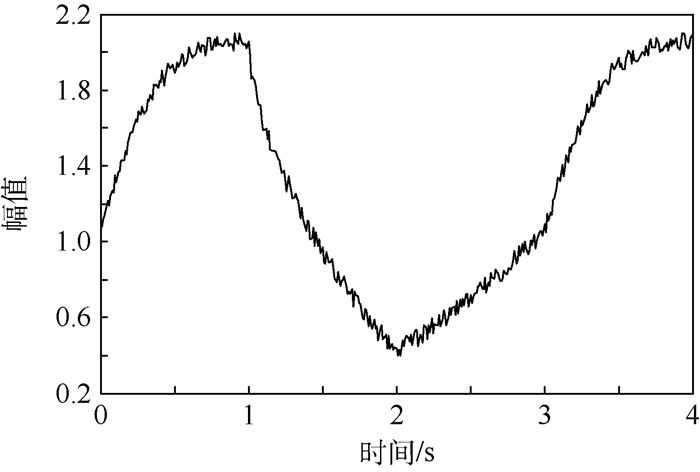 |
| 图 3 混合系统行为 Fig. 3 Behavior of hybrid system |
| 图选项 |
2) 使用小波探测奇异点,结果如图 4所示,在0~4 s之中,真实模式切换点为1、2与3 s,探测到的模式切换点分别为0.97、2.05与2.96 s。
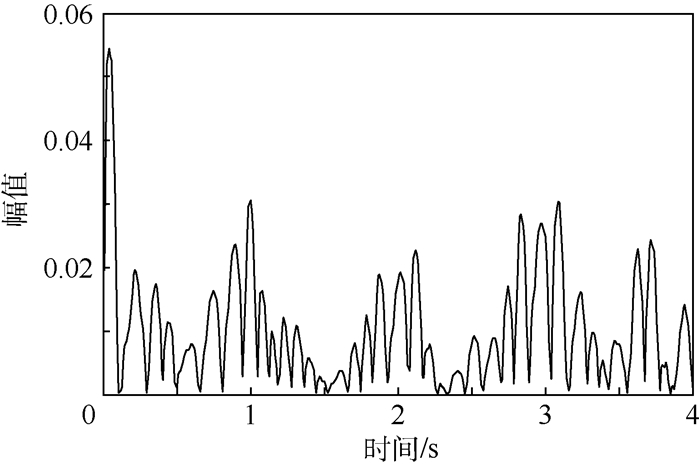 |
| 图 4 模式切换点识别 Fig. 4 Recognition of mode switching points |
| 图选项 |
3) 对历史数据在各个模式下使用SVR单独建模,实验中使用高斯核函数,并使用粒子群优化算法确定参数。
4) 将数据等间隔量化,选取D=1,在模式切换点附近建立D-Markov机。
最终得到系统的EPHA混合模型。该模型所对应的系统行为曲线与经典SVR模型的行为曲线如图 5所示。将2种算法重复实验10次,使用式(18) 均方误差(MSE) 对实验结果进行统计,统计结果见表 1。
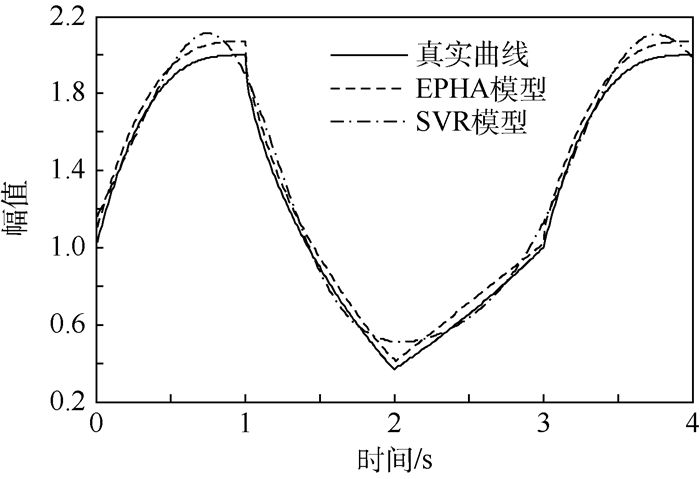 |
| 图 5 EPHA模型与SVR模型系统行为曲线 Fig. 5 System behavior curves of EPHA model and SVR model |
| 图选项 |
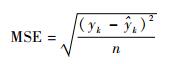 | (18) |
表 1 SVR与EPHA均方误差 Table 1 Mean square error of SVR and EPHA
| 序号 | 均方误差 | |
| SVR | EPHA | |
| 1 | 0.089 6 | 0.071 6 |
| 2 | 0.094 5 | 0.067 9 |
| 3 | 0.094 4 | 0.072 8 |
| 4 | 0.091 6 | 0.073 3 |
| 5 | 0.093 5 | 0.071 8 |
| 6 | 0.089 6 | 0.072 2 |
| 7 | 0.091 2 | 0.070 1 |
| 8 | 0.094 2 | 0.071 6 |
| 9 | 0.093 5 | 0.068 7 |
| 10 | 0.094 5 | 0.072 2 |
| 方差 | 3.95×10-6 | 3.11×10-6 |
| 均值 | 0.092 7 | 0.071 2 |
表选项
式中:yk为第k个数组的观测值
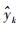
对比2种建模方法,可以看出,EPHA模型比SVR模型更加精确,特别是在模式切换点附近,EPHA有着更为明显的优势,平均误差减少23.19%。另一方面,由表 1中2种模型方差可知,EPHA具有与SVR一样的稳定性。
4 结论 本文针对混合系统数据驱动的建模问题进行了深入研究,提出了EPHA混合模型,并给出了相应的建模方法,经理论分析与实例验证,可以达到如下结论:
1) 本文提出的EPHA混合建模方法能够有效解决混合系统中传统定量建模方法精度差的问题,特别是在模式切换点附近,精确度远高于传统SVR模型,实验表明,建模误差减少约23%。
2) EPHA模型与传统SVR模型的稳定性接近,是一种可靠的数学模型。
3) EPHA混合建模方法能够准确识别混合系统模式切换关系,对通过数据分析系统行为有着极大的帮助。
4) EPHA模型具备良好的适应能力,当放宽假设2与假设3时,仍然能够非常容易地扩展,从而得到准确的混合模型。
参考文献
| [1] | SOLOMATINE D P, OSTFELD A. Data-driven modelling:Some past experiences and new approaches[J].Journal of Hydroinformatics, 2008, 10(1): 3–22.DOI:10.2166/hydro.2008.015 |
| [2] | 陈华舟, 宋奇庆, 石凯, 等. 多维标度线性回归技术应用于人体血清临床指标的FTIR光谱定量分析[J].光谱学与光谱分析, 2015, 35(4): 914–918.CHEN H Z, SONG Q Q, SHI K, et al. Multidimensional scaling linear regression applied to FTIR spectral quantitative analysis of clinical parameters of human blood serum[J].Spectroscopy and Spectral Analysis, 2015, 35(4): 914–918.(in Chinese) |
| [3] | 谭鑫, 潘景昌, 王杰, 等. 基于线指数线性回归的恒星光谱大气物理参数测量[J].光谱学与光谱分析, 2013, 33(5): 1397–1400.TAN X, PAN J C, WANG J, et al. Stellar spectrum parameter measurement based on line index by linear regression[J].Spectroscopy and Spectral Analysis, 2013, 33(5): 1397–1400.(in Chinese) |
| [4] | 谷艳红, 李颖, 田野, 等. 基于LIBS技术的钢铁合金中元素多变量定量分析方法研究[J].光谱学与光谱分析, 2014, 34(8): 2244–2249.GU Y H, LI Y, TIAN Y, et al. Study on the multivariate quantitative analysis method for steel alloy elements using LIBS[J].Spectroscopy and Spectral Analysis, 2014, 34(8): 2244–2249.(in Chinese) |
| [5] | CORTES C, VAPNIK V. Support-vector networks[J].Machine Learning, 1995, 20(3): 273–297. |
| [6] | 李元. 时间序列中变点的小波分析及非线性小波估计[M].北京: 中国统计出版社, 2002: 11-41.LI Y. Wavelet analysis for change points and nonlinear wavelet estimates in time series[M].Beijing: China Statistics Press, 2002: 11-41.(in Chinese) |
| [7] | GUPTA S, RAY A, SARKAR S, et al. GUPTA S, RAY A, SARKAR S, et al.Fault detection and isolation in aircraft gas turbine engines.Part 1:Underlying concept[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2008, 222(3): 307–318.DOI:10.1243/09544100JAERO311 |
| [8] | SARKAR S, YASAR M, GUPTA S, et al. Fault detection and isolation in aircraft gas turbine engines.Part 2:Validation on a simulation test bed[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2008, 222(3): 319–330.DOI:10.1243/09544100JAERO312 |
| [9] | CHAKRABORTY S, SARKAR S, RAY A. Symbolic identification for fault detection in aircraft gas turbine engines[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2012, 226(4): 422–436.DOI:10.1177/0954410011409980 |
| [10] | CHAKRABORTY S, SARKAR S, RAY A, et al.Symbolic identification for anomaly detection in aircraft gas turbine engines[C]//Proceedings of the 2010 American Control Conference.Piscataway, NJ:IEEE Press, 2010:5954-5959. |
| [11] | SARKAR S, MUKHERJEE K, RAY A. Symbolic dynamic analysis of transient time series for fault detection in gas turbine engines[J].Journal of Dynamic Systems Measurement and Control-Transactions of the ASME, 2012, 135(1): 359–370. |
| [12] | MOSTERMAN P J.Hybrid dynamic systems:A hybrid bond graph modeling paradigm and its application in diagnosis[D].Nashville, Tennessee:Vanderbilt University, 1997:13-31. |
| [13] | BREGON A, ALONSO C, BISWAS G, et al.Fault diagnosis in hybrid systems using possible conflicts[C]//8th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes.Laxenburg:IFAC Secretariat, 2012, 8(1):132-137. |
| [14] | HAHN E M, HERMANNS H.Rewarding probabilistic hybrid automata[C]//Proceedings of the 16th International Conference on Hybrid Systems:Computation and Control.New York:ACM, 2013:313-322. |
| [15] | HOFBAUR M W, WILLIAMS B C.Mode estimation of probabilistic hybrid systems[C]//International Workshop on Hybrid Systems:Computation and Control.Berlin:Springer-Verlag, 2002:253-266. |
| [16] | ZHOU G, BISWAS G, FENG W. A comprehensive diagnosis of hybrid systems for discrete and parametric faults using hybrid I/O automata[J].IFAC-PapersOnLine, 2015, 48(21): 143–149.DOI:10.1016/j.ifacol.2015.09.518 |
