在尾缘噪声的理论研究方面,Powell[6]认为尾缘上游壁面边界层中的湍流是尾缘噪声的主要声源。Ffowcs Williams和Hall[7]认为尾缘噪声是由于翼型尾缘对流场中的四极子噪声源声散射引起的,因此假设声源为四极子声源,通过求解半平面格林函数获得了Lighthill理论[8-9]下的半无限长、零厚度平板尾缘噪声模型,并发现了尾缘噪声的五次方速度率规律。Hayden[10]将尾缘噪声模化为尾缘附近的偶极子声源。Chase[11]和Chandiramani[12]认为尾缘噪声是流体压力波动被尾缘声散射造成的。Crighton[13]将尾缘噪声模化成一系列涡流过半无限长平板边缘,同样得到了相应的理论预测模型。Amiet[14]直接把远声场压力与翼型尾缘上游处的壁面气动压力相关联,也获得了预测模型。Howe[15]通过求解有限弦长格林函数得到了低马赫数下的尾缘噪声模型。为了考虑叶片前缘的散射影响,Roger和Moreau[16]通过对Amiet[14]辐射积分参数修正,得到了低马赫数的尾缘噪声模型,发现翼型前缘只对很低频率的噪声具有影响。
由于理论方法包含大量假设,适应范围较窄,很难用于复杂几何翼型和复杂流场。因此近年来各种数值预测方法逐渐受到关注。数值预测方法大致可分为基于非定常流场和基于平均流场的预测方法2类。Wang和Parviz[17]使用大涡模拟(LES)求解了非对称升力体的非定常流场,然后使用Ffowcs Williams和Hall[7]的尾缘噪声积分方程预测了尾缘噪声。由于非定常流场计算耗时,近年来基于平均流场的预测方法逐渐成为研究热点。Ewert等[18]使用平均流场生成随机噪声源,进而使用声波动方程数值模拟噪声在平均流场中的声传播,得到了不错的预测结果。Kamruzzaman等[19]首先使用平均流场模化翼型尾缘附近壁面压力波数频率谱,进而使用散射理论预测远场噪声。Albarracin等[20]也开展了基于平均流场的尾缘噪声预测研究工作,首先使用平均流场对尾缘处的Lighthill应力张量进行声源模化,再结合 Ffowcs Williams和Hall[7]的噪声积分方程预测了尾缘噪声。笔者课题组[21]也发展了一种基于平均流场的翼型尾缘预测方法。
近年来,数值模拟方法越来越广泛,但是数值模拟方法都需要较长的计算时间,这种方法适用于详细设计阶段,对于要求时间短的早期概念设计不适用;然而半经验预测方法计算时间很短,是工程广泛使用的预测手段。Fink[22]在大量实验结果相关分析基础上,给出了预测叶片尾缘噪声的半经验公式。Glegg等[23]通过对风力机宽频噪声测量,也提出了风力机宽频噪声的半经验预测方法。Brooks等[1]系统地测量了NACA0012翼型在不同攻角、不同来流速度以及不同弦长下的边界层流动参数和尾缘噪声,并建立了BPM半经验预测公式。该半经验预测公式BPM在工程中得到了广泛应用,并被集成到了风力机噪声预测软件NAFNoise中[24]。在NAFNoise软件[24]中,边界层参数使用XFOIL进行计算,而不是使用Brooks等[1]的边界层位移厚度的经验模型,使得BPM公式对峰值频率预测更加准确。
虽然半经验预测方法是基于实验数据得到的,但近年来基于物理机制的半经验预测方法[25-27]发展迅速,而且精度较高,速度很快。
大多数的翼型尾缘噪声半经验预测模型中都采用两声源模型,即压力面声源和吸力面声源,而且这2个声源不相关[1]。Heller和Dobrzynski[28]的测量实验结果揭示翼型吸力面边界层对噪声辐射更重要。BPM半经验预测公式也显示吸力面声源是翼型尾缘噪声的主要声源。由于从实验结果中不能直接分离出吸力面声源辐射噪声和压力面声源辐射噪声,因此如何衡量压力面声源的辐射贡献就是个难题。
Brooks等[1]的半经验预测结果表明:当攻角较大时,或者对于较厚的风力机翼型,BPM半经验预测公式往往高估高频频谱[21]。因此本文将首先分析BPM半经验预测公式高估高频频谱的原因,进而对传统的翼型湍流边界层尾缘噪声BPM半经验预测公式进行了改进。
1 BPM半经验预测公式的分析与改进 传统的BPM方法假设翼型尾缘噪声由不相干的压力面声源和吸力面声源共同产生[1]。因而总的声压级可以表示为
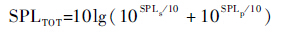 | (1) |
式中:SPLs和SPLp分别为吸力面和压力面声源辐射产生的声压级。
Brooks等[1]根据Ffowcs Williams和Hall[7]的模型对尾缘噪声实验数据进行归一化处理,得到吸力面噪声源产生的声压级预测公式为
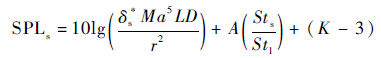 | (2) |
式中:r为声辐射距离;Ma为来流马赫数;δs*和L分别为吸力面尾缘处的边界层位移厚度和翼展长度;D为指向性函数;函数A(·)为频谱函数,其自变量Sts=fδs*/U∞为以吸力面尾缘处的边界层位移厚度为参考长度的斯特劳哈数,f 为频率,U∞为远前方来流速度;St1为吸力面声辐射频谱的峰值无量纲频率;K为幅值修正函数。
同样的,压力面噪声源产生的远场声压级预测公式为
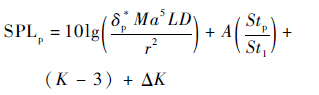 | (3) |
式中:δ*p为压力面尾缘处的边界层位移厚度;Stp=fδp*/U∞为以压力面尾缘处的边界层位移厚度为参考长度的斯特劳哈数;ΔK为压力面相对于吸力面的声压贡献,其具体表达式为
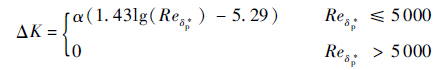 | (4) |
式中:α为来流攻角;Reδp*为以压力面尾缘边界层位移厚度δp*为参考长度的雷诺数。
为了更清楚地衡量压力面声源噪声辐射贡献与吸力面声源噪声辐射贡献之比,将声压级转化为声功率,可以得到吸力面和压力面声功率之比为
 | (5) |
式中:Πp和Πs分别为压力面和吸力面的声功率。
将式(4)代入式(5)可以看出
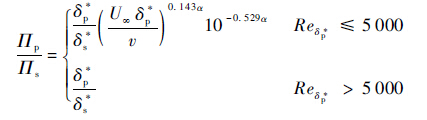 | (6) |
式中:v为空气的运动黏性系数。
从式(6)可以看出,压力面的声压贡献取决于基于压力面位移厚度的雷诺数以及攻角。当雷诺数Reδp*>5 000时,压力面声源与吸力面声源的声功率之比正比于压力面与吸力面的边界层位移厚度之比。
由于Ffowcs Williams和Hall[7]的翼型尾缘噪声模型没有对尾缘处的压力波动详细描述,不能反映压力面声源与吸力面声源声功率差异,因为压力面声源和吸力面声源的辐射贡献主要取决于声源强度。因此,Howe[29-30]采用声散射理论对尾缘噪声进行了深入分析,得到的翼型尾缘噪声理论模型为
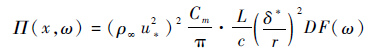 | (7) |
式中:ρ∞为远场密度;u*为尾缘处的边界层摩擦速度;c为声速;F(ω)为无量纲频谱函数;Cm为经验系数。
Howe[29-30]的理论模型采用了Chase[31]的壁面压力波动频率波数谱描述流场,在高频范围具有较高精度的预测结果,但是该模型的频谱函数F(ω)需要尾缘边界层的湍流信息来确定,比如峰值频率的确定。为了获得该理论模型需要的边界层湍流信息,目前往往使用CFD方法模拟平均流场,进而计算边界层湍流信息,而平均流场计算往往需要较长时间。
从式(7)可以看出在Howe[29-30]的理论模型中,不论压力面声源还是吸力面声源的声功率都与相应面的边界层位移厚度的平方成正比,因此压力面声源与吸力面声源的声功率之比为
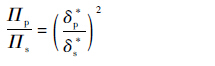 | (8) |
通过比较式(8)和式(6)可以发现:2种尾缘噪声模型对于压力面和吸力面声源的声功率之比不一致;相比于BPM半经验预测公式,Howe[29-30]尾缘噪声模型中压力面声源噪声辐射要小。
由于高频噪声主要来自于压力面噪声源贡献,基于上述分析,笔者认为:BPM半经验预测公式对翼型湍流边界层尾缘噪声在高频范围常常高估是由于BPM高估了压力面噪声源的声压贡献。
为了提高BPM半经验预测公式在高频范围的预测精度,笔者根据Howe[29-30]理论模型对BPM半经验预测公式进行了如下改进,将传统BPM半经验预测公式中的压力面声源噪声辐射与吸力面声源噪声辐射之比由原来的与边界层位移厚度一次方成正比改进为与边界层位移厚度的二次方成正比,就可以得到新的压力面声源噪声辐射贡献参数为
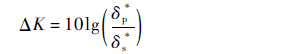 | (9) |
将式(9)代替式(4)代入式(3)就可以得到改进后的BPM半经验预测公式。
2 半经验预测公式验证 2.1 计算工况及网格 本文选择第三届机体噪声标准算例1[32]中的翼型湍流边界层尾缘宽频噪声问题进行验证。表 1列出了5种计算工况,前4种工况对应的翼型为NACA0012翼型,第5种工况对应的翼型为较厚的风力机翼型DU-96-W-180。工况1、工况2和工况3,雷诺数Re一致,攻角α不同。工况4与工况1,攻角一致,来流速度U∞不同。
表 1 计算工况 Table 1 Computation cases
| 工况 | 翼型 | U∞/ (m·s-1) | Re/106 | α/(°) |
| 1 | NACA0012 | 56.0 | 1.5 | 0 |
| 2 | NACA0012 | 54.8 | 1.5 | 4 |
| 3 | NACA0012 | 53.0 | 1.5 | 6 |
| 4 | NACA0012 | 37.7 | 1.0 | 0 |
| 5 | DU-96-W-180 | 60.0 | 1.1 | 4 |
表选项
本文采用开源计算流体力学软件OpenFOAM模拟这5种工况的平均流场。由于这5种工况的来流速度都较低,可压性可以忽略,因此使用不可压求解器,湍流模型选择SST(Shear Stress Transport)两方程模型。
本文采用的计算网格、计算边界条件设置,以及平均流场计算结果参见文献[21]。
2.2 翼型边界层参数计算及对比 传统的翼型湍流边界层尾缘噪声BPM半经验预测公式以及改进后的BPM半经验预测公式都需要翼型尾缘处的压力面和吸力面边界层位移厚度作为输入参数[1],因为边界层位移厚度决定着频谱的峰值频率。因此首先对边界层位移厚度参数进行计算和对比,确保边界层位移厚度参数具有较高精度。
图 1给出了工况1、工况2和工况3的翼型尾缘吸力面和压力面边界层位移厚度随攻角的变化关系以及对比结果。图中不仅给出了本文计算的边界层位移厚度,而且也给出了另外3个研究机构(德国宇航局DLR、斯图加特大学IAG和丹麦理工大学DTU)的计算结果[33],另外也给出了Brooks等[1]的半经验预测公式得到的边界层位移厚度公式。图 1(a)给出了吸力面边界层位移厚度与攻角的关系,可以看出,随着攻角的增加,位移厚度增加,这主要是由于攻角增加导致翼型尾缘吸力面边界层变厚引起的。从图 1(b)可以看出,随着攻角的增加,压力面边界层位移厚度减小,这是由于攻角增加导致翼型尾缘压力面的边界层厚度变薄导致的。从图 1对比可以看出不论压力面和吸力面边界层,计算结果都比Brooks等[1]的半经验预测值小;这主要是因为Brooks等[1]实验测试时给翼型前缘安装了湍流诱导装置,导致实验测量得到的边界层变厚。而不同研究机构计算得到的边界层位移厚度基本一致。
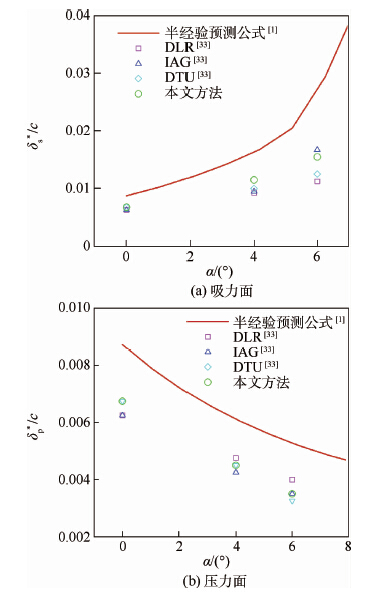 |
| 图 1 边界层位移厚度随攻角的变化 Fig. 1 Variation of boundary displacement thickness withangle of attack |
| 图选项 |
图 2给出了翼型尾缘吸力面和压力面边界层动量厚度(θs和θp)随攻角的变化关系。从图 2(a)可以看出,随着攻角增加,翼型尾缘吸力面边界层动量厚度随攻角增加而增加,这主要是由于吸力面边界层随攻角变厚引起的;从图 2(b)可以看出,随着攻角增加,翼型尾缘压力面边界层动量厚度随攻角增加而减小,这主要是由于压力面边界层随攻角变薄引起的;还可以看出不论压力面和吸力面边界层动量厚度,计算结果都比Brooks等[1]的半经验预测值小;这主要是因为Brooks等[1]实验测试时给翼型前缘安装了湍流诱导装置,导致实验测量得到的边界层变厚。
图 3给出了当攻角α=0时,翼型尾缘边界层位移厚度δ0*和动量厚度θ0随雷诺数的变化关系。可以看出随着雷诺数增大,不论位移厚度还是动量厚度都变小了,这主要是因为当来流速度增大后,翼型尾缘边界层厚度减小导致的。还可以看出不同研究机构计算得到的边界层厚度参数基本一致,但都比Brooks等[1]的半经验预测值小;这主要是因为Brooks等[1]实验测试时给翼型前缘安装了湍流诱导装置,导致实验测量得到的边界层变厚。
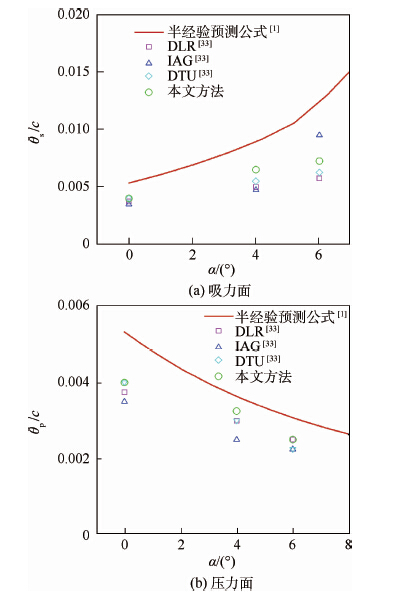 |
| 图 2 边界层动量厚度随攻角的变化 Fig. 2 Variation of boundary momentum thickness withangle of attack |
| 图选项 |
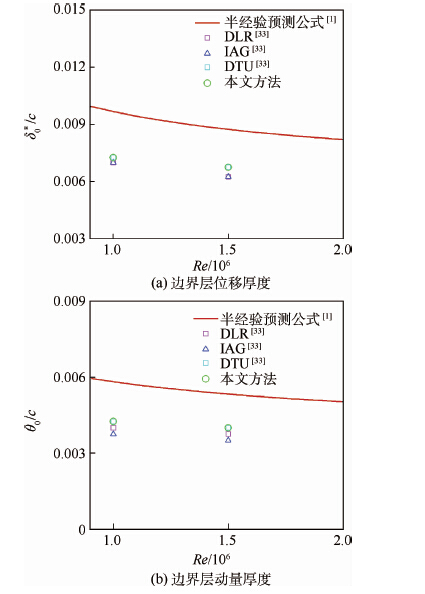 |
| 图 3 攻角为0时边界层厚度随雷诺数的变化 Fig. 3 Variation of boundary thickness with Reynolds numberwhen angle of attack equals to zero |
| 图选项 |
2.3 远场噪声半经验预测 为了预测翼型尾缘噪声的远场频谱,本文观察者的位置选择与尾缘噪声标准算例[32]中一致,观察者位于翼型尾缘正下方,距离翼型尾缘r=1 m。
图 4(a)给出了工况1的远场噪声预测结果对比,SPL1/3为远场的噪声声压级。从给出的改进后的预测结果和没有改进的BPM预测结果可以看出,当攻角为0时,改进后的预测频谱与没有改进的预测频谱几乎一致,这主要是因为压力面和吸力面的噪声贡献一致,而且2种方法预测的结果与实验结果符合很好。当攻角从0增加到4°时,图 4(b)给出了工况2的预测频谱对比。从对比可以看出,改进后的预测频谱相比于没有改进的预测频谱,在中高频改进很多。图 4(c)给出了攻角为6°时工况3的预测频谱对比。可以看出没有改进的频谱在高频的预测结果明显大于实验结果,而改进后的预测结果改进很多,与实验结果符合很好。图 4(d)给出了工况4的预测频谱对比,由于工况4的攻角为0,因此两者预测结果基本一致,与实验结果也吻合很好。图 4(e)给出了风力机翼型的尾缘噪声预测结果对比。可以看出没有改进的BPM预测结果在高频远远大于实验频谱,这主要是由于BPM高估了压力面声源的贡献。而改进后的BPM预测频谱在整个频率范围都在误差范围之内,与实验结果吻合很好。
 |
| 图 4 工况1~工况5的噪声预测对比 Fig. 4 Comparison of noise prediction for Case 1-Case 5 |
| 图选项 |
3 结 论 1) 分析比较了传统BPM半经验预测公式与Howe尾缘噪声模型,发现传统BPM半经验预测公式在高频范围预测较大主要是由于传统BPM半经验预测公式高估了压力面声源噪声辐射。
2) 改进了传统BPM半经验预测公式中的压力面声源噪声辐射与吸力面声源噪声辐射之比。将原来的压力面声源与吸力面声源的声辐射贡献之比正比于边界层位移厚度之比改进为边界层位移厚度的二次方之比。
3) 使用改进后的BPM半经验预测公式对NACA0012翼型和风力机厚翼型DU-96-W-180进行了远场噪声预测,与实验结果对比发现:改进后的BPM半经验预测公式对不同翼型、不同攻角下都具有较高精度。
参考文献
| [1] | ?BROOKS T F,POPE D S,MARCOLINI M A.Airfoil self-noise and prediction:NASA-RP-1218[R].Hampton,Virginia:NASA Langley Research Center,1989. |
| [2] | YANNICK R,MOREAU S,MAUUEL H,et al.Fan trailing-edge noise prediction using RANS simulations:AIAA-2010-3720[R].Reston:AIAA,2010. |
| [3] | ANA G S,TOM H,HOWARD H.Experimental investigation into trailing edge noise sources:AIAA-2006-2476[R].Reston:AIAA,2006. |
| [4] | ROBERT G R,MILLER G,GUO Y P,et al.Airframe noise studies-review and future direction:NASA-CR-213767[R].Hampton,Virginia:NASA Langley Research Center,2005. |
| [5] | WAGNER S, BAREIB R, GUIDATI G. Wind turbine noise[M].Berlin: Springer, 1996: 67-80. |
| [6] | POWELL A. On the aerodynamic noise of a rigid flat plate moving at zero incidence[J].Journal of the Acoustical Society of America, 1959, 31(12): 1649–1653.DOI:10.1121/1.1907674 |
| [7] | FFOWCS WILLIAMS J E, HALL L H. Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane[J].Journal of Fluid Mechanics, 1970, 40: 657–670.DOI:10.1017/S0022112070000368 |
| [8] | LIGHTHILL M J. .On sound generated aerodynamically:I.General theory[J].Proceedings of the Royal Society of London, Series A:Mathematical and Physical Sciences, 1952, 211(1107): 564–581.DOI:10.1098/rspa.1952.0060 |
| [9] | LIGHTHILL M J. On sound generated aerodynamically:II.Turbulence as a source of sound[J].Proceedings of the Royal Society of London, Series A:Mathematical and Physical Sciences, 1954, 222(1148): 1–32.DOI:10.1098/rspa.1954.0049 |
| [10] | HAYDEN R E.Noise from interaction of flow with rigid surfaces:A review of current status of prediction techniques:NASA CR-2126[R].Washington,D.C.:NASA,1972. |
| [11] | CHASE D M. Noise radiated from an edge in turbulent flow[J].AIAA Journal, 1975, 13(8): 1041–1047.DOI:10.2514/3.60502 |
| [12] | CHANDIRAMANI K L. Diffraction of evanescent waves with applications to aerodynamically scattered sound and radiation from unbaffled plates[J].Journal of the Acoustical Society of America, 1974, 55(1): 19–29.DOI:10.1121/1.1919471 |
| [13] | CRIGHTON D G. Radiation from vortex filament motion near a half-plane[J].Journal of Fluid Mechanics, 1972, 51(2): 357–362.DOI:10.1017/S0022112072001235 |
| [14] | AMIET R K. Noise due to turbulent flow past a trailing edge[J].Journal of Sound and Vibration, 1976, 47(3): 387–393.DOI:10.1016/0022-460X(76)90948-2 |
| [15] | HOWE M S. Edge-source acoustic Green's function for an airfoil of arbitrary chord with application to trailing-edge noise[J].Quarterly Journal of Mechanics and Applied Mathematics, 2001, 54(1): 139–155.DOI:10.1093/qjmam/54.1.139 |
| [16] | ROGER M, MOREAU S. Broadband self-noise from loaded fan blades[J].AIAA Journal, 2004, 42(3): 536–544.DOI:10.2514/1.9108 |
| [17] | WANG M, PARVIZ M. Computation of trailing-edge flow and noise using large-eddy simulation[J].AIAA Journal, 2000, 38(12): 2201–2209.DOI:10.2514/2.895 |
| [18] | EWERT R,APPEL C,DIERKE J,et al.RANS/CAA based prediction of NACA0012 broadband trailing edge noise and experimental Validation:AIAA-2009-3269[R].Reston:AIAA, 2009.http://www.cnki.com.cn/Article/CJFDTOTAL-HKDI201601017.htm |
| [19] | KAMRUZZAMAN M,LUTZ T,HERRIG A,et al.RANS based prediction of airfoil trailing edge far field noise:impact of isotropic and anisotropic Turbulence:AIAA-2008-2867[R].Reston:AIAA,2008. |
| [20] | ALBARRACIN C A,DOOLAN C J,JONES R F,et al.A RANS-based statistical noise model for trailing edge noise:AIAA-2012-2181[R].Reston:AIAA,2012. |
| [21] | 柏宝红, 李晓东. 一种基于平均流场的翼型尾缘宽频噪声预测方法[J].航空动力学报, 2016, 31(1): 115–123.BAI B H, LI X D. A RANS-based prediction method for the airfoil broadband trailing edge noise[J].Journal of Aerospace Power, 2016, 31(1): 115–123.(in Chinese) |
| [22] | FINK M R. Experimental evaluation of theories for trailing edge and incidence fluctuation noise[J].AIAA Journal, 1975, 13(11): 1472–1477.DOI:10.2514/3.60559 |
| [23] | GLEGG S A L, BAXTER S M, GLENDENNING A G. The prediction of broadband noise from wind turbines[J].Journal of Sound and Vibration, 1986, 118(2): 217–239. |
| [24] | MORIARTY P.NAFNoise:A program for calculating 2d airfoil noise.Design code[EB/OL].Golden,Colorado:National Wind Technology Center,2003[2016-03-17].https://nwtc.nrel.gov/NAFNoise. |
| [25] | GUO Y P. Slat noise modeling and prediction[J].Journal of Sound and Vibration, 2012, 331(15): 3567–3586.DOI:10.1016/j.jsv.2012.03.016 |
| [26] | GUO Y P. A component-based model for aircraft landing gear noise prediction[J].Journal of Sound and Vibration, 2008, 312(4): 801–820. |
| [27] | GUO Y P. Flap side edge noise modeling and prediction[J].Journal of Sound and Vibration, 2013, 332(16): 3846–3868.DOI:10.1016/j.jsv.2013.02.029 |
| [28] | HELLER H H, DOBRZYNSKI W M. Unsteady surface pressure characteristic on aircraft components and far field radiated airframe noise[J].Journal of Aircraft, 1978, 15(12): 809–815.DOI:10.2514/3.58453 |
| [29] | HOWE M S. Trailing edge noise at low Mach numbers[J].Journal of Sound and Vibration, 1999, 225(2): 211–238.DOI:10.1006/jsvi.1999.2236 |
| [30] | HOWE M S. Trailing edge noise at low mach numbers, Part 2:Attached and separated edge flows[J].Journal of Sound and Vibration, 2000, 234(5): 761–775.DOI:10.1006/jsvi.1999.2861 |
| [31] | CHASE D M. Modeling the wavevector-frequency spectrum of turbulent boundary layer wall pressure[J].Journal of Sound and Vibration, 1980, 70(1): 29–67.DOI:10.1016/0022-460X(80)90553-2 |
| [32] | HERR M,BAHR C,KAMRUZZAMAN M.Workshop category 1:Trailing-edge noise[C]//Proceedings of the AIAA/CEAS Third Workshop on Benchmark Problems for Airframe Noise Computations (BANC-Ⅲ).Reston:AIAA,2014. |
| [33] | HERR M,EWERT R,RAUTMANN C.Broadband trailing-edge noise predictions-overview of BANC-Ⅲ results:AIAA-2015-2847[R].Reston:AIAA,2015. |
