Rossano[5]和Gu[6]等运用机器人末端与球面、圆柱面等特殊几何形状的接触并根据不同接触位形建立了不相容方程组得到机器人基坐标系的标定结果,但这种方法是建立在机器人的末端工具具有特殊结构的基础上的,并且这种方法对特殊几何形状的精度要求很高。任永杰等[7]对机器人轴1和轴2分别进行单轴运动,运动过程中通过激光跟踪仪[8]得到末端靶标数据实现机器人基座标系标定,但是这种方法需要获取大量的数据,不能实现快速标定。王伟等[1]也使用激光跟踪仪进行测量标定,应用单位四元数表示法得到了机器人基坐标系与测量坐标系的姿态关系,然而这种方案的前提是法兰坐标系或基坐标系直接通过激光跟踪仪的测量得到,不能解决具有隐藏法兰坐标系的串联机器人的标定问题。本文针对具有隐藏机器人基坐标系和法兰坐标系的串联机器人提出了一种快速标定的新方法,并通过实验验证应用标定结果并结合一种新的位姿补偿算法后能够极大地提高机器人的定位精度。
1 标定模型的建立 机器人具有固定在机器人底盘的基坐标系{OB}以及固定在机器人末端的法兰坐标系{OF},这2个坐标系通常是隐藏的,在使用机器人进行标定或定位操作时,需要建立一个测量坐标系{OP},同时在末端固定至少3个靶标点PP1、PP2、PP3得到末端相对于测量坐标系关系,这样标定模型就建立完成。标定过程就是需要知道测量坐标系相对于机器人基坐标系的位姿矩阵TP。在建立模型时,末端3个靶标点在测量坐标系{OP}下的坐标是已知的,机器人法兰坐标系相对于基坐标系的位姿可以通过机器人面板得到(也可以根据机器人各关节角度得到DH参数得到[9-11])。
2 标定理论 2.1 等价变换法得到标定方程 根据图 1所示的标定模型,当控制串联机器人达到一个新的位姿后,图 1中相应的矩阵TBF、TPF变化为TBF2、TPF2,靶标点P1、P2、P3在测量坐标系{OP}中的坐标PP1、PP2、PP3变化为2PP1、2PP2、2PP3,如图 2所示。为了求解需要标定的矩阵TP,本文提出了一种基于等价变换法建立矩阵方程的方法。
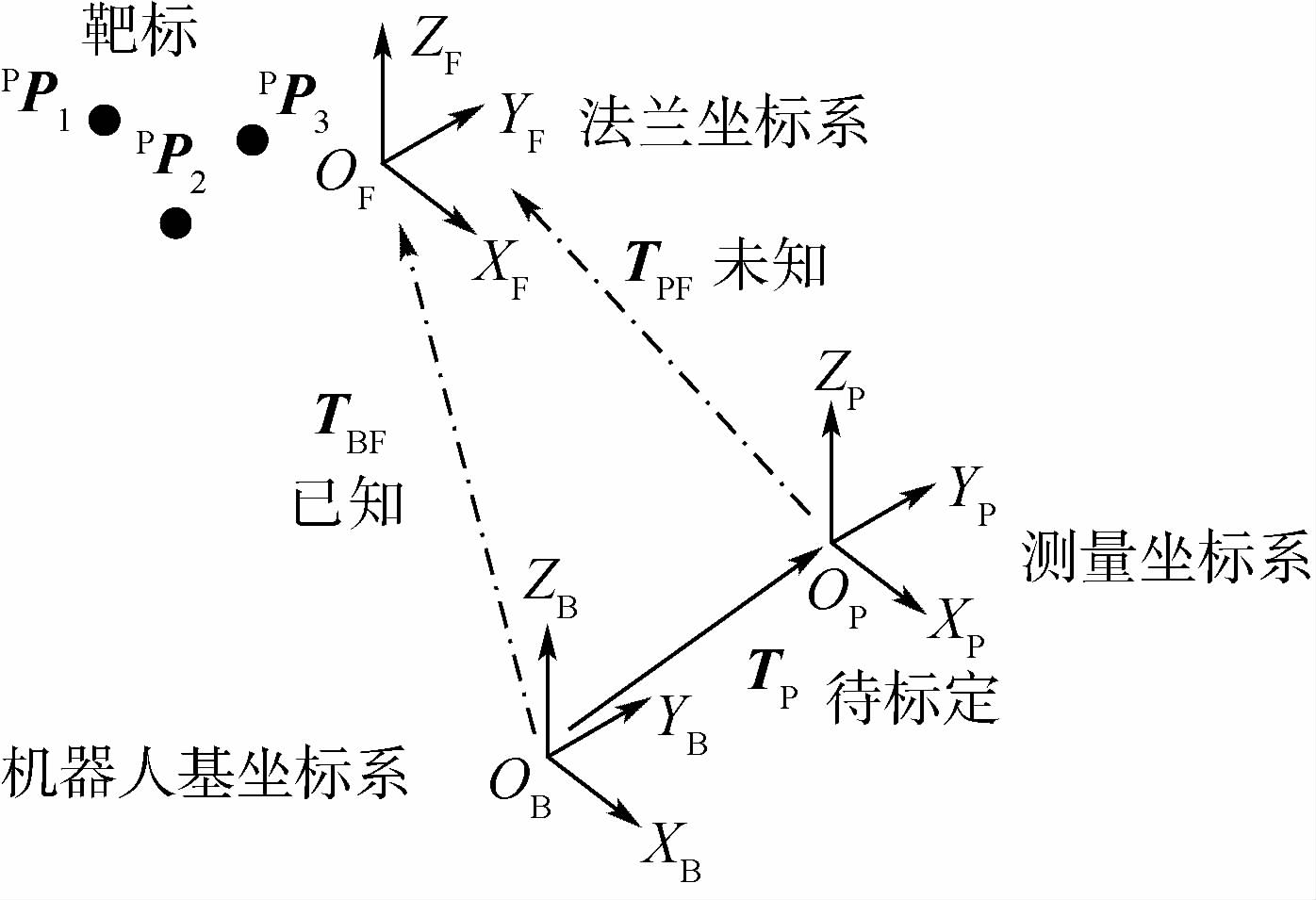 |
| 图 1 标定模型 Fig. 1 Calibration model |
| 图选项 |
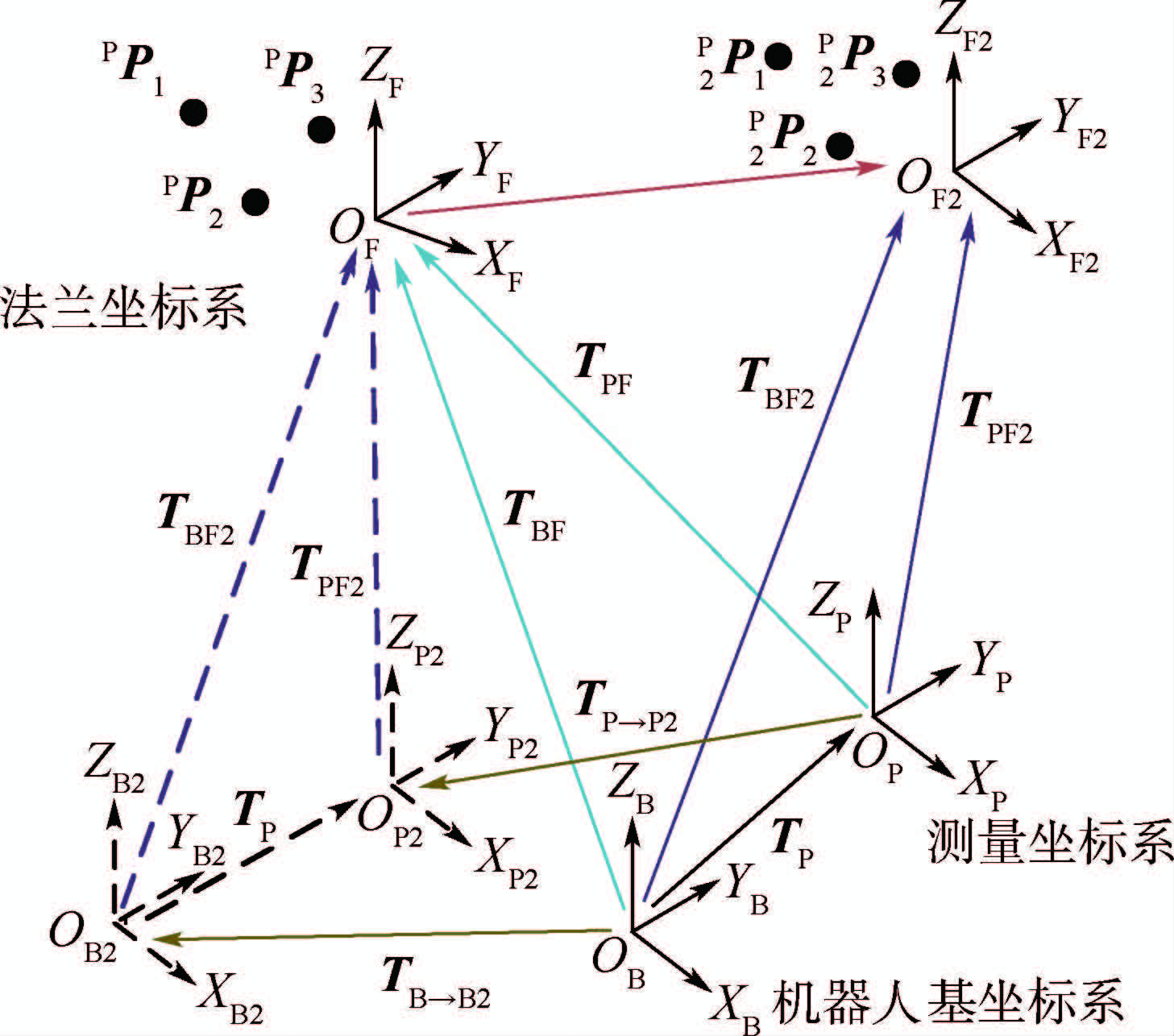 |
| 图 2 等价变换法坐标系模型 Fig. 2 Coordinate system model of equivalenttransformation method |
| 图选项 |
等价变换法:如图 2,法兰坐标系由{OF}变换到{OF2}可以转换为法兰坐标系不变,机器人基坐标系{OB}和测量坐标系{OP}变换到机器人基坐标系{OB2}和测量坐标系{OP2},变换完成后只要保证法兰坐标系{OF}相对于机器人基坐标系{OB2}和测量坐标系{OP2}的位姿关系分别为TBF2和TPF2,即可保证坐标系{OB2}和{OP2}的位姿关系为TP。
由第1节所述,矩阵TBF和矩阵TBF2可以通过求解得到,进而可以得到TB→B2。而TPF和TPF2由于法兰坐标系是隐藏的,但是靶标点P1、P2、P3在测量坐标系{OP}及测量坐标系{OP2}中的坐标是已知的,应用SVD法[12-13]求解得到TP→P2。
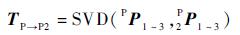 | (1) |
根据图 2中封闭的矩阵关系可以得到
 | (2) |
由此可以得到结论:TB→B2~TP→P2,由TB→B2变换到TP→P2的相似变换矩阵为TP。
将上述的位姿齐次矩阵转化为姿态位置矩阵描述,可得对于任意的末端坐标系中的坐标点[X Y Z]T均满足下述的等式关系:
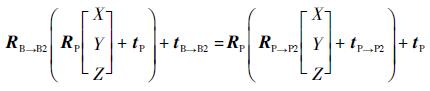 | (3) |
由于对于任意的坐标[X Y Z]T式(3)均成立,则可得到等式关系如下:
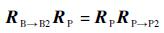 | (4) |
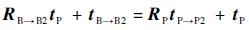 | (5) |
2.2 应用罗德里格矩阵的方程变换 根据姿态矩阵可以分解为2种形式罗德里格矩阵[14-16]的表示,姿态矩阵中的9个未知量由3个变量表示并避免了求解过程中存在矩阵逆的情况,进而极大地简化了计算。
将RP进行罗德里格矩阵变换可得
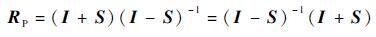 | (6) |
将式(6)代入式(4)可得
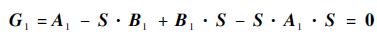 | (7) |
式中:
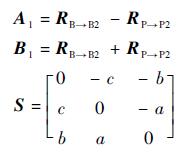 |
由于RP是关于(a,b,c)的函数,并且RP是RB→B2变换到RP→P2相似变换矩阵,仅通过2组数据得到上述关系式(7)无法得到RP的解,因此还需要一组数据建立另一个如式(4)所示的方程。相应地需要控制机器人达到新的位姿并测量新位姿下的3个靶标点坐标。
 | (8) |
式中:A2=RB→B3-RP→P3;B2=RB→B3+RP→P3。
2.3 应用最小二乘法求解变换矩阵 由式(7)和式(8)得到的是关于变量(a,b,c)的三元二次矩阵方程,虽然对RP的求解比变换前容易,但得出解析解依旧困难。
为得到RP中的变量(a,b,c),采用最小二乘法进行求解,其过程是首先建立最小二乘法的目标函数,然后应用牛顿迭代法完成变量(a,b,c)求解。
根据最小二乘法建立目标函数:
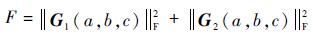 | (9) |
决定姿态矩阵RP的变量a、b、c包含在式(9)中的矩阵S中,将F分别对a、b、c求偏导:
 | (10) |
式中:sum()表示矩阵中各元素的和。
同理其他各式为
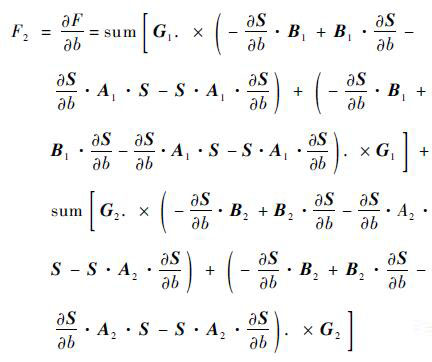 | (11) |
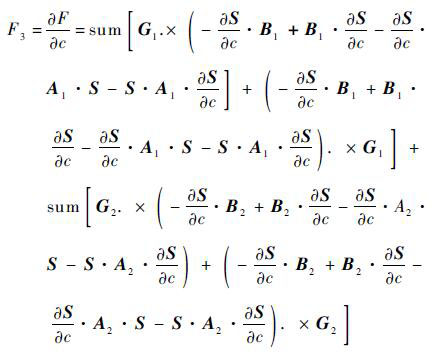 | (12) |
给定一初值x(0)=(a0 b0 c0),将其与已知值代入式(10)~式(12),求出初始误差值||F(x(0))||,如果||F(x(0))||<ε(ε为精度值),则x(0)为所求;如果||F(x(0))||≥ε,构造牛顿迭代方程。令
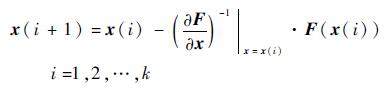 |
其中:
 |
进行多次迭代,直到满足||F(x(s))||<ε,那么x(s)=(as bs cs)就是所求的解,将求解结果代入式(6)就可以得到标定矩阵中的姿态矩阵RP。
最后根据式(5),并结合上述所求解的姿态矩阵RP,即可求得位置向量tP,求解方法如下:
 | (13) |
3 标定试验 在机器人基坐标系标定试验中,试验系统由API激光跟踪仪、3个靶标座和KUKA标准工业机器人KR210 R2700组成,如图 3所示。
 |
| 图 3 标定试验系统 Fig. 3 System of calibration experiment |
| 图选项 |
首先将3个靶标座固定在机器人末端;然后控制KUKA机器人运动到某一位姿,记录下此时面板显示的位姿信息X、Y、Z、A、B、C,同时测量机器人末端3个靶标点的坐标PP1、PP2、PP3;重复上一步操作,记录下6组数据。将实验结果进行记录,结果如表 1所示。
表 1 标定试验记录 Table 1 Records of calibration experiment
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| X/mm | 787.08 | 1 034.80 | 781.15 | 920.70 | 845.21 | 1 260.31 |
| Y/mm | 652.11 | 421.65 | 789.07 | 716.23 | 624.32 | 779.90 |
| Z/mm | 1 397.13 | 1 510.33 | 1 421.27 | 1 300.67 | 1 336.91 | 1 256.55 |
| A/(°) | -17.88 | 3.59 | 15.65 | 34.18 | 0.52 | 26.86 |
| B/(°) | -34.95 | -14.42 | 13.12 | 14.70 | 26.71 | 50.43 |
| C/(°) | -131.82 | -108.07 | -77.79 | -48.75 | -122.20 | -80.52 |
| 靶标点PP1/mm | -1 451.694 1 | -1 532.075 4 | -1 389.275 6 | -1 388.278 1 | -1 465.091 5 | -1 104.085 2 |
| 1 261.126 1 | 939.940 5 | 1 342.042 8 | 1 159.200 2 | 1 207.296 0 | 920.818 0 | |
| 870.637 0 | 1 016.827 0 | 975.633 1 | 864.795 4 | 882.391 6 | 836.600 1 | |
| 靶标点PP2/mm | -1 481.243 6 | -1 511.547 8 | -1 356.844 6 | -1 341.088 7 | -1 492.635 2 | -1 124.393 0 |
| 1 176.577 6 | 874.397 1 | 1 337.026 3 | 1 197.063 4 | 1 173.368 3 | 946.855 1 | |
| 849.137 2 | 955.521 8 | 889.580 0 | 795.399 4 | 801.334 9 | 750.644 5 | |
| 靶标点PP3/mm | -1 429.139 9 | -1 466.628 8 | -1 306.996 3 | -1 288.543 3 | -1 413.111 0 | -1 046.697 3 |
| 1 170.211 8 | 853.476 0 | 1 275.929 2 | 1 125.866 1 | 1 127.190 6 | 891.396 3 | |
| 928.905 5 | 1 037.245 2 | 943.469 3 | 831.433 4 | 827.094 3 | 747.072 6 |
表选项
进行数据处理,因为上述具有6组数据,每3组数据就会计算出一组标定结果,因此上述数据共有C63=20组结果。将标定得到的矩阵TP转化为位置信息和姿态信息,姿态信息用ZYX欧拉角进行表示,为了验证标定方法的准确性,将这20组结果中的位姿信息绘制曲线图(见图 4),观察结果。
 |
| 图 4 标定结果 Fig. 4 Records of calibration experiment |
| 图选项 |
根据图 4可知,由标定得到的姿态角偏差在±0.04°以内,位置偏差在1 mm以内,因此证明这种标定方法是正确的。将20组标定结果得到的ZYX姿态角Ar、Br、Cr及位置Xr、Yr、Zr、取平均值,得到标定试验结果,如表 2所示。
表 2 标定试验结果 Table 2 Results of calibration experiment
| 参数 | Xr/mm | Yr/mm | Zr/mm | Ar/(°) | Br/(°) | Cr/(°) |
| 数值 | 2 614.63 | 1 173.67 | 490.06 | 55.31 | -0.08 | -0.21 |
表选项
4 补偿实验 由于这种标定方法依赖于机器人控制器给出的末端位姿结果,这对标定精度具有一定的影响,因此应用标定结果控制机器人到达指定靶标点时的直接定位精度不一定很高。另外,串联机器人本身的直接定位精度并不高,即使应用精确测量仪器的标定方法也只能在一定程度上提高直接定位精度,若进一步提高串联机器人的定位精度,则需要对机器人进行位姿补偿进而达到目标点。
补偿实验的过程:①在机器人末端贴3个靶标点;②记录下机器人操作面板初始位姿、初始位姿下机器人末端靶标点在测量坐标系的坐标以及目标靶标点在测量坐标系的坐标;③通过控制串联机器人运动使末端的3个靶标点与目标靶标点重合,记录运动完成后机器人位姿及3个靶标点坐标;④若3个靶标点没有与目标靶标点重合,运用补偿算法得到机器人的运动位姿控制机器人运动,记录运动后的3个靶标点坐标。
4.1 原 理 本文根据等价变换法提出了一种新的位姿补偿算法,并且在之后的补偿实验中证明了这种新补偿算法比一种通用的补偿算法具有更高的补偿精度。
通用补偿算法原理:根据初始位姿靶标点和目标靶标点可以计算出目标位姿,控制机器人运动到目标位姿后,靶标点并未与目标靶标重合。根据此时测量得到的当前靶标点坐标和初始位姿的靶标点可以得到此时测量的位姿,用目标位姿减去测量得到的位姿得到位姿变化量ΔD,然后将位姿变化量加上当前面板位姿作为目标位姿进行机器人的补偿运动。
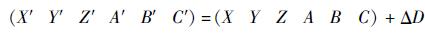 | (14) |
新补偿算法原理如图 5所示,当机器人达到目标位姿时,测量当前靶标点P1、P2、P3并未与目前靶标点与目标靶标mP1、mP2、mP3重合,由等价变换可知,当前靶标点与目标靶点相差一个变换矩阵ΔT,将这个变换矩阵与当前面板位姿得到的变换矩阵T相乘即可作为目标位姿进行机器人的补偿运动。当然这种新的补偿算法也具有通用性。
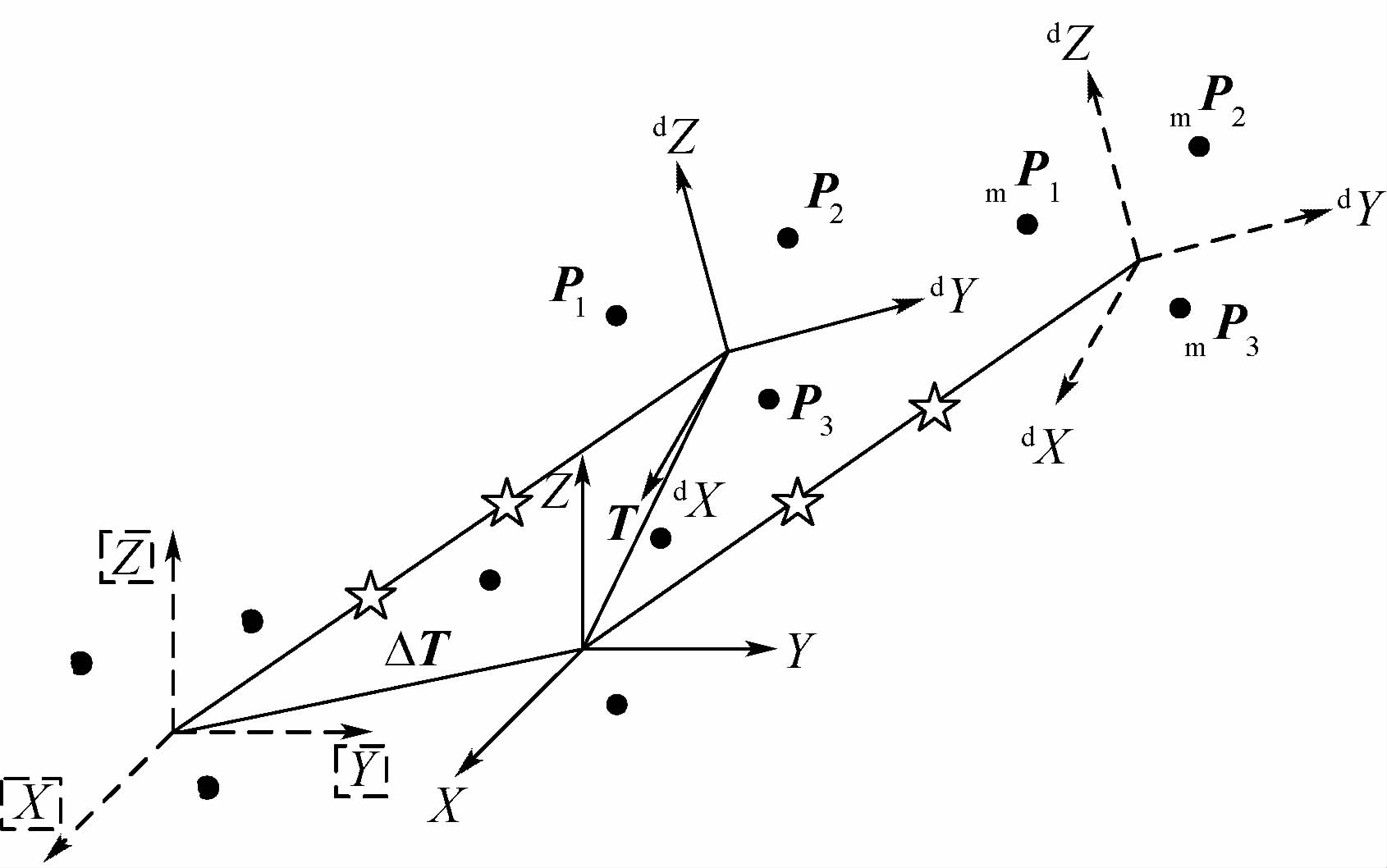 |
| 图 5 新补偿算法原理 Fig. 5 Principle of the new compensation algorithm |
| 图选项 |
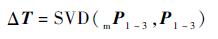 | (15) |
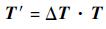 | (16) |
式中:T为补偿或运动需要达到的目标位姿;T为根据当前面板位姿信息得到的位姿矩阵;SVD(mP1~3,P1~3)为应用SVD法得到当前靶标点相对于目标靶标点的变换矩阵。
4.2 分 析 为了验证新的补偿算法比通用补偿算法具有更高的补偿精度,首先进行的补偿实验是分别应用2种补偿算法控制机器人由相同的初始位姿运动到相同的目标靶标,然后为了验证新的补偿算法较高的补偿精度不是偶然因素产生的,进行多次实验验证这种新补偿算法。
按照通用补偿算法原理进行补偿实验得到数据如表 3所示。
表 3 通用补偿算法补偿实验靶标数据记录 Table 3 Target data records in compensation experimentwith universal compensation algorithmmm
| mm | ||||
| 靶标序号 | 初始靶标 | 目标靶标 | 补偿前 | 补偿后 |
| 靶标点1 | -1 408.80 | -1 455.28 | -1 455.39 | -1 455.30 |
| 1 398.80 | 1 263.11 | 1 263.22 | 1 263.21 | |
| 1 027.63 | 848.95 | 849.21 | 848.94 | |
| 靶标点2 | -1 416.39 | -1 463.87 | -1 463.99 | -1 463.87 |
| 1 347.08 | 1 211.64 | 1 211.75 | 1 211.74 | |
| 1 081.34 | 902.76 | 903.00 | 902.74 | |
| 靶标点 | -1 416.51 | -1 450.18 | -1 450.29 | -1 450.18 |
| 1 400.22 | 1 262.90 | 1 263.00 | 1 263.00 | |
| 1 140.48 | 961.97 | 962.22 | 961.95 | |
表选项
以运动完成后靶标点与目标靶标点的距离作为误差的数值量,给出3个靶标点补偿前和补偿后的误差值计算表,如表 4所示。
表 4 通用补偿算法补偿前后靶标误差值 Table 4 Target error values before and afteruniversal compensation algorithmmm
| mm | |||
| 过程 | 靶标点1 | 靶标点2 | 靶标点3 |
| 补偿前 | 0.30 | 0.29 | 0.29 |
| 补偿后 | 0.10 | 0.10 | 0.10 |
表选项
按照新补偿算法原理进行补偿实验得到数据如表 5所示。
表 5 新补偿算法补偿实验靶标数据记录1 Table 5 Target data record 1 in compensation experiment with the new compensation algorithmmm
| mm | ||||
| 靶标序号 | 初始靶标 | 目标靶标 | 补偿前 | 补偿后 |
| 靶标点1 | -1 408.82 | -1 455.28 | -1 455.34 | -1 455.30 |
| 1 398.83 | 1 263.11 | 1 263.31 | 1 263.13 | |
| 1 027.55 | 848.95 | 849.28 | 848.95 | |
| 靶标点2 | -1 416.41 | -1 463.87 | -1 463.94 | -1 463.88 |
| 1 347.13 | 1 211.64 | 1 211.85 | 1 211.66 | |
| 1 081.25 | 902.76 | 903.07 | 902.75 | |
| 靶标点3 | -1 416.52 | -1 450.18 | -1 450.25 | -1 450.18 |
| 1 400.27 | 1 262.90 | 1 263.10 | 1 262.91 | |
| 1 140.39 | 961.97 | 962.29 | 961.97 | |
表选项
根据误差的数值量表示,给出3个靶标点补偿前和补偿后的误差值计算表,如表 6所示。
表 6 新补偿算法补偿前后靶标误差值 Table 6 Target error values before and after the new compensation algorithmmm
| mm | |||
| 过程 | 靶标点1 | 靶标点2 | 靶标点3 |
| 补偿前 | 0.39 | 0.38 | 0.39 |
| 补偿后 | 0.03 | 0.02 | 0.02 |
表选项
为了验证新的补偿算法较高补偿精度不具有偶然性,需要进行多组补偿实验进行验证,下面给出另一组实验数据。将3个机器人末端靶标拆掉后重新粘贴靶标,并根据新补偿算法重新进行补偿实验。对补偿数据进行记录及处理如表 7所示。
表 7 新补偿算法补偿实验靶标数据记录2 Table 7 Target error values before and after the new compensation algorithmmm
| mm | ||||
| 靶标序号 | 初始靶标 | 目标靶标 | 补偿前 | 补偿后 |
| 靶标点1 | -1 630.62 | -1 470.65 | -1 470.99 | -1 470.67 |
| 631.62 | 385.45 | 385.36 | 385.43 | |
| 888.57 | 875.46 | 876.05 | 875.47 | |
| 靶标点2 | -1 632.82 | -1 458.37 | -1 458.74 | -1 458.38 |
| 681.02 | 434.08 | 433.99 | 434.06 | |
| 940.35 | 926.55 | 927.13 | 926.57 | |
| 靶标点3 | -1 648.09 | -1 473.47 | -1 473.83 | -1 473.49 |
| 611.25 | 364.67 | 364.57 | 364.65 | |
| 947.85 | 937.06 | 937.64 | 937.08 | |
表选项
由表 3~表 6,基于等价变换法的新补偿算法比通用补偿算法具有较高的补偿精度,经过一次补偿后,新的补偿算法精度能够达到0.03 mm以内,而通用的补偿算法只能够达到0.10 mm。由表 5~表 8,在应用本文中标定方法得到的位姿,并结合本节中新补偿算法后,机器人能够达到很高的定位精度,精度值约为0.03 mm。为达到更高精度,可进行第2次、第3次补偿运动。
表 8 补偿前后靶标误差值 Table 8 Target error values before and after compensation
| mm | |||
| 过程 | 靶标点1 | 靶标点2 | 靶标点3 |
| 补偿前 | 0.69 | 0.69 | 0.69 |
| 补偿后 | 0.03 | 0.03 | 0.03 |
表选项
5 结 论 本文提出并实施了一种等价变换建立矩阵方程实现机器人基坐标系与测量坐标系位姿快速标定的方法,通过这种标定方法结合补偿算法后,能够提高了机器人的定位精度。
1) 串联机器人仅运动2次得到3组靶标数据就可以完成机器人坐标系与测量坐标系的位姿标定,因此这种标定方法具有快速性。
2) 通过测量多组数据得到20组标定结果,标定结果相似,因此这种标定方法具有正确性。
3) 通过补偿实验,验证了应用标定方法得到的结果结合一种新的补偿算法后能够极大提高串联机器人的定位精度(精度约0.03 mm)。
参考文献
| [1] | 王伟, 刘立冬, 王刚, 等. 基于四元数表示法的机器人基坐标系标定方法[J].北京航空航天大学学报, 2015, 41(3): 411–417.WANG W, LIU L D, WANG G, et al. Calibration method of robot base frame by quaternion form[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 411–417.(in Chinese) |
| [2] | 宋月娥, 吴林, 张连新, 等. 弧焊机器人离线编程系统标定模块的开发[J].机器人, 2001, 23(7): 695–697.SONG Y E, WU L, ZHANG L X, et al. Calibration module development of arc welding robot off-line programming system[J].Robot, 2001, 23(7): 695–697.(in Chinese) |
| [3] | 齐飞, 平雪良, 刘洁, 等. 关于工业机器人标定方法的研究[J].机床与液压, 2015, 43(21): 32–36.QI F, PING X L, LIU J, et al. Research of calibration method on industrial robot[J].Machine Tool & Hydraulics, 2015, 43(21): 32–36.(in Chinese) |
| [4] | 张博, 魏振忠, 张广军. 机器人坐标系与激光跟踪仪坐标系的快速转换方法[J].仪器仪表学报, 2010, 31(9): 1986–1990.ZHANG B, WEI Z Z, ZHANG G J. Rapid coordinate transformation between a robot and a laser tracker[J].Chinese Journal of Scientific Instrument, 2010, 31(9): 1986–1990.(in Chinese) |
| [5] | GAN Z,ROSSANO G,LI X,et al.Method for calibrating and programming of a robot application:US,Patent 6,822,412[P].2004-11-23. |
| [6] | GU X, FENG C. A calibration procedure for a system of two coordinated manipulators[J].International Journal of Robotics and Automation, 1995, 10(4): 152–158. |
| [7] | 任永杰, 邾继贵, 杨学友, 等. 利用激光跟踪仪对机器人进行标定的方法[J].机械工程学报, 2007, 43(9): 195–199.REN Y J, ZHU J G, YANG X Y, et al. Method of robot calibration based on laser tracker[J].Chinese Journal of Mechanical Engineering, 2007, 43(9): 195–199.DOI:10.3901/JME.2007.09.195(in Chinese) |
| [8] | NUBIOLA A, BONEV I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J].Robotics and Computer Integrated Manufacturing, 2013, 29(1): 236–245.DOI:10.1016/j.rcim.2012.06.004 |
| [9] | 黄晓辰, 张明路, 张小俊, 等. 机器人坐标系建立的改进DH法[J].农业机械学报, 2014, 45(10): 313–319.HUANG X C, ZHANG M L, ZHANG X J, et al. Improved DH method to build robot coordinate system[J].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 313–319.(in Chinese) |
| [10] | 戚祯祥, 叶超强, 吴建华, 等. 基于MDH模型的工业机器人标定算法与实验研究[J].制造业自动化, 2015, 37(2): 15–18.QI Z X, YE C Q, WU J H, et al. Research on the algorithm and experiment of robot calibration based on MDH model[J].Manufacturing Automation, 2015, 37(2): 15–18.(in Chinese) |
| [11] | 周爱国, 周飞, 吕刚, 等. 关节臂式坐标测量机的运动学与工作空间分析[J].机械传动, 2015, 39(1): 48–51.ZHOU A G, ZHOU F, LV G, et al. Kinematics and workspace analysis for articulated arm coordinate measuring machine[J].Journal of Mechanical Transmission, 2015, 39(1): 48–51.(in Chinese) |
| [12] | 李新友, 陈五一. 基于奇异值分解的刚体位姿误差检测方法[J].计算机集成制造系统, 2011, 17(9): 1981–1987.LI X Y, CHEN W Y. Detection of pose errors for a rigid body based on singular value decomposition method[J].Computer Integrated Manufacturing Systems, 2011, 17(9): 1981–1987.(in Chinese) |
| [13] | 黄鹏, 王青, 丽江熊, 等. 激光跟踪仪三维坐标转换综合优化方法[J].计算机集成制造系统, 2015, 21(11): 2912–2920.HUANG P, WANG Q, LI J X, et al. Comprehensive optimization for three-dimensional coordinate transformation of laser tracker[J].Computer Integrated Manufacturing Systems, 2015, 21(11): 2912–2920.(in Chinese) |
| [14] | CAYLEY A. On the motion of rotation of a solid body[J].Cambridge Mathematic Journal, 1843, 3: 224–232. |
| [15] | RODRIGUES O. Des lois géométriques qui régissent les déplacements d'un système solide dans l'espace,et de la variation de s coordonnées provenant de ses déplacements consideérés indépendamment des causes qui peuvent les produire[J].Journal des Mathématiques Pures et Appliquées, 1840, 5: 380–440. |
| [16] | 陶武勇, 鲁铁定, 吴飞, 等. 罗德里格矩阵坐标变换模型的结构总体最小二乘估计[J].工程勘察, 2015(4): 56–60.TAO W Y, LU T D, WU F, et al. Algorithm of structure total least squares in coordinate transformation based on Lodrigues matrix[J].Geotechnical Investigation & Surveying, 2015(4): 56–60.(in Chinese) |
