国内外对无人机航迹规划已做了大量的研究。文献[2]将规划区域栅格化,用栅格的颜色表示不同威胁程度,通过在浅色的栅格区域中搜索航迹点进行二维静态航迹规划。文献[3-5]通过在威胁区域设定人工势场,实现对威胁的避障,但采用势场法,当航迹搜索到某势场均衡处时容易陷入停滞。文献[6]将航迹规划分为学习和查询2个阶段,提出了在稀疏路线图上实时搜索初始航迹和在精细路线图上启发式搜索后备航迹的规划方法。文献[7-10]根据无人机实时探测的信息,对环境进行预测,再进行规划,实现实时航迹规划,但因为需要不断地更新环境信息,使得计算量较大。文献[11]通过在遗传算法中引入基因对比度以此提高优良基因的遗传概率,航迹规划算法的实时性得以提高。
这些专家****对航迹规划的研究都做了大量的工作,但还有一些值得改进和需要继续深入研究的地方。目前,对二维航迹规划研究较充分,而三维航迹规划有待进一步研究,静态规划与实时规划难以同时兼顾。
在传统航迹规划中,通常都是设定指定的步长进行航迹节点扩展,对于采用动态步长进行节点扩展的研究甚少。采用动态步长搜索策略,可以在威胁区域附近实现精细搜索,在无威胁自由空间区域实现大步长搜索,所以,本文提出了一种基于动态步长的无人机航迹规划方法。
在进行航迹规划时,通常根据已掌握的环境信息进行事先规划,得到一条静态参考航迹。但由于战场环境瞬息万变,当出现新的突发威胁时,需要及时修正航迹,尽快逃离危险区域[6],所以对于遭遇突发威胁时的航迹重规划的研究是非常必要的,无人机需要具备一定的实时规划能力。本文通过在突发威胁区域附近设置子目标点,实现对突发威胁的动态规避。
航迹规划考虑的因素众多,是一个NP-hard问题,随着规划空间的增加,复杂程度和求解时间呈指数性增长。对于传统的航迹规划算法,直接在三维空间进行航迹搜索,搜索空间大,约束条件多,而且航迹在精度上要求高,使得航迹规划计算量非常大[11]。基于此,本文提出了一种将三维空间转化为2个二维平面的规划,可以简化问题的复杂性。
1 航迹规划建模 1.1 无人机约束条件 由于无人机受气动特性和机动性能的约束,需要考虑以下条件[12]。
1)最大航程
因携带的燃料是有限的,最大航程是一定的。假设第i段航迹长度为li,最大航程为Lmax,则必须满足:
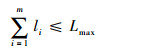 | (1) |
2)最小转弯半径
最小转弯半径指无人机改变航向,在水平面内做圆周运动时,圆周的最小半径。根据文献[13],最小转弯半径满足如下关系式:
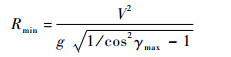 | (2) |
式中:V为无人机飞行速度大小;γmax为最大倾斜角。通过控制倾斜角,就可以使无人机满足最小转弯半径的约束。
3)最低飞行高度
无人机在飞行时,为保证安全,必须与地面保持一定的高度,如果高度过低,容易坠毁。假设无人机与地面的最小安全高度为Hsafe,假设第i段航迹的最低高度为Hi, min,需满足以下条件:
 | (3) |
4)最大俯仰角
无人机在向上爬升或向下俯冲时,不能超过最大俯仰角,如果超过最大俯仰角将会造成飞机失速,产生严重后果。因而,假设无人机的最大俯仰角为θf,zi和zi+1分别为第i和i+1航迹点的高度,则在高度方向上,需要满足以下条件:
 | (4) |
1.2 威胁模型 无人机在飞行途中,会遇到各种各样的威胁,主要包括:地形障碍、敌方雷达、防空导弹、高射炮、恶劣的天气气候等。在航迹规划过程中,威胁约束是一个不可忽略的因素。通常为保证安全,无人机都选择绕过威胁覆盖的区域,尽可能地避开威胁。当前的大部分无人机由于飞行速度慢,高度较低,所以在面对敌方防空导弹和高射炮时容易被击落,可以说是发现即摧毁。但是,现代防空导弹和高射炮只有在雷达发现目标之后的前提下,才能发挥出应有的作用,对无人机构成威胁。因此,本文暂且只考虑地形障碍和敌方雷达对无人机构成的威胁。
1.2.1 山峰威胁 无人机在执行威胁区域突防时,由于山峰可以对雷达形成探测盲区,无人机需要借助地形的遮蔽作用,实行低空突防[14-15]。但进行低空突防时,由于飞行高度比较低,容易发生碰撞,所以地形威胁主要来自于山峰,本文采用如下函数建立山峰威胁概率模型[12]:
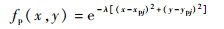 | (5) |
式中:(xpj, ypj)为第j个山峰中心点在平面上的位置坐标;λ为一个参数,可以通过λ来调节山峰在二维规划平面上威胁作用距离;(x, y)为无人机在二维规划平面上的位置;fp(x, y)为关于无人机位置到山峰中心点坐标(xpj, ypj)的距离的函数,表示发生碰撞的概率。同时在三维空间中,赋予(x, y)点一高度惩罚值h(x, y),表示无人机在飞越该位置时,至少要大于高度h(x, y):
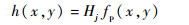 | (6) |
式中:Hj为第j个山峰中心点的高度。
1.2.2 雷达威胁 参考文献[16]中的方法,将威胁和障碍规划为一个统一的模型,用等效地形来近似模拟雷达威胁。将雷达威胁覆盖区域的地形抬升,表示成不可逾越的山峰威胁,高度值采用式(6)中的方法。采用这种模型可以简化航迹规划过程中威胁的表达,将所有的威胁统一转化为地形处理,以便占用较少的时间和系统资源。雷达威胁概率模型为
 | (7) |
式中:fr(x, y)为雷达威胁概率; (xrq, yrq)为第q个雷达的位置坐标;
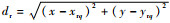
1.3 突发威胁规避策略
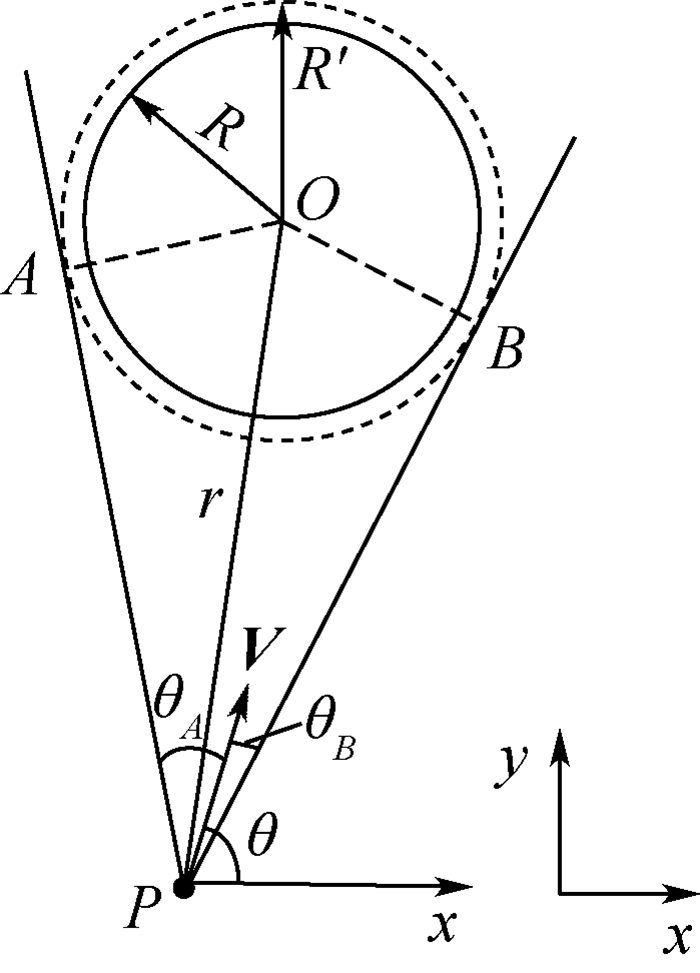
1.3.1 设置子目标点 假设在某时刻,无人机沿预先规划的参考航迹飞行到位置P(xP, yP),通过机载雷达探测到有一突发威胁源O(xO, yO),威胁源的作用半径为R,威胁源与无人机距离为r。如果无人机继续按预先规划的参考航迹飞行,将进入威胁区域。无人机与威胁源之间的关系如图 1所示。
 |
| 图 1 设置子目标点 Fig. 1 Sub-goal setting |
| 图选项 |
此时,无人机不能再按预先规划的参考航迹飞行,需要启动实时规划,重新规划航迹。本文在此提出了一种设置子目标点的方法,通过设置子目标点,引导无人机尽快地摆脱突发威胁,逃离威胁区域。
子目标点的设置是实现实时规划的关键,设置子目标点,可以启发引导航迹节点扩展时朝子目标点方向搜索,从而使无人机改变航向,从原有航迹改出,及时规避突发威胁。由Dubins路径[17]可知,当无人机由威胁源的边界飞行时,恰好能绕过威胁,并且航程是最短的。受此启发,考虑到无人机自身尺寸,以及恰好沿威胁边界飞行时,处于危险边缘状态,如果航行时稍有差错,将进入威胁区域,不能保证绝对的安全,所以对威胁做“膨化”处理,将威胁作用半径R扩大α(α>1)倍,得到膨化后的威胁作用半径R′(R′=α×R)。由无人机当前位置P向膨化后的威胁圆做切线PA和PB,切点分别为A和B,则A点和B点就是我们需要设置的子目标点。
1.3.2 子目标点位置计算 当前速度V与x轴正方向的夹角为θ,PA与当前速度V之间的夹角为θA,PB与当前速度V之间的夹角为θB,根据图 1所示的几何关系,可知:
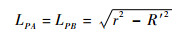 | (8) |
式中:LPA表示PA的长度,LPB同理。B的位置坐标(xB, yB)为
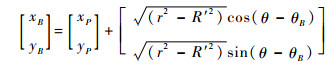 | (9) |
A的位置坐标(xA, yA)为
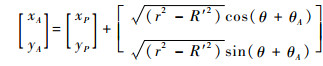 | (10) |
θ-θB满足如下关系:
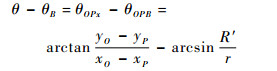 | (11) |
式中:θOPx表示PO与Px之间的夹角,θOPB,θOPA同理。θ+θA满如如下关系:
 | (12) |
将式(11)代入式(9),式(12)代入式(10)可求得A、B两点的坐标。
1.3.3 规避方向和子目标点的选择 在确定A和B两点的位置之后,需要判定无人机是采用逆时针规避威胁还是顺时针规避威胁,由于A、B两点还可能在其他威胁覆盖区域范围之内,所以除了单纯地比较θA和θB的大小外,还需要比较A、B两点处威胁概率的大小,具体判定依据以下4条准则:
1)如果θA>θB并且threat (A)>threat (B),说明顺时针方向规避威胁比逆时针方向规避时航向调整小,航程更短,并且B点威胁概率小于A点,此时选择B点作为需要设置的子目标点。
2)如果θA < θB并且threat (A) < threat (B),说明逆时针方向规避威胁比顺时针方向规避时航向调整小,航程更短,并且A点威胁概率小于B点,此时选择A点作为需要设置的子目标点。
3)如果θA>θB并且threat (A) < threat (B),但是threat (B)-threat (A) < C,其中C为常值,表示无人机可接受的威胁阈值,则优先选择航向调整小,航程短的规避方向,此时选择B点作为需要设置的子目标点;如果threat (B)-threat (A)>C,则优先选择安全系数更高的规避方向,选择A点作为需要设置的子目标点。
4)如果θA < θB并且threat (A)>threat (B),但是threat (A)-threat (B) < C,则优先选择航向调整角度小,航程短的规避方向,此时选择A点作为需要设置的子目标点;如果threat (A)-threat (B)>C,则优先选择安全系数更高的规避方向,选择B点作为需要设置的子目标点。
1.4 动态步长调整策略 为使无人机能快速规划出可行航迹,同时避免频繁调整航向和姿态,理想的状态是:在无威胁的自由空间,航迹搜索的步长应该设置为较大值,加快航迹的搜索;然而,在接近威胁区域时,为保证飞行安全,应当精细规划,步长设置应较小,确保无人机能成功规避威胁。因而,有必要采用一种可以动态调整步长的方法,动态调整步长有利于得到较优航迹,更符合实际飞行状况。
据此,设定步长s动态调整方法如下:
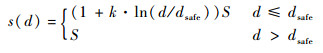 | (13) |
式中:

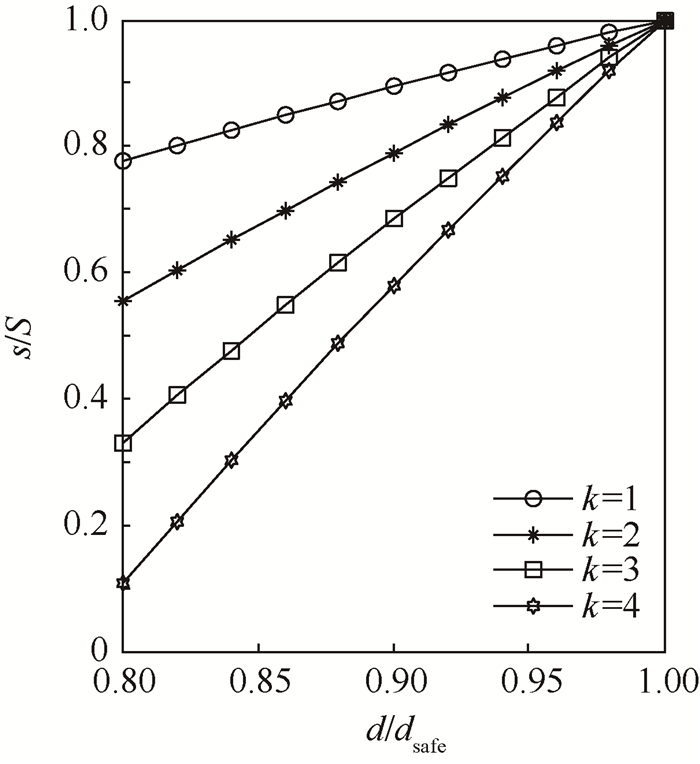
根据实际飞行情况,由于无人机探测到威胁源,并且,随着距离越近,机载雷达对威胁的感知和判断准确率提高,因而不可能过于靠近威胁源飞行。因此,在小于安全距离飞行时,取与威胁源的距离在0.8 dsafe~dsafe之间,则在小于安全距离飞行时,步长动态调整如图 2所示。
 |
| 图 2 小于安全距离时步长动态调整 Fig. 2 Step dynamic adjustment when distanceis less than safe distance |
| 图选项 |
可见,建立关于无人机与威胁源中心距离的动态步长调整策略,可以有效控制搜索步长。随着距离的增大,航迹搜索的步长逐渐增大,从而加快搜索速度,缩短算法运行时间;而距离减小,靠近威胁源时,航迹搜索的步长逐渐减小,实现精细搜索,避免误进入威胁区域,有效规避威胁。通过不同调整幅度结果的对比,可知k取[2,3]时较为合适。因为我们希望在越靠近威胁时,步长越小越好,但又不能过小,过小产生的航迹节点大量增多,导致冗余,航迹搜索时间增加,无人机沿此航迹飞行时,姿态将变换频繁,不利于飞行,并且无人机飞过该步长的距离时,飞行的时间很短,可能出现时间不够重新规划一次航迹的情况。而若调整幅值取较小值时,显然可供调整的步长范围太小,与固定步长搜索航迹差异不大。
1.5 节点扩展 在许多航迹规划的方法中,将规划区域栅格化,航迹节点扩展限制在了栅格线的交叉点上,这种方法得到的航迹不够平滑,并且扩展方向限定为0°、45°。针对这种局限性,本文采用以下方法:以当前位置P为圆心,步长s为半径做圆,根据最小转弯角φmax的限制,得到如图 3所示的扇形区域,然后在圆弧上等距取N个点,分别计算这N个点的启发函数值,启发函数值最小的点即是下一个待扩展节点。
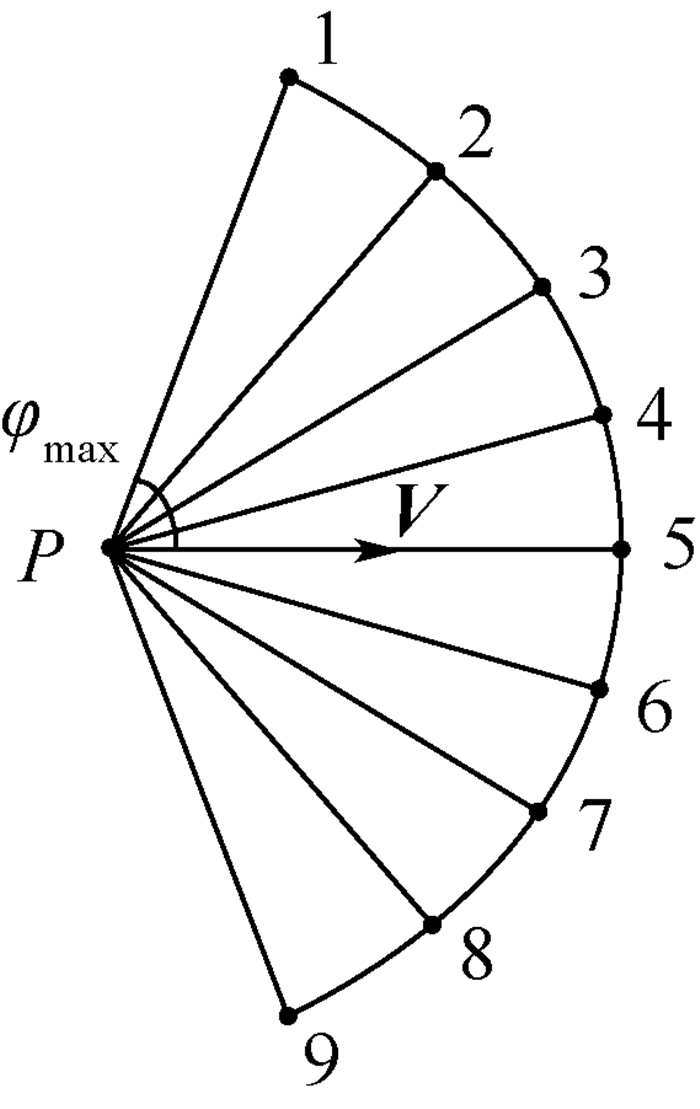 |
| 图 3 圆形节点扩展示意图 Fig. 3 Schematic diagram of circular expanding nodes |
| 图选项 |
圆弧上第n(n=1,2,…,N)个节点an启发函数值计算如下:
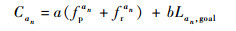 | (14) |
式中:Lan, goal为圆弧节点an与目标点的距离;fpan和fran分别为an处山峰威胁概率和雷达威胁概率;a和b为比例系数,采用文献[18]中的方法可确定a和b的值。
1.6 目标函数 航迹规划的最终目的是规划一条满足无人机性能约束、威胁小、安全性高、航程较短、消耗少的航迹。基于此,建立目标函数为
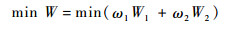 | (15) |
式中:W1为整条航迹的威胁代价,设整条航迹共有m个航迹节点,则
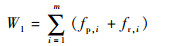 | (16) |
其中:fp, i和fr, i分别为第i个航迹节点的山峰威胁概率和雷达威胁概率。
除去起飞阶段和降落阶段燃油的消耗,在某种程度上,燃油的消耗与航程成正比,所以,在此只考虑总航程,而不再单独考虑燃油的消耗。用W2表示总航程,具体表达式如下:
 | (17) |
ω1、ω2为比例系数,用于调节威胁代价和航程代价量纲不同的影响,通过调节权系数,可以实现规划安全优先或者是航程优先的航迹。
1.7 高度规划 当无人机根据地形,进行跟踪飞行时,能最大限度地利用地形隐蔽自己,但在飞行的过程中,需要与地面保持合适的高度。无人机飞行高度较低时,不易被发现,被敌方雷达探测并被击毁的危险性降低,如图 4中曲线2所示,容易实现低空突防。但另一方面,由于无人机受自身结构和机动能力的影响,飞行高度降低时,撞地坠毁的危险性增加,如图 4中曲线1所示。因此,如何选择合适的安全间隙高度Hsafe,是确定理想的地形跟随航迹非常重要的一步。由图 4中,综合曲线1和曲线2得到曲线3,在Hsafe处,无人机的撞地危险和被探测危险之和最小,所以可以确定Hsafe即安全间隙高度。通常情况下,它的范围一般在60~300 m[19]。
 |
| 图 4 Hsafe的确定 Fig. 4 Determination of Hsafe |
| 图选项 |
在确定安全间隙高度后,在二维航迹规划中,我们已得到参考航迹,并可知道参考航迹节点在二维平面投影点处地形高度,所以,最理想的状态是将每一个二维平面投影点处地形高度叠加安全间隙高度Hsafe,就得到航迹节点在三维空间的位置,然后将这些航迹节点连接得到三维航迹。然而,由于地表起伏较大,凹凸不平,简单地通过叠加Hsafe得到的航迹显然不够平滑,并且无人机受机动性能约束,很难按此航迹飞行,所以需要根据无人机最大俯仰角的限制,对航迹进行修正平滑处理。
2 算法流程 根据第1节建立的规划模型,确定算法流程如下。
2.1 静态二维参考航迹规划 步骤1??初始化参数,确定规划区域,并对规划区域的地形和雷达威胁进行建模,得到其威胁概率模型,将当前位置初始化为起始点,目标点位置为终点。
步骤2??从当前位置出发,根据当前无人机位置与威胁的距离,按照步长调整策略,得到扩展步长。
步骤3??根据1.5节中节点扩展方法得到下一个待扩展节点,作为下一个飞行位置,无人机从当前节点位置飞到规划的下一位置。
步骤4??判断此时的待扩展节点是否为目标点;若是,则转步骤5;若否,则将此时的扩展节点作为当前节点,转步骤2。
步骤5??规划结束,得到参考航迹。
2.2 二维实时航迹规划 步骤1??从起始位置出发,按照参考航迹飞行。
步骤2??判断是否探测到突发威胁,并且沿参考航迹飞行是否会进入突发威胁区域,若是,按照1.3节中的方法设置子目标点,转步骤3;若否,继续按照参考航迹飞行。
步骤3??启动实时规划,以当前位置为起点,子目标点为终点,规划得到第1段航迹;然后,更新起点为子目标点,初始目标点位置为终点,规划得到第2段航迹。按新规划的航迹飞行。
步骤4??判断是否到达目标点,若是,转步骤5;若否,转步骤2。
步骤5??规划结束,得到实时规划航迹。
2.3 三维航迹规划 步骤1??根据2.1节和2.2节的方法得到二维静态或实时规划航迹。
步骤2??按照1.7节中的方法启动高度规划得到高度剖面航迹。
步骤3??二维平面规划航迹与高度剖面航迹合成,得到三维航迹。
3 仿真实验 3.1 规划空间 仿真实验在Pentium 4(2.93 GHz),1.21 GB内存的PC机上进行,运行环境为Windows XP,采用MATLAB进行仿真。设定规划区域为65 km×65 km,起始位置为(0,0,2) km,目标位置为(65,65,4) km,威胁半径膨化系数α=1.2,设定比例调节系数a=ω1=5,b=ω2=1×10-3,步长调整幅值k=3,最大转弯角φmax=60°,最大俯仰角θf=30°,威胁阈值C=0.1,节点扩展时取N=8,假设无人机的雷达探测半径为6 km,雷达和山峰威胁的参数如表 1所示。
表 1 威胁具体参数 Table 1 Specific parameters of threats
| 威胁类型 | 中心坐标/km | 中心点高度/km | λ |
| 山峰1 | (10,6) | 25 | 0.10 |
| 山峰2 | (16,32) | 28 | 0.08 |
| 山峰3 | (36,22) | 18 | 0.05 |
| 山峰4 | (32,42) | 30 | 0.10 |
| 雷达1 | (47,40) | 32 | 0.10 |
| 雷达2 | (47,46) | 32 | 0.08 |
| 雷达3 | (50,10) | 40 | 0.08 |
表选项
地形采用丘陵地形与山峰地形以及雷达威胁等效地形叠加, 得到航迹规划区域如图 5所示。
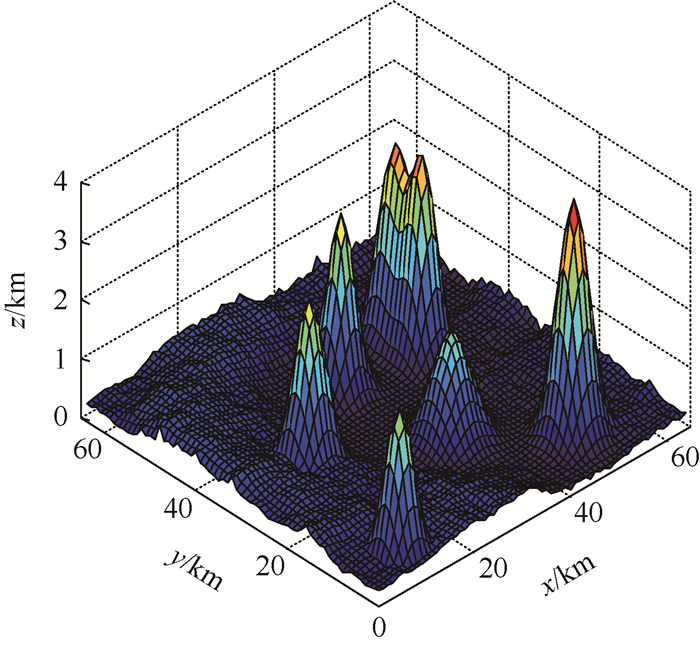 |
| 图 5 航迹规划区域 Fig. 5 Path planning area |
| 图选项 |
3.2 动态步长结果对比 为研究动态步长调整策略对航迹轨迹规划结果的影响,分别选取了基准步长S=0.6,1.0,3.0,5.0 km时,对固定步长搜索与动态步长搜索2种不同策略下的航迹规划进行了仿真,仿真规划得到的航迹如图 6所示。
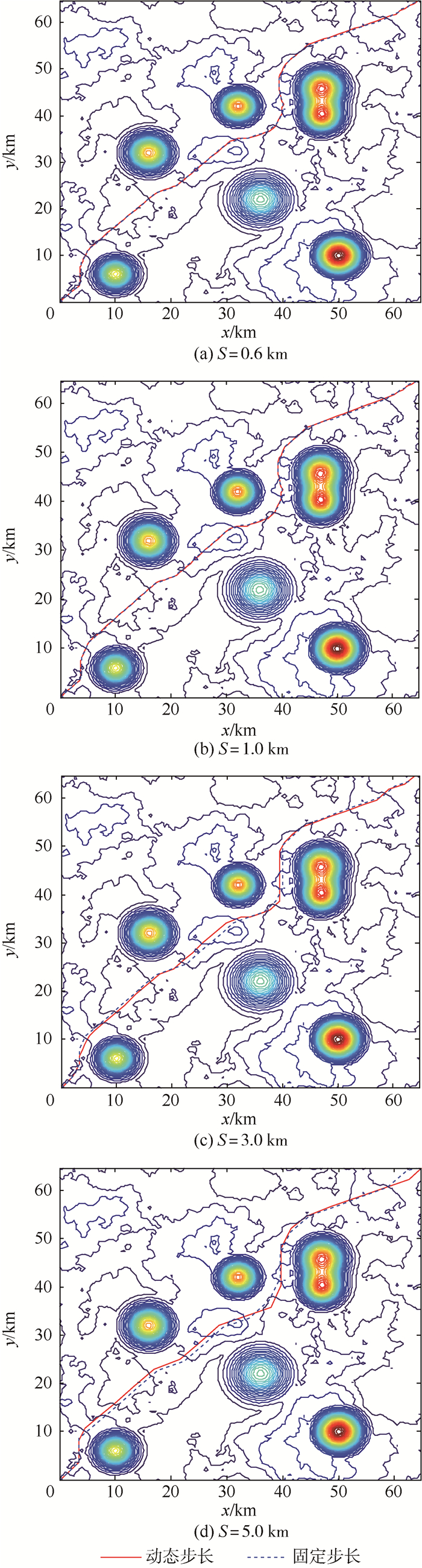 |
| 图 6 固定步长与动态步长航迹仿真 Fig. 6 Path simulation with fixed step and dynamic step |
| 图选项 |
对2种不同搜索步长策略下的航迹规划仿真100次,以排除随机误差的影响,对航迹节点数、时间、航程、平均威胁概率进行统计,得到其平均值结果如表 2所示。
表 2 固定步长与动态步长仿真结果对比 Table 2 Comparison of simulation results between fixed step and dynamic step
| S/km | 步长策略 | 节点数 | 时间/s | 航程/km | 平均威胁概率 |
| 0.6 | 动态步长 | 217 | 2.177 | 99.459 | 0.034 |
| 固定步长 | 166 | 2.156 | 99.351 | 0.028 | |
| 1.0 | 动态步长 | 129 | 2.076 | 99.472 | 0.038 |
| 固定步长 | 100 | 2.066 | 99.400 | 0.040 | |
| 3.0 | 动态步长 | 42 | 1.988 | 98.943 | 0.099 |
| 固定步长 | 33 | 1.979 | 99.449 | 0.195 | |
| 5.0 | 动态步长 | 25 | 1.971 | 98.263 | 0.269 |
| 固定步长 | 20 | 1.965 | 99.078 | 0.580 |
表选项
从图 6(a)、图 6(b)可知,在取基准步长S≤1.0 km时,采用固定步长搜索与动态步长搜索得到的航迹几乎重合,同时从表 2中航程与平均威胁概率的统计结果可知,2种不同步长策略下航程与威胁概率相差较小,变化不明显,说明在采用小步长搜索时,对步长进行动态调整对航迹规划的优化作用较小,究其原因是此时的航迹已经趋近于最优。并且,会造成节点数增多,使得航迹调整次数增多,规划时间延长,所以,综合看来,在采用小步长搜索时,适宜采用固定步长的策略进行航迹规划。
从图 6(c)、图 6(d)可知,在取基准步长S>1.0 km时,采用动态步长搜索策略与固定步长搜索策略航迹明显有所不同。从表 2中的统计结果也可知,在采用大步长搜索时,虽然动态步长搜索的航迹较固定步长搜索的航迹节点数增多、时间延长,但随着S的增大,二者越来越接近。从规划的航程来看,动态步长搜索的航迹要优于固定步长搜索的航迹,航程更短;并且,从整条航迹受到威胁的程度来看,动态步长搜索航迹的平均威胁概率要明显小于固定步长搜索航迹的平均威胁概率,安全性更高。说明,在采用大步长搜索航迹时,动态调整步长,可以使无人机在靠近威胁区域飞行时,快速改出,逃离威胁区域。所以,在采用大步长搜索时,适宜采用动态步长进行航迹规划。
从图 6(a)~图 6(d)可知,取不同的基准步长时,采用固定步长与动态步长搜索规划得到的航迹大致方向相同,没有出现与其他航迹搜索方向有明显的偏差。另外,随着搜索步长的增大,航迹的平滑性有所下降。
3.3 二维航迹规划 取基准步长S=0.6 km,采用动态步长搜索得到二维投影平面的静态参考航迹。当无人机沿预先规划的参考航迹飞行时,如图 7所示,到达(16,22.6) km处探测到突发威胁,突发威胁的中心坐标为(20,26) km,威胁作用半径为4.2 km,并且如果继续沿着预先规划航迹飞行时将进入突发威胁区域。此时,以当前位置为起始点,按照1.3节中的方法设置子目标点,启动实时规划,得到实时规划的航迹如图 8所示。
 |
| 图 7 等高线投影面静态规划航迹 Fig. 7 Static path planning on contour projective plane |
| 图选项 |
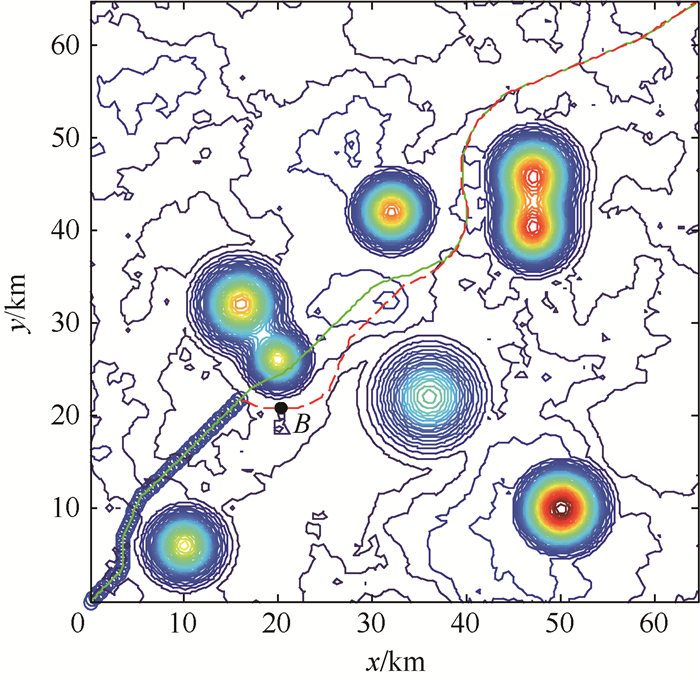 |
| 图 8 等高线投影面实时规划航迹 Fig. 8 Real-time path planning on contour projective plane |
| 图选项 |
图 8中红色虚线为实时规划的航迹,从图中可以看出,针对出现的突发威胁,通过设置子目标点B,可以重新规划出新的航迹,使无人机成功规避突发威胁,安全到达目标点。实时规划总共用时约1.8 s,如果无人机当前速度是360 km/h,从启动实时规划到规划结束无人机总共飞行距离为0.18 km, 相对于与突发威胁的距离较小,所以,在实时规划算法中,我们是以当前发现威胁的位置作为实时规划的起始点,而没有额外考虑无人机在实时规划时间段内沿参考航迹走过的距离。从规划的用时来看,符合实时规划运算速度快的要求,说明本文提出的实时规划算法是有效的。
3.4 高度规划 假设无人机安全间隙高度为150 m,为保证充足的裕量,实验环境下取安全间隙高度为200 m。为保证航迹可飞,符合无人机机动性能约束,采用三次样条插值,并加入俯仰角限制条件,对高度数据进行平滑处理,分别得到与图 7、图 8中静态二维参考航迹和实时规划航迹相对应的高度剖面图,如图 9和图 10所示。图中:L表示二维航迹的航程;蓝色部分表示地表剖面;红色线表示规划的高度剖面飞行轨迹。从图中可知,高度面规划的航迹可以较好地对地形进行跟踪,充分利用地形进行隐蔽,整条航迹较为平滑,适合无人机飞行。
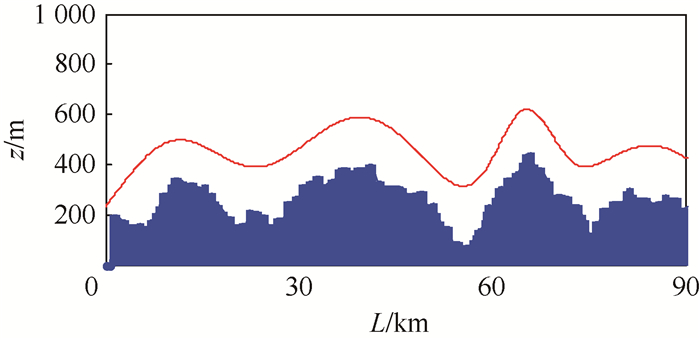 |
| 图 9 静态规划航迹高度剖面图 Fig. 9 Height profile map of static path planning |
| 图选项 |
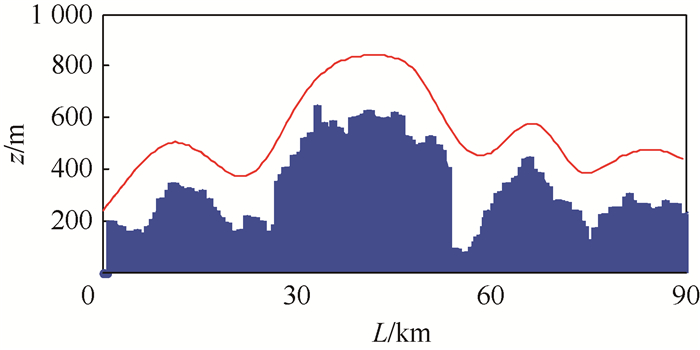 |
| 图 10 实时规划航迹高度剖面图 Fig. 10 Height profile map of real-time path planning |
| 图选项 |
3.5 三维航迹规划 在得到二维投影平面的航迹和高度剖面的航迹后,将二者合成,得到最终的三维静态规划航迹与遭遇突发威胁后的实时规划航迹,分别如图 11和图 12所示。
 |
| 图 11 静态规划三维航迹 Fig. 11 Static 3D path planning |
| 图选项 |
 |
| 图 12 实时规划三维航迹 Fig. 12 Real-time 3D path planning |
| 图选项 |
由图 11和12可知,三维航迹可以有效地避开静态威胁,通过设置子目标点可以成功对突发威胁进行规避。三维航迹巧妙地利用地形,对地形进行跟踪飞行,并且从图中可以看出航迹都是在丘陵地带上空穿过,有效降低了飞行高度,有利于实现低空突防。
4 结论 本文方法具有以下优点:
1)当基准步长为大步长时,采用动态步长进行航迹规划,航程更短,威胁程度降低。
2)可以实现对地形的跟踪,有利于低空突防,求解的复杂度降低,得到较为满意的航迹。
3)可以成功规避突发威胁,实现实时规划。
但本文只考虑了单一突发威胁,对于多突发威胁没有涉及。为了更好地适应未来作战环境,对于多突发威胁的无人机航迹规划,是一个值得深入研究的问题。
参考文献
| [1] | 沈林成, 陈璟, 王楠. 飞行器任务规划技术综述[J].航空学报, 2014, 35(3): 593–606.SHEN L C, CHEN J, WANG N. Overview of air vehicle mission planning techniques[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 593–606.(in Chinese) |
| [2] | BAE K Y, KIMB Y D, HAN J H. Finding a risk-constrained shortest path for an unmanned combat vehicle[J].Computer and Industrial Engineering, 2015, 80: 245–253.DOI:10.1016/j.cie.2014.12.016 |
| [3] | 姚远, 周兴社, 张凯龙, 等. 基于稀疏A*搜索和改进人工势场的无人机动态航迹规划[J].控制理论与应用, 2010, 27(7): 953–959.YAO Y, ZHOU X S, ZHANG K L, et al. Dynamic trajectory planning for unmanned aerial vehicle based on sparse A* search and improved artificial potential field[J].Control Theory & Applications, 2010, 27(7): 953–959.(in Chinese) |
| [4] | OSCAR M, ULISES O R, ROBERTO S. Path planning for mobile robots using bacterial potential field for avoiding static and dynamic obstacles[J].Expert System with Application, 2015, 42(12): 5177–5191.DOI:10.1016/j.eswa.2015.02.033 |
| [5] | MENG G L, GUO J L, SUN F Q, et al.UAV real-time path planning using dynamic RCS based on velocity vector field[C]//26th Chinese Control and Decision Conference, CCDC 2014.Piscataway, NJ:IEEE Press, 2014:1376-1380. |
| [6] | 严平, 丁明跃, 周成平, 等. 飞行器多任务在线实时航迹规划[J].航空学报, 2004, 25(5): 485–489.YAN P, DING M Y, ZHOU C P, et al. On-line real-time multiple-mission route planning for air vehicle[J].Acta Aeronautic et Astronautica Sinica, 2004, 25(5): 485–489.(in Chinese) |
| [7] | PENG Z H, LI B, CHEN X T, et al.Online route planning for UAV based on model predictive control and particle swarm optimization algorithm[C]//10th World Congress on Intelligent Control and Automation.Piscataway, NJ:IEEE Press, 2012:397-401. |
| [8] | SHEKHAR R C, KEARNEY M, SHAMES I. Robust model predictive control of unmanned aerial vehicle using waysets[J].Journal of Guidance, Control, and Dynamics, 2015, 38(10): 1898–1907.DOI:10.2514/1.G000787 |
| [9] | WU J, ZHANG D H, PEI D H.Autonomous route planning for UAV when threats are uncertain[C]//6th IEEE Chinese Guidance, Navigation and Control Conference, CGNCC 2014.Piscataway, NJ:IEEE Press, 2014:19-22. |
| [10] | REDDING J, AMIN J N, BO?KOVIC J D.A real-time obstacle detection and reactive path planning system for autonomous small-scale helicopters[C]//AIAA Guidance, Navigation and Control Conference and Exhibit 2007.Reston:AIAA, 2007, 1:989-1010. |
| [11] | 何平川, 戴树岭. 一种改进UAV三维航迹实时规划算法[J].北京航空航天大学学报, 2010, 36(10): 1248–1251.HE P C, DAI S L. Improved 3-D real-time trajectory algorithm for UAV[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(10): 1248–1251.(in Chinese) |
| [12] | 张帅, 李学仁, 张鹏, 等. 基于改进A*算法的无人机航迹规划[J].飞行力学, 2016, 34(3): 39–43.ZHANG S, LI X R, ZHANG P, et al. UAV path planning based on improved A* algorithm[J].Flight Dynamics, 2016, 34(3): 39–43.(in Chinese) |
| [13] | 常波, 王瑞. 基于几何法的无人机航迹规划[J].计算机系统应用, 2015, 24(1): 109–113.CHANG B, WANG R. Path planning based on geometric method for unmanned aerial vehicles[J].Computer System Applications, 2015, 24(1): 109–113.(in Chinese) |
| [14] | 占伟伟, 王伟, 陈能成, 等. 一种利用改进A*算法的无人机航迹规划[J].武汉大学学报·信息科学版, 2015, 40(3): 315–320.ZHAN W W, WANG W, CHEN N C, et al. Path planning strategies for UAV based on improved A* algorithm[J].Geomatics and Information Science of Wuhan University, 2015, 40(3): 315–320.(in Chinese) |
| [15] | 温乃峰, 苏小红, 马培军, 等. 低空复杂环境下基于采样空间约减的无人机在线航迹规划算法[J].自动化学报, 2014, 40(7): 1376–1390.WEN N F, SU X H, MA P J, et al. Sampling space reduction-based UAV online path planning algorithm in complex low altitude environments[J].Acta Automatic Sinica, 2014, 40(7): 1376–1390.(in Chinese) |
| [16] | ZHAN B C, MAO Z L, LIU W Q, et al. Geometric reinforcement learning for path planning of UAVs[J].Journal of Robotic System, 2015, 77(2): 391–409.DOI:10.1007/s10846-013-9901-z |
| [17] | 关震宇, 杨东晓, 李杰, 等. 基于Dubins路径的无人机避障规划算法[J].北京理工大学学报, 2014, 34(6): 570–575.GUAN Z Y, YANG D X, LI J, et al. Obstacle avoidance planning algorithm for UAV based on Dubins path[J].Transaction of Beijing Institute of Technology, 2014, 34(6): 570–575.(in Chinese) |
| [18] | 郑昌文.飞行器航迹规划方法研究[D].武汉:华中科技大学, 2003:22-25.ZHENG C W.Research on route planning for air vehicles[D].Wuhan:Huazhong University of Science and Technology, 2003:22-25(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10487-2006109890.htm |
| [19] | 蔡满意. 飞行控制系统[M].北京: 国防工业出版社, 2007: 144-145.CAI M Y. Flight control system[M].Beijing: National Defence Industry Press, 2007: 144-145.(in Chinese) |
