在以往的研究中,通常直接将弹目相对距离与接近速度的比值作为TGO,并将其作为经典方法。但此方法仅在弹道较为平直或处于平行接近状态时,具有一定有效性;如果拦截弹在飞行过程中机动幅度较大,则该方法误差较大。
目前对于TGO估计方法的研究,一类是直接解析法:York和Pastrick[5]首先提出了一种基于求解线性二次控制问题的TGO估计方法;Jeon等[6]在线性条件下得出了TGO关于初始弹目距离与框架角的表达式,降低了弯曲追踪轨迹带来的误差;Liu等[7]求得了TGO二次方程得近似解,其中对拦截弹速度变化带来的影响做了补偿;Kim等[8]根据制导律的2个增益常量预测飞行轨迹,得出了基于经典估计方法的补偿系数;马国欣等[9]将偏置比例导引中的构造角作为微分变量,并求解得出了作为指数形式参与的TGO估计多项式;李辕等[10]针对顺轨拦截情况,分别提出了拦截非机动和机动目标的TGO估计方法;刘剑锋和庄志洪[11]通过导引头一阶微分信息推导出的TGO估计方法与非线性卡尔曼(GHK)滤波算法具有较好匹配性。
另一类是迭代递推法:Riggs[12]通过建立一个简易的拦截弹切向加速度模型以解算平均加速度,从而补偿速度变化对TGO估计的影响;Hull等[13]基于对TGO的粗略估计,随着拦截轨迹的改变,进行递次求近得到的TGO精确值;Dhananjay和Ghose[14]采用数值内插法递推估计TGO,虽然不需在每一个制导周期进行解算,但具有较大计算量;Tahk等[15]在TGO的递归计算中,对非零框架角引起的估计误差进行了补偿;常青等[16]对TGO估计时,将目标在视线方向上的平均加速度进行加权,引入算法降低了Riggs估计法的误差;张友安和马国欣[17]在拦截弹框架角变化区间的不同分段内,采用迭代法求解TGO。
通过对比可知,直接解析法运算量小,利于在线实时解算,但估计精度略低;迭代递推法虽然有精度优势,但计算过程十分复杂,实时性不强。另外,随着近年来越来越多的顺轨制导律[18-20]提出,也需有相应的TGO估计方法,而目前的成果主要针对逆轨拦截模式。因此,研究高精度、运算简单且对拦截模式具有针对性的TGO估计方法十分必要。
1 TGO估算 1.1 基础理论 因本文的TGO是在线性条件下计算,其制导律[21]是在一定的几何关系下,将视线角和框架角近似为“小角度”,从而消除三角函数得到的线性制导指令。虽然推导过程中存在基于小角度近似的情况,但结论公式普遍适用。理论分析过程中,均将目标和拦截弹考虑成质点,并忽略重力带来的影响。
经典比例制导律的指令形式为
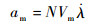 | (1) |
式中:am为拦截弹加速度; N为导航比; Vm为拦截弹速度; λ为视线角。
拦截弹攻击静止目标的几何关系如图 1所示。
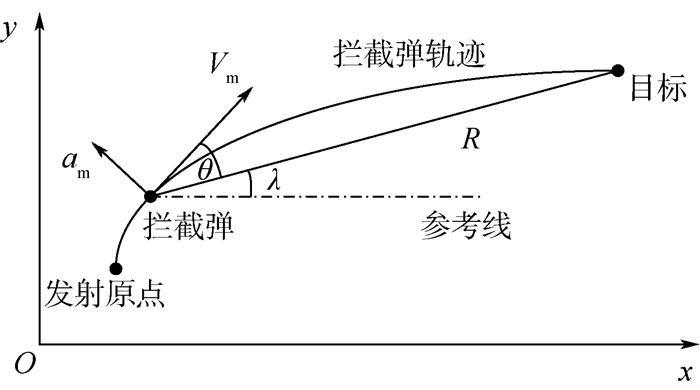 |
| 图 1 平面几何关系 Fig. 1 Planar interception geometry |
| 图选项 |
设拦截弹位置为(xm, ym),目标位置为(xt, yt),则视线角可近似为
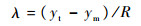 | (2) |
由R=Vctgo,ctgo为剩余拦截时间,Vc为拦截弹接近速度,并将式(2)按时间微分后得
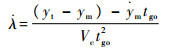 | (3) |
在线性条件下,λ和θ均为小角,则可近似取
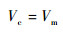 | (4) |
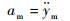 | (5) |
结合式(1)、式(3)~式(5)可得
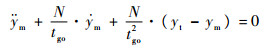 | (6) |
为便于解算,逆向考虑拦截全过程,将拦截活动看作是拦截弹从目标位置发射,飞向发射原点。令tgo=(R0-r)/Vc,r∈[0, R0],其中R0为目标与发射原点的距离,将式(6)转化为以r为自变量的函数:
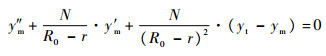 | (7) |
按照初始条件:r=0,ym(0)=ym0=yt,y'm(0)=y'm0,求解欧拉-柯西方程式(7)得
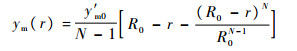 | (8) |
将式(8)对r求导得
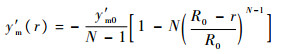 | (9) |
拦截弹轨迹长度为
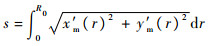 | (10) |
在线性条件下,近似取xm(r)=r,y′m(r)为小量,按照泰勒级数可得
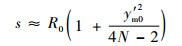 | (11) |
由于视线角λ较小,则s≈Vmtgo,y′m0(r)≈θ,代入式(11)得
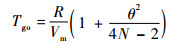 | (12) |
1.2 逆轨拦截运动目标TGO估计 TGO估计的主要思想是通过预测出拦截弹与目标的碰撞点,然后按照拦截静态目标的时间估计方法对剩余拦截时间进行估计。拦截弹在逆轨模式下拦截目标的几何关系如图 2所示。
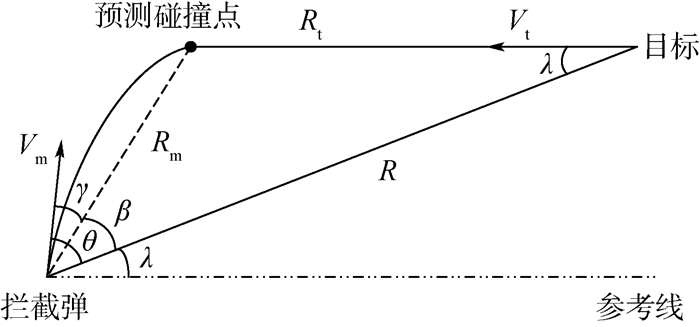 |
| Vt—目标速度;Rt—目标与预测碰撞点间的距离;Rm—拦截弹与预测碰撞点间的距离;β—预测内框角;γ—预测外框角。 图 2 逆轨拦截几何关系 Fig. 2 Head-on interception geometry |
| 图选项 |
假设拦截弹直接飞向处于预测碰撞点处的静止目标,则估计剩余飞行时间为
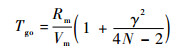 | (13) |
式中:预测外框角可表示为γ=θ-β。
由于在实际情况下,各预测量均是未知的,以下的推导则是为了消掉这些未知量。
为便于分析,取拦截弹与目标速度比为
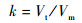 | (14) |
目标与预测碰撞点间距离可表示为
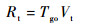 | (15) |
根据图 2可得出目标和拦截弹距离预测碰撞点的三角关系为
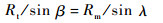 | (16) |
由于β和λ为小角,式(16)可近似为
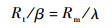 | (17) |
将式(13)~式(15)代入式(17)化简后得
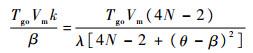 | (18) |
通过求解方程得
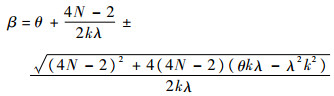 | (19) |
按照泰勒级数方法展开根号下内容,可取得预测内框角有效值为
 | (20) |
根据图 2可得出拦截弹距离预测碰撞点距离和弹目距离的三角关系为
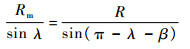 | (21) |
由于λ和β为小角,式(21)可近似为
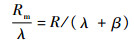 | (22) |
将式(20)和式(22)代入式(13)得
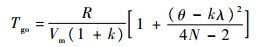 | (23) |
1.3 顺轨拦截运动目标TGO估计 拦截弹在顺轨模式下拦截目标的几何关系如图 3所示。
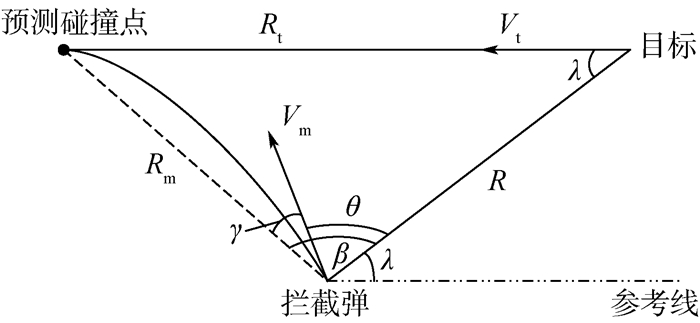 |
| 图 3 顺轨拦截几何关系 Fig. 3 Head-pursuit interception geometry |
| 图选项 |
根据图 3可得出目标和拦截弹距离预测碰撞点的关系可近似为
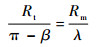 | (24) |
将式(13)~式(15)代入式(24)化简后,通过求解方程,可取得预测内框角有效值为
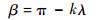 | (25) |
根据图 3可得出拦截弹距离预测碰撞点距离和弹目距离的三角关系可近似为
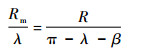 | (26) |
将式(25)和式(26)代入式(13)得
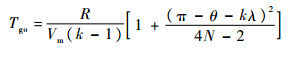 | (27) |
2 仿真验证 仿真验证主要与韩国的Tahk小组和印度的Ghose小组近年提出的TGO估计方法作对比。
Tahk小组根据几何关系推导出TGO估计的解析式[15]:
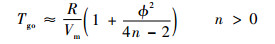 | (28) |
可直接用以TGO计算(?为拦截弹速度倾角),以下简称解析法;Ghose小组是通过方程
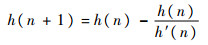 | (29) |
经数次递推后预测拦截点(h为出目标飞行路径长度)再根据目标速度解算TGO[14],以下简称递推法。此外,由于经典TGO估计法(Tgo=R/VC,VC为弹目接近速度)应用广泛,也将其作为对比对象。
仿真采用MATLAB在CPU主频为2.6 GHz的PC机上进行,仿真步长选取为0.000 2 s。
2.1 不同框架角下的TGO仿真验证 通过仿真,分别在不同初始框架角下,计算各方法所估计出的TGO误差:逆轨模式下,分别与其他3种方法对比;顺轨模式下,解析法和递推法不再适用,仅与经典法对比,结果如图 4所示。同时,随机选取某次拦截全过程,分别记录4种方法估计TGO所需CPU时间,等间隔采样50个值,结果如图 5所示。
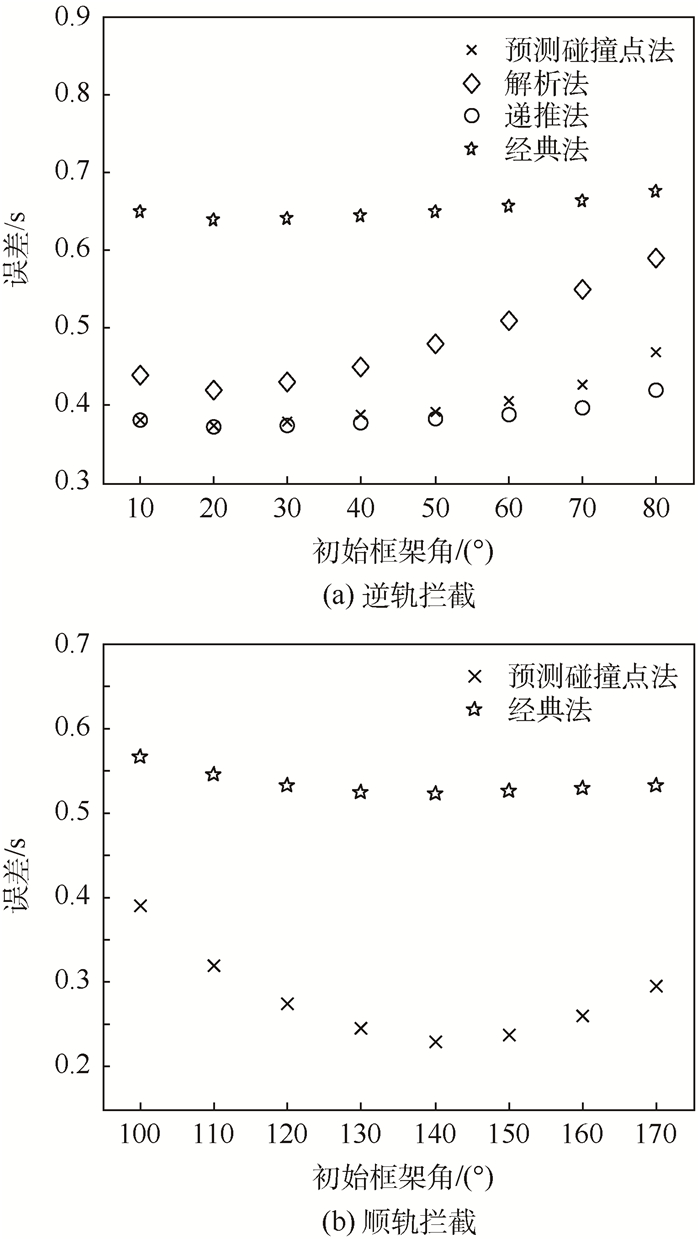 |
| 图 4 不同初始框架角下TGO估计误差 Fig. 4 TGO estimation error at different initial heading errors |
| 图选项 |
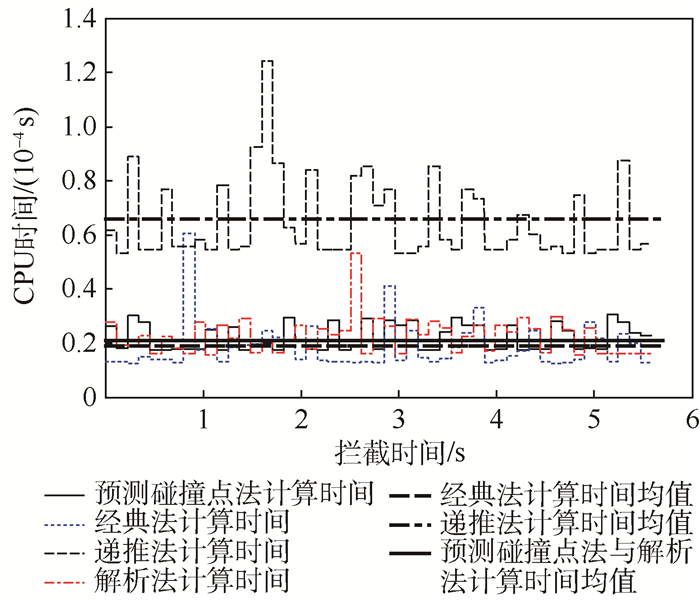 |
| 图 5 TGO估计所需CPU时间 Fig. 5 CPU time of TGO estimation |
| 图选项 |
由图 4可知,对于不同框架角下的TGO初始值估计,经典法与预测碰撞点法相比,均存在较大的估计误差。在逆轨模式下,预测碰撞点法与解析法相比估计精度有较大提高;但与递推法相比,在框架角较大时,精度下降。这是由于预测碰撞点法通过“小角度”近似消除框架角的三角函数,框架角在接近90°时,线性条件下的近似虽然合理,但误差有所增大;而递推法在多步迭代计算过程中存在误差补偿修正,故框架角较大时估计效果更好。
由图 5可知,经典法计算最简单,TGO估计所需CPU时间最少,其均值小于2×10-5 s;预测点估计法与解析法所用时间相近,均值都为2.1×10-5 s;递推法运算量最大,所需平均时间为6.576×10-5 s,实时性最差。这是由于递推法在计算过程中通常需要迭代4~5步,TGO估计值才能趋于平稳,因而计算时间最长。
随着制导律不断采用最优化算法,其本身计算量已较难达到实时性要求,而对于TGO的估算应尽量为运算周期节约时间。递推法虽然在框架角较大时有一定优势,但在制导全过程中,实时性不高,故在以下的仿真中,不作为对比对象。
在逆轨模式下,分别选取初始框架角为10°、40°、70°,采用比例系数为3的纯比例(PPN)制导律完成目标拦截仿真;在顺轨模式下,分别选取框架角为110°、140°、170°,采用比例系数为3的负比例(RPN)制导律完成目标拦截仿真。各仿真完成后,确定拦截总时间tf,取实时的剩余拦截时间tgo=tf-t,得到各方法的TGO估计误差如图 6所示。
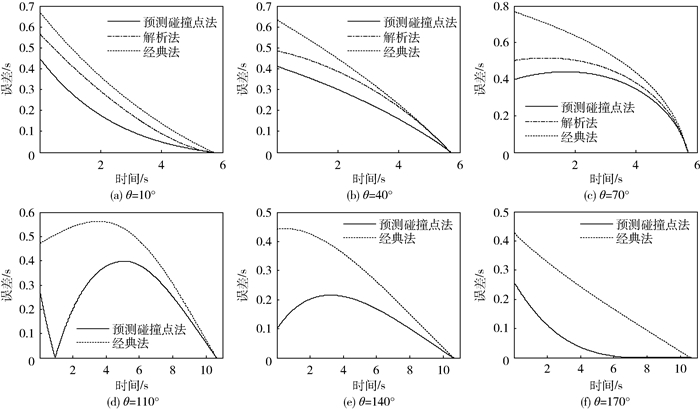 |
| 图 6 不同初始框架角下拦截过程TGO估计误差 Fig. 6 TGO estimation error during interception at different initial heading errors |
| 图选项 |
由于解析法仅在逆轨拦截模式下有效,因而在顺轨拦截模式下仅与经典TGO估计法作比较。从图 6中可知,逆轨模式下预测碰撞点法不论在初始时刻还是拦截全过程中,都具有最高的估计精度,解析法次之,经典法误差最大;顺轨拦截模式下,预测碰撞点法较经典法同样具有全面优势。其中,当框架角选取为110°拦截时间在1 s时,预测碰撞点的估计误差发生正负变化,是由算法系数项中π-θ-kλ随框架角和视线角改变而发生正负偏转所导致。
2.2 TGO估计对制导律性能的影响 为进一步验证TGO估算方法对制导律性能的影响,在不同初始路径倾角下,直接将各方法的估算值用以制导运算。仿真参数如表 1所示。
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 取值 |
| 目标速度/(m·s-1) | 1 500 |
| 拦截弹速度/(m·s-1) | 600 |
| 初始弹目距离/m | 10 000 |
| 拦截弹失效距离/m | 30 |
| 初始视线角/(°) | 8 |
| 目标初始路径倾角/(°) | 0 |
| 导航比 | 3 |
表选项
拦截弹进入失效距离后,重复执行失效前最后的制导指令。逆轨拦截的仿真结果如表 2和图 7所示(图中1~4为表 2中的方案1~方案4)。表 2中控制力按照∫|a|dt[22]进行计算,图 7(b)中的误差为估计值与实际值的差值。
表 2 逆轨拦截各方案结果 Table 2 Head-on interception results of different scenarios
| 方案 | 初始路径倾角/(°) | TGO估计方法 | 实际飞行总时间/s | 初始加速度/g | 控制力/(m·s-1) |
| 1 | 75 | 预测碰撞点法 | 5.09 | -12.45 | 106.464 3 |
| 2 | 75 | 解析法 | 4.96 | -13.01 | 125.068 5 |
| 3 | 20 | 预测碰撞点法 | 4.74 | 22.05 | 201.831 3 |
| 4 | 20 | 解析法 | 4.79 | 22.21 | 202.419 2 |
表选项
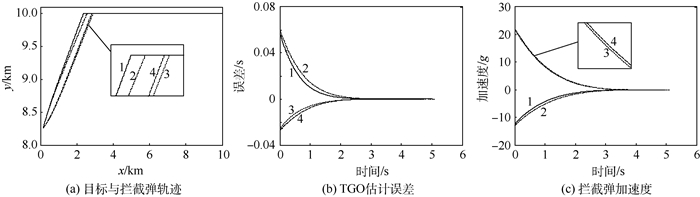 |
| 图 7 逆轨拦截仿真结果 Fig. 7 Simulation results of head-on interception |
| 图选项 |
由仿真结果可知,在不同初始路径倾角条件下,采用预测碰撞点法的TGO估计误差小于解析法,从而其初始加速度和控制力都较小。在初始路径倾角为75°时,由图 7(b)中前2 s的曲线可知,预测碰撞点法的TGO估计误差收敛性更强,这是由于式(23)中将弹目速度比k作为预测碰撞框架角θ-kλ的增益,对实际框架角变化更为敏感。而TGO误差直接反映在拦截弹指令加速度上,虽然预测碰撞点法飞行时间较长,但由图 7(c)可知在4 s以后,加速度趋近于0,拦截基本趋于平行接近,对时间的积分数值很小,故而最终控制力具有明显优势。
顺轨拦截目标的初始参数见表 1,结果见表 3和图 8。仿真结论与逆轨拦截相似,不再赘述。
表 3 顺轨拦截各方案结果 Table 3 Head-pursuit interception results of different scenarios
| 方案 | 初始路径倾角/(°) | TGO估计方法 | 实际飞行总时间/s | 初始加速度/g | 控制力/(m·s-1) |
| 1 | 105 | 预测碰撞点法 | 10.77 | 5.14 | 94.97 |
| 2 | 105 | 经典法 | 10.93 | 4.84 | 111.45 |
| 3 | 160 | 预测碰撞点法 | 10.94 | -9.43 | 182.59 |
| 4 | 160 | 经典法 | 10.75 | -10.55 | 209.71 |
表选项
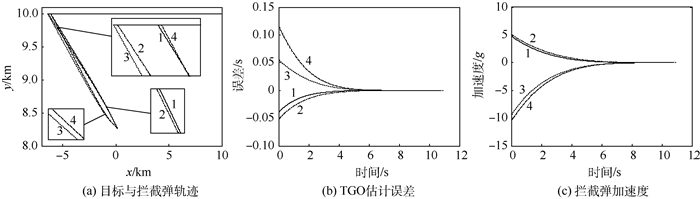 |
| 图 8 顺轨拦截目标仿真结果 Fig. 8 Simulation results of head-pursuit interception |
| 图选项 |
在拦截机动目标的仿真中,参数不变,目标采用1 g加速度进行恒值机动。为方便与拦截非机动目标的仿真对比,初始路径倾角选择20°和160°,仿真结果如表 4及图 9所示。
表 4 拦截机动目标各方案结果 Table 4 Results of different scenarios for maneuvering target interception
| 方案 | 拦截模式 | 初始路径倾角/(°) | TGO估计方法 | 实际飞行总时间/s | 控制力/(m·s-1) |
| 1 | 逆轨 | 20 | 预测碰撞点法 | 4.75 | 218.096 1 |
| 2 | 逆轨 | 20 | 解析法 | 4.80 | 220.716 4 |
| 3 | 顺轨 | 160 | 预测碰撞点法 | 10.99 | 233.670 2 |
| 4 | 顺轨 | 160 | 经典法 | 10.82 | 254.189 3 |
表选项
 |
| 图 9 拦截机动目标仿真结果 Fig. 9 Simulation results of maneuvering target interception |
| 图选项 |
结合图 7(b)、图 8(b)和图 9(b)可知,在目标机动情况下,由于目标路径改变,导致TGO估计误差初值有所增加。当初始路径倾角为20°时,预测碰撞点法的估计误差初值增大了0.004 s,解析法增大了0.005 s;初始路径倾角为160°时,预测碰撞点法的估计误差初值增大了0.053 s,经典法增大了0.071 s。对于机动目标,预测碰撞点法虽然误差变大,但估计精度和制导性能仍优于其他两者。
3 结?论 1)?针对顺/逆轨拦截模式,提出了基于预测碰撞点的剩余拦截时间估计方法。该方法基于线性的RPN/PN制导律,通过假设出的预测碰撞点,求解二阶微分方程并积分得出拦截弹路径,建立拦截弹和目标飞行时间的等式,进而得出预测碰撞点位置和剩余拦截时间。通过与3种不同TGO估计方法对比,验证了基于预测碰撞点TGO估计法的有效性,并具有精确度高、控制力小等特点。
2)?本文提出的TGO估计方法所需参数少、计算简单、实时性好,其思想对于不同制导律都易于移植和实施,尤其是算法复杂多变的最优制导律。
参考文献
| [1] | RYOO C, CHO H, TAHK M. Time-to-go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on Control Systems Technology, 2006, 14(3): 483–492.DOI:10.1109/TCST.2006.872525 |
| [2] | KIM K B, KIM M, CHOI J W. Modified receding horizon guidance law with information on small accurate time-to-go[J].IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 725–729.DOI:10.1109/7.845274 |
| [3] | TANAKA A, MAEDA H. Studies on the time-to-go indexing control scheme for an automatic aircraft landing system[J].Transactions of the Japan Society for Aeronautical and Space Sciences, 1973, 16(31): 1–18. |
| [4] | WHANG I, RA W.Time-to-go estimation filter for anti-ship missile application[C]//Society of Instrument and Control Engineers (SICE).Piscataway, NJ:IEEE Press, 2008:247-250. |
| [5] | YORK R, PASTRICK H. Optimal terminal guidance with constraints at final time[J].Journal of Spacecraft and Rockets, 1977, 14(6): 381–382.DOI:10.2514/3.57212 |
| [6] | JEON I, LEE J, TAHK M. Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology, 2006, 14(2): 260–266.DOI:10.1109/TCST.2005.863655 |
| [7] | LIU P, SUN R, LI W. Homing guidance law with falling angle and flying time control[J].Journal of Harbin Institute of Technology, 2014, 21(1): 55–61. |
| [8] | KIM T H, LEE C H, TAHK M J. Time-to-go polynomial guidance with trajectory modulation for observability enhancement[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 55–73.DOI:10.1109/TAES.2013.6404091 |
| [9] | 马国欣, 张友安, 李君. 带导引头视场限制的多约束导引律及剩余时间估计[J].系统工程与电子技术, 2014, 36(8): 1609–1613.MA G X, ZHANG Y A, LI J. Guidance law with multiple constraints and seeker field-of-view limit and the time-to-go estimation[J].Systerms Engineering and Electronics, 2014, 36(8): 1609–1613.(in Chinese) |
| [10] | 李辕, 闫梁, 赵继广, 等. 顺轨拦截模式剩余飞行时间估计方法研究[J].航空学报, 2015, 36(9): 3032–3041.LI Y, YAN L, ZHAO J G, et al. Method of time-to-go estimation for head-pursuit interception mode[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 3032–3041.(in Chinese) |
| [11] | 刘剑锋, 庄志洪. 利用导引头测角信息进行遭遇段剩余飞行时间估计的算法[J].兵工学报, 2006, 27(1): 27–31.LIU J F, ZHUANG Z H. The algorithm of time-to-go using angle information provided by seeker during missile-target encounter[J].Acta Armamentarii, 2006, 27(1): 27–31.(in Chinese) |
| [12] | RIGGS J T L.Linear optimal guidance for short range air-to-air missile[C]//Proceedings of National Aerospace and Electronics Conference NAECON'79.Piscataway, NJ:IEEE Press, 1979:757-764. |
| [13] | HULL D G, RADKE J J, MACK R E. Time-to-go prediction for homing missiles based on minimum-time intercepts[J].Journal of Guidance, Control, and Dynamics, 1991, 14(5): 865–871.DOI:10.2514/3.20725 |
| [14] | DHANANJAY N, GHOSE D. Accurate time-to-go estimation for proportional navigation guidance[J].Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1378–1383.DOI:10.2514/1.G000082 |
| [15] | TAHK M, RYOO C, CHO H. Recursive time-to-go estimation for homing guidance missiles[J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 13–24.DOI:10.1109/7.993225 |
| [16] | 常青, 邢超, 李言俊. 利用导弹轴向加速度估算剩余飞行时间的新方法[J].弹箭与制导学报, 2002, 22(4): 112–114.CHANG Q, XING C, LI Y J. A new method for time-to-go using the acceleration along the axis of missile[J].Journal of Projectiles Rockets Missiles and Guidance, 2002, 22(4): 112–114.(in Chinese) |
| [17] | 张友安, 马国欣. 大前置角下比例导引律的剩余时间估计算法[J].哈尔滨工程大学学报, 2013, 34(11): 1409–1414.ZHANG Y A, MA G X. Time-to-go estimation algorithm for the proportional navigation guidance law with a large lead angle[J].Journal of Harbin Engineering University, 2013, 34(11): 1409–1414.(in Chinese) |
| [18] | PRASANNA H M, GHOSE D. Retro-proportional-navigation:A new guidance law for interception of high-speed targets[J].Journal of Guidance, Control, and Dynamics, 2012, 35(2): 377–386.DOI:10.2514/1.54892 |
| [19] | SHIMA T. Intercept-angle guidance[J].Journal of Guidance, Control, and Dynamics, 2011, 34(2): 484–492.DOI:10.2514/1.51026 |
| [20] | TAL S, GOLAN O M. Head pursuit guidance[J].Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1437–1444.DOI:10.2514/1.27737 |
| [21] | ZARCHAN P. Tactical and strategic missile guidance[M].3rd edReston: AIAA, 2002: 15. |
| [22] | YUAN P, CHERN J. Ideal proportional navigation[J].Journal of Guidance, Control, and Dynamics, 1992, 15(5): 1161–1165.DOI:10.2514/3.20964 |
