针对同轴共轭像祛除问题,早期提出的数字相减法[10, 11]、远场记录法[12]和叠加法[13, 14]等只适用于电子全息显微术或者X射线全息显微术,而各种数字信号处理方法,如DSP线性滤波[15]、逆卷积滤波[16]等只能抑制共轭像而无法对其完全消除,严重制约了相位测量的精度。Yamaguchi和Zhang[17]提出的相移全息技术,即通过连续调节参考光的相位获得多幅全息图后,再采用四则运算方法祛除零级项以及共轭像。相移算法在消除同轴数字全息共轭像的干扰方面确实是一种比较有效的方法,但是相移全息由于要求每次的相移量都要相等,所以它需要高精密的相移装置和稳定的记录条件。相移装置的精密性会直接影响再现像质量,而且很难做到实时观测成像。相位恢复算法是一种比较适用的方法,它通过在物面和记录面之间往复迭代,以在恢复出成像面上的物光复振幅分布的同时达到祛除像面共轭像的效果[18, 19, 20]。但是现有已提出的相位恢复算法得到的都是包裹相位像,而被测物体的纵向深度通常都是大于单测量波长的,所以鲍鹏等[21, 22]通过在迭代过程中引入合成相位,实现了在共轭像祛除的同时获取相位连续分布的解包裹相位信息。但是由于这种迭代算法以全息图强度的均方根乘以随机相位做为迭代的初始值,并且在物面不添加任何的收敛限制条件,所以其收敛速度很慢,而且若想得到高质量的再现像,则需要大量的迭代次数以及足够多的记录波长。
本文提出一种基于多波长同轴数字全息图的相位恢复算法,利用角谱法在物面和4个波长下记录的全息面之间进行迭代计算,实现再现成像面中共轭像的祛除。在迭代计算过程中以归一化全息图的幅值作为记录面的约束条件,以物体的吸收系数和相位分布作为物面的约束条件,有效提高了算法的收敛速度以及减少了迭代过程中使用的全息图幅数。同时,由于在迭代过程中引入了合成波长,有效地扩展了测量范围,实现了再现成像面中共轭像祛除的同时获得连续分布的相位信息。数值仿真和实验结果皆证明了该方法的有效性。
1 迭代算法实验装置示意图如图 1所示,该实验系统又通常被称为盖伯全息。可调谐激光器出射的偏振光通过扩束准直单元(BE,由空间滤波器以及准直透镜组成)后成为均匀分布的平行光。当平行光透过物体后,经过物体(S)的衍射光作为物光,而周围未经过物体的直通光则作为参考光,物光与参考光在CMOS相机的光敏面上发生干涉形成全息图。CMOS相机被放置在距离物体z处,分别在照明波长为λ11、λ12、λ21和λ22条件下记录4幅数字全息图。这4幅全息图被分为2组,且λ11和λ21之间的记录波长间隔应与λ12和λ22之间的记录波长间隔相同。
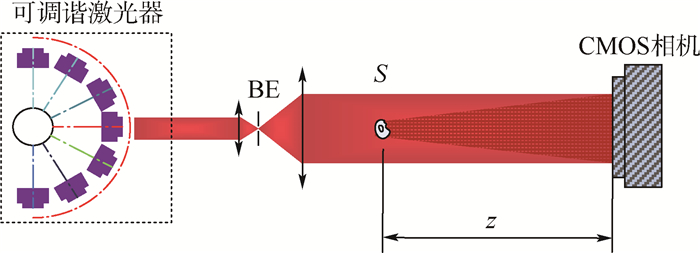 |
| 图 1 同轴数字全息实验系统光路图 Fig. 1 Schematic diagram of the setup for in-line digital holography |
| 图选项 |
迭代算法的具体流程如下:
1)首先估计2个初始相位值φλi1(x,y)(i=1,2),其中(x,y)为记录波长为λi1时记录面的笛卡儿坐标系。接着exp(jφλi1(x,y))乘以各自的归一化全息图强度的平方根,得到记录波长为λi1条件下记录面的复振幅分布信息,其中归一化的全息图是由包含样品的全息图强度Hλi1(x,y)除以在相同实验条件下无样品时记录的背景全息图强度Gλi1(x,y)后得到的。于是记录面的复振幅分布可以表示为

2)用角谱法[23]将记录面的复振幅分布Uλi1(x,y)逆向回传到物面,得到物面的复振幅分布为
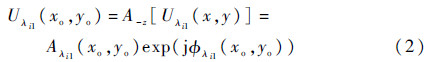
式中:(xo,yo)为物面的笛卡儿坐标系;A-z[]为用角谱法逆向传播距离z;Aλi1(xo,yo)和φλi1(xo,yo)分别为Uλi1(xo,yo)的振幅和相位信息。由于平行光穿过样品后光波的振幅只会减弱或保持不变,因此,由真实归一化全息图复振幅反向传回物面的幅值分布应不超过1。在相位恢复算法最初迭代过程中,物面波前振幅分布超过1的区域是由离焦共轭像造成的,随着离焦共轭像在迭代过程中被逐渐祛除,最终的物面部分点的振幅分布应不超过1。因此在物面波前振幅分布超过1的区域,其幅值应被替换为1,而相应的相位分布应置为0,于是物面更新后的复振幅分布为

3)比较2个物面上所获得的相位分布,计算合成相位:
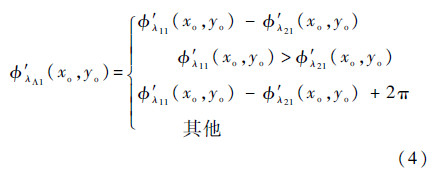
式中:φ′λi1(xo,yo)为U′λi1(xo,yo)的相位值;λΛ1为合成波长:
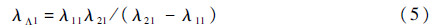
物体的表面形貌高度h(xo,yo)与合成相位之间的关系为
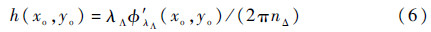
式中:nΔ=n-n0为样品与其周围介质的折射率差。因此,这2组记录波长的选取应使最后获得的合成波长大于物体表面形貌的最大高度,以避免相位包裹。基于式(6),利用合成相位φ′λΛ1(xo,yo)将φ′λi1(xo,yo)替换为下一记录波长λi2对应的相位值,而相应的振幅则不变。
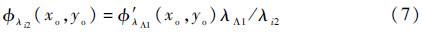
4)λi2对应物面的复振幅分布应为
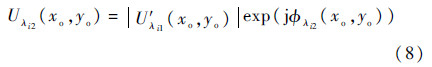
5)用角谱法将Uλi2(xo,yo)正向传播到记录面,得到记录波长为λi2的记录面的复振幅分布。之后使用该记录面归一化的全息图强度的平方根替换幅值,而保持相位值不变,并做为迭代算法步骤2)的输入值,开始新一轮的迭代。同轴数字全息物面波前重建的精度在迭代传播过程中得到了提升,其共轭像在多次的迭代后最终消除。由于在迭代算法过程中,引入了合成波长进行光学解包裹,因此该算法中所获得的相位值已经是一个连续分布的相位信息,所以可以直接换算得到对应物体的表面形貌分布信息。
2 仿真分析2.1 算法仿真结果及比较分析为了验证本文所提出的算法的可行性,本文首先选用了一个简单物体进行仿真实验。该物体是一组在透明背景上的5个字母,这5个字母具有均匀的吸收系数20%和分别为5、8、12、16和20 μm的高度分布,其幅值和相位分布见图 2(a)。被检测物体受限于512像素×512像素的方形区域中。模拟的相机为1 024像素×1 024像素,且每个像素尺寸大小为6.7 μm×6.7 μm。模拟的2组照明光波长分别为643.1 nm、644.0 nm以及658.1 nm、659.0 nm,物面到相机的记录距离为140 mm。利用角谱法得到的在记录波长分别为643.1 nm和658.1 nm条件下仿真的归一化后全息图见图 2(b)。经过100次迭代之后,所获得的再现结果如图 2(c)中所示。物面复振幅分布已经完全消除了共轭像的影响,由图中线扫描可知其幅值和高度分布已经完全恢复到预设值。为了更好地评价这种相位恢复算法,本文选取了鲍鹏等[22]的方法,基于双系列的记录面强度值的相位复原(PRDS)算法作为比较。该方法同样采用多波长条件下记录的一系列同轴数字全息图用于返复迭代计算,以复原物面的复振幅分布,但是在记录面以及物面上并未添加任何的约束条件。由于该算法要求每组的记录幅数不少于10幅[22],所以在该算法中模拟的2组照明光波长分别为643.1~644.0 nm及658.1~659.0 nm,间隔距离为0.1 nm,记录距离仍为140 mm。其共轭像祛除效果见图 2(d),结果表明在100次迭代后,该算法无法完全去除复振幅分布中共轭像的影响,通过线扫描也可以发现物面的幅值和高度没有恢复到预设值。通过对比图 2(c)和图 2(d)中的结果可知,在相同的迭代次数下,本文提出的算法可以使用较少的记录波长获得更优于PRDS算法的再现像成像质量。
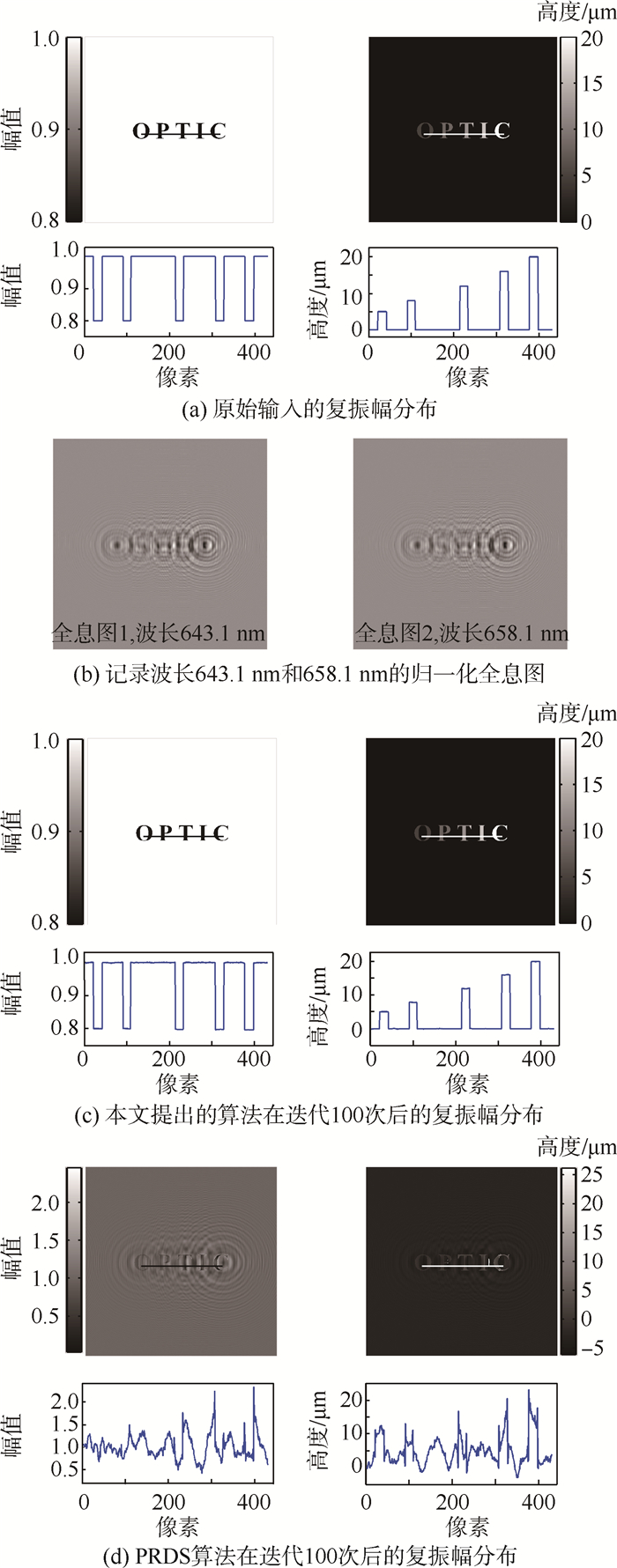 |
| 图 2 仿真实验结果 Fig. 2 Simulation experimental results |
| 图选项 |
迭代收敛速度是评价相位恢复算法的关键性因素,其可以用均方根误差E来评估:
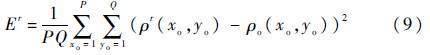
式中:ρ(xo,yo)为相位恢复后物面得到的幅值或高度分布;ρo(xo,yo)为预设的物面的幅值或高度分布;P和Q为物面尺寸;r为迭代次数。为了更清晰地显示比较效果,采用均方根误差的lg指数表示收敛效果。迭代收敛速度比较结果见图 3,与PRDS算法相比,本文提出的算法拥有更快的收敛速度,而且在经过相同的迭代次数之后,本文提出的算法具有更好的共轭像祛除效果。
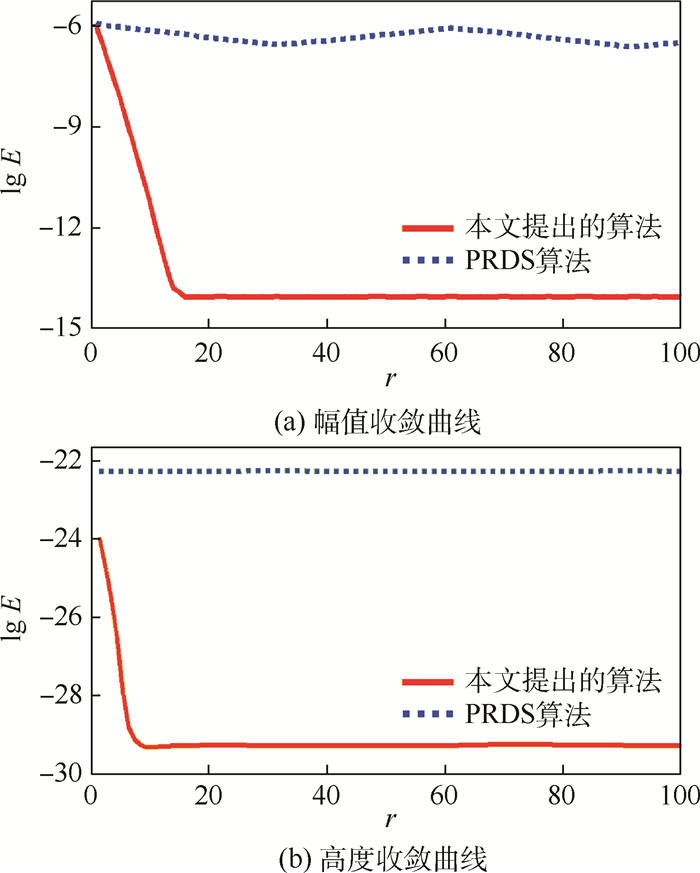 |
| 图 3 迭代收敛速度比较 Fig. 3 Comparison of convergence rates |
| 图选项 |
2.2 不同参数条件下的收敛特性对本文提出的算法在对应不同实验参数下的收敛特性予以评估。仿真物体如图 4(a)所示,其仍具有均匀的吸收系数20%,但是采用“lena”的灰度值分布来表征物体表面形貌高度分布特征。图 4(b)中的曲线所表示是在该算法中,对应于不同的波长间隔丨λ1i-λ2i丨分别为2、5、10、15和20 nm时,算法在经过相同的迭代次数后的共轭像祛除效果。从曲线中可以看出,算法在较大的波长间隔时具有更快的收敛速度及更好的祛除效果,然而当波长间隔分别为15 nm及20 nm时,算法具有相同的收敛速度与祛除效果。其原因可能是因为较小的波长间隔引入了更大的合成波长,从而更进一步地扩大了噪声。所以在该算法中,波长间隔的选取应使其噪声水平满足于一定的要求。图 4(c)中表示的是该算法在迭代过程中使用不同幅数的数字全息图时的收敛特性。从曲线中可以看出,当每一组中的数字全息图的幅数M从31幅降低到2幅时,算法的收敛速度与最终的祛除效果都几乎相同。也就是说,本文提出的算法,由于在记录面以及物面上添加了一定的收敛限制条件,使得算法的收敛特性已不再依赖于在迭代过程中所使用的数字全息图的幅数。反观PRDS算法,它要求用于迭代算法中每组的数字全息图的幅数不少于10幅[22]。所以本文提出的算法可在使用较少的数字全息图的前提下,达到预期的收敛速度以及祛除效果。该算法在对应不同物体表面最高形貌高度(hmax=2,12,15,20,25 μm)时的收敛特性如图 4(d)中所示。由图 4(d)中的曲线可以得出,随着物体表面最高形貌高度的不同,算法的收敛速度基本一致。但是当物体表面最高形貌高度为2 μm时,算法在相同的迭代次数之后对共轭像的祛除效果并不理想。随着物体表面最高形貌高度逐渐增大,算法在相同的迭代次数之后对共轭像的祛除效果也越加理想,说明该算法更适用于物体表面最高形貌高度较大的情况。
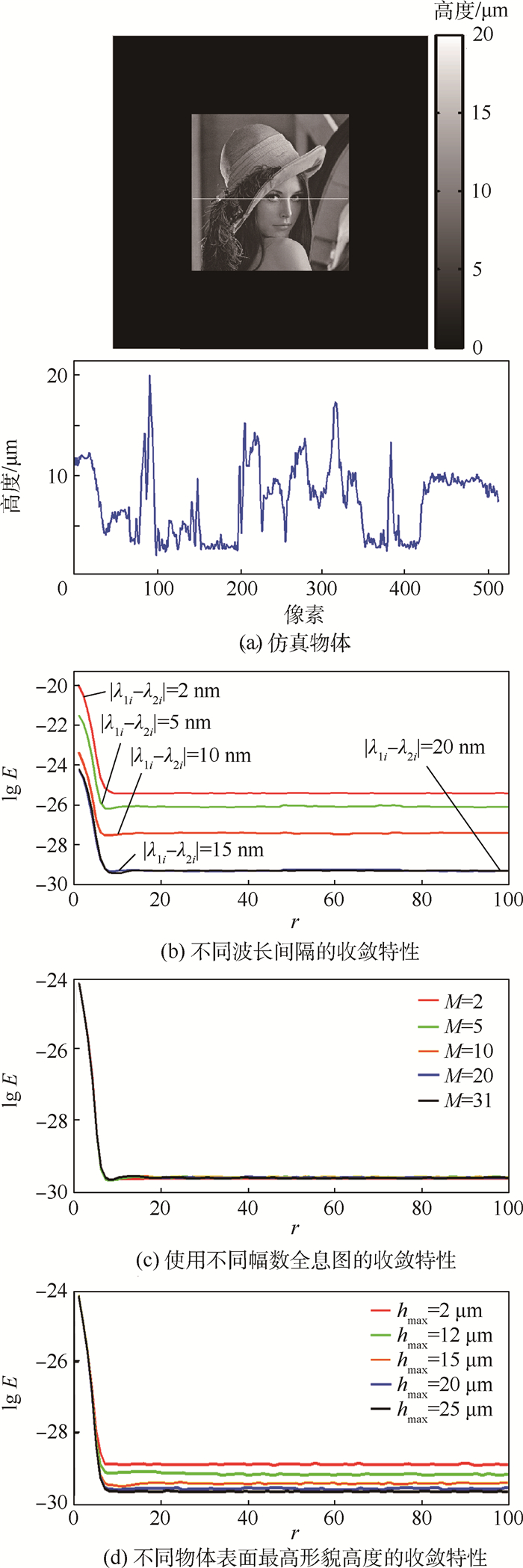 |
| 图 4 不同实验参数条件的收敛特性结果 Fig. 4 Convergence performance results under different experimental parameter conditions |
| 图选项 |
3 实 验为了验证迭代算法的正确性,选取相位调制型光栅作为样品。光栅折射率为1.5,其凹槽高度为20 μm,光栅周期为300 μm。光源为韩国Nanobase公司生产的Xperay-TL系列的可调谐半导体激光器,输出光功率为50 mW。CMOS相机为加拿大Lumenera公司生产的L-125型号相机,1 280像素×1 024像素,单元像素尺寸为6.7 μm×6.7 μm。CMOS相机被放置到距离物体100 mm处,相应的背景全息图则在移除物体后进行拍摄获取。实验中在照明光波长为643.1~644.0 nm以及658.1~659.0 nm、间隔距离为0.1 nm时记录全息图。精确的记录距离可由拉普拉斯二阶微分自聚焦算法自动获取[24]。实验结果见图 5。图 5(a)和图 5(b)中所示的是在记录波长为643.1 nm和658.1 nm,记录距离为100 mm时归一化的数字全息图。PRDS算法[22]中使用全部记录的全息图,其在经过100次迭代之后所获得的物体实际表面形貌分布如图 5(c)中所示。图 5(e)和图 5(g)分别为图 5(c)中直线的线扫描曲线以及白色虚线框内区域的三维显示。图 5(e)和图 5(g)中的结果表明,再现图像仍然受共轭像的影响,而且PRDS算法的收敛速度很慢,共轭像祛除效果并不理想。而本文提出的算法中只使用记录波长分别为643.1 nm、644.0 nm以及658.1 nm、659.0 nm的数字全息图,其在经过100次迭代之后所获得的物体实际表面形貌分布如图 5(d)所示。图 5(f)和图 5(h)分别为图 5(d)中直线的线扫描曲线以及白色虚线框内区域的三维显示。从图 5(f)和图 5(h)中可以看出,光栅边缘清晰锐利,光栅外部分的背景高度分布均匀,表明共轭像已完全祛除,而且实验所获得的光栅周期与凹槽深度皆与给定的光栅参数相符。从光栅的再现结果可以看出,采用本文所提出的算法进行迭代计算后,物面波前重建已经完全祛除共轭像的影响,物体信息得到了比较好的复原,再现图像质量得到明显提高。
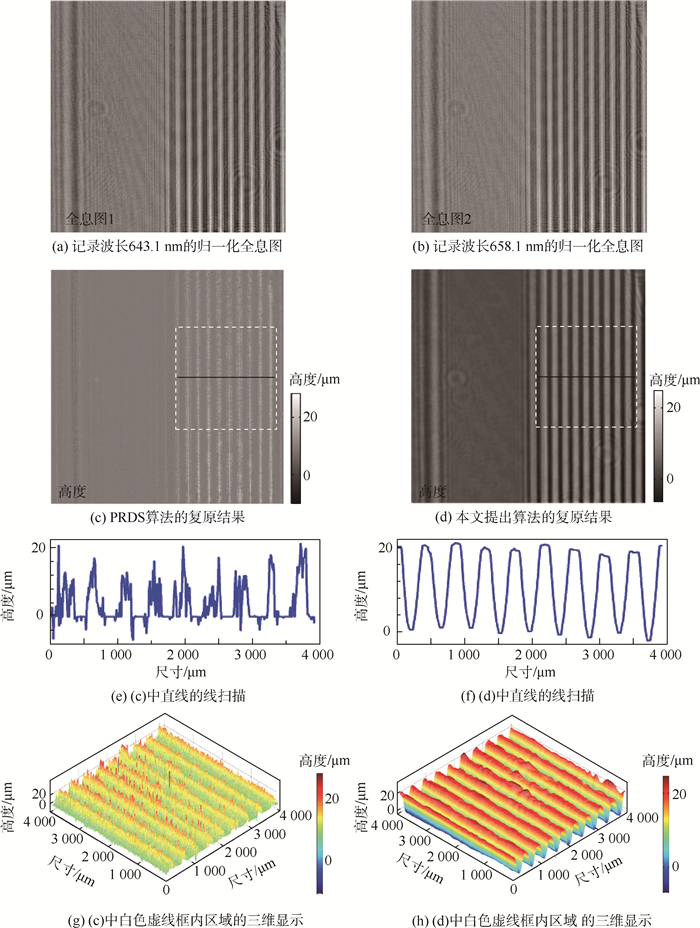 |
| 图 5 光栅形貌复原结果 Fig. 5 Results of binary phase grating |
| 图选项 |
4 结 论针对同轴全息中3项混叠的问题,本文提出了一种基于多波长的相位恢复算法以消除共轭像,数值仿真与实验结果表明:
1)通过在记录面以及物面添加一定的收敛限制条件后,该算法以较少的迭代次数以及较少的记录波长精确地复原物面的复振幅分布,得到了高质量的再现像。
2)由于在迭代过程中引入了合成波长,所以获得的相位值已经是一个连续分布的相位信息,可以直接换算得到对应物体的表面形貌分布。
3)通过使用不同实验参数(如波长间隔、全息图幅数以及物体表面最高形貌高度等)对迭代算法的收敛速度以及共轭像祛除效果影响的仿真分析,得出波长间隔的选取会同时影响算法的收敛速度以及共轭像祛除效果,所以波长间隔的选取应使其噪声水平满足于一定的要求。而由于记录面以及物面收敛限制条件的添加,算法的收敛特性已不再依赖于迭代过程中所使用的数字全息图的幅数。物体表面最高形貌高度的不同并不影响算法的收敛速度,但会影响最后的重构精度。
该实验装置结构简单并且无需参考光,可有效降低噪声以及环境对其的影响,提供了一种更为高效的检测手段。
参考文献
| [1] | VIJAY R S, ANAND A.In-line digital holography for dynamic metrology of MEMS[J].Chinese Optics Letters,2009,7(12):1117-1122. |
| Click to display the text | |
| [2] | DEMOLI N. Real-time monitoring of vibration fringe patterns by optical reconstruction of digital holograms:Mode beating detection[J].Optics Express,2006,14(6):2117-2122. |
| Click to display the text | |
| [3] | PU S L, ALLANO D,PATTE-ROULAND B,et al.Particle field characterization by digital in-line holography:3D location and sizing[J].Experiments in Fluids,2005,39(1):1-9. |
| Click to display the text | |
| [4] | KEMPER B, BALLY G.Digital holographic microscopy for live cell applications and technical inspection[J].Applied Optics,2008,47(4):A52-61. |
| Click to display the text | |
| [5] | NUGENT K A. Twin-image elimination in Gabor holography[J].Optics Communications,1990,78(3):293-299. |
| [6] | REN Y, CHEN C,CHEN R,et al.Optimization of image recording distances for quantitative X-ray in-line phase contrast imaging[J].Optics Express,2011,19(5):4170-4181. |
| Click to display the text | |
| [7] | LEE D J, WEINER A M.Optical phase imaging using a synthetic aperture phase retrieval technique[J].Optics Express,2014,22(8):9380-9394. |
| Click to display the text | |
| [8] | GAO P, PEDRINI G,ZUO C,et al.Phase retrieval using spatially modulated illumination[J].Optics Express,2014,39(12):3615-3618. |
| Click to display the text | |
| [9] | LEI T, NICK L,DOMíNGUEZ-CABALLERO J A,et al.Quantitative measurement of size and three-dimensional position of fast-moving bubbles in air-water mixture flows using digital holography[J].Applied Optics,2010,49(9):1549-1554. |
| Click to display the text | |
| [10] | BRAGG W L, ROGER G L.Elimination of the unwanted image in diffraction microscopy[J].Nature,1951,167(4240):190-191. |
| Click to display the text | |
| [11] | ROGERS G. In-line soft-X-ray holography:The unwanted image[J].Optics Letters,1994,19(1):67. |
| Click to display the text | |
| [12] | DEVELIS J, PARRENT G,THOMPSON B.Image reconstruction with fraunhofer holograms[J].Journal of the Optical Society of America,1966,56(4):423-427. |
| Click to display the text | |
| [13] | TONG S,LI H, HUANG H.Energy extension in three-dimensional atomic imaging by electron emission holography[J].Physical Review Letters,1991,67(22):3102-3105. |
| Click to display the text | |
| [14] | LIN J, COWLEY M.Reconstruction from in-line electron holograms by digital processing[J].UltramieroAcopy,1986,19(2):179-189. |
| Click to display the text | |
| [15] | ONURAL L, SCOTT P D.Digital decoding of in-line holograms[J].Optical Engineering, 1987,26(11):1124-1132. |
| Click to display the text | |
| [16] | MALEKI M H, DEVANEY A J.Noniterative reconstruction of complex-valued objects from two intensity measurements[J].Optical Engineering,1994,33(10):3243-3253. |
| Click to display the text | |
| [17] | YAMAGUCHI I, ZHANG T.Phase-shifting digital holography[J].Optics Letters,1997,22(16):1268-1270. |
| Click to display the text | |
| [18] | KOREN G, JOYEUX D,POLACK F.Twin-image elimination in in-line holography of finite-support complex objects[J].Optics Letters,1991,16(24):1979-1981. |
| Click to display the text | |
| [19] | ZHANG Y, PEDRINI G,OSTEN W,et al.Whole optical wave field reconstruction from double or multi in-line holograms by phase retrieval algorithm[J].Optics Express,2003,11(24):3234-3241. |
| Click to display the text | |
| [20] | LATYCHEVSKAIA T, FINK H. Solution to the twin image problem in holography[J].Physical Review Letters,2007,98(23):233901. |
| Click to display the text | |
| [21] | BAO P, ZHANG F C,PEDRINI G,et al.Phase retrieval using multiple illumination wavelengths[J].Optics Letters,2008,33(4):309-311. |
| Click to display the text | |
| [22] | BAO P, PEDRINI G,OSTEN W.Optical surface profile measurement using phase retrieval by tuning the illumination wavelength[J].Optics Communications,2012,285(24):5029-5036. |
| Click to display the text | |
| [23] | YU L,KIM M K. Wavelength-scanning digital interference holography for tomographic 3D imaging using the angular spectrum method[J].Optics Letters,2005,30(16):2092-2094. |
| Click to display the text | |
| [24] | GUO C S, YUE Q Y,WEI G X,et al.Laplacian differential reconstruction of in-line holograms recorded at two different distances[J].Optics Letters,2008,33(17):1945-1947. |
| Click to display the text |
