为了提高基于图像梯度分布的局部特征描述子的不变性、实时性及准确性,提出了一种新的梯度分布统计模型。用模值累积梯度方向直方图作为离散边缘积分函数,使用非参数估计方法实现该函数的精确估计。针对视觉导航应用中十分重要的图像匹配算法的旋转不变性问题,提出了基于径向采样网格的SIFT描述子,降低特征向量维数和运算复杂度。
1 模值累积方向直方图的统计模型直方图是一种概率密度函数的离散形式,对它的估计方法分为2种:参数估计和非参数估计。若在局部领域内像素的梯度方向分布形态已知,则估计称为参数估计,反之则称为非参数估计。如设方向分布为方向统计学的混合正态分布,方向分布估计为参数估计[10]。本文设分布函数形态是未知的,用非参数估计方法描述特征向量,这种情况下不仅考虑到梯度方向,而且也考虑到梯度模值。
1.1 关于模值累积梯度方向直方图的数学模型设D为连续图像局部领域,ξ和η分别为局部领域内像素点的梯度模值和方向。ξ的变化区间为Ω1=[0,M],η的变化区间为Ω2=[0,2π]。记Ω=Ω1×Ω2,ζ=(ξ,η)为概率空间(Ω,,P)上的二维随机变量,联合分布函数为
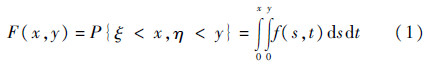
式中:x和y为随机变量ξ和η取的实数值,联合概率密度函数f(x,y)是未知的。将边缘积分算子定义为
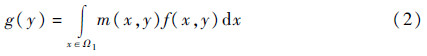
式中:m(x,y)为可积函数;g(y)为关于y的边缘积分函数。
设m(x,y)=x时,边缘积分函数为

本文将模值累积梯度方向直方图作为式(3)的边缘积分函数g(y)。假如m(x,y)=1,g(y)是边缘概率密度函数,而且是只考察方向的直方图。当m(x,y)为x与边缘概率密度函数fη(y)之比时,g(y)为η的条件数学期望。由于联合概率密度函数f(x,y)未知,用像素的梯度模值和方向角估计边缘积分函数。所以边缘积分函数估计就是非参数估计。
1.2 边缘积分函数的非参数估计设(Xi,Yi)为样本向量,Xi为像素的梯度模值,Yi为方向角,N为样本容量。式(3)中,关于联合概率密度函数f(x,y)和边缘积分函数的估计量用核函数法[11]可得到

式中:Kx和Ky为核函数;hx,hy为窗口的宽,且为常量。
核函数是一元函数,必须满足下面的条件:

由式(3)和式(4)可知,关于边缘积分函数的估计量为
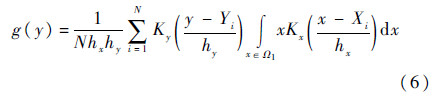
若核函数满足下面的条件:
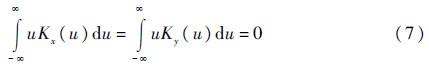
则边缘积分函数的估计量可为
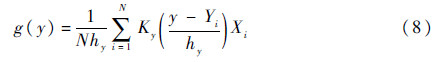
2 基于离散边缘积分函数的SIFT特征向量描述一般SIFT算法运算复杂度较大,其中描述子计算时间大约占总运算时间的40%。本文提出一种基于径向采样网格和边缘积分值估计的SIFT描述子,目的在于提高匹配效率而降低运算复杂度。
2.1 径向采样特征点提取及主方向计算和SIFT算法相同,但采样网格以及特征向量结构并不一样。标准SIFT算法将局部区域选取为正方形[12, 13, 14, 15],通过直角坐标采样网格,将特征点周围的区域划分为d×d(一般4×4)个子区域。将局部区域坐标轴旋转至主方向后,组成对每个子区域的8个方向梯度直方图。坐标轴旋转公式为

式中:u和v为旋转前局部区域内采样点的坐标;u′和v′为坐标轴旋转后新坐标;θ为旋转角度。图 1(a)显示坐标轴旋转结果。对求出的u′和v′的值进行四舍五入时,会产生误差。图上白色点的坐标变换结果不正确。θ在15°~45°区间变化时,白色点的占有率由5%~18%单调递增。其他区间也一样。因此,计算基于种子点和像素点之间距离的权重时会产生误差。
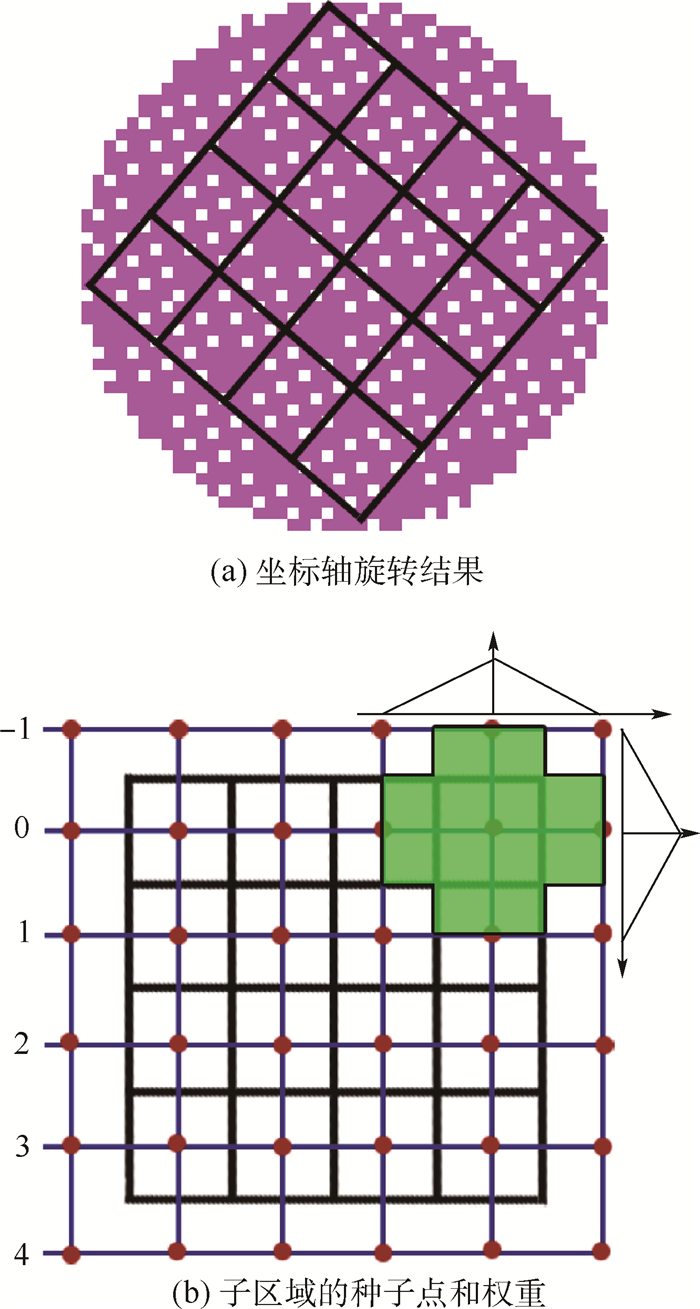 |
| 图 1 SIFT局部区域 Fig. 1 SIFT local region |
| 图选项 |
结果,全图片的旋转角度为30°以上时,基于直角坐标采样网格的SIFT算法的匹配效率下降。
为了提高SIFT算法的旋转不变性,有研究提出极坐标采样网格及环采样网格,但径向采样网格最适合用来实现局部区域的梯度分布特性。具体来说,极坐标采样方法采用17个子区域的16方向直方图构成272维特征向量。随后,用主成分分析(PCA)将维数降低为128维。弱点是每个子区域的像素数目不同,而此前进行关于图像数据库的PCA运算,要得到本征向量,所以若图像数据库不同,则匹配效果下降。环采样网格方法将局部区域划分为8个环形区域,计算关于8个环子区域的8维梯度方向直方图,每个子区域的像素数目不同而且较小,因此,不能表明统计特性,独特性下降。本文提出径向采样网格,局部区域选取为圆形区域。圆形区域的径向采样网格有3个优点:
1)轻易选定对关键点的局部区域,其与图像旋转及主方向无关,不需要坐标轴旋转变换。
2)使局部区域跟主方向计算过程中的圆形区域一致。
3)用圆的对称性轻易决定像素点存在于哪个子区域。
每个子区域的像素数目一致,不仅满足旋转不变性,而且有可能拓展到椭圆形区域来满足仿射不变性。图 2显示径向采样网格。
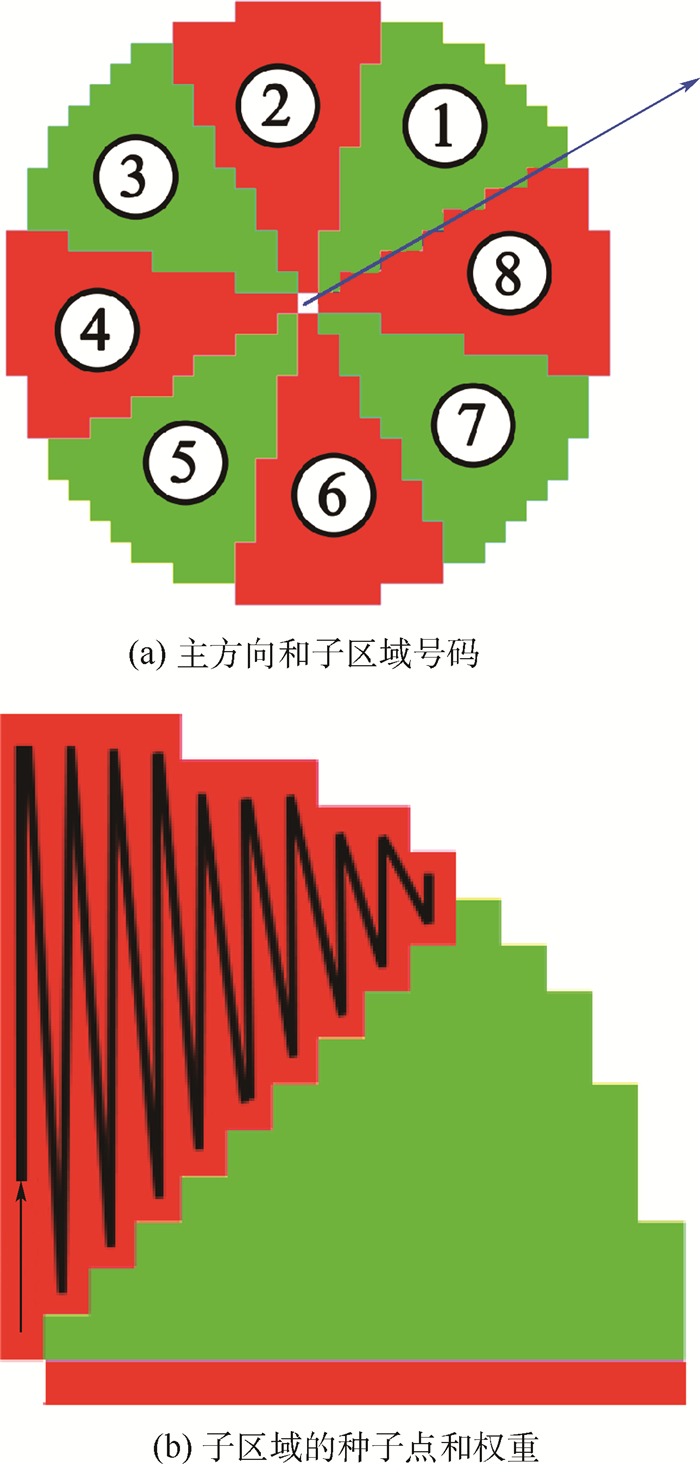 |
| 图 2 M=8,半径14的径向采样网格 Fig. 2 M=8, radial sampling grid of radius 14 |
| 图选项 |
如局部区域大小不同,独特性和运算复杂度也不同。SIFT算法[3, 4]采用大小为W×W的正方形区域,实际上,每组内3个层的局部区域大小平均为24×24、32×32及36×36。文献[3]用brisenham运算来实现径向采样,局部区域大小可变。将3个层的局部区域设定成半径为11、14和17的圆形区域。为了决定像素点存在于哪个子区域,需计算像素点的圆心角。设该角度为β。运行程序之前,如图 2(b)所示,对一个子区域内的像素采用“之”字型的排列方法,计算每个像素点的β角,记录在程序里。运行时,用圆的对称性得到其他子区域内所有像素点的β角。设主方向为α,径向采样数为M,像素点存在的子区域号码为m。设α和β的取值在[-180,180)时:

式中:[·]为取整数维。最后子区域号码确定需要一次乘运算和一次减运算。
2.2 特征描述设梯度方向和局部区域主方向为y,在式(8)中将该变量离散得到特征向量。设径向采样子区域为Dm(m=1,2,…,M),边缘积分函数为gm(y)。
由于每个子区域的函数估计方法一致,不失一般性,只在一个子区域上估计离散边缘积分函数g(y)。设对N个子区域内像素点的样本向量为(Xi,Yi)。
首先采用式(11)来变换Yi,yi属于区间[0,8)。

随后,估计在离散点y=ykc的边缘积分值。由式(12)的ykc量化为K个值。
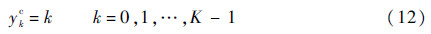
设hx=hy=1,核函数Kx和Ky分别为
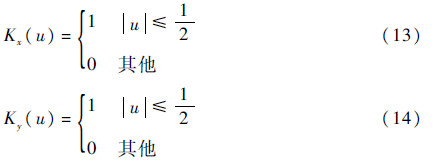
该核函数满足条件式(5)和式(7),由式(8)、式(11)及式(12),估计在离散点ykc的边缘积分值。该估计量为

该估计量不仅是无偏估计量,而且是相合估计量(证明略)。若核函数Ky为式(16),它和SIFT的方向权重一致。
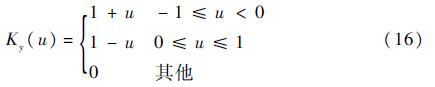
由式(15),能够得到M个子区域的离散边缘积分函数,即模值累积梯度方向直方图。最后将所有子区域的直方图连接成为M×K维的特征向量。
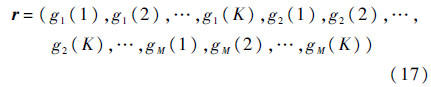
因此特征向量维数为M×K。设M=8,K=8,得到64维特征向量。
为了适应光照变化进行规范化处理,将上限设为Tr=0.25时其效果最好。标准SIFT、GLOH和Ring[8]以0.2、0.23和0.35为描述最合理。图 3依次表示直角坐标采样网格(SIFT[9])、极坐标采样网格(GLOH)、环采样网格(Ring)和径向采样网格(本文)区域标准化之前的梯度方向直方图。
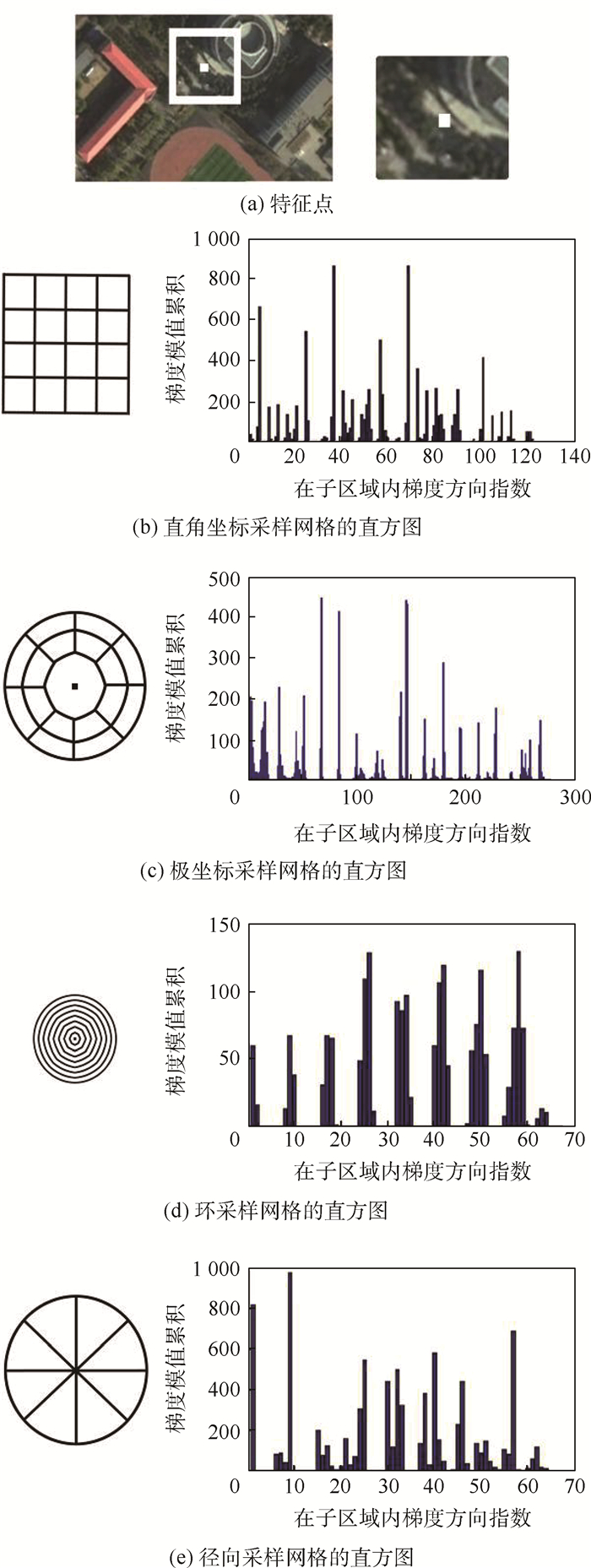 |
| 图 3 在同一特征点关于不同描述子的直方图 Fig. 3 Histogram for different descriptors at the same feature point |
| 图选项 |
从图 3可以看出,在GLOH中1~16的成分值较大而在Ring中循环性较强。本文的目的在于提高独特性而得到较高的查全率,所以没考虑去除掉错误匹配对,只考察基于l1距离的穷举匹配基准。将参考图像特征向量zi的集合设为Z,测试图像的特征向量设为r,2个向量之间的距离l1设为d(r,zi),那么Mr为
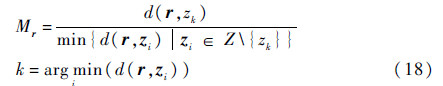
若其值小于某种阈值TM、r和zi被认为匹配对。图 4表示按照大小顺序排列的对于参考图像特征点的测试图像特征点的穷举匹配基准。可以看出匹配对与非匹配对之间的穷举匹配基准差距越大,对匹配对分类的正确率越高。
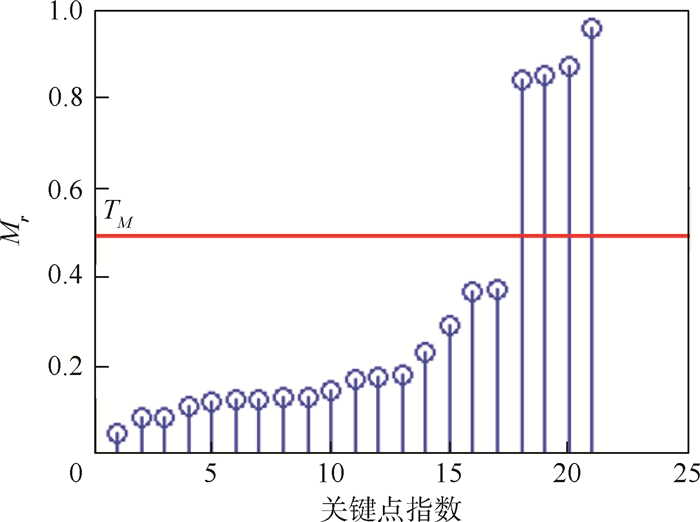 |
| 图 4 顺序排列的穷举匹配基准 Fig. 4 Ordered exhaustion matching criterion |
| 图选项 |
3 实验结果本文采用2类图像数据:①牛津建视觉几何数据库(http://www.robots.ox.ac.uk/);②目的在于遥感图像与航空图像一起匹配的图像数据。其参考图像为http://map.baidu.com/提供的遥感图像,而测试图像为在3D-google earth软件中得到的模拟航空图像及CSUAV数据库(https://www.sdms.afrl.af.mil/)。所有算法均在Window7,32位操作系统下运行,电脑配置为内存2 G,AMD,X2 B24 CPU3G.本文及其他描述子则使用作者提供的源代码在VC++2008平台运行,也在MATLAB2012(a)平台运行来显示了中间计算结果。
3.1 按照旋转角的描述子的匹配指标基于视角的导航与定位一定要满足在描述阶段中旋转变换及仿射变换的鲁棒性,特别是对于-180°~180°之间旋转变换的不变性。本文考虑到描述子的对称性,所以只考察0°~180°的范围。参考图像与测试图像特征点的提取方法跟SIFT一致,而通过选择不同的描述子,决定特征向量,在匹配阶段要抓住正确的匹配对,所以没有采用RANSAC或OSRA来除掉匹配后的错误匹配,只是采用基于l1距离的穷举匹配法。
实际上正确的匹配对设为正匹配对,而其个数设为Np,分类后正匹配对个数为NTP,没有成为正匹配对的个数设为NFN,此时Np=NTP+NFN。在匹配方法不变的情况下,描述子的描述能力越强,正匹配对个数越多。其指标作为查全率tp,而其计算公式为

本文关注关于旋转变换的描述子的查全率。首先选择在1 m分辨率的遥感图像(参考图像)及旋转180°的模拟航空图像(测试图像)中恰当的区域而选取较少个数的特征点,然后采用最新版本的SIFT[9]与本文的方法来得到有顺序的穷举匹配指标进行对比,如图 5所示。
 |
| 图 5 遥感图像和模拟航空图像 Fig. 5 Remote sensing image and simulated aerial image |
| 图选项 |
阈值与SIFT一致设为TM=0.497 1。若穷举匹配指标小于阈值,其被认为匹配。图 6顺序的穷举匹配指标的对比,由图 6得知,与已有的SIFT相比,在旋转角较大的情况下,正匹配对个数有一定增加,从而提高查全率。
 |
| 图 6 顺序的穷举匹配指标对比 Fig. 6 Comparison for ordered exhaustion matching value |
| 图选项 |
采用2种参考图像(图 7(a)和图 7(b))的旋转图像(图 7(c)和图 7(d)),跟随旋转角的典型描述子的查全率如图 8所示。测试结果显示,最新版本SIFT和本文的查全率较高,2种方法之间的平均查全率差距为20%。GLOH的尺度不变性及压缩鲁棒性较好,但10°以上的范围内旋转变换的鲁棒性很差[6]。
 |
| 图 7 参考图像与旋转图像 Fig. 7 Reference image and rotated image |
| 图选项 |
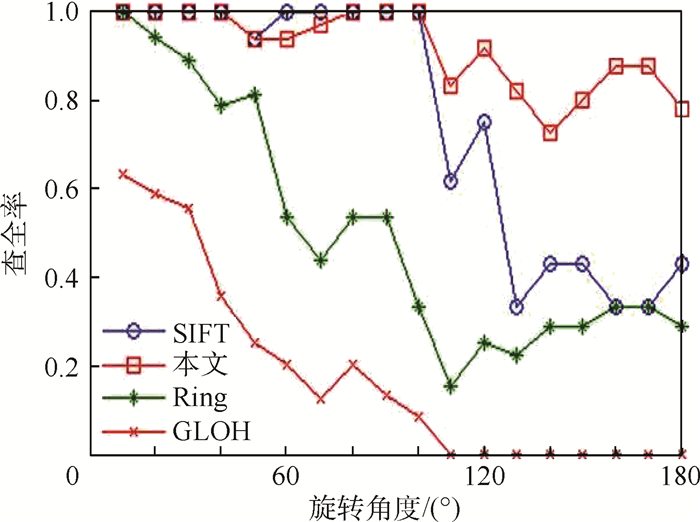 |
| 图 8 关于旋转角度的查全率 Fig. 8 Recall for rotation angle |
| 图选项 |
图 9为从CSUAV数据库得到的遥感图像(参考图像)和无人机实拍的图像(测试图像)。图 9(a)上3个四边形区域对应图 9(b)中3幅图像。
如图 9所示,对于测试图像,除了旋转变换之外,影子、噪声、光照及尺度变化的影响也比较大。此时,本文算法的查全率下降为42%~63%,而最新版本SIFT查全率为16%~28%,2种算法的差距为23%。还需要别的匹配方法。
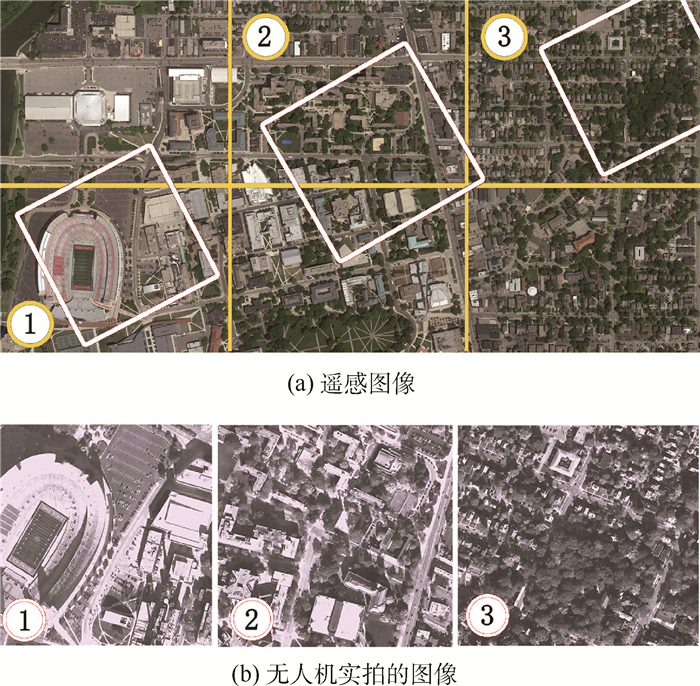 |
| 图 9 遥感图像和无人机实拍的图像 Fig. 9 Remote sensing image and UAV image |
| 图选项 |
3.2 描述子的描述指标及查全率基于局部区域统计特性的描述子的描述能力,与该描述子的特征向量包括多少非相关成分有关。采用基于方差极大值化法的主成分分析,从特征向量提取非相关成分。假设按照某一个描述子得到p维特征向量ri,i=1,2,…,Nd。其中Nd为特征点的个数。以其特征向量为行向量组成Nd×p矩阵。对于其输入矩阵的列进行归一化,设为R。RRT的本证值按大小排列而得到λ1,λ2,…,λp。用式(20)来计算具有80%以上的贡献率的主成分个数。
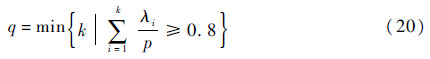
q/p比率越近于1,在特征向量中不需要的成分越少。另一方面,在随着p增加而q也增加的情况下,基于描述子得到的特征向量中说明变量的个数也越大。因此,加权主成分个数设为描述指标。其公式为

其次,一定要对于其输入矩阵的列进行归一化。采用图像数据库,得到15 800个特征向量,其描述指标计算结果如表 1所示。较大的描述指标不一定提高查全率,但却是提高查全率的必要条件之一。较小的描述子是不能期待较高的查全率的。
表 1 描述指标计算结果Table 1 Computational result of description indicator
| 算法 | p | q | Q |
| GLOH | 272 | 110 | 44.48 |
| 本文 | 64 | 32 | 16 |
| SIFT-(4×4) | 128 | 38 | 11.3 |
| Ring | 64 | 20 | 6.25 |
| SIFT-(2×2) | 32 | 14 | 6.125 |
表选项
3.3 描述子的运算复杂度标准SIFT描述方法一般将正方形局部区域划分为4×4个子区域,在每个子区域将方向直方图描述为8维向量。此时,由图 2(b)可知,除子区域之外,也考虑到它的上下左右的小区域。基于像素点与种子点之间的距离,像素点与特征点之间的距离及梯度方向,得到梯度模值的权重。因此,计算一个像素的权重时,需要13次乘运算。GLOH描述算法除对每个像素需8次乘运算以外,还需要128次乘运算来进行主成分变换。环采样需一次乘运算。本文提出了径向采样,只需要2次。由于特征点向量的维数也降低为64维,降低匹配的运算复杂度及运算时间。
对图 10显示的图像提取SIFT特征点,得到关于各种算法的描述时间(表 2)。
 |
| 图 10 描述时间计量图像 Fig. 10 Image for measuring description time |
| 图选项 |
表 2 各种算法的描述时间Table 2 Description times of different methods
| Id | 特征点数 | 描述时间/s | |||
| SIFT | GLOH | 本文 | Ring | ||
| 1 | 2 025 | 1.235 | 1.358 | 1.078 | 1.008 |
| 2 | 1 853 | 1.219 | 1.275 | 1.053 | 1.054 |
| 3 | 1 329 | 1 | 1.137 | 0.906 | 0.897 |
| 4 | 1 237 | 0.937 | 1.082 | 0.828 | 0.831 |
| 5 | 1 126 | 0.875 | 0.897 | 0.781 | 0.774 |
| 6 | 902 | 0.723 | 0.816 | 0.662 | 0.652 |
| 7 | 784 | 0.614 | 0.593 | 0.532 | 0.498 |
| 8 | 522 | 0.359 | 0.341 | 0.328 | 0.307 |
| 9 | 368 | 0.265 | 0.254 | 0.218 | 0.220 |
| 10 | 235 | 0.219 | 0.206 | 0.187 | 0.190 |
表选项
4 结 论本文在建立模值累积梯度方向直方图的统计模型基础上,提出了一种新的SIFT描述子,得到以下结果:
1)实验结果表明基于径向采样网格与边缘积分值的特征描述运算可实现较为优异旋转不变性,例如10°~100°之间的查全率为98%,在全区间的是91%。
2)该运算降低了复杂度,能够实现实时性。
3)提出的特征向量包括较多的非相关成分,匹配可能性较大。
4)特征向量维数较少,会提高图像检索速度。
为使本文提出的算法能处理各种类型的图片,仍需要优化预备工作和检索实现过程的各项参数。
参考文献
| [1] | WU H Y, CAI Z H,WANG Y X.Vision-based auxiliary navigation method using augmented reality for unmanned aerial vehicles[C]//IEEE International Conference on Digital Object Identifier. Piscataway,NJ:IEEE Press,2012:520-525. |
| [2] | KOUSKOURICLAS R, BADEKAS E,GASTERATOS A.Simultaneous visual object recognition and position estimation using SIFT[C]//Proceedings Second International Conference on Intelligent Robotics and Applications.Berlin:Springer-Verlag,2009:866-875. |
| Click to display the text | |
| [3] | ZHENG M G, WU C D,CHEN D Y,et al.Rotation and affine-invariant SIFT descriptor for matching UAV images with satellite images[C]//Proceedings of IEEE Chinese Guidance Navigation and Control Conference.Piscataway,NJ:IEEE Press,2014:2624-2628. |
| [4] | LOWE D G. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110. |
| Click to display the text | |
| [5] | DALAL N, TRIGGS B.Histograms of oriented gradients for human detection[C]//Proceedings of IEEE Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE Press,2005:886-893. |
| Click to display the text | |
| [6] | MIKOLAJCZYK K, SCHMID C.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(10):1615-1630. |
| Click to display the text | |
| [7] | VEDALDI A. An open implementation of the SIFT detector and descriptor:UCLA-CSD-070012[R].Los Angeles:UCLA, 2007. |
| Click to display the text | |
| [8] | ZHAO J,XIN F T. Improved SIFT features in image retrieval using[C]//International Conference on Computer Research and Development.Piscataway,NJ:IEEE Press,2011:393-397. |
| Click to display the text | |
| [9] | MOREL J M, YU G.ASIFT:A new framework for fully affine invariant image comparison[J].SIAM Journal on Imaging Sciences,2009,2(2):438-469. |
| Click to display the text | |
| [10] | TANG H, TANG F.AH-SIFT:Augmented histogram based SIFT descriptor[C]//IEEE International Conference on Image Processing.Piscataway,NJ:IEEE Press,2012:2357-2360. |
| Click to display the text | |
| [11] | WU J,CUI Z,SHENG V S,et al. A comparative study of SIFT and its variants[J].Measurement Science Review,2013,13(3):122-131. |
| Click to display the text | |
| [12] | LOWE D G. Method and apparatus for identifying scale invariant features in an image and use of same for locating an object in an image:US 6711293[P].2004-03-24. |
| Click to display the text | |
| [13] | BROWN M, GANG H,WINDER S.Discriminative learning of local image descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(1):43-57. |
| Click to display the text | |
| [14] | GIL A,MOZOS O M, BALLESTA M,et al.A comparative evaluation of interest point detectors and local descriptors for visual SLAM[J].Machine Vision and Applications,2010,21(6):905-920. |
| Click to display the text | |
| [15] | TAKEZAWA K. Introduction to nonparametric regression[M].Hoboken,NJ:John Wiley & Sons,2006:103-230. |
