由于航空作动器密封环境存在流、固与热相互耦合,现有密封设计理论难以描述其真实情况,受实验手段的限制,也无法真实测量密封机理存在的问题。
密封研究可追溯到1930年[2]。随着计算科学的迅猛发展,利用仿真技术描述工程物理模型成为重要的科研手段[3],很多****利用有限体积法计算往复密封泄漏与摩擦规律。Salant等[4, 5, 6, 7, 8]提出带空化因子的Reynolds方程,利用有限体积法计算O形圈、U形圈、斯特封以及多级密封等密封形式性能,并进行对比;Schmidt等[9]建立O形圈密封面混合润滑理论模型,并利用ABAQUS软件对该模型进行仿真,证明了这种模型描述密封的准确性;ngün等[10]提出用有限元法求解往复密封中存在的轴对称流固耦合、橡胶与不锈钢混合润滑问题。以往****都是针对低压常温范围内的作动器往复密封提出建模方法,缺少复杂环境的作动器密封性能研究。
本文以Trelleborg公司的航空作动器Turcon VL密封结构为研究对象,建立基于混合润滑理论的密封面关系,揭示航空高压、高温及低速对密封性能的影响。
1 建 模如图 1所示,航空作动器密封包括活塞密封(piston seal)和杆密封(rod seal)。杆密封的目的是阻止油液泄漏到环境,与阻止内泄漏的活塞密封相比要求更高。其工作过程包括外冲程(outstroke)和内冲程(instroke)两部分:外冲程时,作动杆受到负载压力作用,容腔(1)内高压,容腔(2)内低压;内冲程时,作动杆受到负载拉力,容腔(1)低压,容腔(2)高压。因此,对于右侧衬套中杆密封,外冲程承受低压,而内冲程承受高压。当作动杆外冲程时,会带出去一部分流体,内冲程时,会带回,在一个作动循环内,流体泄漏量就是带出流体与带回流体量之差[11]。
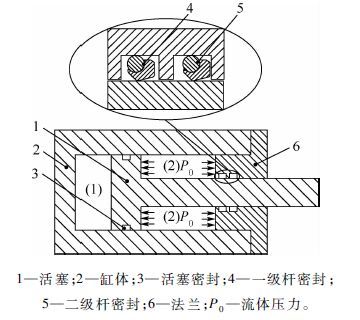 |
| 图 1 航空液压作动器简图 Fig. 1 Sketch of aircraft hydraulic cylinder |
| 图选项 |
往复运动过程中,密封面间不是绝对光滑的,微观织构凸起与作动杆接触,导致密封面间无法产生纯流体润滑,同时存在流体动压润滑与干摩擦[5],如图 2所示。由于密封材料(橡胶与聚四氟乙烯(PTFE))粗糙度比作动杆材料(不锈钢)大很多,因此认为作动杆表面绝对光滑,只考虑密封材料表面粗糙度。设密封面沿x轴坐标接触,接触宽度为L。
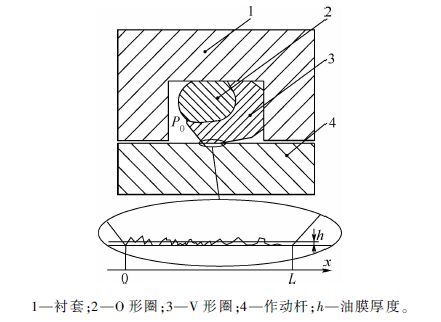 |
| 图 2 密封面接触状态 Fig. 2 Contact state of sealing interface |
| 图选项 |
宏观与微观并存的密封结构有2种建模方法:离线法(off-line method)和在线法(on-line method)[4, 5, 6, 7, 8]。在线法是将宏观与微观的计算一起迭代。而离线法是利用小变形原理:油膜厚度h非常小,与密封材料粗糙度同一数量级,由于h变动不会引起整个密封变形,因此密封整体结构变形提供密封面总压。本文利用离线法对Turcon VL密封进行建模,其工作环境参数见Trelleborg样本[12]。
1.1 宏观接触模型基于接触面小变形理论,利用ANSYS求解密封接触面接触压力Ps(此接触压力由密封宏观几何模型提供,称为宏观接触压力)。选取PLANE183单元作为平面计算单元,网格划分5 709个单元;CONTA169作为接触单元;TARGE172作为目标单元,摩擦系数f=0.1。O形圈材料为丁腈橡胶(NBR),V形圈材料为聚四氟乙烯,作动杆与衬套材料为不锈钢。丁腈橡胶力学性能用Mooney-Rivlin超弹性体模型描述,其二参数简化模型为[13-14]
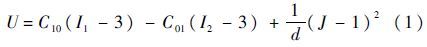
式中:C为偏应变率系数,C10=0.202,C01=6.858;d为体积变化率,d=0.000 11;U为应变能;I1和I2分别为不同方向的偏应变率;J为体积率。
在ANSYS中先将衬套向下挤压密封,在此动作下提取密封面接触压力作为外冲程宏观接触压力;在左端施加流体35 MPa压力,提取此时密封面接触压力作为内冲程宏观接触压力,如图 3所示。
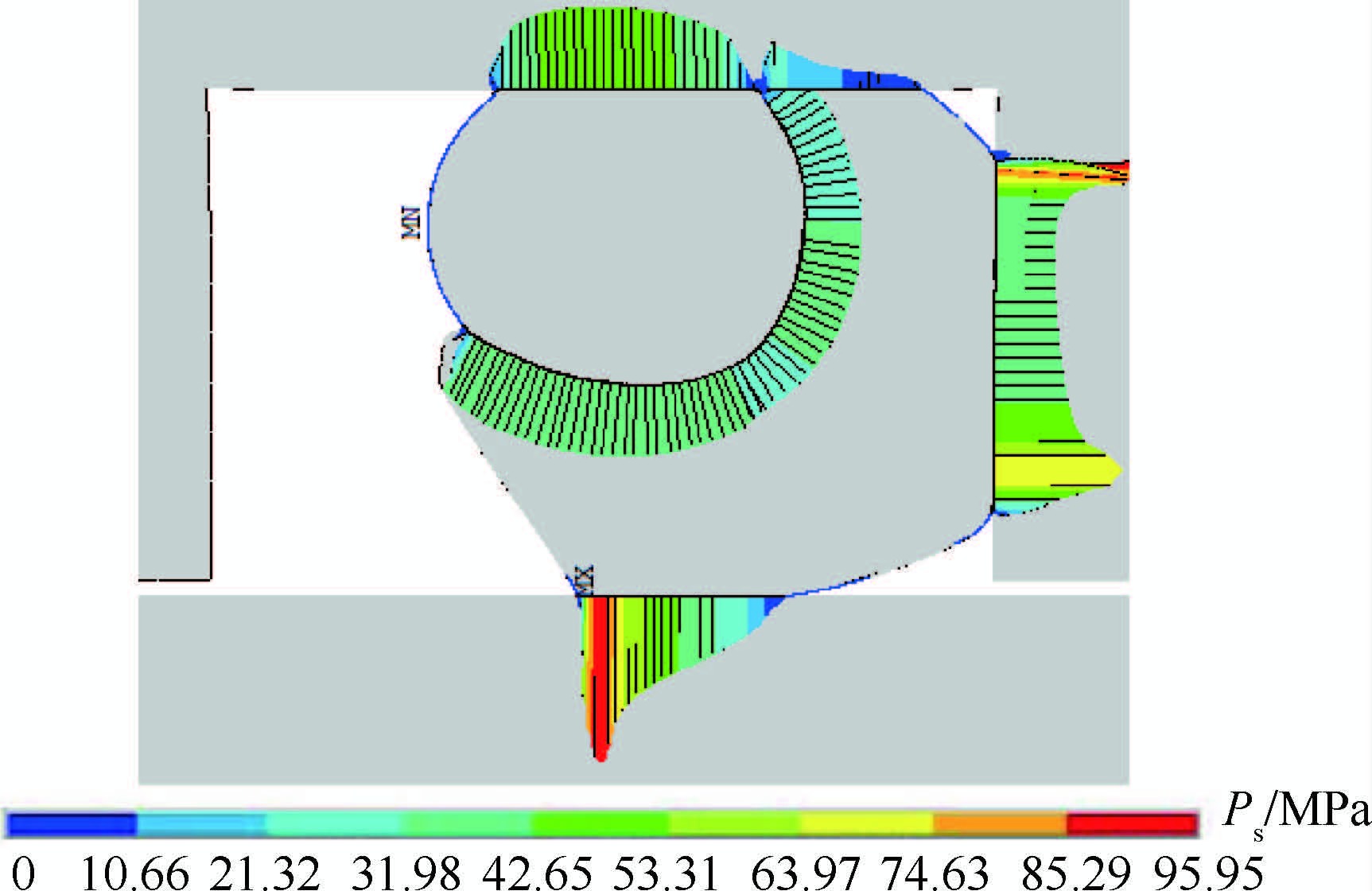 |
| 图 3 Turcon VL密封宏观接触模型 Fig. 3 Macro contact model of Turcon VL seal |
| 图选项 |
1.2 油膜模型密封面润滑油膜运动模型为Reynolds方程[15]:
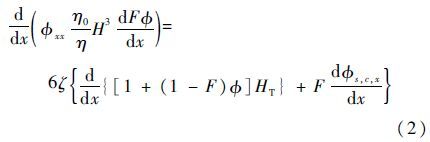
式中:所有参数无量纲,H为膜厚;Φ为流体压力;η为流体实际黏度;η0为参考黏度;ζ为作动杆往复速度;HT为截断膜厚;Φxx为压力流因子;Φs,c,x为剪切流因子[16, 17];F为空化因子,Pl为油膜压力,当Φ<0时,F=0,Pl=0,否则F=1,Pl=Φ。
利用有限体积法计算流体模型,用Jacobi迭代法根据膜厚求解流体压力Φ。根据Φ可求得由流体产生的剪切应力为
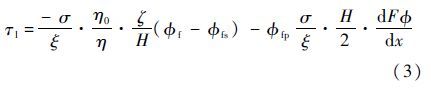
和单次往复循环作动杆带出或带回的流体量为
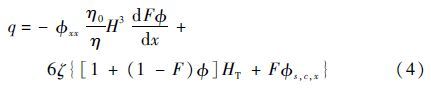
式中:σ为密封表面无量纲RMS粗糙度;ξ为无量纲密封表面特征;Φf、Φfs和Φfp为剪切应力因子。
与密封接触的作动杆直径D=25.4 mm,作动速度v=100 mm/s,液压油参考黏度(25℃)η0=0.043 Pa·s,初始空化因子F=1。
1.3 微观接触模型利用Greenwood-Williamson(G-W)模型作为密封面摩擦接触模型[18],此模型利用Gauss分布简化Hertz模型获得
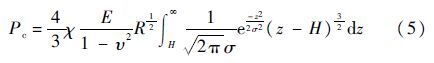
式中:Pc为接触压力; χ为L形圈粗糙凸起密度;σ为RMS粗糙度,σ=0.2 μm;R为粗糙度平均半径,R=1 μm,这3个参数都与其表面形貌有关,通过三维光学表面形貌仪测定;z为接触表面粗糙凸起坐标;E为L形圈弹性模量,E=43 MPa,υ为泊松比,υ=0.499 7。由此可以通过H求解接触压力Pc(由于是与微观粗糙度接触得到,称Pc为微观接触压力),进而求得固体摩擦剪切应力为

式中:f为摩擦系数。
1.4 变形模型聚四氟乙烯弹性模量比不锈钢小很多,因此忽略不锈钢变形。依据小变形理论,忽略聚四氟乙烯材料的非线性特性,用弹性变形理论计算流体压力引起的L形圈变形[19]。
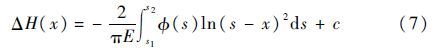
式中:s为x轴上附加坐标;ΔH(x)为橡胶变形引起的油膜厚度变化;c为常数。
1.5 传热模型假设环境温度不变,但往复运动过程中固体、流体摩擦会生热,导致温度升高。不锈钢比聚四氟乙烯传热系数大很多,因此假设热量完全传递到作动杆上。低速运动的传热模型为[20]
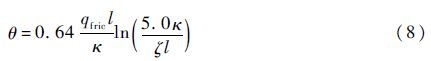
式中:l为作动行程,l=100 mm;κ为传热系数,κ=150 J/m·s;θ为无量纲上升温度;qfric为摩擦产生的热量。

1.6 多场耦合模型固体与流体摩擦产热升温对材料与流体性质有影响,尤其是流体黏度,受到温度和流体压力综合作用
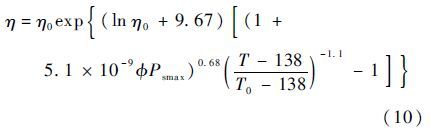
式中:Psmax为最大宏观接触压力;T为油膜中实际温度;T0为参考温度。此外,考虑到油膜压力Pl、微观接触压力Pc以及宏观接触压力Ps的关系:

因此,流体、接触、变形与温度相互耦合。沿x轴方向分94个点,按照图 4流程在MATLAB中将方程离散化并求解,收敛精度为10-3。
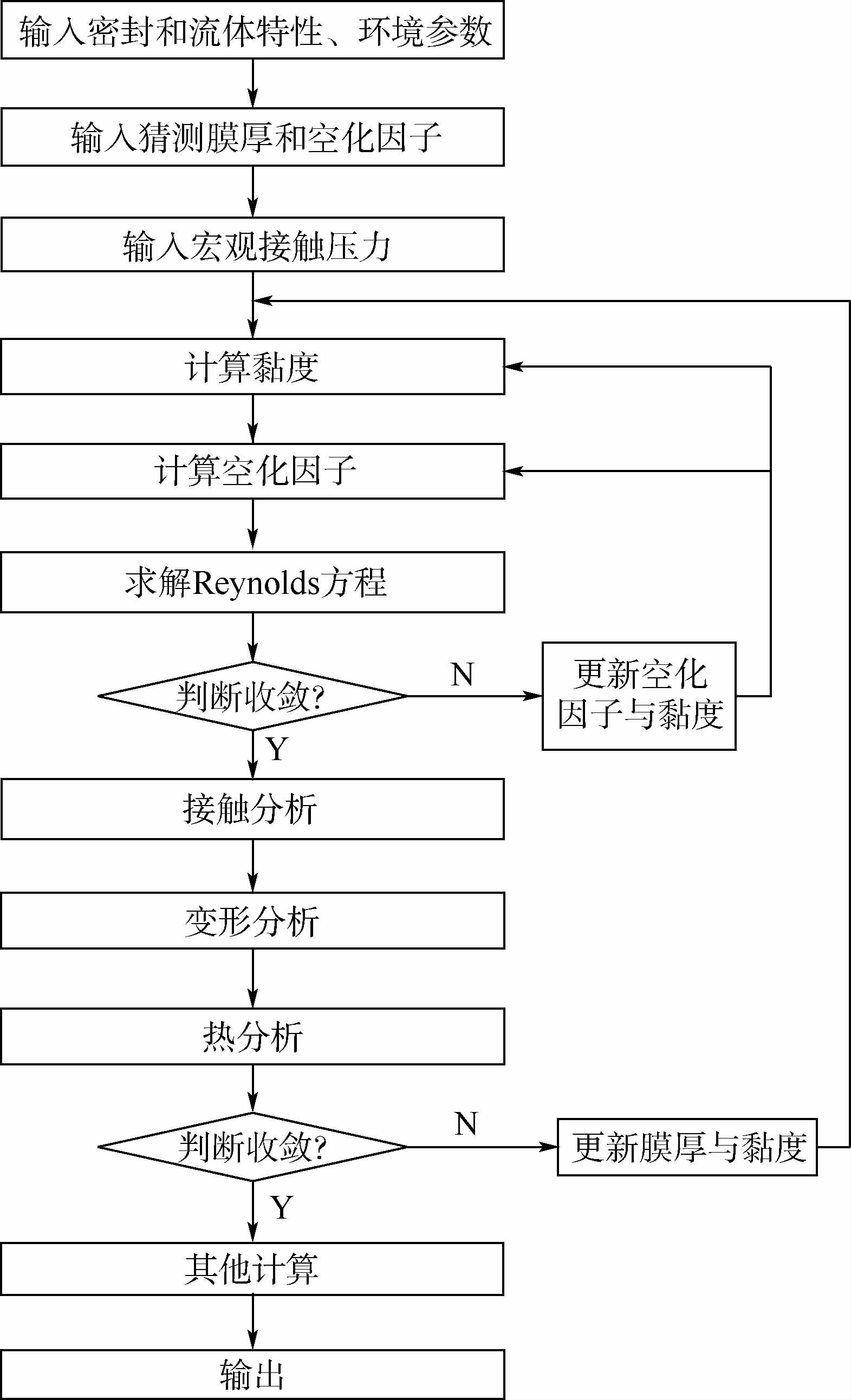 |
| 图 4 计算流程 Fig. 4 Computational procedure |
| 图选项 |
2 航空作动器密封性能分析2.1 压力对作动器密封性能影响高压是航空液压作动器的重要特点,最高压力可达35 MPa。不同流体压力密封状态不同,不仅改变密封形状,还会与温度一起改变流体黏度。
图 5为Turcon VL密封分别于0、10、20和35 MPa 4种流体压力下的密封面宏观接触压力。压力越大,接触宽度越大,接触压力也越大。为方便比较,将接触宽度末端坐标统一。35 MPa压力下宏观接触压力达到92.31 MPa。曲线左边边界条件是流体压力。
 |
| 图 5 不同流体压力下的宏观接触压力 Fig. 5 Macro contact pressures at different fluid pressures |
| 图选项 |
图 6为35 MPa下内冲程宏观接触压力、微观接触压力及油膜压力沿接触宽度分布,此过程满足方程(11),即微观接触压力与流体压力之和等于宏观接触压力。左侧压力边界条件是流体压力。
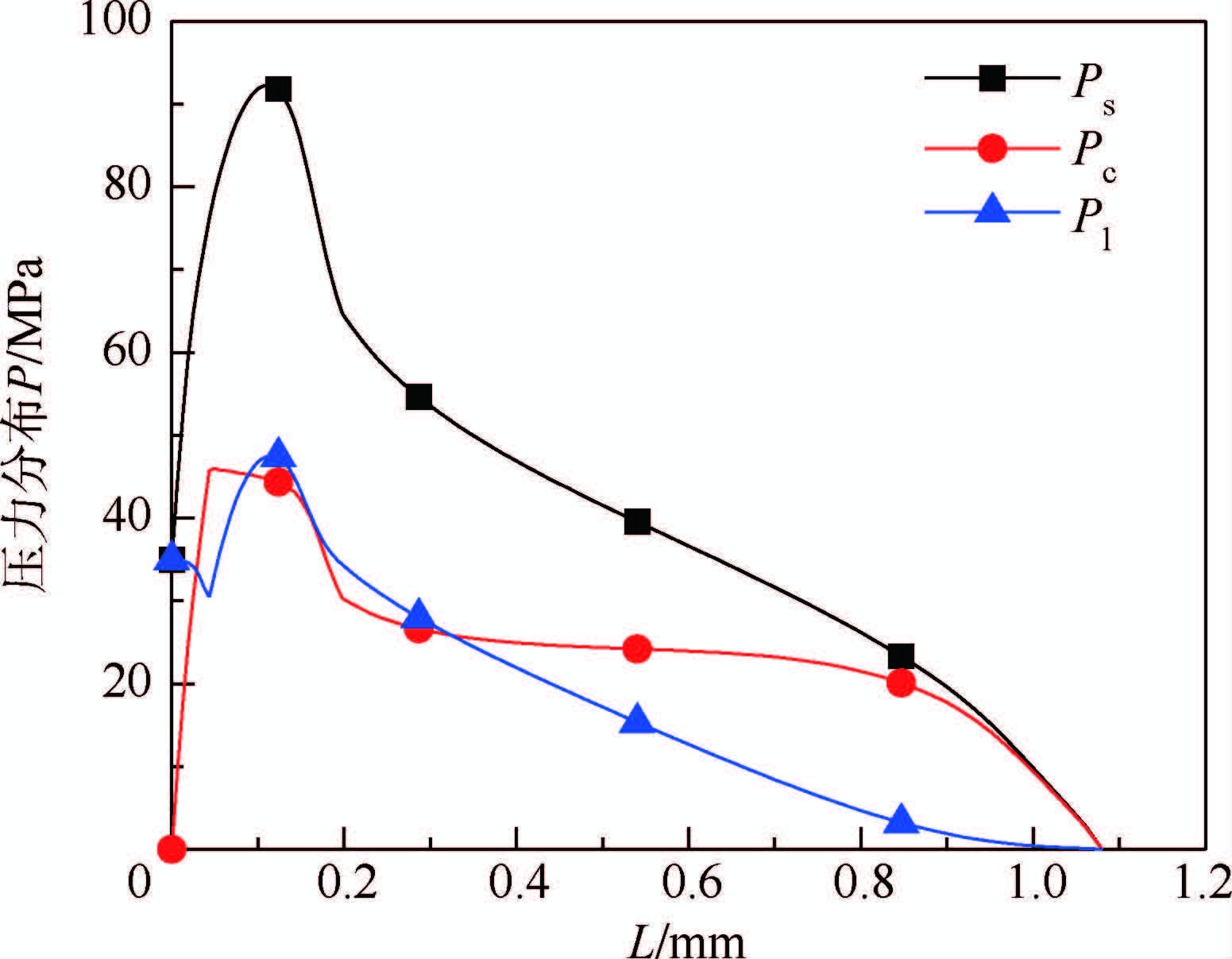 |
| 图 6 35 MPa压力分布(内冲程) Fig. 6 Distribution of pressure 35 MPa (instroke) |
| 图选项 |
图 7为不同流体压力下的油膜压力分布,外冲程流体压力设为0 MPa。理应在内冲程0 MPa和外冲程时出现空化现象,而有压力时不出现空化是由于负压被流体压力补偿,由图 7中下凹尖端可见。空化现象会产生噪声与汽蚀,但由于密封面内空间较小,空化危害不大。与图 5对比看出,油膜压力随流体压力增大而增大。
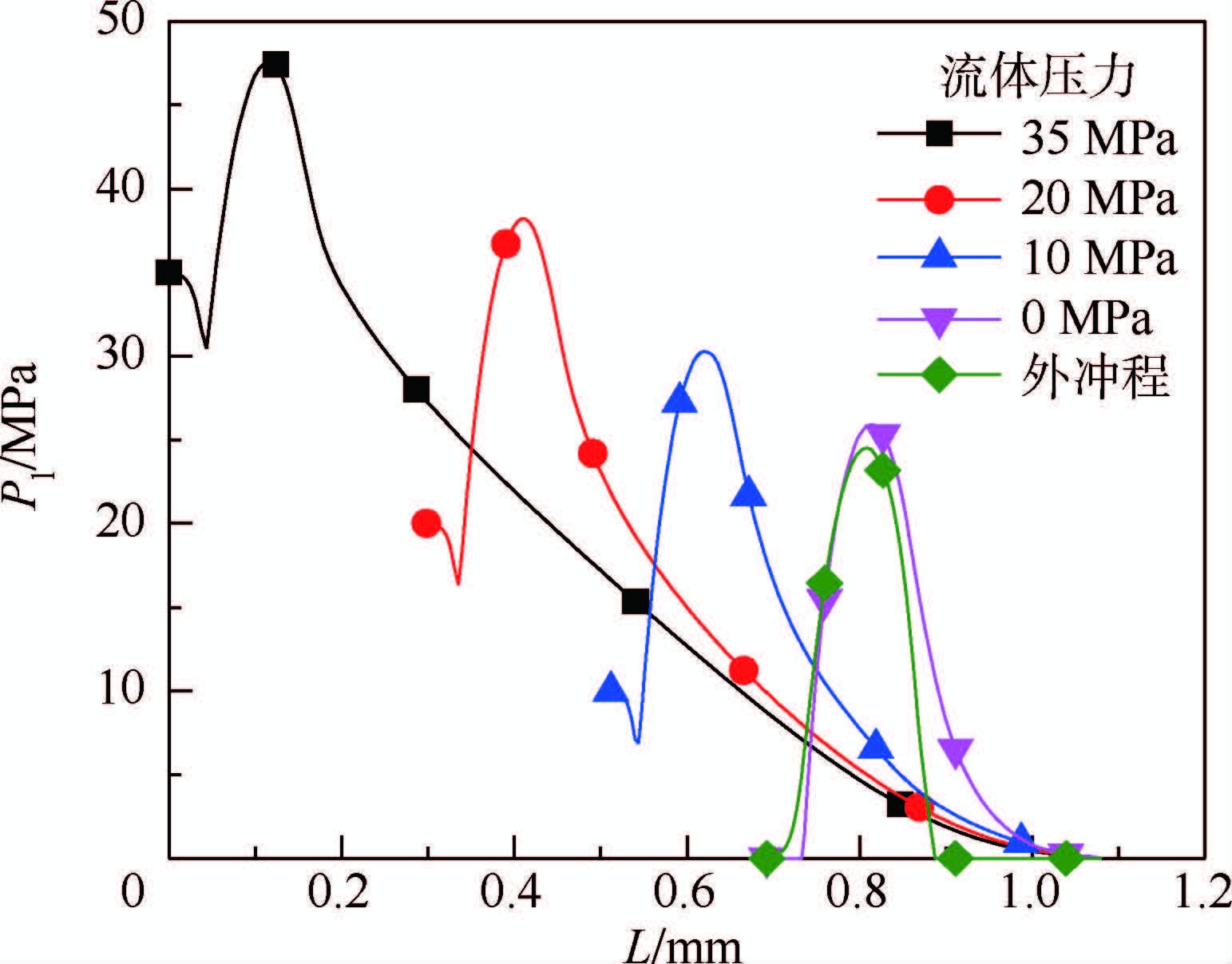 |
| 图 7 不同流体压力下的油膜压力(内冲程) Fig. 7 Oil film pressures at different fluid pressures(instroke) |
| 图选项 |
图 8为不同流体压力下的微观接触压力。不同流体压力下微观接触压力基本相同,由此亦可证明宏观接触压力变化仅影响油膜压力。由于Turcon VL密封结构特点,接触区左端一段微观接触压力大,此段磨损也较严重。图 9为膜厚分布,在其他量确定的情况下,由于G-W摩擦接触模型性质,膜厚与接触压力分布一一对应,由此说明最小膜厚区域是磨损最大区。作动杆带出流体量取决于密封面油膜厚度最小处,此段是Turcon VL密封主要工作区域,也是易磨损区。
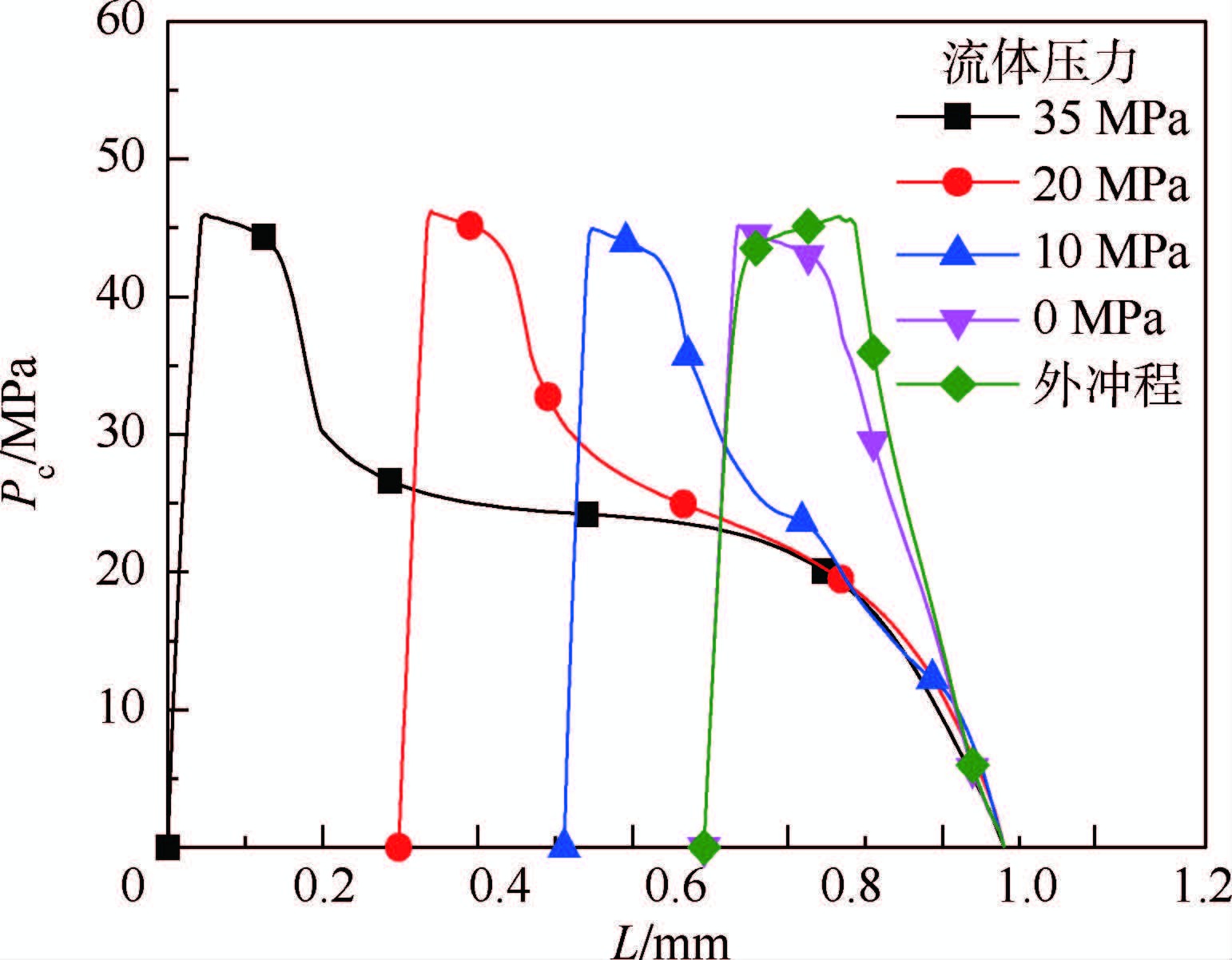 |
| 图 8 不同流体压力下的微观接触压力 Fig. 8 Micro contact pressures at different fluid pressures |
| 图选项 |
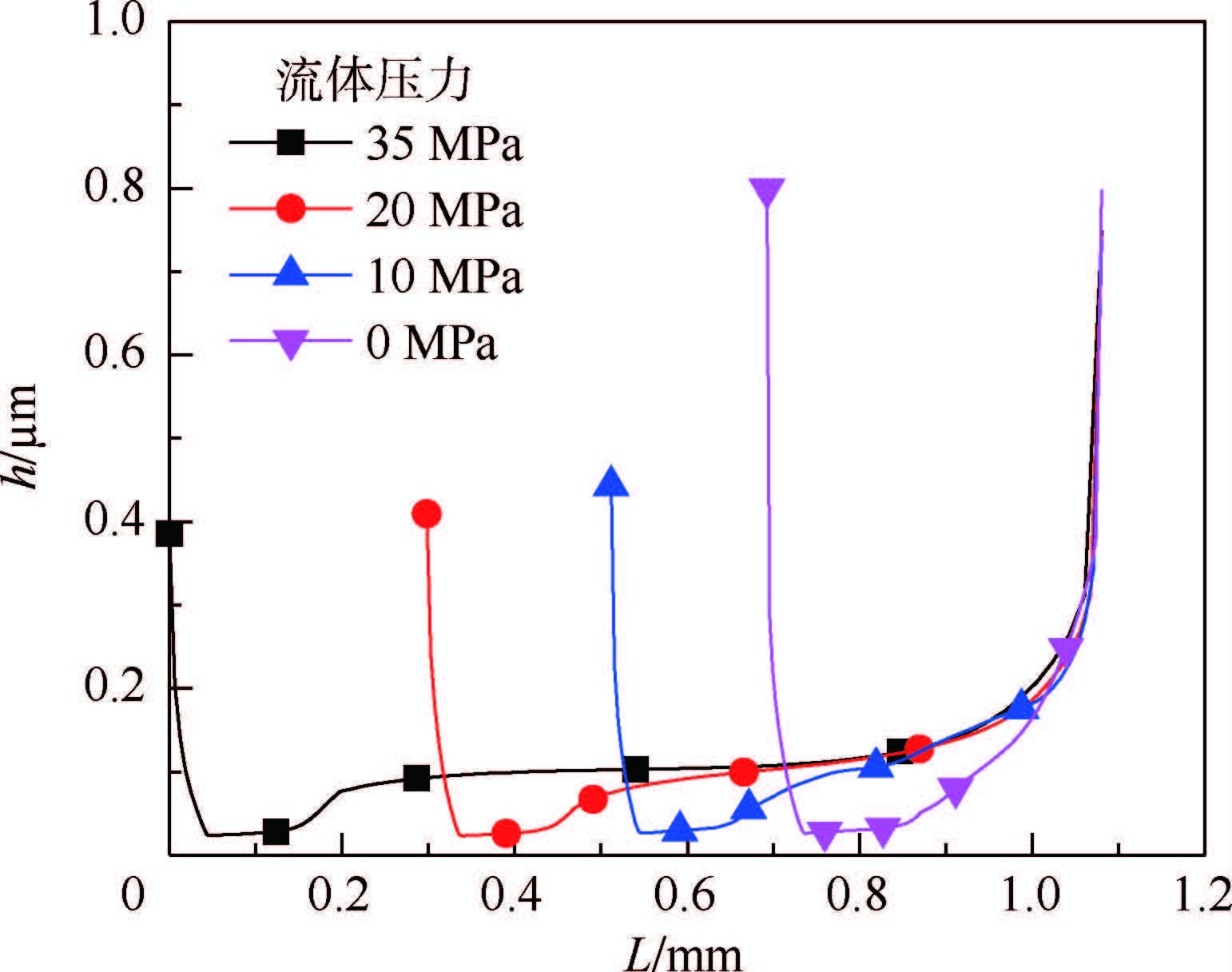 |
| 图 9 不同流体压力下油膜厚度(内冲程) Fig. 9 Oil film thicknesses at different fluid pressures(instroke) |
| 图选项 |
图 10与图 11分别为不同流体压力下Turcon VL密封泄漏量Q与摩擦力Ff。其中,泄漏量表示每个往复循环周期内作动杆带出流体与带回流体之差。 Müller和Nau[11]提到用弹流润滑描述密封特点,若接触压力分布形成不对称三角形,可以利用密封的泵回作用吸回泄漏出的油液而做到零泄漏。但用混合润滑理论描述的密封面力学特征并非如此。如图 10所示,泄漏量随流体压力增大而增大,在无压力和10 MPa压力下,Turcon VL密封泄漏量为负,在20 MPa和35 MPa时,泄漏量为正。由于作动速度小,流体黏度引起的摩擦力很小,摩擦力主要来源于微观接触压力。不同流体压力下摩擦力变化见图 11。由图 8可知,不同流体压力下微观接触压力分布整体相同,但由于流体压力越大,接触宽度越大,因此摩擦力越大。
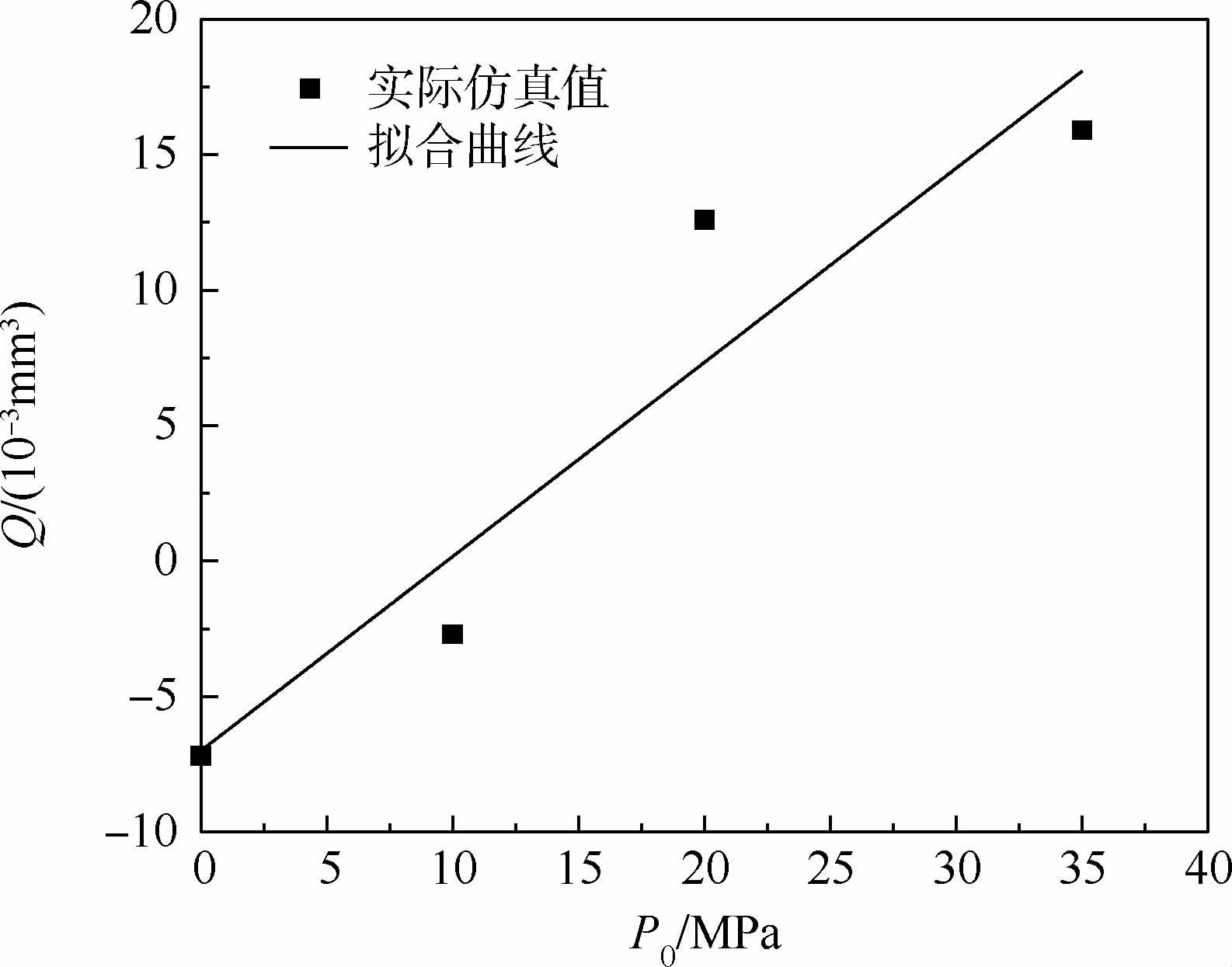 |
| 图 10 不同流体压力下泄漏量 Fig. 10 Leakages at different fluid pressures |
| 图选项 |
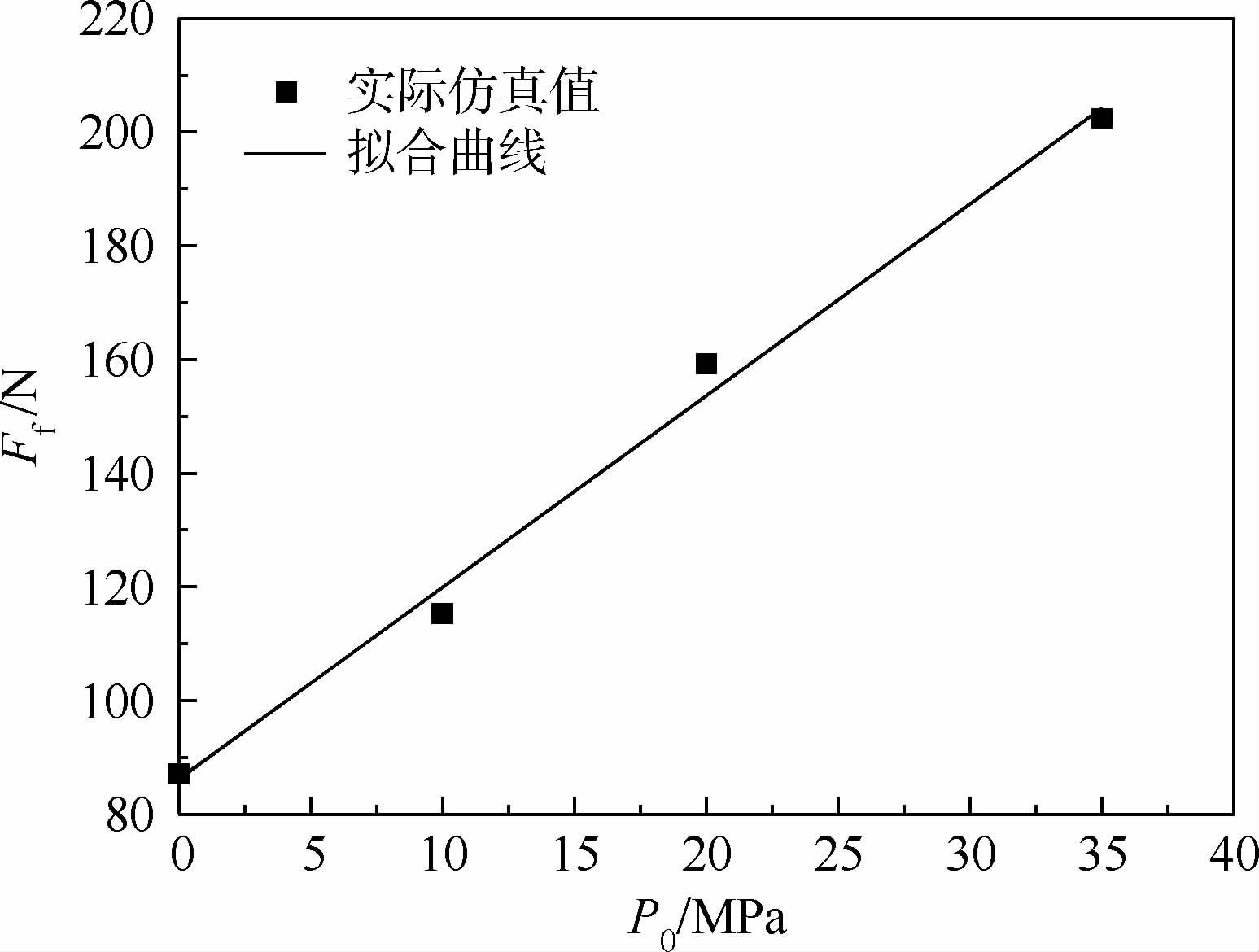 |
| 图 11 不同流体压力下摩擦力 Fig. 11 Frictions at different fluid pressures |
| 图选项 |
2.2 温度对作动器密封性能影响航空往复动密封环境另一特点是宽温,温度范围为-55~135℃。高温对流体黏度影响极大,如方程(10)表示,温度与流体压力共同影响流体黏度。温度越高,流体黏度越低。本文主要分析高温环境引起流体黏度降低对航空往复动密封的影响;而极低温度主要影响密封材料特性,不是本文研究重点。
图 12所示为航空高温(135℃)以及常温(25℃)下密封面内压力对比。高温环境会造成微观接触压力增大而油膜压力降低,油膜承载能力下降,摩擦磨损加剧。由于摩擦主要来自微观接触压力,高温导致摩擦增大,而由于摩擦生热又使温度更高,形成一种正反馈,对密封非常不利。
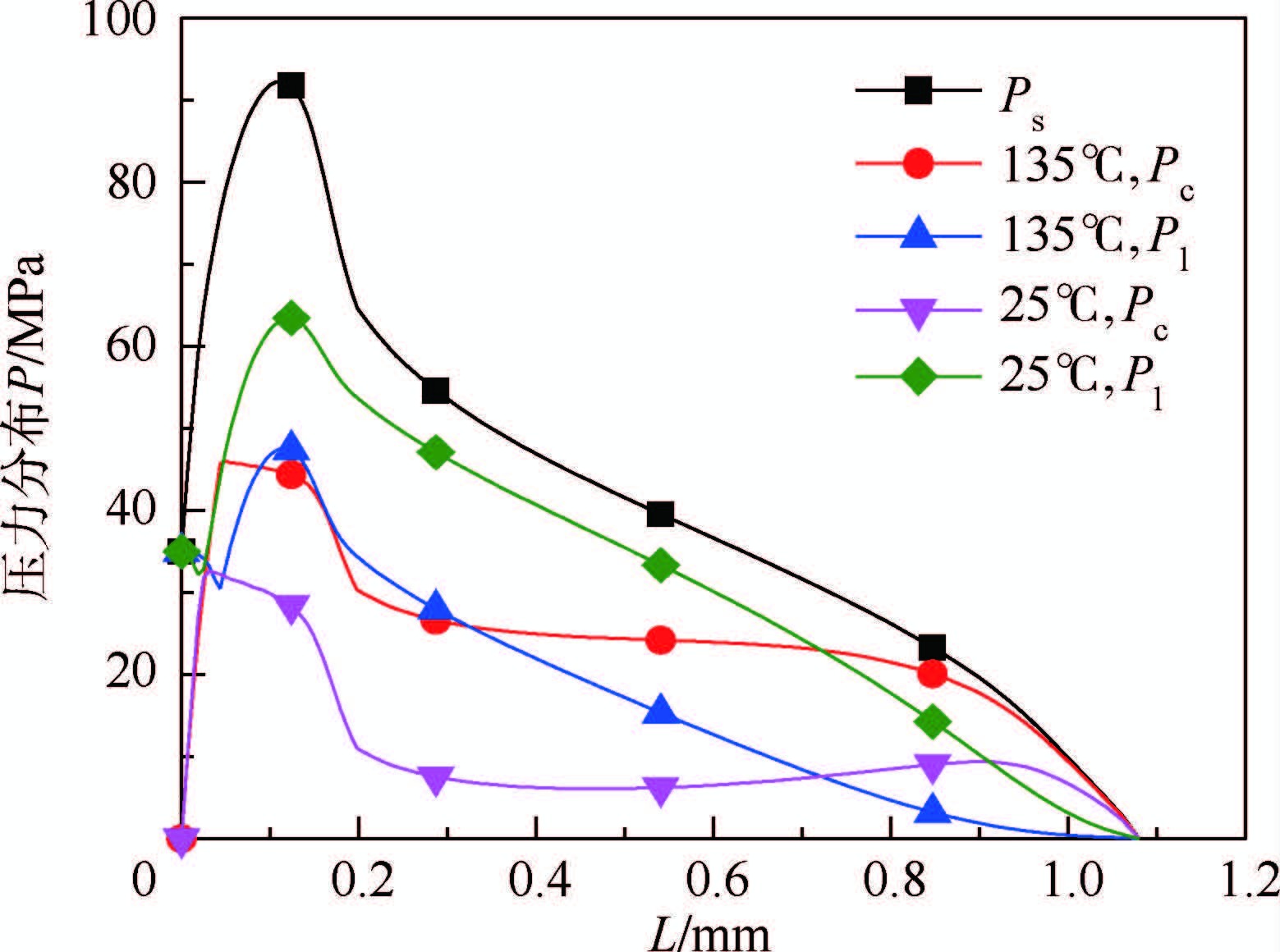 |
| 图 12 高温与常温压力对比(内冲程) Fig. 12 Pressure comparison between high temperature and normal temperature(instroke) |
| 图选项 |
通过计算获得135℃下内外冲程作动杆与密封面间摩擦力分别为202.37 N和227.41 N,25℃下内外冲程摩擦力分别为153.15 N和232.27 N。对比可知,高温令摩擦磨损严重。
图 13所示为不同温度密封面间油膜厚度,25℃下油膜厚度是135℃的2倍多。油膜厚度和流体黏度同时影响密封泄漏。若流体黏度不变,则油膜厚度越大,泄漏量越大。但若黏度增大,泄漏量将减小,因此必须综合考虑确定密封泄漏量。135℃下每次往复循环泄漏量为0.002 7 mm3,而25℃下为-0.014 2 mm3,即不泄漏。
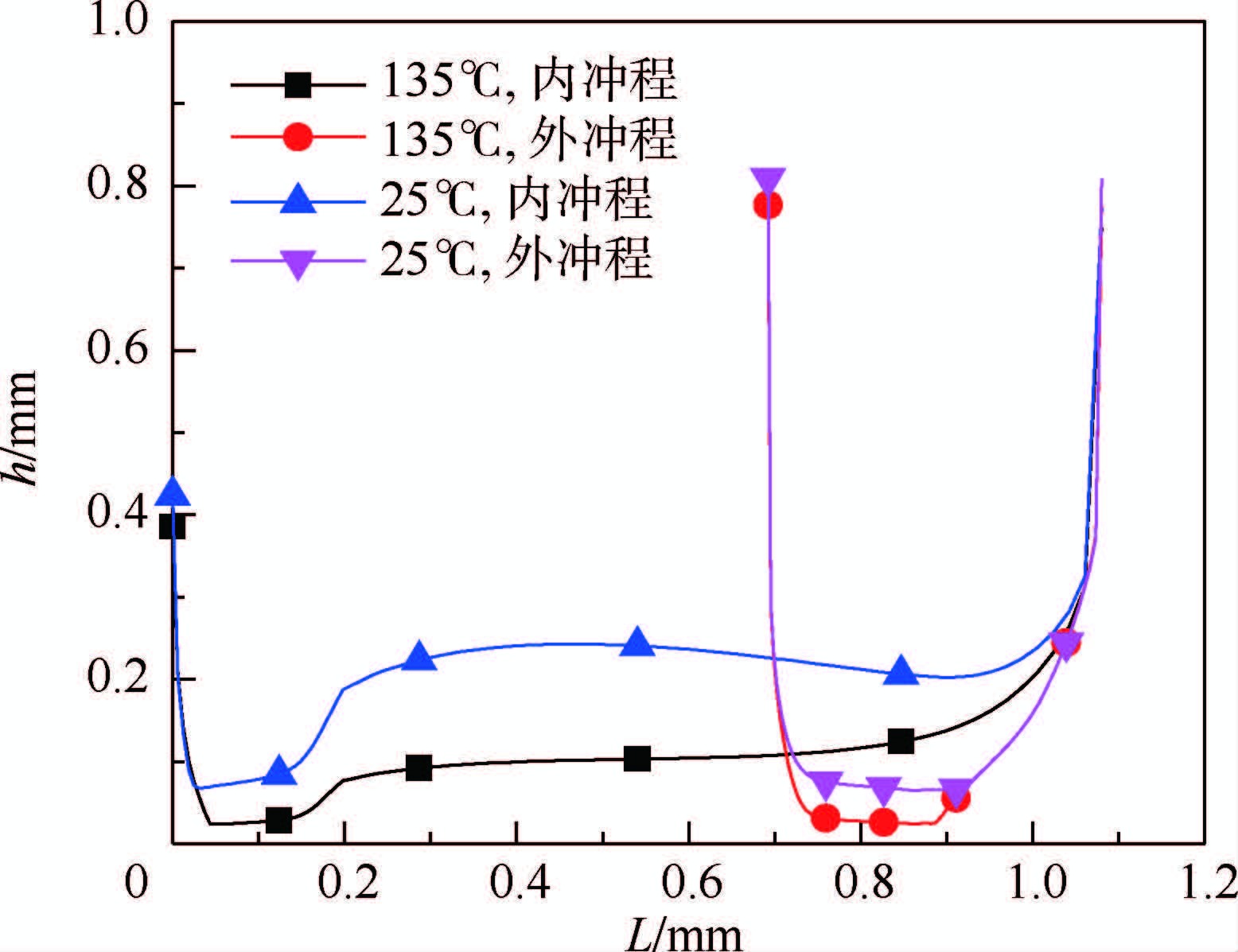 |
| 图 13 高温与常温油膜厚度对比 Fig. 13 Oil film thickness comparison between high temperature and normal temperature |
| 图选项 |
2.3 作动速度对作动器密封性能影响除压力和温度外,作动速度对密封性能也有一定影响,因为运动速度直接影响密封面间油膜形成能力,而油膜压力与厚度决定密封泄漏量与摩擦力。
图 14为不同作动速度下内外冲程分别形成的油膜厚度。很明显,作动速度越快,油膜厚度越大,0.2 m/s作动速度是0.01 m/s的2倍左右,主要是由于动压支承作用的结果。
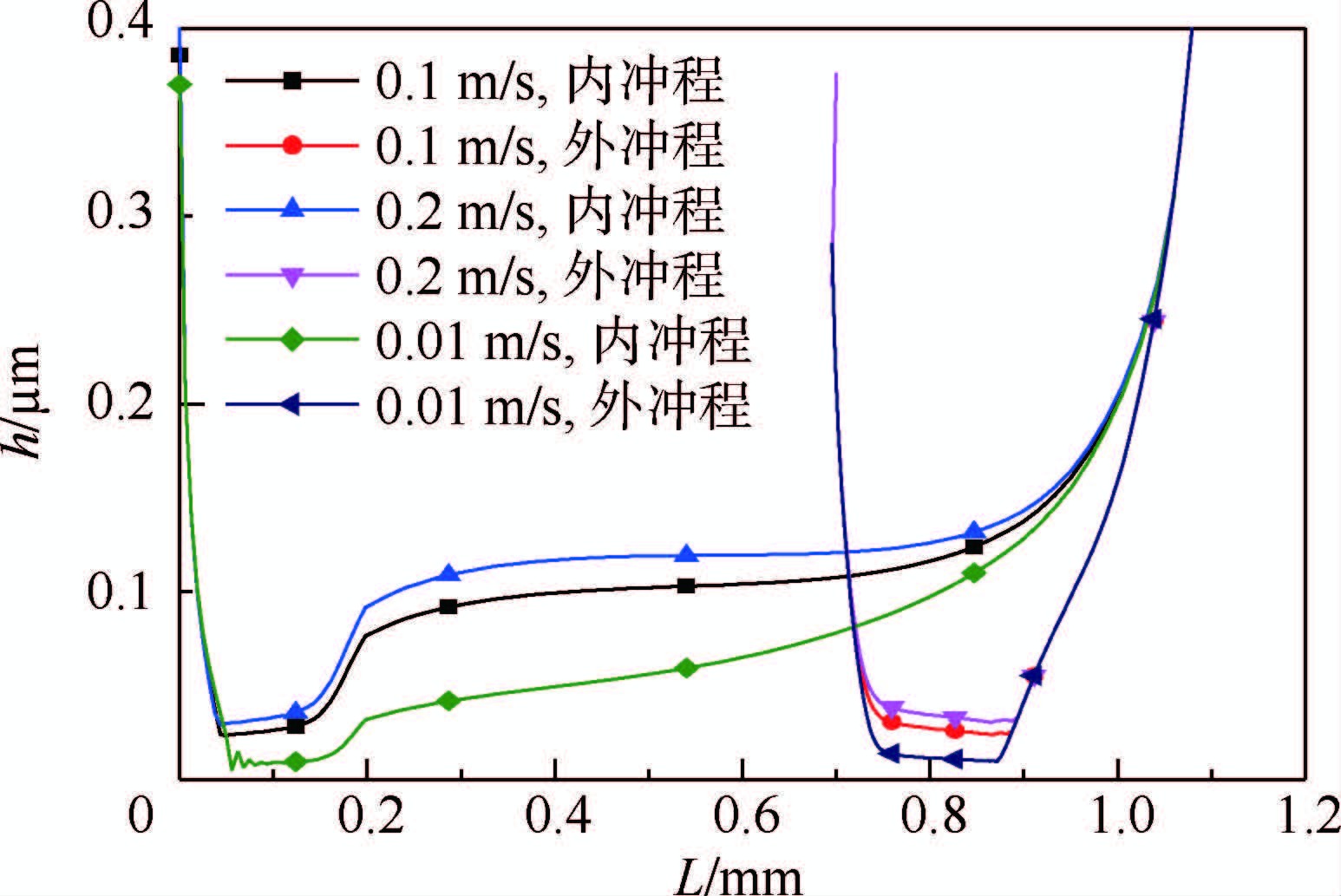 |
| 图 14 不同作动速度下油膜厚度对比 Fig. 14 Oil film thickness comparison among different velocities |
| 图选项 |
图 15所示为不同作动速度下泄漏量对比。随着作动速度增加,泄漏量也增加,且增加量逐渐递减。主要原因是由于作动速度增大,油膜厚度增大,跟随作动杆运动的油液增多。
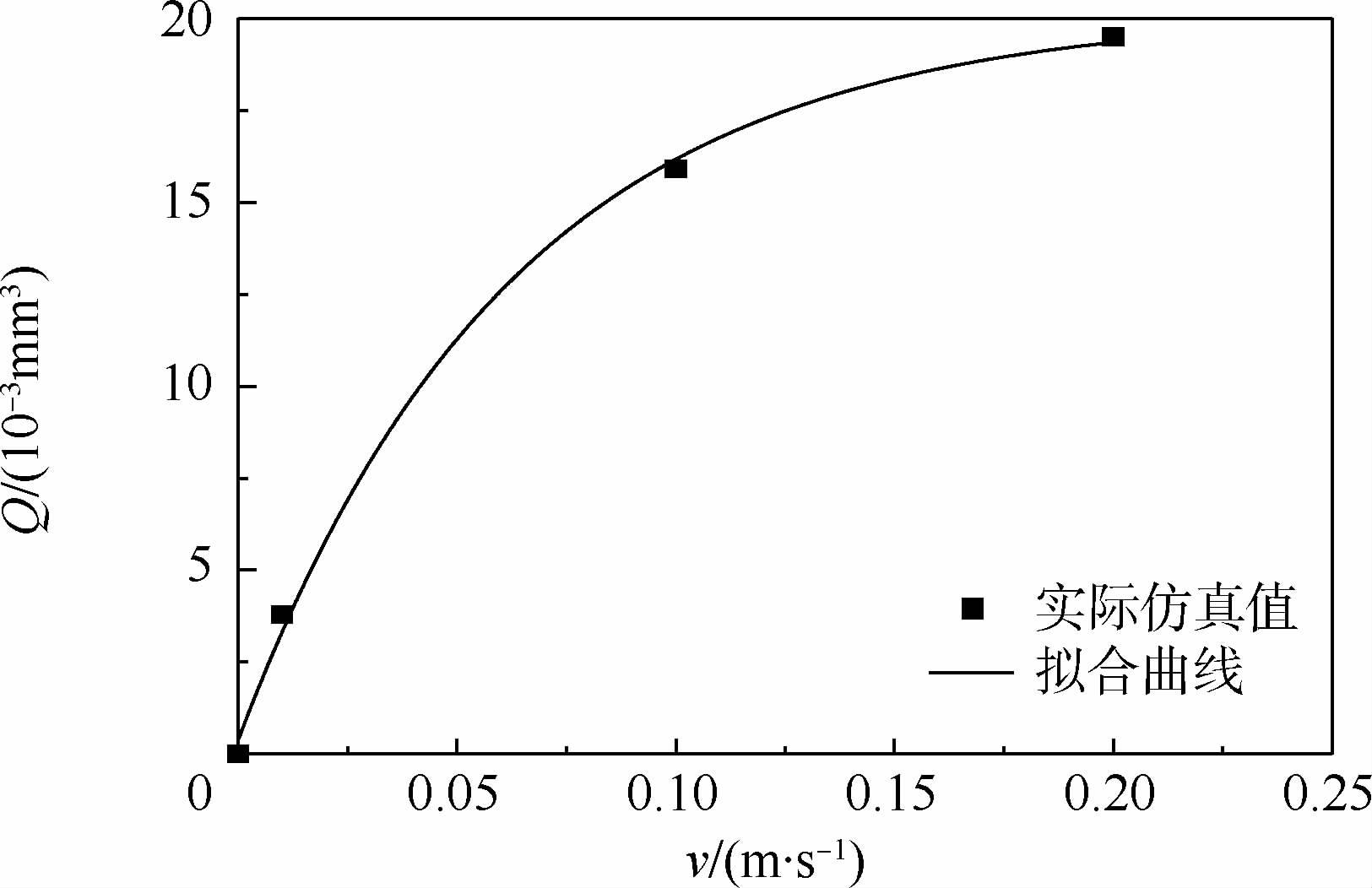 |
| 图 15 不同作动速度下泄漏量对比 Fig. 15 Leakage comparison among different velocities |
| 图选项 |
图 16所示为不同作动速度下密封与作动杆间摩擦力。随作动速度增大,摩擦力减小,即摩擦磨损减小。由此可知,在航空作动器中,低速作动由于油膜较薄会加快密封磨损。
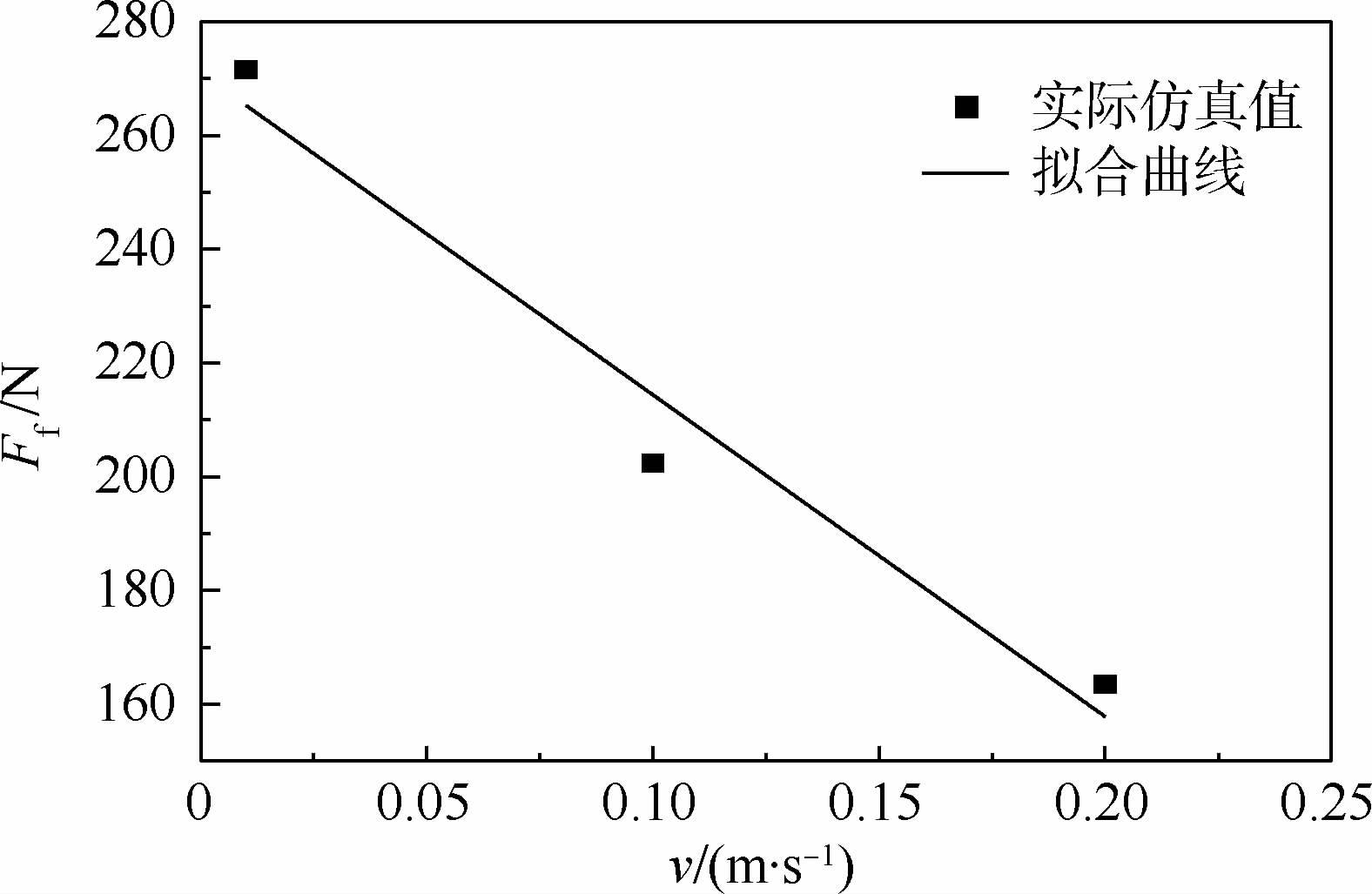 |
| 图 16 不同作动速度下摩擦力对比 Fig. 16 Friction comparison among different velocities |
| 图选项 |
3 结 论基于混合润滑模型,分别在高压、高温以及不同作动速度下对Turcon VL密封进行分析:
1) 高压降低密封性能,增大泄漏且加剧摩擦磨损,缩短密封寿命。因此压力越高,对密封挑战越大。
2) 高温通过降低流体黏度,大幅增加泄漏且加剧摩擦磨损。高温与摩擦生热效应形成正反馈,使工作温度更高,密封效果更差。
3) 高速作动会导致泄漏量增多,而低速作动不易形成油膜,摩擦加大。在航空作动器启动与停机时,摩擦最大,磨损最严重,而作动速度提升后泄漏量会有增大。
参考文献
| [1] | 王占林. 飞机高压液压能源系统[M].北京:北京航空航天大学出版社,2004:2-3. WANG Z L.The aircraft high pressure hydraulic energy system[M].Beijing:Beihang University Press,2004:2-3(in Chinese). |
| [2] | NIKAS G K. Eighty years of research on hydraulic reciprocating seals:Review of tribological studies and related topics since the 1930s[J].Journal of Engineering Tribology,2010,224(1):1-23. |
| Click to display the text | |
| [3] | NAU B S. An historical review of studies of polymeric seals in reciprocating hydraulic systems[J].Journal of Engineering Tribology,1999,213(3):215-226. |
| Click to display the text | |
| [4] | YANG B,SALANT R F.Elastohydrodynamic lubrication simulation of O-ring and U-cup hydraulic seals[J].Journal of Engineering Tribology,2011,225(7):603-610. |
| Click to display the text | |
| [5] | SALANT R F,MASER N,YANG B.Numerical model of a reciprocating hydraulic rod seal[J].Journal of Tribology,2007,129(1):577-583. |
| [6] | YANG B,SALANT R F.Numerical model of a reciprocating rod seal with a secondary lip[J].Tribology Transactions,2008,51(2):119-127. |
| Click to display the text | |
| [7] | YANG B,SALANT R F.Numerical model of a tandem reciprocating hydraulic seal[J].Journal of Tribology,2008,130(3):032201-1-032201-7. |
| Click to display the text | |
| [8] | YANG B,SALANT R F.Soft EHL simulations of U-cup and step hydraulic seals[J].Journal of Tribology,2009,131(2):021501-1-021501-10. |
| Click to display the text | |
| [9] | SCHMIDT T,ANDRE M,POLL G.A transient 2D-finite-element approach for the simulation of mixed lubrication effects of reciprocating hydraulic rod seals[J].Tribology International,2010,43(10):1775-1785. |
| Click to display the text | |
| [10] | ÖNGVN Y,ANDRÉ M,BARTEL D,et al.An axisymmetric hydrodynamic interface element for finite-element computations of mixed lubrication in rubber seals[J].Journal of Engineering Tribology,2008,222(3):471-481. |
| Click to display the text | |
| [11] | MVLLER H K,NAU B S.Fluid sealing technology principles and applications[M].New York:Marcel Dekker Inc.,1998:112-117. |
| [12] | TRELLEBORG. Airspace sealing systems[EB/OL].[2015-03-12].http://tss-static.com/remotemedia/media/globalformastercontent/downloadsautomaticlycreatedbyscript/catalogs/aerospace_gb_en.pdf. |
| Click to display the text | |
| [13] | ANSYS Inc. ANSYS elements reference[Z].ANSYS Release 15.0.2014. |
| [14] | TRELOAR L R G. The physics of rubber elasticity[M].New York:Oxford University Press,1975:65-74. |
| [15] | PAYVAR P,SALANT R F.A computational method for cavitation in a wavy mechanical seal[J].Journal of Tribology,1992,114(1):199-204. |
| Click to display the text | |
| [16] | PATIR N,CHENG H S.An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J].Journal of Tribology,1978,100(1):12-17. |
| Click to display the text | |
| [17] | PATIR N,CHENG H S.Application of average flow model to lubrication between rough sliding surfaces[J].Journal of Tribology,1979,101(2):220-229. |
| [18] | GREENWOOD J A,WILLIAMSON J B P.Contact of nominally flat rough surfaces[J].Proceedings of the Royal Society A,1966,295(1442):300-319. |
| Click to display the text | |
| [19] | 黄平. 润滑数值计算方法[M].北京:高等教育出版社,2012:137-140. HUANG P.The numerical calculation method of lubrication[M].Beijing:Higher Education Press,2012:137-140(in Chinese). |
| [20] | BHUSHAN B. Principles and applications of tribology[M].New York:Wiley,1999:407-408. |
| [21] | 温诗铸,黄平.摩擦学原理[M].4版.北京:清华大学出版社,2012:10-11. WEN S Z,HUANG P.Principle of tribology[M].4th ed.Beijing:Tsinghua University Press,2012:10-11(in Chinese). |
