螺栓连接结构具有构造简单、可操作性好等特点^[1],因此在机械结构系统中被广泛应用,如航空发动机机匣和转子的连接^{[2, 3]}.近年来,航空发动机不断向高转速、高推重比发展,使得螺栓连接结构对整机模型动力特性影响越来越大.从20世纪80年代开始,美国NASA报告^[4]和Sandia实验室白皮书^[5]就有关于螺栓连接结构的研究内容.可见,螺栓连接结构建模方法研究一直是结构动力学研究领域的热点问题^{[6, 7, 8]}.
起初,人们将螺栓连接结构接触面设置为刚性连接,忽略所有接触面对整体结构的影响,这样处理使得结构刚度增加从而影响其动力学特性.随着有限元法和接触理论的发展,Liu等^{[2, 3, 9]}建立了三维实体有限元模型,即精细有限元模型.该模型保留了结构的几何特征,需使用较小的单元尺寸进行网格划分,从而导致模型自由度数目庞大,因此在航空发动机整机建模中不宜采用.为了降低问题规模,Ahmadian等^{[10, 11]}利用弹簧、阻尼单元对螺栓连接结构进行建模,并通过试验结果对刚度、阻尼系数进行修正,但是这些方法均将螺栓连接结构面—面接触简化为点—点接触而且忽略了剪切刚度,因此运用到复杂机械模型中仍存在困难,特别是在航空发动机螺栓连接结构建模中,上述方法均存在局限性.
在复杂机械连接结构中,Ahmadian等^[12]运用薄层单元法^{[13, 14]}对AWE-MACE机构中的连接部位进行动力学建模,将连接结构面—面接触等效为厚度很薄的实体单元,并运用优化算法结合模态试验结果对薄层单元材料参数进行修正;马双超等^[15]将薄层单元法运用到航空发动机领域,对静子机匣焊接部位进行动力学建模,并运用模态试验结果对材料参数进行动力学修正.由此可知,薄层单元能够模拟复杂机械中的连接结构并保持结构完整性,但薄层单元法还未应用到航空发动机螺栓连接结构建模领域中,更没有从最基本的力学原理出发给出航空发动机螺栓连接结构薄层单元法建模原理、薄层单元材料参数理论推导以及应用前景.
因此,本文以薄层单元法为基础,探讨航空发动机螺栓连接结构薄层单元建模原理,确定薄层单元相关材料参数,并与精细有限元模型结果进行对比,从而验证薄层单元法的正确性和应用前景.
1 薄层单元法建模原理图 1所示为某航空发动机典型螺栓连接,其中包括两个部件间的连接,如进气机匣与风扇机匣螺栓连接(图 1(a))和加力扩散器与加力筒体螺栓连接(图 1(b)),以及多个部件间的连接,如燃烧室后套壁、低压涡轮机匣与涡轮后承力框架螺栓连接(图 1(c)).根据结构主要承载方式及连接件定位要求的不同,航空发动机螺栓连接可以分为以下3种形式:①普通螺栓连接;②带止口螺栓连接;③精密螺栓连接,详细分类如表 1所示.这3种连接形式有其共同点:①均带有法兰安装边;②螺栓连接的构件多为薄壁圆筒;③承受载荷主要为轴向载荷、弯矩、横向载荷和扭矩.因此根据共同点可将其简化为短粗薄壁圆筒螺栓连接结构(见图 2)作为分析模型.

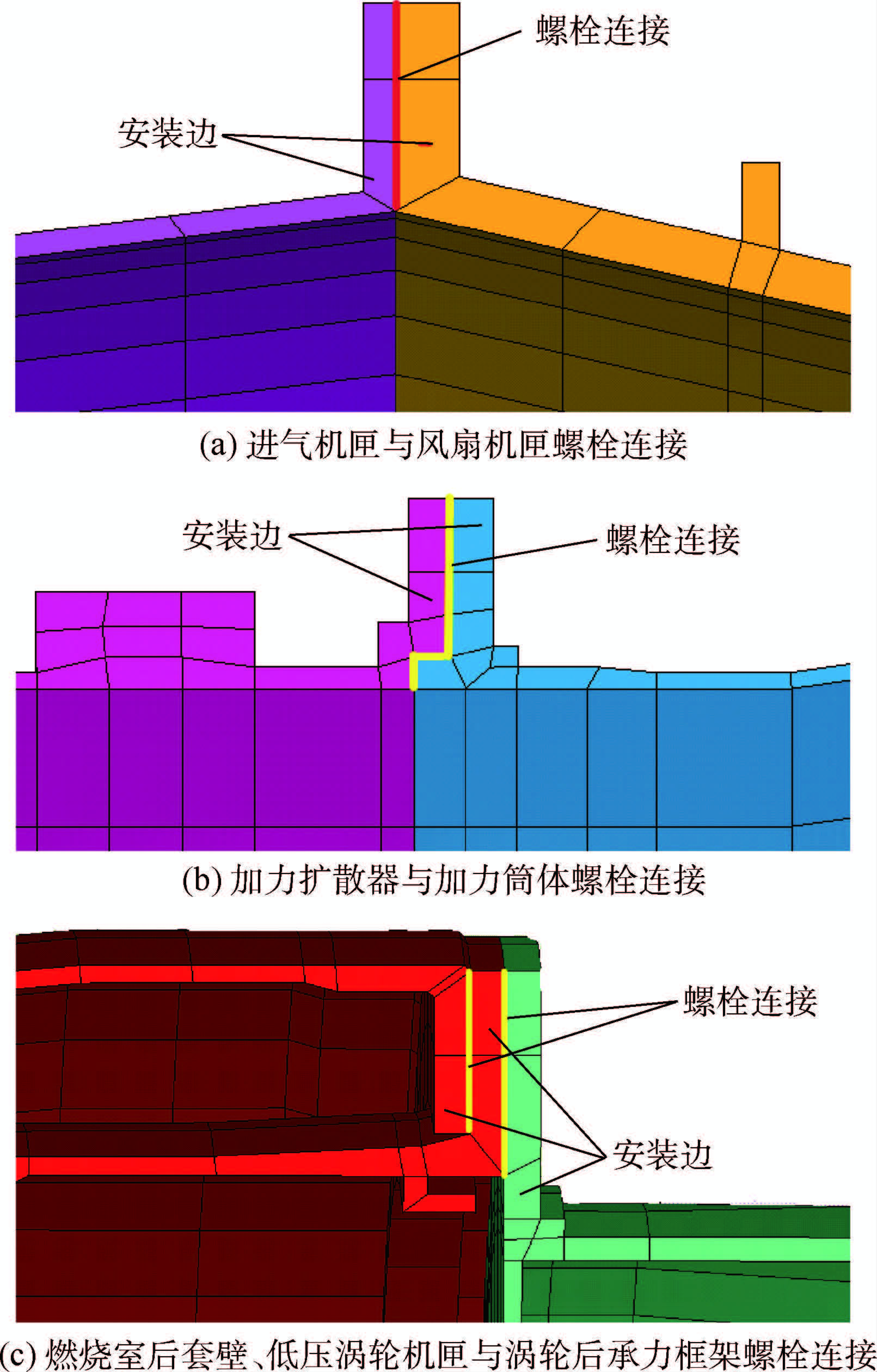图 1 某航空发动机典型螺栓连接结构 Fig. 1 Typical aero-engine bolted joints structure

图选项

图 2 薄壁圆筒螺栓连接结构 Fig. 2 Bolt joints thin-walled cylinder structure

图选项

表 1 航空发动机螺栓连接分类Table 1 Classification of aero-engine bolted joints

螺栓类型	普通 螺栓连接	带止口 螺栓连接	精密 螺栓连接
特殊结构	无	止口	在螺杆与 螺孔间无空隙
定位要求	低	一般	高
承载切向载荷方式	安装边 接触面摩擦	止口	螺杆与螺孔挤压
承载切向载荷大小	小	大	大
是否承载轴向载荷	是	是	是
是否承载弯曲载荷	是	是	是

表选项


当螺栓预紧力足够大或者外界激励幅值相对小时^{[13, 6]},可以忽略螺栓连接处的非线性性质并将其线性化.航空发动机螺栓连接在结构装配、组装和定位起重要作用,而且为了尽可能减小螺栓连接带来的刚度损失,经常使用带止口螺栓连接^{[2, 3]}和精密螺栓连接并使用较大预紧力进行预紧,因此忽略航空发动机螺栓连接结构的非线性,运用薄层单元法对航空发动机螺栓连接进行参数化建模,考虑3个刚度作用,即轴向刚度、弯曲刚度、剪切刚度.首先介绍薄层单元法有限元计算方程的形成过程,然后给出螺栓连接结构轴向、弯曲、剪切刚度的数学表达形式,最后进行小结.
1.1 薄层单元法有限元计算方程形成薄层单元可用通用四面体或六面体单元生成.假设薄层单元为8节点六面体实体单元,节点坐标系为笛卡儿坐标系.8节点六面体实体单元中任一点位移坐标(x,y,z)与节点坐标(x_i,y_i,z_i)的关系可表示为
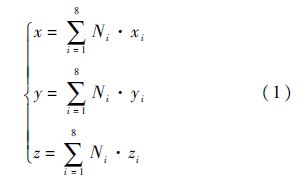
式中：N_i为形函数.
根据弹性力学基本方程,单元应变(ε)、单元应力(σ)与节点(a)的关系为
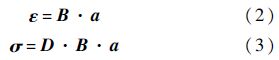
式中：B为几何矩阵；D为弹性矩阵.
忽略螺栓连接结构对接面各方向耦合刚度^{[16, 17]},则弹性矩阵为
式中:c₁₁、c₂₂、c₃₃为3个方向的弹性模量;c₄₄、c₅₅、c₆₆为3个平面的剪切模量,弹性矩阵所在坐标与节点坐标系一致.
根据虚功原理,单元刚度矩阵为
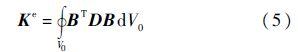
式中：V₀为有限元单元的体积.
集合单元刚度矩阵K^e和节点力向量F^e形成螺栓连接结构刚度矩阵K和节点载荷向量F,得到静力学有限元计算方程:

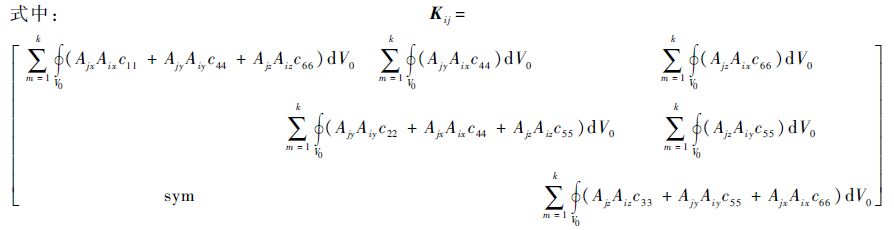
其中：i,j=1,2，…,n；∂N_i/∂x=A_ix；∂N_i/∂y=A_iy；∂N_i/∂z=A_iz；k≤8为某节点所在单元的个数.结构刚度矩阵K是3n×3n阶矩阵,包括了薄层单元和非薄层单元.
对于薄层单元厚度的选择,Desai等^{[14, 15, 18]}都对其进行了研究.结果表明,如果不考虑界面的附加质量和阻尼,厚度的影响会很小.下面给出螺栓连接结构轴向、弯曲和剪切刚度的数学表达形式.
1.2 轴向刚度螺栓连接结构轴向刚度定义如图 3所示,假设薄壁圆筒一端固定,另一端在圆筒中心节点j上施加轴向载荷F_N,其中x为轴向方向,y、z代表薄壁圆筒结构横向方向.结构的轴向位移Δl_x由节点i的轴向位移值X_i表示,则螺栓连接结构轴向刚度定义为

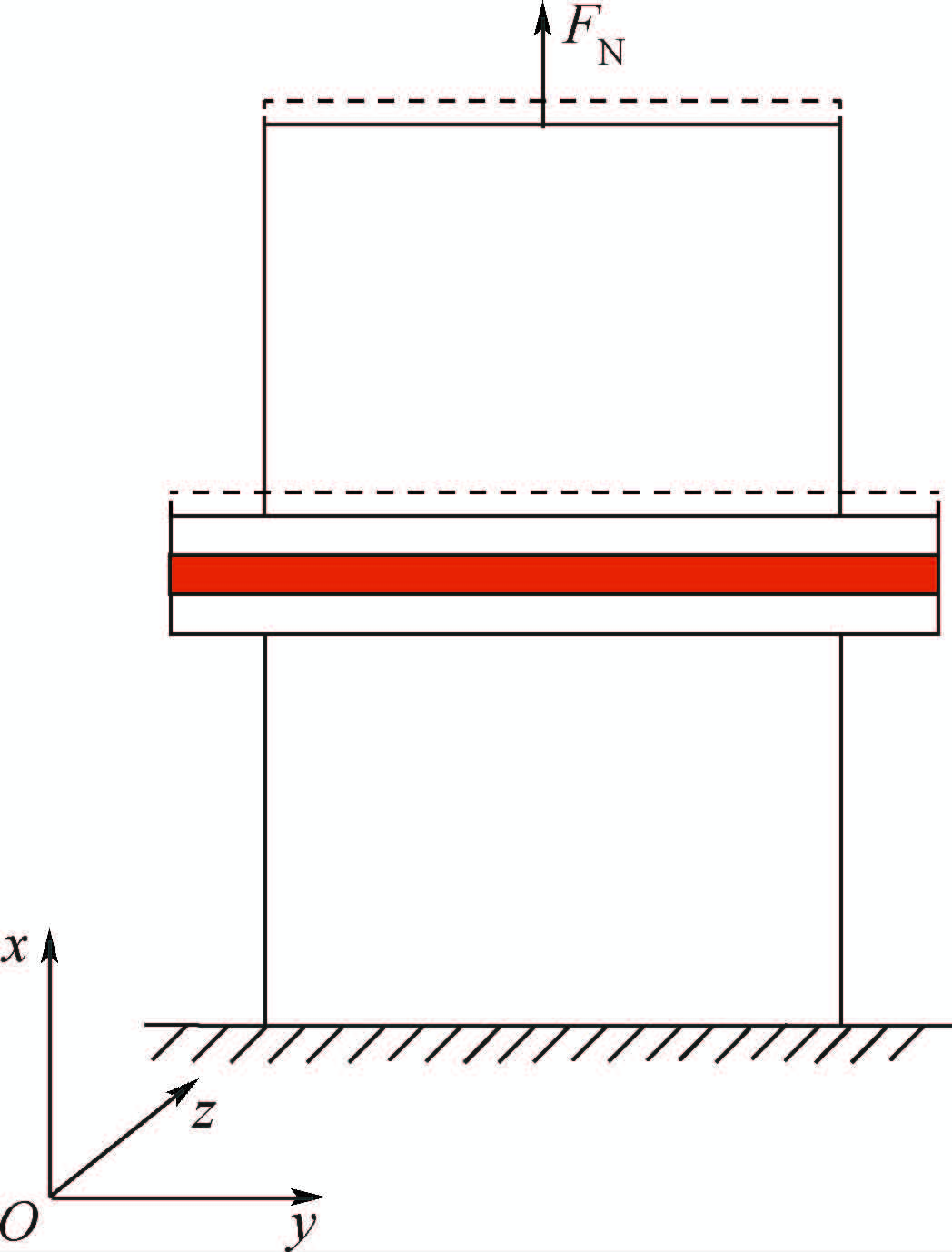图 3 螺栓连接结构轴向刚度定义 Fig. 3 Definition of axial stiffness of bolted joints structure

图选项

代入边界条件和载荷,求解式(6)可得
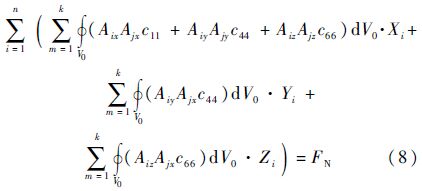
式中：X_i、Y_i、Z_i为节点位移.
对于薄层单元,厚度h较单元其他两个方向的特征尺寸小得多,所以在图 3所示的节点坐标系xyz下,可近似认为^[19]
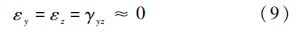
代入形函数N_i可得
而且当螺栓连接结构受到轴向力作用时,结构的横向位移几乎为0,即
将式(10)和式(11)代入式(8),轴向刚度简化为
结构刚度矩阵K包括薄层单元和非薄层单元.从式(12)可以看出,当结构的截面尺寸和单元类型确定时,轴向刚度k_N由轴向弹性模量c₁₁确定.因此,当非薄层单元材料属性不变时,轴向刚度k_N由薄层单元轴向弹性模量确定.
1.3 弯曲刚度根据文献^[20]可知,当薄壁圆筒螺栓连接结构受到横向载荷作用时,基于连接结构的轴向刚度,可以获取其等效弯曲刚度,即连接结构的弯曲刚度可由轴向刚度表示:
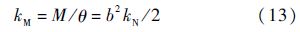
式中:M为弯矩；θ为转角；b为圆筒的外径.
从式(13)可以看出,螺栓连接结构弯曲刚度k_M与轴向刚度k_N、截面尺寸有关.因此在薄壁圆筒尺寸确定情况下,弯曲刚度k_M由薄层单元轴向弹性模量确定.
1.4 剪切刚度螺栓连接结构剪切刚度定义如图 4所示,假设薄壁圆筒一端固定,另一端在圆筒中心节点j上施加y向剪切载荷F_Sy.横向剪切力作用产生的结构横向位移由节点i′的y向位移值Δl_y表示,则螺栓连接结构的y向剪切刚度可定义为

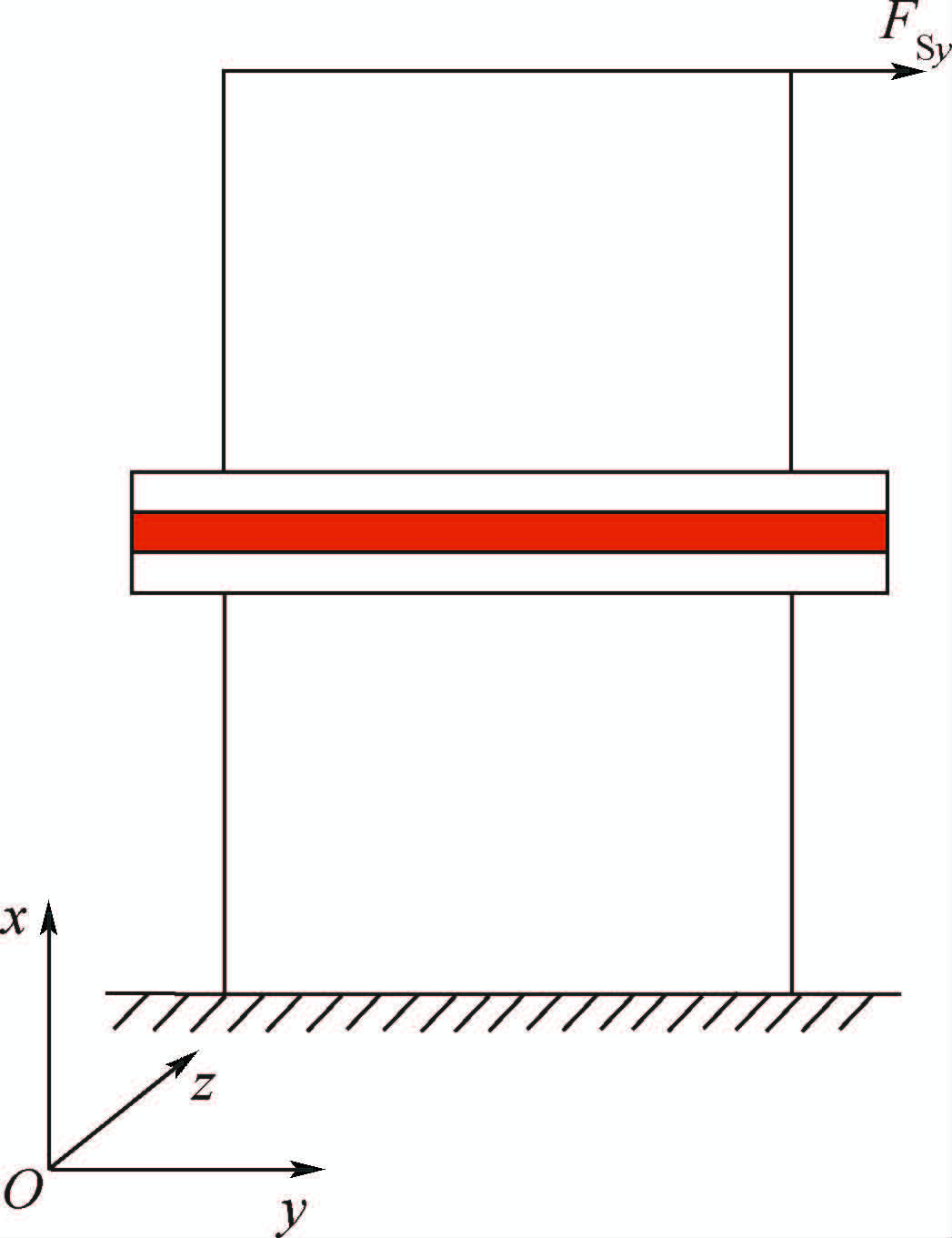图 4 螺栓连接结构剪切刚度定义 Fig. 4 Definition of shear stiffness of bolted joints structure

图选项

代入边界条件和载荷,可得

同理^[21],将式(10)代入式(15),螺栓连接结构y向剪切刚度简化为
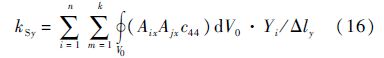
同理,螺栓连接结构z向剪切刚度为
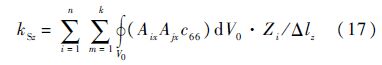
式(16)和式(17)表明螺栓连接的剪切刚度与剪切模量有关,因此当非薄层单元的材料属性和结构截面尺寸不变时,剪切刚度k_S由薄层单元剪切模量决定,其中xy平面剪切模量决定y向剪切刚度,xz平面剪切模量决定z向剪切刚度.
综上所述,航空发动机螺栓连接结构的轴向刚度、弯曲刚度可由薄层单元轴向弹性模量确定,剪切刚度可由薄层单元横向剪切模量来确定.
2 薄层单元对连接刚度影响规律第1节详细叙述了航空发动机螺栓连接结构薄层单元法建模原理,现阐述薄层单元材料参数对连接刚度的影响规律.
2.1 建 模图 5所示为薄层单元薄壁圆筒螺栓连接结构有限元模型,单元类型为SOLID185.由于航空发动机螺栓连接结构轴向、弯曲刚度由薄层单元轴向弹性模量确定,剪切刚度由薄层单元横向剪切模量确定,为了使薄层单元材料参数互不影响且忽略各个方向耦合刚度^{[13, 17]},将其设置为正交各向异性材料,材料属性设置如表 2所示.

图 5 薄壁圆筒螺栓连接有限元模型 Fig. 5 Finite element model of thin-walled cylinder bolted joints

图选项

表 2 有限元模型材料属性Table 2 Material properties of finite element model

单元

单元类型

密度/(kg·m-3)

材料属性

弹性模量/GPa

剪切模量/GPa

泊松比

x

y

z

xy

yz

xz

xy

yz

xz

薄层

SOLID185

7 850

正交各向异性

180

180

180

180

180

180

0

0

0

其他

SOLID185

7 850

各向异性

210

80.7

0.3

表选项


在该模型中,x轴代表圆筒的轴向,y、z轴分别代表圆筒的横向,那么薄层单元的E_x、E_y、E_z分别表征连接处轴向(x向)、横向(y向、z向)的刚度,G_xy、G_yz、G_xz分别表征xy平面、yz平面、xz平面的剪切刚度.因此在该模型中,对轴向、弯曲刚度起决定作用的是轴向(x向)弹性模量E_x,对剪切刚度起决定作用的是xy、xz平面的剪切模量G_xy、G_xz.由于航空发动机螺栓连接结构大多数是带止口的螺栓连接或精密螺栓连接,剪切刚度可认为是无限大,因此本节中不对剪切刚度进行验证,只验证轴向刚度和弯曲刚度的建模原理.
2.2 轴向刚度影响规律对图 5所示的有限元模型一端完全约束,另一端施加载荷为2 kN的轴向力,改变薄层单元材料参数,得到对轴向刚度的影响规律.
2.2.1 剪切模量对轴向刚度的影响保证弹性模量E不变,改变剪切模量G(3个平面值一致).图 6所示为轴向刚度随剪切模量G改变的变化曲线图.研究表明:①当薄层单元弹性模量E分别为100、10、1 GPa时,随着剪切模量G的变化,轴向刚度几乎不变,说明剪切模量对轴向刚度几乎没有影响;②当弹性模量E较小时(1 GPa),随着剪切模量的改变,轴向位移有一定改变,但变化程度在3%以内.根据式(8)可以看出,当弹性模量E较小时,A_i1A_j1c₁₁、A_i2A_j2c₄₄、A_i3A_j3c₆₆的共同影响造成了这种结果,但这种影响可以忽略.

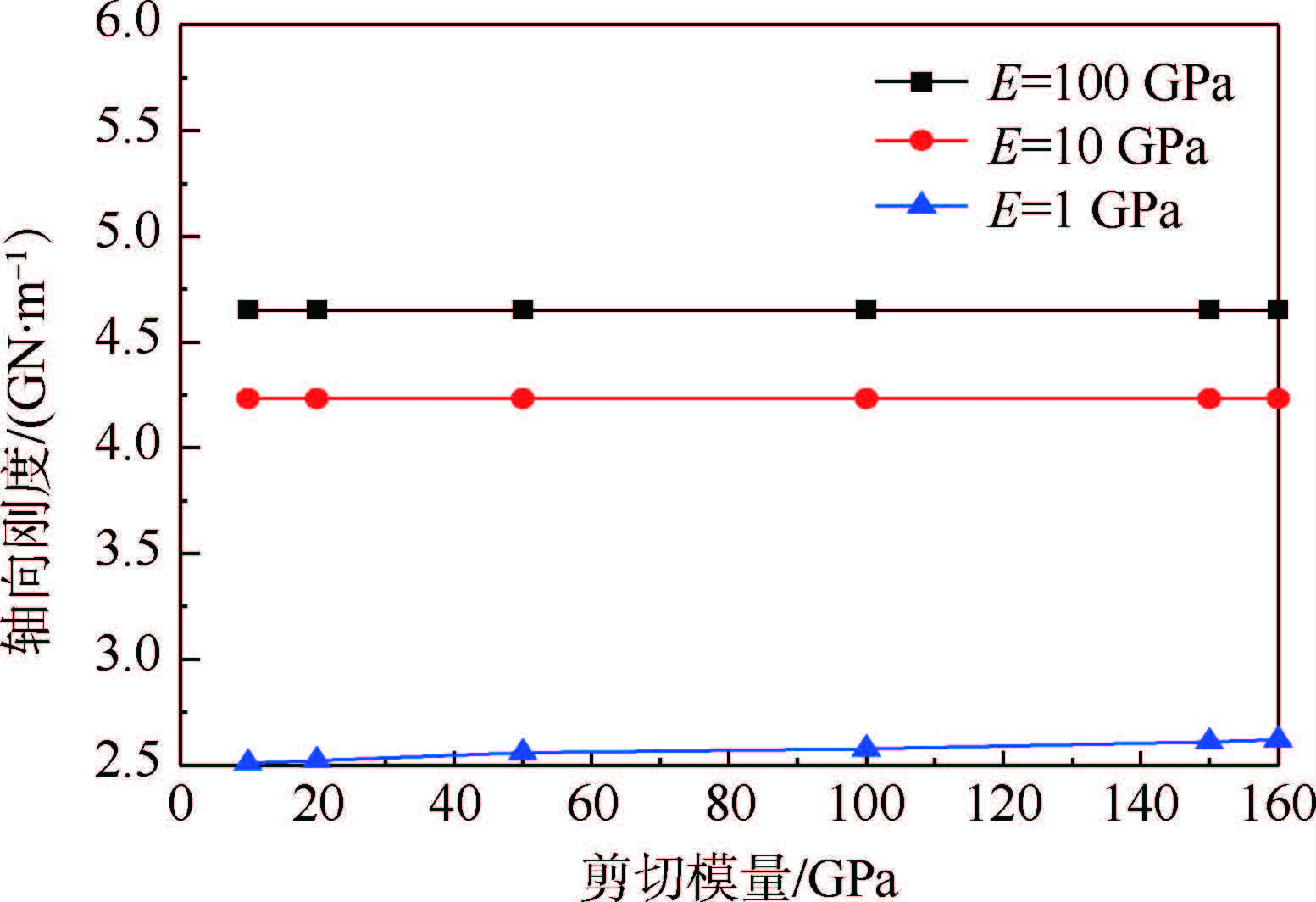图 6 剪切模量对轴向刚度的影响Fig. 6 Influence of shear modulus on axial stiffness

图选项

2.2.2 弹性模量对轴向刚度的影响保证剪切模量G不变(均取180 GPa),然后依次改变E_x、E_y、E_z(值不变时取10 GPa).图 7所示为轴向刚度随弹性模量E_x、E_y或E_z改变的变化曲线图.研究表明:①当剪切模量一定时,改变弹性模量E_y、E_z值,轴向刚度几乎不变,说明E_y、E_z对机匣轴向刚度没有影响;②当剪切模量一定时,改变弹性模量E_x,轴向刚度有明显变化,说明轴向弹性模量对轴向刚度有很大影响,特别是当E_x较小时影响更大.
现分析轴向弹性模量对轴向刚度具体影响规律.从图 7可以看出:①随着轴向弹性模量的减小(160~18 GPa),轴向刚度线性逐渐减小,但刚度变化趋势并不明显;②当弹性模量减小到一定时(18 GPa附近),轴向刚度突然减小,并存在一个明显的拐点;③当通过拐点之后,机匣轴向刚度又线性减小,但刚度变化趋势比160~18 GPa间大很多.

图 7 不同方向弹性模量对轴向刚度的影响Fig. 7 Influence of elastic modulus on axial stiffness

图选项

从上述分析可知,轴向弹性模量对机匣轴向刚度影响是存在两段线性变化的区间,这主要是随着轴向弹性模量的改变,整个机匣承受轴向力的部位发生了变化,造成轴向位移分布发生了变化.如图 8所示,当轴向弹性模量较大时,薄层单元处的轴向刚度比较大,并且与圆筒部分轴向刚度值相差不大,因此整个圆筒结构共同承受轴向力,机匣轴向位移云图是均匀分布的,如图 8(a)所示.随着轴向弹性模量逐渐减小,此时薄层单元处轴向刚度也逐渐减小,并且与圆筒部分轴向刚度相差越来越大,因此逐渐从整个圆筒结构共同承受轴向力变为连接处薄层单元单独承受,此时轴向变形主要发生在薄层单元,机匣圆筒部分主要发生轴向刚性位移,如图 8(b)所示.这也解释了轴向弹性模量的改变引起整个结构轴向刚度非线性变化的原因.

图 8 Ex=160 GPa和1.8 GPa时机匣轴向位移图 Fig. 8 Axial displacement when Ex is 160 GPa and 1.8 GPa

图选项

2.3 弯曲刚度影响规律对图 5所示的机匣有限元模型一端完全约束,另一端施加载荷为2 kN·m的弯矩,改变薄层单元的材料属性参数,得到对弯曲刚度的影响规律.
2.3.1 剪切模量对弯曲刚度的影响保证弹性模量不变,改变剪切模量G,图 9所示为弯曲刚度随着剪切模量G改变的变化曲线图.研究表明:①当薄层单元弹性模量E分别为100、10、1 GPa时,随着剪切模量G的变化,弯曲刚度几乎不变,说明剪切模量对弯曲刚度没有影响;②当弹性模量E较小时(1 GPa),随着剪切模量的改变,弯曲刚度有一定改变,但变化程度在3%以内.这主要是因为当弹性模量E较小时,A_i1A_j1c₁₁、A_i2A_j2c₄₄、A_i3A_j3c₆₆共同影响造成的结果,但这种影响可以忽略.

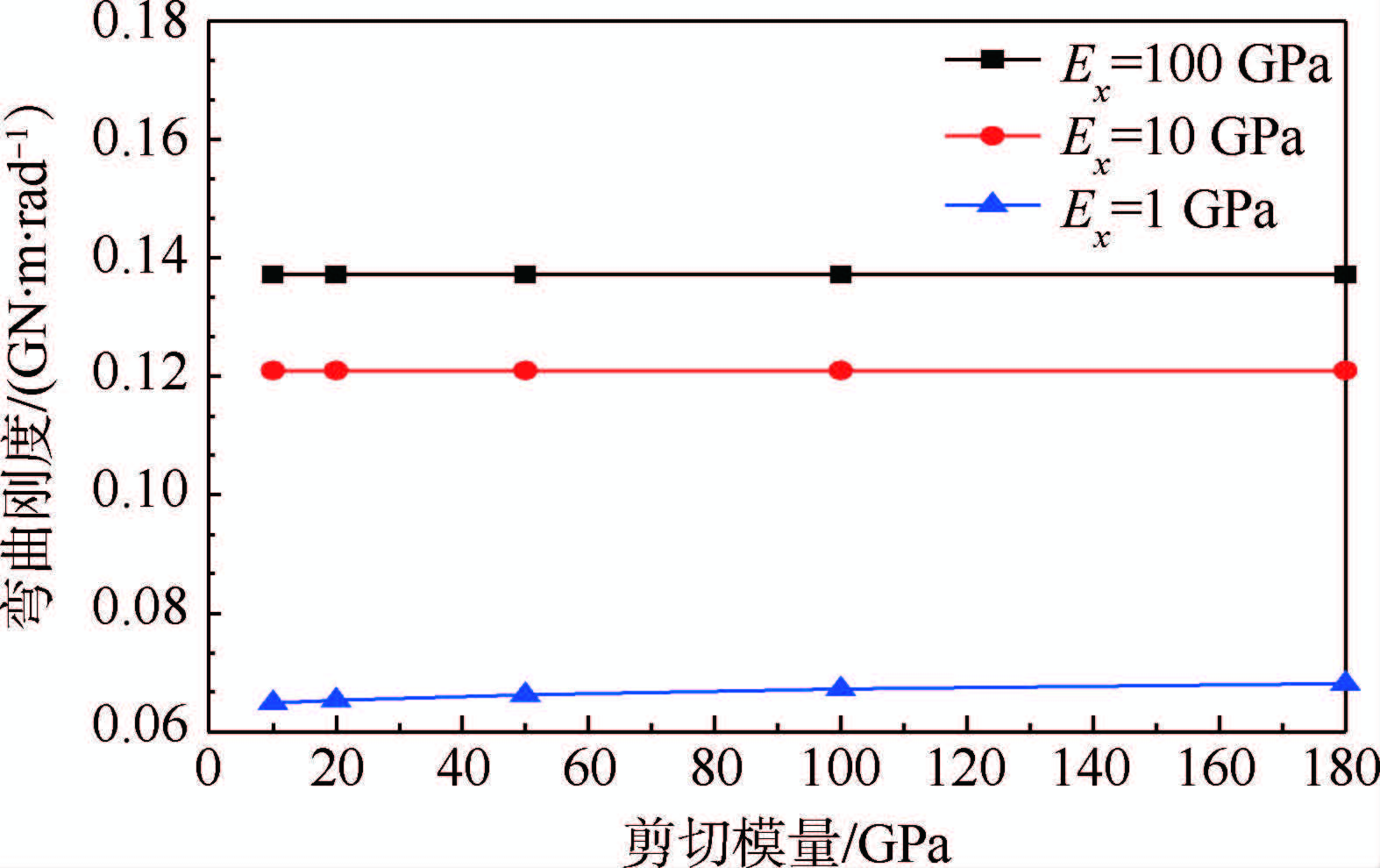图 9 剪切模量对弯曲刚度的影响Fig. 9 Influence of shear modulus on bending stiffness

图选项

2.3.2 弹性模量对弯曲刚度的影响保证剪切模量G不变(取180 GPa),依次改变E_x、E_y、E_z(值不变时取10 GPa).图 10所示为弯曲刚度随着弹性模量改变的变化曲线图.研究表明:①当剪切模量一定时,改变弹性模量E_y、E_z值,弯曲刚度几乎不变,说明E_y、E_z对机匣弯曲刚度没有影响;②当剪切模量一定时,改变轴向弹性模量,弯曲刚度有明显变化,说明轴向弹性模量对机匣弯曲刚度有很大影响.
现分析轴向弹性模量对弯曲刚度的影响规律.从图 10中可以看出:①随着轴向弹性模量的减小(160~18 GPa),弯曲刚度线性逐渐减小,但刚度变化的趋势并不大;②当轴向弹性模量减小到一定程度(18 GPa附近),弯曲刚度突然减小,并存在明显的拐点;③当通过拐点后,弯曲刚度又线性减小,但刚度变化趋势比160~18 GPa间大.

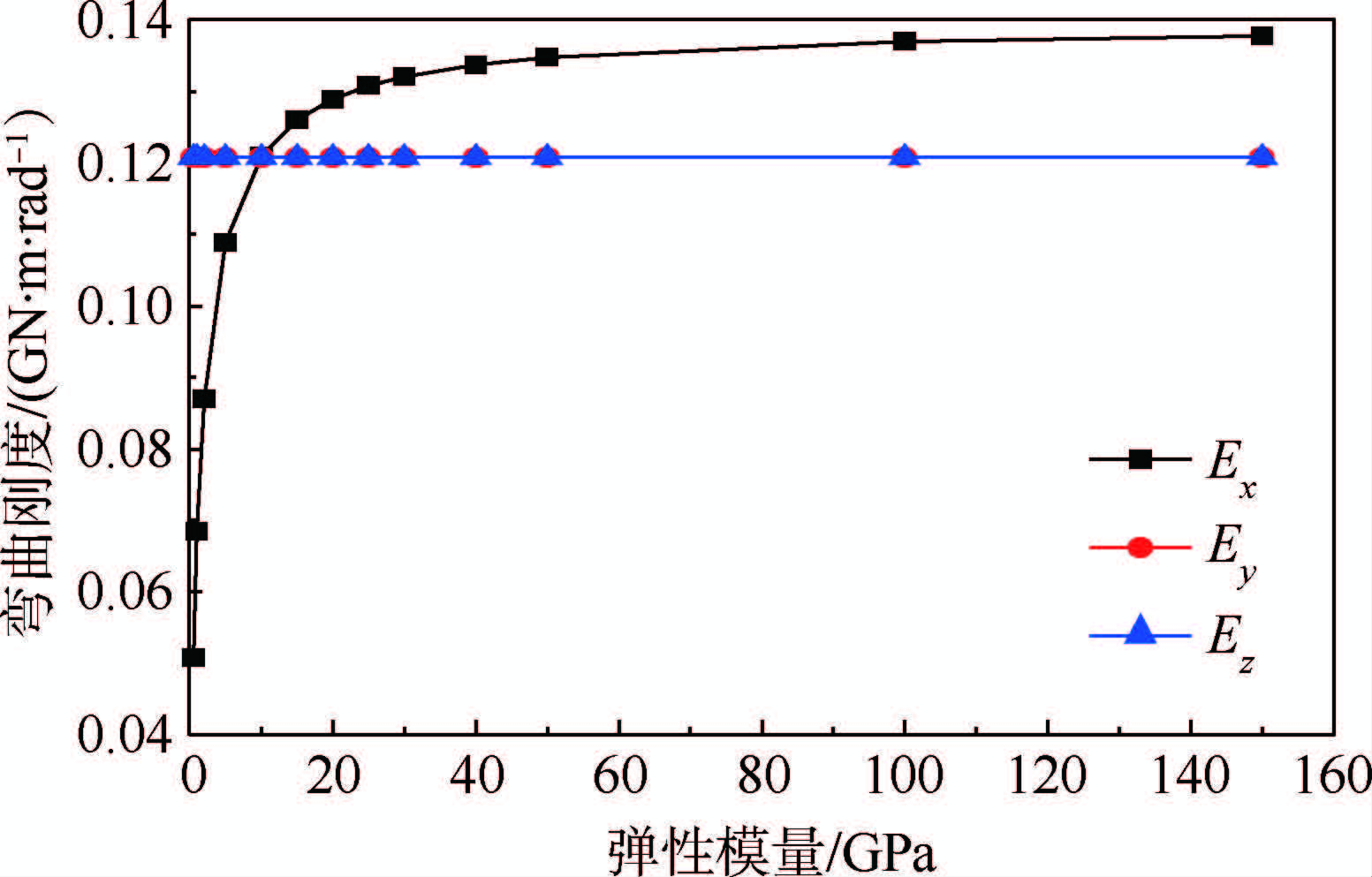图 10 不同方向弹性模量对弯曲刚度的影响Fig. 10 Influence of elastic modulus on bending stiffness

图选项

从上述分析可知,轴向弹性模量对弯曲刚度影响主要是存在两段线性变化的区间,这主要是随着轴向弹性模量的改变,整个圆筒承受弯矩的部位发生了变化,从而造成位移分布改变.如图 11(a)所示,当轴向弹性模量较大时,薄层单元处的轴向刚度较大,与圆筒部分的轴向刚度值相差不大,因此在受到弯矩作用时,整个机匣共同承受弯矩,螺栓连接结构和机匣作为整体发生弯曲变形,机匣Von Mises位移云图是均匀分布的.当轴向弹性模量逐渐减小,此时薄层单元轴向刚度逐渐减小,并且与圆筒部分轴向刚度相差越来越大,因此在受到弯矩作用时,弯矩逐渐从整个圆筒共同承受变为连接处薄层单元单独承受,此时变形主要发生在薄层单元,为轴向变形,存在受拉侧和受压侧,且受拉侧和受压侧轴向位移一致,机匣圆筒部分主要发生刚性转角位移,如图 11(b)所示.这也解释了轴向弹性模量的改变引起整个结构弯曲刚度非线性变化的原因.

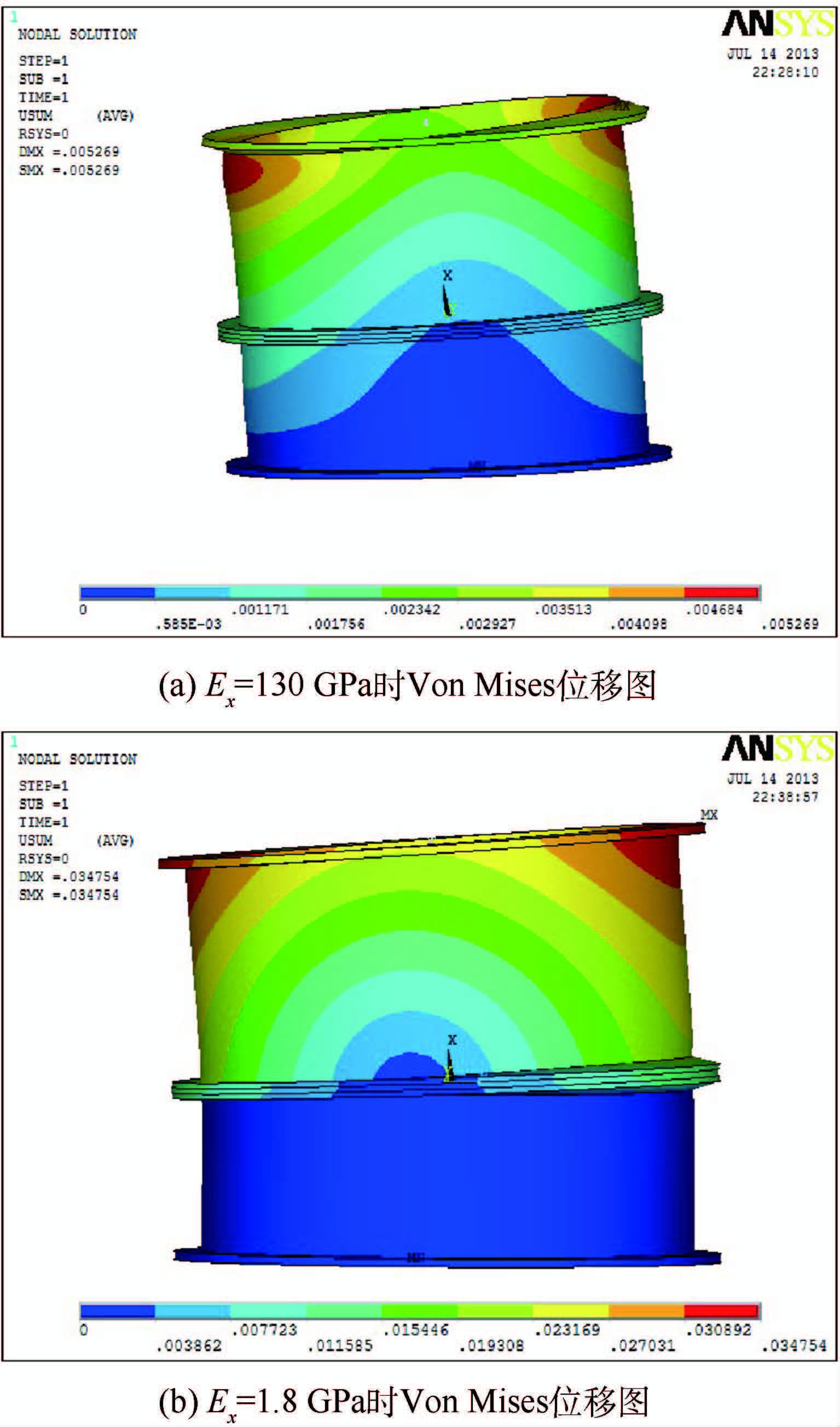图 11 Ex=130 GPa和1.8 GPa时机匣Von Mises位移图 Fig. 11 Von Mises displacement of casing when Ex is 130 GPa and 1.8 GPa

图选项

3 薄层单元法材料参数确定第1节和第2节详细阐述了航空发动机螺栓连接薄层单元法建模原理以及薄层单元材料参数对薄壁圆筒连接刚度的影响规律,本节给出薄层单元相关材料参数的理论表达式并研究螺栓连接结构参数对连接刚度的影响规律.
由于航空发动机螺栓连接结构大多数是带止口的螺栓连接或精密螺栓连接,剪切刚度可认为是无限大,因此本节中不考虑结构的剪切刚度,只给出轴向弹性模量的理论表达式.
3.1 螺栓连接轴向刚度理论表达式对于一般薄壁圆筒螺栓连接结构,去掉圆筒部分,保留安装边及螺栓,那么连接区域可以分为3个部分:①螺杆连接区域;②螺栓预紧力夹紧区域;③安装边对接面连接区域,如图 12所示,其中螺栓连接结构的轴向连接刚度主要由①、②决定.

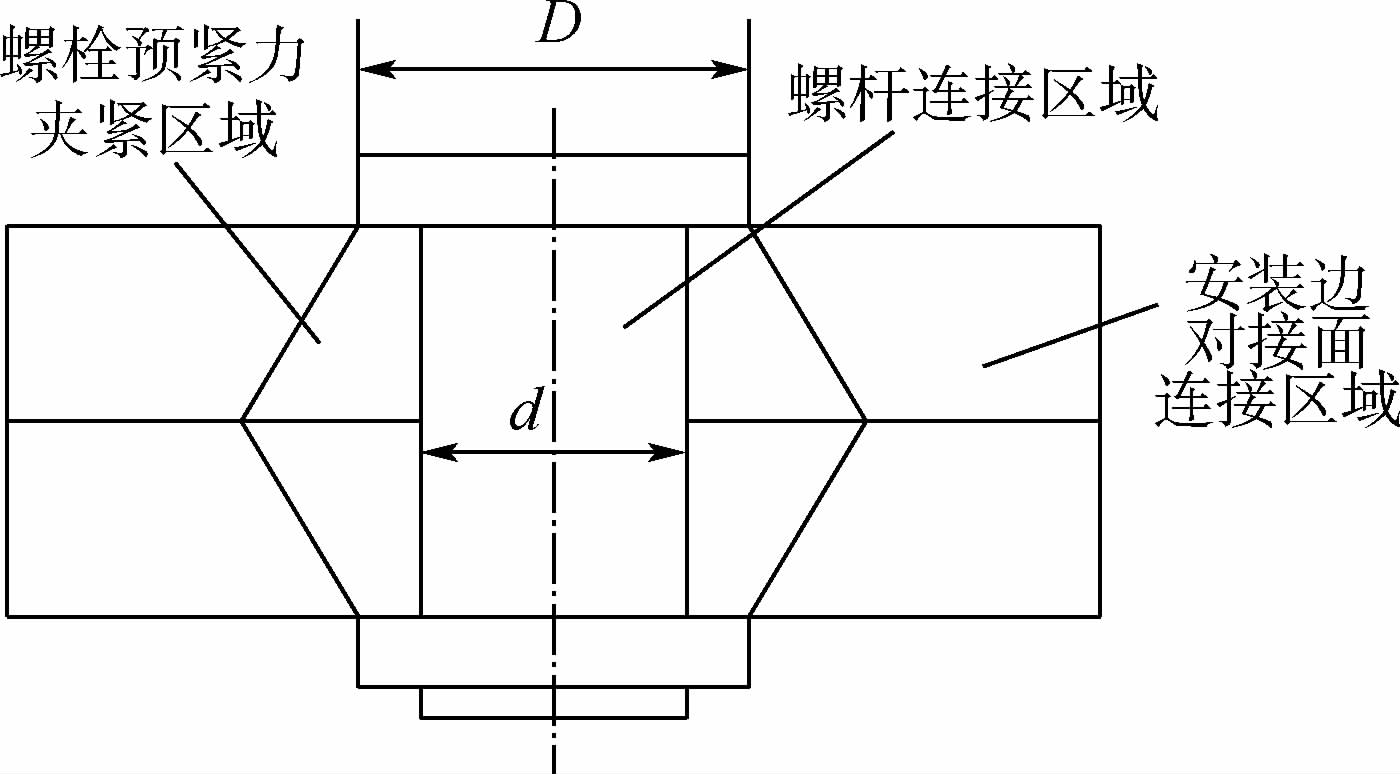图 12 螺栓连接结构连接区域 Fig. 12 Connection region of bolted joints structure

图选项

对于螺杆连接区域,螺杆轴向刚度^[21]可以表示为
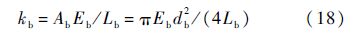
式中:A_b为螺杆截面面积；d_b为螺杆直径;L_b为螺杆等效长度,可表示为L_b=L+(1.95－β/2－υ)d_b^[22],其中L、β和υ分别为螺孔长度、无量纲系数及螺杆泊松比,这充分考虑了螺母、垫片等对连接刚度的影响;E_b为螺杆弹性模量.在本文中L_b取L.
对于螺栓预紧力夹紧区域,该区域可近似为对称的切去顶端的圆锥形区域,可得每块安装边轴向连接刚度^[23]为
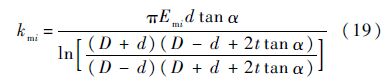
式中:E_mi(i=1,2)为安装边弹性模量;t为安装边厚度;α为半锥形角,与螺栓预紧力F_p大小有关.
对于安装边厚度不同的螺栓连接结构,如图 13所示,螺栓预紧力压紧区域为上下对称的去顶端圆锥区域加中间的圆环区域,圆环柱状区域的轴向连接刚度可表示为
式中:A_c为圆环面积;t′为圆环柱状区域厚度.

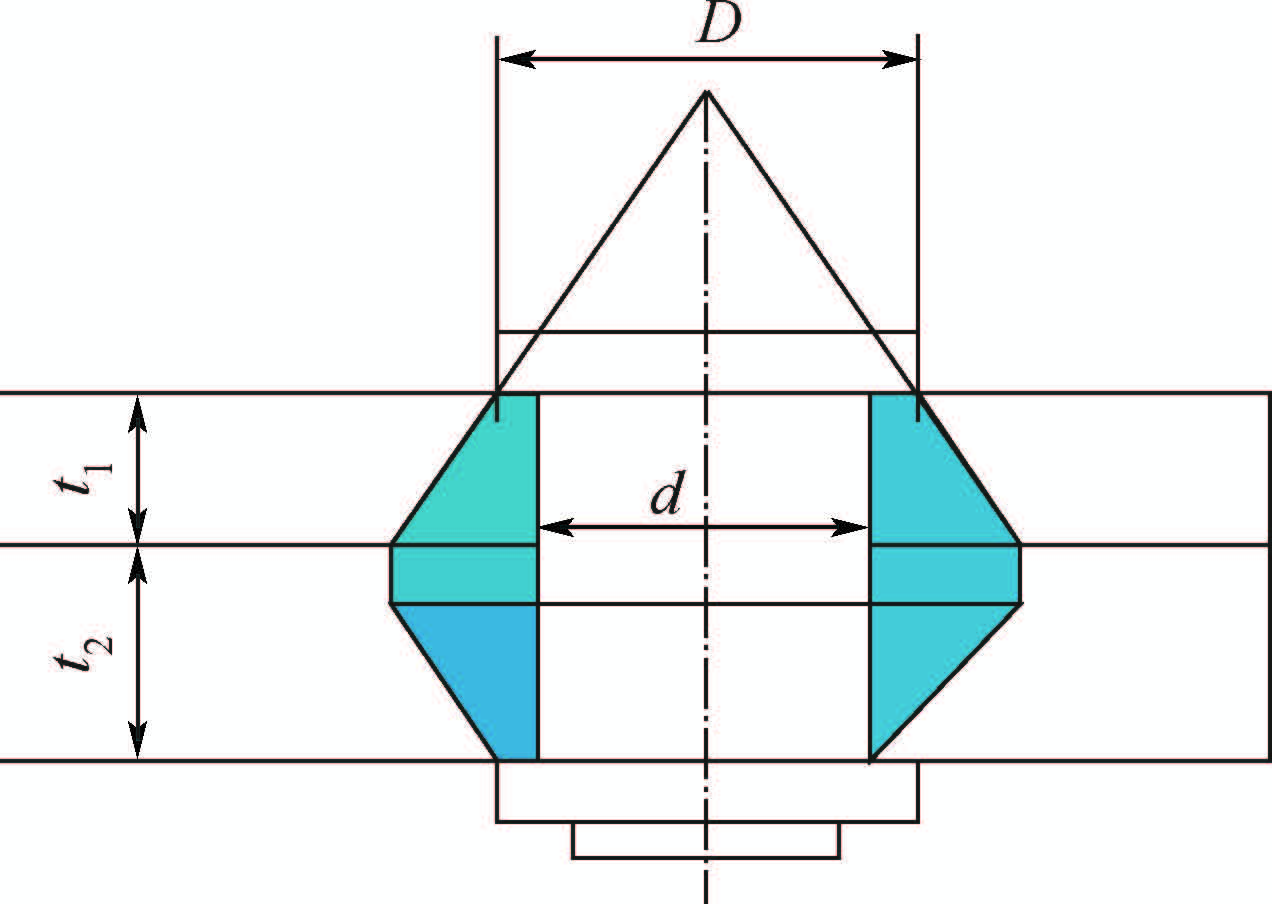图 13 安装边厚度不同的螺栓连接结构 Fig. 13 Bolted joints structure of different thickness flange

图选项

因此整个螺栓预紧力夹紧区域轴向连接刚度为

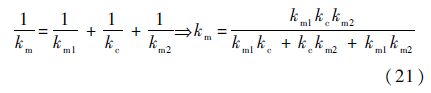
那么图 12所示整个螺栓连接轴向刚度可表示为(式(7)为整个薄壁圆筒的轴向刚度)
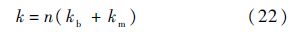
式中:n为整个法兰边周向螺栓的个数.
可见,整个螺栓连接轴向、弯曲刚度与螺杆弹性模量E_b、螺杆直径d_b、螺孔长度L以及安装边弹性模量E_mi、螺栓预紧力F_p、螺母压紧区域半径D、螺栓数目n有关.
3.2 结构参数对轴向刚度的影响下面探讨螺栓连接结构参数对轴向刚度的影响规律,主要研究螺栓数目n和螺栓预紧力F_p对其的影响.
假设两安装边的厚度一致,安装边以及螺栓的材料属性一样,其他结构参数如图 14所示,那么螺栓连接轴向刚度可表示为

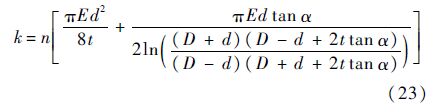
图 14 精细有限元模型 Fig. 14 Detailed finite element model

图选项

3.2.1 螺栓数目对轴向刚度的影响当螺栓连接其他结构参数都确定,螺栓预紧力为3 kN时,螺栓个数与连接刚度的变化曲线如图 15所示.从图中可以看出,轴向刚度随着螺栓数目的变化线性增加,说明螺栓个数越多,螺栓连接轴向刚度越大.

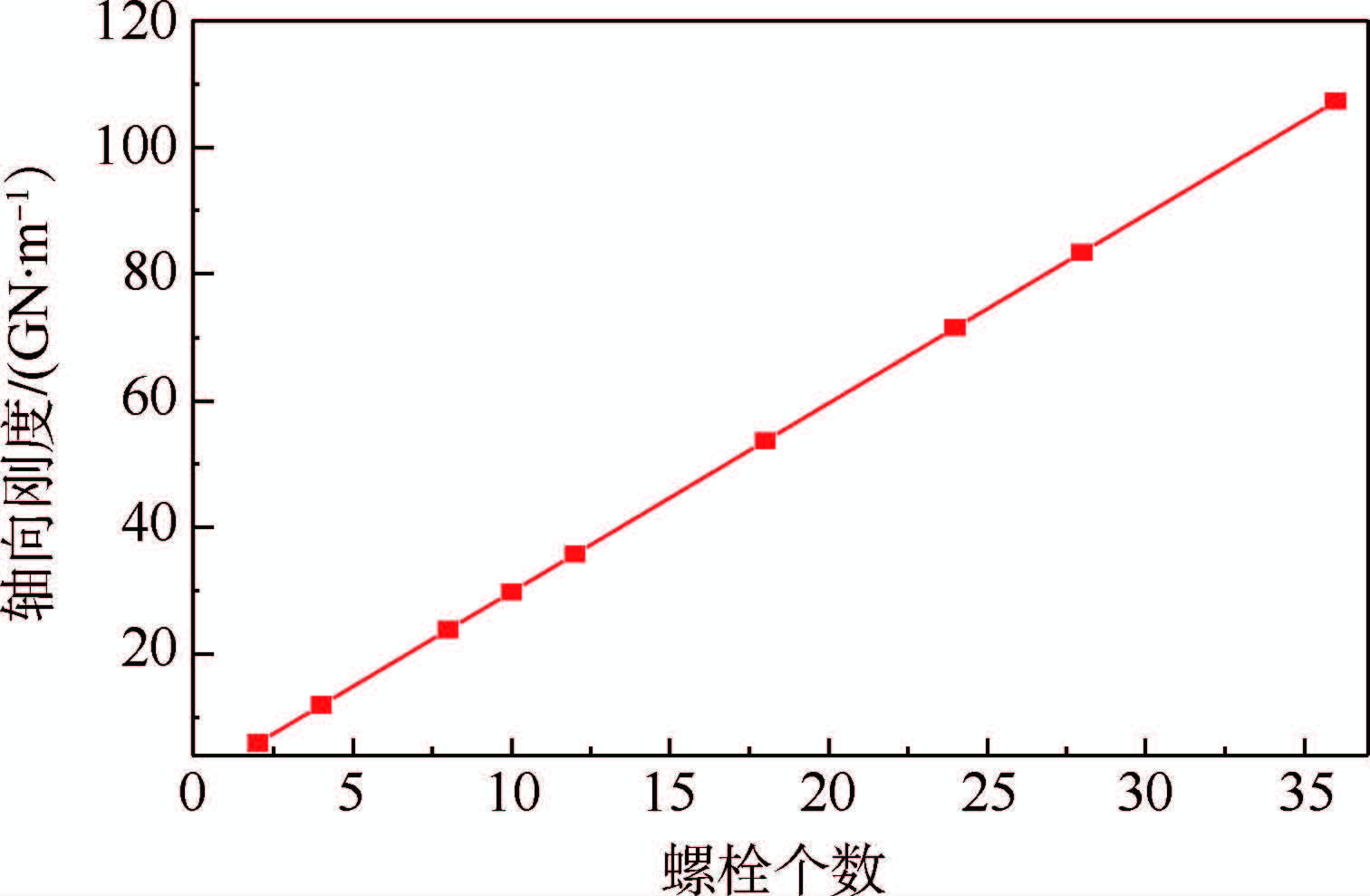图 15 螺栓个数对连接刚度影响Fig. 15 Influence of bolt numbers on joint stiffness

图选项

3.2.2 螺栓预紧力对轴向刚度的影响由于半锥形角α与螺栓预紧力有关,因此通过半锥形角α作为中介研究螺栓预紧力对连接刚度的影响规律.当螺栓连接其他结构参数都确定,螺栓个数为12时,螺栓预紧力与连接刚度的变化曲线如图 16所示.从图中可以看出,当螺栓预紧力较小时,轴向刚度随着螺栓预紧力的增加几乎线性增加;当预紧力增加到一定程度时,轴向刚度趋近不变,说明此时螺栓连接已接近于刚性连接.

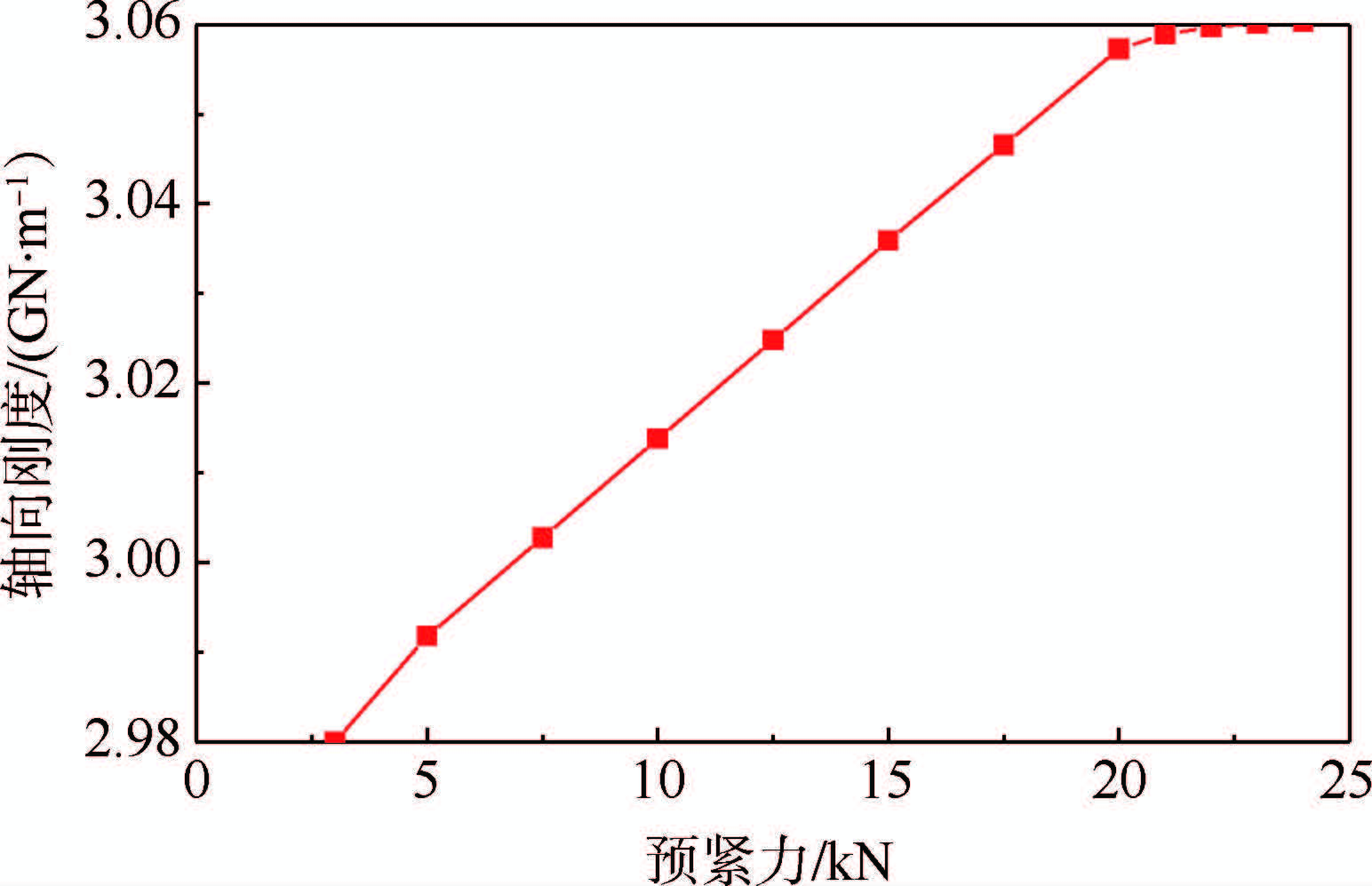图 16 螺栓预紧力对连接刚度影响Fig. 16 Influence of bolt preload on joint stiffness

图选项

3.3 薄层单元材料参数理论表达式如图 17所示,当用薄层单元法对航空发动机螺栓连接结构进行参数化建模时,结构轴向刚度可表示为(去掉圆筒,保留安装边和螺栓)
式中:k₁、k₂、k₃分别为上安装边、薄层单元以及下安装边的刚度,表示为k_i=E_iA_i/L_i,其中E_i、A_i和L_i分别表示各部分的轴向弹性模量、横截面积以及厚度.

图 17 螺栓连接薄层单元 Fig. 17 Thin-layer element of bolted joints

图选项

因此,薄层单元轴向弹性模量与连接刚度的关系为
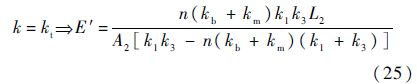
4 应 用第1~3节对薄层单元法的建模原理、材料参数对连接刚度的影响规律以及材料参数的确定进行了详细的阐述.现在将薄层单元法应用到实际的结构中,并与精细有限元模型的结果进行对比,从而验证薄层单元法的正确性和应用前景.
首先,通过精细有限元模型计算薄壁圆筒螺栓连接结构的轴向刚度和弯曲刚度以作为标准刚度;然后,通过第3节内容得到薄层单元的材料参数,并计算出薄层单元薄壁圆筒的轴向、弯曲刚度;最后,将两个模型的结果进行对比.
4.1 精细有限元模型方法图 14所示为薄壁圆筒精细有限元模型,法兰边周向有12个M9的螺栓,建模过程中充分考虑螺栓预紧力(PRETS179单元模拟,设置为3 kN)、螺母与法兰边、螺栓头与法兰边以及法兰边对接面间的接触(TARGE170和CONTA174单元模拟),单元类型为SOLID185,整个结构有88 333个单元数和95 917个节点数,结构的弹性模量为210 GPa,密度为7 850 kg·m^-3,泊松比为0.3.
将该结构一端固定,另一端分别施加轴向载荷和弯曲载荷,从而得到轴向刚度和弯曲刚度(第1节的定义)的变化曲线,如图 18所示.

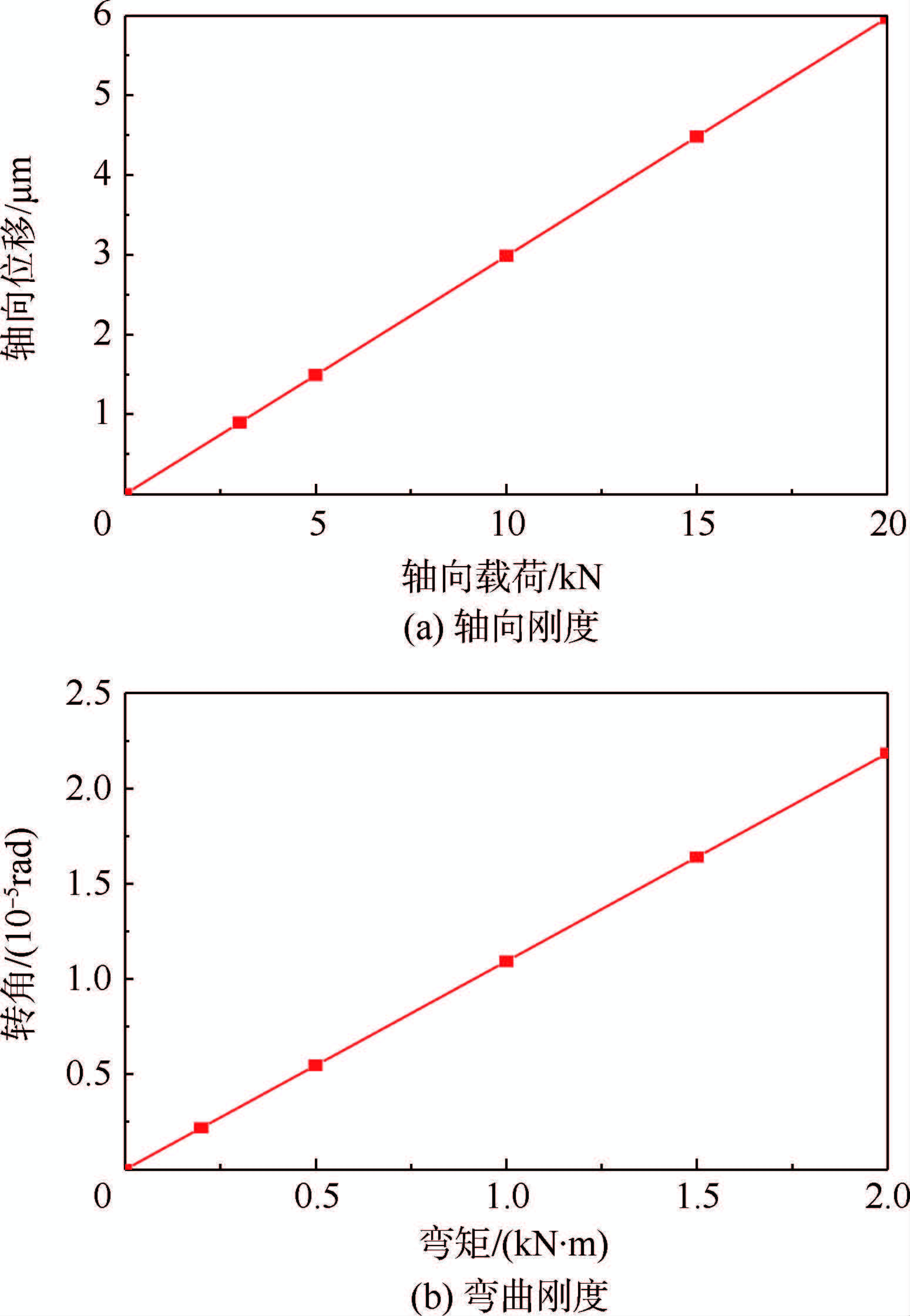图 18 刚度变化规律 Fig. 18 Change law of stiffness

图选项

从图 18中可以看出:①结构轴向位移随着轴向载荷的增加线性变化,结构转角随着弯曲载荷的增加线性变化,说明结构的轴向刚度、弯曲刚度随着外载荷的增加不改变;②通过计算,轴向刚度为3.35 GN/m,弯曲刚度为9.16×10⁷N·m/rad.
4.2 薄层单元法运用薄层单元法对该结构建模,薄层单元厚度为h(h=3 mm),单元类型SOLID185,整个结构共有19 927单元数和28 161节点数,薄层单元材料属性为正交各向异性材料,横向弹性模量为100 GPa,剪切模量为300 GPa,泊松比为0.尺寸如图 17所示,螺杆直径d=9 mm,安装边厚度t=7 mm,螺母压紧区域直径D=14 mm,薄层单元厚度h=3 mm,螺栓个数n=12,螺栓预紧力3 kN对应的半锥形角位α=16°,通过第3节相关内容计算得到薄层单元轴向弹性模量E=2.62 GPa.将该结构一端固定,另一端分别施加轴向载荷和弯曲载荷,从而得到薄层单元模型的弯曲刚度为9.71×10⁷ N·m/rad,轴向刚度为3.58 GN/m.
4.3 对 比将薄层单元薄壁圆筒螺栓连接结构的轴向刚度和弯曲刚度与精细有限元模型的结果进行对比,详细的对比结果如表 3所示,可以得出以下结论:
1) 通过薄层单元法建立的薄壁圆筒螺栓连接结构的轴向刚度、弯曲刚度与精细有限元模型(标准值)相比,弯曲刚度与轴向刚度分别只相差6%和6.8%.
2) 精细有限元模型的轴向、弯曲刚度影响因素为螺杆直径、螺栓数目、螺栓孔位置、法兰边厚度、预紧力,而薄层单元法模型的影响因素则只有轴向弹性模量.
3) 薄层单元模型的单元数和节点数分别比精细有限元模型少78%和71%.
4) 薄层单元模型的计算时间相对精细有限元模型少98%.
综上所述,薄层单元法能够很好地模拟航空发动机螺栓连接结构且能保证正确性,具有很好的应用前景.
表 3 薄层单元模型与精细有限元模型对比Table 3 Comparisons between detailed FE model and thin-layer element model

模型	轴向 弹性模量/GPa	弯曲刚度/ (N·m·rad-1)	轴向刚度/ (N·m-1)	刚度影响因素	单元数	节点数	计算时间/ min
精细有限元模型	210	9.16×107	3.35×109	螺杆直径、螺栓数目、螺栓孔位置、法兰边厚度、预紧力	88 333	95 917	49
薄层单元模型	2.62	9.71×107	3.58×109	轴向弹性模量	19 927	28 161	1
比例/%		6	6.8		78	71	98

表选项


5 结 论本文将薄层单元法应用到航空发动机领域,从航空发动机螺栓连接结构出发,以薄层单元法为基础,给出了航空发动机螺栓连接结构薄层单元法参数化建模原理,研究了薄层单元材料参数对螺栓连接刚度的影响规律,并从理论上给出了薄层单元相关材料参数的表达式,最后将该方法应用到实际结构中,并与精细有限元模型结果进行对比,验证了薄层单元法的正确性和应用前景.研究结果表明:
1) 薄层单元法能很好地模拟航空发动机螺栓连接结构.
2) 薄层单元剪切模量对轴向、弯曲刚度几乎没有影响;横向弹性模量对轴向、弯曲刚度几乎没有影响.
3) 薄层单元轴向弹性模量对轴向、弯曲刚度起决定作用;薄层单元剪切模量对剪切刚度起决定作用.
4) 螺栓连接的螺栓数目与轴向连接刚度呈线性变化规律.
5) 当螺栓预紧力较小时,轴向刚度随着螺栓预紧力的增加线性增加;当预紧力增加到一定程度时,轴向刚度趋近不变,说明此时螺栓连接已接近于刚性连接.
6) 通过精细有限元模型与薄层单元模型结果的对比,薄层单元模型刚度值与精细有限元模型相差在7%以内,而且计算时间、模型规模较精细有限元模型均大幅减少.

参考文献

[1]	Bickford J H.An introduction to the design and behavior of bolted joints[M].2nd ed.New York:Marcel Dekker,Inc.,1990:1-8.
[2]	Liu S G,Wang J,Hong J,et al.Dynamics design of the aero-engine rotor joint structures based on experimental and numerical study[C]//Proceedings of ASME Turbo Expo.New York:ASME,2010:GT2010-22199.
[3]	樊宁.航空发动机连接结构刚度非线性及其对转子动力学影响[D].北京:北京航空航天大学,2013. Fan N.Studies on dynamic characteristics of the joint in the aero-engine rotor system[D].Beijing:Beijing University of Aeronautics and Astronautics,2013(in Chinese).
[4]	Belvin W K.Modeling of joints for the dynamic analysis of truss structures,NASA-L-16163[R].Washington,D.C.:NASA,1987.
[5]	Gregory D L,Martinez D R.On the development of methodologies for constructing predictive models of structures with joints and interfaces,SAND2001-0003P[R].Albuquerque:Sandia National Laboratories,2001.
[6]	Ibrahim R A,Pettit C L.Uncertainties and dynamic problems of bolted joints and other fasteners[J].Journal of Sound and Vibration,2005,279(3-5):857-936.
	Click browse the original
[7]	Groper M.Microslip macroslip in bolted joints[J].Experimental Mechanics,1985,25(2):171-174.
	Click browse the original
[8]	Gaul L,Nitsche R.The role of friction in mechanical joints[J].Applied Mechanics Reviews,2001,54(2):93-106.
	Click browse the original
[9]	Kim J,Yoon J C,Kang B S.Finite element analysis and modeling of structure with bolted joints[J].Applied Mathematical Modelling,2007,31(5):895-911.
	Click browse the original
[10]	Ahmadian H,Jalali H.Identification of bolted lap joints parameters in assembled structures[J].Mechanical Systems and Signal Processing,2007,21(2):1041-1050.
	Click browse the original
[11]	Boeswald M,Link M,Meyer S.Experimental and analytical investigations of non-linear cylindrical casing joints using base excitation testing[C]//2003 IMAC-XXI:Conference & Exposition on Structural Dynamics.Kissimmee:Society for Experimental Mechanics,2003:1-9.
[12]	Ahmadian H,Mottershead J E,James S,et al.Modelling and updating of large surface-to-surface joints in the AWE-MACE structure[J].Mechanical Systems and Signal Processing,2006,20(4):868-880.
	Click browse the original
[13]	Desai C S,Zaman M M,Lightner J G,et al.Thin-layer element for interfaces and joints[J].International Journal for Numerical and Analytical Methods in Geomechanics,1984,8(1):19-43.
	Click browse the original
[14]	Sharma K G,Desai C S.Analysis and implementation of thin-layer element for interfaces and joints[J].Journal of Engineering Mechanics,1992,118(12):2442-2462.
	Click browse the original
[15]	马双超,臧朝平,兰海波.某航空发动机机匣的动力学模型修正[J].航空动力学报,2013,28(4):878-884. Ma S C,Zang C P,Lan H B.Dynamic model updating of an aero-engine casing[J].Journal of Aerospace Power,2013,28(4):878-884(in Chinese).
	Cited By in Cnki (3) | Click to display the text
[16]	Ahmadian H,Ebrahimi M,Mottershead J E,et al.Identification of bolted-joint interface models[C]// Proceedings of the 2002 International Conference on Noise and Vibration Engineering.Leuven:Katholieke Universiteit Leuven,2002:1741-1747.
[17]	Iranzad M,Ahmadian H.Identification of nonlinear bolted lap joint models[J].Computers and Structures,2012,96-97:1-8.
	Click browse the original
[18]	Pande G N,Sharma K G.On joint interface elements and associated problems of numerical ill-conditioning[J].International Journal for Numerical and Analytical Methods in Geomechanics,1979,3(3):293-300.
	Click browse the original
[19]	黄耀英,吴中如,王德信.薄层单元基本假设和简化探讨[J].力学与实践,2008,30(2):49-52. Huang Y Y,Wu Z R,Wang D X.Discuss on fundamental assumption and simplification of thin-layer element[J].Mechanics in Engineering,2008,30(2):49-52(in Chinese).
	Cited By in Cnki (4) | Click to display the text
[20]	栾宇.航天器结构中螺栓法兰连接的动力学建模方法研究[D].大连:大连理工大学,2012. Luan Y.Study on dynamic modeling of bolted flange connections in aerospace structures[D].Dalian:Dalian University of Technology,2012(in Chinese).
	Cited By in Cnki (1)
[21]	Williams J G,Anley R E,Nash D H,et al.Analysis of externally loaded bolted joints:Analytical, computational and experimental study[J].International Journal of Pressure Vessels and Piping,2009,86(7):420-427.
	Click browse the original
[22]	Pedersen N L,Pedersen P.Stiffness analysis and improvement of bolt-plate contact assemblies[J].Mechanics Based Design of Structures and Machines,2008,36(1):47-66.
	Click browse the original
[23]	Oskouei R H,Keikhosravy M,Soutis C.Estimating clamping pressure distribution and stiffness in aircraft bolted joints by finite-element analysis[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2009,223(7): 863-871.
	Click browse the original