电磁成形技术提高成形极限主要有2个机制[1]:①颈缩的惯性稳定(inertial stabilization of necks);②惯性熨烫(inertial ironing)。Golovashchenko[2]的研究表明汽车车身铝合金(6111-T4和5754)电磁成形极限高于传统准静态成形极限。然而,通过电磁成形难以实现几何复杂的零件的一次成形,研究者于是开发了电磁辅助成形工艺。Shang和Daehn[3]将电磁成形技术与传统拉深工艺复合,使用车身铝合金(Al 6111-T4)实现了远远超过传统方法所能获得的拉深成形深度。Psyk等[4]从面向应用的角度归纳了多种电磁成形技术的直接成形工艺和组合工艺,多数表现出成形性提高的特点。
由于电阻率较高,电磁成形技术用于高强钢的研究相对较少。Park等[5]使用电导率高的Al 1050作为驱动片进行了高强钢DP780的成形实验。此外,电磁成形技术也被证明能够用于高强钢的回弹矫形[6, 7]。
成形极限的研究关注零件破裂时的应变,却少有研究者关注电磁与传统成形几何特征一致时的应变特征。铝合金不仅被引入汽车工业[2],更是航空工业广泛使用的合金材料。尤其是在航空领域,铝合金零件的使用寿命和力学性能备受研究者关注。
金属发生塑性变形后,力学性能会发生相应的改变。Lee等[8]提到铝合金成形中的大应变会导致橘皮缺陷。Pol k[9]对比应力幅值和应变幅值对疲劳寿命的影响,指出应变幅值是决定疲劳寿命的决定因素。Al-Rubaie等[10]指出7050-T7451l铝合金的疲劳寿命随着预应变水平增加而降低。而电磁体积力效应有利于分散变形[11]。因此,可以简单地认为,同样的零件,如果使用电磁成形方法加工的零件的应变峰值比采用传统成形方法时低,加工的零件将拥有更好的使用性能,如更高的疲劳寿命。
弯曲变形是金属加工成形过程中的一种典型变形形式。弯曲部分的金属内侧受压,外侧受拉。通常用弯曲实验来测定金属的弯曲变形行为。
本文以通用航空铝合金2024-T3为研究对象,开展了电磁V弯与机械V弯数值模拟和实验研究,分析了2种成形方法下V形圆角半径相同的试件圆角处的应变分布特征。
1 电磁成形原理 电磁成形(Electromagnetic Forming,EMF)是一种基于电磁感应原理的高速成形技术。成形时,蓄能电容器放电,在放电回路中产生瞬态脉冲放电电流。激励电流流过工具线圈,在线圈附近激发出瞬态脉冲强磁场。根据电磁感应原理,线圈磁场在被加工试件(通常为高电导率金属,如铝和铜)中诱导出感应涡电流,被加工试件进而受洛伦兹力作用发生变形,达到金属成形的目的。平板金属电磁成形原理如图 1所示[4]。图中:C为蓄能电容;Li和Ri分别为电磁成形机的电感和电阻。
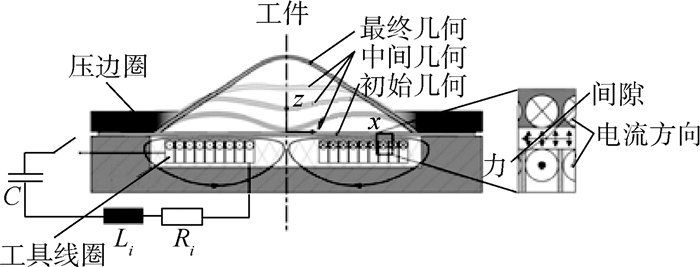 |
| 图 1 金属平板EMF原理[4]Fig. 1 EMF principle of metal plate[4] |
| 图选项 |
电磁成形过程电路结构如图 2所示[4]。图中:Rcoil、Icoil和Lcoil分别为工具线圈的电阻、电流和电感;Rworkpiece、Iworkpiece和Lworkpiece分别为工件的电阻、电流和电感;U0为电容器充电电压。
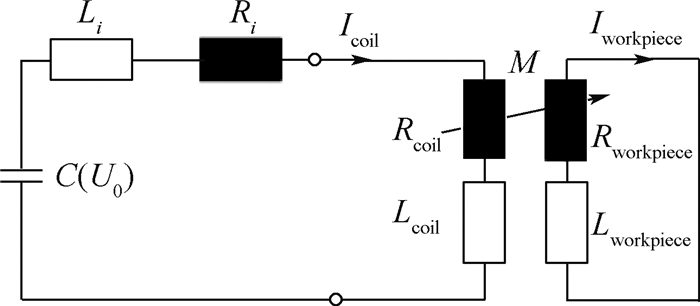 |
| 图 2 EMF过程电路结构[4]Fig. 2 Circuit structure of EMF process[4] |
| 图选项 |
电磁成形时板料受到的洛伦兹力为[12]

式中: J 为工件中的涡流密度; B 为磁通量密度。
2 实验材料及方法 2.1 实验材料与研究方法 实验材料选用2024-T3铝合金,是一种广泛使用的航空铝合金。矩形试件规格为100 mm×40 mm×1.8 mm。试件上印制直径2.5 mm的圆形应变测量网格。2024-T3铝合金准静态真实应力-真实应变曲线[13]见图 3。
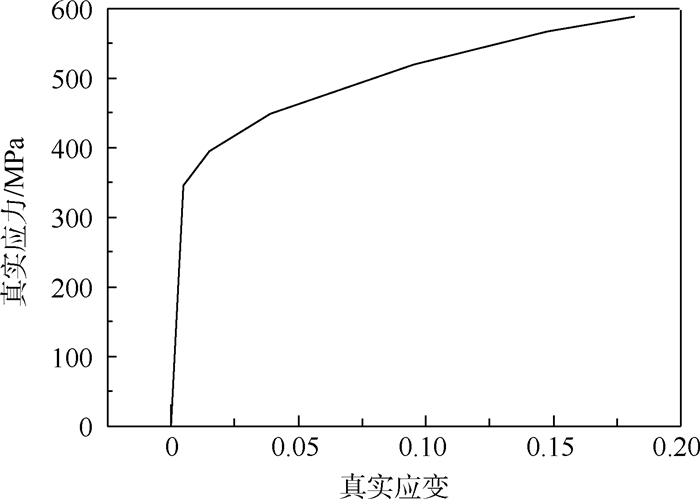 |
| 图 3 2024-T3准静态真实应力-真实应变曲线[13]Fig. 3 Quasi-static true stress-true strain curve of 2024-T3[13] |
| 图选项 |
首先,进行电磁V弯实验,根据电磁V弯试件的实际V形弯曲圆角半径确定机械V弯的凸模半径;然后进行机械V弯实验,以保证实验结果具有可比性;最后对比分析电磁V弯和机械V弯试件V形弯曲圆角处的应变特征。应变特征分析采用了2种对比方式:①实验对比,通过ISM-PM200数码显微镜测量变形前后网格的变化计算出实际应变进行对比;②数值模型对比,以电磁V弯数值模型的V形弯曲半径为依据,建立传统机械V弯数值模型,并提取弯曲圆角处的应变数值结果进行对比。
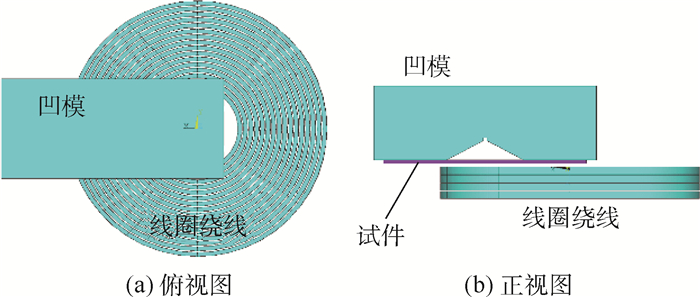
2.2 电磁V弯实验 电磁V弯实验使用的工具线圈和V形凹模分别如图 4(a)和图 4(b)所示。实验所用工具线圈是由华中科技大学提供的一个4层平面螺旋线圈,它能提供比单层线圈更大的电磁力。 线圈的几何参数和电参数见表 1。凹模V形型腔两侧壁夹角为120°,凹模圆角半径为3 mm,型腔深度10 mm。图 5为电磁V弯线圈、凹模和板料的实验设置,图中可以看出工具线圈的绕线、试件、凹模的相对位置。实验装置由液压机提供压紧力。电磁成形机蓄能电容器电容为80 μF,充电电压为18 kV。
 |
| 图 4 电磁成形线圈和V形凹模Fig. 4 Tool coil and V-shaped die in EMF |
| 图选项 |
表 1 工具线圈几何参数与电参数Table 1 Geometric and electric parameters of tool coil
| 参数类型 | 参数值 |
| 电阻/Ω | 0.001 |
| 电感/H | 2×10 -6 |
| 横截面积/mm 2 | 2×4 |
| 层数 | 4 |
| 每层匝数 | 16 |
| 匝间距/mm | 0.8 |
| 层间距/mm | 0.4 |
表选项
 |
| 图 5 电磁V弯线圈、凹模和板料的实验设置 Fig. 5 Experimental set-up of coil,die and sheet metal in electromagnetic V-bending |
| 图选项 |
2.3 机械V弯实验 图 6为机械V弯实验装置。机械V弯使用的V形凹模与电磁V弯相同;机械V弯凸模圆角半径根据电磁V弯实际加工的试件设定,以保证通过2种方法成形试件的V形圆角半径相同,使得应变对比具有可比性。受限于线圈结构,电磁V 弯中的板料无法发生纯弯曲。机械V弯中的压板压力对板料的变形行为存在较大影响。采用压板螺栓结构压边是为了使板料具有与电磁V弯相同的初始变形条件,提高可比性。凸模运动速度为15 mm/min,成形后保持压力6 000 kg持续30 s。
 |
| 图 6 机械V弯实验装置Fig. 6 Mechanical V-bending experiment set-up |
| 图选项 |
3 数值模型 3.1 电磁V弯数值模型 电磁成形数值模拟涉及2个主要的物理场:电磁场和结构场。顺序耦合和松散耦合是实现2个物理场之间的数据传递的2种耦合策略。松散耦合策略虽然计算精度相对较差,但计算成本更低,研究中也被广泛使用。Bartels等[14]进行了松散耦合和顺序耦合2种策略特点的对比研究,并给出了对应的流程图。本文采用松散耦合策略,即首先求解电磁场模型,得到板料上的电磁力;然后将各个时间步的电磁力直接加载到结构场中的板料上,求解板料的变形
本文使用商业有限元代码ANSYS/Emag求解电磁场计算板料上的电磁力;用有限元代码LS-DYNA求解结构场,计算试件的变形。为了保证电磁力的正确传递,板料在电磁场和结构场中的网格划分方式、单元形状、单元编号及单元节点编号均保持一致。
ANSYS/Emag电磁场模型的单元类型和单元自由度选择如下:板料用SOLID97实体单元,AX、AY、AZ、VOLT自由度;线圈用SOLID97实体单元,AX、AY、AZ自由度;空气用SOLID97实体单元,AX、AY、AZ自由度;远场区域使用INFIN111单元,AX、AY、AZ自由度。线圈简化为同心圆环,使用BFE命令直接加载电流密度(JS)作为电磁场计算的激励源。电流密度由实验中实际测量的电流换算。图 7为用于电磁场计算的实际测量电流(充电电压18 kV)。电磁场模型中的板料和线圈网格如图 8所示。
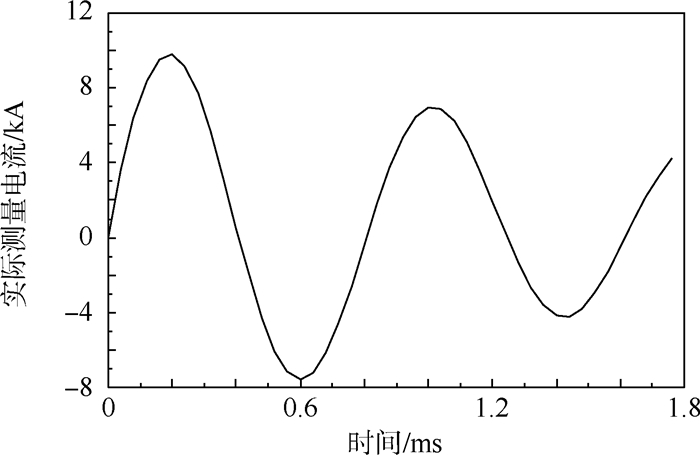 |
| 图 7 实际测量电流Fig. 7 Measured actual currents |
| 图选项 |
 |
| 图 8 电磁场中的板料与线圈网格 Fig. 8 Sheet metal and coil meshing in electromagnetic field |
| 图选项 |
LS-DYNA结构场中板料、凹模和压边板都使用SOLID164显示动力单元,凹模和压边板均设定为刚体,且锁死凹模和压边板的位移和转动自由度。板料和模具之间设有很小的初始间隙以避免板料与模具出现网格初始穿透导致的接触问题。板料与模具的摩擦系数设定为0.25。结构场有限元网格如图 9所示。
 |
| 图 9 结构场有限单元网格Fig. 9 Structural field finitc element mesh |
| 图选项 |
结构场中板料采用Cowper-Symonds率相关本构模型,应变率参数取值[15]为:C=6 500 s-1,P=4。松散耦合方法由于不考虑板料变形对电磁场的影响,结构场中电磁力加载时间取第1个电流脉冲的一部分,为0~0.13 ms[16]。
3.2 机械V弯数值模型 使用LS-DYNA进行机械V弯数值仿真,数值模型如图 10所示。单元的选择,模具和板料间隙的设定,摩擦系数的设定都与电磁V弯结构场保持一致。尽管实验中螺栓压板结构提供的下压力不能被精确控制,但图 9和图 10所示结构场数值模型中的初始间隙和摩擦系数设置相同,即可在数值仿真中排除压板压力不同产生的影响。变形发生的初始条件相同,进而能确定应变特征的差异是由变形方式不同造成的,而不必严格区分板料是拉弯还是纯弯。
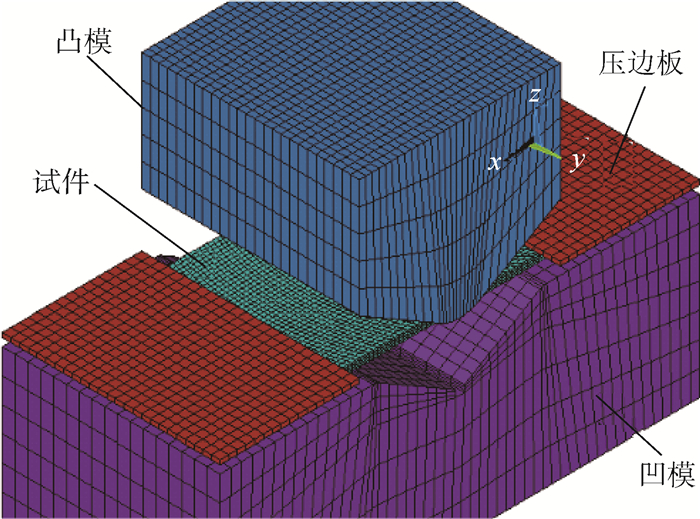 |
| 图 10 机械V弯数值模型Fig. 10 Numerical model of mechanical V-bending |
| 图选项 |
4 结果与讨论 4.1 电磁V弯试件的几何特征 电磁V弯实验结果与数值结果的纵向轮廓和横向轮廓分别如图 11和图 12所示。
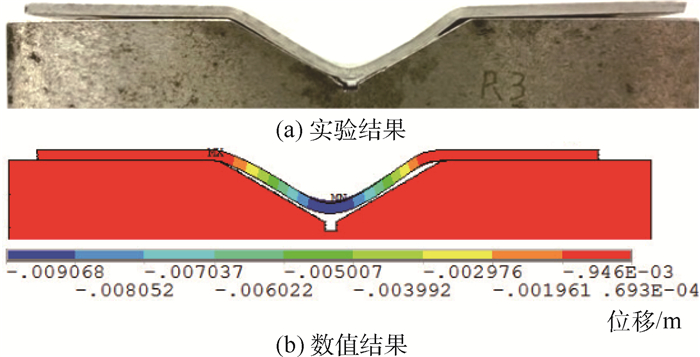 |
| 图 11 电磁V弯试件纵向轮廓Fig. 11 Longitudinal profile of V-bending part formed by electromagnetic forming |
| 图选项 |
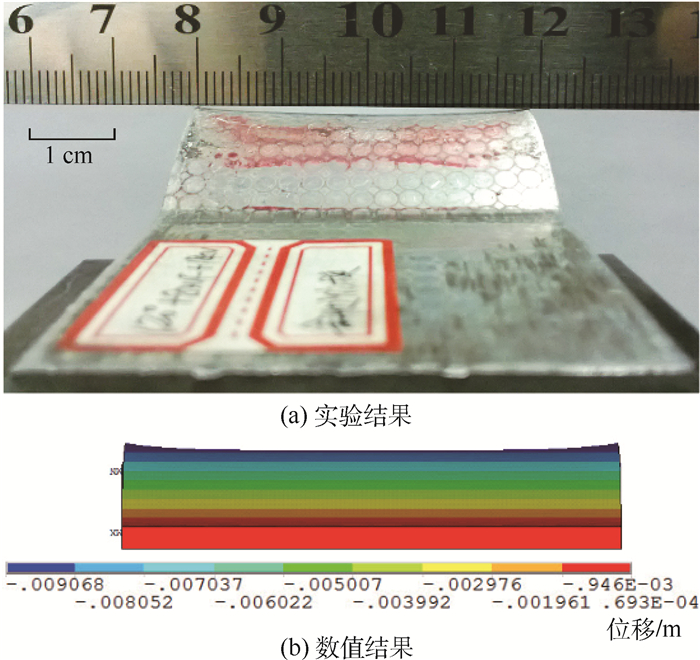 |
| 图 12 电磁V弯试件横向轮廓 Fig. 12 Transverse profile of V-bending part formed by electromagnetic forming |
| 图选项 |
由图 11和图 12可见电磁V弯松散耦合数值模型能够反映成形试件的实际几何特征。图 13所示为电磁V弯试件的测量几何参数。R为V形弯曲圆角外侧半径。R1、R2和R3为沿试件横向3个不同位置的V形圆角外侧半径值。Δh为马鞍的高度差。数值模型中只测量了R2。实验试件R1、R3不相等,是由于试件与线圈的位置不严格对称所致。电磁V弯试件以及松散数值模型的几何参数如表 2所示。试件变形呈马鞍特征与试件上的电磁力分布直接相关。图 14为垂直于试件表面的电磁力分量云图。2条竖直线之间的部分为电容放电之前,试件位于凹模型腔上方的部分。远离和靠近线圈中心的两端分别用A和B标示。由图 14可知,V形型腔上方的板料两侧边缘位置有电磁力集中现象。
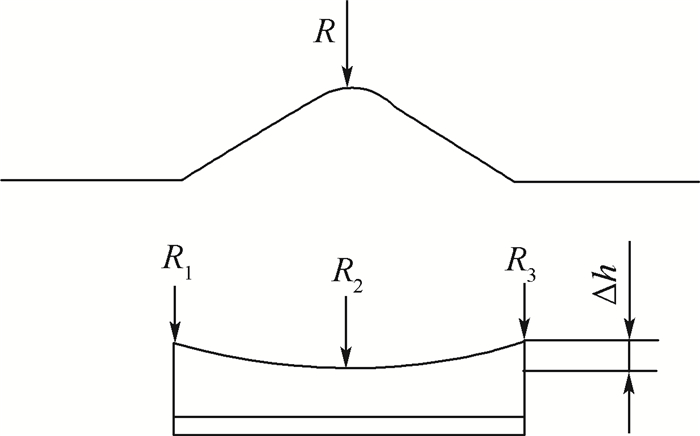 |
| 图 13 试件几何参数Fig. 13 Geometrical parameters of formed part |
| 图选项 |
表 2 电磁V弯试件几何参数Table 2 Geometrical parameters of formed part by electromagnetic V-bending
| 试件类型 | 几何参数 | |||
| R 1/mm | R 2/mm | R 3/mm | Δ h/mm | |
| 实验 | 6.0 | 11.5 | 8.5 | 0.78 |
| 数值 | - | 9.5 | - | 0.39 |
表选项
 |
| 图 14 试件表面的电磁力分布云图 Fig. 14 Distribution contours of electromagnetic force on formed part surface |
| 图选项 |
几何特征的具体数值存在差异,这与采用了低精度的松散耦合策略有关。但该数值模型具有与实际零件相同的几何特征,说明该模型(包括参数设定)能够反映板料的变形特点,可用于分析板料的变形行为。
4.2 电磁与机械V弯应变特征对比 4.2.1 数值模型应变对比电磁V弯数值模型预测的V形圆角外侧半径R2为9.5 mm,忽略板料厚度的变化,取试件的名义尺寸,则内径为7.5 mm。为使机械V弯与电磁V弯的数值结果具有可比性,机械V弯数值模型凸模圆角半径设为7.5 mm。同时也进行了凸模圆角半径分别为9.0 mm和10.0 mm的机械V弯数值模拟,以扩大与电磁V弯试件对比的范围。
图 15和图 16分别为弯曲试件V形圆角,半径R2所在位置,沿试件长度方向(纵向)的外侧拉应变和内侧压应变分布曲线。图中EMF表示电磁成形实验结果;R7.5、R9.0和R10.0分别表示凸模圆角半径为7.5 mm、9.0 mm和10.0 mm时的机械V弯数值结果。
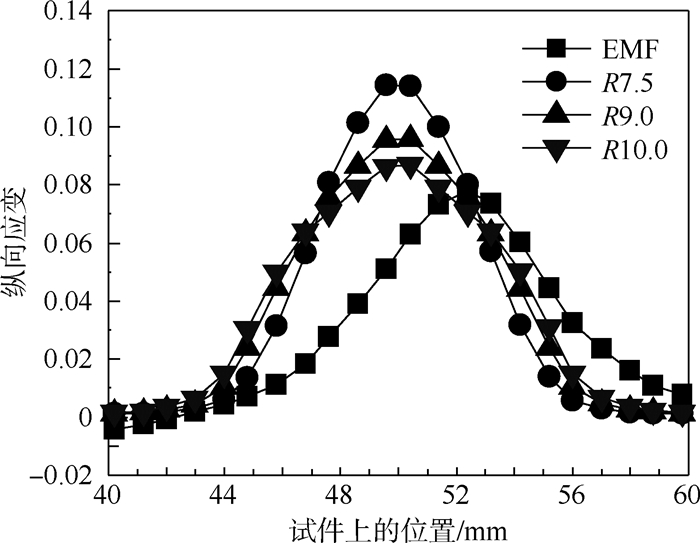 |
| 图 15 试件V形圆角外侧纵向拉应变Fig. 15 Longitudinal component tensile strain at outer radius of V-shaped corner of formed part |
| 图选项 |
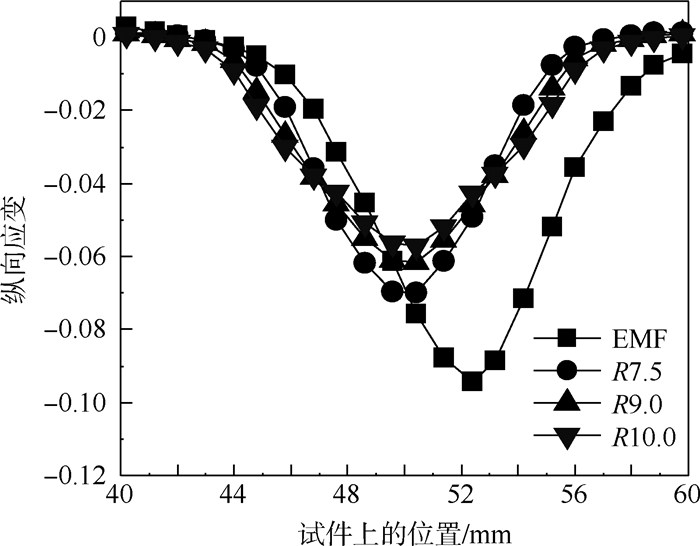 |
| 图 16 试件V形圆角内侧纵向压应变 Fig. 16 Longitudinal component of compressive strain at inner radius of V-shaped corner of formed part |
| 图选项 |
1) 应变峰值大小
由图 15可知,当V弯试件V形圆角内侧半径同为7.5 mm时,电磁V弯虚拟试件V形圆角外侧纵向拉应变的峰值远远低于机械V弯,两者相差31.7%。
当机械V弯的凸模圆角半径增加,V形圆角处的变形程度减小。由图 15可以看出,机械V弯凸模圆角半径为9.0 mm和10.0 mm时,试件V形圆角处的纵向拉应变峰值依然大于弯曲内径为7.5 mm的电磁V弯试件。
2) 变形区域大小
由图 15和图 16可知,在V形弯曲圆角处,用电磁成形方法所得应变曲线的“波形”比用传统机械冲压方法得到的“波形”要宽,尤其是图 16所示V形圆角内侧的压应变表现更为明显。这表明电磁V弯试件V形圆角附近有更大范围的金属材料参与了变形。由于电磁力分布不对称,试件应变值较大的区域也相应向电磁力较大的一侧移动。
4.2.2 实际零件应变对比 塑性成形过程中,板料受拉变形超过一定程度会产生多种缺陷,降低材料的使用性能。因此,V弯试件V形圆角外侧的变形是研究重点。同时也因为V形圆角受压侧的应变更难测量,所以只测量了R2位置的纵向拉应变。
为使机械V弯试件V形圆角外侧半径与电磁V弯试件V形圆角外侧半径R2相同,采用不同半径值的凸模进行机械V弯,然后,用半径规测量并选取出V角外侧半径同为11.5 mm的机械V弯试件与电磁V弯试件对比圆角外侧纵向拉应变。用于应变对比的试件如图 17所示。
 |
| 图 17 V形圆角外径相同的V弯试件Fig. 17 Formed parts by V-bending with the same outer radius of V-shaped corner |
| 图选项 |
表 3为测量的V弯试件V形圆角外侧纵向拉应变值。由表 3可知,电磁V弯试件的应变值比机械V弯低13.9%。尽管松散耦合电磁V弯数值模型的弯曲圆角半径与实验结果之间存在偏差,但实验试件间应变对比的结果与数值模型间应变对比的结果趋势相符,即同等弯曲半径下,电磁V弯试件的拉应变峰值低于传统机械V弯。
表 3 V弯试件V形圆角外侧纵向拉应变Table 3 Longitudinal component of tensile stain at outer radius of V-shaped corner of formed part by V-bending
| 试件类型 | 纵向应变 |
| 电磁V弯 | 0.075 8 |
| 机械V弯 | 0.088 0 |
表选项
5 结 论 通过电磁与机械2种V弯成形方法,加工出电磁V弯试件和机械V弯试件,分析了相同V形圆角半径下的电磁V弯试件和机械V弯试件的应变分布特征,结果表明:
1) 相同弯曲半径下,电磁V弯试件V形圆角外侧拉应变峰值低于机械V弯试件。
2) 电磁V弯比机械V弯有更大范围的金属材料参与弯曲变形。
电磁成形是脉冲电磁体积力作用下的高速成形,弯曲圆角拉应变峰值低、参与变形的材料范围大。因此,塑性变形导致的材料损伤程度更低,采用电磁成形技术可获得比传统成形方法具有更优使用性能和更长使用寿命的零件。
致 谢 感谢潘龙、范志松和冯飞在研究过程中的帮助。
参考文献
| [1] | MAMALIS A G,MANOLAKOS D E,KLADAS A G,et al.Electromagnetic forming and powder processing:Trends and developments[J].Applied Mechanics Reviews,2004,57(4):299-324. |
| Click to display the text | |
| [2] | GOLOVASHCHENKO S F.Material formability and coil design in electromagnetic forming[J].Journal of Materials Engineering and Performance,2007,16(3):314-320. |
| Click to display the text | |
| [3] | SHANG J H,DAEHN G.Electromagnetically assisted sheet metal stamping[J].Journal of Materials Processing Technology,2011,211(5):868-874. |
| Click to display the text | |
| [4] | PSYK V,RISCH D,KINSEY B L,et al.Electromagnetic forming-A review[J].Journal of Materials Processing Technology,2011,211(5):787-829. |
| Click to display the text | |
| [5] | PARK H I,KIM D,LEE J,et al.Experimental study on electromagnetic forming of high strength steel sheets with different dimensions of aluminum driver plate[C]//Proceedings of ICHSF 2014.Dortmund:Forming Technology and Lightweight Construction,TU Dortmund University,2014:237-242. |
| [6] | IRIONDO E,ALCARAZ J L,DAEHN G S,et al.Shape calibration of high strength metal sheets by electromagnetic forming[J].Journal of Manufacturing Processes,2013,15(2):183-193. |
| Click to display the text | |
| [7] | IRIONDO E,GUTIERREZ M A,GONZALEZ B,et al.Electromagnetic impulse calibration of high strength sheet metal structures[J].Journal of Materials Processing Technology,2011,211(5):909-915. |
| Click to display the text | |
| [8] | LEE P S,PIEHLER H R,ADAMS B L,et al.Influence of surface texture on orange peel in aluminum[J].Journal of Materials Processing Technology,1998,80-81(3):315-319. |
| Click to display the text | |
| [9] | POLÁK J.Plastic strain-controlled short crack growth and fatigue life[J].International Journal of Fatigue,2005,27(10-12):1192-1201. |
| Click to display the text | |
| [10] | AL-RUBAIE K S,DEL GRANDE M A,TRAVESSA D N,et al.Effect of pre-strain on the fatigue life of 7050-T7451 aluminium alloy[J].Materials Science and Engineering:A,2007,464(1-2):141-150. |
| Click to display the text | |
| [11] | 刘大海,周文华,李春峰.电磁力体积力效应对AA5052板材动态成形性的影响[J].塑性工程学报,2013,20(6):62-67. LIU D H,ZHOU W H,LI C F.Influence of body force effect of the pulsed magnetic forces on the dynamic forming limits of AA5052 sheets[J].Journal of Plasticity Engineering,2013,20(6):62-67(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [12] | VANBENTHYSEN R,THIBAUDEAU E,KINSEY B L.Effect of specimen planar area on electromagnetic flanging[J].Journal of Manufacturing Processes,2013,15(2):194-200. |
| Click to display the text | |
| [13] | GAO X,KIM J.Modeling of ductile fracture:Significance of void coalescence[J].International Journal of Solids and Structures,2006,43(20):6277-6293. |
| Click to display the text | |
| [14] | BARTELS G,SCHÄTZING W,SCHEIBE H P,et al.Comparison of two different simulation algorithms for the electromagnetic tube compression[J].International Journal of Material Forming,2009,2(S1):693-696. |
| Click to display the text | |
| [15] | SOHONI G S,WALAME M V,TANDON V,et al.Dynamic behavior characterization of lead at high strain rates using high speed photography for finite element simulation[C]//Proceedings of IMECE 2005.New York:ASME,2005:1-6. |
| Click to display the text | |
| [16] | XIONG W R,WANG W P,WAN M,et al.Effect of the duration of electromagnetic pulse force on the rebound suppression in V-bend experiment[C]//Proceedings of ICHSF 2014.Dortmund:Forming Technology and Lightweight Construction,TU Dortmund University,2014:335-344. |
| Click to display the text |
