Libby等通过观测发现蜥蜴、壁虎等从高空下落时可以利用尾巴的摆动调节其空中身体姿态,从而达到平稳着陆的目的[1]。文献[2]据此设计了带刚性尾巴的机械小车,当小车从高空跌落时,可通过尾巴的摆动改变下落姿态。美国密歇根大学Zhao等在跳跃机器人上加装单自由度尾巴以增加机器人的空中姿态稳定性,取得了很好的效果[3]。除尾巴以外,研究人员对生物翅膀拍动也进行了大量研究,认为翅膀对空中姿态也起着积极作用。如天蛾能通过翅膀的扭转运动实现身体姿态的俯仰运动[4],大黄蜂能通过调节翅膀拍动方向与速度实现前飞与悬停[5],飞鸟通过翅膀拍动与身体扭转的协调运动实现空中急速转弯[6],蝗虫在飞行中能通过翅膀的运动调节飞行姿态以躲避障碍物[7, 8]。仿生学的研究成果为机器人的设计提供了思路,德国FESTO公司研制的仿生机械蜻蜓“BionicOpter”,依靠改变翅膀拍动的角度改变飞行姿态,可实现蜻蜓的几乎所有动作,如前飞、急转弯和悬停等[9],其两侧翅膀运动相似。翅膀在仿生跳跃机器人上的应用,目前还仅限于利用滑翔以增强机器人的跳跃距离。如Woodward和Sitti研究发现蝙蝠可以利用前翼实现跳跃和滑翔运动,由此得到灵感,设计了一种跳跃与滑翔结合的微小型机器人,实现了跳跃机器人空中滑翔运动[10]。Kovac等对比分析了蝗虫、蝙蝠、蝴蝶翅膀构型,设计了一种滑翔翼,安装在研制的小型蚂蚱跳跃机器人上,实现跳跃起飞和滑翔滞空的运动[11]。Desbiens等设计了一种折叠翼安装于跳跃机器人上,用于增强跳跃性能[12]。
蝗虫能通过翅膀的拍动实现空中身体的转动,最后以理想姿态着陆。由此得到启发,本文提出利用翅膀进行机器人的空中姿态调整并且分析了翅膀拍动对机器人空中姿态的影响,搭建了仿蝗虫空中姿态调整机器人实验平台,验证了利用翅膀进行空中姿态调整的正确性和有效性。
1 蝗虫实验观测 采集健康活跃、体态均匀的东亚飞蝗进行实验观测。将蝗虫背部向下由高空自由下落,利用高速摄像机(FASTCAM 1280 PCI,Photron,USA,拍摄速率500帧/s)记录蝗虫自由下降过程中的翅膀拍动及身体滚转情况。
以蝗虫头部为坐标原点建立随体坐标系O0x0z0,如图 1所示,z0由蝗虫腹部指向背部,x00与z0垂直。定义蝗虫翅膀由腹部拍向背部方向为上拍,反之为下拍,上拍角度为正。左前翅、右前翅、左后翅与右后翅拍动角度分别以θ1、θ2、θ3与θ4表示,身体与竖直方向夹角为θ5。
 |
| 图 1 坐标系及测量角度Fig. 1 Coordinate system and measuring angles |
| 图选项 |
图 2为蝗虫下落过程中,两对翅膀的拍动角度以及身体滚转角度变化情况。由图 2(a)与图 2(b)可以看出,蝗虫翅膀拍动频率基本一致,约为29次/s,但是左右翅膀拍动存在明显的不对称现象,其幅值、相位均存在差异,且下拍与上拍时间也不相等。图 2(c)表示蝗虫在140 ms内能将其身体角度由165°调整到约40°并以正常姿态着陆。
 |
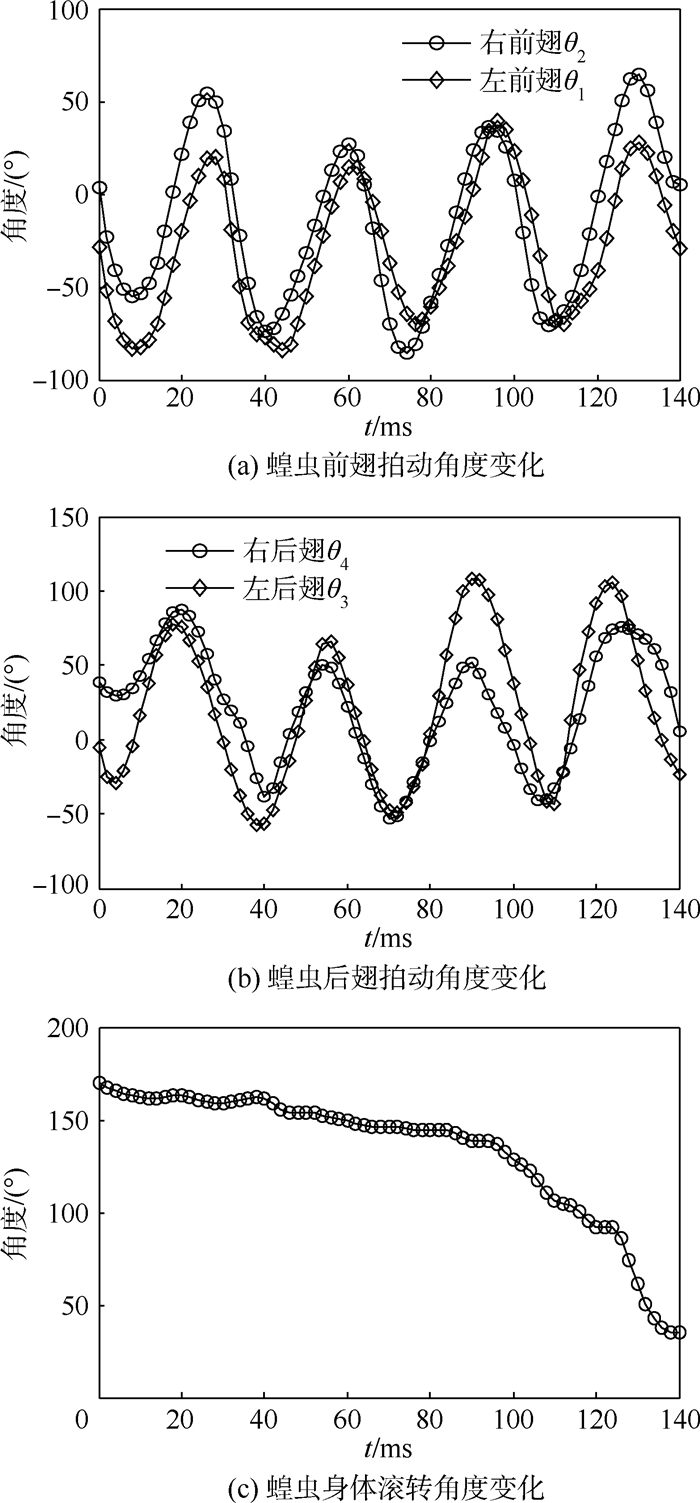| 图 2 蝗虫下落时翅膀拍动角度及身体滚转角度变化Fig. 2 Variations of flapping wings’ angles and body rolling angle when locust falling down |
| 图选项 |
图 2表明蝗虫能通过改变翅膀拍动的幅度、相位以及下拍与上拍的时间,使得左右翅膀呈现不对称运动,促使身体产生滚转从而调节其空中姿态保证平稳落地,由此得到启发,可利用翅膀的不对称运动进行机器人空中姿态调整。
2 实验样机设计 仿蝗虫空中姿态调整机器人由仿生机构本体、驱动系统、姿态感测系统、数据传输系统以及计算机控制系统组成,其中扑翼机构与传动结构为设计的重点。
扑翼运动包括拍打、挥摆和扭转3种模式,这3个自由度的复杂运动模式决定了昆虫扑翼的高升力和飞行的灵巧性。由于高频空间扑翼机构的实现难度较大,且本文主要是研究翅膀对机器人空中姿态调整的作用,因此,为简化结构,采用单对平面扑翼机构形式。如图 3(a)所示,电机通过减速齿轮系统带动曲柄摇杆机构上下摆动,实现翅膀的上下扑动。通过实验观测发现蝗虫左右翅膀拍动频率是相同的,故该仿蝗虫空中姿态调整机器人采用一个电机驱动。其左右翅膀的不对称运动可通过手动调节曲柄位置以改变翅膀拍动的幅度与初始相位而实现。由于两对翅膀传动结构相似,以左翅为例进行分析,建立机构简图如图 3(b)所示,O1为曲柄转动中心,O2为扑翼转动中心,驱动杆
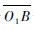长为L1,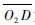
为翅膀支撑骨架,扑动关节C与中心O2点的距离为L3,连杆BC 长度为L2。O1与O2之间水平距离为a,竖直距离为b,则O1与O2之间距离
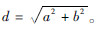当电机带动齿轮驱动曲柄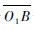作旋转运动时,设电机转动频率为f,扑翼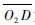将以相同频率作上下扑动。 |
| 图 3 扑翼机构结构图Fig. 3 Structure of flapping wing |
| 图选项 |
以O1点为坐标原点建立坐标系O1x1y1,以O2为坐标原点建立坐标系O2x2y2,设在地面坐标系中,O1坐标为(0,0),则O2点的坐标为(-a,b),B点轨迹可以表示为
C点轨迹为
式中:β为曲柄O1B与x1方向的夹角;φ为摆动杆O2D与x2方向的夹角。根据机构约束关系,有
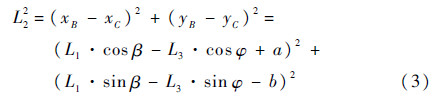
为使翅膀上拍与下拍阶段产生不同的作用力,则需保证翅膀上拍与下拍阶段速度不同,故该机构具有急回特性。急回特性程度可用行程速度变化系数K表示,K越大,则急回特性越明显,一般取值范围为K∈(1,2),本文中K取1.4。设计机构扑翼最大摆动角度ψ为60°。根据曲柄摇杆机构的设计方法[13],可计算得出各杆件尺寸如表 1所示。
表 1 各杆件尺寸及参数值Table 1 Size of each rod and values of parameters
| 参数 | L 1 | L 2 | 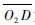| a | b | L 3 |
| 尺寸/mm | 3 | 10.6 | 140 | 13.5 | 8 | 10 |
表选项
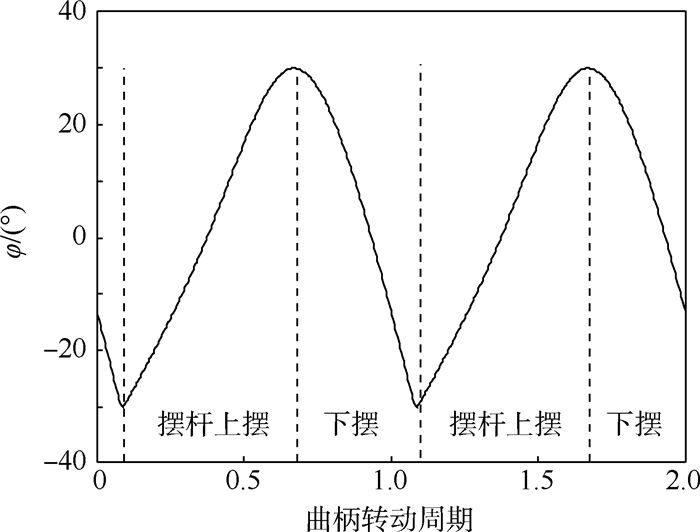
将表 1各参数代入式(3),可计算得出电机转动周期与摆杆摆动角度关系如图 4所示。由图可以看出,摆杆运动存在急回特性,摆动角度与设计值相符,故满足要求。
 |
| 图 4 电机匀速转动时摆杆摆动规律Fig. 4 Rods swing rule when motor rotating uniformly |
| 图选项 |
3 翅膀影响分析 由于蝗虫翅膀拍动时,翅膀扭转存在一个偏转角度,因此拍动中相对于前进方向产生一个迎角。本结构无法实现翅膀的扭转,但是可以将翅膀倾斜安装,倾斜安装角为2°。图 5为翅膀拍动简易模型,设翅膀展向距离旋转中心r处翅膀弦长为cA(r),所受气动力为dF,翅膀拍动时,左翅对机身产生的力矩为M1,右翅产生的力矩为M2。
 |
| 图 5 翅膀拍动模型 Fig. 5 Wings flapping model |
| 图选项 |
3.1 力与翅膀拍动关系 根据流体力学原理[14],翅膀拍动时,其所受力为
式中:ρ为空气密度；A为翅膀面积；U为流速；CL为升力系数。由于本文限制机体向前运动,因此翅膀上某点处空气流速等于该点的线速度,即为r
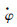(t),其可由式(3)求解得出。根据Dickinson总结的经验公式[15],升力系数为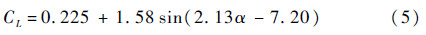
式中:α为迎角。则翅膀扑动时所产生的升力为
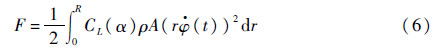
式中:R为翅膀整个展向距离,即为
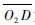尺寸,取为140 mm(见表 1)。代入机构尺寸及ρ=1.25×103 kg/m3,则可以得出气动力(F)与拍动频率(f)关系,如图 6(a)所示。由图可知,翅膀拍动产生的气动力与拍动频率有关,频率越高,产生的气动力越大。 |
| 图 6 翅膀拍动频率、振幅与气动力关系Fig. 6 Relationships between wings flapping frequencies,amplitudes and aerodynamic forces |
| 图选项 |
当左右翅膀拍动频率一致时,改变曲柄位置,可以改变翅膀拍动幅值(ψ),代入机构尺寸,结合式(6),可计算出不同幅值情况下,一个拍动周期内上拍与下拍时翅膀所受气动力值,设翅膀下拍时产生气动力为正,上拍时为负。如图 6(b)所示,下拍时气动力整体大于上拍时气动力,且振幅越大,产生的气动力也越大。
3.2 力矩与翅膀拍动关系 为分析翅膀拍动对姿态的影响,需要计算翅膀所受力对躯体产生的力矩变化情况。由图 5可知翅膀上距离转轴距离为r处产生的气动力对机身的力矩为
对式(7)沿着翅膀展向积分可得拍动时,单侧翅膀上所受力对机体产生总力矩:
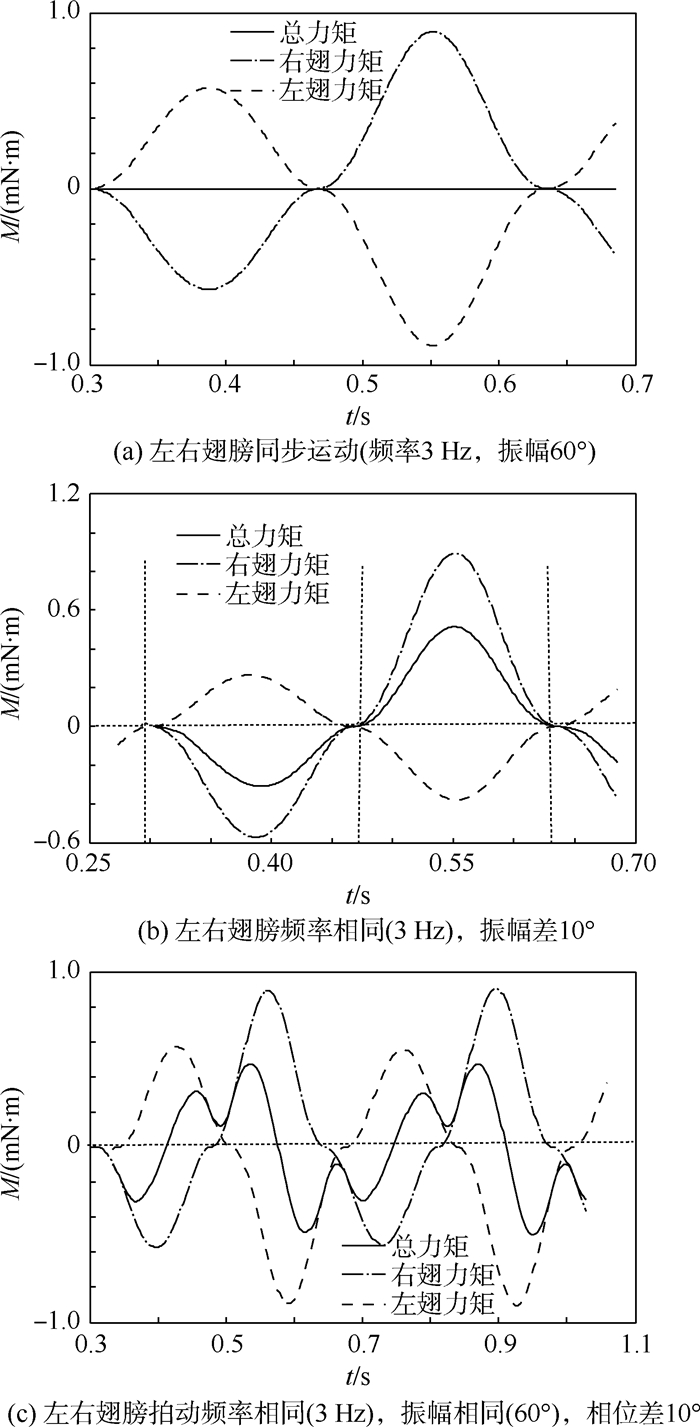
设机体所受力矩顺时针为正(见图 5),则当左右翅膀同步拍动时,翅膀所产生气动力相同,但其对机体产生力矩相反,故合力矩为零,如图 7(a)所示,此时,两翅膀所受力对机体的合力矩为零,翅膀拍动主要提供升力与前进的动力。当翅膀拍动频率不变(3 Hz),振幅不同时,如图 7(b)所示,减小右翅的拍动角度为±25°,则左右 翅膀产生的力矩将不再相等,此时产生的合力矩不为零。在合力矩作用下,机体将产生转动。由于下拍阶段的力矩大于上拍阶段的力矩,则下拍合力矩大于上拍合力矩,机体将逆时针旋转。当左右翅膀拍动频率与幅值均相等,而相位不同时,如图 7(c)所示,频率为3 Hz,振幅为60°,右翅初始相位相对左翅延后约10°,则左右翅膀对机体合力矩呈震荡趋势。分析图 7(c)发现,合力矩为正与为负时正好相等,故将使得机体左右摇摆但是无法产生持续的旋转效果。
 |
| 图 7 左右翅膀同步与不同步拍动时力矩变化Fig. 7 Variations of torques when left and right wings flapping synchronously and asynchronously |
| 图选项 |
分析可知,当左右翅膀同步拍动时,机体相对稳定,拍动频率增大可提高升力但是对姿态影响不大;当左右翅膀有着相位差时,翅膀拍动可使机体左右摇摆却不能产生持续旋转作用;当左右翅膀拍动幅值不同时,产生的合力矩将促使机体产生转动。因此,可通过改变左右翅膀拍动的幅值改变机体空中姿态。
4 实验验证 为验证利用翅膀进行空中姿态调整机理的正确性与可行性,搭建了实验平台,如图 8所示,由仿蝗虫空中姿态调整机器人系统、实验支架、计算机控制及实时显示系统以及摄像系统组成。机器人置于实验支架上,可绕支架轴自由转动,但俯仰与偏航自由度被限制。通过姿态感应器测量机体的滚转角度,通过摄像系统记录翅膀拍动与机体姿态变化情况,通过计算机控制系统调控电机转速以及显示姿态角度变化情况。
 |
| 图 8 仿蝗虫空中姿态调整实验平台Fig. 8 Experimental platform of air posture adjustment inspired by locust |
| 图选项 |
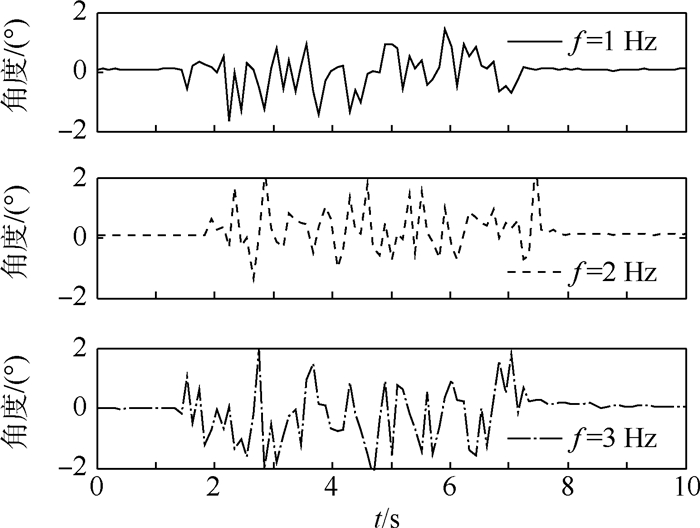
当左右翅膀同步拍动时,即左右翅膀相位、振幅、拍动频率一致,如图 9所示,机体先处于静止状态(0~2 s左右),当翅膀拍动时(2~8 s左右),出现抖动;当翅膀停止拍动时(8~10 s左右),机体静止。整个过程机体滚转角度变化较小。当拍动频率提高时,机体抖动幅度略有增大,但是整体幅值变化较小,在±2°之内,姿态较稳定。因此,翅膀的同步拍动不会引起机体的滚转运动。此时,翅膀的拍动主要提供升力与前飞动力。
 |
| 图 9 翅膀同步拍动机体滚转姿态变化情况Fig. 9 Effects on airframe rolling posture when wings flapping synchronously |
| 图选项 |
当左右翅膀拍动不同步时,如右翅拍动幅值相对左翅减小,但是左右翅拍动频率一致,此时将引起机体的滚转运动。如图 10(a)所示,当拍动频率为1 Hz时,机体滚转角度约为3°;当拍动频率为2 Hz时,机体滚转角度约为10°;当拍动频率为3 Hz时,机体滚转角度约为19°。当左右翅膀拍动幅值一定,但是存在一定相位差时,如图 10(b)所示,翅膀拍动带来机体的左右摇摆,振动 幅值相对左右翅膀同步拍动要大,且随着拍动频率的增加,幅值也增大,但是未出现机体向着同一个方向旋转的情况。因此可以认为,此时左右翅膀产生的力矩周期性变化,使得机体在平衡位置左右摆动。实验结果与理论分析基本一致。
 |
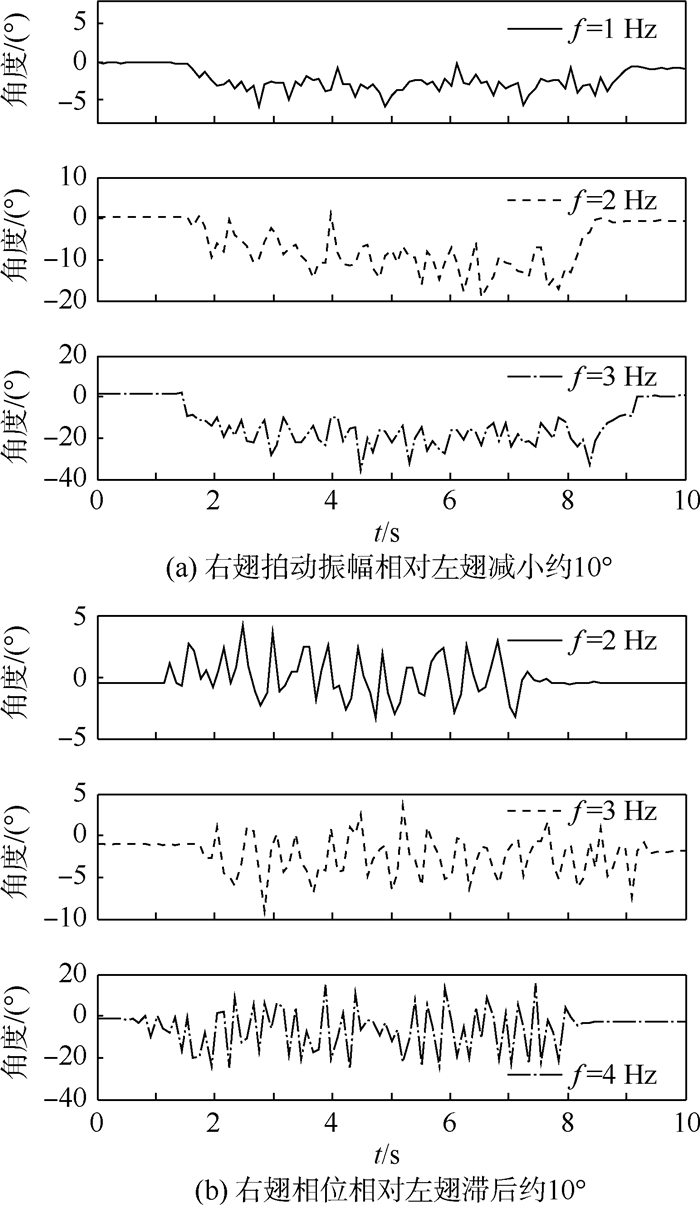| 图 10 翅膀不同步运动时对机体滚转姿态的影响Fig. 10 Effects on airframe rolling posture when wings flapping asynchronously |
| 图选项 |
该实验证明,当左右翅膀同步拍动时,翅膀主要提供升力与前飞动力,左右翅膀产生的旋转力矩将相互抵消,机体较稳定;当左右翅膀拍动频率一致、振幅不同时,翅膀的拍动将引起机体的滚转运动,拍动频率越高,滚转效果越明显;当左右翅膀拍动频率、振幅一致,但是相位存在差异时,翅膀的拍动带来力矩周期性变化,此时机体将在平衡位置左右摇摆,拍动频率越高,摇摆幅度越大。因此,可以通过改变左右翅膀拍动的振幅以调节仿蝗虫机器人空中姿态,可通过提高拍动频率以提高姿态调整的效率。
5 结 论 1) 设计了仿蝗虫空中姿态调整机器人系统,利用曲柄摇杆机构实现翅膀的摆动。计算得出了存在急回特性的机构尺寸值并分析了电机匀速转动时摇杆的摆动规律。
2) 分析了翅膀同步与不同步运动产生的气动力与力矩变化情况以及对机体的作用。分析发现翅膀拍动频率越大,气动力越大。翅膀同步拍动对机体产生的力矩为零;左右翅膀拍动振幅不同时,将产生促使机体旋转的力矩;当左右翅膀拍动相位不同时,对机体产生的合力矩呈现周期性变化。
3) 搭建了实验验证平台并进行了仿蝗虫机器人空中姿态调整实验。通过实验发现左右翅膀同步拍动主要提供升力与前进动力,并不能进行滚转姿态的调节;左右翅膀振幅不同时,可使得机体产生滚转运动,此时拍动频率越高,滚转效果越明显;左右翅膀相位不同时,仅使得机体在平衡位置来回摆动,拍动频率越高,摆动幅值越大,与理论分析基本一致,验证了蝗虫通过翅膀不对称运动进行空中姿态调整的机理。
4) 该实验证明了通过翅膀不同步运动进行机器人空中姿态调节的正确性与可行性。通过改变左右翅膀的拍动幅度进行滚转运动的调节,通过提高拍动频率提高调节效率。为仿蝗虫机器人空中姿态调整的设计提供了依据。
本文翅膀拍动幅值的改变主要通过手动调节连杆与齿轮连接位置实现,在实际空中姿态调整机器人设计中,可采用2个电机驱动2套齿轮旋转以实现左右翅膀拍动的不同步。
参考文献
| [1] | LIBBY T,MOORE T Y,CHANG-SIU E,et al.Tail-assisted pitch control in lizards,robots and dinosaurs[J].Nature,2012,481(7380):181-184. |
| Click to display the text | |
| [2] | CHANG-SIU E,LIBBY T,TOMIZUKA M,et al.A lizard-inspired active tail enables rapid maneuvers and dynamic stabilization in a terrestrial robot[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).Piscataway,NJ:IEEE Press,2011:1887-1894. |
| [3] | ZHAO J,ZHAO T,XI N,et al.Controlling aerial maneuvering of a miniature jumping robot using its tail[C]//2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).Piscataway,NJ:IEEE Press,2013:3802-3807. |
| Click to display the text | |
| [4] | CHENG B,DENG X,HEDRICK T L.The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta)[J].The Journal of Experimental Biology,2011,214(24):4092-4106. |
| Click to display the text | |
| [5] | XU N,SUN M.Lateral dynamic flight stability of a model bumblebee in hovering and forward flight[J].Journal of Theoretical Biology,2013,319:102-115. |
| Click to display the text | |
| [6] | SU J Y,TING S C,YANG J T.How a small bird executes a sharp turning maneuver:A mechanical perspective[J].Experimental Mechanics,2012,52(7):693-703. |
| Click to display the text | |
| [7] | ROBERTSON R M,JOHNSON A G.Collision avoidance of flying locusts:Steering torques and behaviour[J].Journal of Experimental Biology,1993,183(10):35-60. |
| Click to display the text | |
| [8] | ROBERTSON R M,KUHNERT C T,DAWSON J W.Thermal avoidance during flight in the locust locusta migratoria[J].Journal of Experimental Biology,1996,199(6):1383-1393. |
| Click to display the text | |
| [9] | GAISSERT N,MUGRAUER R,MUGRAUER G,et al.Inventing a micro aerial vehicle inspired by the mechanics of dragonfly flight[M].Towards Autonomous Robotic Systems.Berlin,Heidelberg:Springer,2014:90-100. |
| [10] | WOODWARD M A,SITTI M.Design of a miniature integrated multi-modal jumping and gliding robot[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS).Piscataway,NJ:IEEE Press,2011:556-561. |
| Click to display the text | |
| [11] | KOVAC M,HRAIZ W,FAURIA O,et al.The EPFL jumpglider:A hybrid jumping and gliding robot with rigid or folding wings[C]//IEEE International Conference on Robotics and Biomimetics.Piscataway,NJ:IEEE Press,2011:1503-1508. |
| Click to display the text | |
| [12] | DESBIENS A L,POPE M T,CHRISTENSEN D L,et al.Design principles for efficient,repeated jumpgliding[J].Bioinspiration & Biomimetics,2014,9(2):025009. |
| Click to display the text | |
| [13] | 程友联,吴晓红.曲柄摇杆机构的参数设计法[J].机械设计,2010(9):60-62. CHENG Y L,WU X H.Parameter design method of crank-rocker mechanism[J].Journal of Machine Design,2010(9):60-62. |
| Cited By in Cnki (13) | Click to display the text | |
| [14] | OERTEL H,ERHARD P,ASFAW K,et al.Prandtl-essentials of fluid mechanics[M].New York:Springer,2010:212-259. |
| [15] | DICKINSON M H,LEHMANN F O,SANE S P.Wing rotation and the aerodynamic basis of insect flight[J].Science,1999,284(5422):1954-1960. |
| Click to display the text |
