基于LD的RIOG中,为了检测Sagnac效应产生的谐振频差,通过电流调谐将LD的中心频率锁定在谐振腔的谐振频率处[13].由于驱动电流的调节同时改变LD的输出频率和光强,必然引入强度噪声.文献[14]已经分析了光源强度噪声对开环RIOG性能的影响,得到光源强度噪声对陀螺性能的影响与固有零偏值相关.为了消除开环RIOG中的这种电流调谐致强度噪声,文献[15]提出了基于模拟减法电路的强度噪声抑制方案.但是该方案存在两个不足之处:①需要增加新的电路器件,不利于系统的小型化;②模拟减法电路控制精度低,容易受环境因素的影响.文献[16]基于声光移频器实现了RIOG的闭环检测,理论上可以消除光源强度噪声对陀螺性能的影响,但是声光移频器不仅增加了光路器件,还引入了新的噪声源,不利于系统集成和陀螺精度的提高.本文在研究LD电流调谐致强度噪声的特性基础上,提出了基于频率锁定位置的强度噪声抑制方案,该方案采用数字补偿方法,不需要增加任何光路和电路器件,利于系统的小型化.本文还搭建了实验系统,验证了方案的可行性,有效抑制了开环RIOG的电流调谐致强度噪声.
1 电流调谐致强度噪声分析与抑制 1.1 RIOG基本原理 图 1给出了基于LD的开环RIOG结构框图,LD发出的光经光隔和集成光学调制器后,被分为两束相等的光,并受到集成光学调制器的三角波相位调制作用.两束光经耦合器C1耦合进入集成光学谐振腔,在谐振腔内分别沿顺时针和逆时针方向传输.传输不同圈数的顺时针光和逆时针光经耦合器C2耦合出谐振腔时分别发生多光束干涉,干涉光强由光电探测器PD1和PD2探测.当陀螺旋转时,顺时针光与逆时针光的谐振频差与旋转角速度成正比.为了检测该谐振频差信号,频率锁定环路根据PD2的解调输出反馈控制LD的驱动电流,将LD的中心频率锁定在逆时针光的谐振频率处,而信号检测环路根据PD1的解调输出得到正比于角速度的陀螺输出信号.
 |
| IL(t)—LD的输出光强;IIN(t)—集成光学谐振腔的输入光强;IPD(t)—集成光学谐振腔的输出光强;CW—顺时针方向;CCW—逆时针方向图 1 基于LD的开环RIOG结构框图Fig. 1 Structure block diagram of open-loop RIOG based on LD |
| 图选项 |
1.2 电流调谐致强度噪声分析 根据图 1所示的开环RIOG检测原理,LD的中心频率与逆时针光的谐振频率相等,但随着应力、温度、旋转角速度等因素的变化,逆时针光的谐振频率在不断变化.当LD的中心频率与逆时针光的谐振频率不相等时,频率锁定环路根据PD2解调得到的误差信号反馈控制LD的驱动电流,调整其中心频率,实现LD中心频率对逆时针光谐振频率的实时锁定.此时,LD的驱动电流i(t)与逆时针光的谐振频率fCCW之间的关系为
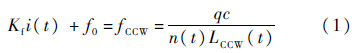
式中:Kf为LD的电流调谐系数;f0为LD的初始频率;q为纵模阶数;c为真空中的光速;n(t)为集成光学谐振腔的折射率;LCCW(t)为逆时针光路的等效腔长.
LD的输出光强IL(t)和驱动电流i(t)的关系如图 2所示,其中ith为LD的阈值电流.当LD的驱动电流小于阈值电流时,如图 2中区域Ⅰ所示,LD的输出只有很微弱的光,并且输出光强与驱动电流无关.当LD的驱动电流大于阈值电流时,输出光强随着驱动电流的增大而增加,并且输出光强和驱动电流之间近似为线性关系,如图 2中区域Ⅱ所示.RIOG中LD工作在区域Ⅱ,在该区域内光强IL(t)和驱动电流i(t)的关系可以近似表示为[15]

式中:KI为LD的强度调节系数.
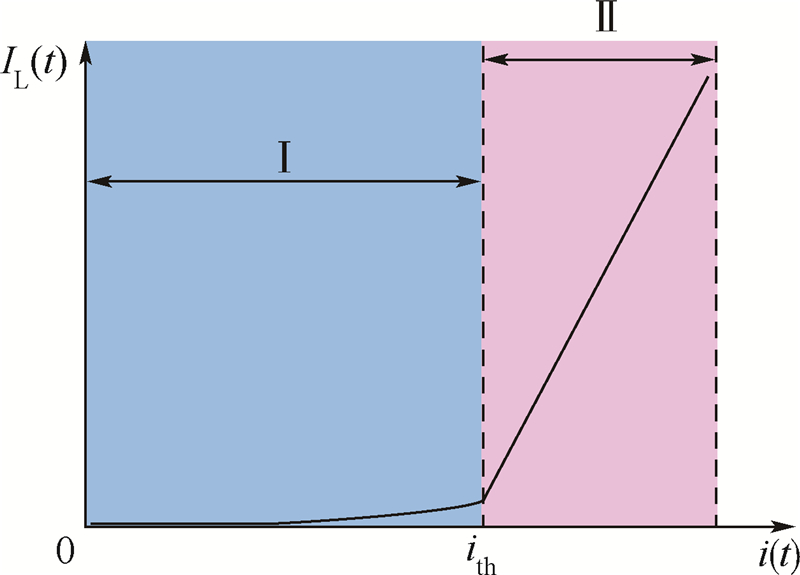 |
| 图 2 LD的输出光强与驱动电流之间的关系示意图Fig. 2 Illustration of relationship between intensity of LD and its driven current |
| 图选项 |
将式(1)代入式(2),得到
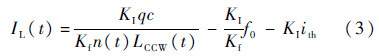
因此,通过电流调谐实现频率锁定的同时,必然改变LD的输出光强,引入光源强度噪声.这种电流调谐致强度噪声同时受环境因素和旋转角速度的影响,频率分量比较复杂,无法通过传统数字滤波滤除,严重影响RIOG的性能[13].
RIOG中的电流调谐致强度噪声可以等效为光源强度波动噪声,它通过改变谐振曲线影响陀螺的性能.对于图 1中LD的输出光强IL(t),由于光隔和集成光学调制器的作用,逆时针光入腔前的光强可以表示为IIN(t)=KlossIL(t),Kloss为光强入腔前的损耗系数.当LD的中心频率与逆时针光的谐振频率之差为ΔfCCW(t)时,集成光学谐振腔的输出光强IPD(t)可以表示为[17]

式中:Γ为谐振曲线的半高全宽.
根据式(4),对于一定的频差ΔfCCW(t),谐振腔的输出光强IPD(t)与LD的输出光强IL(t)之间为线性关系.图 3给出了当谐振腔的输入光强IIN分别为0.9I0、1.0I0、1.1I0、1.2I0时的仿真谐振曲线,从图 3中可以看出,当LD的输出光强波动引起入腔光强变化时,会线性改变谐振曲线的形状.根据三角波相位调制解调原理,对于相同的调制参数,谐振曲线的变化会改变陀螺输出环路的增益,造成陀螺标度因数的变化,最终影响RIOG的性能[18, 19].
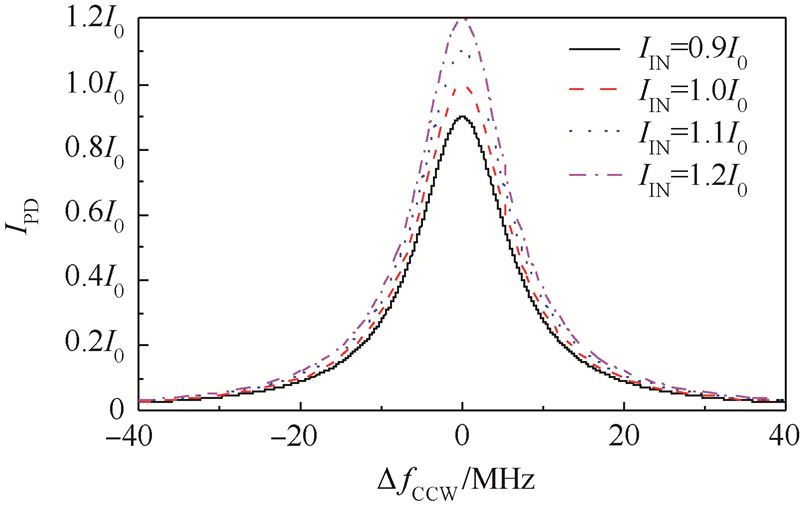 |
| 图 3 谐振腔输入光强波动对谐振曲线的影响Fig. 3 Fluctuation influence of resonator’s input intensity on resonance curve |
| 图选项 |
文献[14]已经分析了光源强度波动对开环RIOG输出的影响,陀螺输出Gout(t)与光源强度IL(t)之间为线性关系,并且与陀螺的固有零偏值相关.开环陀螺输出Gout(t)可以表示为
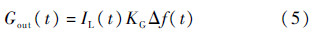
式中:Δf(t)为顺逆时针光之间的谐振频差,其中包含陀螺的固有非互易频差;KG为陀螺输出与Δf(t)之间的归一化比例系数.依据式(5)所示的线性关系,为了消除电流调谐致强度噪声对陀螺性能的影响,可监测LD输出光强的变化,然后对RIOG的输出进行实时补偿.
三角波相位调制等效于方波频率调制[20],当LD的中心频率被锁定在逆时针光的谐振频率时,LD的中心频率与逆时针光的谐振频率之差为零.此时,如图 4所示,逆时针光路的输出为一恒定光强值Ilock,结合式(4),可以得到频率锁定时的输出光强Ilock可以表示为
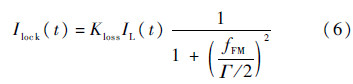
式中:fFM为三角波相位调制等效的方波频率调制幅度.
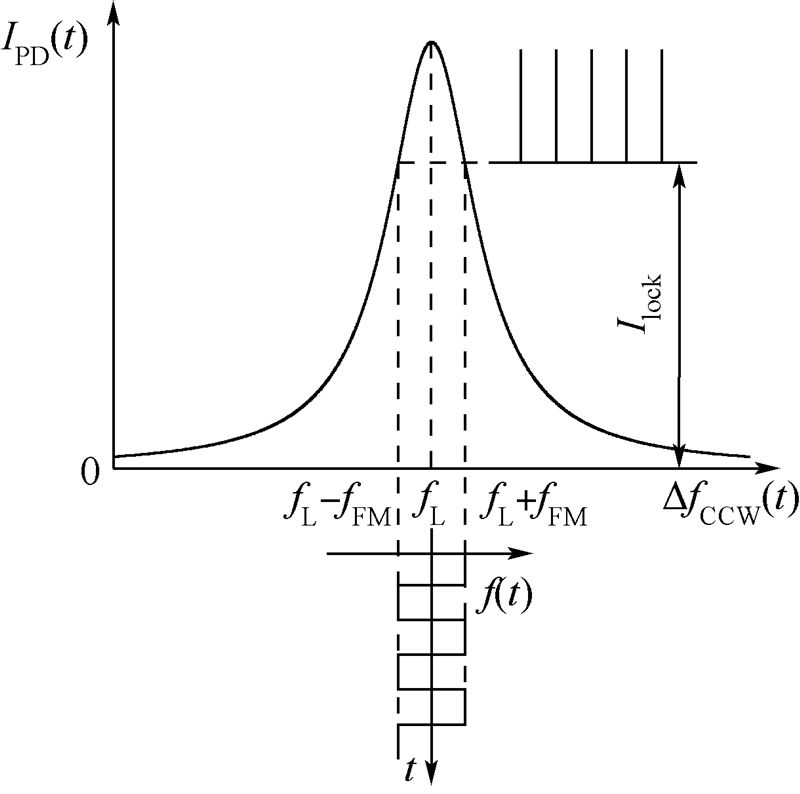 |
| 图 4 频率锁定条件下的谐振腔输出光强Fig. 4 Output intensity of resonator under condition of frequency locking |
| 图选项 |
根据式(6),Ilock(t)与IL(t)之间为线性关系.因此,可以建立Ilock(t)与陀螺输出之间的理论模型,然后通过Ilock(t)实时地监测LD输出光强的变化,并对光源强度波动进行补偿,为消除开环RIOG中的电流调谐致强度噪声提供一种方法.
1.3 抑制方案基于第1.2节分析,提出了基于频率锁定位置的强度噪声抑制方案.基本原理方案如图 5所示,PD2的输出电压给出了频率锁定位置,它与频率锁定时逆时针光路的输出光强成正比,并且实时反应了LD输出光强的变化趋势.信号检测环路一方面采集PD2输出的电压直流信号,用于监测LD的光强波动情况,得到补偿系数;另一方面根据PD1得到解调输出信号,将解调输出信号与补偿系数相乘,消除光强波动对陀螺输出的影响,达到抑制电流调谐致强度噪声的目的.
 |
| 图 5 基于频率锁定位置的强度噪声抑制方案示意图Fig. 5 Scheme illustration of intensity noise suppression based on frequency locking position |
| 图选项 |
在频率锁定条件下,假定图 5中LD的初始光强I0与PD2输出的初始频率锁定位置Dlock之间有如下比例关系:

式中:Klock为两者之间的比例系数.式(7)对光强I0求导,可以得到PD输出频率锁定位置的变化量为

根据式(8),当LD的初始光强I0受强度变化量ΔI0(t)影响时,RIOG的输出可以表示为
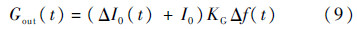
结合式(8)和式(9),得到反映光源强度变化趋势的补偿系数为
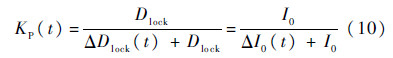
将RIOG的输出Gout(t)乘以补偿系数KP(t),得到
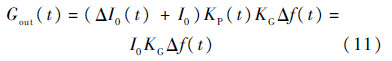
因此,补偿之后RIOG的输出Gout(t)中不再包含强度变化因子ΔI0(t),消除了强度噪声对陀螺性能的影响.
2 实验结果与讨论 根据图 1建立了RIOG实验系统,其中LD的中心波长为1550nm,洛伦兹线宽为1.17kHz,最大输出光功率为20mW;集成光学谐振腔的长度为18.8cm,半高全宽为13.4MHz;调制三角波的频率为1MHz,调制电压峰峰值为20V;光电探测器PD1和PD2均采用PIN-FET组件,响应度为0.92A/W.光电探测器PD1和PD2的输出电压经A/D转换后到达可编程逻辑器件的现场可编程门阵列(Field-Programmable Gate Array,FPGA),频率锁定、信号检测和实时补偿都基于FPGA实现.
根据RIOG的谐振特性,当集成光学谐振腔的入射光频率与谐振腔的谐振频率之差线性变化时,谐振腔的输出可探测到谐振曲线.实验中默认短期内谐振腔的谐振频率保持不变,通过控制FPGA线性调节LD的驱动电流对LD扫频,测试得到集成光学谐振腔输出的谐振曲线如图 6所示,验证了驱动电流对LD的线性调谐特性.当扫频出现谐振峰时,启动FPGA内部的频率反馈控制模块,完成LD中心频率对逆时针光谐振频率的锁定.频率锁定之后,PD2探测到的谐振腔输出如图 7所示,由于三角波相位调制等效的方波频率调制作用,在每个方波频率调制周期内,调制频率切换时会产生一个尖峰脉冲信号,造成谐振腔的输出并非理想的直流电压信号.为了提高频率锁定位置的采集精度,信号采样时应避开尖峰脉冲区域,一个解调周期内的理想信号采样区域如图 7中阴影所示.根据三角波相位调制解调原理[17],图 7中信号采样区域①和②的共模分量反应了频率锁定位置,并且该共模分量不受频率锁定误差的影响,可用于实时监测LD输出光强的变化.
 |
| 图 6 集成光学谐振腔的谐振曲线Fig. 6 Resonance curve of integrated optic resonator |
| 图选项 |
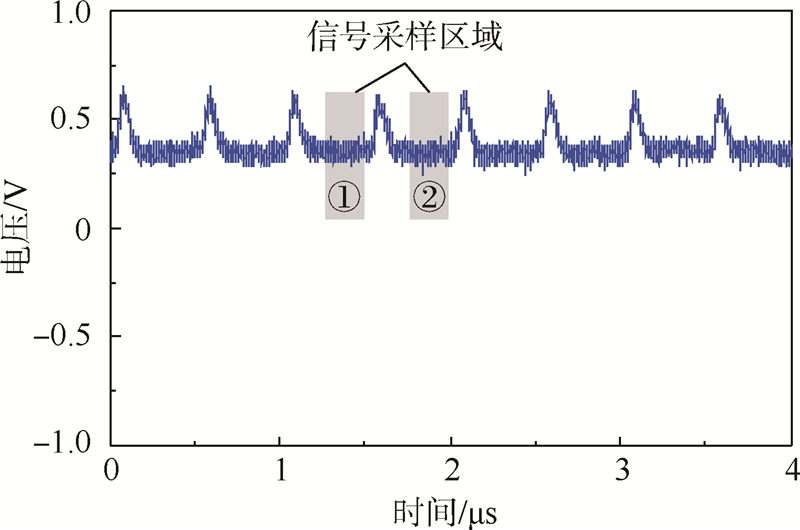 |
| 图 7 频率锁定时的PD2输出Fig. 7 Output of PD2 under condition of frequency locking |
| 图选项 |
为了验证频率锁定位置与LD输出光强之间的线性关系,在频率锁定条件下,同时采集了光电探测器PD2的输出和LD的光强输出.图 8和图 9分别给出了PD2输出的频率锁定位置数字量和LD的光强输出数字量,从图 9中可以看出,受电流调谐和环境因素的影响,LD输出的光强中叠加了一个低频噪声,该噪声无变化规律,但它与频率锁定位置的变化趋势一致.将频率锁定位置数字量与光强数字量相除,图 10给出了数据处理结果,两者的比值与光强波动无关,表明频率锁定位置可以实时地反应LD输出光强的变化趋势.
 |
| 图 8 频率锁定位置输出Fig. 8 Output of frequency locking position |
| 图选项 |
 |
| 图 9 LD光强输出Fig. 9 Intensity output of LD |
| 图选项 |
 |
| 图 10 频率锁定位置与LD光强之比Fig. 10 Ratio between frequency locking position and LD intensity |
| 图选项 |
理论模型的精确度严重制约了实时补偿算法的效果,而频率锁定位置数字量与光强数字量的比值在一定程度上反映了模型的精确度.从图 10中可以看出,两者之间的比值并非严格的直线,它围绕均值存在±0.5的误差,分析主要有3个方面的原因:①频率锁定位置与输出光强的信号采集环路非互易,存在时间延时,影响两者的相关性;②信号采集环路中的器件受环境噪声的影响,使两路信号分别产生增益误差,并将误差引入比值当中;③RIOG系统中光学器件受环境因素产生了光学误差,并随着光电转换引入采集结果当中.因此,为了提高实时补偿效果,实验中不但选择了环境性能较好的光路和电路器件,还保持频率锁定环路和信号检测环路的器件互易性,尽可能提高理论模型的精确度.
采集得到频率锁定位置的基础上,根据式(10)计算得到补偿系数,然后将补偿系数与PD1的解调输出相乘,实现对LD强度噪声的实时补偿,消除了强度噪声产生的陀螺标度因数变化.为了对比补偿算法对电流调谐致强度噪声的抑制效果,图 11给出了实时补偿前后2h的陀螺静态测试数据,从图中可以看出,补偿之前陀螺输出与光强变化保持一致,显然受到电流调谐致强度噪声的影响.而补偿之后陀螺输出与光强波动不相关,证明光源强度噪声得到了有效抑制.对比补偿前后的陀螺性能,RIOG的零偏稳定性由0.768(°)/s提高到了0.103(°)/s,有效改善了陀螺输出精度.
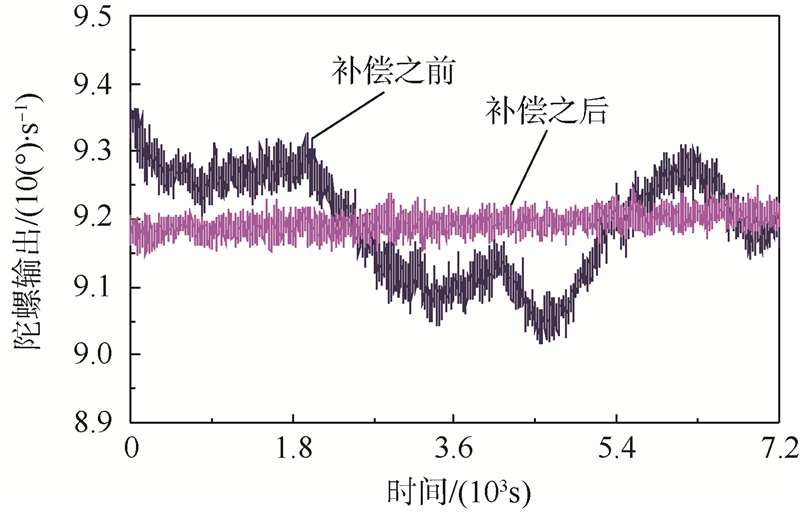 |
| 图 11 补偿前后陀螺输出结果Fig. 11 Gyro output before and after compensation |
| 图选项 |
基于频率锁定位置的强度噪声抑制方案不仅适用于陀螺静态测试,还同样适用于陀螺转动实验.当陀螺发生转动时,由于集成光学谐振腔中逆时针光的谐振频率会发生变化,频率锁定环路会调节LD的中心频率实时跟踪并锁定逆时针光的谐振频率.虽然在频率跟踪与锁定过程中会存在频率锁定误差,但频率锁定位置为图 7中采样区域①和采样区域②的共模分量,不受频率锁定误差的影响,仍可实时监测LD输出光强的变化,对光源强度波动进行补偿.此外,该方案基于FPGA对开环RIOG的输出进行实时数字补偿,既不会影响陀螺的动态特性,又不需要增加任何光路和电路器件,利于系统的小型化.
3 结 论 本文在分析RIOG中电流调谐致强度噪声特性的基础上提出了一种基于频率锁定位置的强度噪声抑制方案,经理论分析和实验验证表明:
1) RIOG中的电流调谐致强度噪声可等效为光源强度波动噪声,它通过改变谐振曲线影响陀螺的性能.
2) 频率锁定位置与LD输出光强之间为线性关系,利用频率锁定位置可实时监测LD输出光强的波动.
3) 该方案基于FPGA对开环RIOG的输出进行实时数字补偿,既不会影响陀螺的动态特性,又不需要增加任何光路和电路器件.
4) RIOG的零偏稳定性由0.768(°)/s提高到0.103(°)/s,验证了方案的可行性.
为进一步提高该方案对电流调谐致强度噪声的抑制的效果,仍需改善理论模型的精确度.
参考文献
| [1] | Hervé C L.光纤陀螺仪[M].张桂才,王巍,译.北京:国防工业出版社,2002:157-167.Hervé C L.The fiber-optic gyroscope[M].Translated by Zhang G C,Wang W.Beijing:National Defense Industry Press,2002:157-167(in Chinese). |
| [2] | Mario N A,Caterina C,Francesco D O,et al.Advances in gyroscope technologies[M].Berlin:Springer-Verlag,2010:37-46. |
| [3] | Feng L S,Wang J J,Zhi Y Z,et al.Transmissive resonator optic gyro based on silica waveguide ring resonator[J].Optics Express,2014,22(22):27565-27575. |
| Click to display the text | |
| [4] | Suzuki K,Takiguchi K,Hotate K.Monolithically integrated resonator microoptic gyro on silica planar lightwave circuit[J].Journal of Lightwave Technology,2000,18(1):66-72. |
| Click to display the text | |
| [5] | Sanders G A.Critical review of resonator fiber optic gyroscope technology[J].SPIE Fiber Optic Sensors,1992,CR44:115-133. |
| [6] | Takiguchi K,Hotate K.Partially digital-feedback scheme and evaluation of optical Kerr-effect induced bias in optical passive ring-resonator gyro[J].IEEE Photonics Technology Letters,1991,3(7):679-681. |
| Click to display the text | |
| [7] | Meyer R E,Ezekiel S,Stowe D W,et al.Passive fiber-optic ring resonator for rotation sensing[J].Optics Letters,1983,8(12):644-646. |
| Click to display the text | |
| [8] | Zarinetchi F,Ezekiel S.Observation of lock-in behavior in a passive resonator gyroscope[J].Optics Letters,1986,11(6):401-403. |
| Click to display the text | |
| [9] | Smith P,Zarimetchi F,Ezekiel S.Narrow-linewidth stimulated Brillouin fiber laser and applications[J].Optics Letters,1991,16(6):393-395. |
| Click to display the text | |
| [10] | Wang X J,He Z Y,Hotate K.Reduction of polarization-fluctuation induced drift in resonator fiber optic with twin 90° polarization-axis rotated splices gyro by a resonator[J].Optics Express,2010,18(2):1677-1683. |
| Click to display the text | |
| [11] | 肖树妹,梅海平,黄宏华,等.半导体激光器电流频率调制率的测量[J].红外与激光工程,2010,39(增刊):74-77.Xiao S M,Mei H P,Huang H H,et al.Measuring current-induced frequency modulation ratio in semiconductor diode laser[J].Infrared and Laser Engineering,2010,39(Sup.):74-77(in Chinese). |
| Cited By in Cnki | |
| [12] | Jin Z H,Yu X H,Ma H L.Resonator fiber optic gyro employing a semiconductor laser[J].Applied Optics,2012,51(15):2856-2864. |
| Click to display the text | |
| [13] | Lei M,Feng L S,Zhi Y Z,et al.Current modulation technique used in resonator micro-optic gyro[J].Applied Optics,2013,52(2):307-313. |
| Click to display the text | |
| [14] | Lei M,Feng L S,Zhi Y Z,et al.Effect of intensity variation of laser in resonator integrated optic gyro[J].Applied Optics,2013,52(19):4576-4581. |
| Click to display the text | |
| [15] | Lei M,Feng L S,Zhi Y Z,et al.Experiments on resonator micro-optic gyro using external cavity laser diode[J].Optical Engineering,2012,51(10):104602. |
| Click to display the text | |
| [16] | 王文怡,王慧泉,陈妍,等.双路闭环谐振式微光学陀螺[J].中国激光,2012,39(12):12080003.Wang W Y,Wang H Q,Chen Y,et al.Double closed-loop resonator micro optic gyro[J].Chinese Journal of Lasers,2012,39(12):12080003(in Chinese). |
| Cited By in Cnki | |
| [17] | Feng L S,Zhi Y Z,Lei M,et al.Suppression of frequency locking noise in resonator fiber optic gyro by differential detection method[J].Optics & Laser Technology,2014,62:109-114. |
| Click to display the text | |
| [18] | Zhi Y Z,Feng L S,Lei M,et al.Low-delay,high-bandwidth frequency-locking loop of resonator integrated optic gyro with triangular phase modulation[J].Applied Optics,2013,52(33):8024-8031. |
| Click to display the text | |
| [19] | 洪灵菲,张春熹,冯丽爽,等.谐振式微光学陀螺标度因数及其非线性度分析[J].北京航空航天大学学报,2012,38(8):1046-1050.Hong L F,Zhang C X,Feng L S,et al.Investigation on scale factor and output nonlinearity in resonator micro-optic gyro[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(8):1046-1050(in Chinese). |
| Cited By in Cnki | |
| [20] | 洪灵菲,张春熹,冯丽爽,等.谐振式微光学陀螺偏置频率调制技术研究[J].光学技术,2011,37(5):627-631.Hong L F,Zhang C X,Feng L S,et al.Bias-frequency-modulation used in resonator-optic gyro[J].Optical Technology,2011,37(5):627-631(in Chinese). |
| Cited By in Cnki (2) |
