以上多尺度问题中的“微观”部分,其尺度在波长的分数量级,而很多的实际工程问题中,其微观尺度在波长的几十分之一,无法进行网格剖分及求解.
对于典型的具有松散连接结构如网状天线,其网格尺度均在几十分之一波长以下,而电性能则需要在几十个乃至上百个波长尺度的范围内进行求解,由于多尺度电磁结构中的微观结构的剖分密度远大于其他部分,致使矩阵的条件数恶化,在求解中收敛很慢,甚至不收敛.丝网结构会造成电磁波因为绕射效应的泄露,而丝网节点处的金属结的非理想接触会引起网状天线的无源互调.该结构属于典型的多尺度、非线性无源互调(PIM)的电大尺寸电磁问题.
金属接触非线性引起的无源互调的散射机理及其数值计算最早由意大利Pelosi课题组于1999年提出[15, 16, 17],该课题组将时域物理光学方法(TD-PO)的应用推广于非理想导体和非线性环境,给出由于两种不同的金属相互接触时所产生的非线性无源互调的计算模型.在TD-PO方法中,假设入射波为平面波,通过引入模拟两种不同金属相互搭接而产生的金属结的非线性因子,求解相互搭接的金属在电磁波照射下所产生的空间散射场,并对该散射场进行傅里叶变换求得各阶无源互调产物,实现对不同金属相互接触而产生的无源互调的预测.
但是,TD-PO方法中的入射波被近似为平面波,仅适用于辐射源位于散射目标的散射远区时的情形,只能对一些典型简单的微波结构进行理论验证,无法计算实际复杂微波部件工作时产生的无源互调,并且在电大环境下采用TD-PO时域算法所带来的误差积累是不可忽视的.
含有多尺度、非线性的电大尺寸电磁问题的分析具有重要的实际工程背景,对于计算电磁学的发展带来了新的挑战.本文提出的多尺度等效方法、场路结合数值分析方法是解决多尺度、非线性电大尺寸电磁工程问题分析的关键技术.
1 多尺度问题的等效分析方法多尺度电磁工程问题无法利用现有的数值计算方法如有限元、矩量法及其快速算法等进行几何剖分运算,会导致矩阵求解无法收敛,甚至连几何剖分都无法完成.但是,微观结构由于数量规模和材料结构的原因,其宏观影响却必须通过数值计算来分析评估.等效方法是解决这一矛盾的有效手段,等效方法是指将微观结构对于宏观结构中电磁行为的影响以边界条件的形式等效,并加入宏观结构中进行求解.这种等效方法将问题分为两个阶段:第1个阶段是研究微观结构的电磁响应,并将其等效为边界条件;第2个阶段计算不含有具体微观结构、但含有其等效边界条件的宏观电磁问题.多尺度问题的等效方法化难为易,既解决了直接求解方法中的数值离散化带来的计算难题,也充分考虑了微观结构的电磁效应.具有松散接触的周期性微观结构如丝网反射面、频率选择表面、天线罩高频段特性分析等的多尺度电大尺寸问题均可采用等效分析方法进行数值分析.文献[18]推导了多层极薄层边界条件,解决了天线罩高频段特性分析多尺度电大尺寸的计算,这一技术已集成入ANSYS HFSS软件,并为国内多个重要军工单位解决了新型产品的论证和设计.
松散连接是指金属相互接触面之间存在间隙的连接情况,并形成MIM(Metal Insulator Metal)结构,如图 1所示.图 1中有5种接触状态:①金属接触;②接触面之间夹有金属膜氧化物;③接触面之间夹有绝缘介质;④微小空气间隙;⑤较大空气间隙.①和②形成电流的主要通道,形成收缩电阻和接触电阻;②中的氧化物依靠隧道效应和穿透薄膜的金属桥进行导电,属于半导体接触导电,是非线性的;③则不导电,电流绕到金属接触处通过;在空气间隙④和⑤处电流环绕间隙流过.当电流遇到阻抗Z,产生间隙电压,间隙电压是潜在的,可能激活任何一个半导体而产生无源互调效应[19].接触面的等效电路模型如图 2所示,其V-I特性是非线性的.
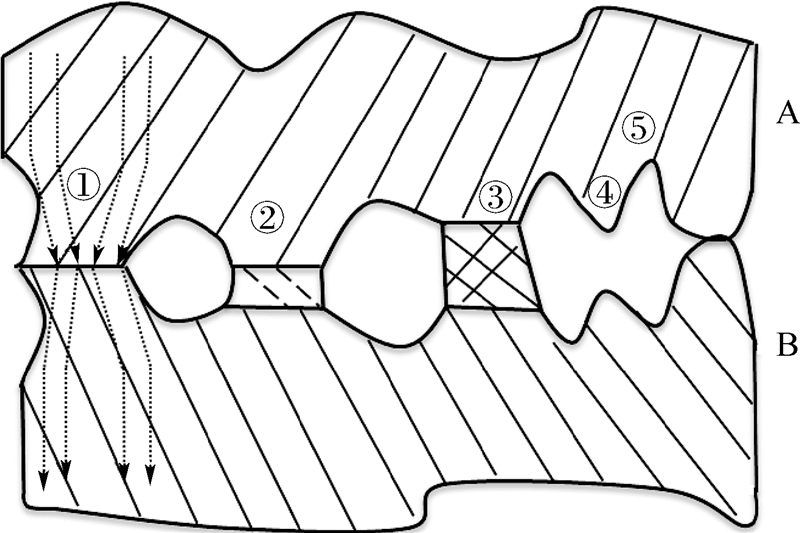 |
| 图 1 松散连接接触面Fig. 1 Contact surface of metallic connection |
| 图选项 |
美国Rahmat-Samii教授等应用Floquet方法研究了不考虑电接触模型(即理想搭接)情况下周期性反射面天线(mesh antenna)的特性,主要研究周期结构单元的尺寸和形状等因素对于反射特性的影响[20].对于搭接的影响,以理想连接和完全断开两种极端情况作为极限来评估.而本文的多尺度等效分析方法首先要对松散连接的周期性单元结构进行电磁建模,并在金属结处引入金属搭接的电接触模型,即图 2所示的等效RLC边界条件,采用Floquet方法求解周期平面结构的电性能参数,多尺度等效方法的计算流程如图 3所示.
 |
| 图 2 松散连接接触面的等效电路Fig. 2 Equivalent circuit of metallic connection contact surface |
| 图选项 |
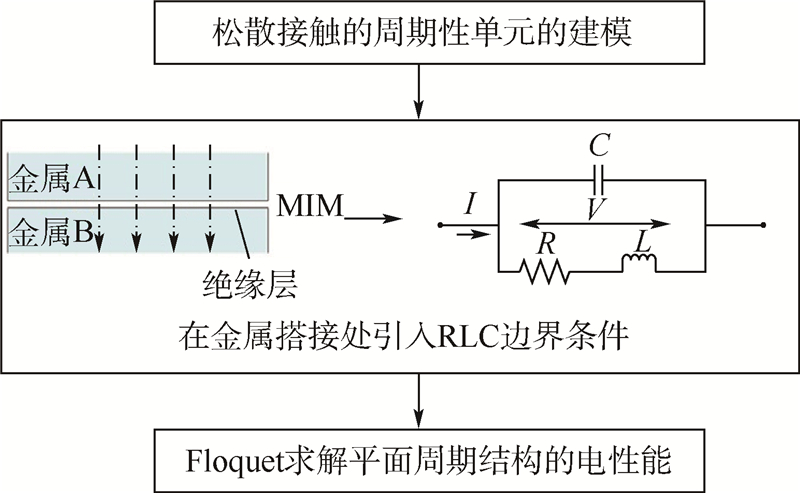 |
| 图 3 多尺度结构等效方法流程图Fig. 3 Flow diagram of equivalent method for multi-scale structure |
| 图选项 |
2 非线性问题的场路结合分析方法实际微波结构中金属部件上的各种不均匀性(镀层、法兰连接面、搭接、焊点、螺钉等)在电磁场的激励下,其金属结中的自由电子运动会产生非线性响应.如果有两个或者以上频率的电磁波同时激励,则会产生高阶交互调频谱上电磁波,这种效应称为无源互调效应.在收发系统中,3阶互调波等会恰好落在工作频带,会对微波接收机产生干扰,对于宽带的收发系统而言,7阶互调波甚至9阶互调波都会对接收机的正常工作产生影响.
对于实际工程中电大尺寸环境中的非线性问题,由于非线性效应非常弱,一般均在-170 dB以下,很容易和远大于波长级电尺寸问题中的数值误差积累混淆.所以,时域方法很难应用于实际电大尺寸问题中.
本文提出了场路结合的数值分析方法,在计算电大尺寸范围内的激励电磁场分布时采用频域全波方法,获得精确的非线性结处的激励场分布,然后结合非线性结的伏安特性求取其各阶互调分量,再采用频域全波方法评估其在电大尺寸范围内的影响,如图 4所示.
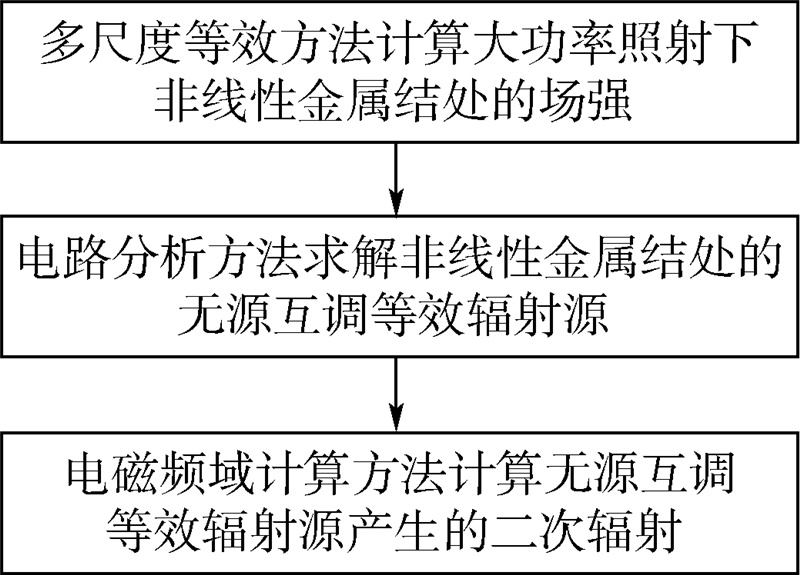 |
| 图 4 场路结合方法分析无源互调的流程图Fig. 4 Flow diagram of coupled field-circuit method for PIM analysis |
| 图选项 |
3 数值实例3.1 多尺度问题的等效分析方法的应用建立图 5所示的印刷平面网状周期结构,其表面由铜条带构成,介质层的相对介电常数为4.7,厚度为1.78 mm.采用频域全波计算方法结合Floquet理论对该结构的传输特性进行数值计算,计算频率为2~15 GHz[20].
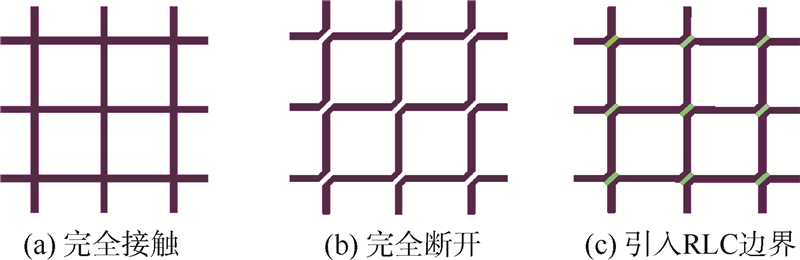 |
| 图 5 周期结构的平面网状反射面Fig. 5 Planar mesh reflector with periodic structure |
| 图选项 |
使用图 3所示的等效计算方法对上述所示的平面网状周期结构进行计算,计算结果如图 6所示.与文献[20]中的实验数据进行比较,在不考虑电接触特性时本文方法计算与其预测结果和测量数据符合,验证了本文等效分析方法的准确性.
 |
| 图 6 不同接触状态下的传输损耗Fig. 6 Transmission loss for different connections |
| 图选项 |
从图 6可以看出,平面丝网结构在金属结搭接处的开路、短路和存在电阻、电容3种状态下引起的传输损耗是有很大区别的.
3.2 场路结合数值分析方法的应用考虑双载波频率情况,互调的频率fIM可以表示为:fIM=mf1+nf2,其中f1、f2为输入载波频率,m、n为非零整数.建立如图 3所示的平板验证模型,使用喇叭天线作为馈源,由金属平板形成的单个金属结距离喇叭天线0.3 m,金属结部分的等效电路模型采用式(1).假设频率分别为f1=11 GHz,f2=12.6 GHz的两个电磁波垂直照射到平板上,计算分析该金属结的3阶、5阶互调干扰.
天线和微波接头处的金属结的非线性效应可用式(1)所示的电路模型来等效[16]:
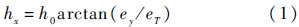
式中:h0和eT为待定的系数;hx为沿非线性金属结的磁场强度;ey为垂直于非线性金属结的电场强度;而h0、eT的值决定了非线性金属结的材料与非线性程度.
使用图 4所示的场路结合数值分析方法对图 7所示的验证模型进行计算,首先对图 3的单个金属结以及喇叭馈源进行电磁建模,采用频域计算方法求得金属结的表面电场,并在非线性区域对表面电场进行积分求得非线性区域的电压降,求得3阶和5阶互调产物的功率电平.再次利用频域计算方法求解3阶和5阶互调产物作为激励所激发的空间二次辐射场,在接收端口处对电场进行积分得到的无源互调功率结果如表 1所示,与测量数据[16]比较可以看出,虽然存在一定的误差,但仍可认为预测结果与测量数据基本符合,初步验证了本文场路结合数值分析方法的准确性.
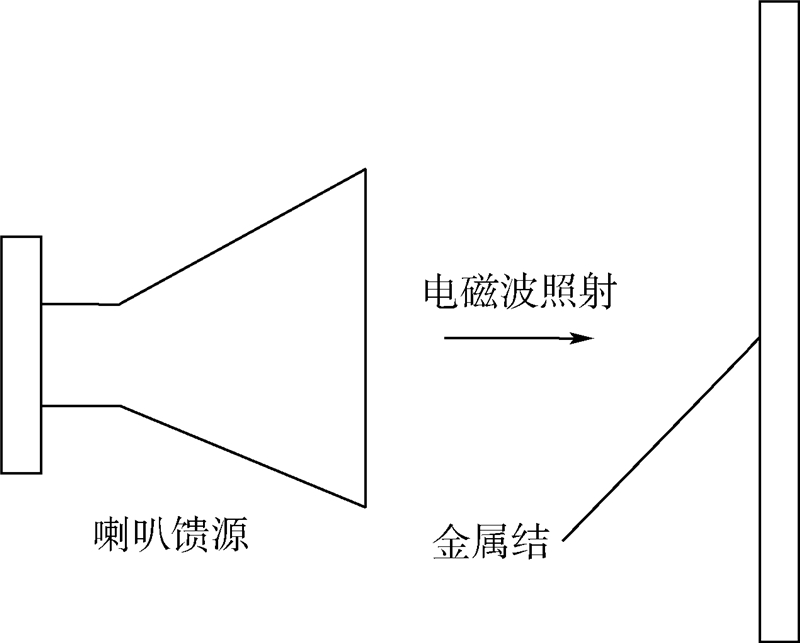 |
| 图 7 金属结无源互调计算模型Fig. 7 PIM computed model of metallic junction |
| 图选项 |
表 1 3阶和5阶无源互调测试结果和计算结果Table 1 Measured and computed PIM levels of third order and fifth order
| 互调阶数 | 每个频点处输入功率/W | 测试结果/dBm | 本文计算结果/dBm |
| 3阶 | 100 | -104 | -102 |
| 170 | -100 | -97 | |
| 5阶 | 100 | -125 | -123 |
| 170 | -116 | -114 |
表选项
4 结论本文介绍了含有微观结构的多尺度电大尺寸的松散连接的周期结构的等效计算方法,以及计算电大尺寸微波部件无源互调的场路结合数值分析方法,可以得出以下结论:
1) 由丝网反射面电性能的计算结果可知,网面上金属结的电接触特性对整个丝网的电性能会产生较大的影响,必须建立正确合理的丝网单元的电磁模型,才能得到准确的丝网反射面的电性能.而多尺度等效分析方法可以有效地对含有微观结构的电大尺寸微波部件的电性能以及该结构对宏观结构电性能的影响进行评估.
2) 提出的场路结合数值分析方法解决了频域计算方法无法求解非线性物质结构的电磁响应问题.
3) 场路结合数值分析方法可以分析具有松散连接结构的电大尺寸微波部件的无源互调,相比时域计算方法,产生的误差较小.
参考文献
| [1] | Geers M G D, Kouznetsova V G, Brekelmans W A M.Multi-scale computational homogenization: Trends and challenges[J].Journal of Computational and Applied mathematics, 2010, 234(7):2175-2182. |
| Click to display the text | |
| [2] | Kevrekidis I G, Gear C W, Hummer G.Equation-free:The computer-aided analysis of complex multiscale systems[J].AIChE Journal, 2004, 50(7):1346-1355. |
| Click to display the text | |
| [3] | Umashankar K R, Nimmagadda S, Taflove A.Numerical analysis of electromagnetic scattering by electrically large objects using spatial decomposition technique[J].IEEE Transactions on Antennas and Propagation, 1992, 40(8):867-877. |
| Click to display the text | |
| [4] | Notaros B M, Popovic B D, Weem J P, et al.Efficient large-domain MoM solutions to electrically large practical EM problems[J].IEEE Transactions on Microwave Theory and Techniques, 2001, 49(1):151-159. |
| Click to display the text | |
| [5] | Tzoulis A, Eibert T F.A hybrid FEBI-MLFMM-UTD method for numerical solutions of electromagnetic problems including arbitrarily shaped and electrically large objects[J].IEEE Transactions on Antennas and Propagation, 2005, 53(10):3358-3366. |
| Click to display the text | |
| [6] | Bagci H, Yilmaz A E, Jin J M, et al.Fast and rigorous analysis of EMC/EMI phenomena on electrically large and complex cable-loaded structures[J].IEEE Transactions on Electromagnetic Compatibility, 2007, 49(2):361-381. |
| Click to display the text | |
| [7] | Li M K, Chew W C.Multiscale simulation of complex structures using equivalence principle algorithm with high-order field point sampling scheme[J].IEEE Transactions on Antennas and Propagation, 2008, 56(8):2389-2397. |
| Click to display the text | |
| [8] | Jiang M, Hu J, Zhao R, et al.Hybrid IE-DDM-MLFMA with forward-backward method for conducting body of translation[C]∥Proceedings of the 2012 International Conference on Electromagnetics in Advanced Applications.Piscataway:IEEE Press, 2012:263-265. |
| Click to display the text | |
| [9] | Shao H, Hu J, Lu W, et al.Analyzing large-scale arrays using tangential equivalence principle algorithm with characteristic basis functions[J].Proceedings of the IEEE, 2013, 101(2):414-422. |
| Click to display the text | |
| [10] | Pan X M, Sheng X Q.Preconditioning technique in the interpolative decomposition multilevel fast multipole algorithm[J].IEEE Transactions on Antennas and Propagation, 2013, 61(6):3373-3377. |
| Click to display the text | |
| [11] | Li M M, Chen R S, Wang H X, et al.A multilevel FFT method for the 3-D capacitance extraction[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2013, 32(2):318-322. |
| Click to display the text | |
| [12] | Li M M, Li C Y, Ong C J, et al.A novel multilevel matrix compression method for analysis of electromagnetic scattering from PEC targets[J].IEEE Transactions on Antennas and Propagation, 2012, 60(3):1390-1399. |
| Click to display the text | |
| [13] | Li M M, Francavilla M A, Vipiana F, et al.A doubly hierarchical MoM for high-fidelity modeling of multiscale structures[J].IEEE Transactions on Electromagnetic Capability, 2014, 56(5):1103-1111. |
| Click to display the text | |
| [14] | Li M M, Francavilla M A, Vipiana F, et al.Nested equivalent source approximation for the modeling of multiscale structures[J].IEEE Transactions on Antennas and Propagation, 2014, 62(7):3664-3678. |
| Click to display the text | |
| [15] | Bolli P, Naldini A, Pelosi G, et al.Passive intermodulation scattering in a time domain physical optics framework[C]∥Proceedings of International Symposium on Nonlinear Electromagnetic Systems(ISEM).Pavia:ISEM, 1999:121-124. |
| Click to display the text | |
| [16] | Selleri S, Bolli P, Pelosi G.A time domain physical optics heuristic approach to passive intermodulation scattering[J].IEEE Transactions on Electromagnetic Compatibility, 2001, 43(2):203-209. |
| Click to display the text | |
| [17] | Bolli P, Pelacchi P, Pelosi G, et al.Passive intermodulation on large reflector antennas[J].IEEE Transactions on Antennas and Propagation Magazine, 2002, 44(5):13-20. |
| Click to display the text | |
| [18] | 刘莹, 谢拥军.多层介质天线罩的数值分析[J].电波科学学报, 2011, 26(3):550-555.Liu Y, Xie Y J.Numerical analysis of multi-layer dielectric radome[J].Chinese Journal of Radio Science, 2011, 26(3):550-555(in Chinese). |
| Cited By in Cnki (5) | |
| [19] | 罗一锋.舰船通信系统的无源互调研究[J].现代电子技术, 2010(23):39-44.Luo Y F.Approach to passive intermodulation in ship communication system[J].Modern Electronics Technique, 2010(23):39-44(in Chinese). |
| Cited By in Cnki (6) | |
| [20] | Imbriale W A, Galindo-Israel V, Rahmat-Samii Y.On the reflectivity of complex mesh surfaces[J].IEEE Transactions on Antennas and Propagation, 1991, 39(9):1352-1365. |
| Click to display the text |
