与此同时,科学技术的进步使得更多的研究手段用于探索该问题.其中,有限元方法(Finite Element Method,FEM)具有适用于工程中较为复杂的地质形态、易于边界处理的特点;能够给出弹性波的基本运动学、动力学信息[9],有助于深入地研究模型的内在力学特性及其在岩石中的传播机制.FEM的基本思想最早可以追溯到1943年[10].1960年,Clough第一次提出了“有限元法”的概念.随后,FEM开始用于动力学分析.1978年,Aoki等[11]就采用FEM分析了含有单裂纹结构的动力学问题.1986年,Taylor等[12]采用FEM研究了含微裂纹脆性岩石的断裂行为.1998年,Ma等[13]采用显式有限元分析程序Autodyn模拟了爆炸载荷激发下岩石中的冲击波传播问题.2001年,Garboczi和Berryman[14]采用FEM讨论了含有夹杂材料的等效弹性参数.2006年,Grechka及Kachanov[15]采用三维FEM分析了含小间距交叉排布的裂纹对于各向同性岩石的等效弹性参数的影响.2013年,Gaede等[16]采用三维FEM计算了各向异性弹性岩石基体中,任意方向的孔洞缺陷周围的应力集中问题.
目前,关于岩石的FEM多侧重于静力问题的研究.然而在实际工程测量中,主要采用地震勘探技术,该方法是利用人工激发地震波,通过拾取测点地震波记录来推断地质形态.因而,有必要采用动力学FEM建立有效岩石模型.本文根据Hudson理论,将岩石简化为含有定向周期均匀分布裂纹的线弹性体,采用FEM构建三维模型,商用FE软件Nastran求解弹性动力学方程,可得到各结点的位移、速度、加速度,以及各单元的应力随时间分布,进而得到弹性波在岩石中完整的传播过程;与Hudson理论解的对比验证了FEM模型的有效性,并定量地讨论了Hudson理论的适用范围;基于本文的FEM模型,分析了弹性波在裂纹介质中的频散效应,裂纹微结构对弹性波传播动力学特性的影响;通过研究含裂纹介质中等效弹性常数的变化规律,讨论了传播介质特性的反演问题.
1 基本方程1.1 Hudson裂纹介质理论Hudson在20世纪80年代就对含有裂纹结构的弹性模型做了很好的研究总结[9].在该理论中,Hudson将岩石假设为含有平行定向均匀分布的圆币形裂纹;微结构的尺寸远小于入射波长,即可以使得弹性波在裂纹附近发生衍射绕过缺陷、裂纹位置;裂纹在弹性体中占有很小的比率.
基于文献[9]模型,Hudson应用平均位移场理论,提出了裂纹介质的等效弹性模型[6]:
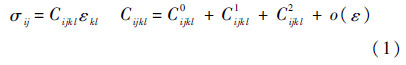
式中:σij和εkl分别为应力、应变张量分量;Cijkl为弹性模量,对于三维问题,i,j,k,l=1,2,3;ε为裂纹密度;o(ε)为高阶扰动小量.忽略高阶小量,二阶近似为
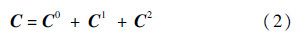
式中:C为四阶张量；C0为无裂纹介质的弹性模量;C1为每个裂纹分别独立作用产生的修正项;C2为由两裂纹间耦合作用产生的修正项.这里假设介质中所有裂纹法向相同,沿x3轴方向分布,单位矢量为[0 0 1]T,裂纹模型如图 1所示.
 |
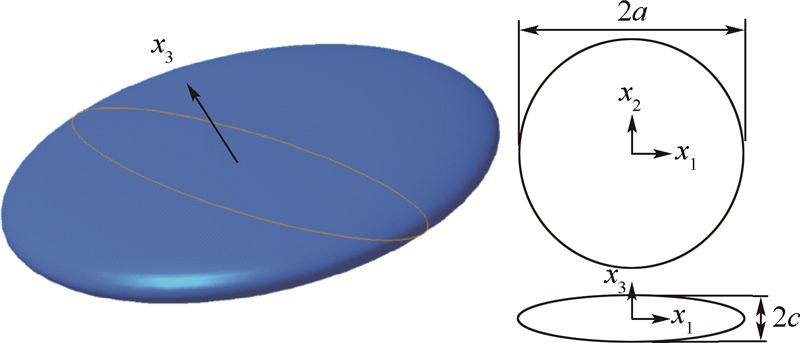| a—裂纹的平均半径；2c—裂纹厚度；x1、x2和x3—空间内3个正主轴.图 1 Hudson裂纹模型Fig. 1 Hudson’s crack model |
| 图选项 |
基体为各向同性线弹性材料,裂纹均匀分布,其等效弹性模量为
式中:
其中:ρ为岩石密度;vP和vS分别为纵波、横波波速;λ和μ为Lame常数;ν为泊松比；E为弹性模量.对于法向为x3轴的干裂纹,则有:
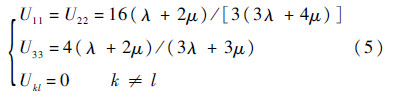
采用Voigt拉直公式[17],将C转化为二阶张量,即
式中：
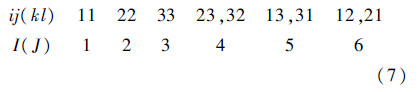
则广义Hooke定律[17]可以写为
将式(3)代入式(8)中,可以看出由于共向均匀排列裂纹的存在,岩石通常不再是各向同性材料,在地震勘探中一般用Thomsen参数描述材料的各向异性[18]：
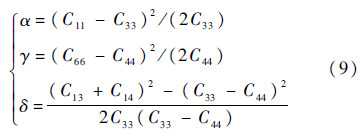
其大小反映各向异性程度.将弹性模量代入,得到一阶修正结果为
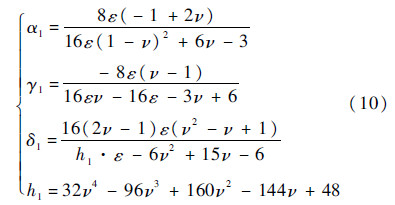
同理可得到二阶修正弹性模量的Thomsen参数.1.2 FEM动力学方程波在介质中传播是动力学研究的重要领域,主要研究短暂作用于介质边界或内部的载荷所引起的位移、速度变化在介质中向周围传播、散射规律,在建筑结构抗震设计、人工地震勘探、无损探伤等领域中都有广泛应用.运动方程[19]为
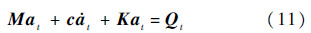
这里采用中心差分方法,有
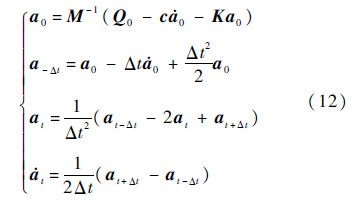
式中:M、c和K分别为质量、阻尼和刚度矩阵;Qt、at、
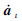和at分别为t时刻结点载荷、位移、速度和加速度向量;a0、 
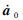、a0和a-Δt分别为初始位移、速度、加速度向量和t=-Δt时刻位移向量;at-Δt和at+Δt分别为t=t-Δt和t=t+Δt时刻位移向量.中心差分为条件稳定算法,时间步长Δt需要满足一定的条件,选择最小单元的最小边长,记为L,近似估计[19]: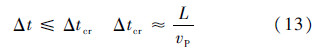 
式中:Δtcr为临界时间步长.2 数值结果与讨论2.1 Hudson理论波速岩石基体选择为各向同性线弹性材料,其泊松比ν的范围为
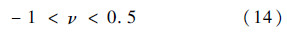
在式(14)范围内,由式(9)可知,对于一阶和二阶修正弹性模量张量都只有ε=0时,才能表征为各向同性材料.
对于正交异性材料,其弹性模量在实验室中通常采用测量波在介质中的P波、S波波速计算得到:
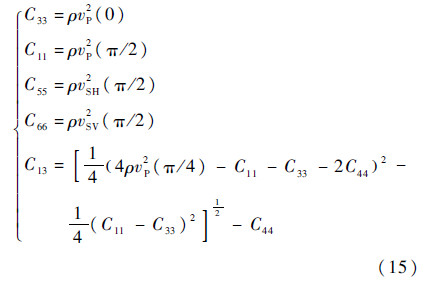
式中:vSV为横波波速竖直分量;vSH为横波波速水平分量.定义两个无量纲数ζ和η,分别用来表征含裂纹的C11与无裂纹C110和C33与无裂纹C330的差异,表达形式为
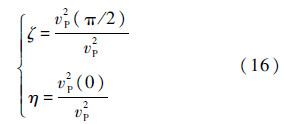
图 2和图 3分别为Hudson裂纹介质一阶等效弹性模量(ζ1与η1)和二阶修正等效弹性模量与无裂纹基体的比值(ζ2与η2)关于ε与ν的变化曲面,曲线为投影面的等值线.从图 2和图 3中可以看出,ν的影响要大于裂纹密度ε的作用,且相对于C11来说,C33的变化趋势更为显著;在图 2中随着ε变化,比值出现负值,这显然是与实际情况相违背的,而图 3会出现比值显著大于1的情形,波速远大于无裂纹基体,即裂纹密度的增大反而使得岩石刚度远大于无裂纹情形,这一点也是与真实情况不符的.综上,Hudson裂纹介质理论不仅建立在低裂纹密度的基础上,实际上,对无裂纹基体ν也有一定要求,只有基体ν在某一范围内时,该理论才成立,尤其当ν接近0.5时,Hudson理论显然不再适用.
 |
| 图 2 ζ、η关于ε与ν的一阶修正Fig. 2 First-order correction of ζ,η with respect to ε and ν |
| 图选项 |
 |
| 图 3 ζ、η关于ε与ν的二阶修正Fig. 3 Second-order correction of ζ,η with respect to ε and ν |
| 图选项 |
2.2 算例分析本文计算模型材料为岩石,无裂纹岩石近似为各向同性线弹性材料,弹性参数[9]及相应的理论波速分别为
有效研究区域尺寸选为100 m×100 m×100 m,时间步长Δt选为50 μs,为满足式(13),最小网格尺寸L应大于0.22 m.
2.2.1 频率影响弹性模量的测量分为静力法和动力学方法.用(准)静力加载法得到静弹性模量;根据弹性波在岩石中的传播速度测得的则是动弹性模量,其值与入射频率有关. 虽然理想弹性问题与频率无关，然而模型的大小会限制拾取结果的准确程度,因而在激励选择方面有必要考虑频率的影响.
图 4为不同频率下得到的vP相对于理论值(见式(17))的误差.从图 4中可以看出,该模型尺寸下,当f≥200 Hz时,vP不再随频率增大,此时得到的弹性模量略大于其静弹性参数,且f=100 Hz 时的值更接近理论结果.
 |
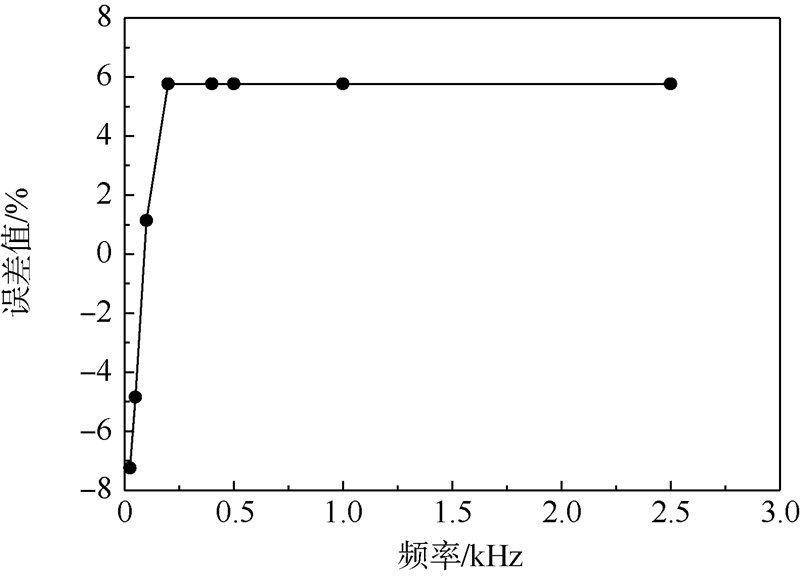| 图 4 误差值随频率变化Fig. 4 Variation of error with respect to frequency |
| 图选项 |
基于Hudson等效介质理论,计算模型裂纹周期排布,近似均匀分布,入射波需满足长波假设,即入射波长λin满足:
式中:fn为模型固有频率.裂纹尺寸平均半径a可以选为2 m,当材料整体尺寸远大于材料小尺寸特征参数时,可不计小尺寸效应影响[20],模型可等比缩放.2.2.2 裂纹密度影响三维FEM模型中,裂纹周期近似均匀分布且裂纹法向为x3方向,x1x2平面内,波速vP(π/2)在各方向近似相同.在x1Ox2平面内,在侧边中点处沿x1方向激励产生弹性波,中线处每隔相等距离设置测点,进而得到平均波速值.图 5为采用FEM得到的vP(π/2)与一阶、二阶Hudson理论值的比对结果.在图 5中,当裂纹密度ε≤0.117时,3种方法得到的结果相近,速度误差不大于5%;当ε>0.117时,Hudson二阶修正结果呈上升趋势,与经验结果不符;在该周期均匀裂纹模型条件下,采用FEM得到的结果与Hudson一阶修正结果更相近;而之前,曾新吾等[9]采用边界元方法(Boundary Element Method,BEM)得出了vP(0)的值与Hudson理论的二阶近似结果吻合更好的结论,裂纹密度ε>0.19时,Hudson裂纹介质理论与BEM分析结果不再吻合.当数值模拟结果与Hudson理论公式不再相符时,是否还能将岩石视为等效弹性体,是值得讨论的.
 |
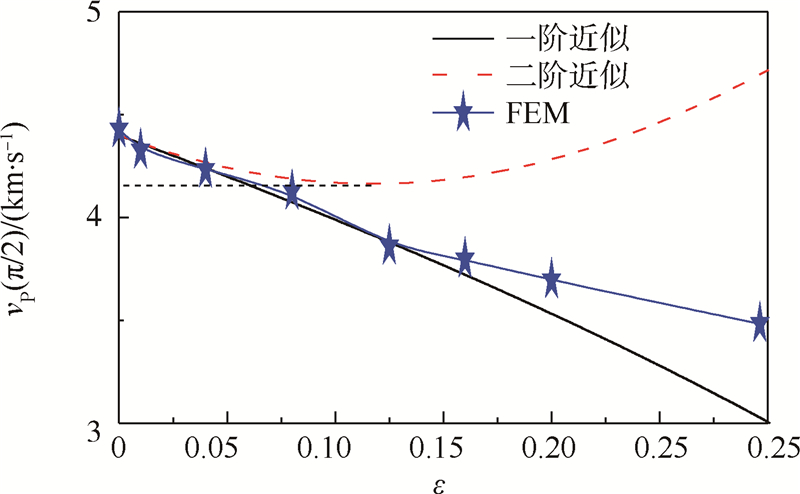| 图 5 vP(π/2)随裂纹密度ε变化Fig. 5 Variation of vP(π/2) with respect to ε |
| 图选项 |
图 6为ε=0.125时,x1Ox2平面内的,在不同时刻,各单元结点沿x1方向位移ux1的色谱图.从该图中可以清楚地看到P波的传播过程,波前近似为半球状,说明在各方向的vP(π/2)近似相同,即弹性模量C11和C22相同,在该裂纹密度条件下,周期拓扑结构仍可近似为均匀排布,且等效介质理论仍可成立.
 |
| 图 6 ε=0.125,在5,10,20和40 ms时刻的ux1Fig. 6 ux1 of ε=0.125 at t=5,10,20,and 40 ms |
| 图选项 |
图 7为ε=0.3时,ux1的色谱图,从t=20 ms时刻的图谱可以看到,波前不再呈现出半球状,说明该周期拓扑、裂纹密度下的计算模型,不再适用等效介质理论.对于该拓扑结构下ε>0.3的FEM模型,由于孔隙过多,弹性波在传播的过程中,在基体内不断地散射,造成能量的损耗,在距离激励点不远处就没有观测数据产生,即没有位移产生.
 |
| 图 7 ε=0.3,在5,10,20,40 ms时刻ux1Fig. 7 ux1 of ε=0.3 at t=5,10,20,40 ms |
| 图选项 |
2.2.3 纵横比影响在FEM研究中,于x1Ox3平面内,在侧边中点处沿x3方向激励产生弹性波,采用相同方法布置测点.模型裂纹密度ε=0.04,裂纹平均半径a=2 m.图 8为κ=0.5时，ux3的色谱图，其中：图 8(a)和图 8(b)分别为κ=0.510,κ=0.5在x1Ox3平面内的,不同时刻下,各结点沿x3方向位移ux3的色谱图.由于波长远大于微结构尺度,且裂纹比例较小,波前仍呈现出半球状,说明在该模型条件下,各方向的vP值仍相同,即C11≈C33,与图 6和图 7对比,说明裂纹密度ε对于该材料的各向异性的影响要远大于纵横比κ的作用.
 |
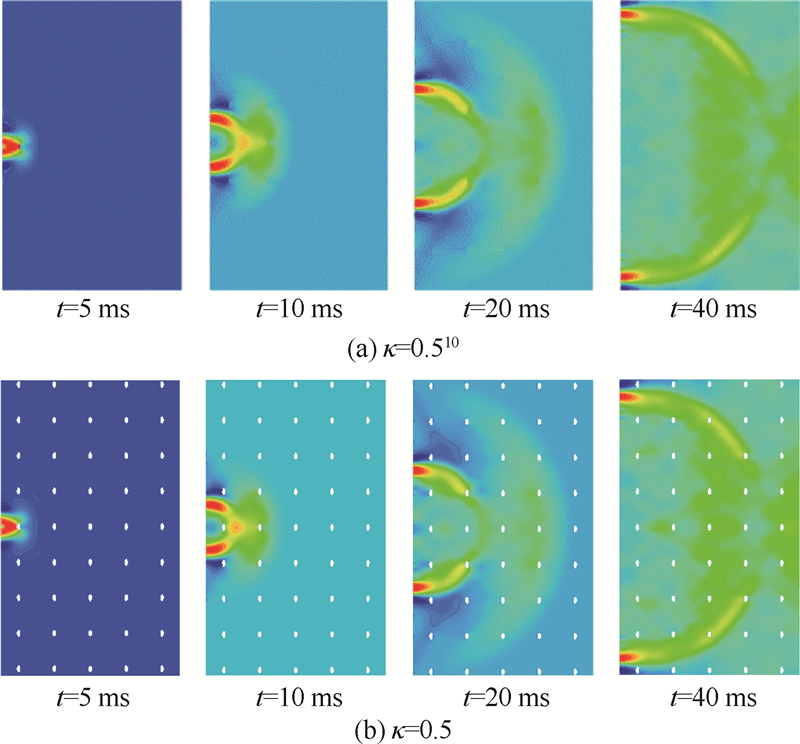| 图 8 κ=0.5,在5,10,20和40 ms时刻的ux3Fig. 8 ux3 of κ=0.5 at t=5,10,20,and 40 ms |
| 图选项 |
图 9为采用FEM得到的结果与Hudson理论值的对比图像.图中,κ=c/a为横纵比,κ=0表示无裂纹情形;当κ>0.001时,与裂纹法向平行方向波速vP(0)急剧下降,0.001<κ≤0.062 5时,采用FEM得到的值在Hudson一阶和二阶近似理论值之间,在κ=0.062 5时,vP(0)略有回升,不排除FEM网格划分的影响;当κ≥0.125时,采用FEM得到的结果不再满足Hudson理论,但误差不超过2%,在合理范围内.Hudson理论中,干裂纹密度与裂纹厚度c无关,而采用FEM也存在横纵比κ不同,但波速相同的情况,即0.59≤κ≤0.55,0.125≤κ≤0.9时,在该条件下如何根据勘测数据推断岩石微结构特征是值得进一步分析的问题,这将有助于在石油、地质勘探等领域的实际应用.
 |
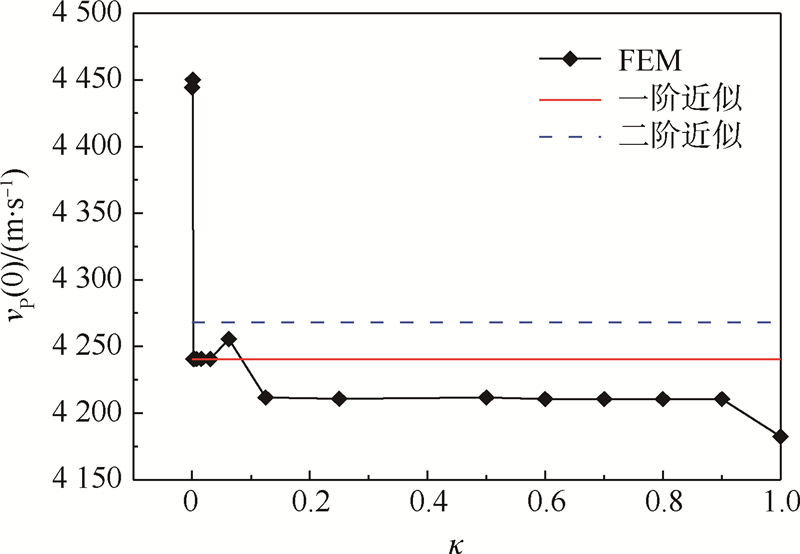| 图 9 ε=0.04时的vP(0)随κ变化Fig. 9 Variation of vP(0) at ε=0.04 with respect to κ |
| 图选项 |
图 10为当0.55≤κ≤1及0.55≤κ≤1时,ux3时域响应.图 10(a)和图 10(b)分别为0≤κ≤0.55,0.55≤κ≤1时距激励74 m处的结点x3方向位移随时间变化曲线.图 10中,出现裂纹使得弹性模量减小,刚度降低,这也就解释了无裂纹的时域响应波峰小于有裂纹的情形;当0.510≤κ≤0.58时,随着κ的增大,曲线的首波峰振幅呈下降趋势;当0.58≤κ≤0.57时,振幅略有回升,这可能是动应力集中作用减弱的结果;0.57≤κ≤1时,随着κ的增大,ux3呈单调下降趋势.
 |
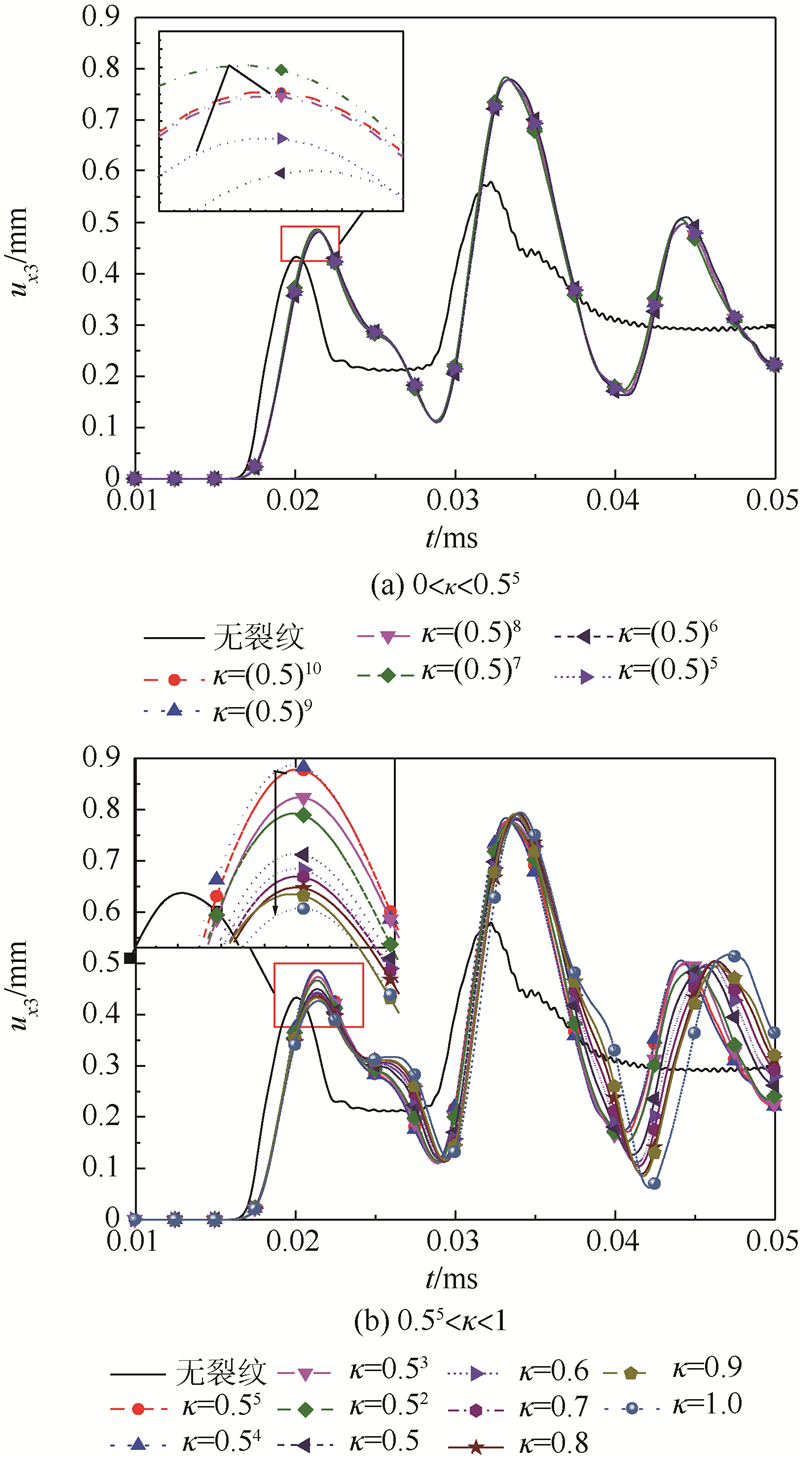| 图 10 当(0.5)5≤κ≤1及(0.5)5≤κ≤1时,ux3时域响应Fig. 10 Time domain response of ux3 when 0≤κ≤(0.5)5 and (0.5)5≤κ≤1 |
| 图选项 |
3 结 论1) 采用FEM可以用于研究弹性波在含裂纹介质中的传播问题;Hudson理论适用于低裂纹密度,泊松比不接近0.5的常规弹性材料.
2) 在给定模型条件下,激励入射频率对于弹性模量的测量有一定影响,本文模型的适用频率为100 Hz.
3) 对于C11(C22),裂纹密度ε≤0.117时,FEM与Hudson一阶和二阶的理论值误差不大于5%;0.117<ε≤0.125,Hudson含裂纹理论不再适用,但该模型仍然可视为等效介质,有必要探索适用范围更广的等效理论;ε>0.3时,该周期拓扑条件下,等效理论或许不再适用.
4) 裂纹密度ε对于该材料的各向异性的影响要远大于纵横比κ的作用.
5) ε=0.04时,通过时域响应即可判定弹性体是否具有裂纹;随纵横比增大,测得C33值有所下降,位移时域响应的首波振幅基本呈现减小趋势.
参考文献
| [1] | Guéguen Y,Kachanov M.Mechanics of crustal rocks[M].Vienna:Springer,2011:73-125. |
| [2] | Mackenzie J K.The elastic constants of a solid containing spherical holes[J].Proceedings of the Physical Society.Section B.1950,63(1):1. |
| Click to display the text | |
| [3] | Eshelby J D.The determination of the elastic field of an ellipsoidal inclusion,and related problems[J].Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences,1957,241(1226):376-396. |
| Click to display the text | |
| [4] | Bristow J R.Microcracks,and the static and dynamic elastic constants of annealed and heavily cold-worked metals[J].British Journal of Applied Physics,1960,11(2):81. |
| Click to display the text | |
| [5] | Walsh J B.The effect of cracks on the compressibility of rock[J].Journal of Geophysical Research,1965,70(2):381-389. |
| Click to display the text | |
| [6] | Hudson J A.Overall properties of a cracked solid[C]//Mathematical Proceedings of the Cambridge Philosophical Society.Cambridge:Cambridge University Press,1980,88(2):371-384. |
| Click to display the text | |
| [7] | Hudson J A.Seismic wave propagation through material containing partially saturated cracks[J].Geophysical Journal International,1988,92(1):33-37. |
| Click to display the text | |
| [8] | Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal International,1981,64(1):133-150. |
| Click to display the text | |
| [9] | 曾新吾,韩开锋,张光莹.含裂缝介质中的弹性波传播特性[M].北京:科学出版社,2013:1-5,18-40,98-121.Zeng X W,Han K F,Zhang G Y.Elastic wave propagation characteristics in cracked media[M].Beijing:Science Press,2013:1-5,18-40,98-121(in Chinese). |
| [10] | Courant R.Variational methods for the solution of problems of equilibrium and vibrations[J].Bulletin of American Mathematical Society,1943,49(1):1-23. |
| Click to display the text | |
| [11] | Aoki S,Kishimoto K,Kondo H,et al.Elastodynamic analysis of crack by finite element method using singular element[J].International Journal of Fracture,1978,14(1):59-68. |
| Click to display the text | |
| [12] | Taylor L M,Chen E,Kuszmaul J S.Microcrack-induced damage accumulation in brittle rock under dynamic loading[J].Computer Methods in Applied Mechanics and Engineering,1986,55(3):301-320. |
| Click to display the text | |
| [13] | Ma G W,Hao H,Zhou Y X.Modeling of wave propagation induced by underground explosion[J].Computers and Geotechnics,1998,22(3):283-303. |
| Click to display the text | |
| [14] | Garboczi E J,Berryman J G.Elastic moduli of a material containing composite inclusions:Effective medium theory and finite element computations[J].Mechanics of Materials,2001,33(8):455-470. |
| Click to display the text | |
| [15] | Grechka V,Kachanov M.Effective elasticity of rocks with closely spaced and intersecting cracks[J].Geophysics,2006,71(3):D85-D91. |
| Click to display the text | |
| [16] | Gaede O,Karpfinger F,Jocker J,et al.Comparison between analytical and 3D finite element solutions for borehole stresses in anisotropic elastic rock[J].International Journal of Rock Mechanics and Mining Sciences,2012,51:53-63. |
| Click to display the text | |
| [17] | Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:Tools for seismic analysis of porous media[M].Cambridge:Cambridge University Press,2009:21-76. |
| [18] | Thomsen L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966. |
| Click to display the text | |
| [19] | 王勖成.有限单元法[M].北京:清华大学出版社,2003: 468-520.Wang X C.Finite element method[M].Beijing:Tsinghua University Press,2003:468-520(in Chinese). |
| [20] | Liu N,Wang Y,Li M,et al.Nonlinear buckling analyses of a small-radius carbon nanotube[J].Journal of Applied Physics,2014,115(15):154301. |
| Click to display the text |
