目前,大部分关于ICT特征模型分析的研究主要关注于对特定节点移动模型的分析,研究者针对随机游走(Random Walk,RW)模型、随机路点(Random Waypoint,RWP)模型[2,6]和随机方向(Random Direction,RD)模型[2, 6, 7]等移动模型的ICT分布规律开展了一定的研究[2, 4, 6, 7].但是,这些研究过多地考虑了节点的移动特性,使得这些模型缺乏普适性.另外,也有一些研究者将实际的轨迹数据集用于ICT分布的研究[3, 8],虽然这些模型可以通过全局统计拟合ICT的方法给出一个普适的简单ICT分布,但由于忽略了节点对的历史接触信息,导致这些模型的准确性存在不足.
前期研究结果表明两个节点对的ICT呈指数分布[3, 7, 8, 9, 10],在此基础之上,本文提出了一个可靠性数学模型——基于ICT分布的接触模型(ICT Distribution-based Contact Model,IDCM),并证明了两个节点对的ICT的指数参数只与历史接触次数和节点对的累积ICT有关.IDCM提供了一个具有普适性的ICT分布,且具有较好的准确性和简洁性,对DTN中的转发算法优化、路由协议设计和网络性能分析具有非常重要的指导意义.
1 相关工作由于ICT在很大程度上反映了节点的移动特性,掌握ICT的特性对于DTN中的路由协议设计和网络性能分析具有重要的指导意义,因此在过去几年中,研究者们进行了大量关于DTN中的ICT特性的研究.在文献[11]中,Thrasyvoulos等首先为节点移动定义了epoch的概念,并证明了在给定的一段时间内,以epoch为基础的RD模型和RWP模型中的任意两个节点发生接触的epoch次数服从几何分布,同时也求出了ICT分布的平均值,但Thrasyvoulos并没有继续推导出ICT的具体分布形式.Muhammad和Simon[7]在Thrasyvoulos研究的基础上,基于epoch的概念研究了RWP和RD两种理论移动模型下节点的ICT分布,他们以假设发生接触的epoch次数服从几何分布为前提,结合时间因素,进一步推导出ICT服从指数分布,同时利用失效率的定义,推导出了指数参数的表达形式.文献[12]也以epoch为节点移动模式来研究ICT的分布和参数特征.但是,基于epoch的理论研究方法主要关注节点的分布情况、epoch长度、节点运动方向和节点运动速度等运动细节特征,缺乏普适性,对于难以获得节点运动细节特征的DTN场景,基于epoch的ICT分布模型将不再适用.
而另一些研究者则利用马尔可夫链模型和基于统计的方法对两个节点之间的ICT分布和参数特征进行研究[4, 13].但这一方法的前提是所研究的随机变量必须满足马尔可夫链过程,也就是说,事件在未来发生的概率与过去无关,只与上一时刻有关,事实上,在很多移动模型中这一点是很难满足的.例如,文献[13]中,作者考虑携带移动设备的一群人在几个固定的地点(例如学校的宿舍、咖啡厅、实验室)之间移动,且假设人们的移动是一个时齐的马尔科夫过程,在此基础之上建立了ICT的分布模型.而实际上人的移动具有一定的习惯性(比如喜欢学习的人经常会去实验室或者自习室),因此节点(人)的下一时刻的状态与历史信息有很大的相关性,而并不仅仅与前一时刻的状态有关,因此在这种场景下,马尔科夫链模型不再适用.
也有研究从实际的车辆、行人的移动轨迹出发,利用统计分析的方法得到了ICT分布特性,文献[3]基于实际的出租车轨迹数据集,提出了一个确定的ICT分布.文献[1]通过对西雅图的城市公交车数据集进行分析,发现了节点的ICT服从幂律分布.文献[5]通过对USCD、MITcell、MITbt等数据集进行分析,提出了ICT的幂律分布和指数衰减模型.然而,在真实的移动网络中很难获得实验数据,同时针对特定数据集所获得的研究成果难以适用于其他的数据集中,缺乏适应性.针对现有研究中的缺陷和不足,通过对节点运动做出一般性假设,然后基于可靠性方法给出了一个具有普适性的ICT分布模型IDCM,最后采用定数截尾实验对模型进行验证.
2 模型抽象IDCM是一个可靠性数学模型.在这节中首先介绍用于简化实际移动场景的两条基本假设,然后给出了IDCM的基本符号和定义的解释.
2.1 模型假设为了简化研究模型,在推导接触间隔时间ICT的分布时,本文做出如下两条基本假设.
假设1 在不重叠的时间段内,节点A、B接触次数是互相独立的.
假设2 接触持续时间相对接触间隔时间忽略不计.
以上假设阐述了在实际DTN环境中节点对之间接触的主要统计特性.假设1认为在不重叠的时间段内,任意一个节点对的相遇次数是互相独立的,也就是说节点的移动是相互独立的,这符合人们的认识,例如,车辆的运动路线和方式主要由其驾驶员来决定.假设2认为接触持续时间相对接触间隔时间而言可以忽略不计,本文通过采集随机方向模型、随机路点模型、北京市出租车网络以及口袋转换网络(Pocket Switched Network,PSN)[14]的节点移动数据,对平均接触时间和平均接触间隔时间进行了统计.如表 1所示,根据统计 结果可以看出,无论是理论移动模型产生的仿真数据,还是实际采集的节点移动数据,其平均接触时间都远远小于平均接触间隔时间,这说明了假设2的合理性.
表 1 平均接触时间与平均接触间隔时间Table 1 Average contact time and average inter contact time
| 数据集 | 平均接触时间/s | 平均接触间隔时间/s |
| RD | 13.7 | 14160.4 |
| RWP | 13.7 | 10340.8 |
| 北京市出租车网络 | 44.6 | 2904.3 |
| 口袋转换网络 | 176.8 | 12710.8 |
表选项
这些假设给出了合理的抽象且有利于IDCM建模,下面介绍IDCM的基本符号和定义的解释.
2.2 符号和定义假设一个区域面积大小为S的网络中存在M个移动节点,节点集合Φ={A,B,C,…},节点A在t时刻的位置表示为LA(t).每一个节点都有一个半径为R的圆形传输范围,每当两个节点进入彼此通信范围,能够进行数据传输时,称为发生了一次接触,该次接触一直持续到节点离开双方的通信范围.考虑到假设2,忽略接触的持续时间,则节点对(A,B)发生接触的时刻为(t0,t1,…ti,…),ti∈{t LA(t)－LB(t) ≤R}.N(t)表示节点对在时间段(0,t］内的接触次数,NA,B(t)表示节点对(A,B)在时间段(0,t］内的接触次数.Pn(t)表示节点对在时间段(0,t］内接触n次的概率,PA,Bn(t)表示节点对(A,B)在时间段(0,t］内接触n次的概率.
下面给出两个重要的定义.
定义1 接触间隔时间ICT.ICT表示节点对的接触时刻与上一次接触时刻之间的间隔时间,对于节点对(A,B)而言,ICTA,Bi=ti+1－ti.为了书写方便,在之后的部分用T表示ICT,用TA,B表示节点对(A,B)的接触间隔时间,用TA,Bi表示节点对(A,B)的第i个接触间隔时间,即第i次接触时刻和第i+1次接触时刻之间的间隔时间.
定义2 瞬时接触强度λ(t).瞬时接触强度表示节点对在(0,t］时间段内的平均接触次数,对于节点对(A,B)而言,λA,B(t)=NA,B(t)/t.
3 基于ICT分布的接触模型在定数截尾实验的基础上,将节点对的历史接触信息和ICT分布结合起来进行分析,并得出了一个可靠性数学模型——IDCM.IDCM证明了节点对的ICT服从指数分布且指数参数仅与历史接触数量和累积ICT相关.
3.1 节点对的ICT分布分析在这节通过分析节点对的接触统计特征,然后确定节点对的ICT分布.
定理1 任意节点对在时间段(0,t］内的接触的累积分布函数为
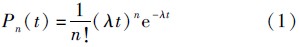
式中:n为节点对在时间段(0,t］内的接触数量.
证明 如果把接触看作节点之间的一条随时间变化的无向边的话,那么容迟网络可以看作是一个随机网络[15, 16, 17],根据随机图[15, 18]的理论,节点对的接触数量应服从泊松分布,即N(t)~Possion(λt),所以对于任意节点对,都有
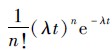,即定理1的结果. 证毕 定理2 任意节点对的ICT的概率密度函数为
证明 对于节点对(A,B)而言,T是非负随机变量,即TA,B≥0.事件{TA,B>K}(其中K为实验的时间)意味着在时间段(0,K］内没有出现接触,也就是{TA,B>K}={NA,B(K)=0}.由NA,B(t)~Possion(λA,Bt),可以得到P{NA,B(K)=0}=P0(K)=
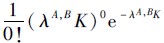那么F(K)=P(TA,B≤K)=1－P(TA,B>K)=1－e－λA,BK,因此节点对(A,B)的ICT的概率密度函数f(TA,B)=F′(TA,B)=λA,Be－λA,BTA,B.由于节点对(A,B)是从移动模型里随机抽取的,所以对任意节点对都有f(T)=F′(T)=λe－λT,因此可以说明任意节点对的ICT服从指数分布,即T~exp(λ). 证毕
3.2 参数估计在定数截尾实验中,选取节点对(A,B),假设可以获得r个ICT,由于每个ICT之间是相互独立的且同一个节点对的指数参数是相同的,另一方面,已经证明了ICT服从指数分布,即TA,B~exp(λA,B),那么对于r个ICT可以得到TA,Biidi ~exp(λA,B)(1≤i≤r，iid表示每个Ti独立同分布).在此基础之上,分析了指数参数λ的点估计和区间估计.
3.2.1 指数参数的点估计 定理3 定数截尾实验中的指数参数的点估计为
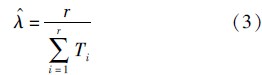
证明 对于节点对(A,B)而言,由TA,Biidi ~exp(λA,B)(1≤i≤r),可以得到多个ICT的联合密度函数为
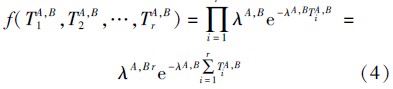
假设指数参数λA,B依赖于历史接触信息,应用杰弗莱彻方法[8]计算λA,B的贝叶斯估计的先验分布π(λA,B). I (λA,B) 表示参数λA,B的Fisher信息矩阵,因为
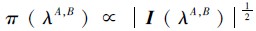并且 I (λA,B) 很容易由 I (λA,B) =
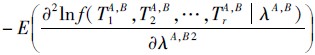获得,所以可以得到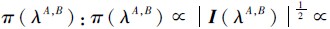
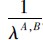. 因此,得到h(λA,B TA,B1,TA,B2,…,TA,Br):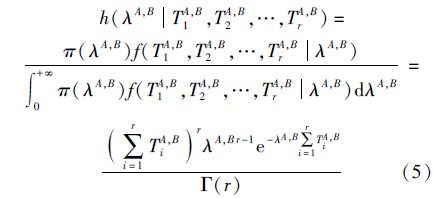
可以看出
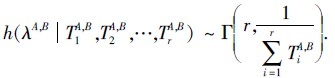根据贝叶斯估计,可以获得指数参数的估计量: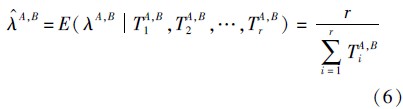
由于节点对(A,B)是从移动模型里随机抽取的,所以对任意节点对都有
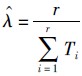,即定理3. 证毕 从定理3可以看出,移动节点对的指数参数只与它们的历史接触数量和累积ICT有关.因此,不能把任意两个节点对的指数参数视为相同.这个结论和文献[4, 5]中的结论形成强烈对比.
由于点估计量不能反映指数参数λ的正确性,因此,在定理4中,基于区间估计的方法分析了λ的适用范围.
3.2.2 指数参数的区间估计 定理4 在定数截尾实验中,节点对的指数参数λ在1－α概率下的置信区间为
证明 对于节点对(A,B)而言,假设Zi=2λA,BTA,B.由
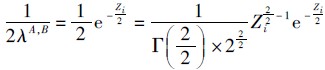,可以得到Zi的概率密度函数为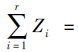
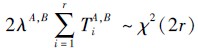,所以Zi~χ2(2).进一步,
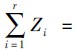则
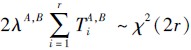,即2λA,Btr~χ2(2r).对于参数λA,B的区间估计,就是找到一个区间[λ ,λ],使得 P(λ ≤λA,B≤λ )=1－α,当α<0.5时,可得到:P(χ2α/2(2r)≤2λA,Btr≤χ21－α/2(2r))= 1－α,则P
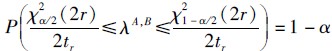,即得到参数λA,B的区间估计为:
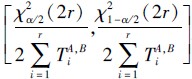.由于节点对(A,B)是从移动模型里随机抽取的,所以对任意节点对而言,指数参数λ在1－α概率下的置信区间为
,即定理4. 证毕 通过IDCM可以看出,节点对的ICT分布的指数参数的点估计量和置信区间都依赖于节点对的历史接触数量和累积ICT.因此,对于DTN的路由协议设计和网络性能分析而言,历史接触信息具有重要意义.
4 仿真验证在本节中对IDCM进行仿真验证,并和两个理论模型(RD和RWP)、两个真实轨迹数据集(北京市出租车网络和PSN)进行对比,并利用判决系数R2来验证理论模型和实际数据仿真结果的差异.
4.1 仿真的参数设置在RD和RWP移动模型仿真中,设置了100个节点在100m×100m的区域内进行仿真.节点的传输半径R=10m,速度设置为vmin=0m/s,vmax=10m/s,定数截尾实验里的节点接触次数设置为r=150.在实际轨迹数据仿真中,本文选取了出租车轨迹数据集,该数据集是由约10000辆携带有商用GPS接收器和GPRS无线通信模块的出租车在北京市的一块25km×25km的区域内移动一天(2010-06-15)所产生的,随机选取了接触数量为35的一对出租车进行对比.另外,对比分析了剑桥大学计算机实验室的PSN数据,该数据集是由4组人携带小型蓝牙设备(iMotes)移动5天所产生的,本文随机选取了接触数量为150的两个人进行对比.
4.2 确定性相关系数本文选取了相关系数R2来度量模型和观察值之间的吻合程度,计算公式为
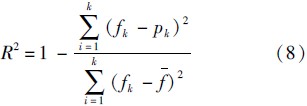
式中：
,表示观察值，每一个观察值都有一个与之相对应的模型值pk=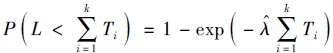
(k=1,2,…,r),此处的r为不同移动模型中两个节点的接触次数,λ ^ 为指数参数估计量,L为时间区间 0,
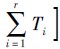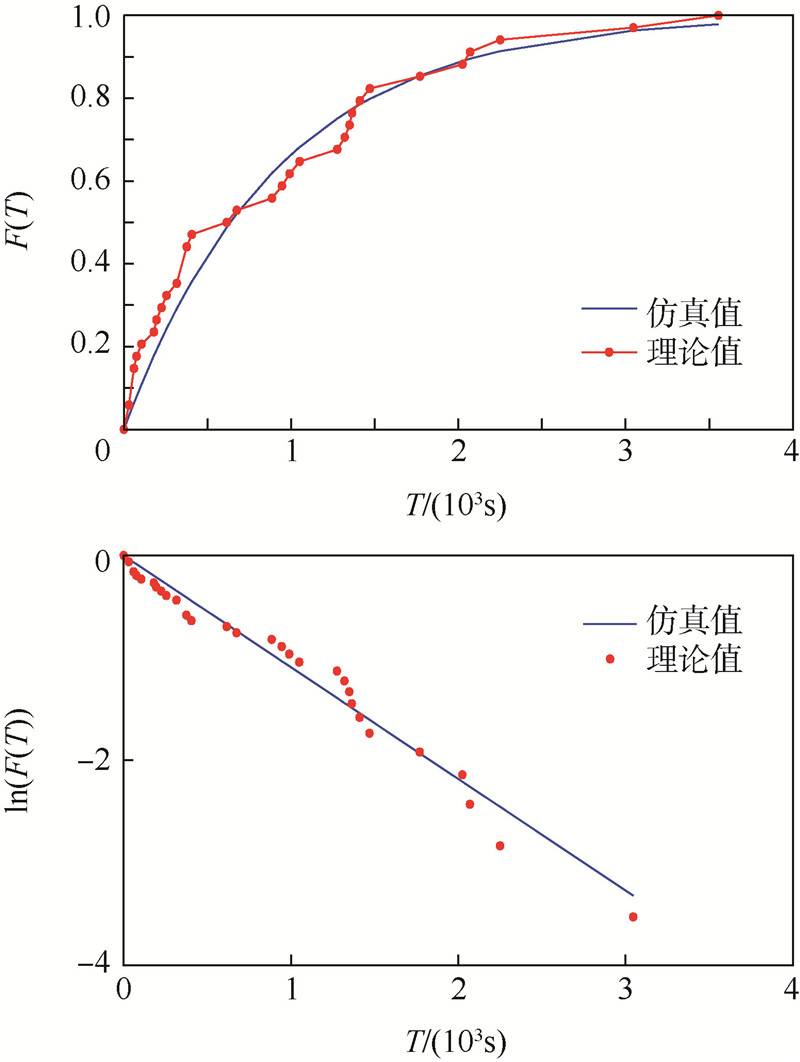
的随机变量；f - 为观察值的均值.因此,R2越大,模型的准确性越高.4.3 仿真结果通过比较RD、RWP和真实移动轨迹的仿真结果与理论结果,验证了IDCM的准确性.如图 1~图 4(F(T)为接触间隔时间T的累积分布函数)和表 2所示,本文方法的理论结果和仿真 结果匹配较好,无论是理论移动模型还是真实数R2均大于0.935.同时,本文也在对数坐标上给出了ICT的CCDF的经验估计.从图中可以看出,仿真结果和理论结果很匹配,对数值呈现出线性下降的趋势.因此可以看出在RWP、RD、北京市出租车网络和PSN中,节点的ICT均呈指数分布.这个结论和文献[1, 5]中的幂律分布形成对比.
 |
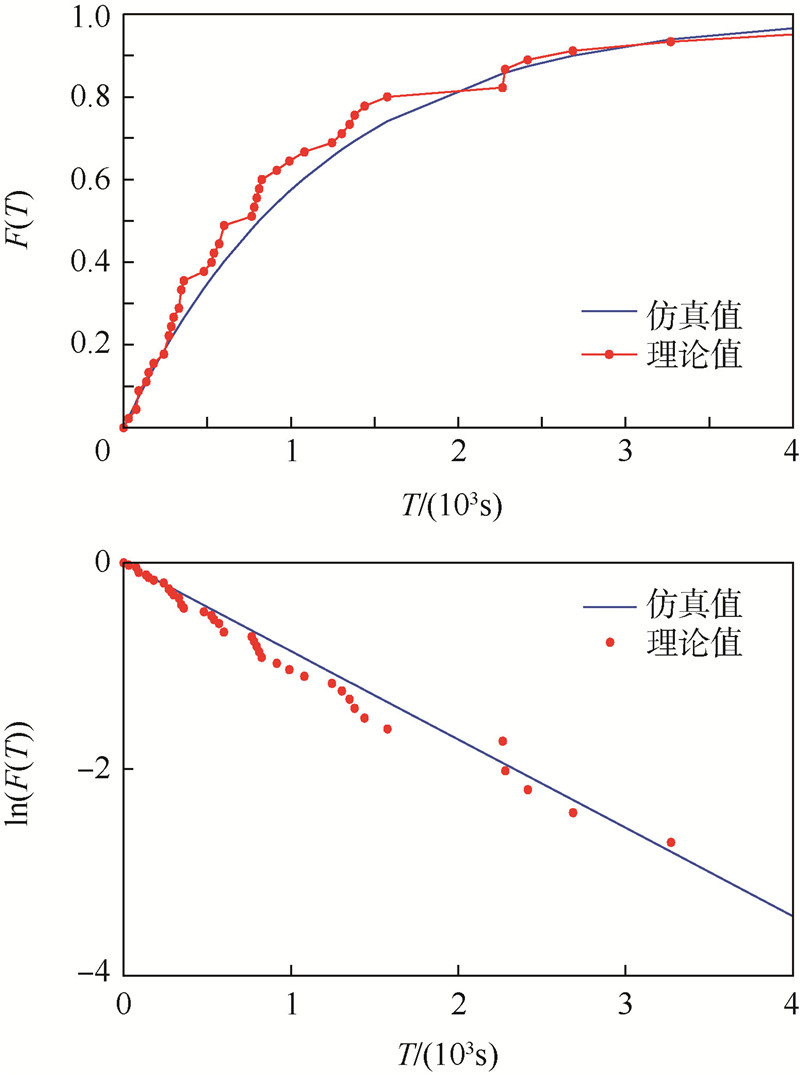| 图 1 RD模型的理论和仿真结果Fig. 1 Theoretical values and simulation results of RD model |
| 图选项 |
 |
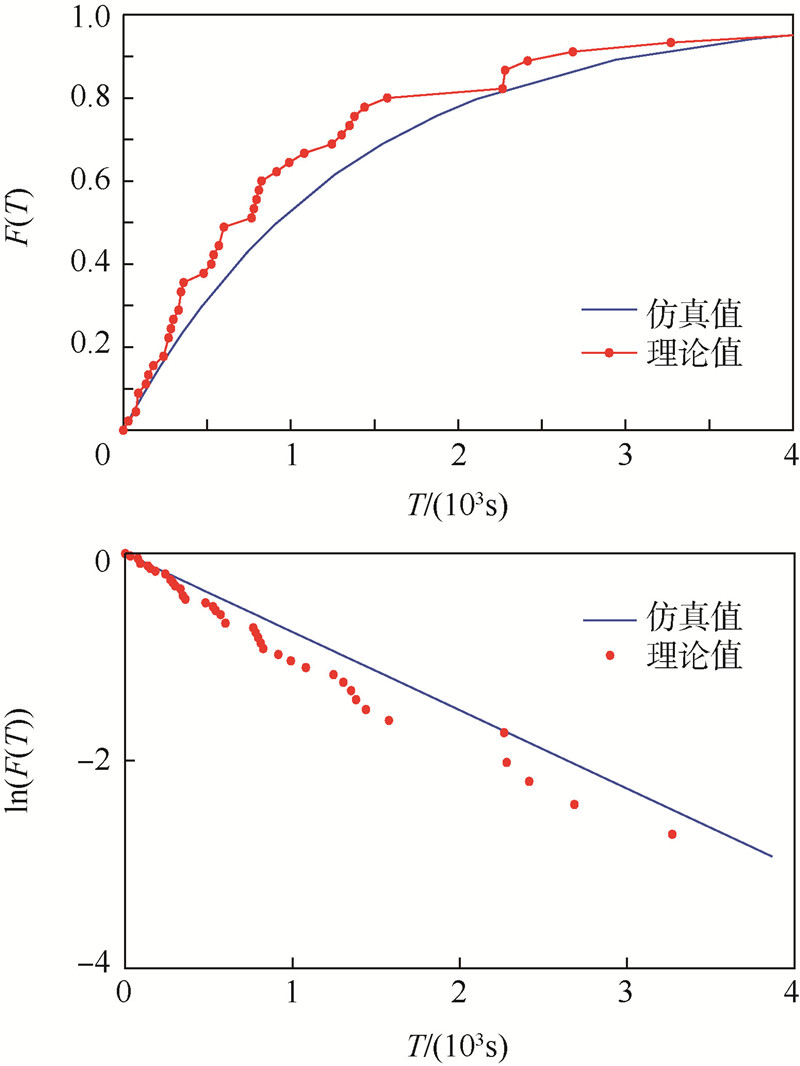
| 图 2 RWP模型的理论和仿真结果Fig. 2 Theoretical values and simulation results of RWP model |
| 图选项 |
 |
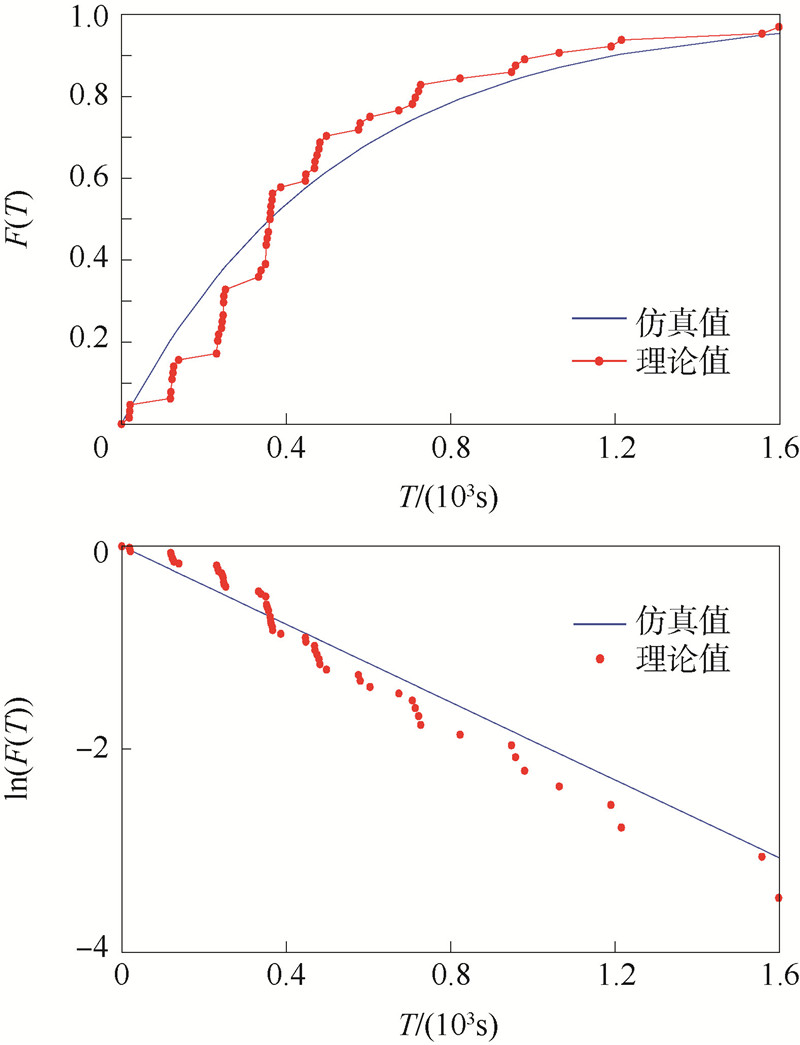
| 图 3 北京出租车网络的理论和仿真结果Fig. 3 Theoretical values and simulation results of Beijing taxi network |
| 图选项 |
 |
| 图 4 PSN的理论和仿真结果Fig. 4 Theoretical values and simulation results of PSN |
| 图选项 |
表 2 通过IDCM模型计算获得的R2Table 2 R2 of IDCM model calculation
| 移动模型和轨迹数据集 | R2 |
| RD | 0.9703041 |
| RWP | 0.9515668 |
| 北京市出租车网络 | 0.9542103 |
| 口袋交换网 | 0.9351140 |
表选项
目前也有一些研究者基于对特定数据集的分析,得出ICT的指数分布模型[3, 6, 19, 20],其中比较典型的是文献[3]中的模型.文献[3]通过对上海市的2109辆出租车一个月的轨迹数据集进行分析,得出了ICT的指数分布模型,并且基于统计拟合的方法计算得出了指数参数λ的值.为了验证本文模型的准确性,将IDCM与文献[3]中的基于统计拟合参数的指数模型进行了对比.为了获得每个节点对的ICT分布,比较了IDCM的R2和文献[3]所提出的模型的R2.表 3展示了通过文献[3]中的统计拟合方法获得的指数参数.
表 3 通过统计拟合ICT模型获得的λTable 3 λ of ICT statistic fitting model
| 数据集 | λ |
| RD | 0.000654144 |
| RWP | 0.000585178 |
| 北京市出租车网络 | 0.00077527 |
| 口袋转换网络 | 0.00092036 |
表选项
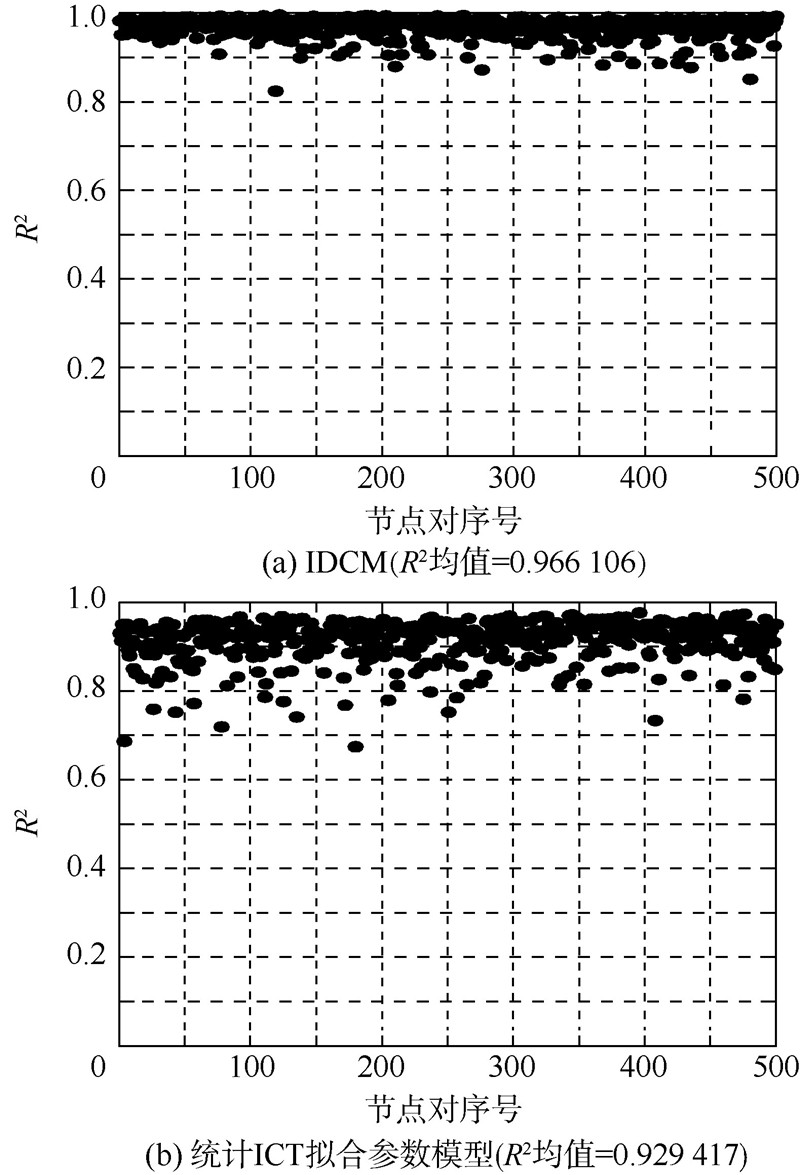
图 5~图 8说明了IDCM和文献[3]的统计拟合模型的R2的比较结果.
从图 5~图 8中可以看出,IDCM的理论值和实际值的R2均值比其他模型的R2均值要大.例如,北京出租车网络和PSN的IDCM的R2均值为0.822和0.789,比文献[3]中的模型的R2要高14.64%和15.01%.实验结果表明,IDCM可以获得比文献[3]中的模型准确度更高的节点对的ICT分布.
 |
| 图 5 RD模型的R2比较Fig. 5 R2 comparison of RD model |
| 图选项 |
 |
| 图 6 RWP模型的R2比较Fig. 6 R2 comparison of RWP model |
| 图选项 |
 |
| 图 7 北京出租车网络的R2比较Fig. 7 R2 comparison of Beijing taxi network |
| 图选项 |
 |
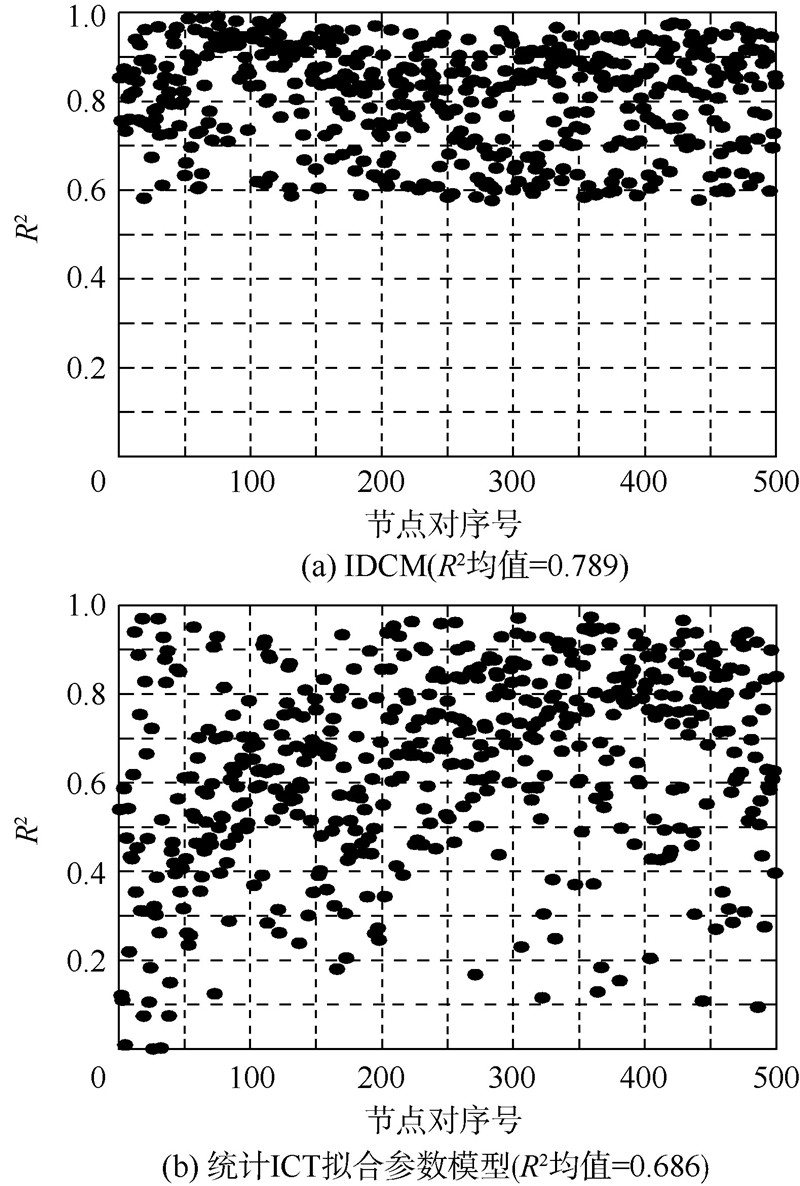| 图 8 PSN的R2比较Fig. 8 R2 comparison of PSN |
| 图选项 |
5 结 论1) 研究了移动模型和真实轨迹数据集中的节点对的ICT分布.在可靠性数学理论和定数截尾实验的基础上,构建了IDCM,证明了任意一个移动模型只要服从本文提出的2个基本假设,则其节点对的ICT服从指数分布.
2) IDCM表明指数分布参数仅与节点对的历史接触次数和累积ICT有关.
3) 理论分析和仿真结果表明IDCM可以准确地描述ICT的统计特性,与其他研究中的幂律分布相比,IDCM提供了一个更加准确的指数分布模型.
4) 仿真结果表明,与目前基于参数拟合的指数分布模型相比,IDCM具有更高的准确性.
5) IDCM模型虽然方便,但在实际场景的应用中也存在一些问题.例如,每一个节点需要记录与其他所有节点的历史接触信息,随着网络规模的增大,数据量将会很大,因此节点的数据存储将会是一个问题.而且,随着节点运动时间越长,历史信息的时效性也会下降,因此在设计路由算法时,节点历史相遇信息的更新也是一个需要考虑的问题.此外,当节点接触较频繁时,数据的更新也会较快,因此节点的能量约束也将会是一个需要考虑的问题.
6) 在下一步工作中,计划在IDCM的基础上研究一些自适应的模型来改善目前网络中的性能分析.同时,IDCM也为研究者们关于目前DTN中的算法和协议的优化提供了一定的指导.
参考文献
| [1] | Ahmed S A, Salil S K S.Characterization of a large-scale delay tolerant network[C]//Local Computer Networks (LCN).Piscataway,NJ:IEEE Press,2010:56-63. |
| Click to display the text | |
| [2] | Karagiannis T, le Boudec J,Vojnovic M.Power law and exponential decay of intercontact times between mobile devices[J].IEEE Transactions on Mobile Computing,2010,9(10):1377-1390. |
| Click to display the text | |
| [3] | Zhu H Z, Li M L,Fu L Y,et al.Impact of traffic influxes:Revealing exponential intercontact time in urban VANETs[J].IEEE Transactions on Parallel and Distributed Systems,2011,22(8):1258-1266. |
| Click to display the text | |
| [4] | Li Y, Jiang Y R,Jin D P,et al.Energy-efficient optimal opportunistic forwarding for delay-tolerant networks[J].IEEE Transactions on Vehicular Technology,2010,59(9):4500-4512. |
| Click to display the text | |
| [5] | Sharma G, Mazumdar R R.Delay and capacity tradeoffs for wireless ad hoc networks with random mobility[J].IEEE/ACM Transactions on Networking,2007,15(5):981-992. |
| Click to display the text | |
| [6] | Muhammad A, Simon R.A simulation study of common mobility models for opportunistic networks[C]//Simulation Symposium.Piscataway,NJ:IEEE Press,2008:43-50. |
| Click to display the text | |
| [7] | Muhammad A, Simon R.Characteristics of common mobility models for opportunistic networks[C]//ACM Second Workshop Performance Monitoring and Measurement of Heterogeneous Wireless and Wired Networks.New York:ACM,2007:105-109. |
| Click to display the text | |
| [8] | Zhang X L, Kurose J,Levine B N,et al.Study of a bus-based disruption-tolerant network:Mobility modeling and impact on routing[C]//Proceedings of the Annual International Conference on Mobile Computing and Networking.New York:ACM,2007:195-206. |
| Click to display the text | |
| [9] | Hu Y T, Wang H Q,Xia C H,et al.On the distribution of inter contact time for DTNs[C]//Local Computer Networks (LCN).Piscataway,NJ:IEEE Press,2012:152-155. |
| Click to display the text | |
| [10] | Sharma G, Mazumdar R R.Scaling laws for capacity and delay in wireless ad hoc networks with random mobility[C]//IEEE International Conference on Communications.Piscataway,NJ:IEEE Press,2004:3869-3873. |
| Click to display the text | |
| [11] | Spyropoulos T, Psounis K,Raghavendra C S.Performance analysis of mobility-assisted routing[C]//Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc).New York:ACM,2006:49-60. |
| Click to display the text | |
| [12] | Li Y,Hui P, Jin D P,et al.Evaluating the impact of social selfishness on the epidemic routing in delay tolerant networks[J].IEEE Communications Letters,2010,14(11):1026-1028. |
| Click to display the text | |
| [13] | Niu J W,Guo J K, Cai Q S,et al.Predict and spread:An efficient routing algorithm for opportunistic networking[C]//Wireless Communications and Networking Conference.Piscataway,NJ:IEEE Press,2011:498-503. |
| Click to display the text | |
| [14] | James S, Richard G,Jon C,et al.The Cambridge/haggle dataset[EB/OL].Cambridge:Cambridge University,2005(2013-01-15).http://crawdad.cs.dartmouth.edu/cambridge/haggle/. |
| Click to display the text | |
| [15] | Erdds P, R Wi A.On random graphs[J].Computer Engineering,1959,109(4):339-340. |
| Click to display the text | |
| [16] | 戴冠中,王林. 复杂网络的Scale-free性、Scale-free现象及其控制[M].北京:科学出版社,2009:1-5. Dai G Z,Wang L.Scale-free property,Scale-free phenomenon and control of complex network[M].Beijing:Science Press,2009:1-5(in Chinese). |
| [17] | 冯允成,吕春连, 杜瑞甫.随机网络及其应用[M].北京:北京航空学院出版社,1987:1-8. Feng Y C,Lv C L,Du R F.Random network and its application[M].Beijing:Beihang University Press,1987:1-8(in Chinese). |
| [18] | Erd s P, Rényi A.On the existence of a factor of degree one of a connected random graph[J].Acta Mathematica Academiae Scientiarum Hungarica,1966,17(3-4):359-368. |
| Click to display the text | |
| [19] | Cai H, Eun D Y.Crossing over the bounded domain:From exponential to power-law intermeeting time in mobile ad hoc networks[J].IEEE/ACM Transactions on Networking,2009,17(5):1578-1591. |
| Click to display the text | |
| [20] | Zhu H Z, Fu L Y,Xue G T,et al.Recognizing exponential inter-contact time in VANETs[C]//2010 Proceedings IEEE INFOCOM.Piscataway,NJ:IEEE Press,2010:101-105. |
| Click to display the text |
