本文给出一种求解瞬态传热问题的高效高精度方法,即采用微分求积法离散空间域,精细积分方法离散时间域,具有解析性好、精度高、计算稳定和能高效处理各种复杂边界条件的特性.
1 微分求积法微分求积法(Differential Quadrature Method,DQM)是一种全域逼近的数值方法,它的基本思想是以全域内各节点函数值的加权和来逼近函数偏导数在某一节点处的值.它与有限元法(Finite Element Method,FEM)有显著的区别:FEM通常采用低阶多项式逼近单元内的函数值,而DQM则是在全域内采用高阶多项式逼近域内某一连续函数;FEM是在单元内逼近函数值,由近似函数求得导数,而DQM综合全域内各节点的信息来直接逼近函数偏导数在某一点的值.因此,DQM用较少网格点就可以获得高的数值精度.
根据微分求积方法,函数f(x)在xi点的k阶导数可近似表示为

式中:N为x方向的结点数;A(k)ij为根据Lagrange函数求得的对应于k阶导数的权系数,A(1)ij可由下面显式计算[12]:
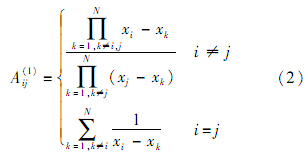
而高阶系数则由递推公式计算[9]:
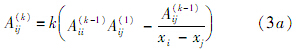
式中:i,j=1,2,…,N,i≠j;2≤k≤N-1,而
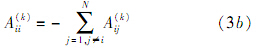
式中:1≤k≤N-1.高维问题的处理与之类似[17].
用微分求积法求解问题,必须选取合理分布的节点.均匀分布是最早被采用也是最简单的节点分布形式.但计算表明,非均匀节点具有更快的收敛速度和更高的求解精度.边界条件处理也是微分求积法中关键问题之一.对于二阶微分方程的求解每个端点只需一个条件,引入边界条件时直接将边界节点坐标代入边界条件即可.对于二阶以上高阶微分方程,每个端点的边界条件不止一个,边界节点却只有一个,因此边界条件的处理不能简单进行.解决这一问题的方法有多种,常见的有方程替代法、变量缩聚法、权系数矩阵修正法和边界自由度增添法.用这些方法可以处理复杂的边界条件.
2 精细积分法精细积分法是计算指数矩阵的一种高精度方法,其要点是利用指数函数加法定理计算指数矩阵的增量.考虑指数矩阵:
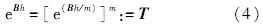
式中: B 为矩阵;h为时间步长;m为任意正整数,通常选取m=2N(N为正整数).令τ=h/m,此时e B h 已经接近单位矩阵 I ,于是可以写成:
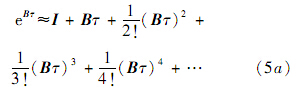
或

由于τ是很小的量,所以式5(a)展开到第5项其精度就足够,其中 T τ相当于 T 的增量矩阵,为小量矩阵.因此计算时,要单独存储 T τ,否则 T τ相对于 I 是很小的数,在计算机舍入计算时其精度丧失殆尽.在计算 T 的时候,先把式(4)进行分解:
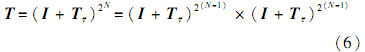
一直分解,共N次.
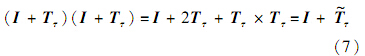
最后计算 T ,即

这样计算的 T 具有计算机的精度[18],这里不再给出具体数值结果.
3 瞬态传热问题考虑隔热结构的热传导问题,如图 1所示.瞬态温度场U是时间和空间的函数,非稳态导热微分方程为

式中:β为传热系数;x、y、z为空间坐标;t为时间.
初始条件:

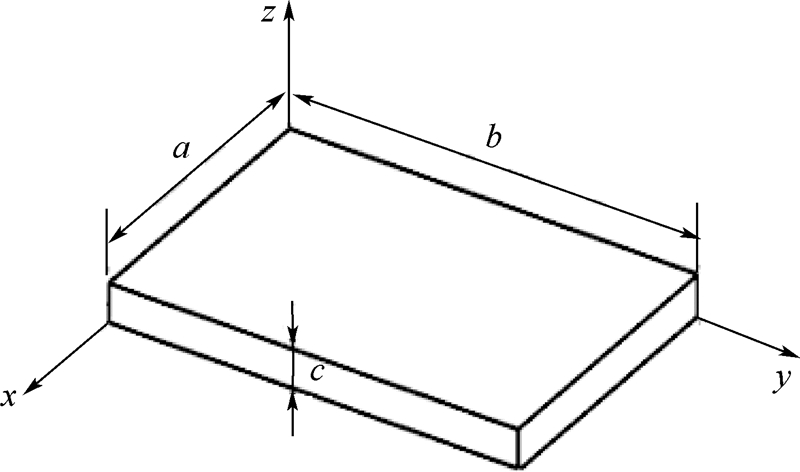 |
| 图 1 隔热材料结构图Fig. 1 Thermal protection material structure |
| 图选项 |
式中:U0为初始温度.
边界条件:
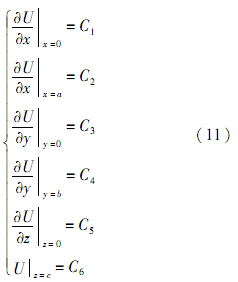
用分离变量法把温度函数空间域分离,即

用微分求积法则离散方程式(9)得
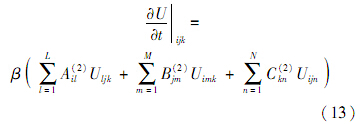
式中:L、M、N分别为x、y、z方向划分的节点数;i、j、k为节点编号,1≤i≤L,1≤j≤M,1≤k≤N;A(2)、B(2)、C(2)分别为关于x、y、z方向二阶导数权系数矩阵.
在求解具体问题时,要用边界条件方程替换方程式(13)中相应的方程.本文选取使切比雪夫多项式等于零的点为节点.离散化的边界条件为

式中:C1jk、C2jk、C3ik、C4ik、C5ij、C6ij为各种可能边界条件.若边界条件是二阶或高阶,其处理方式类似于式(14).
用向量和矩阵可以把域内平衡方程和边界条件方程写成


式中:$\overline {\rm{U}} $为全部结点温度向量;$\overline {{{\rm{U}}_I}} $为域内结点温度向量;$\widetilde {\rm{H}}$和$\widetilde {\rm{D}}$为由权系数组成的矩阵;F为边界条件.为了便于处理边界条件,把方程式(15)改写成
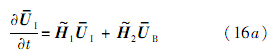
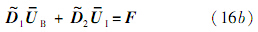
式中:F=[C1 C2 C3 C4 C5 C6]T;$\overline {{U}} $B为边界结点温度向量;$\widetilde {{{\rm{H}}_1}}$、$\widetilde {{{\rm{H}}_2}}$、$\widetilde {{{\rm{D}}_1}}$、$\widetilde {{{\rm{D}}_2}}$为由权系数组成的矩阵.边界条件F可以与时间相关也可以与时间无关.设

式中:F0为时间无关的边界条件向量;F1为时间有关的边界条件向量.
若边界条件都是时间无关向量,则式(17)为

从式(16)消去$\overline {{U}} $ B,再用式(17)替换边界条件F,整理得
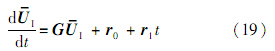
式中:

精细积分方法直接求解的方程是一阶微分方程,方程式(19)仅包含时间的一阶微分,因此不需要降阶,即不需要增加自由度,这也是本文选择精细积分方法的根据.
对方程式(19),根据李级数方法得到其解析解为
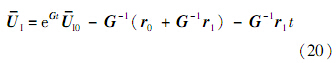
进而可以得到时间递推关系式:
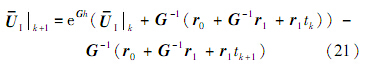
计算式(21)的关键问题就是其中指数矩阵e G h 的计算,其计算方法可参见第2节内容.进而由递推公式(21),可求得域内各节点温度随时间的变化值.
4 数值算例下面用本文方法分析某隔热材料的瞬态温度场.结构尺寸为0.2×0.2×0.025m3,热扩散系数2.47933884×10-7m2/s.
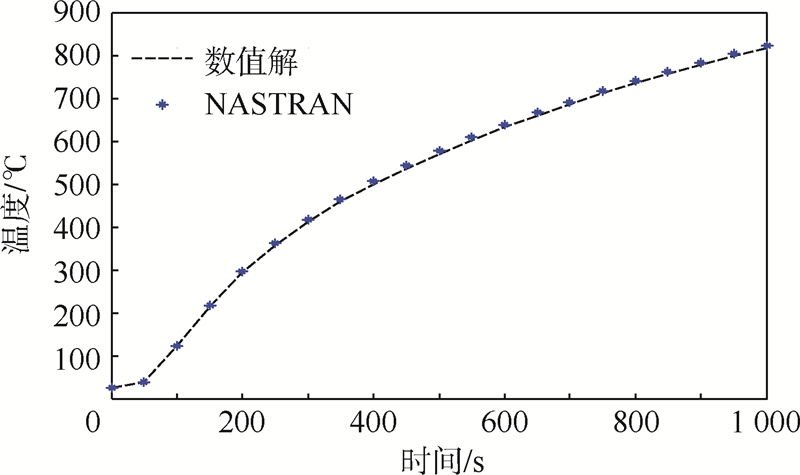
4.1 算 例 1采用三维模型,上表面1200℃恒温,下表面和四周面绝热状态,初始温度为25℃.分别采用微分求积(数值解)和NASTRAN计算它的温度响应.微分求积法中布置节点4×4×10.NASTRAN中划分20×20×10个八节点体单元.图 2给出了两种方法求解的结构下表面一点的温度响应图.图 3给出了两种方法求解的结构中间面一点的温度响应图.图 4给出了NASTRAN计算的982s状态结构的温度响应图.
由图 2~图 4可知:微分求积法计算得到的温度响应曲线和有限元计算结果吻合得很好,可见微分求积和精细积分结合的数值方法能高效高精度地求解瞬态传热问题,布置少量的节点就达到了比较高的精度.
 |
| 图 2 结构下表面一点的温度响应Fig. 2 Temperature response of one point at bottom of structure |
| 图选项 |
 |
| 图 3 结构中间面一点的温度响应Fig. 3 Temperature response of one point in the middle of structure |
| 图选项 |
 |
| 图 4 NASTRAN计算的第982s结构温度响应Fig. 4 Temperature response of structure at 982 s by NASTRAN |
| 图选项 |
4.2 算 例 2考虑如下几种边界条件组合,其中环境温度为25℃.
第1类边界条件(Case1):上表面为1200℃恒温,其他面绝热.此时在式(14)中,C1jk=0,C2jk=0,C3ik=0,C4ik=0,C5ij=0,C6ij=1200.
第2类边界条件(Case2):上表面为1200℃恒温,其他面热交换,对流热交换系数为5000W/m2.C1jk=5000,C2jk=5000,C3ik=5000,C4ik=5000,C5ij=5000,C6ij=1200.
第3类边界条件(Case3):上表面温度变化规律为
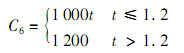
其他边界绝热,C1jk=0,C2jk=0,C3ik=0,C4ik=0,C5ij=0.
第4类边界条件(Case4):上表面温度变化规律为

其他边界绝热,C1jk=0,C2jk=0,C3ik=0,C4ik=0,C5ij=0.
由此可以看出,针对不同的边界条件只需要改变相应的参数即可,求解格式是统一的.微分求积法一方面把二阶或高阶的边界条件并入加权系数中,另一方面把边界条件离散到各个空间点上,大大地简化了边界条件的处理.
图 5给出了3种不同初始温度下,图 1模型中上下表面中点处温度曲线图.由图 5可知前100s 时最下表面温度几乎没有变化,等于初始温度,主要是因为热量是从上表面传递过来的,它的传递是依赖于时间的,在最开始时热量只能传递上层位置;随着时间增长,热量传递加快,下表面温度也增加得越来越快,当达到一定时刻时,上下表面温差小到一定值时,热量传递趋于稳定,曲线又趋于平缓.
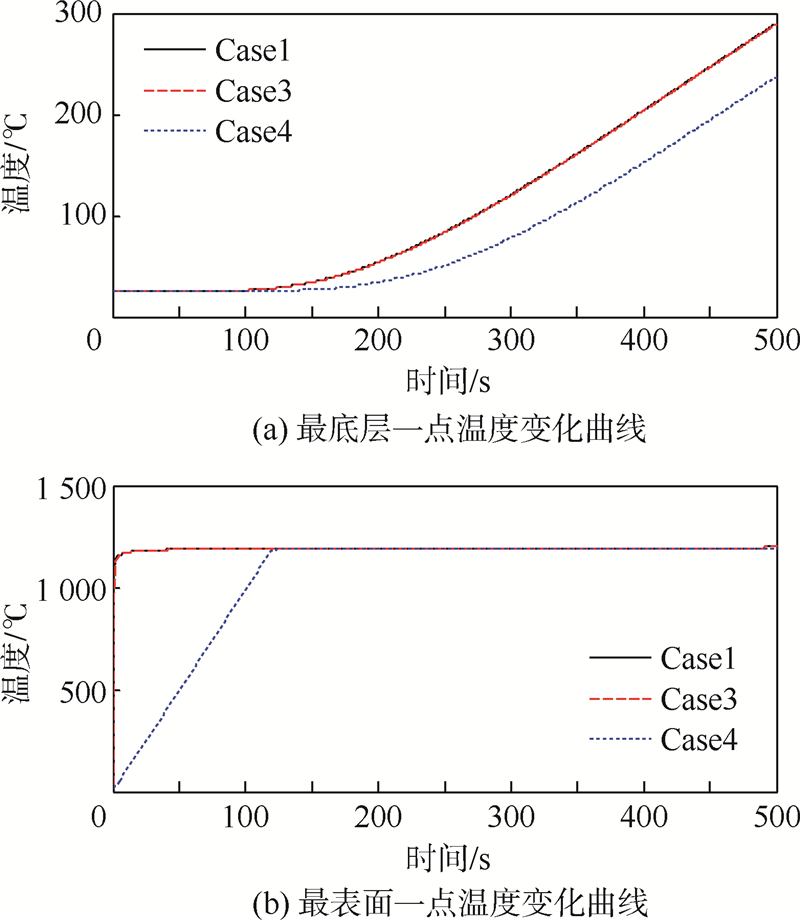 |
| 图 5 3种不同初始温度下的温度响应Fig. 5 Temperature response with three different initial temperatures |
| 图选项 |
图 6给出绝热和热交换两种边界条件下下表面中点温度响应曲线.由图 6可知无论在何种边界下,开始 时刻温度变化缓慢,随着时间增长,温度迅速增加直至最后趋于平稳状态.但对于热交换边界条件,最开始时刻,下表面温度反而会下降,比初始时刻温度还低,之后逐渐增加.由图可知在任意时刻,绝热状态下温度总是比热交换条件高.因而在分析温度响应时正确地确定边界条件是至关重要的.
 |
| 图 6 不同边界条件下结构下表面一点温度响应Fig. 6 Temperature response of one point at bottom of structure with different boundary conditions |
| 图选项 |
5 结 论本文综合利用精细积分法和微分求积法求解了瞬态温度场问题,该做法的优点是充分利用了两种方法的高效高精度特点.
1) 精细积分法对步长的依赖性很小,在有效位数范围内其结果和精确解一致,并且没有因为对方程降阶而增加自由度数的问题.
2) 微分求积法不依赖泛函和变分原理,具有数学原理简单、计算精度高、计算量和内存需求少等优点,能以较少的网格点和较小的计算量求得高精度的数值解.
3) 在处理复杂边界条件时,比如C1类边界条件,微分求积法具有普适性和灵活性.微分求积法具有精度高、效率高等特点,这是高阶方法的优点.
参考文献
| [1] | Civan F, Sliepcevich C M.Application of differential quadrature to transport processes[J].Journal of Mathematical Analysis and Applications,1983,93(1):206-221. |
| Click to display the text | |
| [2] | Bert C W, Jang S K,Striz A G.Two new approximate methods for analyzing free vibration of structural components[J].AIAA Journal,1988,26(5):612-618. |
| Click to display the text | |
| [3] | Bert C W, Malik M.The differential quadrature method for irregular domains and application to plate vibration[J].International Journal of Mechanical Sciences,1996,38(6):589-606. |
| Click to display the text | |
| [4] | Jang S K, Bert C W,Striz A G.Application of differential quadrature to static analysis of structural components[J]. International Journal for Numerical Methods in Engineering,1989,28(3):561-577. |
| Click to display the text | |
| [5] | Bert C W, Wang X,Striz A G.Differential quadrature for static and free vibration analysis of anisotropic plates[J].International Journal of Solids and Structures,1993,30(13):1737-1744. |
| Click to display the text | |
| [6] | Liu F L,Liew K M. Static analysis of Reissner-Mindlin plates by differential quadrature element method[J].ASME Journal of Applied Mechanics,1998,65(3):705-710. |
| Click to display the text | |
| [7] | Wang X, Bert C W.A new approach in applying differential quadrature and free vibration analysis of beams and plates[J].Journal of Sound and Vibration,1993,162(3):566-572. |
| Click to display the text | |
| [8] | Xing Y F, Liu B.A differential quadrature analysis of dynamic and quasi-static magneto-thermo-elastic stresses in a conducting rectangular plate subjected to an arbitrary variation of magnetic field[J].International Journal of Engineering Science,2010,48(12):1944-1960. |
| Click to display the text | |
| [9] | Shu C, Richards B E.Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations[J].International Journal for Numerical Methods in Fluids,1992,15(17):791-798. |
| [10] | Malik M, Bert C W.Differential quadrature solution for steady state incompressible and compressible lubrication problems[J].ASME Journal of Teratology,1994,116(2):296-302. |
| [11] | Quan J R, Chang C T.New insights in solving distributed system equations by the quadrature methods-I.Analysis[J].Computers in Chemical Engineering,1989,13(7):779-788. |
| Click to display the text | |
| [12] | Quan J R, Chang C T.New insights in solving distributed system equations by the quadrature methods-II.Numerical experiments[J].Computers in Chemical Engineering,1989,13(9):1017-1024. |
| Click to display the text | |
| [13] | Tseng A A, Chen T C,Zhao F Z.Direct sensitivity coefficient method for solving two-dimensional inverse heat conduction problems by finite-element scheme[J].Numerical Heat Transfer,Part B:Fundamentals,1995,27(3):291-307. |
| Click to display the text | |
| [14] | 薛齐文,杨海天, 胡国俊.共轭梯度法求解瞬态传热组合边界条件多宗量反问题[J].应用基础与工程科学学报,2004,12(2):113-120. Xue Q W,Yang H T,Hu G J.Solving inverse heat conduction problems with multi-variables of boundary conditions in transient-state via conjugate gradient method[J].Journal of Basic Science and Engineering,2004,12(2):113-120(in Chinese). |
| Cited By in Cnki (9) | |
| [15] | France D M, Chiang T.Analytic solution to inverse heat conduction problem with periodicity[J].Journal of Heat Transfer,1980,102(3):579-581. |
| Click to display the text | |
| [16] | 张驰,石宏,张硕,等. 基于无网格边界元法的瞬态热传导问题研究[J].科学技术与工程,2013,13(26):7638-7643. Zhang C,Shi H,Zhang S,et al.Study on transient heat conduction by meshless boundary element method[J].Science Technology and Engineering,2013,13(26):7638-7643(in Chinese). |
| Cited By in Cnki () | |
| [17] | Xing Y F, Liu B.High-accuracy differential quadrature finite element method and its application to free vibrations of thin plate with curvilinear domain[J].International Journal for Numerical Methods in Engineering,2009,80(13):1718-1742. |
| Click to display the text | |
| [18] | 钟万勰. 结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136. Zhong W X.On precise time-integration method for structural dynamics[J].Journal of Dalian University of Technology,1994,34(2):131-136(in Chinese). |
| Cited By in Cnki (366) | |
