
式中:剪切角γ可根据材料力学确定,即

式中:A为梁的横截面积;p为截面形状系数;G为剪切弹性模量.
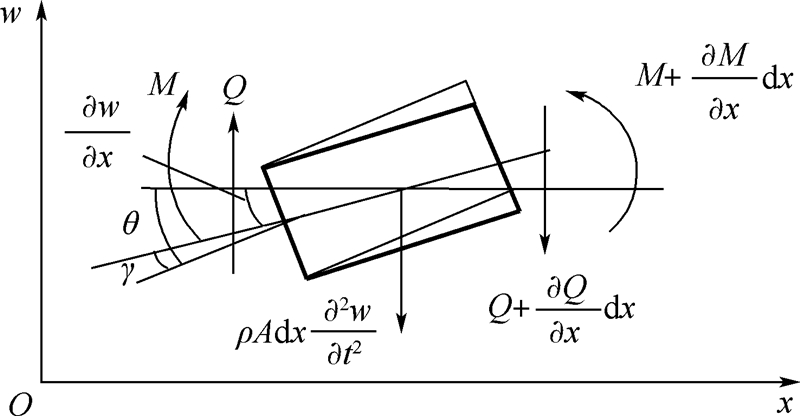 |
| 图 1 Timoshenko梁微段的变形与受力分析Fig. 1 Deformation and force analysis of micro-segment of Timoshenko beam |
| 图选项 |
根据牛顿第二定律和动量矩定理,自由振动的Timoshenko梁的挠度和转角满足式(3):
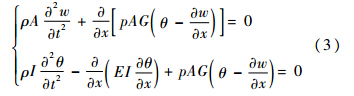
式中:ρ为单位长度上梁的密度;E为梁的弹性模量;I为梁对截面惯性主轴的转动惯量.消去转角θ,得到Timoshenko梁的自由振动微分方程为
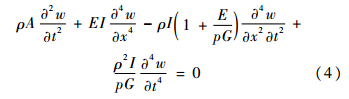
设梁具有如下形式的横向固有振动w(x,t)=W(x)·q(t)
式中:W(x)为梁的振形函数;q(t)为描述运动规律的时间函数.Timoshenko梁的振形函数为
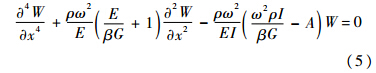
式(5)通解为
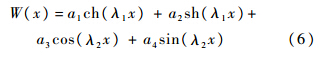
式中:
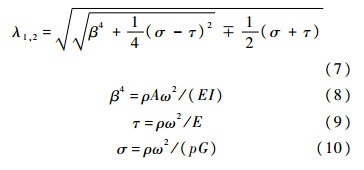
2 传递矩阵和递推公式传递矩阵法[18, 19, 20]是对多自由度系统进行振动分析的一种有效计算方法.用传递矩阵分析系统的振动时,只要对一些阶次很低的传递矩阵进行连续的矩阵乘法运算,计算中只需求解低阶次的传递矩阵和行列式,因此传递矩阵法节省了计算工作量.将整个梁自中间的各个边界条件处断开,形成s段梁,每段梁的振形函数都可用式(5)表示.2.1 场传递矩阵的推导根据梁的性质,梁截面的状态向量是个4×1的矩阵,可以用Z(x)=[Y θ M Q]T进行表示.其中Y为挠度.且满足式(11):
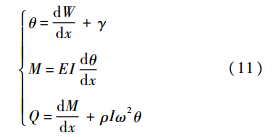
设梁的长度为1,对整个梁做分析,在梁的输入段x=0处,根据梁的性质,有
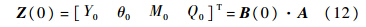
在梁的输入段x=1处,根据梁的性质,有
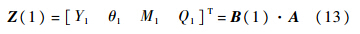
式中:A=[a1 a2 a3 a4]T,为系数矩阵.由式(12)和式(13)可得:
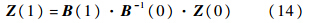
则由场传递矩阵的定义可知,场传递矩阵Hf为
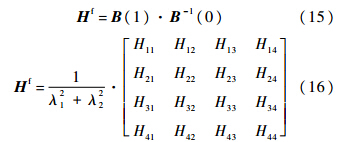
式中:

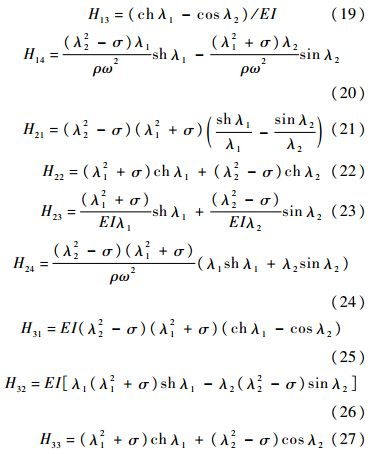
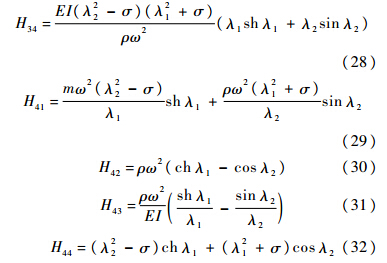
2.2 点传递矩阵的推导设中间的铰支座有k个,每个铰支座的坐标为αi(i=1,2,…,k);集中质量有n个,每个坐标为bi(i=1,2,…,n),质量为mi(i=1,2,…,n),转动惯量为Ji(i=1,2,…,n);拉压弹簧有f个,每个坐标为ci(i=1,2,…,f),刚度为ki(i=1,2,…,f);扭转弹簧有h个,每个坐标为di(i=1,2,…,h),扭转刚度为kθi(i=1,2,…,h).以考虑转动惯量的集中质量的点传递矩阵为例,其他的边界条件类似可得.在集中质量所在的点bi,满足式(33)和式(34):式中:
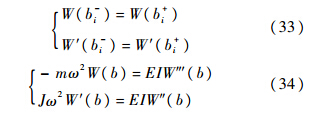
式中:J为梁中间的集中质量的转动惯量.将式(33)和式(34)代入状态矢量的方程中,可得式中:
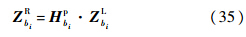
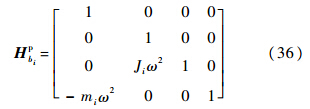
式中:传递矩阵的上标p表示点矩阵;状态矢量的上标R表示状态的末端,本例中为经过传递矩阵的右端;L表示状态的始端,本例中为经过传递矩阵的左端.传递矩阵和状态矢量的下标均表示坐标位置.同理,拉压弹簧的点传递矩阵为
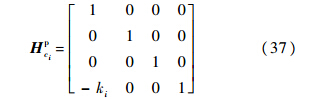
扭转弹簧的点传递矩阵为
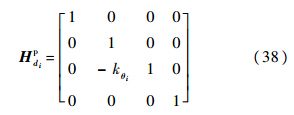
中间的铰支座的点传递矩阵为

2.3 递推公式和频率方程梁的中端从一个边界条件到另一个边界条件经过一段梁和一个力学元件.则体现第i个单元两端状态传递关系的递推公式可表示为
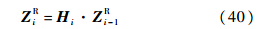
式中:梁端的传递矩阵Hi由该段的场矩阵Hif和该段的点矩阵Hip组成,即

整个系统的传递矩阵H表示为
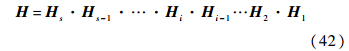
由推导可知,整个系统的传递矩阵H是个4×4的矩阵.可以写成下面的形式:
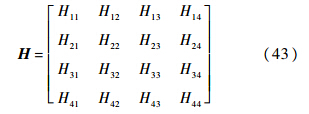
可得梁两端在不同的边界条件下的频率方程如下:固支-自由:
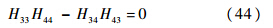
固支-简支:
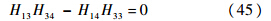
固支-固支:
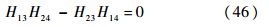
简支-自由:
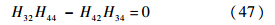
简支-简支:
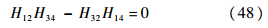
简支-固支:
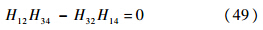
自由-自由:
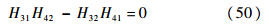
自由-简支:
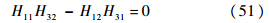
自由-固支:
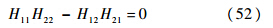
梁两端在不同的边界条件下的振形函数为
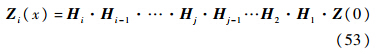
2.4 模型验证按照式(1)~式(53)方法,对两端简支的Timoshenko梁的频率方程进行推导,应用式(16)~式(32)和式(48),得到两端简支的Timoshenko梁的频率方程如下:
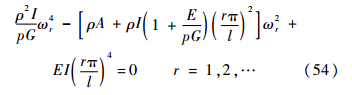
式中:ωr为Timoshenko梁自由振动的第r阶频率.这与文献[21]给出的结论相同.3 Bernoulli-Euler梁的自由振动3.1 Bernoulli-Euler梁的振动微分方程将Timoshenko梁的自由振动方程式(4)中的考虑剪切变形和中性轴的转动惯量的项去掉,即可得出Bernoulli-Euler梁的自由振动方程如下:
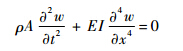
Bernoulli-Euler梁的振形函数为
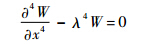
振形函数的通解为W(x)=a1ch(λx)+a2sh(λx)+a3cos(λx)+a4sin(λx)
式中:λ4=[ρA/(EI)]ω2.3.2 场传递矩阵将式(16)中考虑剪切变形和中性轴的转动惯量的项去掉,即可得出Bernoulli-Euler梁的场传递矩阵:
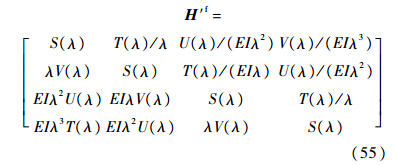
式中:S(x)、T(x)、U(x)和V(x)为Krylov函数.点传递矩阵、递推公式、频率方程和振形函数类似式(33)~式(52)可得出.4 特 例通过简化式(1)~式(53)模型,使简化模型体现一定的工程实践意义,方便工程技术人员应用;并与已有文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]的研究结果进行比较,说明它们可以视为本文提出模型的特例.由于在航空航天、兵器和汽车工业中Bernoulli-Euler梁的相关模型应用较多,根据Bernoulli-Euler梁的简化模型情形,相应的Timoshenko梁模型可按照相同思路得出.4.1 双跨梁情形令k=1、n=f=h=0,可将模型转换成双跨梁的情形,即梁中间只有一个铰支座,位置是αi,将梁分成了两段.引言中提到,先前的用于起落架性能分析的弹性机体看成了自由-自由的Bernoulli-Euler梁,但是应用的对象是上单翼飞机,中单翼飞机如何处理鲜见文献报道;中单翼飞机由于机翼不是一体的,机翼与机身通过加强隔框进行连接,可将连接方式视为铰接.由对称性可取一半的机体,看成悬臂梁加中间铰支座的双跨梁加以分析.按照式(39)、式(44)和式(55)递推,可得其频率方程为
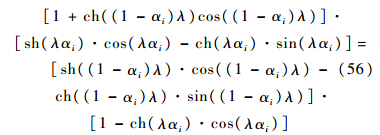
将αi→1,式(56)变成

式(57)为一端固支、一端铰支的频率方程[16].将αi→0,式(56)变成
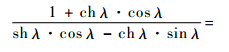
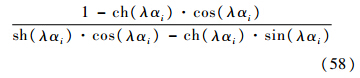
当αi→0时,式(58)是个0/0型的不等式,由三角函数的性质可知,式(58)右边的分子是比分母更高阶的无穷小量,则
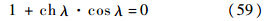
式(59)为悬臂梁的频率方程[20].其他的双跨梁模型,比如简支梁加中间铰支座通过类似的分析也可得出.4.2 悬臂梁带有集中质量的情形令n=1、k=f=h=0,可将模型转换成带有集中质量的情形,即梁中间只有一个集中质量,位置为bi,质量为mi,转动惯量为Ji.先前的用于起落架性能分析的弹性机体看成了自由-自由的Bernoulli-Euler梁,但是没有考虑翼吊式发动机的影响.可以将翼吊式发动机看成是悬臂梁上的集中质量来完善模型.按照式(36)、式(44)和式(55)递推,可得其频率方程为
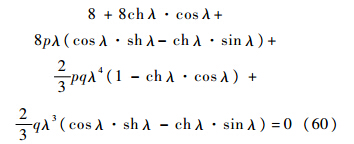
式中:
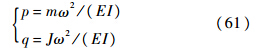
令q=0,可得
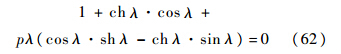
这与文献[3]给出的结论相同.悬臂梁带有任意集中质量的模型可以类似得出,可以看成对带弹机翼的弹性分析的模型.4.3 带有任意拉压弹簧和集中质量的情形令k=h=0,可将模型转换成带有任意个拉压弹簧和集中质量的情形,即梁中间有n个集中质量,位置为bi(i=1,2,…,n),质量为mi(i=1,2,…,n),转动惯量为Ji(i=1,2,…,n);并且梁中间有f个拉压弹簧,每个坐标为ci(i=1,2,…,f),刚度为ki(i=1,2,…,f).特别地,当集中质量和拉压弹簧具有相同的数量,且成对出现在在同一个位置时,即bi=ci(i=1,2,…,n),n=f时,可以用此模型模拟兵器工业上火炮的身管.按照式(36)、式(37)和式(55)递推,频率方程的推导类似可得,如将转动惯性项Ji=0,即可得出文献[5]的结论.5 结 论将工程上常用的单跨梁的传递矩阵推广到了多跨梁;将Bernoulli-Euler梁推广到了Timoshenko梁;将个别的复杂边界条件推广到了一般复杂边界条件,从而使得本文建立的模型具有更普遍的意义和更广泛的实用性.①通过简化模型,推导了双跨梁模型,以梁两端固支-自由为例,给出了其频率方程.当铰支座移至自由端时,频率方程变成了固支-铰支的频率方程;当铰支座移至固定端时,频率方程变成了固支-自由的频率方程.②推导了悬臂梁带有集中质量的模型,给出了频率方程的一般格式,当不考虑转动惯量的影响时,得出的频率方程与已有文献[3]的结论相同.③推导了带有任意拉压弹簧和集中质量的模型,其相应的算例与已有文献[5]的结论相同.④文献[1~10]给出的研究结果可视为本文的一种特例.⑤本文特例中的模型是通过Bernoulli-Euler梁进行推导得出的,实际上通过Timoshenko梁进行推导也可得出相同结果.
参考文献
| [1] | McPherson A E,Evans J J,Levy S.Influence of wing flexibility on force-time relation in shock strut following vertical landing impact,NACA-TN-1995[R].Washington,D.C.:NACA,1949. |
| [2] | 史友进,张曾錩. 大柔性飞机着陆响应弹性机体模型[J].东南大学学报:自然科学版,2005,35(4):549-552. Shi Y J,Zhang Z C.Elastic model for flexible airplane landing impact analysis[J].Journal of Southeast University:Natural Science Edition,2005,35(4):549-552(in Chinese). |
| Cited By in Cnki (18) | |
| [3] | Wang D,Jiang J S,Zhang W H.Frequency optimization with respect to lumped mass position[J].AIAA Journal,2003,41(9):1780-1787. |
| Click to display the text | |
| [4] | 刘天雄,林益明,王明宇,等.航天器振动控制技术进展[J].宇航学报,2008,29(1):1-12. Liu T X,Lin Y M,Wang M Y,et al.Review of the spacecraft vibration control technology[J].Journal of Astronautics,2008,29(1): 1-12(in Chinese). |
| Click to display the text | Cited By in Cnki (30) | |
| [5] | 陆毓琪,王晓锋,张延教,等.具有任意多个弹性与刚性支承及集中质量的梁振动问题[J].弹道学报,1997,9(4):23-28. Lu Y Q,Wang X F,Zhang Y J,et al.Natural vibration of variable cross section continuous beam with arbitrary lumped mass,elastical and rigid supports[J].Journal of Ballistics,1997,9(4):23-28(in Chinese). |
| Click to display the text | Cited By in Cnki (13) | |
| [6] | 芮筱亭,秦英孝,赵海林,等.有任意个集中质量的转管炮的固有振动[J].兵工学报,1994(2):1-5. Rui X T,Qin Y X,Zhao H L,et al.Natural vibration of spin tube gun with multi-lumped masses [J].Acta Armamentarii,1994(2): 1-5(in Chinese). |
| Click to display the text | Cited By in Cnki (3) | |
| [7] | Wang D,Zhou C Y,Rong J.Free and forced vibration of repetitive structures[J].International Journal of Solids and Structures,2003,40(20):5477-5494. |
| Click to display the text | |
| [8] | Chen D W,Wu J S.The exact solutions for the natural frequencies and mode shapes of non-uniform beams carrying multiple spring-mass systems[J].Journal of Sound and Vibration,2002,255(2):299-322. |
| Click to display the text | |
| [9] | Wang B P. Eigenvalue sensitivity with respect to location of internal stiffness and mass attachments[J].AIAA Journal,1993,34(4):791-794. |
| [10] | Ma L,Rui X,Abbas L,et al.Free vibration analysis and physical parameter identification of non-uniform beam carrying spring-mass systems[J].Transactions of Nanjing University of Aeronautics and Astronautics,2012,29(4):345-353. |
| [11] | Гантмахер Ф Р,Крейн М Г.Осцилляционные матрицы и ядра и малые колебания механических систем[M].Москва:Государственное Издательство Технико Теоретической Литературы,1950:82-208. |
| [12] | 王其申,章礼华,王大钧.外伸梁离散系统模态的若干定性性质[J].力学学报,2012,44(6):1071-1074. Wang Q S,Zhang L H,Wang D J.Some qualitative prosperities of modes of discrete system of beam with overhang[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(6):1071-1074(in Chinese). |
| Cited By in Cnki | |
| [13] | 王其申,吴磊,王大钧.多跨梁离散系统的频谱和模态的定性性质[J].力学学报,2009,41(6):947-952. Wang Q S,Wu L,Wang D J.Some qualitative prosperities of frequency spectrum and modes of difference discrete system of multibearing beam[J].Chinese Journal of Theoretical and Applied Mechanics,2009,41(6):947-952(in Chinese). |
| Cited By in Cnki (2) | |
| [14] | 王其申,王大钧. 存在刚体模态的杆、梁连续系统某些振荡性质的补充证明[J].安庆师范学院学报:自然科学版,2014,20(1):1-5. Wang Q S,Wang D J.The supplementary proof of some oscillation property for continuous systems of rod and beam having rigid modes[J].Journal of Anqing Teachers College:Natural Science Edition,2014,20(1):1-5(in Chinese). |
| Cited By in Cnki | |
| [15] | Ariaei A,Ziaei-Rad S,Malekzadeh M.Dynamic response of a multi-span Timoshenko beam with internal and external flexible constraints subject to a moving mass[J].Archive of Applied Mechanics,2013,83(9):1257-1272. |
| Click to display the text | |
| [16] | Ariaei A,Ziaei-Rad S,Ghayour M.Transverse vibration of a multiple-Timos henko beam system with intermediate elastic connections due to a moving load[J].Archive of Applied Mechanics,2011,81(3):263-281. |
| Click to display the text | |
| [17] | Mamandi A,Kargarnovin H M.Dynamic analysis of an inclined Timoshenko beam traveled by successive moving masses/forces with inclusion of geometric nonlinearities[J].Acta Mechanica,2011,218(1-2):9-29. |
| Click to display the text | |
| [18] | Gimena F N,Gonzaga P,Gimena L.Stiffness and transfer matrices of a non-naturally curved 3D-beam element[J].Engineering Structures,2008,30(6):1770-1781. |
| Click to display the text | |
| [19] | Haktanir V,Kiral E.Statical analysis of elastically and continuously supported helicoidal structures by the transfer and stiffness matrix methods[J].Computers and Structures,1993,49(4): 663-677. |
| Click to display the text | |
| [20] | 芮筱亭,来峰,何斌,等.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008:93-94. Rui X T,Lai F,He B,et al.Transfer matrix method of multibody system and its applications[M].Beijing:Science Press,2008:93-94(in Chinese). |
| [21] | 刘习军,贾启芳. 工程振动理论与测试技术[M].北京:高等教育出版社,2004:242-243. Liu X J,Jia Q F.Engineering vibration theory and testing techniques[M].Beijing:Higher Education Press,2004:242-243(in Chinese). |
