后掠角是指从飞机的俯仰方向看,机翼平均气动弦长连线自翼根到翼尖向后歪斜的角度.为了克服因接近声速飞行而急剧增大的空气阻力,突破“音障”,提高飞机的临界马赫数,同时提高飞机的航向稳定性,人们在20世纪30年代提出了后掠翼飞行.
后掠角是引起后掠机翼边界层横流不稳定性的关键参数之一.对于无后掠角的平直机翼,流动不稳定以黏性不稳定为主,而对于有后掠角的横流机翼,流动以无黏的横流不稳定为主.不同的后掠角,除了对机翼的升力、阻力有影响外,对横流不稳定性强度以及转捩位置也有影响.
近几十年,随着航空航天技术的发展,后掠角对机翼横流不稳定性和转捩影响的研究成为国内外研究的热点.早在1960年,Boltz等[5]在低湍流度风洞中研究了后掠角对低速后掠机翼边界层稳定性的影响,发现后掠角为50°时横流不稳定性达到最强.Haynes[6]采用数值方法对比了后掠角为35°、45°、55°时转捩预测eN方法得到的最大幅值增长指数N,发现后掠角为55°时得到的N值最大.Dagenhart等[7]实验发现后掠角为45°时后掠机翼横流不稳定性最强.Bippes等[8, 9, 10]、Malik等[11]、Saric等[12, 13]在三维边界层横流不稳定性及转捩机理方面都做了大量的研究工作.
中国的研究人员大多关注低速情况下后掠角对流动结构、阻力系数、升力系数的影响研究.左林玄和王晋军[14]采用实验方法分析了后掠角对三角翼绕流结构的影响,发现了低雷诺数下不同后掠角时弹性翼绕流的变化规律.马宝峰等[15]采用实验方法研究了大迎角下后掠角对近耦合鸭式布局增升及流态的影响,发现后掠角在40°~45°时增升效果最明显.刘杰等[16]采用数值计算的方法对后掠角为50°的三角翼在不同迎角下的绕流结构及演化进行了研究.左岁寒等[17, 18]采用线性稳定性理论(Linear Stability Theory,LST),线性抛物化稳定性方程(Linear Parabolized Stability Equations,LPSE)研究了无限展长后掠机翼边界层内的驻波不稳定性.徐国亮和符松[2]对可压缩横流失稳及控制的研究进行了综述.黄章峰等[19]研究了后掠角为25°时机翼边界层的横流稳定性特性,并进行了转捩预测,指出引起转捩的扰动波的展向波长约为2 mm.
本文以适航状态的民航后掠机翼为研究对象,研究后掠角对后掠机翼边界层稳定性及转捩的影响.首先采用直接数值模拟的方法计算得到展向无限长后掠机翼的基本流场,然后基于线性稳定性理论分析不同后掠角下后掠机翼边界层的稳定性特征,最后采用eN方法进行转捩预测,为层流化机翼的设计和优化提供理论依据和参考.1 数值方法1.1 计算模型选取的翼型为NACA0012,弦长为1m.在模型中建立正交坐标系,如图 1所示.其中:ξ方向为机翼弦长方向;η方向为机翼法向方向;ζ方向为机翼展向方向;U∞为来流速度;Λ为后掠角;Ut和Wt为横流坐标系下的基本流速度.网格划分后,展向采用周期边界条件,用数值模拟方法计算得到无限展长后掠机翼的基本流场.收敛后,选取流场截面,建立新的坐标系,重新划分网格并做加密处理,得到可用于稳定性分析的基本流场.在新的坐标系下,x的大小为在翼型剖面上距离翼型前缘的壁面弧长距离,方向沿翼型剖面的弧线方向;y的大小为该点到壁面的距离,方向与壁面法向方向相同;U和V分别为x和y方向的平均速度.
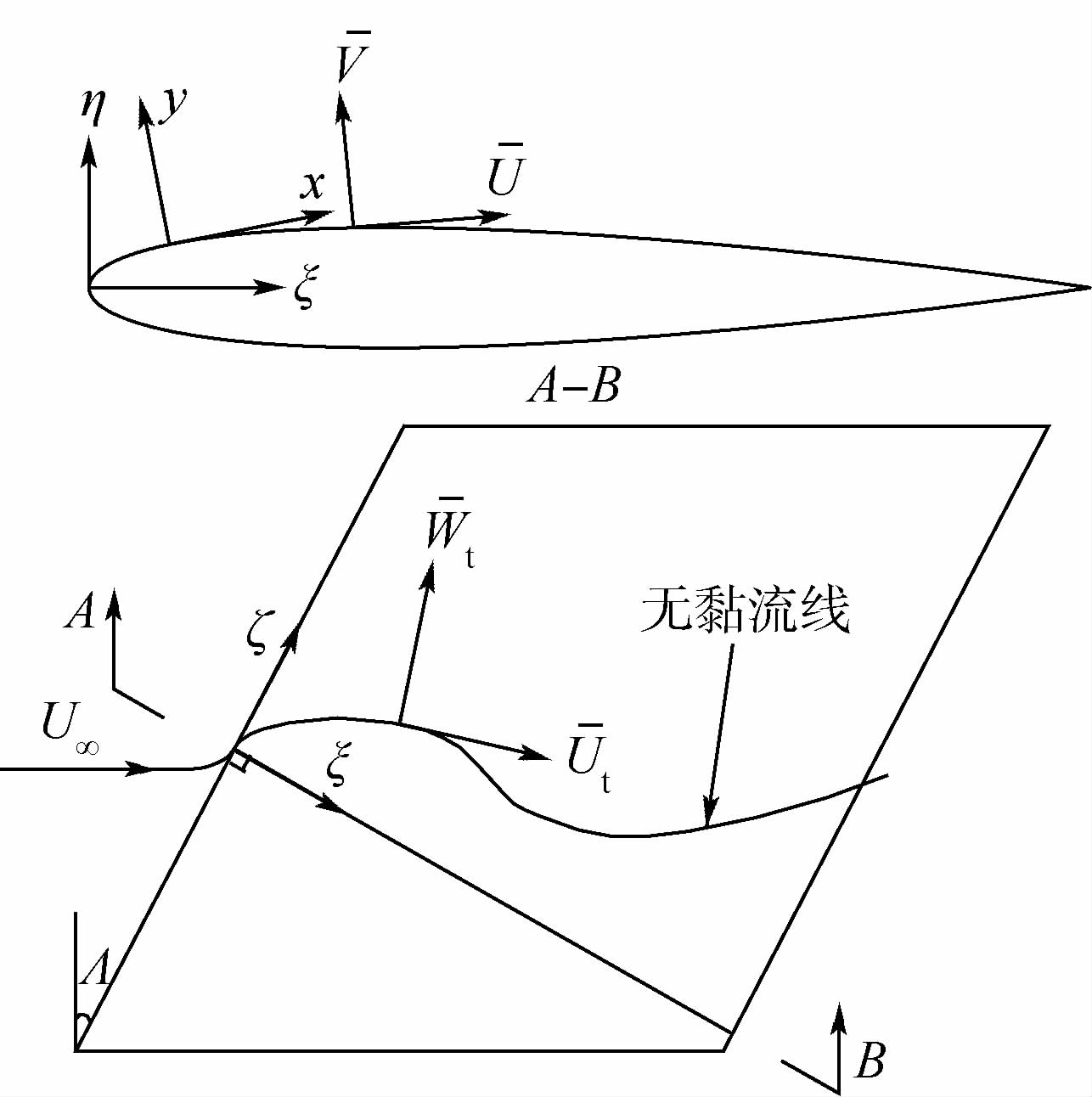 |
| 图 1 模型坐标示意图Fig. 1 Sketch map of model coordinate |
| 图选项 |
1.2 线性稳定性问题及方法将流场分解为基本流与小扰动之和,基于局部平行流假设,基本流Φ={ρ,u,v,w,T},其中U、V=0和W分别为流向、法向和展向速度,ρ和T分别为密度和温度,它们仅是y的函数.小扰动φ′={ρ′,u′,v′,w′,T′}可以写成行进波解的形式.
式中:A为扰动幅值;φ={ρ,u,v,w,T}为特征函数且仅为y的函数;α和β分别为扰动在x和z方向的波数;ω为扰动频率;i为虚数单位;c.c.为共轭复数.
考虑流向曲率,将基本流和小扰动代入正交曲线坐标系下的Navier-Stokes方程并做线化处理即可得到线性稳定性方程,即O-S方程:
式中:f为Re、Φ及其对y的各阶导数和流向曲率的函数.基于基本流场,给定β和ω,采用求特征值的Mueller法就可以得到特征值α以及相应的特征函数φ.
1.3 转捩预测的eN方法转捩预测的常用方法为eN方法,其基本思想[1]是:边界层内各种频率的小扰动波向下游传播时,进入不稳定区域会被放大,不同频率的波开始被放大的位置不同.从扰动波进入不稳定区域开始,沿下游方向计算其累计的线性放大倍数.线性理论中放大倍数以指数形式出现,可用eN表示,即

式中:A0为扰动开始增长的初始幅值.在所有扰动中,若有某一扰动最先达到预设值N时,即可判断转捩发生.
采用空间模式,β、ω为实数,α=αr+αi为复数,αr为α的实部,αi为α的虚部.给定β和ω,通过LST方法得到不同流向位置下的αi,对其积分可得到幅值放大指数n:

式中:x0为扰动开始增长的位置或参考位置.而预测转捩位置的N值则为β和ω所有取值得到的n值的包络值:
1.4 研究对象选取高空10 km处的气体参数,温度为223.3 K,密度为0.413 5 kg/m3,黏性系数为1.458 4×10-5 Pa·s;马赫数为0.7,相应的单位雷诺数为5.945×106/m,为民航飞机巡航时常见的雷诺数;攻角为0°;后掠角Λ分别为10°、15°、20°、25°、30°、40°、45°、50°、60°,研究后掠角对后掠机翼边界层稳定性和转捩的影响.文中的量均为无量纲量.长度采用1 mm无量纲化,以该特征长度定义的雷诺数为5 945,速度用来流速度U∞无量纲化.
2 结果分析2.1 结果验证图 2为计算网格示意图,采用变间距,在机翼
 |
| 图 2 计算网格示意图Fig. 2 Sketch map of computational domain |
| 图选项 |
边界层附近进行局部加密处理:机翼网格两端密中间疏,机翼壁面网格流向最小间距Δx<0.1,最大间距Δx<1;在法向上,一个边界层内布有200个点以上,壁面处法向网格最小间距Δy<0.01.对比了3种不同网格数来验证网格无关性,具体参数如表 1所示.
表 1 3种模型的网格数Table 1 Grid numbers of three kinds of models
| 模型 | 流向点数 | 法向点数 | 总网格数/105 |
| grid-1 | 720 | 300 | 2.16 |
| grid-2 | 1 000 | 400 | 4.00 |
| grid-3 | 1 200 | 500 | 6.00 |
表选项
图 3 (a)给出了3种不同网格数的模型在x=100、200和300位置处的流向速度剖面(马赫数为0.7,攻角为0°,后掠角为25°).可以看出,3种网格数的模型计算得到的流场符合得很好.图 3 (b)为3种不同网格数模型的压力系数Cp曲线,c为机翼弦长.可以看出,3种网格模型计算得到的结果完全重合,说明第1种网格已足够密了.
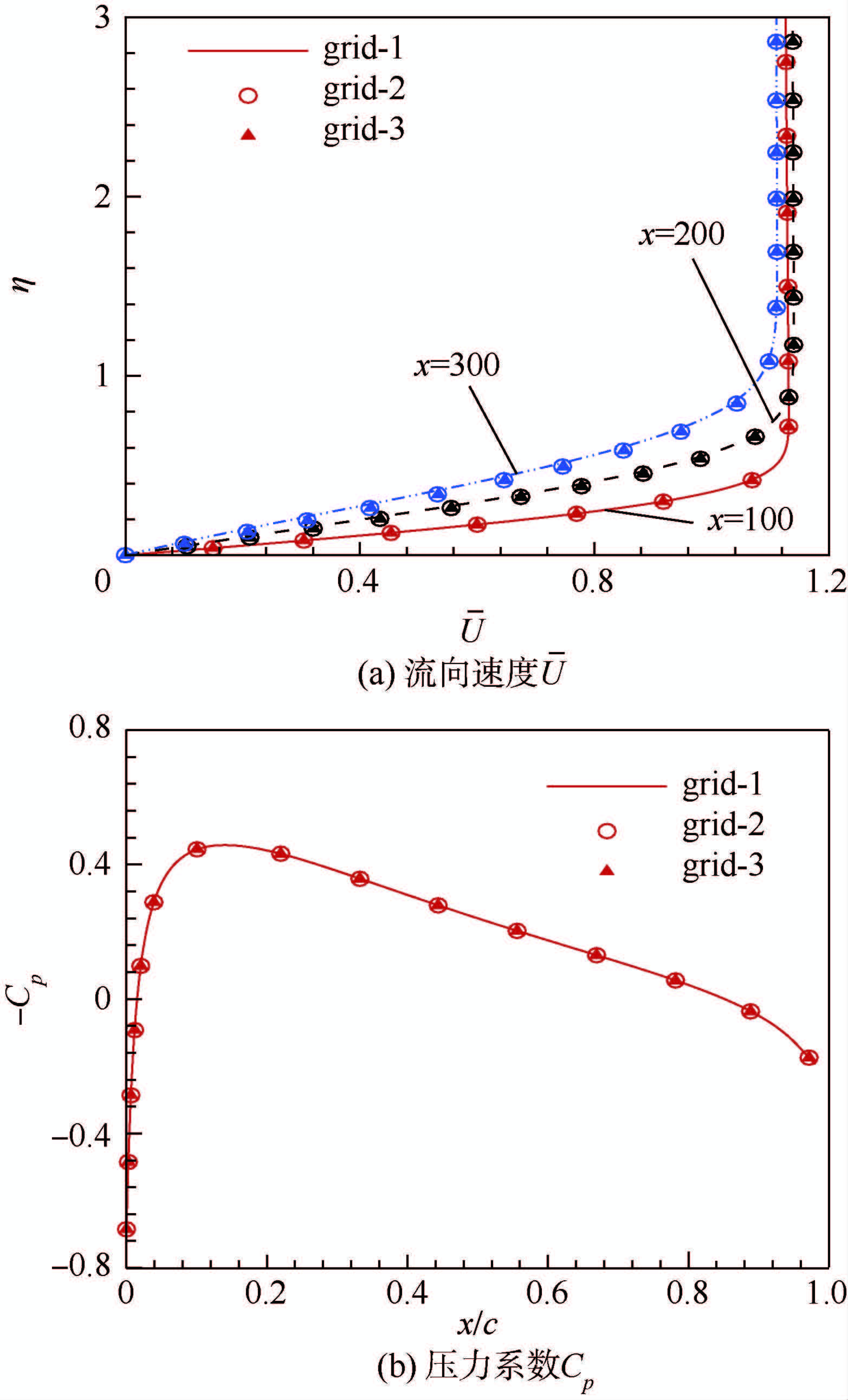 |
| 图 3 3种不同网格数模型的流向速度剖面及压力系数Fig. 3 Profile of flow velocity and pressure coefficient for three kinds of models with different grid number |
| 图选项 |
图 4给出了Ma=0.657 4、Re=1.95×106、攻角为0°、后掠角为0°时的压力系数Cp曲线,同时给出了韩步璋等[20]的实验结果.可以看出本文的数值计算结果与实验结果几乎重合,说明本文采用的计算网格已经足够密,基本流结果准确可靠.
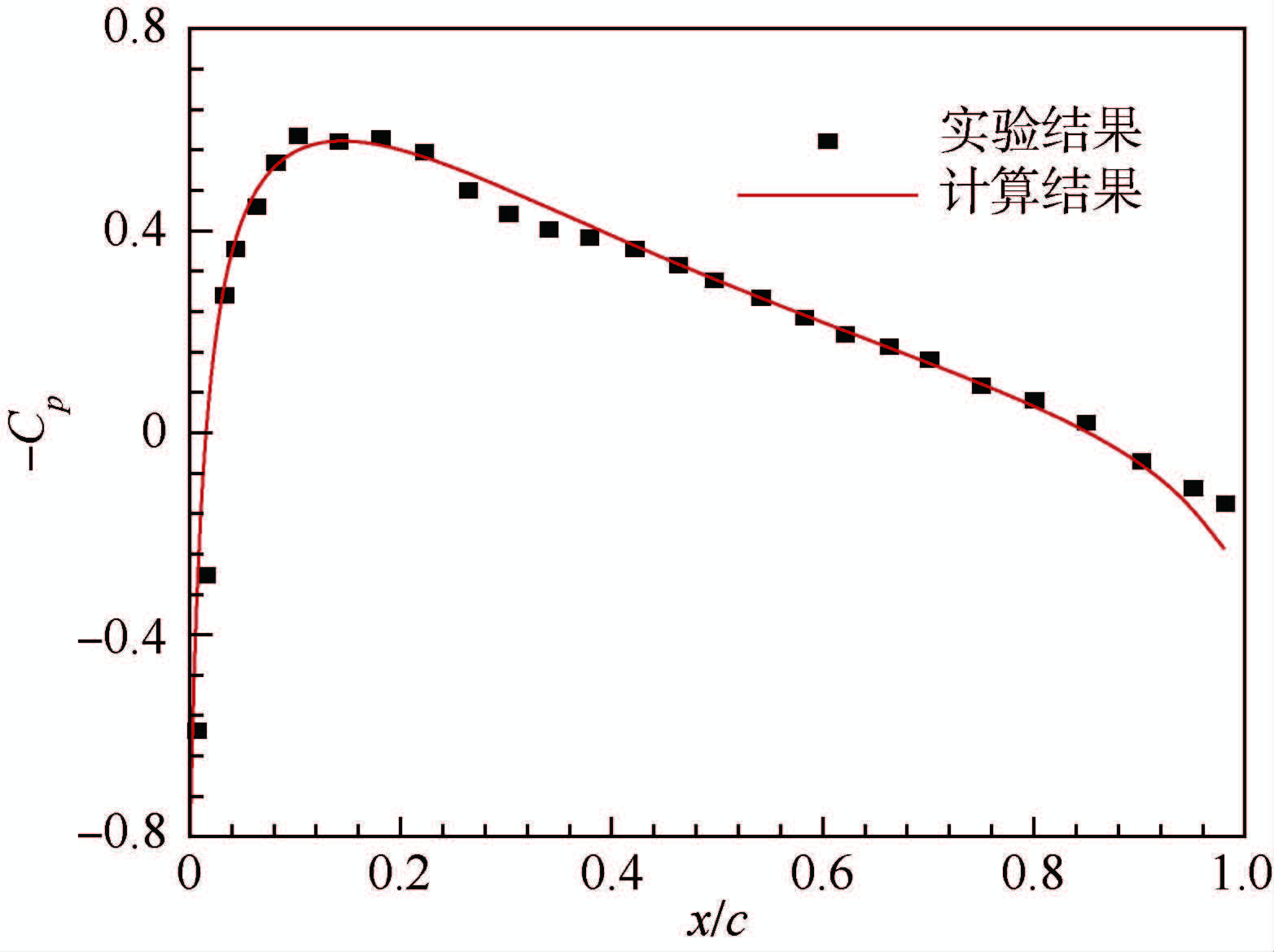 |
| 图 4 压力系数曲线Fig. 4 Pressure coefficient curves |
| 图选项 |
2.2 基本流分析图 5 (a)~图 5 (c)给出了不同后掠角工况下x=100处流向、展向和法向的基本流速度剖面.从图 5 (a)中可以看出,当Λ≤30°时,由于机翼头部的加速效应,在边界层附近的流向速度均大于1.当Λ≥40°时,尽管机翼头部具有加速效应,在边界层附近的流向速度也小于1,因为随着后掠角的增加,更多的流体流向了展向.如图 5 (b)所示,随着后掠角的增加,展向速度也增加.从图 5 (a)和图 5 (b)还可以发现y>1以上的流向速度和展向速度均为常数.由图 5 (c)可看出法向速度V-比流向速度U-小两个量级,满足平行流假设.
图 5 (d)给出了不同后掠角下的压力系数曲线.可以看出在机翼0<x/c<0.8位置处压力系数随后掠角的增大而减小.这是因为随着后掠角的增大,速度在流向的分量逐渐减小,机翼表面压力与来流压力差减小.
图 6所示为在横流坐标下,不同后掠角工况x=100位置处的速度剖面.其中流向速度Ut方向为边界层外沿势流方向,法向速度V-t方向与壁面法向方向相同,横流速度Wt方向则垂直于流向速度和法向速度方向,U-e为边界层外沿处的势流速度.可以看出,随后掠角的增大,流向速度剖面逐渐抬升,说明边界层厚度逐渐增大.横流失稳属于拐点失稳,横流不稳定性强度与横流最大速度直接相关.图 6中横流速度随后掠角的增加先增大后减小,后掠角为40°~50°时横流速度存在最大值,此时横流不稳定性最强,相应的横流扰动最不稳定,其扰动波幅值增长最快;进一步增大后掠角后,由于横流速度峰值减小,横流效应减弱,因而中等后掠角下横流扰动最不稳定.在机翼头部靠近前缘位置(x=100左右),后掠角为45°时横流强度最强,与Dagenhart[7]的结论一致.
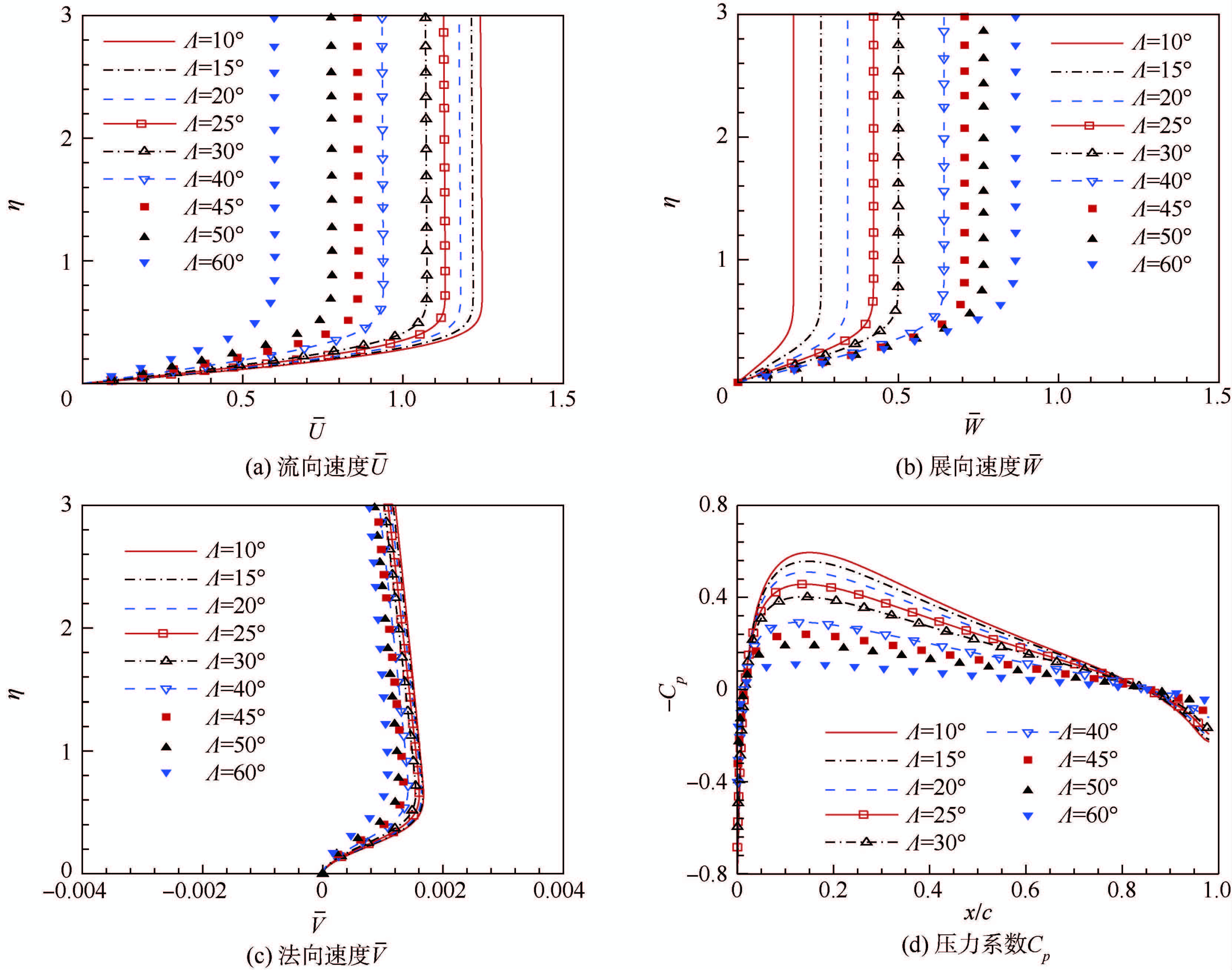 |
| 图 5 后掠角不同时的速度剖面及压力系数Fig. 5 Profile of velocity and pressure coefficient under different sweep angles |
| 图选项 |
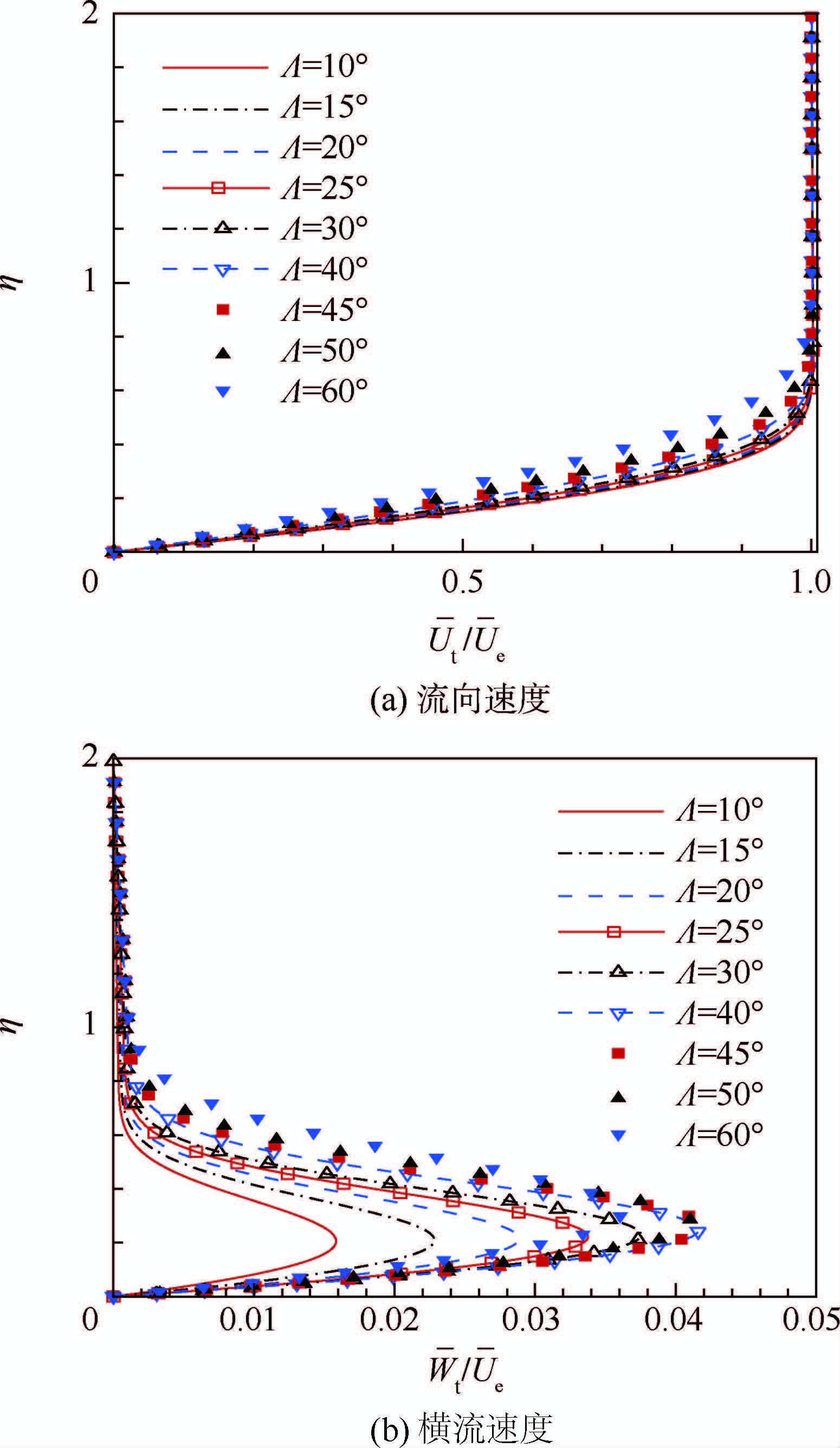 |
| 图 6 横流坐标系下速度剖面Fig. 6 Profile of velocity in cross-flow coordinate |
| 图选项 |
2.3 特征值和特征函数表 2给出了不同后掠角工况下,在x=100位置处不同展向波数的驻波(ω=0)的增长率-αi.可得出,展向波数β=1的驻波在x=100处增长率随后掠角的增加而增大.展向波数β=2和β=3的驻波在x=100处增长率随后掠角的增加先增大后减小.
表 2 不同展向波数的驻波(ω=0)的增长率-αiTable 2 Growth rate of stationary wave (ω=0) with different span-wise wave numbers
| Λ/(°) | -αi | ||
| β=1 | β=2 | β=3 | |
| 10 | -0.005 797 | -0.000 429 | 0.000 464 |
| 15 | -0.002 104 | 0.005 156 | 0.006 881 |
| 20 | 0.001 622 | 0.010 861 | 0.013 037 |
| 25 | 0.005 466 | 0.016 256 | 0.018 445 |
| 30 | 0.009 326 | 0.021 146 | 0.022 821 |
| 40 | 0.016 912 | 0.028 986 | 0.027 137 |
| 45 | 0.020 580 | 0.031 592 | 0.025 659 |
| 50 | 0.024 066 | 0.032 686 | 0.019 476 |
| 60 | 0.029 470 | 0.023 393 | -0.030 135 |
表选项
图 7所示为扰动波(β=1,ω=0)在x=100处的特征函数沿y方向的分布曲线.可以看出,图 7 (a)中|u|达到峰值的位置随后掠角的增大逐渐远离壁面,图 7 (b)中|w|的峰值随后掠角的增大而增大,且达到峰值的位置同样随后掠角的增大而远离壁面.
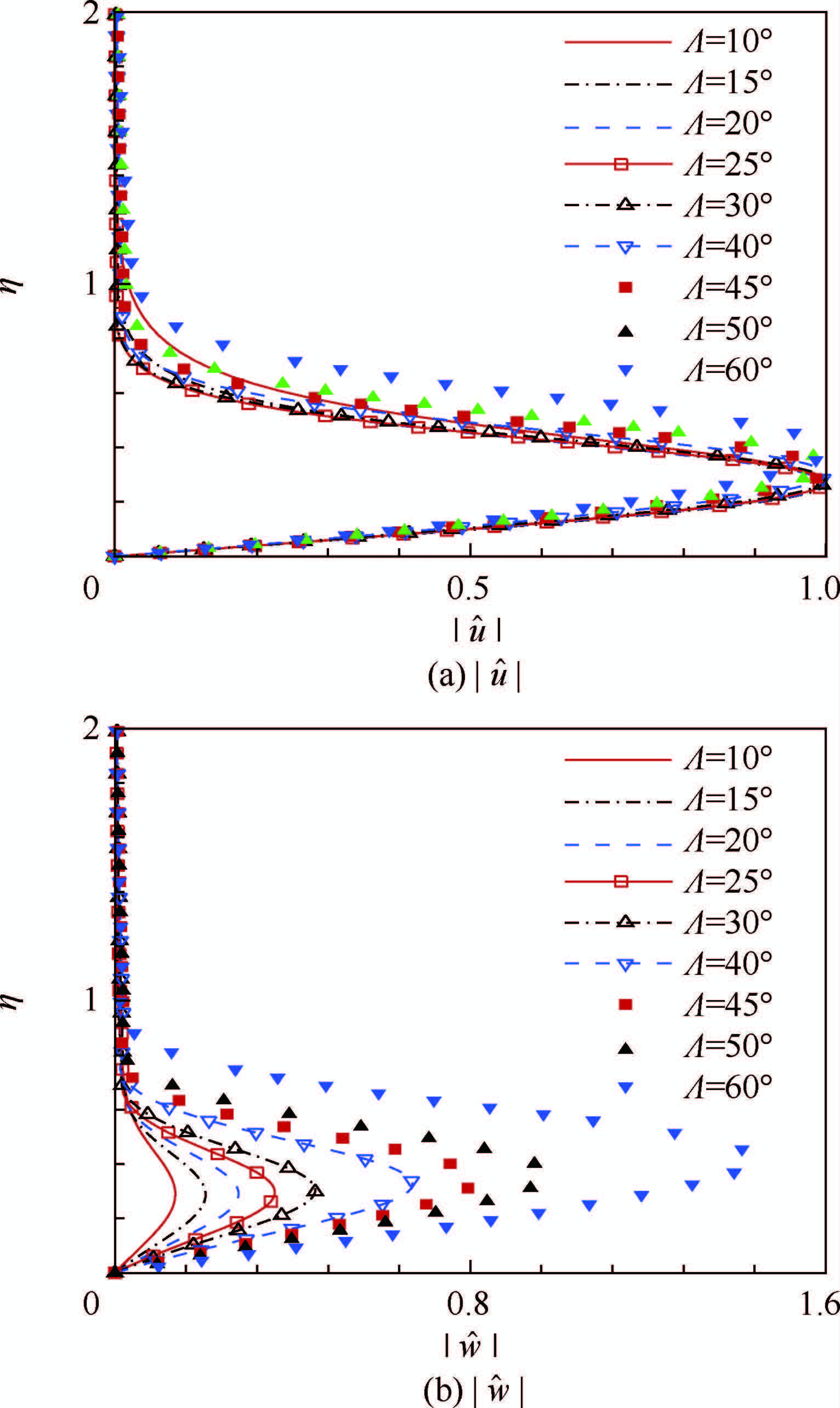 |
| 图 7 扰动波(β=1,ω=0)的特征函数Fig. 7 Eigen-function of disturbance wave (β=1,ω=0) |
| 图选项 |
2.4 中性曲线图 8 (a)给出了不同后掠角时展向波数β=3的中性曲线(-αi=0).可以看出,随着后掠角的增加,中性曲线下支的频率逐渐减小,当后掠角达到40°后不再减小;而中性曲线上支的频率随着后掠角的增加先增大后减小,在后掠角为30°时达到极大值;中性曲线在x方向的范围也是随着后掠角的增加先增大后减小,而且当后掠角为60°时,不稳定区域在x<100的范围内.
图 8 (b)给出的是不同后掠角下驻波(ω=0)的中性曲线.类似地,中性曲线下支的展向波数随着后掠角的增加逐渐减小,而中性曲线上支的展向波数随着后掠角的增加先增大后减小.当后掠角大于30°时,后掠角对驻波的流向增长区域影响较小.后掠角为30°~45°时驻波的中性曲线所包围的不稳定波的范围最大.
当后掠角为零时,势流方向与来流方向一致,其垂直方向没有速度分量,即不存在横流,因而也不存在横流稳定性问题.当后掠角从10°增加到40°时,横流速度近似呈线性增长,无量纲横流速度从0.015增加到0.042,如图 6 (b)所示.因此图 8中的中性曲线范围也成倍地增长.
当后掠角超过45°并继续增加时,来流方向与机翼展向方向夹角逐渐减小,来流在机翼展向方向的流速分量增加,而机翼弦长方向的流速分量减小,其结果使大部分流体顺势沿机翼展向方向流动,而在机翼弦长方向压力梯度影响减小.对于后掠角为90°的极限情况,机翼弦长方向没有压力梯度,同样不存在横流.由于机翼弦长方向压力梯度逐渐减小,机翼表面的边界层厚度将逐渐增加(见图 6 (a)),相应的横流速度的拐点位置也将上升,并且横流速度的最大值也将逐渐减小(见图 6 (b)).因此图 8中的中性稳定曲线范围将逐渐减小,尤其是图 8 (b)中的中性稳定曲线上支下降得很快,从而对于较大展向波数的中性稳定曲线(图 8 (a))范围在流向方向有明显的缩小.
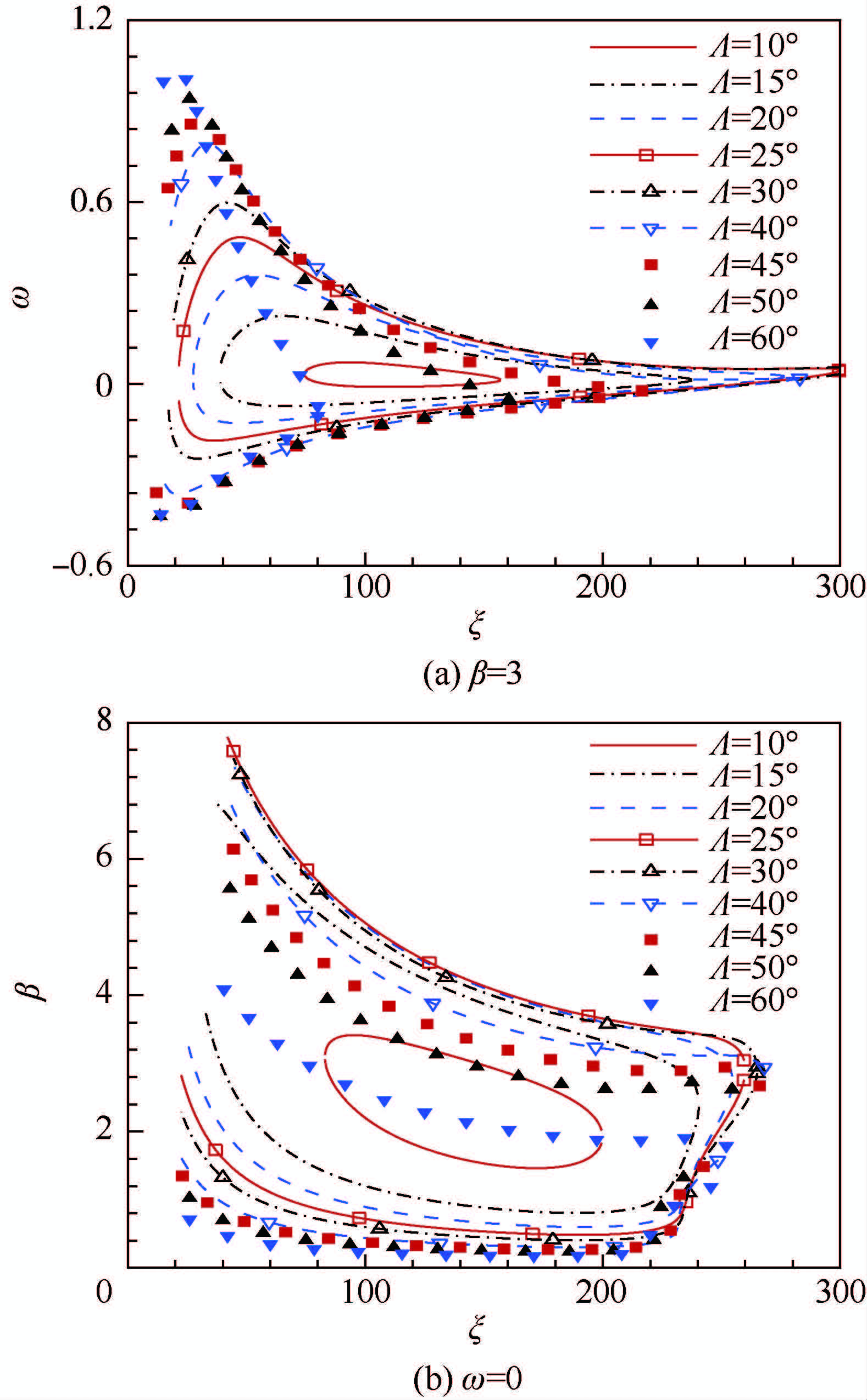 |
| 图 8 中性稳定曲线Fig. 8 Neutral stability curve |
| 图选项 |
2.5 增长率及幅值演化曲线图 9 (a)给出了不同后掠角下驻波(β=2,ω=0)的增长率曲线.可看出在机翼前缘增长率随流向位置的增加先增大后减小.当后掠角为60°时增长率下降较快,增长区域较小.该扰动波在所有后掠角下最远传播到x=270位置后都开始衰减.
取x0=25作为稳定性分析的参考位置,图 9 (b)给出了不同后掠角下该扰动波的幅值演化曲线.虽然在后掠角为30°~45°时驻波的中性曲线所包围的不稳定波的范围最大,但是后掠角为30°~40°时的增长率偏小,相应的幅值放大指数n值也偏小.当后掠角Λ≤50°时,n值随后掠角的增大而增大.但后掠角为60°时,由于其增长的流向范围较小,其n值会有所降低.后掠角为50°时扰动幅值放大指数n达到最大值.该结论与Boltz等[5]和Haynes[6]的发现一致.
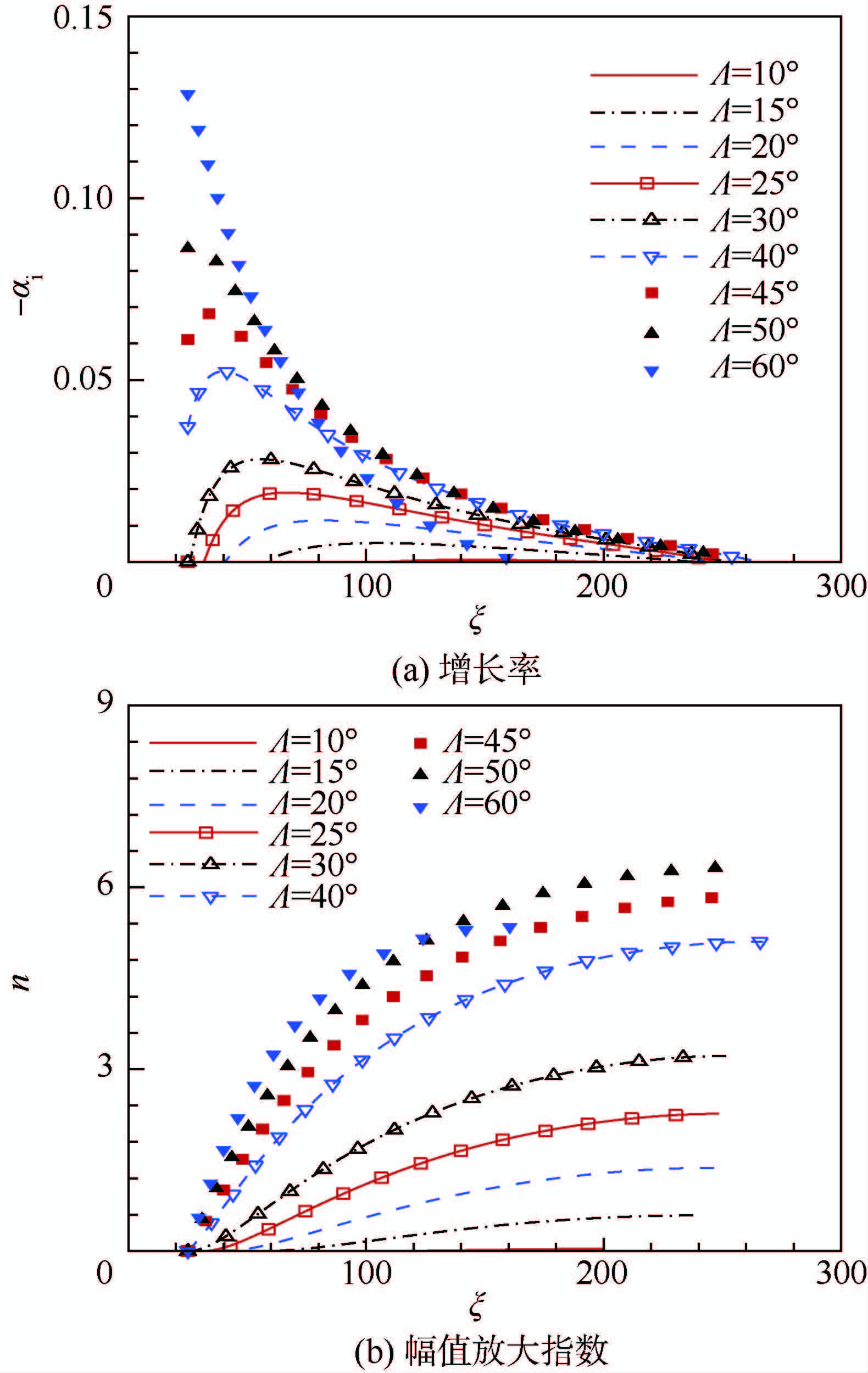 |
| 图 9 驻波(β=2,ω=0)增长率及幅值演化曲线Fig. 9 Growth rate and growth curve of stationary wave (β=2,ω=0) |
| 图选项 |
2.6 N值曲线及转捩预测不同后掠角的N值曲线如图 10所示.可以看出,扰动波的N值随后掠角的增加先增大后减小.后掠角为50°时的N值最大,约为13,说明后掠角为50°时,扰动波传播经过整个增长区域后,其幅值最大可增长e13倍(约44万倍).
 |
| 图 1 转捩预测eN方法的N值曲线Fig. 1 N factor in eN method |
| 图选项 |
eN方法是一种半经验的转捩预测方法,发生转捩的N值需要由实验测量并做出进一步的假定.当计算得到的N值大于预设的N值时即可判定发生了转捩.研究表明,当扰动波的无量纲幅值达到来流的20%就会发生转捩[21].表 3给出了当扰动波放大指数达到给定N值时发生转捩的位置.可以看出,若给定发生转捩的预设值N=9,则后掠角小于30°时不会发生转捩;后掠角大于40°时,随着后掠角的增大,转捩位置向机翼前缘移动.
除转捩发生的位置之外,参考位置处的初始扰动幅值也是工程中人们比较关心的.表 4给出了已知转捩发生位置时,在不同后掠角下的初始扰动幅值A0.由表 4可知,若给定转捩发生的位置x=150,则A0随后掠角的增加而减小;若给定x≥200,则A0随后掠角的增加先减小后增大,且后掠角为50°时初始扰动幅值最小,相应的越容易发生转捩.
表 3 在预设N值发生转捩时的流向位置xTable 3 Transition position x predicted according to pre-setted N factor
| Λ/(°) | 流向位置x | |||
| N=7 | N=8 | N=9 | N=10 | |
| 10 | ― | ― | ― | ― |
| 15 | ― | ― | ― | ― |
| 20 | ― | ― | ― | ― |
| 25 | ― | ― | ― | ― |
| 30 | 274.5 | ― | ― | ― |
| 40 | 120.0 | 151.5 | 198.5 | 307.0 |
| 45 | 99.0 | 121.0 | 149.5 | 193.0 |
| 50 | 86.5 | 103.0 | 124.0 | 152.5 |
| 60 | 71.0 | 82.5 | 97.0 | 125.5 |
表选项
表 4 在x处发生转捩时(A=0.2U∞)的N值以及x0=25处的扰动幅值A0Table 4 N factor at transition position x where A=0.2U∞,and the disturbance amplitude A0 at x0=25 of inducing wave
| Λ/(°) | x=150 | x=200 | x=250 | x=300 | ||||
| N | A0 | N | A0 | N | A0 | N | A0 | |
| 10 | 0.11 | 1.8×10-1 | 0.19 | 1.7×10-1 | 0.25 | 1.6×10-1 | 0.28 | 1.5×10-1 |
| 15 | 1.16 | 6.3×10-2 | 1.47 | 4.6×10-2 | 1.67 | 3.8×10-2 | 1.78 | 3.4×10-2 |
| 20 | 2.63 | 1.4×10-2 | 3.15 | 8.6×10-3 | 3.47 | 6.2×10-3 | 3.66 | 5.1×10-3 |
| 25 | 4.10 | 3.3×10-3 | 4.80 | 1.6×10-3 | 5.21 | 1.1×10-3 | 5.46 | 8.5×10-4 |
| 30 | 5.50 | 8.2×10-4 | 6.34 | 3.5×10-4 | 6.84 | 2.1×10-4 | 7.13 | 1.6×10-4 |
| 40 | 7.96 | 7.0×10-5 | 9.01 | 2.4×10-5 | 9.62 | 1.3×10-5 | 9.96 | 9.5×10-6 |
| 45 | 9.00 | 2.5×10-5 | 10.12 | 8.1×10-6 | 10.74 | 4.3×10-6 | 11.12 | 3.0×10-6 |
| 50 | 9.92 | 9.8×10-6 | 11.07 | 3.1×10-6 | 11.71 | 1.6×10-6 | 12.10 | 1.1×10-6 |
| 60 | 10.29 | 6.8×10-6 | 10.39 | 6.1×10-6 | 10.39 | 6.1×10-6 | 10.39 | 6.1×10-6 |
表选项
3 结 论在采用数值模拟方法得到展向无限长后掠机翼基本流场的基础上,通过求解经典的O-S方程,分析了后掠角对后掠机翼边界层稳定性的影响,采用eN方法进行了转捩预测,得到如下结论:
1) 后掠机翼边界层中横流强度随后掠角的增大先增加后减小.当后掠角为40°~50°时横流强度存在最大值,在机翼头部靠近前缘位置(x=100左右),后掠角为45°时横流强度最强.
2) 后掠角为30°~45°时,扰动波的不稳定区域最大,不稳定驻波的展向波数范围最大.
3) 随着后掠角的增大,扰动波幅值放大指数n先增加后减小.后掠角在50°左右转捩预测eN方法计算的N值最大,引起转捩发生的初始扰动幅值最小,最易发生转捩.
4) 给定预设值N,转捩发生的位置随后掠角的增大逐渐向机翼前缘移动.
需要说明的是飞行巡航时机翼往往存在较小的攻角(或来流迎角),而本文选择的攻角为0°,这样的好处是后掠角对迎风面和背风面的影响是一样的.基于作者的小攻角对后掠机翼边界层稳定性影响的研究,本文的结论在小攻角的情况下定性是一致的,定量上会存在的一定的区别.机翼的后掠角和攻角都会影响到机翼的升力和流动稳定性,因此实际的飞行器巡航状态应该是基于升力恒定的条件下(后掠角和攻角满足一定的关系)不同后掠角或攻角对流动稳定性和转捩位置的影响,这将是作者下一步的工作.
参考文献
| [1] | 周恒, 赵耕夫. 流动稳定性[M].北京: 国防工业出版社, 2004: 77-78. Zhou H, Zhao G F.Hydrodynamic stability[M].Beijing: National Defense Industry Press, 2004: 77-78(in Chinese). |
| Click to display the text | |
| [2] | 徐国亮, 符松. 可压缩横流失稳及其控制[J].力学进展, 2012, 42(3): 262-273. Xu G L, Fu S.The instability and control of compressible cross flows [J].Advances in Mechanics, 2012, 42(3): 262-273(in Chinese). |
| Cited By in Cnki (2) | |
| [3] | Joslin R D. Overview of laminar flow control[M].Hampton, Virginia: National Aeronautics and Space Administration, Langley Research Center, 1998: 3-7. |
| Click to display the text | |
| [4] | 吴永健. 横流不稳定性实验研究[D].南京: 南京航空航天大学, 2002. Wu Y J.Experimental study on crossflow instabilities in the boundary-layer of swept wing[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2002(in Chinese). |
| Cited By in Cnki (1) | |
| [5] | Boltz F W, Kenyon G C, Allen C Q.Effects of sweep angle on the boundary-layer stability characteristics of an untapered wing at low speeds[J].National Aeronautics and Space Administration, NASA Technical Note, 1960: D-338. |
| Click to display the text | |
| [6] | Haynes T S. Nonlinear stability and saturation of crossflow vortices in swept-wing boundary layers[D].Arizona: Arizona State University, 1996. |
| Click to display the text | |
| [7] | Dagenhart J R, Saric W S.Crossflow stability and transition experiments in swept-wing flow[M].National Aeronautics and Space Administration, Langley Research Center, 1999: 7-8. |
| Click to display the text | |
| [8] | Bippes H. Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability[J].Progress in Aerospace Sciences, 1999, 35(4): 363-412. |
| Click to display the text | |
| [9] | Bippes H, Müller B, Wagner M.Measurements and stability calculations of the disturbance growth in an unstable three-dimensional boundary layer[J].Physics of Fluids A: Fluid Dynamics(1989-1993), 1991, 3(10): 2371-2377. |
| Click to display the text | |
| [10] | Bippes H, Wiegel M, Bertolotti F.Experiments on the control of crossflow instability with the aid of suction through perforated walls[C]//IUTAM Symposium on Mechanics of Passive and Active Flow Control.Berlin: Springer, 1999, 53: 165-170. |
| Click to display the text | |
| [11] | Malik M R, Liao W, Li F, et al.DRE-enhanced swept-wing natural laminar flow at high Reynolds numbers, AIAA-2013-0412[R].Reston: AIAA, 2013. |
| Click to display the text | |
| [12] | Saric W S, Carrillo R B, Reibert M S.Nonlinear stability and transition in 3-D boundary layers[J].Meccanica, 1998, 33(5): 469-487. |
| Click to display the text | |
| [13] | Saric W S, Reed H L, White E B.Stability and transition of three-dimensional boundary layers[J].Annual Review of Fluid Mechanics, 2003, 35(1): 413-440. |
| Click to display the text | |
| [14] | 左林玄, 王晋军. 弹性与后掠角对三角翼绕流结构的影响[J].实验流体力学, 2008, 22(2): 29-33. Zuo L X, Wang J J.The effects of flexibility and sweep angle on flow around cropped delta wing[J].Journal of Experiments in Fluid Mechanics, 2008, 22(2): 29-33(in Chinese). |
| Cited By in Cnki (1) | |
| [15] | 马宝峰, 刘沛清, 魏园.大迎角下机翼后掠角对近耦合鸭式布局增升及流态的影响[J].实验流体力学, 2005, 19(3): 73-78. Ma B F, Liu P Q, Wei Y.Effects of wing sweep on lift-enhancement and flow patterns of close-coupled canard-configurations at high incidence[J].Journal of Experiments in Fluid Mechanics, 2005, 19(3): 73-78(in Chinese). |
| Cited By in Cnki (4) | |
| [16] | 刘杰, 刘沛清, 闫指江.中等后掠角三角翼前缘双涡结构的形成机理数值研究[J].空气动力学学报, 2012, 30(6): 767-771. Liu J, Liu P Q, Yan Z J.Numerical investigations of formation mechanism about a dual leading-edge vortex of a delta wing with medium leading-edge sweep angle[J].Acta Aerodynamica Sinica, 2012, 30(6): 767-771(in Chinese). |
| Cited By in Cnki | |
| [17] | 左岁寒, 杨永, 李栋.基于线性抛物化稳定性方程的后掠翼边界层内横流稳定性研究[J].计算物理, 2010, 27(5): 665-670. Zuo S H, Yang Y, Li D.Investigation on cross-flow instabilities in swept-wing boundary layers with linear parabolized stability equations[J].Chinese Journal of Computational Physics, 2010, 27(5): 665-670(in Chinese). |
| Cited By in Cnki (3) | |
| [18] | 左岁寒, 杨永, 李栋, 等.基于线化稳定性理论的后掠翼边界层内横流稳定性研究[J].航空计算技术, 2009, 39(4): 34-36. Zuo S H, Yang Y, Li D, et al.Study on crossflow instability of boundary layer on a swept wing based on linear stability theory[J].Aeronautical Computing Technique, 2009, 39(4): 34-36(in Chinese). |
| Cited By in Cnki | |
| [19] | 黄章峰, 逯学志, 于高通.机翼边界层的横流稳定性分析和转捩预测[J].空气动力学学报, 2014, 32(1): 14-20. Huang Z F, Lu X Z, Yu G T.Cross-flow instability analysis and transition prediction of airfoil boundary layer[J].Acta Aerodynamica Sinica, 2014, 32(1): 14-20(in Chinese). |
| Cited By in Cnki | |
| [20] | 韩步璋, 黄奕裔, 张其威, 等.NACA0012翼型跨音速测压实验研究[J].南京航空航天大学学报, 1987, 19(2): 92-102. Han B Z, Huang Y Y, Zhang Q W, et al.An experiment of pressure measurement for NACA0012 airfoil in a transonic wind tunnel[J].Journal of Nanjing Aeronautical Institute, 1987, 19(2): 92-102(in Chinese). |
| Cited By in Cnki | |
| [21] | Huang Z F, Cao W, Zhou H.The mechanism of breakdown in laminar-turbulent transition of a supersonic boundary layer on a flat plate-temporal mode[J].Science in China Series G: Mechanics and Astronomy, 2005, 48(5): 614-625. |
| Click to display the text |
