编队飞行时,后机利用前机尾涡场上洗气流能够有效降低诱导阻力,改善燃油经济性[3].2009年欧盟提出“2050年航空领域碳排放比2005年降低50%的目标”[4]以及随后Nehrbass[5]、Ning[6-8]、Flanzer[9]、Xue[10]等****针对长距、跨声速、可压缩、黏滞空气尾涡场远场模型的研究,引起了人们对商业航空领域实施编队飞行问题的广泛关注.商业航空编队飞行的研究主要包括气动耦合效应、导航、航空器设计和空中交通运行等4个方面.其中,编队飞行路径规划属于空中交通运行范畴,而编队飞行路径的优劣决定了编队飞行的燃油经济性.
在编队飞行路径规划方面,Ribichini和Frazzoli提出基于贪婪机制的多Agent协商结盟算法以优化编队调度逻辑[11];Bower和Flanzer基于到达时间约束优化编队集结点[12];Kent和Richards将编队路径规划抽象为球面点集上的加权费马点求解问题,基于欧氏平面边加权Steiner最小树的有限几何简化原则建立了最优加权集结拓扑优化模型,利用模拟退火算法优化编队调度逻辑[13];Kent和Richards研究了考虑风场影响的编队路径规划问题[14].上述研究建立编队路径规划的基本模型,形成求解编队路径规划问题的框架和思路,但航空约束特征考虑不足.
Hino提出一种两阶段编队路径规划方法:编队路径拓扑选择(Formation Path Topology Selection,FPTS)和编队路径优化(Formation Path Optimization,FPO)[15].FPTS阶段考虑飞行性能约束,建立实现节油目的的集结包线和脱离包线;FPO阶段在集结包线和脱离包线构成的凸边界内利用时序二次型优化规划集结点和脱离点.Xu等提出一种两阶段编队路径优化框架[16]:首先通过预设航班编队的时间和空间边界约束,利用类似于滤波的方法从大规模航班集合中识别可行编队航班集;然后利用整数规划在可行编队航班集上优化编队调度逻辑.Hino和Xu从编队气动耦合理论出发建立编队路径节点的规划域,使问题的复杂度大为降低,但球面度量考虑不足.
本文针对洲际航空编队路径规划问题,结合编队飞行的航空约束特征和球面度量特征,研究问题建模和几何求解方法.首先基于当量航程概念和编队路径的拓扑特征,建立球面上编队路径规划的基本模型;然后,将编队路径规划问题抽象为递归构造球面点集上基于测地线的加权Steiner最小树问题(Weighted Geodesic Steiner Minimal Tree,WGSMT),推导构造球面3点、4点WGSMT的有限几何简化原则;最后,针对球面避障编队路径规划(Obstacle Avoidance WGSMT,OAWGSMT),给出两阶段编队路径规划方法.
1 问题描述1.1 编队路径根据Bower的定义[12],编队路径由起飞机场、离场集结点、集结航段、航路集结点、编队航段、航路脱离点、脱离航段、进场脱离点和目的地机场构成,如图 1所示.集结点和脱离点分别为航空器加入和脱离编队的点.对于同一机场起飞和降落的子编队,由于航空器在爬升、下降航段尾涡场不稳定,因而设置集结机动区和脱离机动区,同一机场起降航班子编队在机动区内保持正常间隔飞行;机动区的半径通常在100 n mile范围[12].由于飞行区域可能存在飞行限制区、危险天气、通信导航盲区、备降机场位置约束等,需要增加中间衔接航路点以避开不利约束区域.
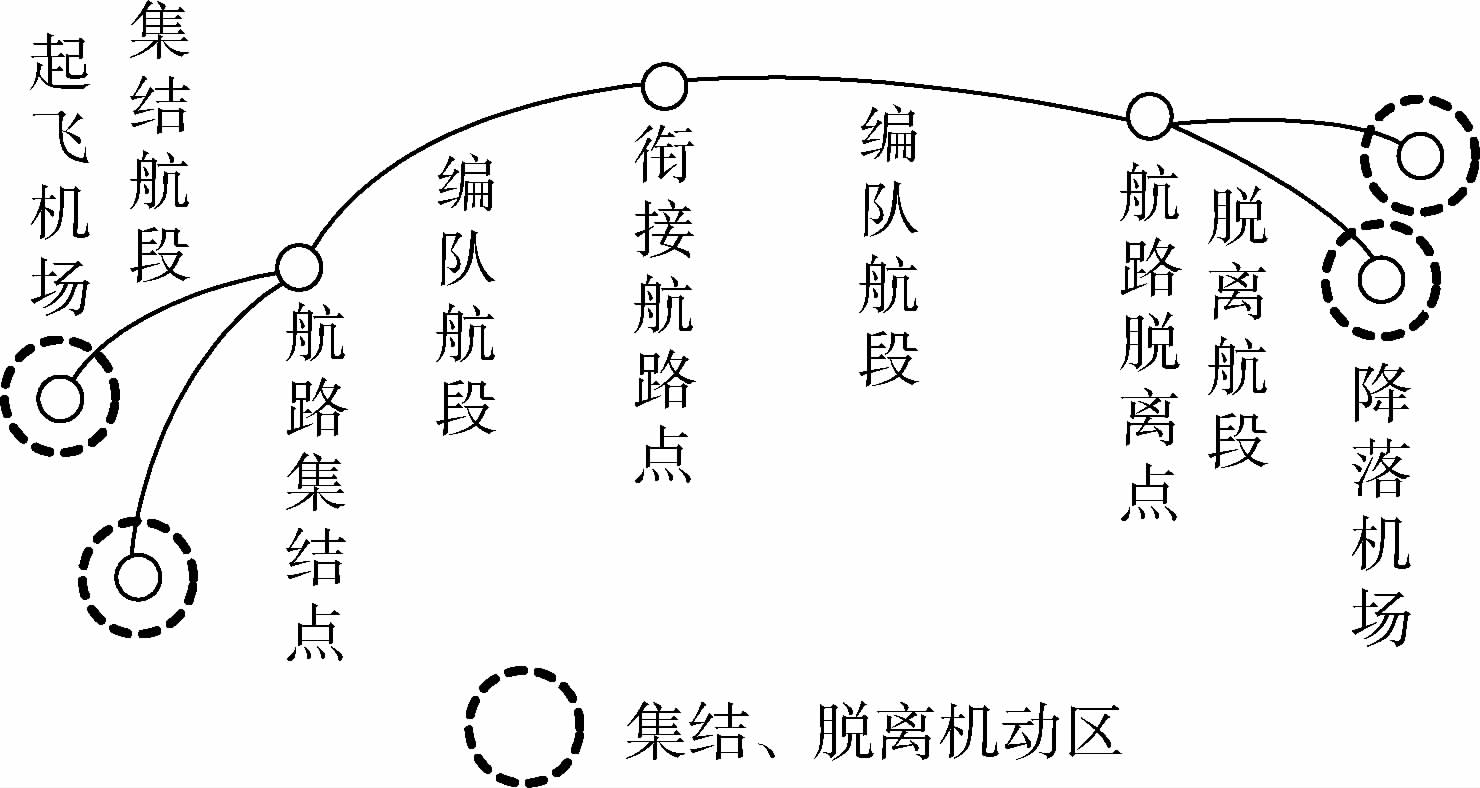 |
| 图 1 编队飞行路径结构Fig. 1 Formation flight path structure |
| 图选项 |
图 1所示编队路径可抽象为图 2所示树状网络T=(D,A,R,B,C).其中D={di,i=1,2,…,m}为根节点集,表示起飞机场集合;A={aj,j=1,2,…,n}为叶节点集,表示降落机场集合;R={ri,i=1,2,…,m-1}和B={bj,j=1,2,…,n-1}分别表示集结点集和脱离点集;C={ck,k=1,2,…,K}表示衔接点集.
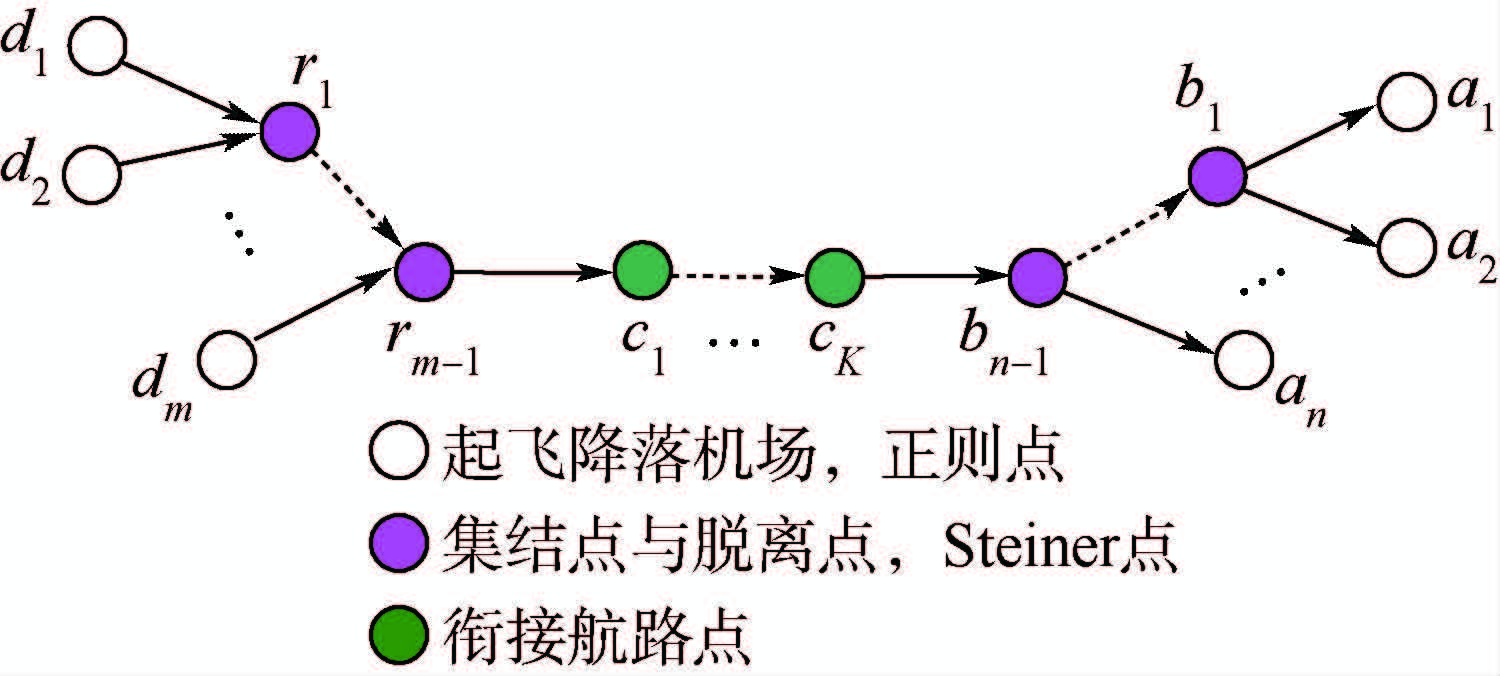 |
| 图 2 编队路径结构抽象出的树状网络Fig. 2 Tree network structure abstracted from formation flight path |
| 图选项 |
如果ri、bj分别是起飞机场di-1、di和降落机场aj-1、aj的集结点和脱离点,记为

如果ri是起飞机场di-1、di和降落机场aj的集结点,记为
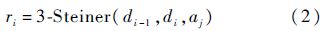
如果bj是起飞机场di和降落机场aj-1、aj的集结点,记为
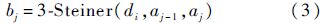
1.2 当量航程规划编队路径需要评价在不同编队调度模式下的燃油经济性,以确定最优编队调度方案.
引入当量航程概念:任何两个节点vi、vj之间的当量航程ge(vi,vj)为其几何航程g(vi,vj)与编队飞行相对燃油里程[3]εij的比值,即
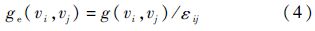
其含义为单机飞行与编队飞行的续航里程之比,其中g(vi,vj)为大圆测度.给定编队调度逻辑下总当量航程越短,编队燃油经济性就越好.
相对燃油里程取决于给定编队队形、编队规模、编队间距、推力设定、大气环境等.假定所有编队航空器为同质航空器,梯形编队,侧向最优间距基于Horseshoe模型确定,纵向间距5~40倍翼展,将q架编队航空器视为一架有效展弦比为单机展弦比q倍的假想航空器并且按照单机最大升阻比飞行,可得到最大相对燃油里程[3]:

1.3 数学模型1.3.1 目标函数对一组候选编队航班集F={fi=<di,ai,qi>|i=1,2,…,I;di∈D,ai∈A,qi∈N},按照规定的编队调度规则在规划衔接所有航班起止点的路径网络T=(D,A,R,B,E,Q,W),在满足相关编队约束的前提下,使编队飞行路径的总当量航程最短,即
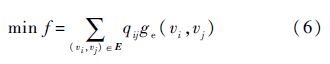
其中:
1) fi=〈di,ai,qi〉表示航班fi的起飞机场、降落机场和机队规模;
2) 编队飞行路径网络T(D,A,R,B,E,Q,W):
D={di|i=1,2,…,m}为所有候选航班的起飞机场集合;
A={aj|j=1,2,…,n}为所有候选航班的降落机场集合;R={ri|i=1,2,…,m-1}为规划的集结点集合;
B={bj|j=1,2,…,n-1}为规划的脱离点集合;
E=[eij]2(m+n-1)×2(m+n-1)为T中节点的邻接矩阵,eij=1表示vi与vj邻接,vi∈D∪R∪B∪A,vj∈D∪R∪B∪A,否则,eij=0;
Q={qij|i=1,2,…,2(m+n-1),j=1,2,…,2(m+n-1)}为各边上的编队规模;
W={wij|i=1,2,…,2(m+n-1),j=1,2,…,2(m+n-1)}为E的权重集合.


1.3.2 当量航程约束对于任意航班,编队当量航程应不劣于单独执行航班任务的当量航程,如图 3所示.

式中:(ri,bj)=4-Steiner(vi,vi′,vj,vj′);〈vi,vj〉为节点vi与vj之间的路径.
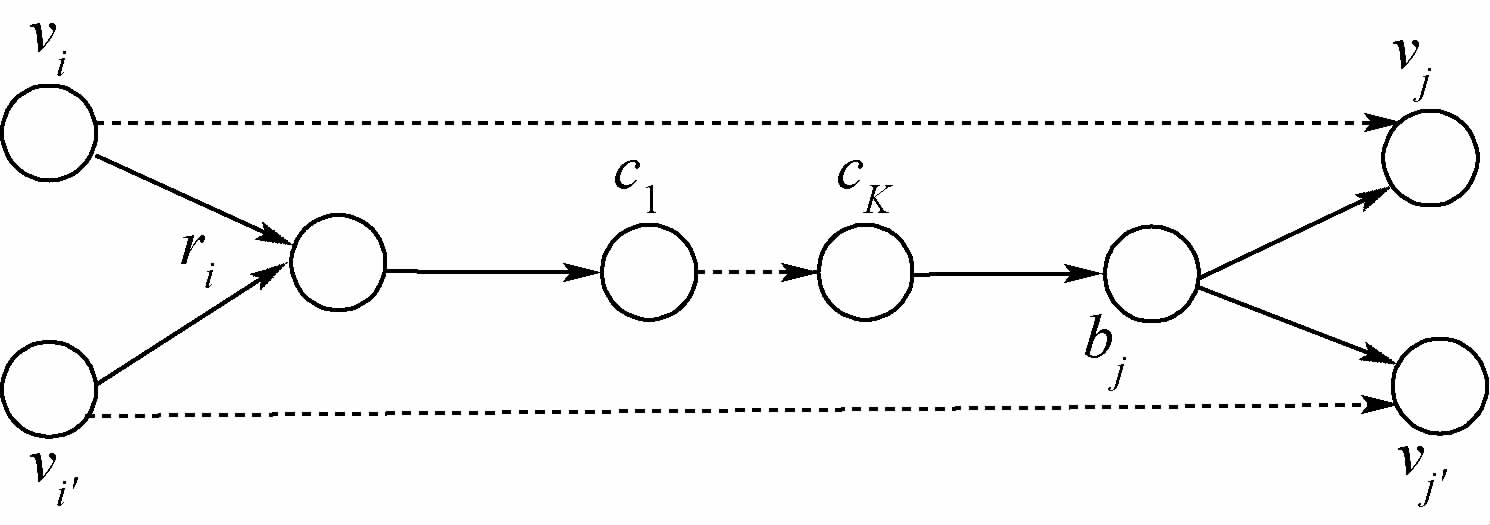 |
| 图 3 当量航程约束Fig. 3 Equivalent voyage constraint |
| 图选项 |
1.3.3 集结时间窗约束对于任一集结点r∈R,若两个航班子编队i和j到达其前驱节点vi和vj的时刻分别为tia和tja,双方应能在最大允许延误时间窗Λi、Λj内和速度包线[Vimin,Vimax]、[Vjmin,Vmaxj]内选择合适的离开时刻ti、tj和速度Vi、Vj,以确保同时到达集结点r.
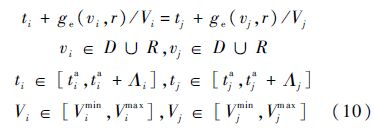
当vi∈D时,Λi表示允许的最大地面延误时间;当vi∈R时,Λi表示允许的最大空中等待时间.
1.3.4 拓扑结构约束规定所有意图编队的航班两两递归集结编队,则编队路径T为Steiner树,如图 2所示.T的拓扑结构应满足:
1) 所有集结点入度不大于2、出度为1,所有脱离点入度为1、出度不大于2.
2) 所有衔接点的出度和入度均为1.
1.3.5 流量平衡约束对于任一集结点和脱离点,由于流入节点的流量必然等于流出节点的流量,因而同一Steiner点关联的3条边存在约束:

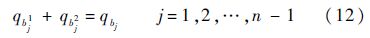
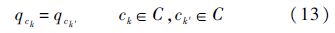

式(11)、式(12)分别表示集结点和脱离点的流量平衡约束,其中rij1、ri2分别为ri的两个前驱节点,b1、bj2为bj的两个后继节点;式(13)为衔接点流量平衡约束,ck和ck′为相邻衔接点;式(14)表示所有意图集结的航班必须全部可达其降落机场.
1.3.6 飞行受限区约束根据航空情报部门发布的航空情报信息所确定的禁止、限制航空器通过或威胁飞行安全的区域称为飞行受限区.要求编队路径不能通过飞行受限区.假定按照圆形公布障碍区域边界(见图 4),飞行受限区约束表示为
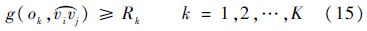
式中:
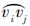 为连接vi与vj大圆劣弧;O={(ok,Rk)|k=1,2,…,K}为障碍物集合,ok为圆心;Rk为受限区半径.由球面三角知识:
为连接vi与vj大圆劣弧;O={(ok,Rk)|k=1,2,…,K}为障碍物集合,ok为圆心;Rk为受限区半径.由球面三角知识: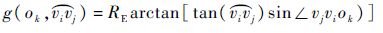
其中:RE为地球半径.
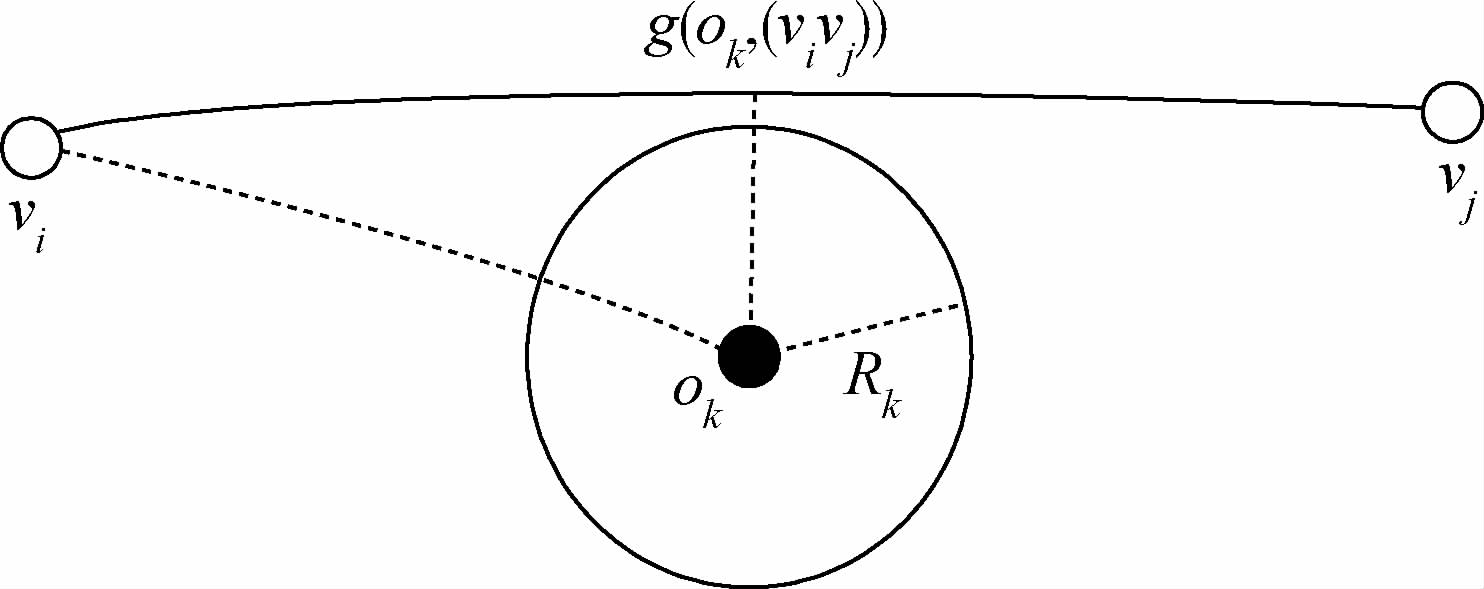 |
| 图 4 飞行受限区限制的编队飞行路径Fig. 4 Formation flight path constrained by flight restricted area |
| 图选项 |
1.3.7 备降机场约束双发延程飞行(Extended-range Twin-engine Operational Performance Standards,ETOPS)是国际民航管理机构为保证双发飞机安全飞行而提出的一项特别要求,指运行航路上有一点到合适机场的距离超过规定60 min飞行(ETOPS 60)或超过180 min飞行(ETOPS 180)的运行[17].考虑航空器编队飞行中的发动机失效风险,要求编队路径任意一点在审定的延程时间内按照单机、单发失效飞行至少能够找到一个适于着陆的备降机场.
编队路径上任意大圆弧段
 满足ETOPS限制的充分必要条件是:包括起降机场和备降机场在内,所有相邻机场的ETOPS圆必须存在一对交点,且交点对必须位于
满足ETOPS限制的充分必要条件是:包括起降机场和备降机场在内,所有相邻机场的ETOPS圆必须存在一对交点,且交点对必须位于 的两侧.否则,需要在相邻机场的ETOPS圆内增加一个衔接点cij1,以确保编队航程全部被所有ETOPS圆最大包络线所覆盖,如图 5所示.图中,χij1、χij2为
的两侧.否则,需要在相邻机场的ETOPS圆内增加一个衔接点cij1,以确保编队航程全部被所有ETOPS圆最大包络线所覆盖,如图 5所示.图中,χij1、χij2为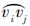 上的备降机场.从而备降机场约束转化为对上述条件的约束满足判定.
上的备降机场.从而备降机场约束转化为对上述条件的约束满足判定.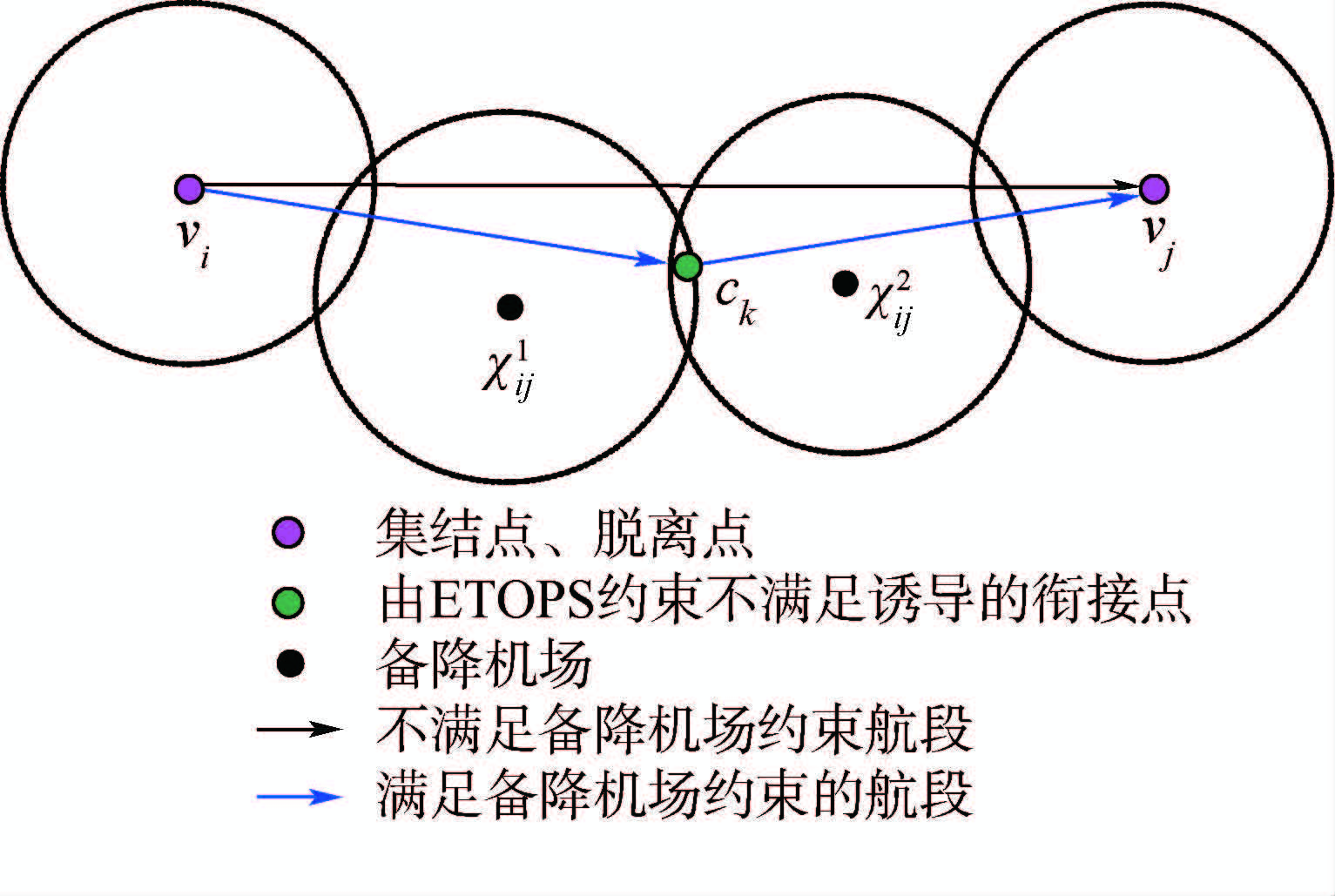 |
| 图 5 备降机场约束不满足时新增中间衔接航路点ckFig. 5 A new connection point ck is added whenever ETOPS constraint is not satisfied |
| 图选项 |
2 WGSMT的有限几何简化观察图 2,由于规定起降机场对间两两编队,因而集结点的入度为2,出度为1;脱离点的入度为1,出度为2.如果将中间衔接航段视为超边,则图 2所示树状结构即为满拓的Steiner树,其中起降机场为正则点,节点度为1,集结点和脱离点为Steiner点,节点度为3,每一个集结点或脱离点均衔接两个正则点和一个Steiner点.满足上述特征的网络称为Steiner树.本文将编队飞行路径规划问题抽象为WGSMT构造问题:规划支撑起降机场集合的最短加权衔接网络.
2.1 基本定义Steiner最小树(Steiner Minimal Tree,SMT)问题是具备NP(Non-Polynomialtime,NP)难的经典几何问题,在网络分析与布局、城市交通规划、大规模集成电路设计、决策优化等领域有着广泛的应用.Courant和Robbins给出了Steiner点满足的基本几何性质[18].Melzak给出了SMT问题的有限几何简化原则,使SMT问题转化为一个有限问题[19].文献[13-14]利用欧氏空间上的角度条件及建立在该角度条件上的有限几何简化原则规划编队路径,球面度量特征考虑不足.
Dolan等给出GSMT(Geodesic Steiner Minimal Tree,GSMT)的定义[20].
定义1 GSMT问题.
给定球面Φ上的点集V={v1,v2,…,vn},设法在Φ上添加点集S={s1,s2,…,sm},构造V∪S的最小支撑树,使其距离最短.
针对编队路径规划,给出几何描述:
定义2 WGSMT问题.
给定球面Φ上图G=(V,E,Q),D∈Φ和A∈Φ是V∈Φ的一个划分,设法在Φ上添加点集R、B,构造V∪R∪B的最小支撑树T=(D,A,R,B,E,Q,W),使其为大圆测度下衔接D与A的最小加权网络.
定义3 OAWGSMT问题.
给定球面Φ上的图G=(V,Q,O),D∈Φ和A∈Φ是对V∈Φ的一个划分,O为障碍物集合,设法在Φ上添加点集R、B、C,构造V∪R∪B的最小支撑树T(D,A,R,B,C,E,Q,W),使其为大圆测度下衔接D与A且不通过O中任意障碍物的最小加权网络.
2.2 WGSMT编队路径存在的充分必要条件Cockayne[21]和Weng[22]推导出GSMT Steiner角恰好为120°.本节推导WGSMT编队路径存在的充分必要条件.
如图 6所示,S为单位球面上不共大圆线的3点A、B、C的Steiner点,其中∠ASB、∠BSC、∠CSA分别称为点A和B、点B和C、点C和A的关联Steiner角.
 |
| 图 6 球面3点的Steiner点Fig. 6 Steiner point of 3 points on sphere |
| 图选项 |
由向量内积定义可得
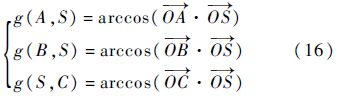
由定义1:
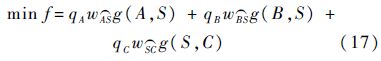
约束条件为

构造拉格朗日函数:
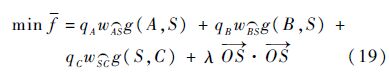
利用拉格朗日乘子法可得球面上任意不共大圆线的3点A、B、C的加权Steiner点S的角度条件为
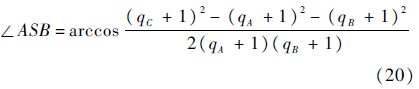
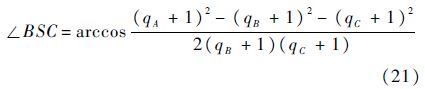

式(20)~式(22)为WGSMT Steiner点存在的角度条件,属于必要但非充分条件.根据1.3.5 节中的流量平衡约束有qC=qA+qB,利用两流出节点流量qA和qB可以确定WGSMT Steiner点的球面位置.
由于编队路径不超过半个球面,即任一条Steiner边或正则边的弧度不超过π,因而只需证明与Steiner点关联的Steiner边和正则边在(0,π)上存在局部极小点.WGSMT Steiner点为局部极小点的充分条件为
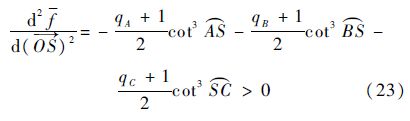
在洲际航空中,合理假设
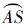 ≈
≈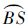 ∈(0,π/2),qA≈qB»1,式(23)可变为
∈(0,π/2),qA≈qB»1,式(23)可变为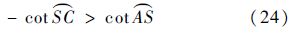
只要π/2<
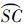 <π且
<π且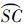 -π/2<π/2-
-π/2<π/2-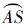 ,即
,即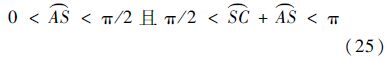
充分条件式(23)自然满足.
式(25)的几何含义为:集结航段小于1/4地球周长,集结与编队航段之和大于1/4大圆且小于1/2大圆.当前洲际航空运输一般在5 000~10 000 n mile之间,恰好位于该运行区间,表明洲际航空最优编队飞行路径存在且唯一.
2.3 WGSMT的有限几何简化由式(20),WGSMT Steiner点必然位于由式(20)所确定的一段小圆劣弧上,同样也必然位于由式(21)、式(22)所确定的小圆劣弧上.由WGSMT Steiner点唯一,由式(20)~式(22)所确定小圆劣弧交于唯一WGSMT Steiner点S,如图 6所示.洲际航空运输中,大圆弧
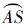 、
、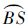 远短于大圆弧
远短于大圆弧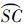 ,在推导相关性质时可以近似应用欧氏平面相关性质以简化问题,因此选择球面圆弧
,在推导相关性质时可以近似应用欧氏平面相关性质以简化问题,因此选择球面圆弧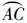 、
、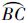 来构造WGSMT Steiner点.
来构造WGSMT Steiner点.假定qA»1,qB»1,利用三角函数公式及流量平衡条件,容易得到
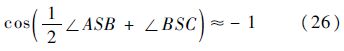
即

同理可得
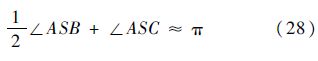
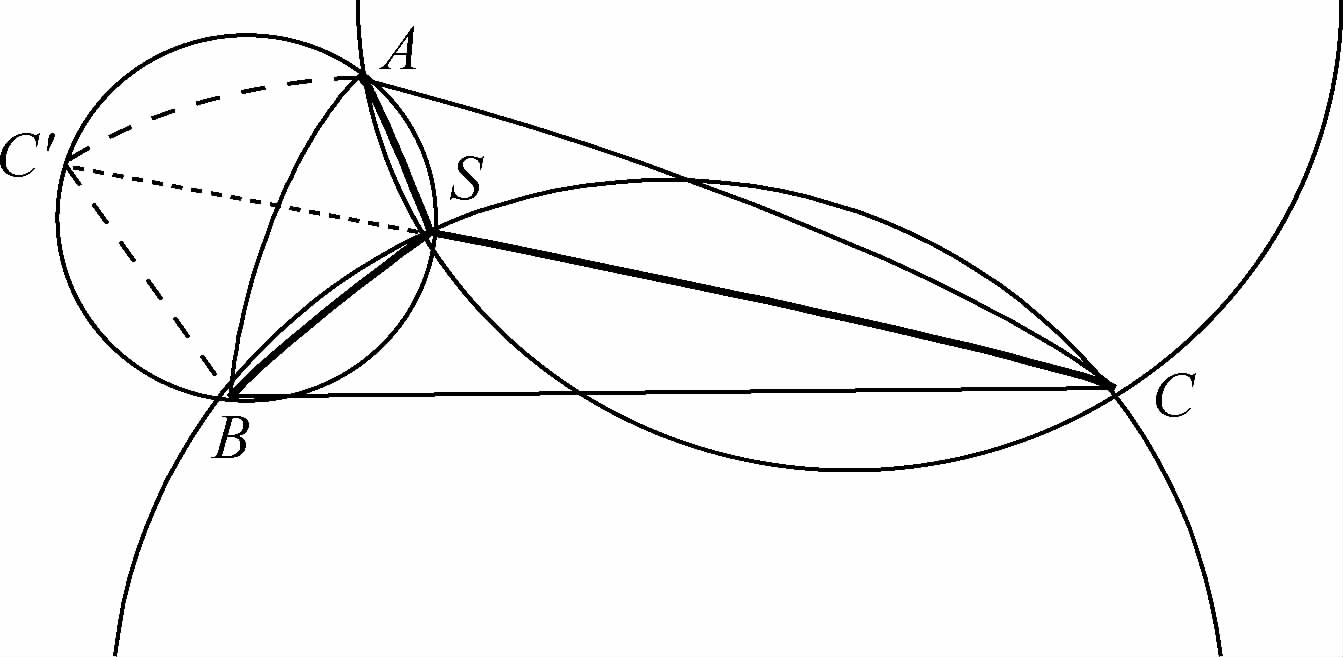
图 7中,利用大圆弧连接
 ,其反向延长线与△ASB的球面外接圆帽相交与点C′.根据式(27)与式(28),立即得到∠ASC′=∠BSC′=½∠ASB,从而
,其反向延长线与△ASB的球面外接圆帽相交与点C′.根据式(27)与式(28),立即得到∠ASC′=∠BSC′=½∠ASB,从而
进而得到构造WGSMT的几何简化原则:
 |
| 图 7 球面3点WGSMT的有限几何简化Fig. 7 Simplifying WGSMT to a finite geometric planning problem of 3 points on sphere |
| 图选项 |
1) 对于球面3点A、B和C,根据式(20)计算∠ASB,进而利用式(29)计算∠ABC′和∠BAC′;在球面点集{A,B,C}的凸包外侧,利用大圆弧
 构造球面等腰△ABC′及其球面外接圆,使满足式(29),则大圆弧
构造球面等腰△ABC′及其球面外接圆,使满足式(29),则大圆弧 与△ABC′球面外接圆交于异于C′的另外一点S即为球面3点A、B和C满足角度条件式(20)~式(22)的WGSMT Steiner点,如图 6所示.
与△ABC′球面外接圆交于异于C′的另外一点S即为球面3点A、B和C满足角度条件式(20)~式(22)的WGSMT Steiner点,如图 6所示.2) 对于球面4点A、B和C、D,在球面点集{A,B,C,D}的凸包外侧,分别利用
 和
和 构造球面等腰
构造球面等腰 和球面等腰△
和球面等腰△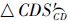 及外接圆,使
及外接圆,使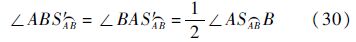
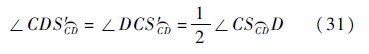
则
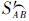
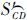 与两球面三角形的外接圆交于异于
与两球面三角形的外接圆交于异于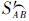 、
、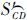 的两交点
的两交点 、
、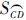 为球面的4点A、B与C、D的WGSMT Steiner点,如图 8所示.
为球面的4点A、B与C、D的WGSMT Steiner点,如图 8所示.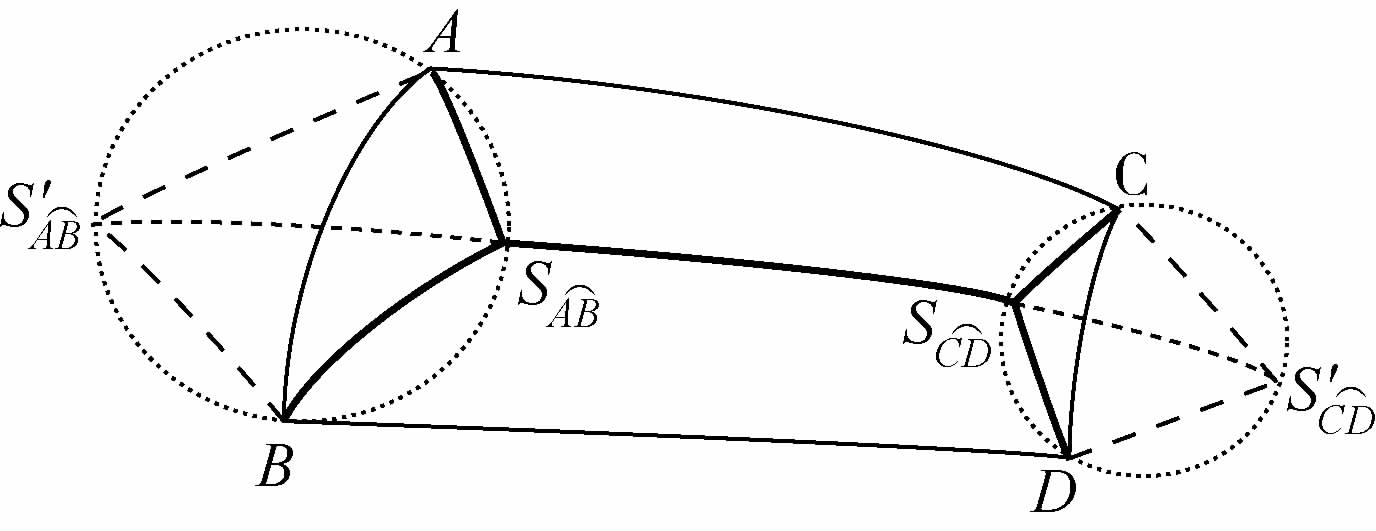 |
| 图 8 球面4点WGSMT的有限几何简化Fig. 8 Simplifying WGSMT to a finite geometric plan problem of 4 points on sphere |
| 图选项 |
3) 对于任意Steiner角,假定为图 7所示∠BSC,若∠BSC<∠BAC,根据上述规则所规划的Steiner点S将位于球面点集{A,B,C}的凸包外侧,此时应取S点为A点,度为2.在编队路径中,表明该点恰位于某一机场.
3 编队飞行路径规划的几何方法编队飞行路径规划问题具有以下特征:
1) 主要编队燃油效益区间为洲际航空运输,满足规划精度要求的规划空间巨大.
2) 边的权重依赖于编队调度方案,具备动态网络流特征.
3) 编队路径具备球面度量特征和航空约束特征,求解困难.
在离散球面空间上利用数值算法规划编队路径具有依赖于离散网格数量的复杂度,而几何方法的复杂度则仅依赖于节点规模.根据编队路径的拓扑特征,编队飞行路径规划问题可以被抽象为一个含动态网络流特征几何规划问题:OAWGSMT构造问题.考虑基于“构造-修复”思想的规划避障编队路径:利用WGSMT有限几何简化原则在球面点集上递归构造WGSMT编队路径;利用可视图方法及WGSMT有限几何简化原则修复WGSMT编队路径得到OAWGSMT编队路径.
基本假设如下:
1) 给定意图编队的航班集合已经满足约束条件式(9)与式(10).实际上,可以从式(9)与式(10)出发,建立可接受编队模式[16]的时间维和空间维判别边界,利用含边界约束的最优层次聚类得到满足式(9)与式(10)的航班集,本文不研究该问题.
2) 同一起飞机场的航班集飞往同一降落机场.如果存在起飞机场di的航班集飞往nj个降落机场an1,an2,…,anj,流量依次为qn1,qn2,…,qnj,则将di分解为nj个与di地理位置相同的虚拟起飞机场dn1,dn2,…,dnj,令(dn1,an1),(dn2,an2),…,(dnj,anj)的流量依次为qn1,qn2,…,qnj;反之,如果存在mi个起飞机场dm1,dm2,…,dmi的航班飞往同一降落机场am,流量分别为qm1,qm2,…,qmi,则将am分解为mi个与am位置相同的虚拟降落机场am1,am2,…,ami,令(dm1,am1),(dm2,am2),…,(dmi,ami)的流量依次为qm1,qm2,…,qmi.
基本步骤如下:
步骤1 构造 WGSMT编队飞行路径.
仅考虑编队路径的约束1.3.4 节与1.3.5节的约束条件,将编队路径规划问题抽象为含流量平衡约束的动态WGSMT构造问题,按照某种启发规则确定节点间的编队调度逻辑,利用球面4点WGSMT有限几何简化原则递归构造如图 9所示的WGSMT编队路径.
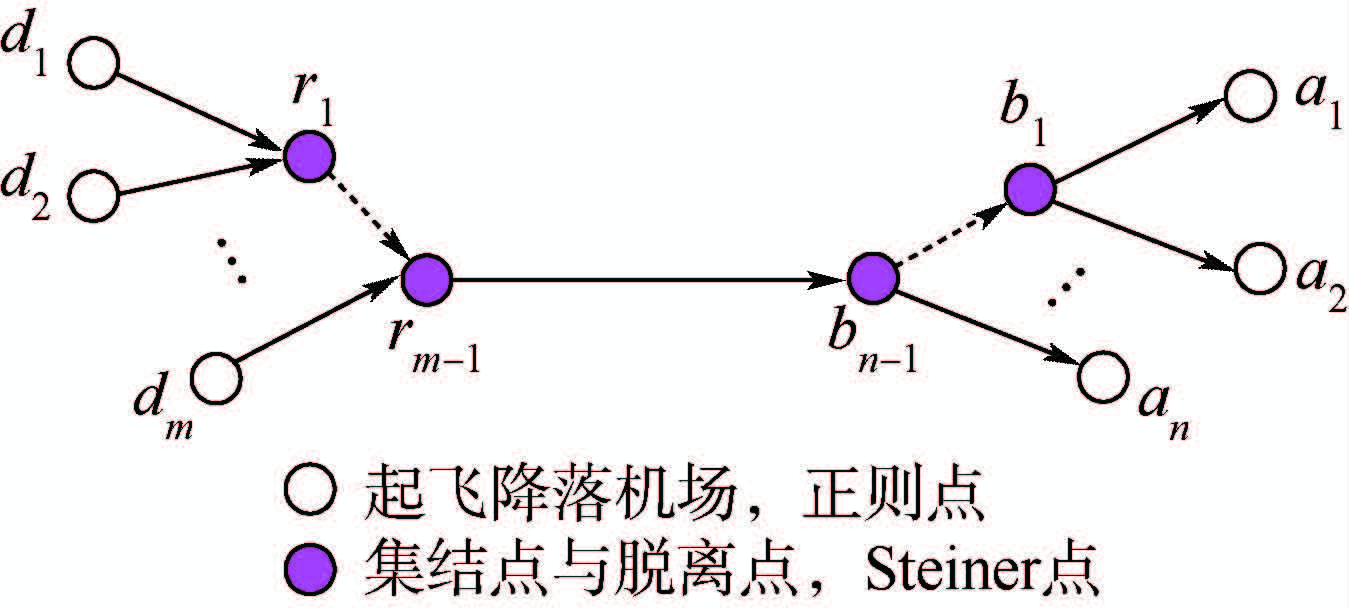 |
| 图 9 WGSMT编队路径Fig. 9 WGSMT formation path |
| 图选项 |
1) 如果D、A非空,按照深度优先规则,基于起降机场对的影响力因子λij,每次从D、A中仅选择λij最大起降机场对(di1,aj1,qi1j1)及与其空间维相似度最高的起降机场对(di2,aj2,qi2j2)构造球面4点的WGSMT.利用WGSMT有限几何简化原则,得到集结点ri1和脱离点bj2,如图 10所示.其中,虚线为当前单独执行任务路径;实线为规划的编队路径.
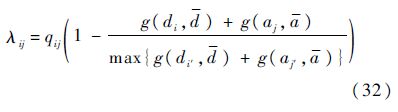
式中:(d,a)为所有起降机场对的几何中心.任意起降机场对,机队规模越大,与所有起降机场对几何中心的位置越近,则影响力因子越大.
 |
| 图 10 球面4点的WGSMT构造Fig. 10 Constructing WGSMT of 4 points on sphere |
| 图选项 |
2) 在D、A中利用(ri1,bj2,qi1j1+qi2j2)取代正则点对(di1,aj1,qi1j1)和(di2,aj2,qi2j2),得到更新后的规划域;转至1),直至完成所有正则点对的构造.
3) 经过前两步1)和2)后,所得到的编队路径可能存在3种情况:
① 所有Steiner点的度恰好为3,WGSMT编队路径满拓.
② 存在Steiner点的度为2,表明某一机场为集结点或脱离点.
③ 存在Steiner点的度大于3,如图 11中的ri1和bj1.出现该情况的原因在于递归构造WGSMT树的过程中,利用Steiner点代替其支撑的正则点进行构造.此路径非几何意义上的最优.修复方法:从di1、di2选择与di3空间相似度较高的一点,假定为di2点,构造r′i2=3-Steiner(di2,di3,ri1);同样,从di1、di2选择与di3空间相似度较高的一点,假定为aj3点,构造bj2=3-Steiner(aj2,aj3,bj1),最终得到如图 12所示的满拓WGSMT.
 |
| 图 11 存在Steiner点的度大于3的WGSMTFig. 11 WGSMT with Steiner points whose degrees are greater than 3 |
| 图选项 |
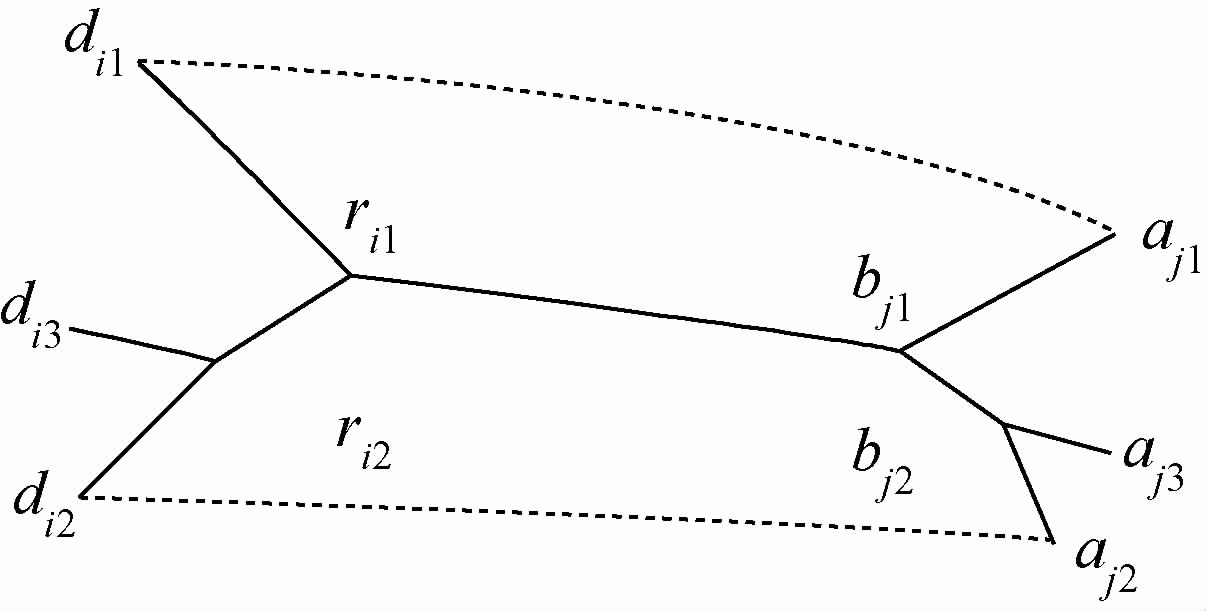 |
| 图 12 修复后的WGSMTFig. 12 Repaired WGSMT |
| 图选项 |
步骤2 OAWGSMT路径规划.
1) 构造rm-1与bn-1之间的最短避障路径.
对于WGSMT路径的主干航段rm-1bn-1,利用可视图方法在球面上规划几何航程最短、满足1.3.6 节和1.3.7节中约束的最短避障路径〈rm-1,c1,…cK,bn-1〉,以取代(rm-1,bn-1),如图 13所示.此时(rm-1,bn-1)≠4-Steiner(rm-2,dm,an,bn-2),因而〈rm-1,c1,…,cK,bn-1〉非vi与vj间的最优路径,但〈c1,c2,…,cK〉是c1与ck间的最优路径.
 |
| 图 13 rm-1与bn-1间的最短避障路径Fig. 13 Shortest obstacle-avoidance path between rm-1 and bn-1 |
| 图选项 |
2) 构造OAWGSMT编队飞行路径.
分别构造r′m-1=3-Steiner(dm,rm-2,c1)和b′n-1=3-Steiner(ck,an,bn-2),以取代rm-1=3-Steiner(dm,rm-2,c1)和bn-1=3-Steiner(ck,an,bn-2).
由于〈c1,…,cK〉是c1与ck之间的最短避障路径,r′m-1为球面点集{dm,rm-2,c1}上满足目标f且满足1.3.4 ~1.3.7节中约束的Steiner点,b′n-1为{ck,an,bn-2}上的满足目标f且满足1.3.4~1.3.7节中约束的Steiner点,因而图 14 所示路径必然为满足目标f最小且满足约束1.3.4~1.3.7节的OAWGSMT编队路径.
 |
| 图 14 OAWGSMT编队路径Fig. 14 OAWGSMT formation path |
| 图选项 |
根据上述分析,不加证明给出下列定理,以支持OAWGSMT编队路径修复算法.
定理1 对于球面不共大圆线3点{A,B,C}的WGSMT Steiner点S及衔接点Ck,支撑{A,B,Ck}的WGSMT Steiner点S′仍是支撑{A,B,C}的OAWGSMT Steiner点,如图 15所示.
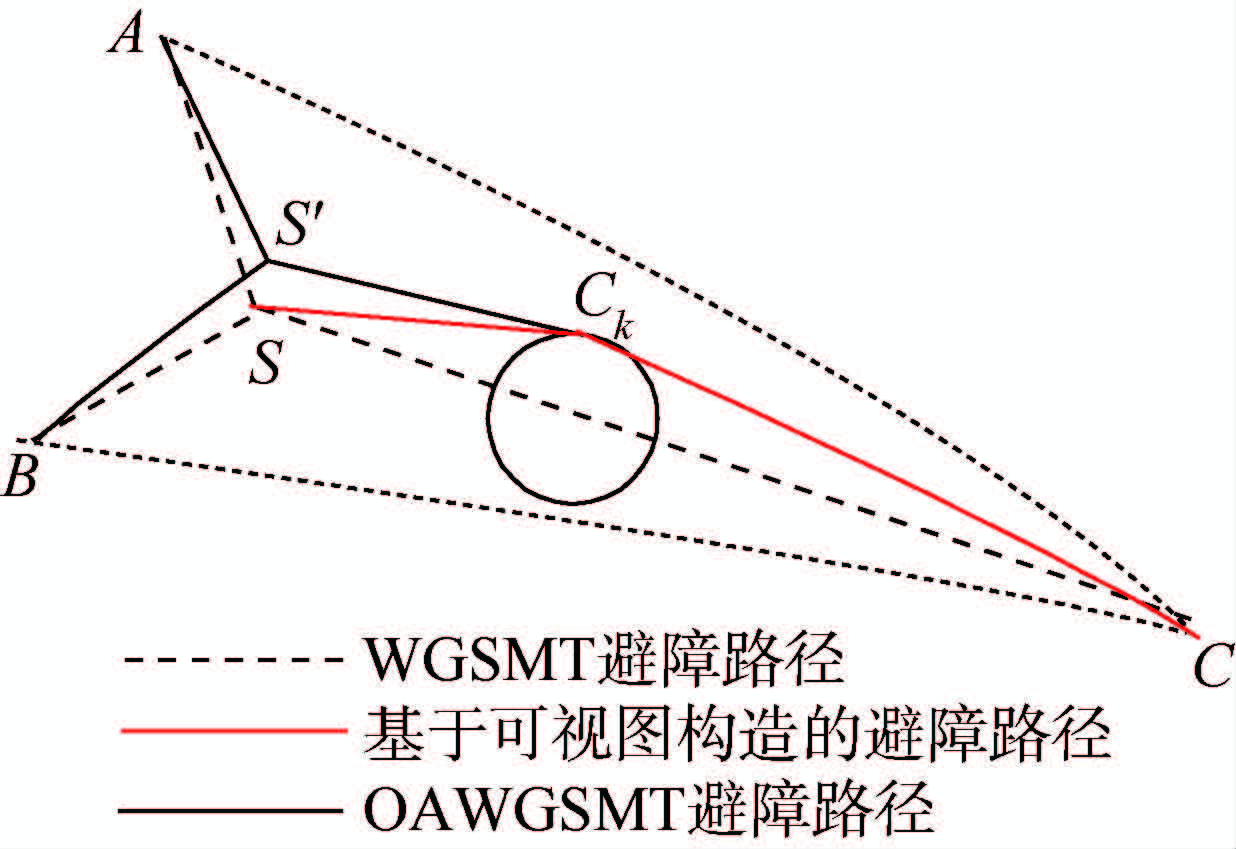 |
| 图 15 球面3点OAWGSMT构造Fig. 15 Constructing OAWGSMT of 3 points on sphere |
| 图选项 |
定理2 对于球面不共大圆线4点{A,B,C,D}的WGSMT Steiner点SAB、SCD及衔接点Ck,支撑{A,B,Ck}的WGSMT Steiner点s′AB和支撑{C,D,Ck}的WGSMT Steiner点s′CD仍是支撑{A,B,C,D}的OAWGSMT的Steiner点,如图 16所示.
 |
| 图 16 球面4点OAWGSMT构造Fig. 16 Constructing OAWGSMT of 4 points on sphere |
| 图选项 |
4 算 例利用表 1所示的实际航班数据验证本文编队飞行路径规划方法的有效性.选择我国东海岸、日本、俄罗斯远东地区、美国阿拉斯加、美国西海岸的部分主要机场构成备降机场集,如表 2所示.机型为Boeing 777-200B,执行ETOPS-180标准,单发失效速度0.80/350 kn,ETOPS-180半径约为1 050 n mile.飞行受限区中心坐标为N46.75E149.68,半径371.75 n mile.
表 1 候选编队航班集Table 1 Candidate flight set
| 起降机场对 | 航班号 | 起飞机场 | 降落机场 | 航班架次 | ||
| 纬度/(°) | 纬度/(°) | 纬度/(°) | 纬度/(°) | |||
| 上海-长滩 | Z2029 | 31.20 | 121.34 | 33.82 | -118.15 | 1 |
| 香港-洛杉矶 | CX880 | 22.31 | 113.91 | 33.94 | -118.41 | 1 |
| 台北-旧金山 | CI004 BR028 | 25.08 | 121.23 | 37.62 | -122.38 | 2 |
| 台北-洛杉矶 | CI008 BR016 | 25.08 | 121.23 | 33.94 | -118.41 | 2 |
| 台北-温哥华 | CI032 BR010 | 25.08 | 121.23 | 49.19 | -123.18 | 2 |
| 台北-奥克兰 | CI053 | 25.08 | 121.23 | 37.71 | -122.34 | 1 |
表选项
表 2 备降机场集Table 2 Alternate aerodromes set
| 名称 | 纬度/(°) | 经度/(°) | 等级 |
| 香港国际机场 | N22.31 | E113.91 | 4F |
| 东京羽田国际机场 | N35.77 | E140.39 | 4F |
| 斯雷登堪察次克机场 | N56.24 | E162.69 | 4D |
| 安克雷奇国际机场 | N61.19 | W150.01 | 4E |
| 旧金山国际机场 | N37.62 | W122.38 | 4E |
表选项
图 17为WGSMT编队路径示意图,图 18为OAWGSMT编队路径示意图.节点上数字表示航班架次,括号中数字表示本场起降航班架次.表 3为WGSMT编队路径与OAWGSMT编队路径经济性评价结果.计算结果表明:
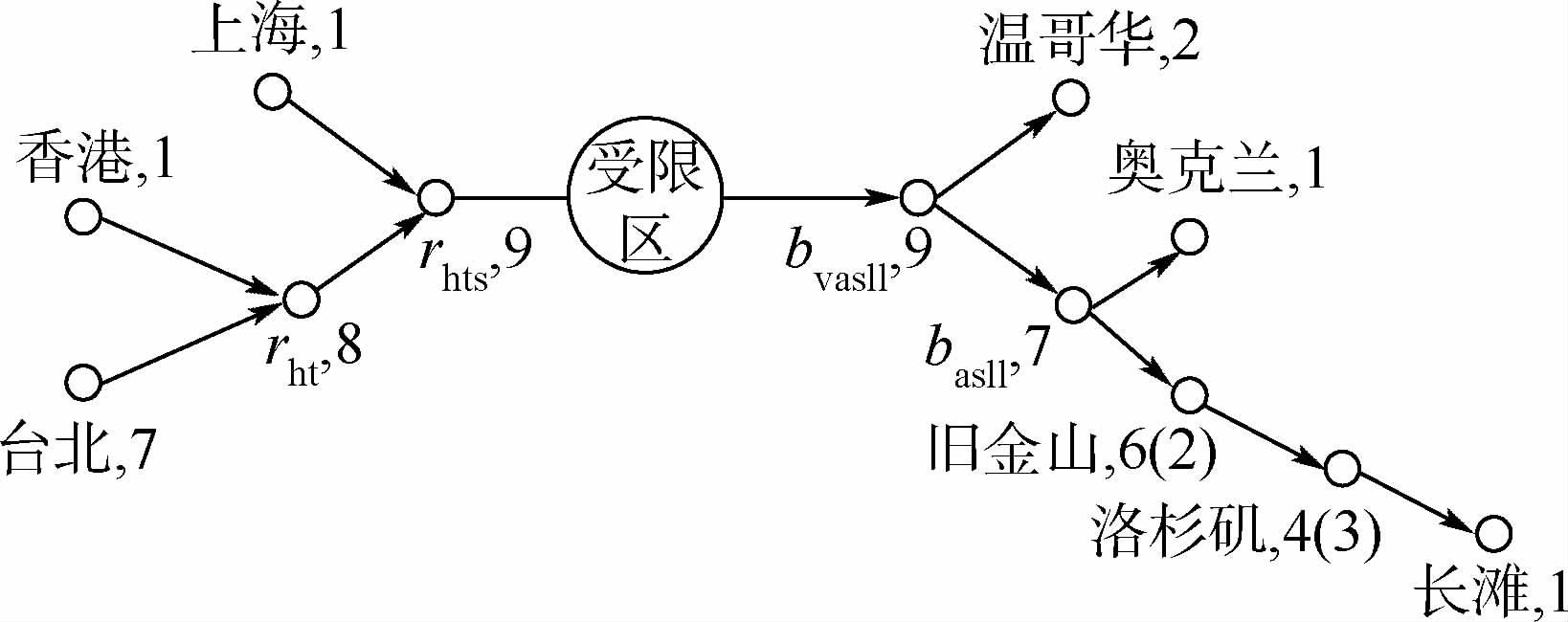 |
| 图 17 WGSMT编队飞行路径Fig. 17 WGSMT formation flight path |
| 图选项 |
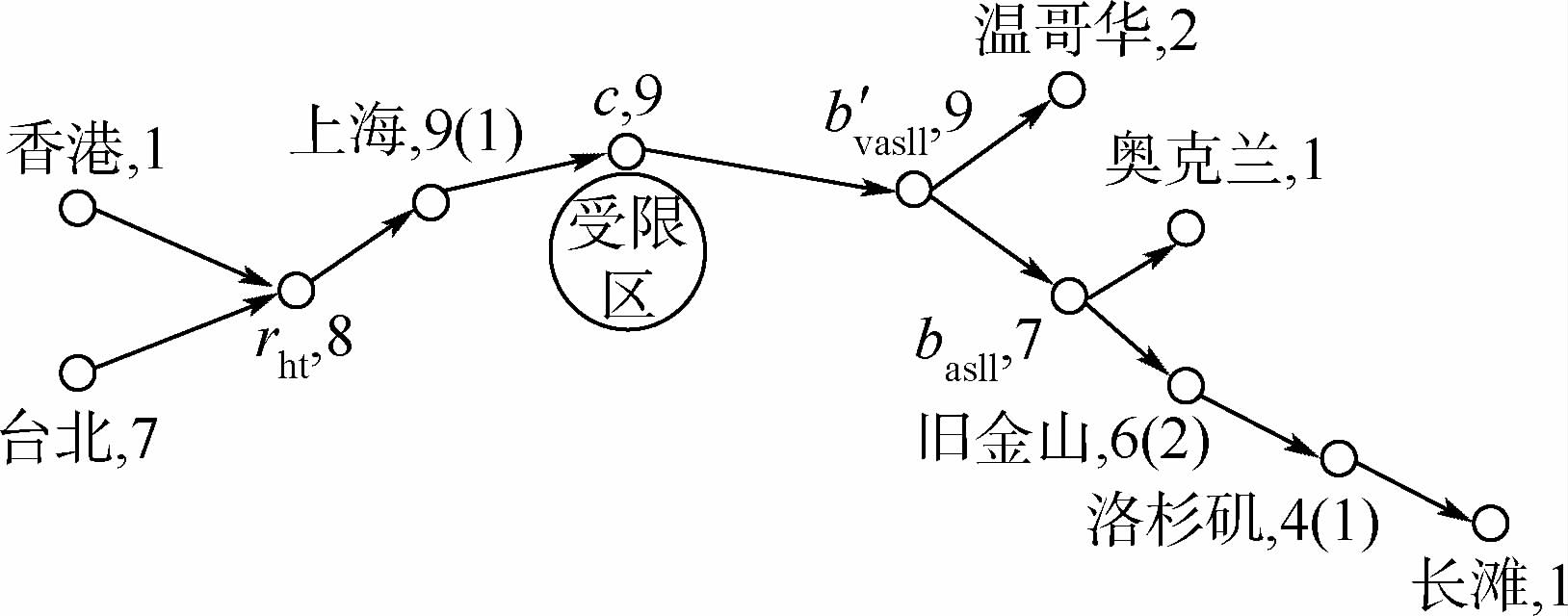 |
| 图 18 OAWGSMT编队飞行路径Fig. 18 OAWGSMT formation flight path |
| 图选项 |
表 3 编队飞行路径的经济效益Table 3 Economic benefits of formation flight path
| 起降机场对 | 起飞机场 | 降落机场 | 架次 | 计划航程/n mile | WGSMT | OAWGSMT | ||||
| 纬度/(°) | 经度/(°) | 经度/(°) | 经度/(°) | 当量航程/n mile | 节省/% | 当量航程/n mile | 节省/% | |||
| 上海-长滩 | 31.20 | 121.34 | 33.82 | -118.15 | 1 | 5 649.29 | 3 281.08 | 41.92 | 3 226.98 | 42.88 |
| 香港-洛杉矶 | 22.31 | 113.91 | 33.94 | -118.41 | 1 | 6 294.23 | 3814 | 39.41 | 3 822.95 | 39.26 |
| 台北-旧金山 | 25.08 | 121.23 | 37.62 | -122.38 | 2 | 5 606.80 | 3 229.43 | 42.40 | 3 238.84 | 42.23 |
| 台北-洛杉矶 | 25.08 | 121.23 | 33.94 | -118.41 | 2 | 5 893.70 | 3 413 | 42.09 | 3 422.19 | 41.93 |
| 台北-温哥华 | 25.08 | 121.23 | 49.19 | -123.18 | 2 | 5 175.85 | 2 977.24 | 42.48 | 3 006.85 | 41.91 |
| 台北-奥克兰 | 25.08 | 121.23 | 37.71 | -122.34 | 1 | 5 605.20 | 3 230.54 | 42.37 | 3 239.95 | 42.20 |
表选项
1) 由于执行ETOPS-180标准,计划航线和编队路径均位于ETOPS一圆内,无不满足备降机场约束的编队航段.
2) WGSMT编队路径有2个满拓的集结点rht和rhts、2个满拓的脱离点bvasll和basll、2个度为2的脱离点“旧金山”和“洛杉矶”;OAWGSMT编队路径有1个满拓的集结点rht,1个度为2的集结点上海,2个满拓的脱离点b′vasll和basll,2个度为2的脱离点“旧金山”和“洛杉矶”,1个衔接点c.两种路径均满足节点度约束和流量平衡约束.
3) 只有“上海-长滩”的OAWGSMT编队路径的燃油经济性优于WGSMT.原因是由于衔接点c的引入,使“上海”由正则点变为集结点,几何航程缩短.
4) 编队飞行的燃油经济性约40%左右,所有编队航空器获得相对均衡的编队燃油经济效益.该结果较为乐观,主要原因在于:
① 未考虑大间距编队飞行时黏性阻力、大气浮力、大气紊流、尾涡碰撞、定位误差等因素影响;
② 未考虑集结机动和脱离机动区范围影响;
③ 未考虑编队稳定性限制的最大编队规模束.
5 结 论1) 针对洲际航空编队飞行路径规划问题,提出当量航程定义,使编队飞行的燃油经济性得以表达;在此基础上,建立了编队路径飞行规划问题在球面上的数学表达.
2) 基于编队路径的拓扑特征,将编队路径规划问题抽象为WGSMT问题,推导出WGSMT Steiner点的角度条件,建立了WGSMT问题的有限几何简化原则,形成了WGSMT Steiner点的编队路径的精确几何构造方法.
3) 针对OAWGSMT编队路径规划问题,证明了衔接点的引入仅改变紧邻的Steiner点的拓扑特征.
4) 在2)和3)的基础上,构造基于“构造-修复”思想的编队飞行路径几何规划方法.
研究形成洲际航空编队飞行路径规划的几何规划的方法基础,使问题复杂度依赖于节点的数量而非球面的离散化网格数量,降低了问题复杂度.
本文仅给出了WGSMT编队路径的几何构造解,为进一步解决大规模洲际航空编队飞行路径规划:①需考虑黏性阻力、大气浮力、大气紊流、尾涡碰撞、定位误差等因素的影响,建立远场涡传播与消散模型及诱导阻力因子的不确定分布模型,提高编队飞行路径规划的精确性和鲁棒性;②结合高空风场模型和动态气象要素影响,考虑编队稳定性限制的最大编队规模约束和最小曲率半径约束,建立更加符合运行实际的洲际航空编队飞行路径规划模型.③在WGSMT几何构造解基础上,结合洲际航空运行区间特征,推导WGSMT Steiner点近似解析解.
参考文献
| [1] | Airport Council International.Global traffic forecast 2006—2025 executive summary,Edition 2007[R].Montreal:Airport Council International,2007. |
| [2] | Rojo J J.Future trends in local air quality impacts of aviation[D].Massachusetts:Massachusetts Institute of Technology,2007. |
| Click to display the text | |
| [3] | Blake W,Multhopp D.Design,performance and modeling considerations for close formation flight,AIAA-1998-4343[R].Reston:AIAA,1998. |
| Click to display the text | |
| [4] | Dijkers H P A,Van Nunen R,Bos D A,et al.Integrated design of a long-haul commercial aircraft optimized for formation flying,AIAA-2011-6969[R].Reston:AIAA,2011. |
| Click to display the text | |
| [5] | Nehrbass J G,Frommer J B,Garison L A,et al.Point to point commercial aircraft service design study including formation flight and morphing[C]//AIAA 4th Aviation Technology,Integration and Operations(ATIO)Forum.Reston:AIAA,2004:20-22. |
| [6] | Ning S A.Aircraft drag reduction through extended formation flight[D].Stanford:Stanford University,2011. |
| [7] | Ning S A,Flanzer T C,Kroo I M,et al.Aerodynamic performance of extended formation flight[J].Journal of Aircraft,2011,48(3):855-865. |
| Click to display the text | |
| [8] | Ning S A,Kroo I M.Compressibility effects of extended formation flight,AIAA-2011-3812[R].Reston:AIAA,2011. |
| Click to display the text | |
| [9] | Flanzer T C,Bieniawski S R,Blake W B,et al.Operational analysis for the formation flight for aerodynamic benefit program,AIAA-2014-1460[R].Reston:AIAA,2014. |
| Click to display the text | |
| [10] | Xue M,Hornby G.An analysis of the potential savings from using formation flight in the NAS,AIAA-2012-4524[R].Reston:AIAA,2012. |
| Click to display the text | |
| [11] | Ribichini G,Frazzoli E.Efficient coordination of multiple-aircraft systems[C]//Proceedings of IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,2003,1:1035-1040. |
| Click to display the text | |
| [12] | Bower G C,Flanzer T C,Kroo I M.Formation geometries and route optimization for commercial formation flight,AIAA-2009-3615[R].Reston:AIAA,2009. |
| Click to display the text | |
| [13] | Kent T,Richards A.A geometric approach to optimal routing for commercial formation flight,AIAA-2012-4769[R].Reston:AIAA,2012. |
| Click to display the text | |
| [14] | Kent T E,Richards A G.On optimal routing for commercial formation flight,AIAA-2013-4889[R].Reston:AIAA,2013. |
| Click to display the text | |
| [15] | Hino T.Real time path planning method of aircraft formations[C]//28th International Congress of the Aeronautical Scicences.Brisbane:ICAS,2012:1-5. |
| Click to display the text | |
| [16] | Xu J S,Ning S A,Bower G C,Kroo I M,et al.Aircraft route optimization for formation flight[J].Journal of Aircraft,2014,51(2):490-501. |
| Click to display the text | |
| [17] | Chiles P.ETOPS redefined[J].AeroSafety World,2007,2(3):88-92. |
| [18] | Courant R,Robbins H.What is mathematics?[M].New York:Oxford University Press,1951. |
| [19] | Melzak Z A.On the problem of Steiner[J].Canadian Mathematical Bulletin,1961,4(2):143-148. |
| [20] | Dolan J,Weiss R,Smith J M G.Minimal length tree networks on the unit sphere[J].Annals of Operations Research,1991,33(7):501-535. |
| Click to display the text | |
| [21] | Cockayne E J.On fermat’s problems on the surface of a sphere[J].Mathematics Magazine,1972,45(4):216-219. |
| Click to display the text | |
| [22] | Weng J F.Steiner trees on curved surfaces[J].Graphs and Combinatorics,2001,17(2):353-363. |
| Click to display the text |
