目前为止,对不稳定燃烧问题的解决主要还是依赖于实验.但不稳定燃烧的发生通常是具有一定概率的,必须通过大量的重复实验才能确保可靠性.此外,限于观测、测量手段的欠缺以及不稳定燃烧现象的复杂性,使得很难通过地面实验对不稳定燃烧进行深入地认识.而且可用的实验结果多数由于保密的原因而不会被公开,这也影响了不稳定燃烧的研究进展.用于预测不稳定燃烧的模拟方法有很多,但从结果来看,能够为发动机设计提供的帮助十分有限.由于数学手段的有限和对物理现象认识的欠缺,大多数的分析方法[2 ,3]都做了简谐波假设及其他大量的简化,使得结果的精度不可预测.20世纪80年代后,计算机资源及计算流体力学(Computational Fluid Dynamics,CFD)的快速发展,使得直接对带反应流的原始Navier-Stokes方程进行求解成为可能.对雷诺平均的Navier-Stokes方程进行非定常求解(Unsteady Reynolds-Averaged Navier-Stokes equations,URANS),可以减少简化假设,但是需要建立关于雾化、蒸发、湍流、化学反应的精确模型,不稳定燃烧的发生机制就隐含在这些模型之中[4, 5].目前还难以实现对上述所有物理过程的精确描述,尤其是在动态压力扰动之下,它们与不稳定燃烧的反馈关系更是尚未深入研究的领域.分离涡模拟(Detached Eddy Simulation,DES)和大涡模拟(Large Eddy Simulation,LES)主要被用于求解与流体不稳定相关的不稳定燃烧中[6],由于采用的是跟URANS相同的物理化学子模型,在求解由雾化、蒸发、化学反应等过程导致的不稳定燃烧时,同样存在困难.尽管计算机性能已得到极大提高,CFD在进行三维计算时的资源和时间消耗仍是工程上难以接受的.此外,高频不稳定燃烧需要精确地求解声波运动,但目前用于求解不稳定燃烧的CFD算法多是二阶精度,在振荡不太大时,声波幅值与数值误差的量级相当,难以判断仿真结果中的不稳定是物理上存在的还是数值误差引发的.
本文旨在发展一套适合于工程应用的、可以快速预测发动机燃烧稳定性的仿真软件.软件采用高精度的计算气动声学(Computational Aeroacoustics,CAA)方法求解三维线性化的声学扰动方程(Acoustic Perturbation Equations,APEs),结合一定的火焰响应模型[7],对不稳定燃烧进行预测.这种方法不必进行简谐波假设,可以考虑非均匀平均场效应,计算效率很高,适合用于工程应用.针对Rocketdyne公司设计的变轨发动机(Orbit Maneuvering Engine,OME)[8]进行燃烧稳定性的数值模拟,对发动机中可能存在的危险振型进行预测.结果表明,预测的危险振型与实验相一致.
1 物理模型及计算方法1.1 OME发动机构型为了研究声腔的阻尼机制,Rocketdyne公司设计了直径约0.21m的OME类型的发动机,主要几何尺寸如图 1所示.
 |
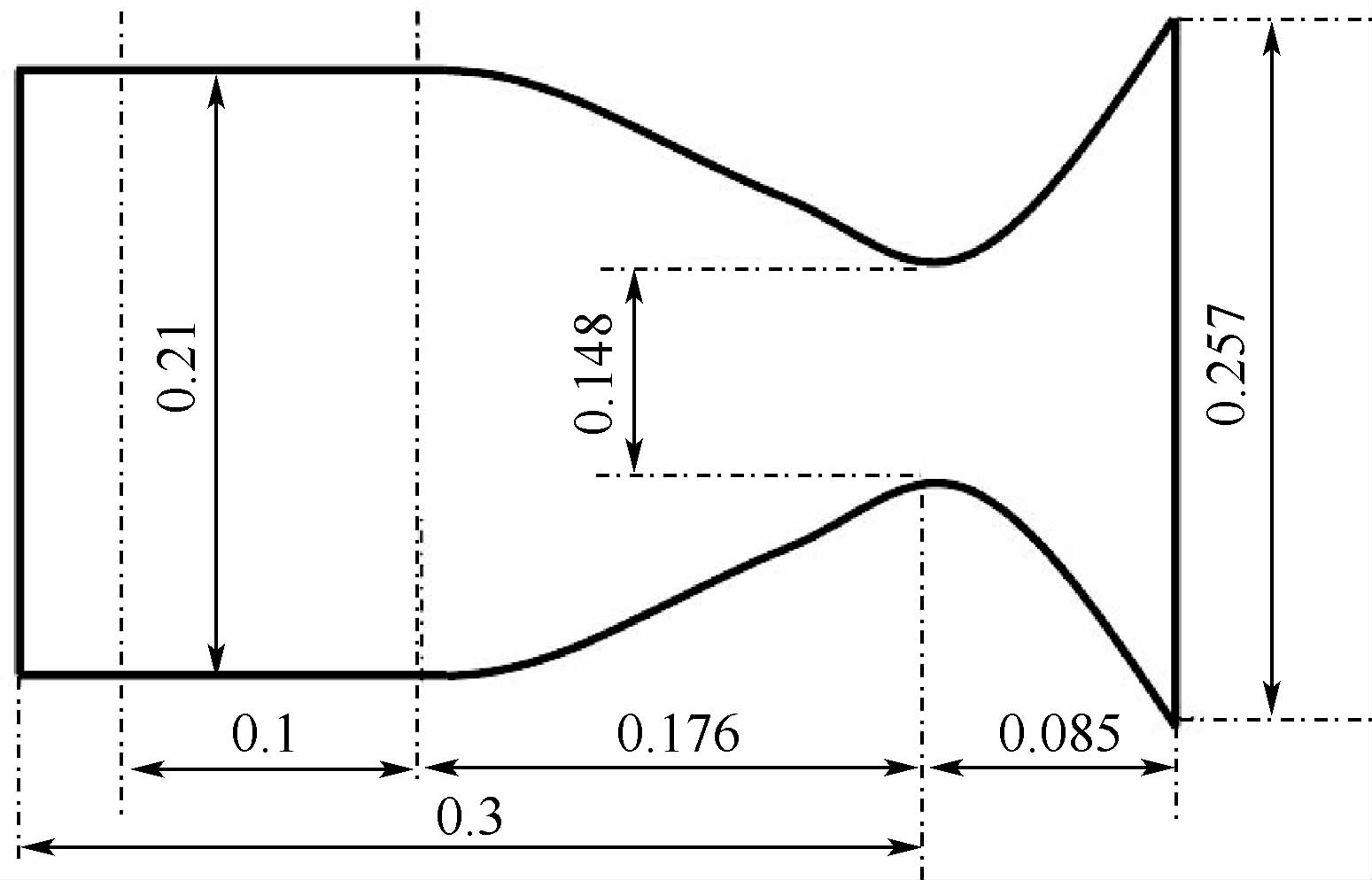| 图 1 OME的几何尺寸(单位：m)Fig. 1 Geometry size of OME (Unit：m) |
| 图选项 |
该发动机采用自燃推进剂(MMH/NTO),混合比1.65,室压0.862MPa.喷注面板采用286对互击式喷嘴,排布成10圈.发动机在进行地面实验时发现存在一阶切向及一阶径向、三阶切向不稳定振型,加入声腔后不稳定得到抑制.本文只研究无声腔时该发动机的稳定性.
1.2 基本方法高频不稳定燃烧属于热声不稳定,发生时的声振荡频率通常大于1kHz,对于尺寸较小的燃烧室,甚至可以达到上万.大部分液体火箭发动机是以扩散燃烧为主,而扩散主要受湍流影响,当高频不稳定燃烧发生时,声波的时间尺度远小于湍流的特征时间尺度,这对于大部分液体火箭发动机都是正确的.在模拟不稳定燃烧问题时,可以假定燃烧流动是稳态的,声波在准稳态环境中传播[9].即:q=q+q′,其中q为任意变量,“-”代表稳态燃烧流动量,“′”代表声场扰动量.
okes方程或其他模拟稳态燃烧流动的方法得到,扰动量通过求解声学扰动方程得到,燃烧和声之间的耦合通过源项实现.
1.3 控制方程声波控制方程采用线性化的声学扰动方程(APEs)[10],方程如式(1)所示:
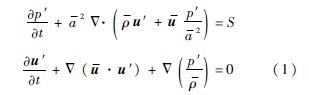
式中;p′为扰动压力;u为扰动速度矢量;u为稳态场速度矢量;ρ为稳态场密度;α为稳态场声速;t为时间;S代表源项.当模拟纯声学问题时,S为具有一定频率的声学振荡的叠加,当模拟热声不稳定问题时,S为
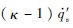，其中κ为比热比，
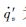为非定常的热释放项，反映了热源与声场之间的耦合.1.4 数值方法声学量通常比流动量小的多,求解时需要采用高精度的数值方法,否则只能通过加密网格的方式来保证精度.Laroche等[11]曾采用二阶迎风的ROE格式对燃烧室中的声波进行时域下的三维模拟,结果显示,每波长至少需要布置80个网格点才能保证精度,导致网格很密,计算量过大.
采用Tam和Webb提出的具有四阶精度的保持色散关系(Dispersion Relation Preserving,DRP)格式[12],具体形式为
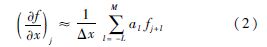
式中:f为原始变量；Δx为网格间距；al为DRP格式系数.对于采用的7点中心差分格式,L=M=3.
DRP格式除了保证低耗散外,还保证了极低的频散,使得格式的声波分辨率理论上甚至可以达到每波长4.4个网格左右.在模拟声波波动时,可以明显减少网格数量.
对于DRP格式不能分辨的高频短波部分,采用Gaitonde和Visbal[13]的高阶紧致滤波方法进行滤波,以保证数值稳定性,如式(3)所示:
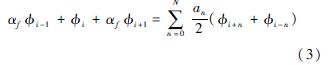
式中:φ为滤波后的变量;φ为滤波前的变量；α及a为滤波的格式系数.
内场采用7点六阶精度格式,靠近边界处采用单侧四阶格式,最边界一层网格不进行滤波.
时间格式采用四阶精度的Adam-Bashforth格式,如式(4)所示:
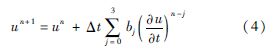
式中:un+1代表第n+1时间层的变量；un代表第n时间层的变量；Δt为时间步长;bj为时间格式的系数.
格式的系数由Tam和Webb进行了低频散的优化[12],计算中CFL数取为0.1.采用MPI平台进行4核并行计算,CPU为主频3.3GHz的i7处理器,进行40万步计算,即时间推进大约0.008s,需要7~8h.
1.5 网格尺度的选取OME在进行地面实验时发现3kHz和6.6kHz 的不稳定振型,因此,当前计算中只需保证10kHz以下波长范围的声波都能得到精确的模拟就足够了.DRP格式的声波分辨率大约为4.4,意味着对于所关心的10kHz以下的声波每波长分布的网格点数大于4.4即可.
根据稳态燃烧流场计算结果,燃烧室内平均声速约为1.13km/s,由于燃烧室内马赫数较低,忽略平均场流速对声波的影响,可估算出最大网格尺度约为26mm.当前采用的声场网格总数约为7万,最大网格尺度为9mm,可以保证足够的网格精度.
1.6 边界条件发动机的喷注面板及壁面均为4阶精度的声学固壁边界[14],其形式如式(5)所示:
式中:“-1”代表“影子网格点”;“0～5”则依次代表边界最外层到内场第6层网格.
对于圆筒形燃烧室,采用单块结构化网格进行计算是困难的,在进行多块计算时,块与块处对接面的参数传递是关键.Gaitonde和Visbal[13]采用重叠网格的方式解决该问题,并指出采用至少5个网格重叠时可以保证与单块计算相当的精度.由于本文采用的是7点DRP格式,为便于在边界处使用中心差分格式,采用7个网格重叠,如图 2所示,箭头指向代表信息传递的方向,其中第4点不传递信息.
 |
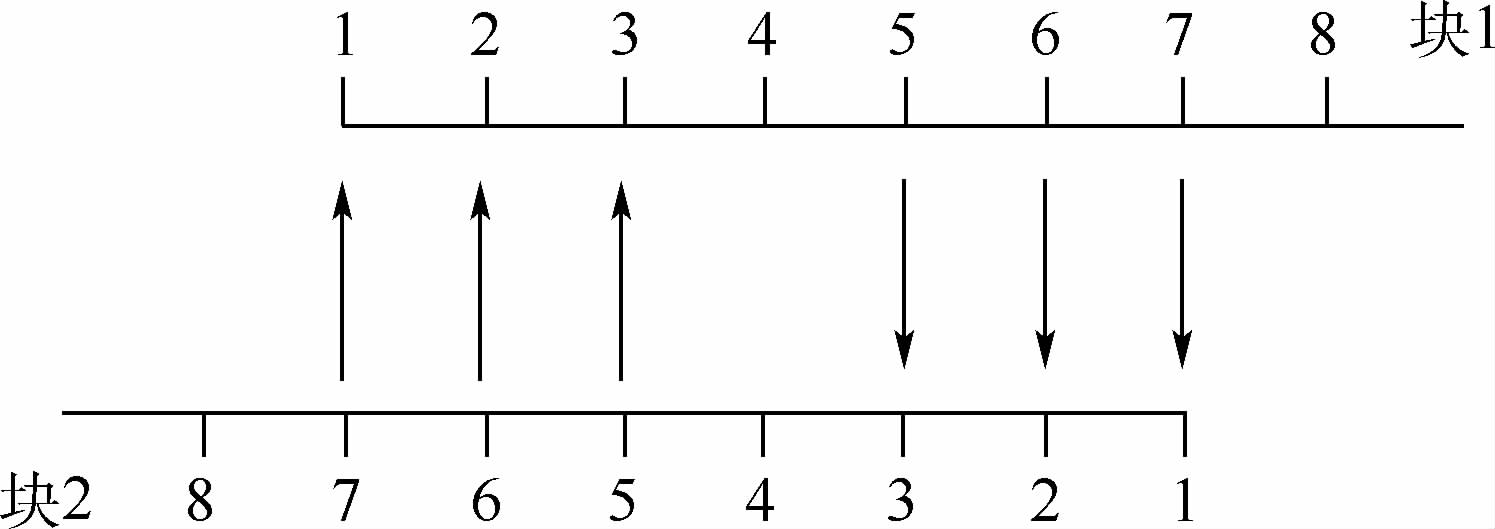| 图 2 7点网格重叠示意图Fig. 2 Schematic of mesh overlap with seven points |
| 图选项 |
由于喷管扩张段为超声速状态,下游的声波无法进入上游,使得在喷管喉部处马赫数达到1的位置,会自动形成一个声学上的封闭面,因此,计算域只取到喷管喉部稍偏下游的位置.在出口处,按超声速出口给定边界条件,所有参数直接外推.
1.7 初始扰动
在计算的初始时刻,需要给定初始扰动作为激发.形式如式(6)所示:
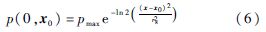
扰动为高斯形式分布的球形波,x0为扰动的中心位置,rs为高斯半径,pmax为扰动最大幅值.
对于激发式不稳定燃烧,初始扰动的幅值大小和位置是具有重要影响的,一方面幅值需要高于一定的阈值,另一方面初始扰动需要布置于燃烧敏感区,否则有可能无法激发不稳定.但对于当前的线性计算,模拟的是自发式的不稳定燃烧,初始扰动对结果影响不大,只是用来模拟燃烧室内存在的随机扰动,但还是要尽量避开重要振型的声压波节位置,以防不能激发某些重要振型.
本文所有计算中,初始扰动位置均位于发动机头部靠近壁面处,监测点位于初始扰动相反的位置,如图 3所示.由于求解的是线性化的方程,为满足线性化要求,初始扰动的最大幅值仅为1kPa.
 |
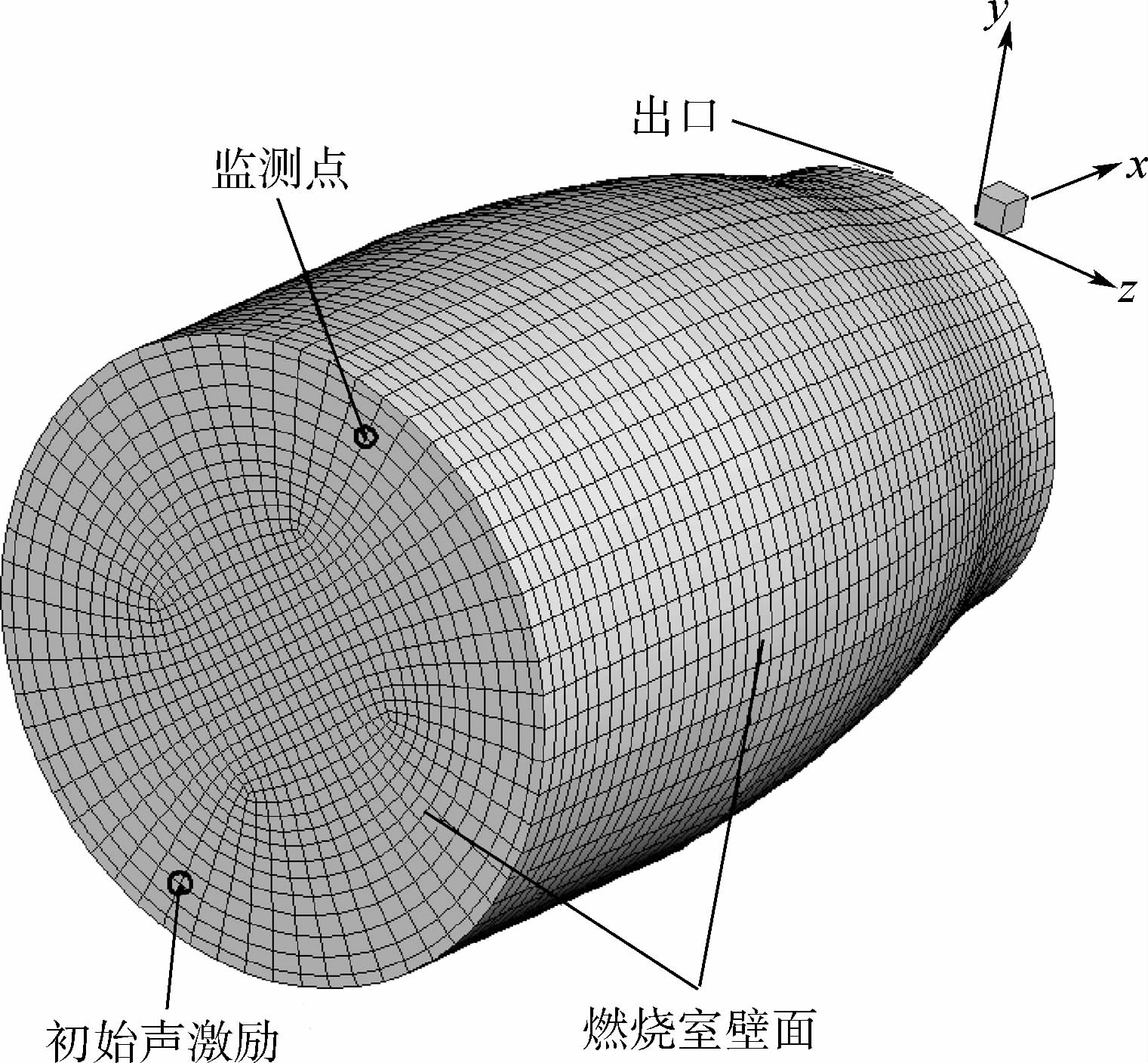| 图 3 初始声学激励及监测点位置图Fig. 3 Position schematic of initial acoustic excitation and monitoring point |
| 图选项 |
2 固有声学频率在进行OME的燃烧稳定性计算之前,需要先对其固有声学频率进行确定.Laudien等[15]曾给出冷试和热试情况下发动机的固有声学频率对比,发现二者的差别在于声速比,给出冷试下的固有声学频率后,根据热试下的平均声速,即可换算出热试下的固有声学频率.
求解固有声学频率时,需要将APEs的源S给定为一系列周期性声源的叠加,以模拟宽频随机声源.声源激发的频率范围为400~3500Hz,每5Hz作为一个间隔,具体形式为
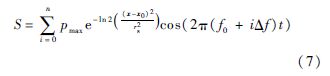
即通过一系列高斯形式分布的周期性压力振荡的叠加模拟声激励源,声源放置在发动机头部靠近壁面处的位置.发动机热试时,喉部处由于达到声速,会自动形成声学封闭端,因此,进行冷试下的固有声学频率计算时,假设喉部处为封闭的,设置为固壁边界.冷试状态下的平均流参数如表 1所示.
表 1 冷态条件下的平均参数Table 1 Mean parameters in cold condition
| 参数 | ρ/(kg·m-3) | c/(m·s-1) | γ | p/Pa |
| 数值 | 1.21 | 340 | 1.4 | 101325 |
表选项
对OME进行固有声学频率的数值计算,监测点的频谱分析如图 4所示.
 |
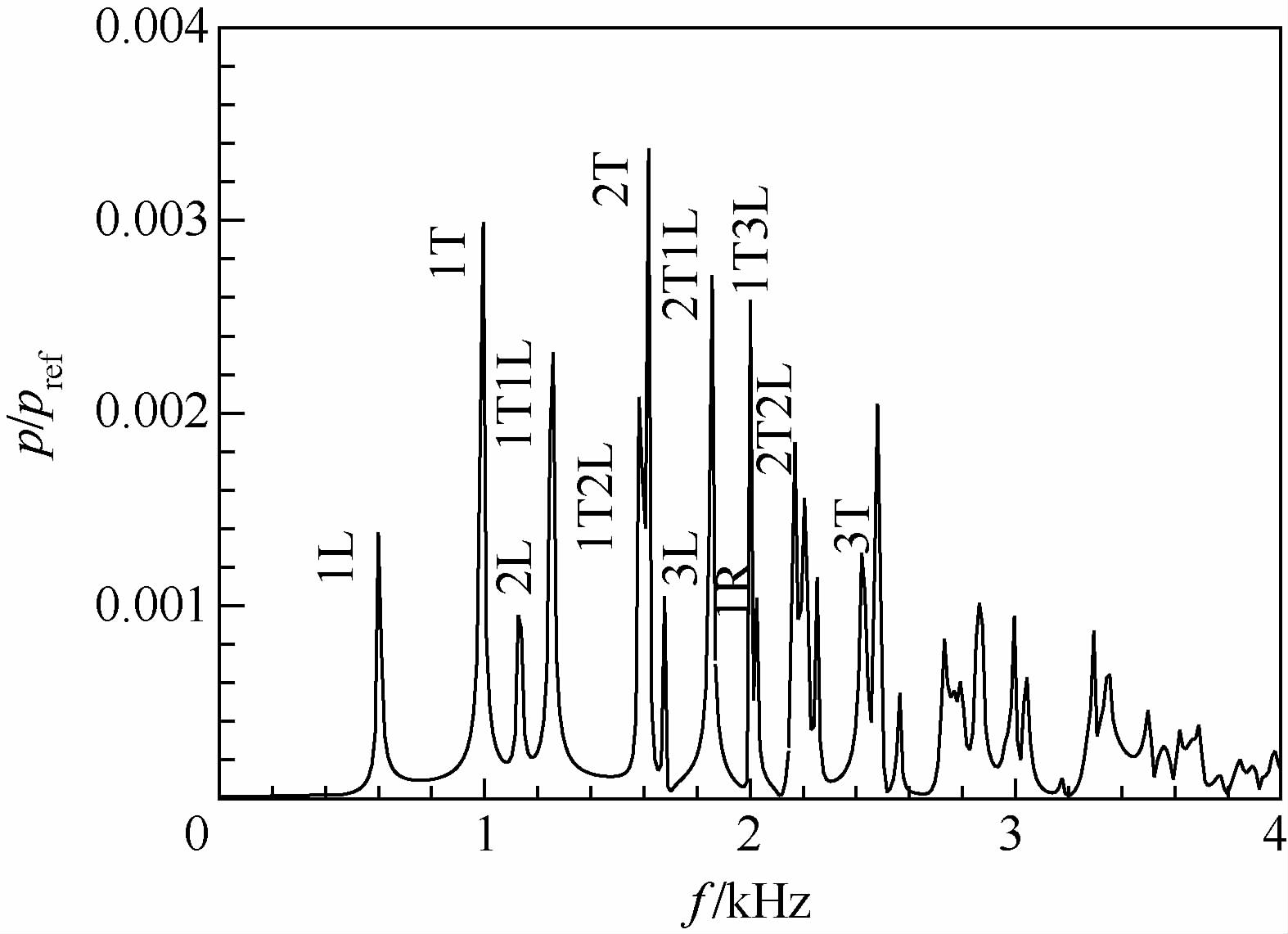| 1L,1L,1R-一阶切向、一阶纵向、一阶径向振型；1T1L-一阶切向和一节纵向的混合振型.图 4 固有频率的频谱分析Fig. 4 Frequency spectra analysis of natural frequencies |
| 图选项 |
图 4中标识出了OME的主要低阶固有频率.为验证数值结果精度,采用基于有限元法的商业软件Comsol求解Helmholtz方程,对OME进行声学固有频率的计算,并与数值结果进行对比,如表 2所示.
表 2 OME的固有频率Table 2 Natural frequencies of OME
| 模态 | 固有频率/Hz | 误差/% | |
| Comsol | 数值结果 | ||
| 1L | 605.0 | 596.3 | -1.4 |
| 1T | 988.1 | 992.4 | 0.4 |
| 2L | 1133.7 | 1134.7 | 0.1 |
| 1T1L | 1253.8 | 1258.5 | 0.4 |
| 2T | 1614.2 | 1623.7 | 0.6 |
| 3L | 1677.5 | 1679.4 | 0.1 |
| 1R | 2018.4 | 2020.6 | 0.1 |
| 3T | 2205.6 | 2203.9 | -0.1 |
表选项
结果显示,数值结果与Comsol结果相差极小,误差基本都在1%以下,证明了本文所用计算代码的精度及有效性.
3 燃烧稳定性计算结果3.1 稳态燃烧流场平均参数对OME进行燃烧稳定性计算前,先通过求解两相燃烧流动的Navier-Stokes方程获得平均流参数,部分结果如图 5所示.其中,气相采用欧拉方法,液相采用Lagrange离散相模型描述,气液相互作用通过气相方程的源项实现.
 |
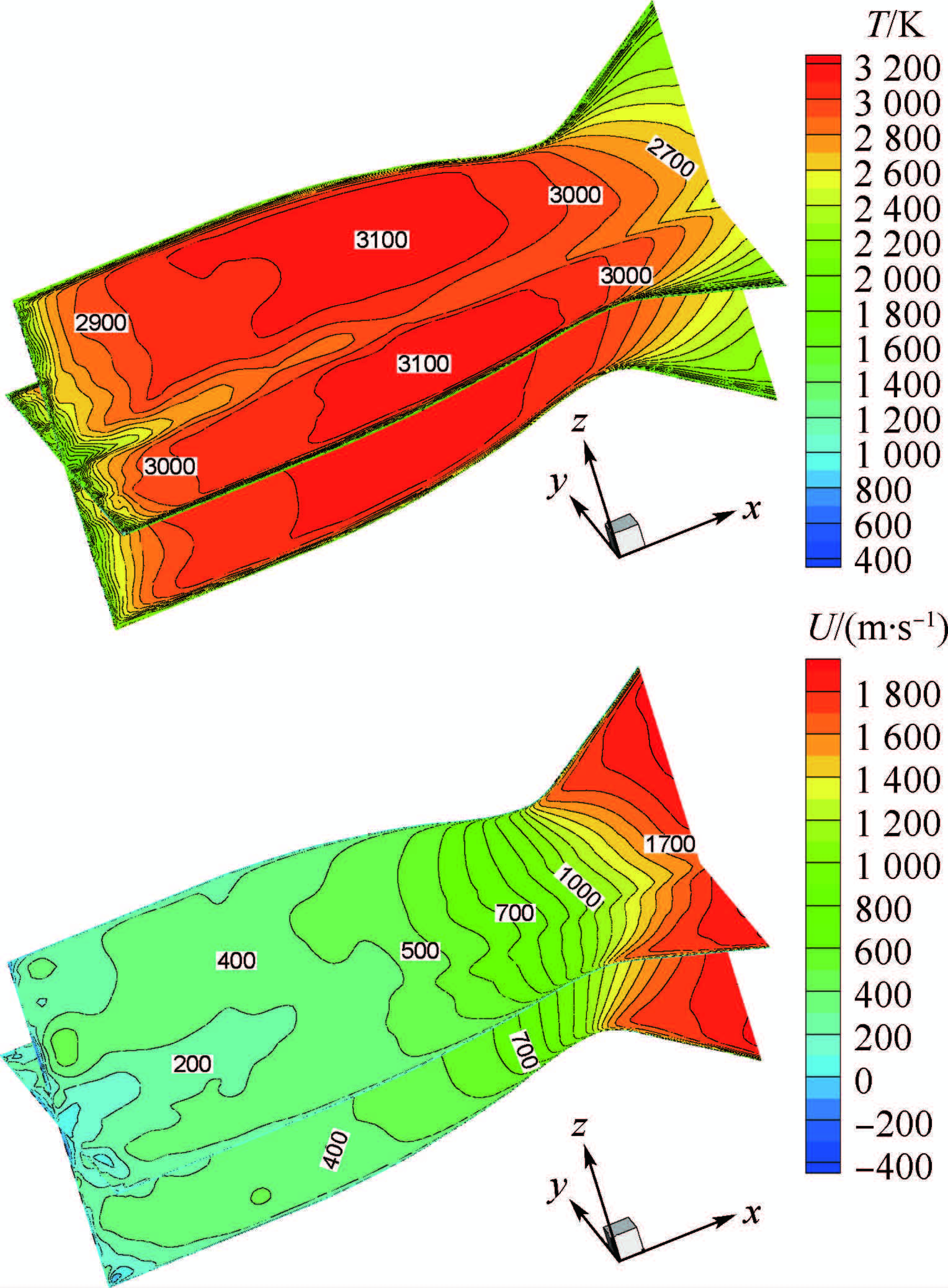| 图 5 温度和轴向速度等值线图Fig. 5 Contour maps of temperature and axis velocity |
| 图选项 |
流场网格与声场网格不同,需要将流场量插值到声场网格上.由于声场计算域只需取到喉部之前的亚声速区,而流场结果显示温度等参数在喉部之前梯度较小,为简化计算,仅考虑速度的非均匀性,而假设压力、温度等参数为一常数.稳态燃烧流场的平均参数值如表 3所示.
表 3 燃烧流场的平均参数Table 3 Mean parameters of combustion flow field
| 参数 | ρ/(kg·m-3) | T/K | c/(m·s-1) | γ | p/MPa |
| 数值 | 0.8 | 3050 | 1130 | 1.19 | 0.84 |
表选项
研究人员认为OME在地面实验时存在1T、1R和3T不稳定振型.冷态固有频率的计算结果里,这3个振型的频率分别为992.4,2020.6,2203.9Hz.根据声速比3.324,热试状态下的1T、1R和3T的频率应为3298.7,6716.5,7325.8Hz.
3.2 热声源项进行不稳定燃烧计算时,需要给定燃烧和声之间的耦合源项.采用Crocco的压力时滞模型,其时域形式为
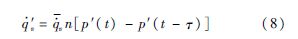
模型中的两个参变量:相互作用指数n和时滞τ,分别代表燃烧和声之间耦合的强弱、热释放波动和声波波动之间的相位差.根据发动机的喷注器类型及相关喷注参数即可给出二者值的范围[16].自燃推进剂的时滞计算公式为
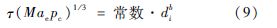
式中:Mae为喷管进口马赫数;pc为燃烧室压力;di为射流直径;b为常数.对于OME采用的两股互击式喷嘴,时滞的范围为
τ=0.0889~0.1968ms
当前计算中,相互作用指数范围为
n=0.10~0.48
根据相互作用指数和时滞的范围,对相互作用指数分别为0.1,0.16,0.2,0.3,0.4,0.48和时滞分别为0.0889,0.11,0.13,0.15,0.17,0.1968ms 时的工况进行了燃烧稳定性的仿真计算.所有结果中的压力均通过平均流的压力值进行了无量纲化.
3.3 相互作用指数对结果的影响相互作用指数反映了燃烧和声之间的耦合强度,值越大,意味着声波能从燃烧中获得的激励越大,不稳定燃烧越容易发生.图 6为时滞0.17ms、相互作用指数分别为0.1和0.16时压力的时间历程.当相互作用指数为0.1时,压力曲线呈现衰减,发动机是稳定的,而为0.16时,压力幅值被放大,此时不稳定燃烧得到激发.也就是说当时滞为0.17ms时,令发动机处于稳定性边界的相互作用指数值介于0.1和0.16之间.对相互作用指数为0.16的压力曲线进行频谱分析,如图 7所示,存在唯一的频率3.2kHz,即一阶切向振型.
 |
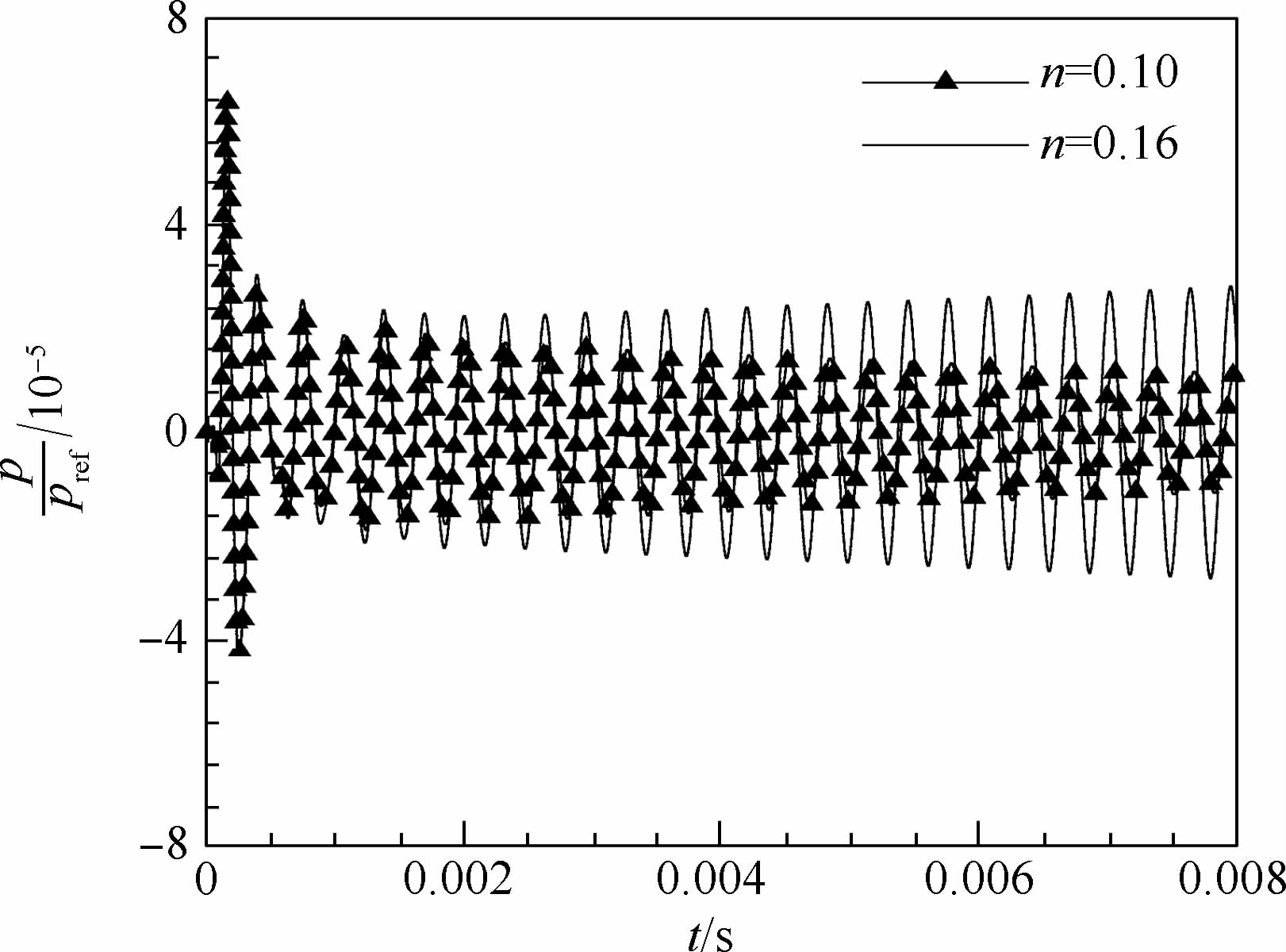| 图 6 不同相互作用指数下的压力时间发展历程Fig. 6 Temporal development of pressure with different values of interaction index |
| 图选项 |
 |
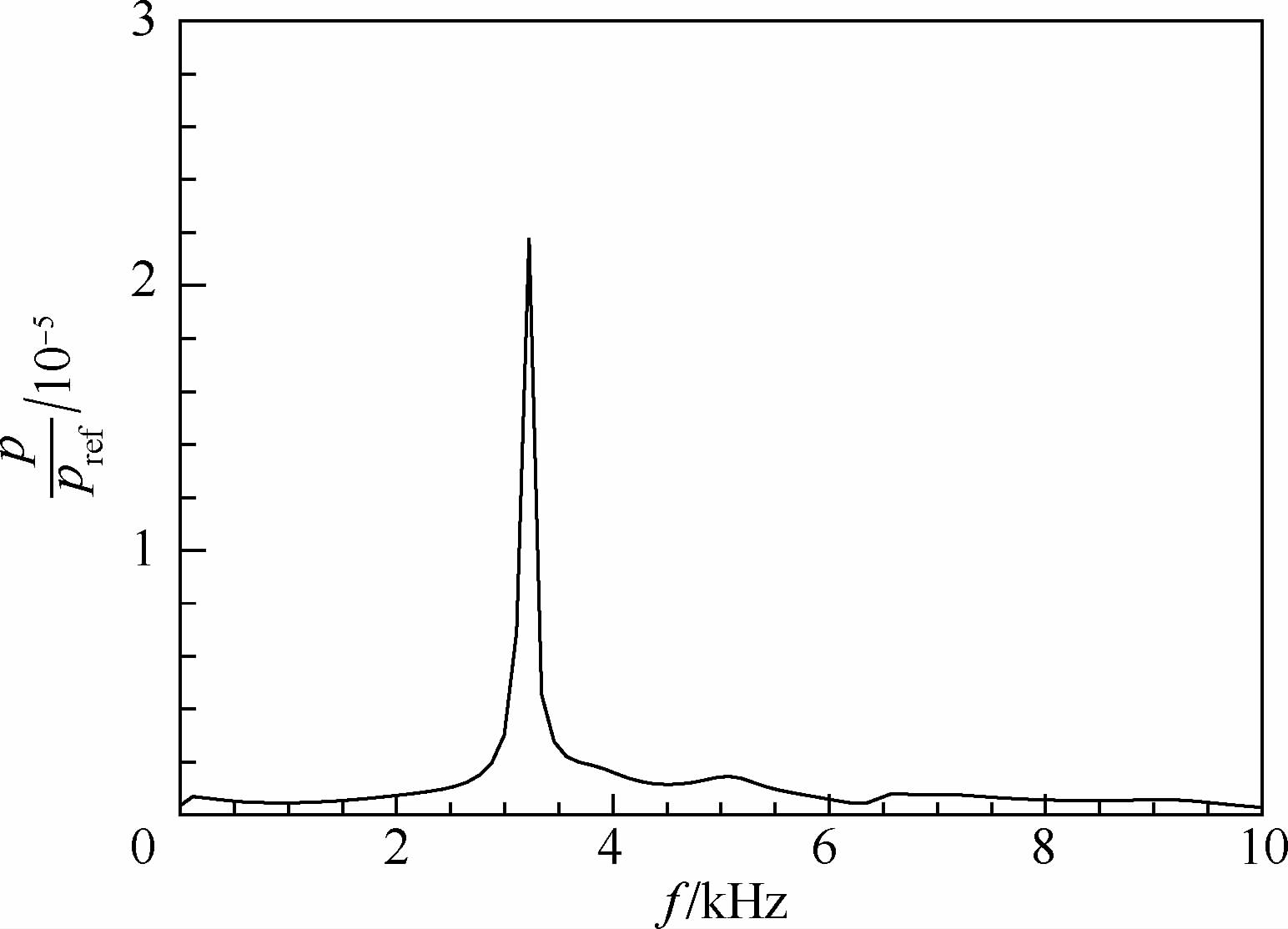| 图 7 n=0.16时的频谱分析Fig. 7 Frequency spectra analysis (n=0.16) |
| 图选项 |
3.4 时滞对结果的影响时滞反映了热释放波动和声波波动之间的相位差,不同的相位差意味着激发的不稳定振型可能不同.图 8为相互作用指数为0.4时,时滞分别为0.0889和0.13ms时的压力时间历程.可见二者相位不一致,且时滞为0.0889ms的压力曲线明显存在不止一个振型.对二者均进行频谱分析,如图 9所示.时滞为0.13ms时,仅存在一个3.2kHz的一阶切向振型;而时滞为0.0889ms时,同时存在3.2kHz的一阶切向振型和6670Hz的一阶径向振型,其中一阶径向振型更为危险.
 |
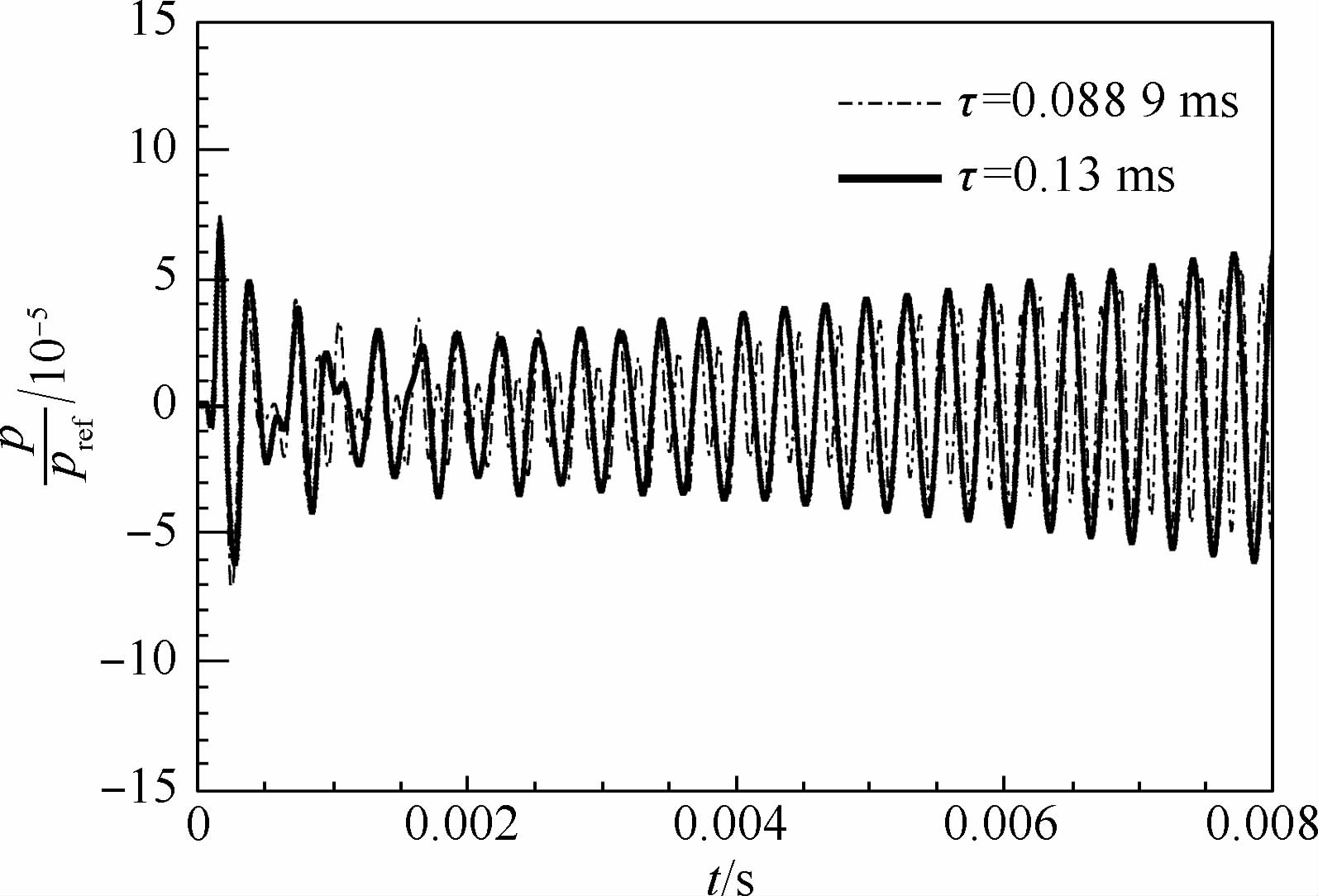| 图 8 压力的时间发展历程(τ=0.0889,0.13ms)Fig. 8 Temporal development of pressure (τ=0.0889,0.13ms) |
| 图选项 |
 |
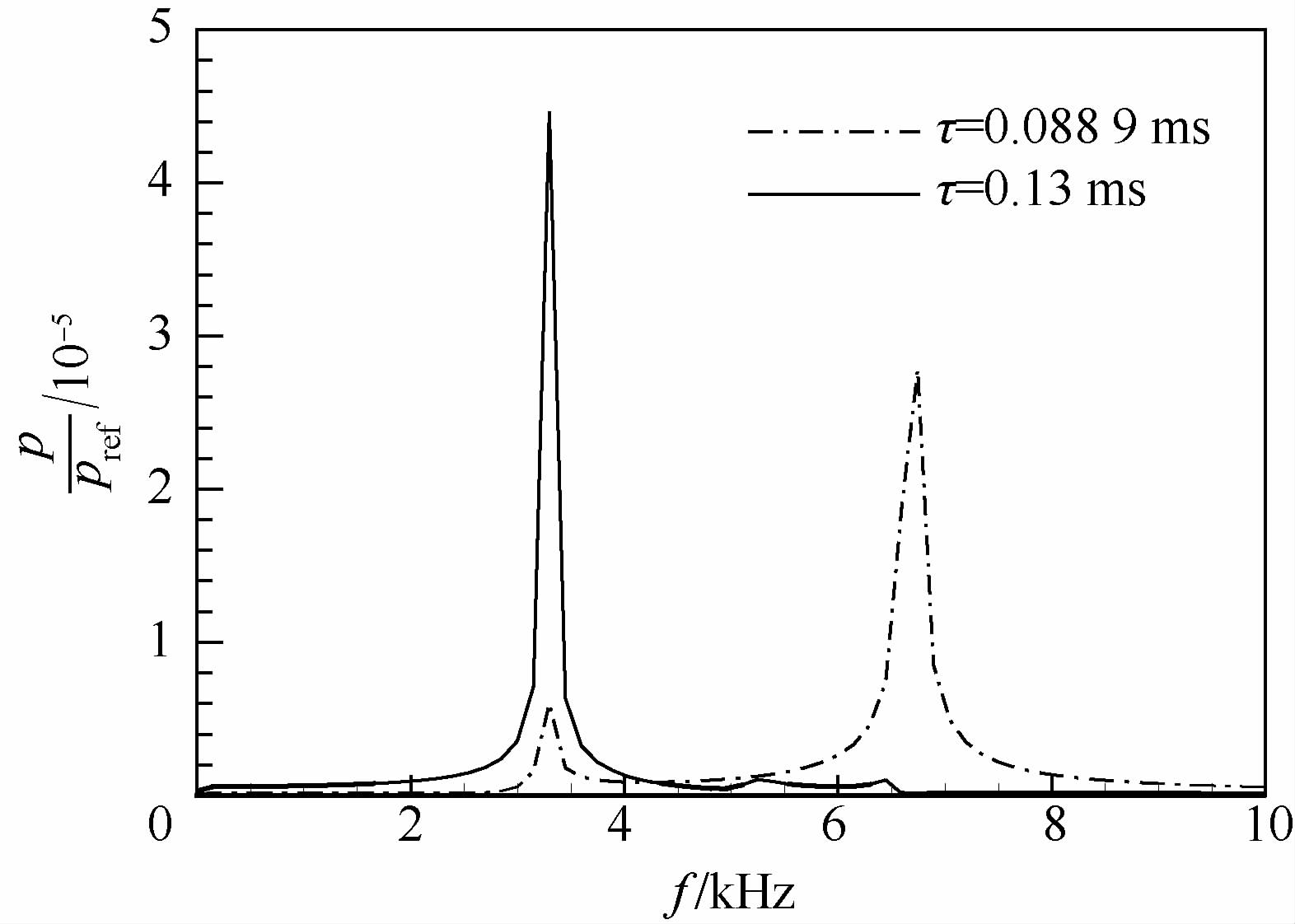| 图 9 频谱分析(τ=0.0889,0.13ms)Fig. 9 Frequency spectra analysis (τ=0.0889,0.13ms) |
| 图选项 |
OME内出现一阶切向或一阶径向不稳定时的声场压力云图,分别如图 10和图 11所示.
 |
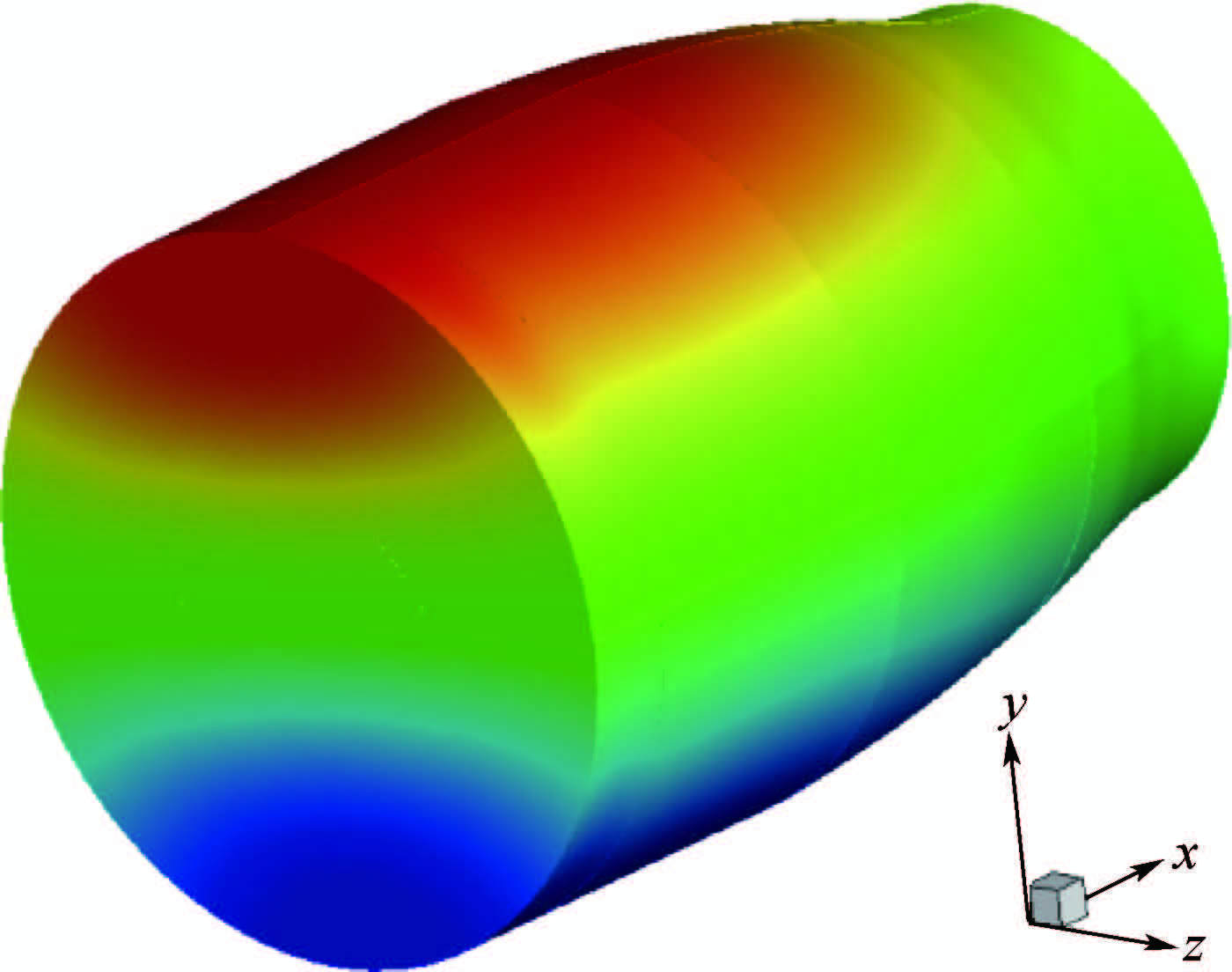| 图 10 1T的声压分布Fig. 10 Acoustic pressure distributions of 1T |
| 图选项 |
 |
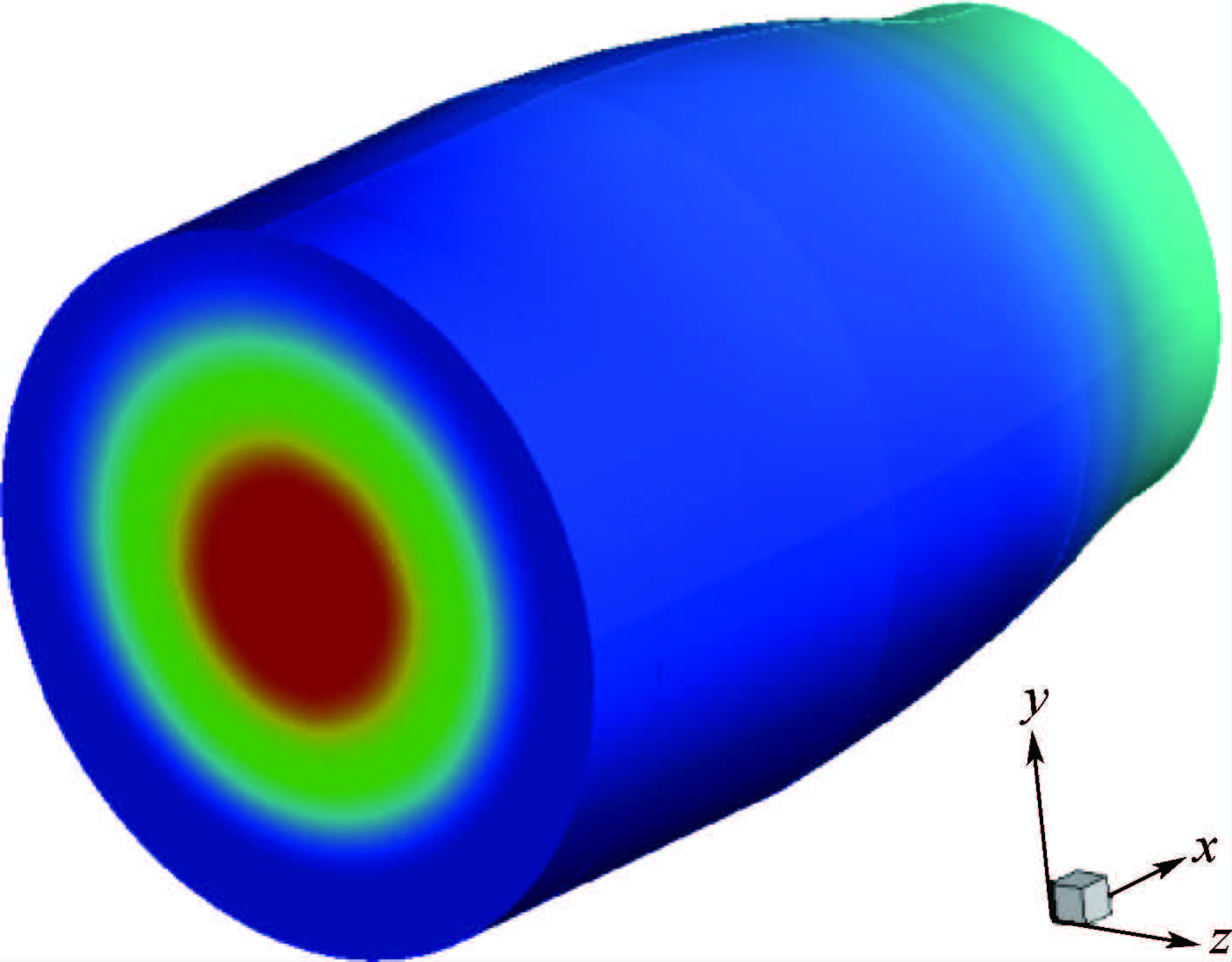| 图 11 1R的声压分布Fig. 11 Acoustic pressure distributions of 1R |
| 图选项 |
由时滞引起的热释放波动和声波波动之间的相位差,一方面决定了将要激发的不稳定振型,另一方面也决定了二者之间的耦合强度.耦合的强弱可以通过瑞利积分来表示:
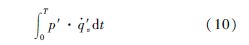
当瑞利积分符号为正时,代表热释放和声波处于同相位关系,由热释放传入声场的能量将可能会使声波幅值得到增长;当瑞利积分符号为负时,代表由热释放传入声场的能量将会使声波幅值变得衰减.瑞利积分式的符号为正,是不稳定燃烧发生的必要条件.
将Crocco的压力时滞模型代入瑞利积分式,并假设声波为正弦形式,则可推导得到使瑞利积分值最大,即热释放和声波同相关系最好时,时滞和频率间的关系[7]为
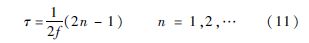
n为大于1的整数.式(11)意味着,当时滞处于某一范围内时,频率为f的某一振型将被激发,而当时滞与频率的关系满足式(11)时,该振型的幅值增长速度应为最快.
但是,瑞利积分只是一个理想化的简单的理论分析,它仅仅是不稳定燃烧发生的必要条件,而非充分条件.对于任何实际的燃烧系统,除了瑞利积分中所包含的热释放和声波间的相位关系外,还存在着各种阻尼项,如:黏性耗散、平均流速度引起的对流效应、平均场的非均匀效应、喷管出口耗散等.这些可能存在的项都会改变时滞和频率之间的关系,使得二者之间可能不再存在这种简单的显式关系.
当相互作用指数为0.4,时滞分别取为0.13,0.15,0.17,0.1968,0.21ms(0.21ms是为了说明问题而加入的)时,数值计算得到的压力时间历程如图 12所示.从图中可以看出,当时滞为0.1968ms 时,压力幅值增长最快.可以大致判断出,对应于压力幅值增长最快的时滞值,应该是位于0.19ms左右.对这5条压力曲线做频谱分析,结果如图 13所示.可知,这5个时滞值都将激发3.2kHz的一阶切向不稳定振型.对于一阶切向振型,通过瑞利积分进行分析,对应于压力幅值增长最快的时滞值应为0.15625ms,显然跟数值计算的结果存在差别.在当前的数值计算中,由于考虑了轴向速度的分布,因此影响结果的主要是平均流速度引起的对流效应、平均场轴向速度的非均匀效应及喷管出口处的耗散.燃烧室壁及喷注面板都采用了刚性壁边界,不存在耗散.黏性耗散在当前计算中未考虑.
 |
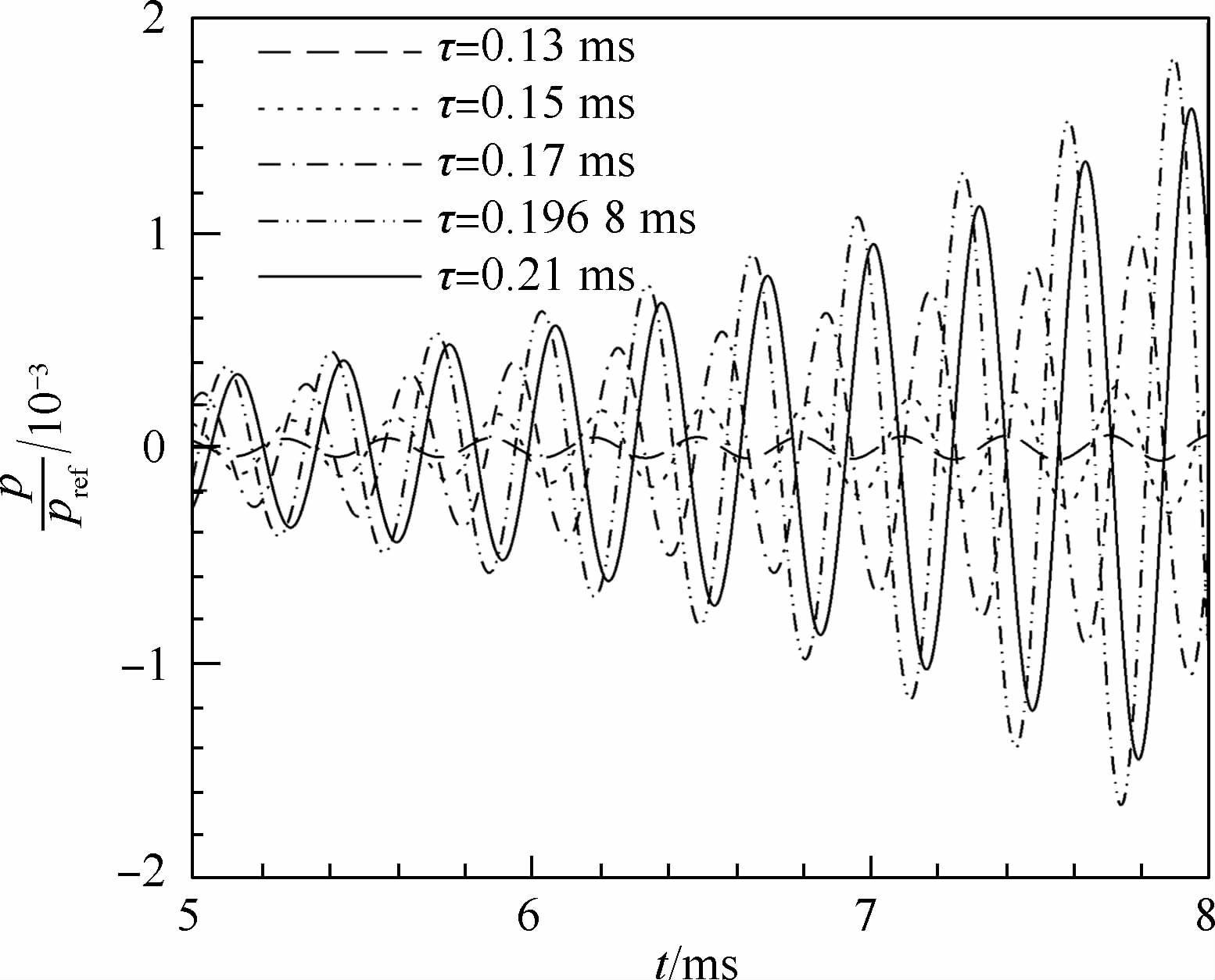| 图 12 不同时滞下的压力时间发展历程Fig. 12 Temporal development of pressure with different values of time lag |
| 图选项 |
 |
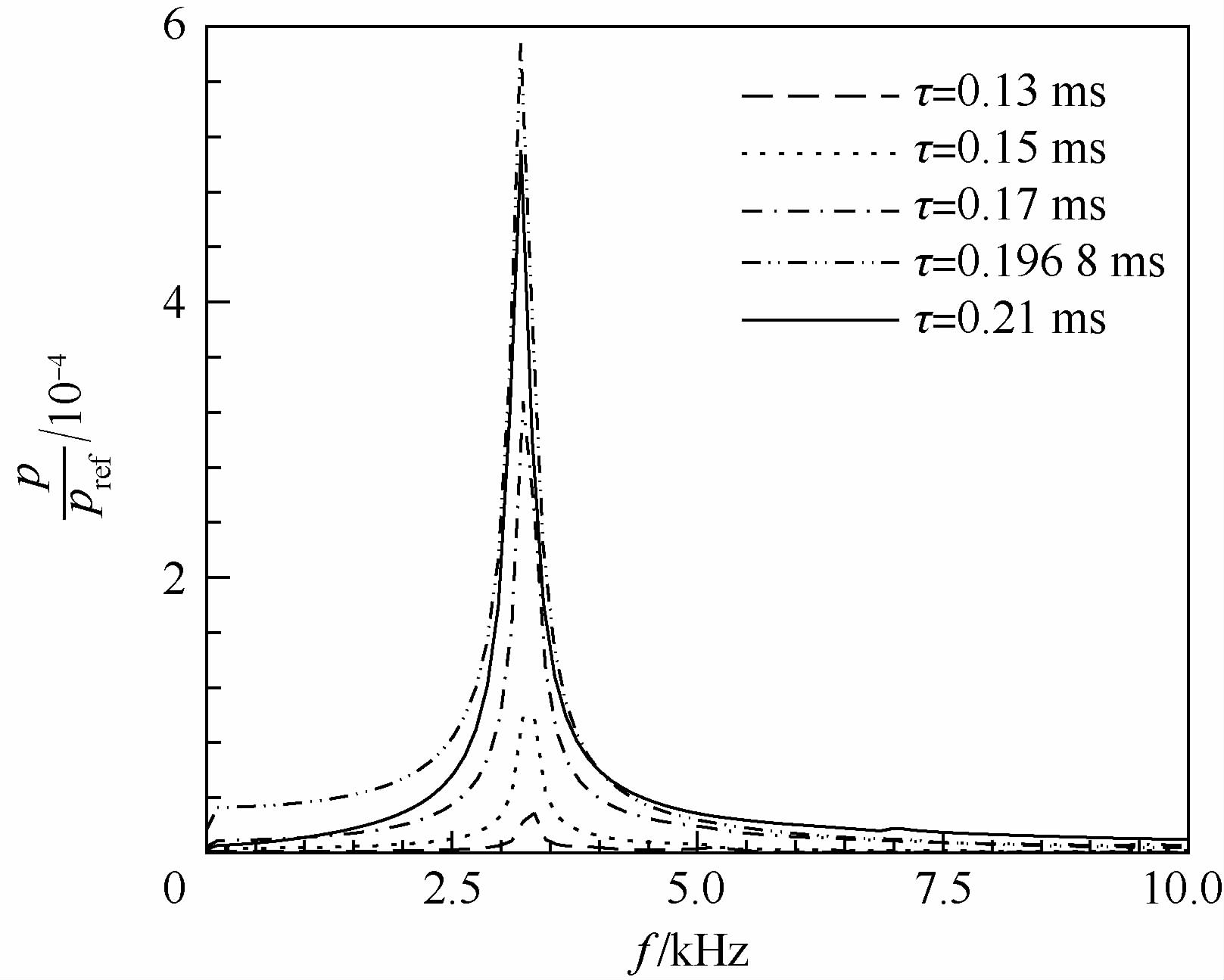| 图 13 不同时滞下的频谱分析Fig. 13 Frequency spectra analysis with different values of time lag |
| 图选项 |
3.5 稳定性极限图对给定的相互作用指数和时滞的参数组合进行燃烧稳定性的仿真计算,给出OME的燃烧稳定性极限图,如图 14所示.
 |
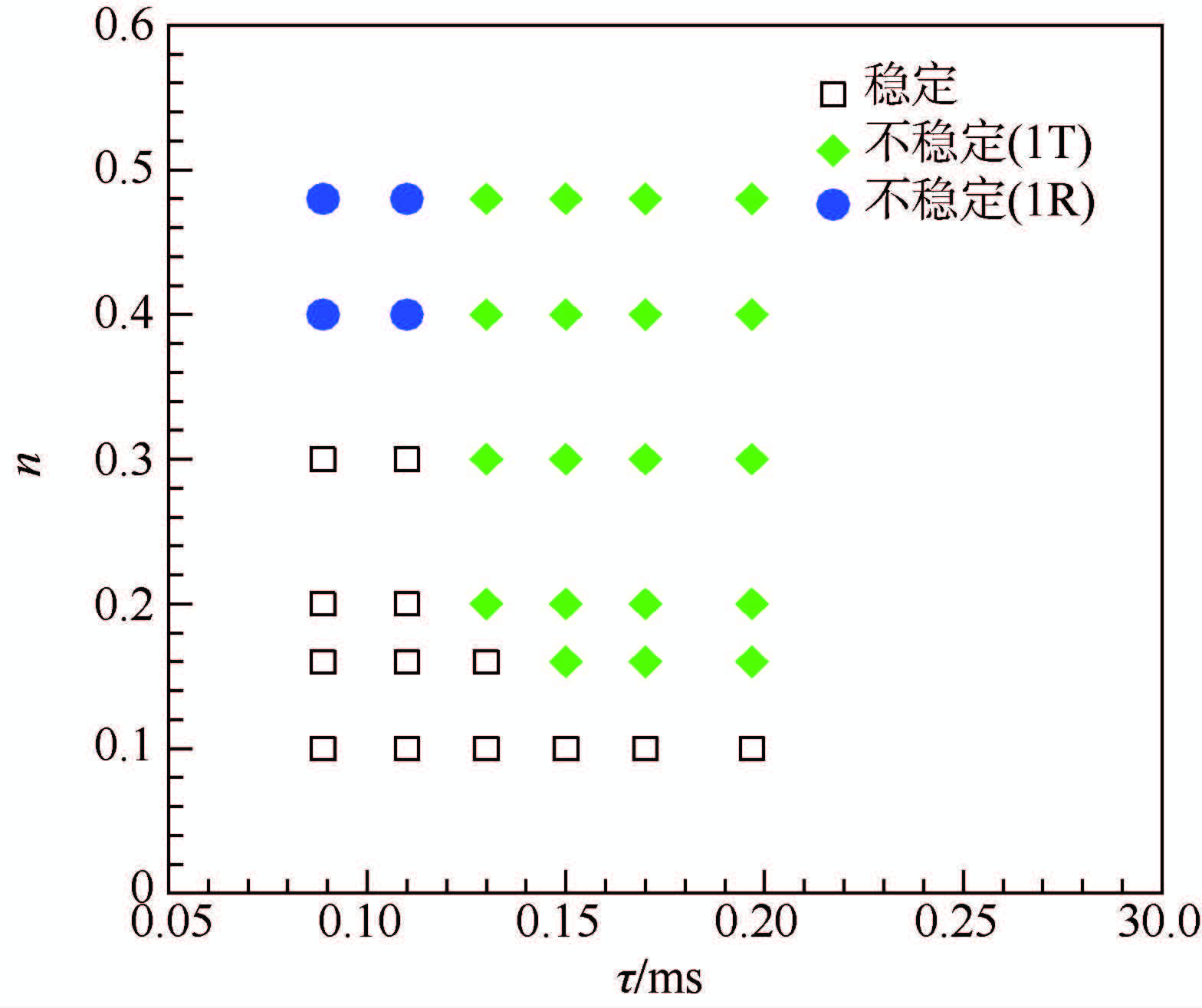| 图 14 OME的稳定性极限图Fig. 14 Stability limit map of OME |
| 图选项 |
稳定性极限图反映了以相互作用指数和时滞为变量的OME的燃烧稳定性情况,给出了OME中最危险的振型,并可以判断OME的稳定性边界.由稳定性极限图可知,在相互作用指数为0.1时,OME是稳定的.当相互作用指数增加至0.16时,OME中可能出现一阶切向不稳定振型.一阶径向不稳定在相互作用指数达到0.4时,才可能出现,意味着其激发需要较高的激励能量.
OME的地面实验中,曾出现3kHz和6.6kHz的不稳定振型,研究人员认为3kHz为一阶切向振型,而6.6kHz为一阶径向或三阶切向振型.仿真计算结果显示,OME在工作时可能出现3.2Hz的一阶切向或6.67Hz的一阶径向不稳定振型,并未发现三阶切向振型的存在.仿真计算的振型频率比实验值偏高,主要是因为燃烧流场参数平均化处理导致的燃烧室内的声速值与真实情况有所偏差.
仿真结果显示,OME在相互作用指数大于0.1时就可能出现不稳定了.实际上,对于自燃推进剂发动机,一般在相互作用指数大于0.6时才会出现不稳定[16].在Pieringer等[7]对Aestus发动机的仿真中,激发不稳定需要的相互作用指数值最低0.16,她指出这是由于计算中仅考虑了由喷管提供的阻尼,对于其他阻尼机制,如黏性耗散,没有考虑,使得激发不稳定所需要的激励变低.在Mitchell等[17]进行的仿真中,仅考虑喷管阻尼时,激发不稳定所需要的相互作用指数值同样偏低.
4 结 论采用计算气动声学方法,对OME进行了高频不稳定燃烧的时域数值仿真,得到如下结论:
1) 计算气动声学方法用于计算发动机的固有声学频率时,具有很高的精度,可以识别几乎所有的低阶振型.结合冷态和热试时的声速比,可帮助识别热试下的不稳定振型.
2) 计算气动声学方法结合Crocco的压力时滞模型,可以预测发动机的高频燃烧稳定性,给出稳定性极限图.对于OME,在时滞的取值范围内,可能激发3.2kHz的一阶切向和6.67kHz的一阶径向不稳定振型.由于一阶径向振型的激发需要更高的激励能量,一阶切向振型相对更加危险.数值计算预测出的不稳定振型与地面试车捕捉到的不稳定振型一致,但是不稳定振型的频率值有偏差,这种偏差主要来自于对稳态燃烧流场所做的平均化处理.相比于平均化所带来的计算便利,这种较小的偏差在工程上是可以接受的.
3) 除燃烧热释放和声波之间的相位关系外,数值计算还包含了平均流速度引起的对流效应、平均场速度的非均匀效应及喷管出口处的耗散,使得得到的最容易激发一阶切向振型的时滞值与由瑞利积分推导得到的理论时滞值有差别.
本文所用方法不需要做大量的简化假设,可以考虑平均流的非均匀效应,且通过引入压力时滞模型又可以避开对物理化学子过程建模的需求,计算量较小,非常适合于工程上用来快速判别发动机的危险振型,为设计提供帮助.
参考文献
| [1] | 刘国球.液体火箭发动机原理[M].北京: 宇航出版社, 1993: 251-252.Liu G Q.The Princple of liquid rocket engine[M].Beijing: Astronautic Publishing House, 1993: 251-252(in Chinese). |
| [2] | Zinn B T. Pulsating combustion, advanced combustion methods[M].London: Academic Press, 1986: 113-181. |
| [3] | Culick F E C.A note on Rayleigh's criterion[J].Combustion Science and Technology, 1987, 56(4-6): 159-166. |
| Click to display the text | |
| [4] | Habiballah M, Lourme D, Pit F.A comprehensive model for combustion stability studies applied to the Ariane Viking engine, AIAA-1988-0086[R].Reston: AIAA, 1988: 1-7. |
| [5] | 尕永婧, 张会强, 王希麟.隔板对燃烧室压力高频自激振荡的抑制作用[J].清华大学学报, 2012, 52(7): 1007-1012. Ga Y J, Zhang H Q, Wang X L.Effects of baffles on self-triggered high frequency pressure oscillations in a thrust chamber[J].Journal of Tsinghua University, 2012, 52(7): 1007-1012(in Chinese). |
| Cited By in Cnki | |
| [6] | Matthew E H, William E A, Charles L M.Analysis of self-excited combustion instabilities using two-and three-dimensional simulations[J].Journal of Propulsion and Power, 2013, 29(2): 396-409. |
| Click to display the text | |
| [7] | Pieringer J, Sattelmayer T, Fassl F.Simulation of combustion instabilities in liquid rocket engines with acoustic perturbation equations [J].Journal of Propulsion and Power, 2009, 25(5): 1020-1031. |
| Click to display the text | |
| [8] | Oberger C L, Hines W S, Falk A Y.High-temperature earth-storable propellant acoustic cavity technology, NASA N75-19460[R].California: Rocketdyne Division, 1974: 1-82. |
| [9] | Kim J S. Effects of turbulence on linear acoustic instability: Spatial inhomogeneity[C]//Progress in Aeronautics and Astronautics.Reston: AIAA, 1995, 169: 431-454. |
| [10] | Ewert R, Schr?der W.Acoustic perturbation equations based on flow decomposition via source filtering[J].Journal of Computational Physics, 2003, 188(2): 365-398. |
| Click to display the text | |
| [11] | Laroche E, Habiballah M, Kuentzmann P.Numerical analysis of liquid rocket combustion instability: Preliminary 3D acoustic calculations[C]//35th Intersociety Energy Conversion Engineering Conference and Exhibit. Reston: AIAA, 2000: 1-9. |
| [12] | Tam C K W, Webb J C.Dispersion-relation-preserving finite difference schemes for computational acoustics[J].Journal of Computational Physics, 1993, 107(2): 262-281. |
| Click to display the text | |
| [13] | Gaitonde D V, Visbal M R.Padé-type higher-order boundary filters for the Navier-Stoke equations[J].AIAA Journal, 2000, 38(11): 2103-2112. |
| Click to display the text | |
| [14] | Tam C K W, Dong Z.Wall boundary conditions for high-order finite-difference schemes in computational aeroacoustics[J].Theoretical and Computional Fluid Dynamics, 1994, 6(5-6): 303-322. |
| Click to display the text | |
| [15] | Laudien E, Pongratz R, Pierro R, et al.Experimental procedures aiding the design of acoustic cavities[C]//Progress in Aeronautics and Astronautics.Reston: AIAA, 1995, 169: 377-402. |
| [16] | Harrje D T, Reardon F H.Liquid rocket combustion instabilities, NASA SP-194[R].Reston: AIAA, 1972. |
| [17] | Milano D, Kirkpatrick A T, Quinlan J M, et al.Computation of acoustic oscillations and combustion stability in a rocket engine with combined hub/blade baffles, AIAA-2009-4866[R].Reston: AIAA, 2009. |
