, 任玉, 关展旭, 王晶 东北大学 信息科学与工程学院, 辽宁 沈阳 110819
收稿日期：2020-01-04
基金项目：国家重点研发计划项目(2019YFE0105000); 矿冶过程自动控制技术国家(北京市)重点实验室开放课题(BGRIMM-KZSKL-2018-09)。
作者简介：王姝(1979-)，女，辽宁沈阳人，东北大学副教授。
摘要：D-S证据理论可应用于多源数据融合领域, 但在处理高度冲突的证据时, 可能会出现反直觉的结果.为解决这一问题, 本文提出了差异信息量的概念及融合方法.首先, 通过信息熵表明证据的相对重要性, 采用散度获取证据可信度.然后利用证据可信度优化证据差异度以得到差异信息量, 经过计算获取数据的最终权重, 并将其作为D-S证据理论中的基本概率分配进行决策.在处理冲突证据、一致证据及不同数量证据等方面的数据融合问题时与其他方法对比, 所提方法收敛更快, 准确度更高.故障诊断的应用实例表明, 所提方法的不确定性更小, 优于现存的其他方法.
关键词：差异信息量D-S证据理论多源数据信息融合决策
Multi-source Data Fusion Method Based on Difference Information
WANG Shu
, REN Yu, GUAN Zhan-xu, WANG Jing School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Shu, E-mail: wangshu@mail.neu.edu.cn.
Abstract: D-S evidence theory can be applied to the field of multi-source data fusion. However, counter-intuitive results may come out when handing highly conflicting evidences. In order to solve this problem, a modified fusion method with the concept of difference information(DI)was proposed. First, information entropy indicated the relative importance of evidence, and divergence was used to obtain the credibility of evidence. Then, the evidence difference was optimized by the credibility of the evidence to obtain difference information(DI). The final weight of the calculated data was used as the basic probability distribution in D-S evidence theory for decision-making. Compared with other methods in dealing with conflicting evidence, consistent evidence, and different amounts of evidence, the proposed method converges faster and has higher accuracy. The application examples of fault diagnosis show that the proposed method has less uncertainty and is better than other existing methods.
Key words: difference information(DI)D-S evidence theorymulti-source datainformation fusiondecision-making
多源数据融合技术在实际应用中发挥着重要作用, 如故障诊断、图像处理、贝叶斯网络的建模问题等[1-4].由于目标的复杂性, 由单个数据源采集到的数据在决策过程中是远远不够的.多源数据融合是对获得的信息进行分析处理以得到正确决策.这些数据需要进行数据融合处理, 充分利用数据之间的相关性及独特性, 提高决策的精度.然而, 在实际应用中, 不精确和不确定性是不可避免的.目前, 为了解决多源信息的融合问题提出了一些研究方法和理论, Jiang等将模糊证据应用在多准则决策中[5], Wen等改进了D-S证据理论中的组合规则[6], Zhang等结合D-S证据理论与Z数对不确定性环境进行评估[7], Xiao基于D数和信息熵提出模糊系统的多准则决策方法[8], Seiti等提出与模糊度相关的模型R数并将其应用于多源决策中[9].
Dempster在1967年提出了证据理论的概念[10], 随后Shafer进一步完善和发展了该理论.D-S(Dempster-Shafer)证据理论为处理不确定信息及群决策方面提供了信息融合方法而且不需要先验信息, 是一种高效率解决不确定问题的办法.同时，极大地扩展了D-S证据理论的应用领域.然而, 该理论的局限在于一票否决问题以及当冲突因子K=1时, 即完全冲突情况下, 无法进行融合.目前为止, 许多****对该问题进行大量的研究, 主要可以分为两类, 一类****认为发生无法融合的情况是由于D-S组合规则本身缺陷导致的, 因此针对组合规则提出改进方法[11-12], 然而这类改进方法会使证据理论的一些性质(如交换性和结合性等)遭到破坏, 更重要的是, 如果冲突结果是由来源信息不准确引起的, 那这样的修改就没有任何作用.另外一类****认为方法本身是完善的, 只是由于信息来源的不准确才导致不符合常规的结果, 相应地对来源信息进行一系列处理[13-15].
本文通过结合信息熵差和散度, 提出基于差异信息量的多源数据融合方法, 能为数据融合提供更好的准确性, 其基本思想是通过差异信息量对不同的证据源进行处理使其获得适当的权重.该方法利用信息熵测得各证据所占信息量的大小, 利用熵差表征证据之间的相对重要性.之后通过Jensen-Shannon散度测得各证据本身的可信程度, 通过可信度权值优化信息熵差计算得出证据的差异信息量, 获得最终的权重, 在此基础上, 得到加权平均证据; 然后采用D-S证据理论将这些加权平均证据进行融合.最后, 通过数值算例和在多传感器故障诊断系统中的应用验证了该方法的合理性、有效性和优越性.
1 理论基础1.1 D-S证据理论D-S证据理论又被称为信念函数理论, 是处理不确定信息的有效工具.它可以在没有先验信息的情况下, 灵活有效地处理不确定性信息.D-S证据理论的优势在于, 它可以将概率分配到由多个对象组成的集合的子集中, 而不是分配到单个对象中, 从而直接表达“不确定性”.此外, 它还能够结合各种证据来得出新的证据.基本概念如下:
定义1 设识别框架(样本空间)Θ是一组相互独立但总体详尽事件的集合, 如式(1)所示:
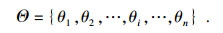 | (1) |
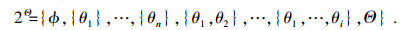 | (2) |
2Θ在[0, 1]上映射,
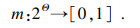 | (3) |
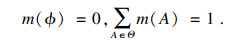 | (4) |
定义3 已知m1和m2的两个独立证据的基本信息分配函数, D-S证据理论的组合规则如下所示:
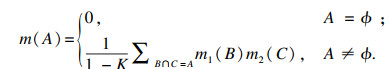 | (5) |
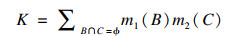 | (6) |
1.2 信息熵信息熵(熵在信息论中的应用)是处理不确定信息的有效方法, 许多****都提出熵的不同改进形式, 目前一种新的信息熵——邓熵——被广泛应用.邓熵是一种度量不确定信息的有效方法.它可以应用于证据理论中, 在证据理论中, 不确定信息用BPA表示.
设Ai是不确定信息的一个事件, Ai包含的元素个数用|Ai|表示, 集合信息熵定义为
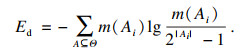 | (7) |
设随机变量X存在两种概率分布形式，m1={m11, m12, …}和m2={m21, m22, …}, 那么m1和m2之间的散度计算方法为
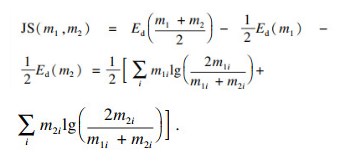 | (8) |
2 基于差异信息量的多源数据融合方法本文提出一种新的多源数据融合方法, 该方法将信息熵和J-S散度相结合得到差异信息量来进行数据融合.所提方法的主要优点如下:
1) 该方法提出差异信息量的概念及融合方法, 同时考虑证据之间的差异以及证据本身的不确定性.此外, 本文方法不仅局限于集合Ai包含元素为1的条件, 还可以扩展到同时存在多个元素的情形.
2) 在处理冲突数据时, D-S证据理论可能会出现反直觉的结果, 本文方法有效地解决了高度冲突的融合问题, 为多源数据融合提出一种新的方法.
3) 本文方法不仅可以处理多传感器或多专家决策等多源信息的数据融合问题, 还能够应用于多源图像融合及人工智能等多个领域, 具有良好的适用性.
本文方法通过J-S散度矩阵获取权重优化信息熵差, 得到证据的差异信息量, 并计算出最终的权重, 由此得到加权平均证据, 最后将所得结果利用D-S证据理论进行多次融合.计算步骤如下:
步骤1 将从各传感器采集到的信号特征信息作为证据, 并将结果以基本信息分配函数BPA(mass函数)的形式给出.
步骤2 根据式(7)计算每个证据mi(i=1, 2, …, n)的信息熵Edi.
步骤3 为了避免在某些情况下给证据分配零权重, 需要求出具体各个证据之间的证据差异量dij:
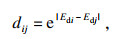 | (9) |
步骤4 列出所有证据的差异度量矩阵(difference measure matrix, DMM),
 |
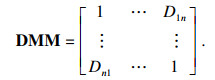步骤5 根据证据的差异度量矩阵, 计算各证据间的证据差异度(evidence difference, ED).
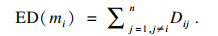 | (10) |
 |
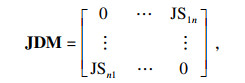步骤7 根据J-S散度度量矩阵计算每个证据的平均散度
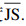
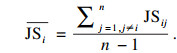 | (11) |
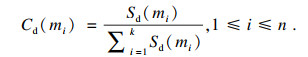 | (12) |
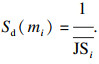
步骤9 利用证据可信度对证据差异度进行优化调整, 得到证据差异信息量(difference information, DI).
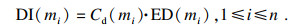 | (13) |
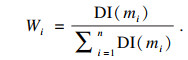 | (14) |
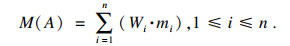 | (15) |
所提方法的流程图如图 1所示.
图 1(Fig. 1)
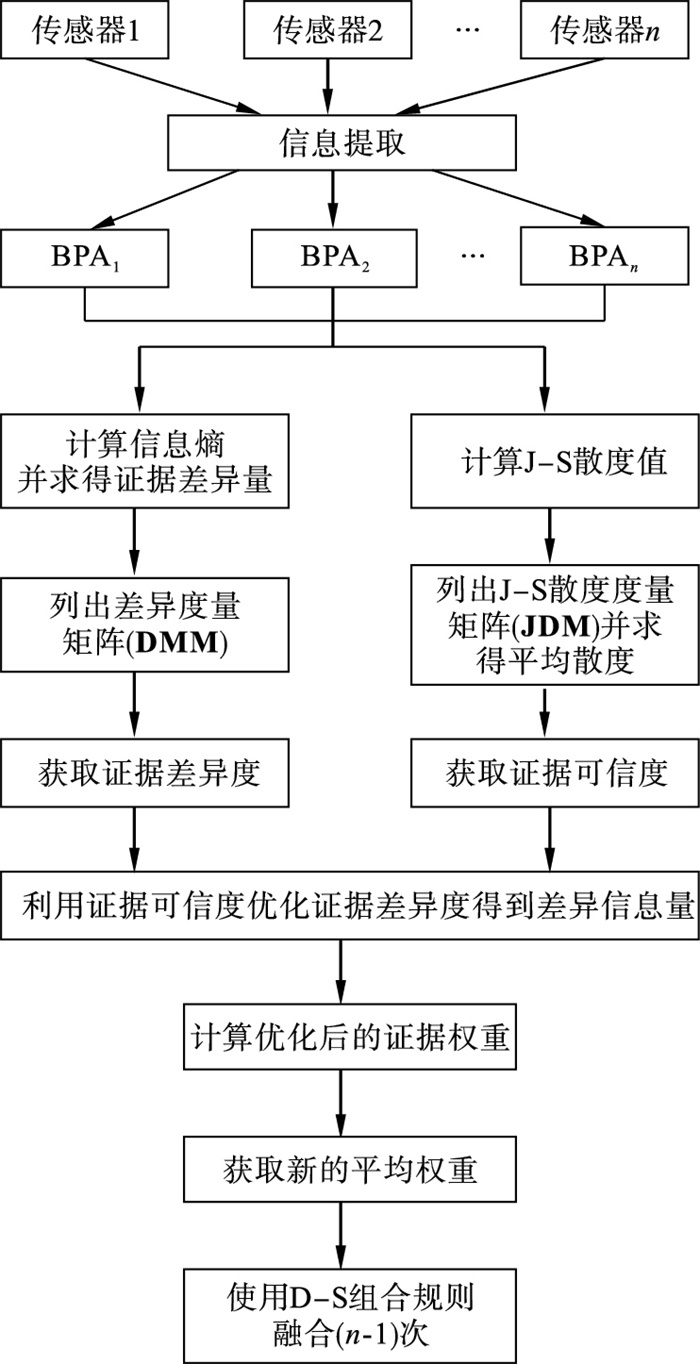 | 图 1 所提方法流程图Fig.1 Flowchart of the proposed method |
3 算例分析基于多传感器的目标识别问题, 从不同类型的传感器收集传感器报告, 并将所得结果以基本信息分配函数BPA的形式表示, 给出一致证据、冲突证据以及既有冲突证据又有一致证据的三种算例分析, 以验证本文所提方法的全面性及准确性.
例1 冲突证据源数据融合(Θ={A, B, C}为三个对象组成的识别框架，见表 1).
表 1(Table 1)
 表 1 冲突数据融合Table 1 Conflict data fusion
| 表 1 冲突数据融合 Table 1 Conflict data fusion |
由表 1数据可以看出, 其中4个传感器结果都较支持{A}, 只有第三个传感器支持{B}且具有更高的确定度, 这几种证据支持不同的假设, 具有冲突性.因此, 无法通过数据直观分析出决策结果.具体的计算结果如下:
根据式(7)计算信息熵,
Ed1=1.122 6, Ed2=1.375 2, Ed3=0.986 3,
Ed4=1.435 4, Ed5=1.318 0.
根据式(9)计算分布差异,
d12=1.287 4, d13=1.146 0, d14=1.367 2,
d15=1.215 8, d23=1.475 4, d24=1.062 0,
d25=1.058 9, d34=1.566 9, d35=1.393 3,
d45=1.124 6.
差异度量矩阵为
 |
ED(m1)=3.203 3, ED(m2)=3.340 6,
ED(m3)=2.906 3, ED(m4)=3.200 4,
ED(m5)=3.373 8.
由式(8)计算散度值,
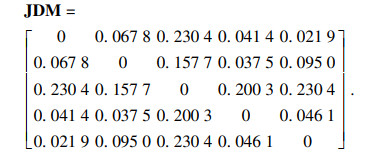
JS(m1, m2)=0.067 8,JS(m1, m3)=0.230 4,
JS(m1, m4)=0.041 4, JS(m1, m5)=0.021 9,
JS(m2, m3)=0.157 7, JS(m2, m4)=0.037 5,
JS(m2, m5)=0.095 0, JS(m3, m4)=0.200 3,
JS(m3, m5)=0.230 4, JS(m4, m5)=0.046 1.
J-S散度度量矩阵为
 |
 |
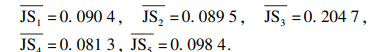Cd(m1)=0.223 1, Cd(m2)=0.225 3,
Cd(m3)=0.098 5, Cd(m4)=0.248 1,
Cd(m5)=0.205 0.
利用式(13)计算优化后的差异信息量，
DI(m1)=0.714 7, DI(m2)=0.752 6,
DI(m3)=0.286 3, DI(m4)=0.794 0,
DI(m5)=0.691 6.
优化后的权重为
W1=0.220 6, W2=0.232 3, W3=0.088 4,
W4=0.245 1, W5=0.213 5.
求得的平均权重为
M({A})=0.543 3, M({B})=0.193 9,
M({C})=0.056 6, M({A, B})=0.071 0,
M({B, C})=0.021 3, M({Θ})=0.113 8.
使用D-S规则融合四次, 得到的结果为{0.993 8 0.005 8 0.000 01 0.000 04 0.004}, 将所得结果与现存方法的结果进行比较, 对比情况如表 2，图 2所示.
表 2(Table 2)
表 2 冲突数据融合结果的对比Table 2 Comparison results of conflicting data fusion
| 表 2 冲突数据融合结果的对比 Table 2 Comparison results of conflicting data fusion |
图 2(Fig. 2)
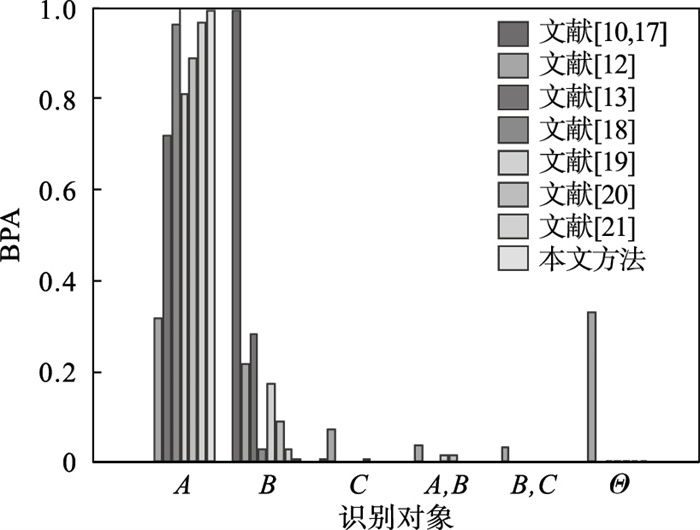 | 图 2 冲突数据融合结果对比Fig.2 Comparison results of conflicting data fusion |
从表 2可以看出, 当收集到相互冲突的证据时, 经典的D-S组合规则会产生不符合逻辑的结果, 不能反映结果的实际分布.在此情况下, 尽管更多的证据支持一个目标, 但最终结果不可能是{A}.此外, 从表中可以看出, 本文方法得到的决策结果正确, 对正确结果的支持度更高, 更能准确决策出结果.本文所提出的方法不但避免证据理论的缺点, 而且对于冲突数据融合的结果比现存方法决策效果更好, 说明所提方法能很好地适用于冲突数据的融合问题.
例2 一致证据融合比较(见表 3).
表 3(Table 3)
表 3 一致证据融合比较Table 3 Comparison of consistent evidence fusion
| 表 3 一致证据融合比较 Table 3 Comparison of consistent evidence fusion |
差异度量矩阵为
 |
 |
W1=0.191 0, W2=0.230 2, W3=0.260 8, W4=0.260 8,
W5=0.057 2.
求得的平均权重为
M({A})=0.577 8, M({B})=0.119 1,
M({C})=0.103 3, M({A, C})=0.199 7.
最后, 使用D-S规则融合四次，得到结果为{0.999 8 0.000 004 0.000 001 0.000 2}, 将所得结果与现存方法的结果相比, 具体情况见表 4.
表 4(Table 4)
表 4 一致证据融合结果Table 4 Results of consistent evidence fusion
| 表 4 一致证据融合结果 Table 4 Results of consistent evidence fusion |
由表 4可知, 在证据一致的情形下, 表 4中采用的方法都可以作出正确决策.在存在几个证据完全一致的特殊情况下, 每种情况的概率相差不大, 但是本文所提方法对{A}决策结果的准确率更高, 其他两种情况的概率均低于其他方法.采用传统的D-S组合规则进行数据融合时{C}, {A, C}的证据信息量为0, {B}的概率高于其他两种方法.虽然文献[13]所提方法也能够进行融合并有效地作出决策, 但与本文所提方法相比, 准确率较低.本文方法不但能够融合同时存在一致证据源的数据, 而且具有比现存方法更小的不确定性.
例3 集合Ai包含元素为1的情形下, 不同数量证据融合比较(见表 5).
表 5(Table 5)
表 5 |Ai|=1时不同数量证据融合Table 5 Fusion of different amounts of evidence when |Ai|=1
| 表 5 |Ai|=1时不同数量证据融合 Table 5 Fusion of different amounts of evidence when |Ai|=1 |
上述两例证明了在集合Ai包含多个元素的情形下, 本文方法对冲突证据、一致证据的数据融合具有更好的融合效果.本例验证了在集合Ai仅包含1个元素时本文所提方法的有效性, 并讨论了在不同数量证据下各方法融合结果的对比情况(见表 6).
表 6(Table 6)
表 6 |Ai|=1时不同数量证据融合结果Table 6 Fusion results of different amounts of evidence when |Ai|=1
| 表 6 |Ai|=1时不同数量证据融合结果 Table 6 Fusion results of different amounts of evidence when |Ai|=1 |
差异度量矩阵为
 |
 |
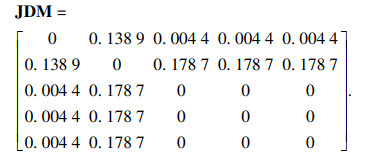DI(m1)=0.969 7, DI(m2)=0.184 6,
DI(m3)=0.832 8, DI(m4)=0.832 8,
DI(m5)=0.832 8.
求得的平均权重为
M({A})=0.509 0, M({B})=0.167 0,
M({C})=0.324 1.
最后, 使用D-S规则融合四次，得到的结果为{0.973 1 0.001 3 0.025 7}, 在融合过程中, 不同数量的证据会对融合结果产生较大的影响, 采用不同的方法融合不同数量证据, 所得结果与现存方法的结果相比较, 具体情况如图 3所示.
图 3(Fig. 3)
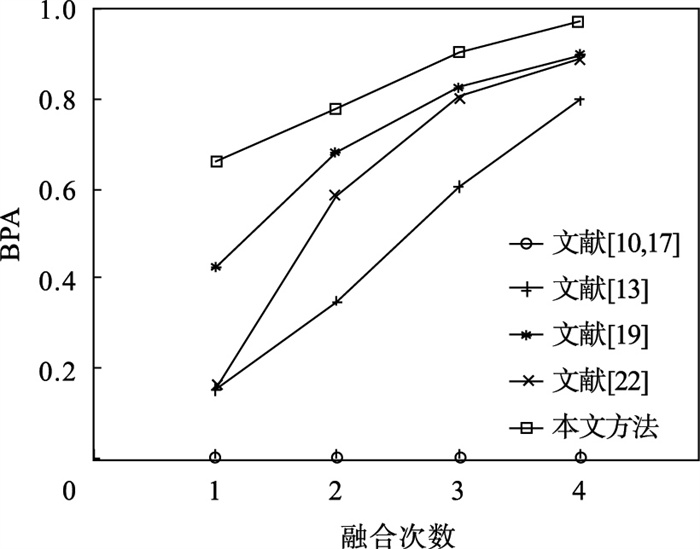 | 图 3 |Ai|=1时不同数量证据融合结果对比Fig.3 Comparison of fusion results of different amounts of evidence when |Ai|=1 |
由图 3可知, |Ai|=1时, 经过n-1次融合, 本文所提方法准确率明显高于其他方法.另外, 第二个证据与其他证据相冲突, 虽然越来越多的证据支持{A}, 但是D-S证据理论的方法并不能得出正确结果.文献[13]在证据数量为3个的情况下, 仍不能识别出证据源m2的错误, 直至证据增加至4个才作出正确判断.此外, 从图 3中可以看出, 本文方法的收敛性能优于其他已有的方法.
4 应用本节将所提方法应用于一个机器故障诊断的案例研究.该系统非常复杂, 系统中的每个因素都以非常复杂的方式相互作用.
为了验证本文方法应用于故障诊断中的有效性, 将S={S1, S2, S3}三个不同位置的传感器信号作为证据源, 对采集到的信号以基本信息分配函数BPA的形式表示.假设机器有F1, F2, F3三种类型的故障, 收集到的传感器数据如表 7所示, 其中Θ为故障组成的识别框架，Θ={F1, F2, F3}.在基于多传感器的故障诊断系统中, 假设真实目标为F1, 从3个不同的传感器中, 系统收集了3个证据源, 如表 7所示.
表 7(Table 7)
表 7 传感器数据Table 7 Sensor data
| 表 7 传感器数据 Table 7 Sensor data |
计算求得的加权平均证据为
M({F1})=0.296, M({F2})=0.239 6,
M({F3})=0.90, M({F1, F2, F3})=0.140 77.
最后, 使用D-S规则融合两次，得到的结果为{0.896 5 0.083 1 0.004 4 0.016 1}, 不同方法所得结果的比较如表 8所示.
表 8(Table 8)
表 8 传感器证据数据融合结果对比Table 8 Comparison of fusion results for sensor evidence data
| 表 8 传感器证据数据融合结果对比 Table 8 Comparison of fusion results for sensor evidence data |
由表 8可知, 本文方法可以诊断出故障类型{F1}, 与文献[21], [23],[24]等方法的诊断结果一致, 即使面对冲突的传感器报告, 这些方法都可以很好地处理冲突的证据.而传统的D-S规则不能很好地处理冲突证据, 得出故障类型为{F2}的错误结果.
此外, 本文方法对故障类型{F1}的置信度最高(89.65 %), 高于文献[21], [23], [24]的方法.本文方法利用信息熵和散度结合处理证据, 考虑了传感器报告的不确定性, 因此具有较高的准确度.由于{F1}故障的置信度为89.65 %, 可以判断{F1}是设备的故障.与其他方法相比, 该方法的性能有了很大的提高.
5 结语在故障诊断和其他传感器数据融合系统中, 来自不同传感器的证据可能会因为复杂环境的影响而不可靠.因此, 如何高效地确定每个证据源的可靠性是非常重要的.本文综合考虑证据之间的相似度和相异度以及证据不确定性的影响, 提出了一种新的数据融合方法.该方法以信息熵和散度为基础, 利用散度度量矩阵求得相应权重, 从而优化信息熵差, 求得证据的最终权重, 并通过证据理论进行融合从而做出准确的决策结果.最后, 通过三个数值例子说明该方法的有效性、合理性.此外, 利用一个故障诊断实例, 说明该方法在确定这些实际故障时更为准确.所提方法可以推广到其他不确定性理论当中, 为多源数据融合提供一种新的理论与方法.
参考文献
| [1] | Amyotte K P. Safety analysis in process facilities: comparison of fault tree and Bayesian network approaches[J]. Reliability Engineering & System Safety, 2011, 96(8): 925-932. |
| [2] | Seixas F L, Zadrozny B, Laks J, et al. A Bayesian network decision model for supporting the diagnosis of dementia, Alzheimers disease and mild cognitive impairment[J]. Computers in Biology and Medicine, 2014, 51C(7): 140-158. |
| [3] | Mori J, Mahal E V. Planning and scheduling of steel plates production.Part I: estimation of production times via hybrid Bayesian networks for large domain of discrete variables[[J]. Computers & Chemical Engineering, 2015, 79(4): 113-134. |
| [4] | Mori J, Mahalec V, Yu J. Identification of probabilistic graphical network model for root-cause diagnosis in industrial processes[J]. Computers & Chemical Engineering, 2014, 71: 171-209. |
| [5] | Jiang W, Wei B. Intuitionistic fuzzy evidential power aggregation operator and its application in multiple criteria decision-making[J]. International Journal of Systems Science, 2018, 49(1/2/3/4): 582-594. |
| [6] | Wen J, Hu W. An improved soft likelihood function for Dempster-Shafer belief structures[J]. International Journal of Intelligent Systems, 2018, 33(6): 1264-1282. DOI:10.1002/int.21980 |
| [7] | Kang B, Zhang P, Gao Z, et al. Environmental assessment under uncertainty using Dempster-Shafer theory and Z-numbers[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11: 2041-2060. DOI:10.1007/s12652-019-01228-y |
| [8] | Xiao F. A multiple-criteria decision-making method based on D numbers and belief entropy[J]. International Journal of Fuzzy Systems, 2019, 21(4): 1144-1153. DOI:10.1007/s40815-019-00620-2 |
| [9] | Seiti H, Hafezalkotob A, Martínez L. R-numbers, a new risk modeling associated with fuzzy numbers and its application to decision making[J]. Information Sciences, 2019, 483: 206-231. DOI:10.1016/j.ins.2019.01.006 |
| [10] | Dempster A P. Upper and lower probabilities induced by a multivalued mapping[J]. Annals of Mathematical Statistics, 1967, 38(2): 325-339. DOI:10.1214/aoms/1177698950 |
| [11] | Lefevre E, Colot O, Vannoorenberghe P. Belief function combination and conflict management[J]. Information Fusion, 2002, 3(2): 149-162. DOI:10.1016/S1566-2535(02)00053-2 |
| [12] | Yager R R. On the Dempster-Shafer framework and new combination rules[J]. Information Sciences, 1987, 41(2): 93-137. DOI:10.1016/0020-0255(87)90007-7 |
| [13] | Murphy C K. Combining belief functions when evidence conflicts[J]. Decision Support Systems, 2000, 29(1): 1-9. DOI:10.1016/S0167-9236(99)00084-6 |
| [14] | Han D, Deng Y, Liu Q. Combining belief functions based on distance of evidence[J]. Decision Support Systems, 2005, 38(3): 489-493. |
| [15] | Zhang Z, Liu T, Chen D, et al. Novel algorithm for identifying and fusing conflicting data in wireless sensor networks[J]. Sensors, 2014(6): 9562-9581. |
| [16] | Lin J. Divergence measures based on the shannon entropy[J]. IEEE Transaction on Information Theory, 1991, 37(1): 145-151. DOI:10.1109/18.61115 |
| [17] | Shafer G A. A mathematical theory of evidence[J]. Technometrics, 1978, 20(1): 106. |
| [18] | Xiao F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy[J]. Information Fusion, 2018, 46: 23-32. |
| [19] | Dong Y, Zhang J, Li Z, et al. Combination of evidential sensor reports with distance function and belief entropy in fault diagnosis[J]. International Journal of Computers, Communications & Control(IJCCC), 2019, 14(3): 329-343. |
| [20] | Liu Z, Dezert J, Quan P, et al. Combination of sources of evidence with different discounting factors based on a new dissimilarity measure[J]. Decision Support Systems, 2012, 52(1): 133-141. |
| [21] | Ma M, Jiyao A N. Combination of evidence with different weighting factors: a novel probabilistic-based dissimilarity measure approach[J]. Journal of Sensors, 2015, 2015(2): 1-9. |
| [22] | Jiang W, Wei B Y, Xie C H, et al. An evidential sensor fusion method in fault diagnosis[J]. Advances in Mechanical Engineering, 2016, 8(3): 1-7. |
| [23] | Fan X, Zuo M J. Fault diagnosis of machines based on D-S evidence theory.Part 1:D-S evidence theory and its improvement[J]. Elsevier Science Direct,, 2006, 27(5): 266-376. |
| [24] | Yuan K, Xiao F, Fei L, et al. Modeling sensor reliability in fault diagnosis based on evidence theory[J]. .Sensors,, 2016, 16(1): 113. DOI:10.3390/s16010113 |
