
 , 程大众1, 耿浩博2
, 程大众1, 耿浩博2 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 澳门大学 科技学院,澳门 999078
收稿日期:2020-11-20
基金项目:国家自然科学基金资助项目(51775094)。
作者简介:赵春雨(1963-),男,辽宁黑山人,东北大学教授,博士生导师。
摘要:主轴回转误差影响车削工件的加工精度, 本文通过对主轴回转误差的分析和研究, 提出了一种基于回转误差的车削工件2-D表面形貌检测方法, 并建立了车削过程数学模型. MATLAB仿真结果表明, 主轴径向回转误差会影响工件的车削半径和表面形貌, 进而造成工件的同轴度误差、圆度误差,并增大表面粗糙度.为验证所提方法的有效性, 搭建了2-D表面形貌检测平台进行数据采集, 得到了主轴在切深方向的回转误差和车削工件的平均半径误差.实验结果表明实验与仿真结果在特性上具有一致性, 验证了方法的可行性, 对机床的性能调试及提高工件的加工质量具有参考价值.
关键词:主轴回转误差表面形貌检测同轴度误差圆度误差表面粗糙度
Research on 2-D Surface Topography Detection Method of Turning Workpieces
ZHAO Chun-yu1

 , CHENG Da-zhong1, GENG Hao-bo2
, CHENG Da-zhong1, GENG Hao-bo2 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Faculty of Science and Technology, University of Macau, Macau 999078, China
Corresponding author: ZHAO Chun-yu, E-mail: chyzhao@mail.neu.edu.cn.
Abstract: Spindle rotation error affects the machining accuracy of turning workpieces. Through analyses and studies of the spindle rotation error, a 2-D surface topography detection method was proposed for turning workpieces based on the rotation error, and the turning process model was established. The MATLAB simulation results showed that the spindle radial rotation error affects the turning radius and surface topography of the workpiece, resulting in the coaxiality error, roundness error and surface roughness. To verify the effectiveness of the proposed method, the 2-D surface topography detection platform for data collection was built, and the rotation error value of the spindle in the depth direction and average radius error of turning workpieces were obtained. The experimental results showed that the experiment and simulation results are consistent in characteristics, which verify the feasibility of the method and have reference value for the performance debugging of the machine tool and improving the processing quality of the workpieces.
Key words: spindle rotation errorsurface topography detectioncoaxiality errorroundness errorsurface roughness
车削加工是回转体零件生产中去除多余材料的主要方法之一.被加工零件的表面形貌是衡量产品质量的重要指标, 因此表面形貌测量、表征及控制一直是该领域研究的焦点[1-2].机床主轴是决定工件和刀具相对运动并传递切削力的核心部件, 其运动误差是影响车削加工精度的主要因素以及衡量机床性能的重要指标之一, 也是决定工件表面形貌的主要因素之一[3].特别是加工应用于航天以及轮船航母等领域的大回转体零件或者在精加工时(切削用量相对于加工工件名义尺寸非常小), 因为工件刚度相对较大, 由切削力引起的受力变形会很小, 此时决定车削工件表面形貌的主要因素通常是机床主轴的运动误差[4].
为了提高工件表面形貌的检测精度, 必须将主轴运动误差从检测结果中分离, 而且主轴运动误差检测方法也成为学术界的研究主题.目前已提出了多种主轴运动误差测量方法, 例如反转法[5]、多探头法[6]和多步法[7].Cappa等[8]对上述三种测量方法及存在的误差进行了综合分析概述.但以上方法均需借助标准棒单纯测量主轴的回转误差, 并且在测量时无法避免工件、测量装置安装误差, 这也会增加其测量误差.
近年来, ****们对主轴运动误差测量方法提出了很多优化措施, Grejda针对反转法进行改进, 消除移动和重新调整位移传感器对检测结果的影响, 并保证频域低通滤波数据结果不失真[9]; Chen等提出利用小波变换、W函数以及PSD频域分析得到主轴回转误差[10].从上述文献可知, 目前的研究内容对车削加工过程中主轴回转误差对被加工工件的表面形貌的影响分析较少, 本文提出了一种基于回转误差测量工件表面形貌的方法.
1 主轴运动误差的描述在国际标准ISO/FDIS230-7中定义, 机床主轴在理想情况下, 只绕中心固定轴线作回转运动, 但是在实际的工作中, 由于机床部件的制造误差、装配误差以及外部各种因素的影响, 导致主轴瞬时回转轴线发生变化, 即造成运动误差[11].主轴在空间上的运动误差主要包括纯径向跳动误差、纯轴向窜动误差和纯倾角摆动误差[12], 如图 1所示.其中纯径向跳动误差和纯倾角摆动误差总称为主轴径向回转误差.
图 1(Fig. 1)
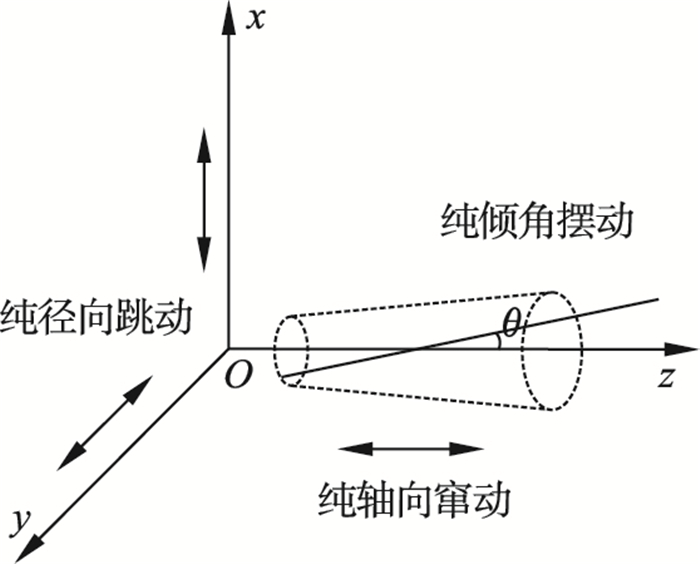 | 图 1 主轴的空间运动误差Fig.1 Spatial motion error of the spindle |
由于主轴理想轴线运动的非确定性, 在测量过程中测得的数据不具有可复制性, 对主轴运动误差测量的描述会比较复杂.根据ASME(American Society of Mechanical Engineers)B89.3.4M标准, 主轴径向回转误差可分解为同步误差和异步误差[13-14].同步误差指主轴回转基频整倍数的那些分量的总和; 异步误差又叫随机误差, 是指总误差减掉同步误差的剩余分量, 包括主轴回转基频整数倍以外的其他误差成分以及基频以内的非周期性谐波成分.主轴径向回转误差δ可由下式表示:
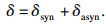 | (1) |
在机床上, 同步误差主要来自于轴承内套和配合轴的圆度制造误差, 会在主轴周期性旋转中重复出现.异步误差是随机的运动误差, 其值被定义为总的运动误差在通过坐标原点的任意方向的误差带的最大宽度, 一般情况下呈近似正态分布, 可以采用多个测量值作平均处理的方法进行减小或消除.
2 建立车削过程数学模型在车削过程中, 主轴的运动误差会导致刀尖与工件理想轴线之间的距离发生变化, 从而造成车削工件的误差.如图 2所示, 假设椭圆实线为主轴的各谐波次数同步运动误差, ai, bi分别为其曲线的长半轴和短半轴.波浪实线为带有异步误差的主轴瞬时回转中心轨迹, 即主轴回转全运动误差.O为主轴理想回转中心(坐标系Oxy原点), x轴为刀具进给方向, O1为主轴实际回转圆心, 两传感器S1和S2在圆周方向相隔180°对称分布, 连线与导轨平行, 其中传感器S1与刀具的轴线位置完全重合, 两传感器与坐标系原点的距离分别为L和H.OA为工件理想加工半径R, 椭圆外接圆对应点与传感器轴线的夹角为φ, 瞬时回转半径O1A与传感器轴线夹角为
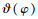
图 2(Fig. 2)
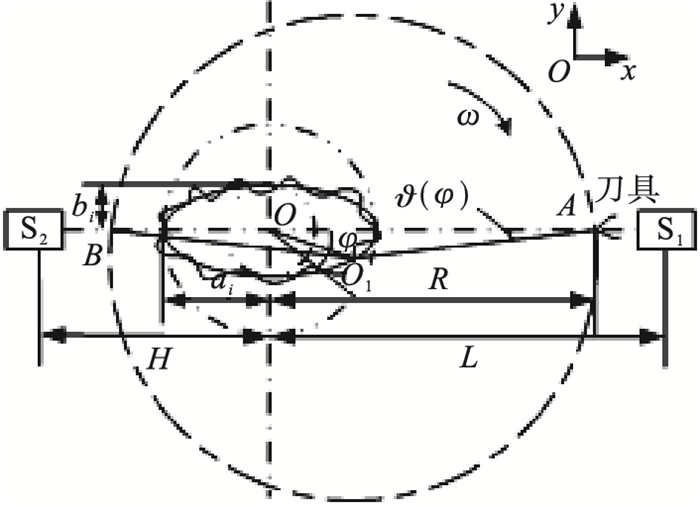 | 图 2 车削工件的2-D截面Fig.2 2-D cross section of the turning workpiece |
由几何关系可得, 实际回转中心O1在坐标系Oxy中的参数方程为
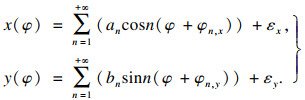 | (2) |
根据异步误差的特点, 可以将其看作是按一定自相似规律分布的, 可用Weierstrass-Mandelbrot函数(简称W-M函数)来生成.该函数模拟的曲线处处连续但不可导, 符合机加工轮廓曲线的特征[15], 其表达式为
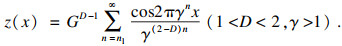 | (3) |
若取分形维数D=1.3, 特征尺度参数G=1×10-4mm, 轮廓曲线微凸体最小频率指数nl=1, 此时轮廓曲线算术平均偏差Ra,ε=5.25μm, 式(2)中异步误差为
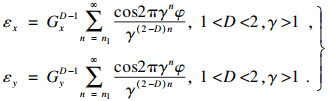 | (4) |
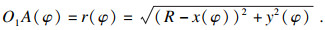 | (5) |
 | (6) |
 | (7) |
 | (8) |
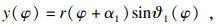 | (9) |
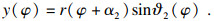 | (10) |
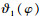
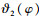
此时传感器S1和S2的测量值lA和lB可分别表示为
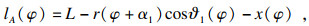 | (11) |
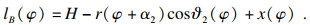 | (12) |
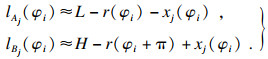 | (13) |
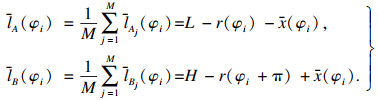 | (14) |
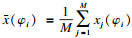
由于主轴运动误差包括同步误差和异步误差, 而异步误差具有随机性, 所以当单点测量数足够大时, x(φi)即为同步误差.
将式(14)中的N对方程求平均, 得
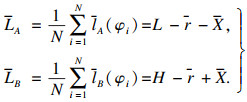 | (15) |
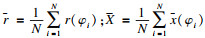
方程(15)两式相加, 得
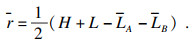 | (16) |
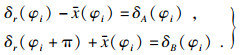 | (17) |
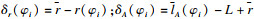
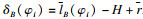
旋转后亦是如此, 不再赘述.得以下超定方程组:
 | (18) |
对于求解超定方程组Ay=b, y=[δr x]T, A为系数矩阵, b=[δA δB]T, 运用最小二乘原理寻求一最近似解y*, 使得‖ε‖22最小, ε=b-Ay*记为误差向量, 即可求得工件半径误差δr与切深方向的同步误差x.
4 测试原理仿真结果分析设定传感器安装位置参数L=60 mm, H=50 mm, 理想半径R=40 mm, 旋转角α0=30°, 每周采样点数N=720.在一般情况下, 具有较低傅里叶级数误差对工件表面形貌造成的影响较为明显, 因此在这里仅分析主轴回转误差傅里叶级数前三项对工件表面形貌的影响.主轴回转误差运动参数如表 1所示.
表 1(Table 1)
| 表 1 主轴回转误差运动参数 Table 1 Spindle rotation error motion parameters |
4.1 同步误差对检测结果的影响仅考虑同步误差, 即式(2)中εx=εy=0, 图 3为传感器的仿真测量结果, 通过对检测数据进行计算, 得工件平均半径为r=40 mm.
图 3(Fig. 3)
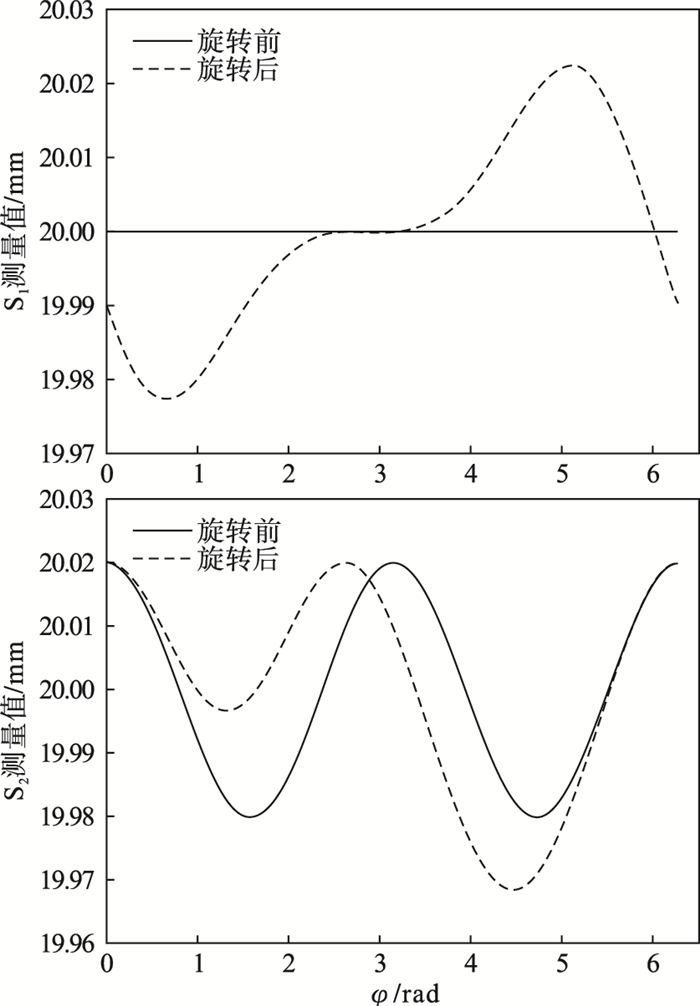 | 图 3 工件旋转前后的测量值Fig.3 Measured values before and after workpiece rotation |
利用最小二乘原理对式(18)求解, 得到车削工件半径误差和主轴在切深方向的回转误差, 仿真结果如图 4~图 6所示.
图 4(Fig. 4)
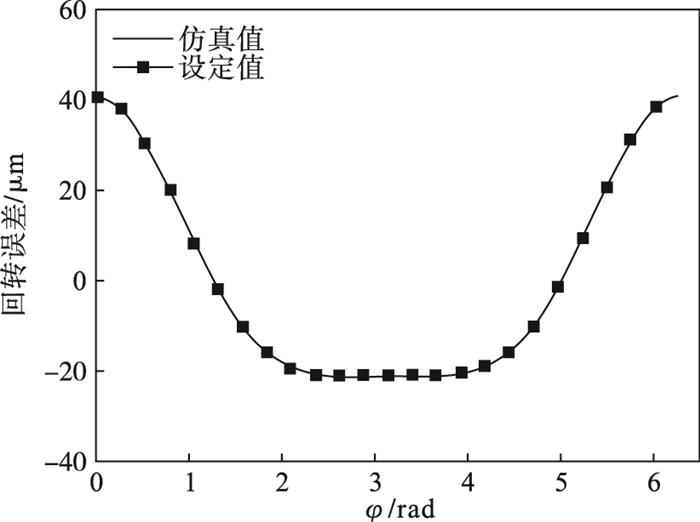 | 图 4 同步误差计算与验证对比Fig.4 Comparison of calculation and verification of synchronization errors |
图 5(Fig. 5)
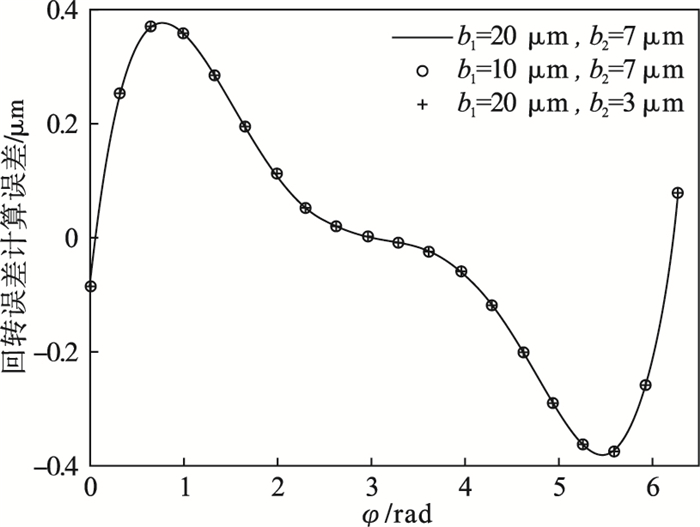 | 图 5 不同参数bi同步误差计算误差对比Fig.5 Comparison of calculation errors of synchronization errors for different error parameters bi |
图 6(Fig. 6)
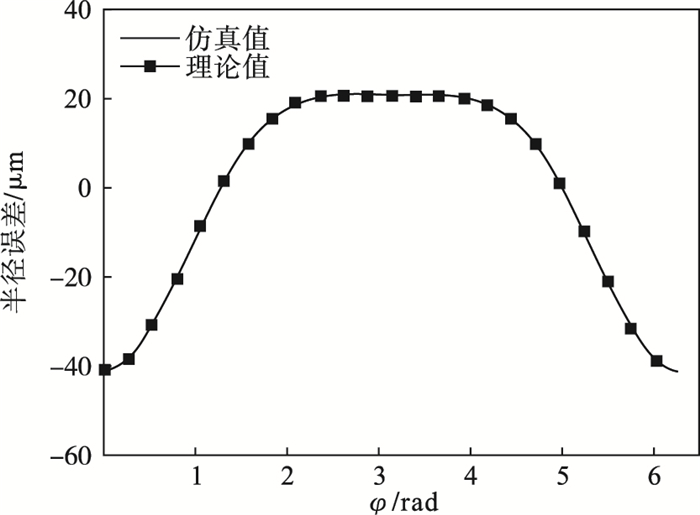 | 图 6 工件半径误差计算与验证对比Fig.6 Comparison of calculation and verification of workpiece radius errors |
从图 4可知, 主轴在切深方向的回转误差运动值通过该测试方法的仿真结果与预先设定相比几乎完全一致, 将仿真值与设定值(理论值)之差定义为计算误差.改变回转误差运动参数bi的大小, 切深方向回转误差计算误差结果如图 5所示, 其最大值与最小值分别为±0.38 μm, 并可以看出其计算误差值几乎不变.
图 6为工件半径平均误差的仿真值与理论值, 对比图 4与图 6, 可以看出切深方向同步误差与半径误差相一致.改变回转误差参数bi的大小, 车削半径误差计算误差结果如图 7所示, 可以看出随着回转误差运动参数bi的增大, 车削工件半径计算误差范围有所增大.但从数值上来看, 与切深方向垂直的方向上的同步误差对测试结果影响很小.
图 7(Fig. 7)
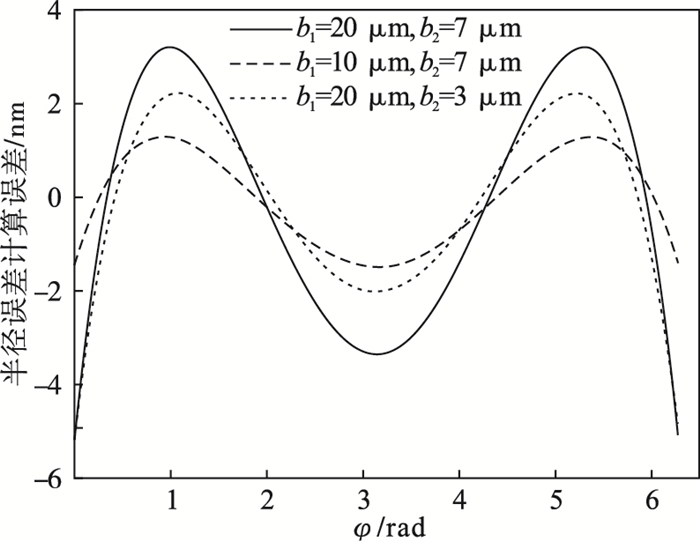 | 图 7 不同参数bi半径误差计算误差对比Fig.7 Comparison of calculation errors of radius errors for different error parameters bi |
将计算所得半径误差δr(φi)加载到平均半径为r的圆上得到r(φi), 利用最小二乘法圆度评定[16], 即可求得圆度误差ε, 从上述计算结果中可以得到回转误差运动参数bi对工件的半径误差的影响很小, 即对工件的圆度误差影响极小, 其值远小于ISO标准中的最高公差等级, 可以忽略不计.
现改变回转运动误差参数ai的值, 利用最小二乘法对车削工件圆度误差进行评定, 得到回转运动误差参数ai对圆度误差的影响规律如图 8所示.
图 8(Fig. 8)
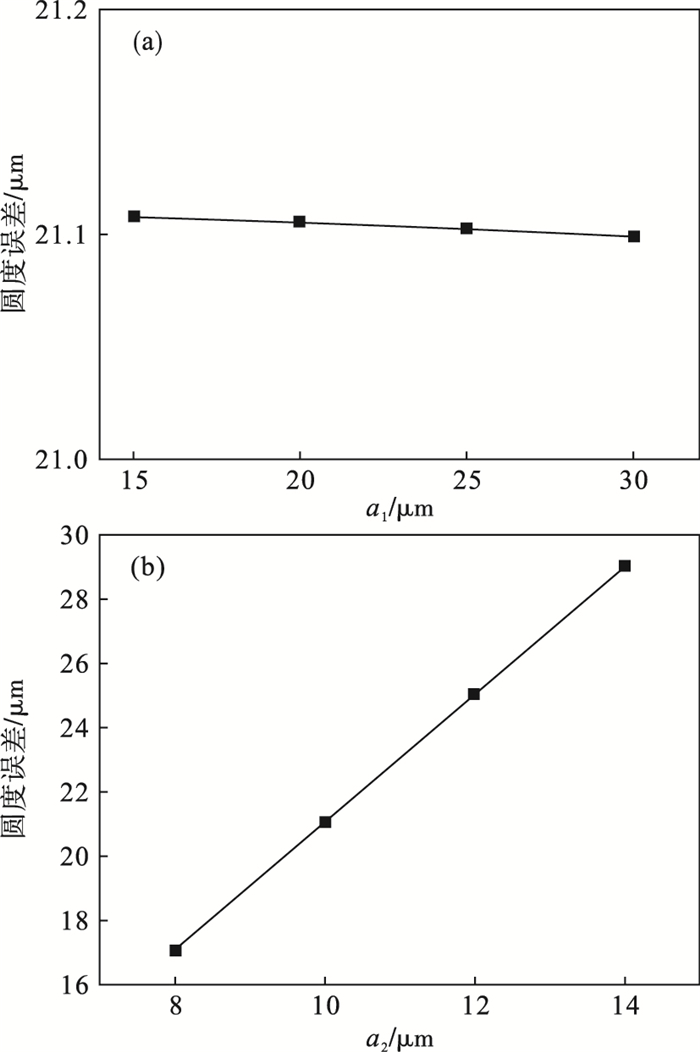 | 图 8 回转运动误差参数ai对工件圆度误差的影响Fig.8 Influence of rotation motion error parameter ai on workpiece roundness error |
从图 8a可以看出, 与主轴转速频率相同的运动误差分量将不影响车削工件的圆度误差, 但是需要指出的是其造成工件横截面轴线的同轴度误差为2a1.从图 8b可知, 主轴运动误差参数ai的二次误差分量对工件横截面的圆度误差造成较大的影响, 第二项傅里叶级数系数a2每增加一个单位值, 圆度误差值就增加两个单位值, 其三次谐波分量与二次谐波分量对圆度误差的影响规律一致, 在这里不在赘述.为更完善地分析高于主轴转速频率的运动误差对圆度误差的影响作用, 通过改变两谐波分量的初始相位差, 得到圆度误差的影响规律如图 9所示.由图 9可知, 随着相位差的变化, 其圆度误差值出现周期性波动变化; 等值的谐波分量系数变化, 其基数值越大, 对圆度误差变化的影响越大.
图 9(Fig. 9)
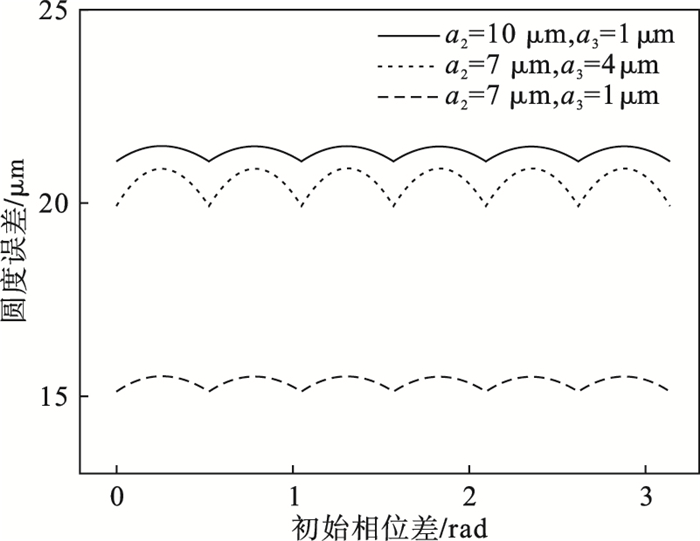 | 图 9 初始相位差对圆度误差的影响规律Fig.9 Influence of initial phase differences on roundness errors |
综上所述, 车削工件圆度误差主要是高于主轴转速频率的切深方向运动误差分量(各谐波分量系数, 初始相位差)综合作用的结果, 且谐波次数越低的分量对工件圆度误差影响越大.
4.2 异步误差对检测结果的影响依据上文给定参数, 按式(4)确定异步误差, 仿真计算工件加工半径.然后, 对其进行测试仿真, 为消除测量过程中异步误差随机性对检测结果的影响, 测试周期为M=50, 作平均处理, 传感器测量结果如图 10所示, 利用式(14)~式(16), 计算平均半径r=40 mm.用最小二乘原理对式(18)求解, 得到在存在异步误差状态下的回转误差计算误差和工件的半径误差仿真结果, 如图 11和图 12所示.
图 10(Fig. 10)
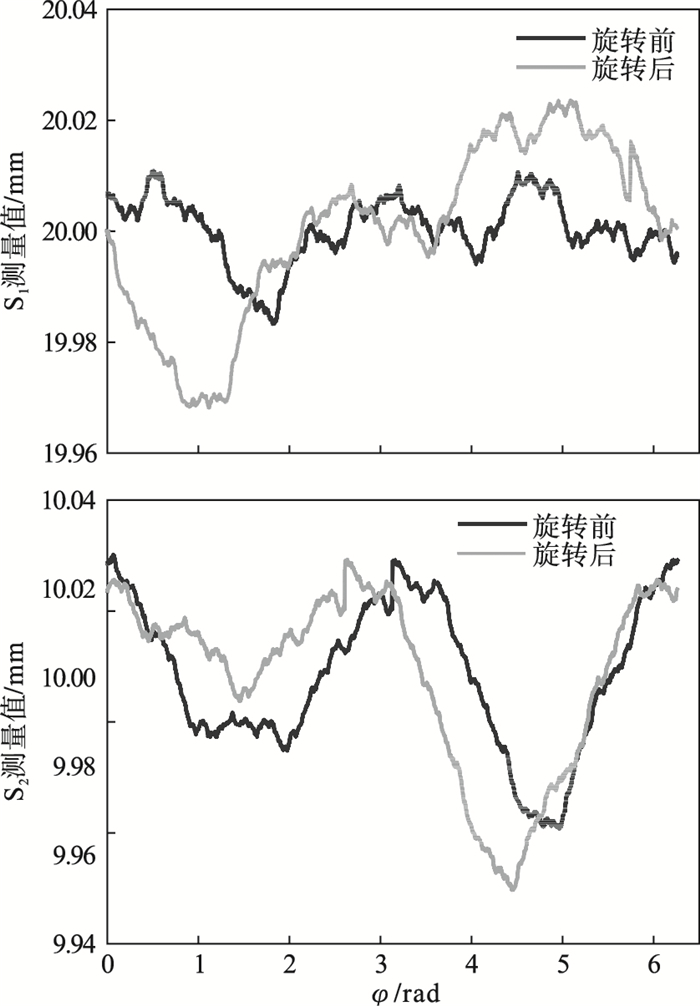 | 图 10 工件旋转前后的测量值Fig.10 Measured values before and after workpiece rotation |
图 11(Fig. 11)
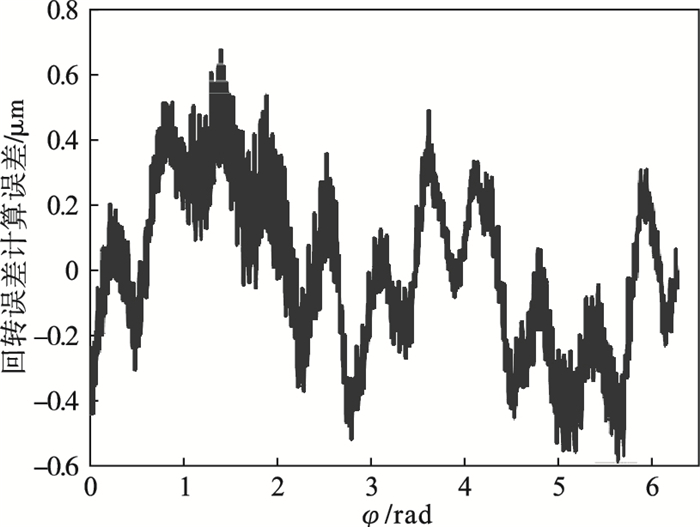 | 图 11 异步误差计算误差Fig.11 Calculation error for asynchronous errors |
图 12(Fig. 12)
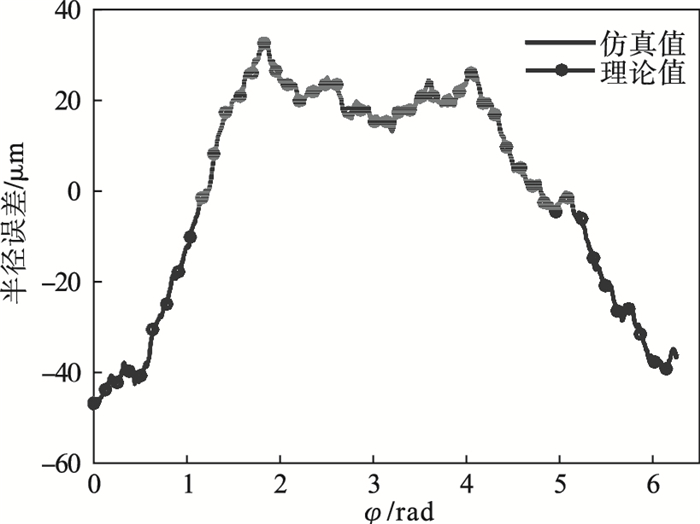 | 图 12 工件半径误差仿真值与理论值对比Fig.12 Comparison of simulation value and theoretical value of workpiece radius errors |
从图 11与图 5对比可知, 在存在异步误差状态下, 通过多周期测量, 主轴切深方向上的回转误差的仿真结果与同步误差设定值相比略有差别, 主要原因是异步误差是服从正态分布的随机误差, 通过多周期测量可以中和掉大部分随机误差, 很大程度上消除了在检测过程中的异步误差对检测结果的影响.
图 12为工件半径误差的仿真值与理论车削半径误差值, 具有很高的重合度, 可见此方法能准确分离车削工件半径误差.将只考虑同步误差造成的平均半径误差(图 6)与引入异步误差后的平均半径误差(图 12)相比, 可得到工件横截面轮廓的粗糙表面形貌, 如图 13所示, 其轮廓算术平均偏差值Ra=5.06 μm, 与异步误差Ra, ε基本一致, 可知异步误差主要影响工件的表面粗糙度.
图 13(Fig. 13)
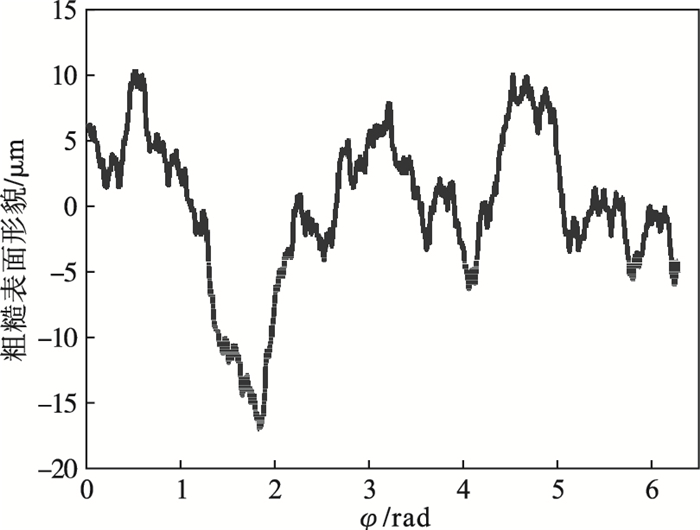 | 图 13 粗糙表面形貌Fig.13 Rough surface topography |
5 实验及计算结果对提出的车削数学模型搭建实验测试系统原理图如图 14所示, 实验将位移传感器在车削工件某一截面呈180°布置, 设定在机床转速为600 r/min的情况下进行车削工作, 并且在同样的转速下进行测量.将旋转前后的测量数据代入本文所提出的算法, 可以得到主轴的同步回转误差值以及切削工件的平均半径误差, 如图 15, 图 16所示, 并对曲线进行了多项式最小二乘拟合.
图 14(Fig. 14)
 | 图 14 测试系统图Fig.14 Physical photo of the test system |
图 15(Fig. 15)
 | 图 15 主轴切深方向同步回转误差Fig.15 Synchronous rotation error of the spindle in cutting depth direction |
图 16(Fig. 16)
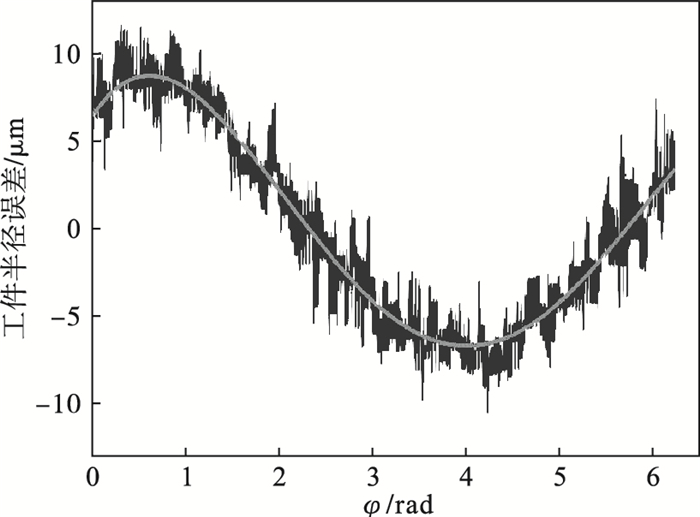 | 图 16 工件平均半径误差Fig.16 Average radius error of the workpiece |
通过对比图 15、图 16与图 4、图 12, 可以看出仿真与实验结果在特性上具有一致性, 车削工件截面轮廓形状几何误差与回转误差有一定的相似性, 通过车削工件截面圆轮廓可得到最小二乘圆半径为27.16 mm, 轮廓算术平均偏差为1.3 μm, 利用最小二乘法求得其圆度误差为3.3 μm.但同时也能看出一些差异: 回转误差存在相位差, 这是由主轴在切削加工时的初始转角不同所导致的; 在实际车削过程中, 表面形貌还受材料属性、刀具磨损、切屑黏结、加工纹理与测量方向的差异、主轴转速不稳定等因素的影响, 检测装置在工作过程中由于受到安装位置振动而导致的检测数值不准确等, 使得测量结果存在误差.
6 结论本文提出以被加工工件为测量标准, 基于机床主轴回转误差检测工件表面形貌的测量方案, 建立了车削过程的数学模型, MATLAB仿真结果表明,主轴运动误差的同步误差一次谐波分量主要造成车削工件的同轴度误差, 对工件的圆度误差没有影响, 二次及以上谐波分量将对工件加工截面的圆度误差产生影响; 而异步误差是造成工件的表面粗糙度的主要原因.最后搭建检测平台, 在主轴转速为600 r/min情况下进行数据采集, 代入本文所提出的误差分离算法, 得到了主轴在切深方向的回转误差值和被加工工件的平均半径误差, 可以看出实验结果与仿真结果在特性上具有一致性.
参考文献
| [1] | Lin C C, Hopfe H H. A surface roughness characterization system[J]. Wear, 1986, 109(1/2/3/4): 79-85. |
| [2] | Shiraishi M, Sato S. Dimensional and surface roughness controls in a turning operation[J]. Journal of Engineering for Industry, 1990, 112(1): 78-83. DOI:10.1115/1.2899298 |
| [3] | Huang P, Lee W B, Chan C Y. Investigation of the effects of spindle unbalance induced error motion on machining accuracy in ultra-precision diamond turning[J]. International Journal of Machine Tools and Manufacture, 2015(94): 48-56. |
| [4] | Qehaja N, Jakupi K, Bunjaku A, et al. Effect of machining parameters and machining time on surface roughness in dry turning process[J]. Procedia Engineering, 2015, 100: 135-140. DOI:10.1016/j.proeng.2015.01.351 |
| [5] | Donaldson R R. A simple method for separating spindle error from test ball roundness error[J]. Annals of CIRP, 1972, 21(1): 125-126. |
| [6] | Sonozaki S, Fujiwara H. Simultaneous measurement of cylindrical parts profile and rotating accuracy using multi-three-point-method[J]. Bulletin of the Japan Society of Precision Engineering, 1989, 54(11): 2095-2100. |
| [7] | Pepin S, Molloy M, Hatch R. Software—the key to making virtual instruments practical[J]. Autotestcon-IEEE, 2003, 1(1): 147-153. |
| [8] | Cappa S, Reynaerts D, Al-Bender F. A sub-nanometre spindle error motion separation technique[J]. Precision Engineering, 2014, 38(3): 458-471. DOI:10.1016/j.precisioneng.2013.12.011 |
| [9] | Grejda R D. Techniques for calibrating spindle with nanometer-error motion[J]. Precision Engineering, 2005, 29: 113-123. DOI:10.1016/j.precisioneng.2004.05.003 |
| [10] | Chen D, Fan J, Zhang F. An identification method for spindle rotation error of a diamond turning machine based on the wavelet transform[J]. International Journal of Advanced Manufacturing Technology, 2012, 63(5/6/7/8): 457-464. DOI:10.1007/s00170-012-3923-8 |
| [11] | The International Organization for Standardization. Test code for machine tools, part 7: geometric accuracy of axes of rotation: ISO 230-7-2015[S]. Switzerland: ISO, 2015. |
| [12] | Martin D L, Tabenkin A N, Parsons F G. Precision spindle and bearing error analysis[J]. International Journal of Machine Tools & Manufacture, 1995, 35(2): 187-193. |
| [13] | Ashok S D, Samuel G L. Modeling, measurement, and evaluation of spindle radial errors in a miniaturized machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59(5/6/7/8): 445-461. |
| [14] | The American Society of Mechanical Engineers. Axes of rotation: methods for specifying and testing: ASME B89.3.4-2010[S]. New York: ASME, 2010. |
| [15] | 陈辉, 胡元中, 王慧, 等. 粗糙表面分形特征的模拟及其表征[J]. 机械工程学报, 2006, 042(009): 219-223. (Chen Hui, Hu Yuan-zhong, Wang Hui, et al. Simulation and characterization of fractal features of rough surfaces[J]. Chinese Journal of Mechanical Engineering, 2006, 042(009): 219-223.) |
| [16] | 邢闽芳. 互换性技术测量[M]. 北京: 清华大学出版社, 2007. (Xing Min-fang. Interchangeability technical measurement[M]. Beijing: Tsinghua University Press, 2007.) |
