
 , 李清良
, 李清良 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2020-07-01
基金项目:国家自然科学基金资助项目(51775101);中央高校基本科研业务费专项资金资助项目(N2024002-18,N180306003).。
作者简介:修世超(1959-), 男, 内蒙古赤峰人, 东北大学教授, 博士生导师。
摘要:针对端面磨削加工接触表面热力学分布特征提出一种基于动态热力耦合效应的理论建模方法.首先, 建立多颗磨粒运动轨迹数学模型; 其次, 基于磨粒运动轨迹与磨粒高度的动态分布特征对加工工件磨削力进行解析求解; 根据求得的磨削力, 运用有限差分法(FDM)对端面磨削工件表面动态热力耦合过程进行分析; 最后, 分别采用有限元法(FEM)和端面磨削实验验证理论分析的合理性.结果表明: 动态热力耦合的均一化程度会引起加工工件表面轮廓高度的差异性, 减小砂轮转速可改善加工工件表面轮廓.
关键词:端面磨削动态热力耦合效应运动轨迹磨削力工件表面轮廓
Dynamic Thermal Mechanical Coupling Effect in Disc Grinding and Its Influence on Workpiece Material Removal Process
XIU Shi-chao, LU Yue, SUN Cong

 , LI Qing-liang
, LI Qing-liang School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: SUN Cong, E-mail: suncong1@mail.neu.edu.cn.
Abstract: A theoretical modeling method based on dynamic thermal mechanical coupling effect is proposed for the thermodynamic distribution characteristics of contact surfaces in disc grinding. Firstly, the mathematical model of movement trajectory of multiple abrasive grains is established. Then, the surface grinding force of the workpiece is modeled analytically based on the dynamic distribution characteristics of movement trajectory and the height of effective abrasive grains. Subsequently, the dynamic thermal mechanical coupling process on the workpiece surface is analyzed with the finite difference method (FDM) according to the grinding force. Lastly, the finite element method (FEM) and disc grinding experiment are applied to verify the rationality of the theoretical analysis respectively. The results show that the workpiece surface profile height is different due to the homogenization degree of the dynamic thermal mechanical coupling. The workpiece surface profile can be improved by reducing the speed of grinding wheels.
Key words: disc grindingdynamic thermal mechanical coupling effectmovement trajectorygrinding forceworkpiece surface profile
端面磨削加工, 砂轮与工件同时旋转, 以面干涉形式实现工件表面材料去除, 因其加工精度、自动化程度较高, 能够一次性对工件完成粗磨、半精磨、精磨和光磨, 提高了加工效率.为此, 端面磨削加工技术受到广泛关注[1].
加工工件质量好坏是影响实际工程进度的重要因素[2].因此, 人们对端面磨削过程作了大量的研究, 主要集中于磨粒运动轨迹、磨削力以及磨削裂纹等方面.Wang等[3]用磨粒轨迹离散点的标准差变异系数描述了端面磨削加工工件表面不均匀性, 并以实验测量的工件表面粗糙度(Ra)、非均匀系数和总厚度变化(TTV)进行验证.杨金双等[4]通过运动学分析构建了端面磨粒运动模型, 并基于离散统计法, 对磨粒轨迹均匀性进行定量评价.Sun等[5]建立了端面磨削力理论模型, 分析了晶圆径向距离和晶圆材料晶界取向对磨削力的影响, 并得出磨削力过大会使工件表面产生裂纹损伤的结论.以往研究重点分析了端面磨削的动态过程以及磨粒高度分布情况, 然而, 磨削过程中工件表面伴随着非线性动态热力耦合效应, 该效应分布的均一化程度会影响工件表面的去除效果.因此, 有必要分析磨削过程中的热力耦合效应对工件表面质量的影响.
针对粉末冶金不锈钢薄片工件的端面磨削加工过程, 本文建立了考虑有效磨粒的运动轨迹及其随机高度分布的端面磨削热力耦合数学模型, 分析端面磨削加工中热力耦合效应对工件表面轮廓的影响规律及去除机理.
1 端面磨削磨粒运动轨迹1.1 端面磨削加工原理如图 1所示, 本文采用HMP-108数控端面磨床, 配有双转轴、基体、端面CBN砂轮、托盘、给料盘和工件固定盘, 工件材料为粉末冶金不锈钢316L, 工件直径? 40 mm, 厚度4 mm.加工时, 砂轮与工件同时旋转, 砂轮竖直向下运动实现进给.
图 1(Fig. 1)
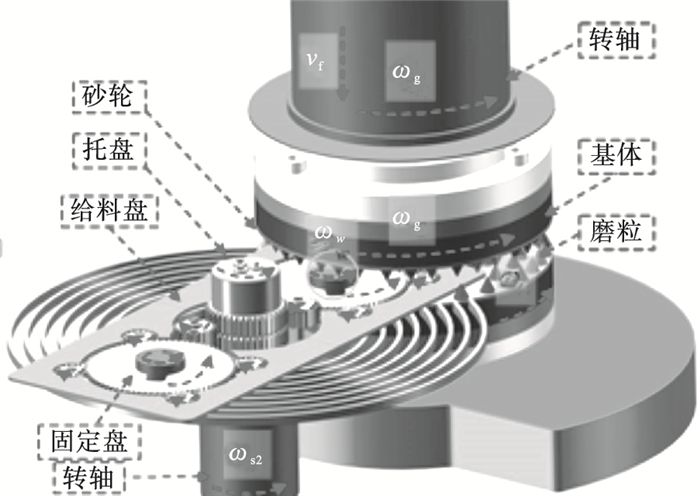 | 图 1 端面磨削系统加工原理Fig.1 Machining principle of disc grinding system |
1.2 磨粒运动轨迹模型工件表面的磨粒轨迹是由多颗有效磨粒与工件表面发生干涉形成的, 普通砂轮上的磨粒是随机分布的, 在加工塑性较大材料时, 往往容易阻塞砂轮磨粒间隙.本文采用工程砂轮[6]中的磨粒方形排布形式, 如图 2所示.
图 2(Fig. 2)
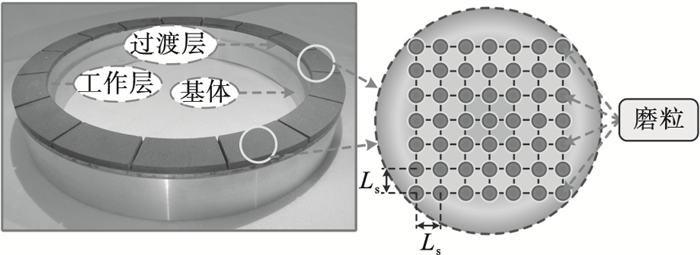 | 图 2 端面砂轮磨粒排布图Fig.2 Diagram of grain arrangement of disc grinding wheels |
根据加工原理, 在砂轮与工件工作表面建立2个坐标系, 分别对应全局坐标系XOY和局部坐标系xoy, 数学原理如图 3所示.
图 3(Fig. 3)
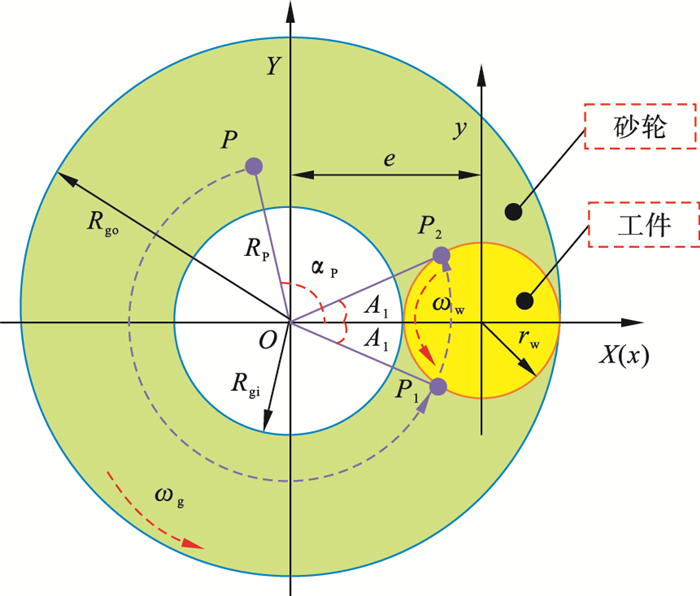 | 图 3 端面磨削磨粒运动学示意图Fig.3 Kinematics diagram of disc grinding abrasive grain |
图中: Rgi和Rgo为砂轮的内外半径, 分别为110 mm和150 mm; rw为工件半径; e为砂轮与工件的圆心距; P为端面砂轮上的任意磨粒; RP和αP分别为磨粒P在全局坐标系中的极径和极角; 2A1为磨粒与工件发生干涉的转角.磨粒P的初始坐标为
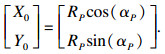 | (1) |
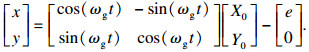 | (2) |
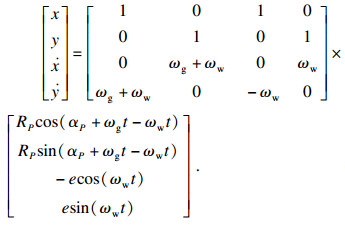 | (3) |
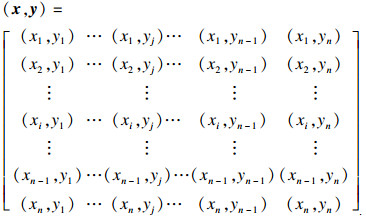 | (4) |
2 端面磨削热力耦合模型2.1 端面磨削动态磨削力分析磨粒轨迹是为了计算磨削力.在端面磨削过程中, 每颗有效磨粒都可看成是具有负前角的切削刃, 假定磨粒结构为尖端带有微平磨损面的圆锥体, 磨削力由三部分构成, 切削力、划擦力和耕犁力[7], 单颗磨粒切削机理如图 4所示.
图 4(Fig. 4)
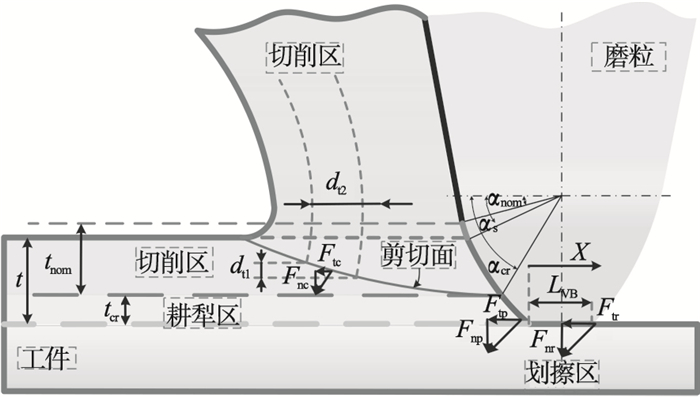 | 图 4 单颗磨粒切削机理Fig.4 Cutting mechanism of single abrasive |
图中: LVB为磨损面长度; αcr和αnom分别为磨粒的临界刃倾角和名义刃倾角; tnom为名义未变形切屑厚度; t为未变形切屑厚度; tcr为由磨粒形状确定的临界未变形切屑厚度.单颗磨粒磨削力受未变形切屑厚度的影响较大, 假设未变形切屑截面呈三角形, 可得体积连续性表达式[8]:
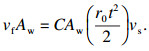 | (5) |
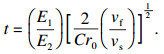 | (6) |
1) 切削力.切向切削力Ftc和法向切削力Fnc.
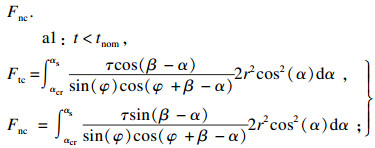 | (7) |
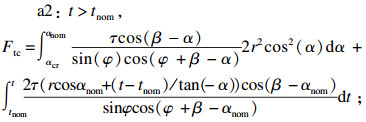 | (8) |
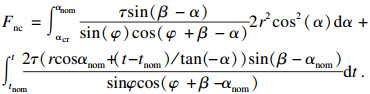 | (9) |
2) 耕犁力.切向耕犁力Ftp和法向耕犁力Fnp分别为
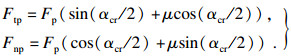 | (10) |
3) 划擦力.切向划擦力Ftr和法向划擦力Fnr分别为
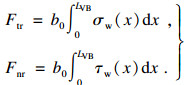 | (11) |
总的切向磨削力为
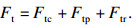 | (12) |
图 5(Fig. 5)
 | 图 5 动态切向磨削力分布Fig.5 Distribution of dynamic tangential grinding force (a)—0.1 s;(b)—0.2 s;(c)—0.6 s. |
2.2 端面磨削动态磨削热FDM模型将加工表面视为二维FDM模型传热平面, 将工件分成有限个网格, 如图 6所示, 每个网格区域中心可视为有效磨粒与工件相接触而形成的热源, 热源散发的热量在网格间相互传递, 网格间的距离定义为Δx=Δy=Δl; 而后, 通过传热偏微分方程来描述端面磨削温度场的形成过程[10]:
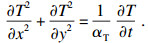 | (13) |
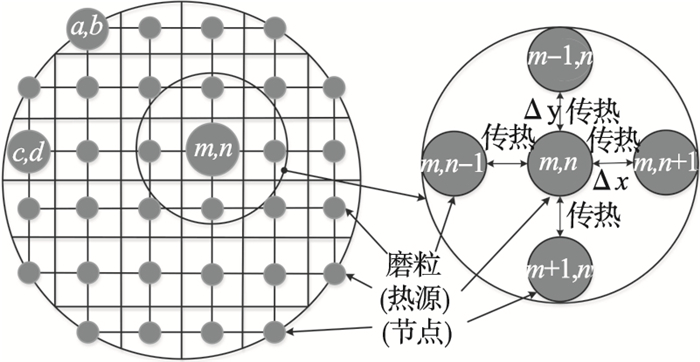 | 图 6 FDM传热模型图Fig.6 Illustration of the FDM heat tansfer model |
式中, αT为热扩散系数,
以差分形式对式(13)进行推导, 可得
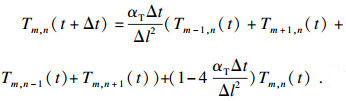 | (14) |
结合传热边界条件, 如图 7所示, 可得
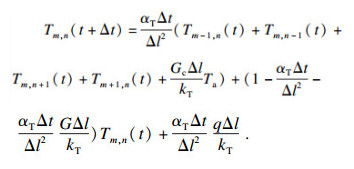 | (15) |
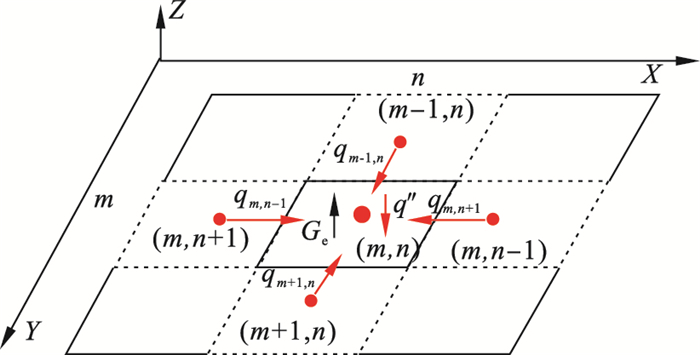 | 图 7 FDM边界条件Fig.7 Boundary conditions of FDM |
式中: Ta为环境温度; Gc为综合对流换热系数.磨粒产生的热流密度q可表示为[11]
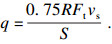 | (16) |
根据FDM磨削传热过程, 不同工况下的温度分布如图 8所示.从图中可以看出, 工件表面温度分布不均匀, 工件边缘区域的温度较高, 进而导致工件表面发生不同程度的微观形变, 因此, 相对于温度较低的工件中心区域, 距工件中心较远的区域会被去除更多的表面材料.此外, 磨削温度随砂轮转速的增大而升高, 因而, 较高的砂轮转速会增大工件表面材料去除的不均匀性.
图 8(Fig. 8)
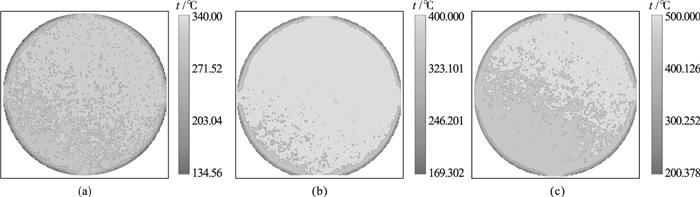 | 图 8 FDM模型中不同转速下的温度分布Fig.8 Temperature distribution under different speeds in FDM model (a)—ng=500 r/min, nw=60 r/min; (b)—ng=750 r/min, nw=60 r/min; (c)—ng=1 000 r/min, nw=60 r/min. |
2.3 端面磨削动态磨削热FEM模型为了验证提出的端面磨削动态温度场FDM模型的准确性, 应用FEM模型对端面磨削动态温度场进行验证分析.将FDM热力耦合计算得到的动态热流密度载荷与对流换热载荷以表格的形式加载到有限元模型中, 建模流程与计算结果分别如图 9与图 10所示.
图 9(Fig. 9)
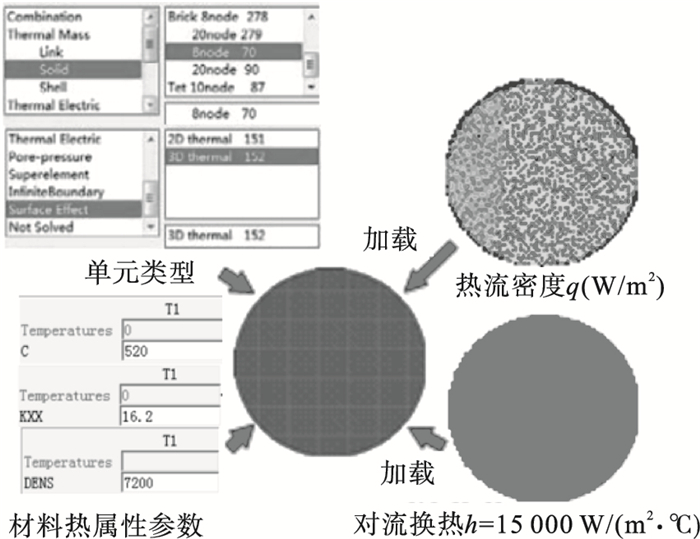 | 图 9 FEM建模过程Fig.9 FEM modeling process |
图 10(Fig. 10)
 | 图 10 FEM模型中不同转速下的温度分布Fig.10 Temperature distribution under different speeds in FEM model (a)— ng=500 r/min, nw=60 r/min; (b)—ng=750 r/min, nw=60 r/min; (c)—ng=1 000 r/min, nw=60 r/min. |
从图 10可以看出, 工件表面温度分布不均匀, 距工件中心较远的区域温度较高.此外, 端面磨削温度随砂轮转速的增加而升高, 温度分布差异也变得更加明显, 因此, 加工工件表面材料形变规律与FDM模型分析规律相似.
如图 11所示, 分别采用FDM与FEM模型计算所得工件中心区域温度变化结果.可以看出, 在不同磨削条件下, FEM与FDM计算结果均匹配良好.因此, 本文所建立的FDM模型可以有效预测端面磨削热力耦合过程.
图 11(Fig. 11)
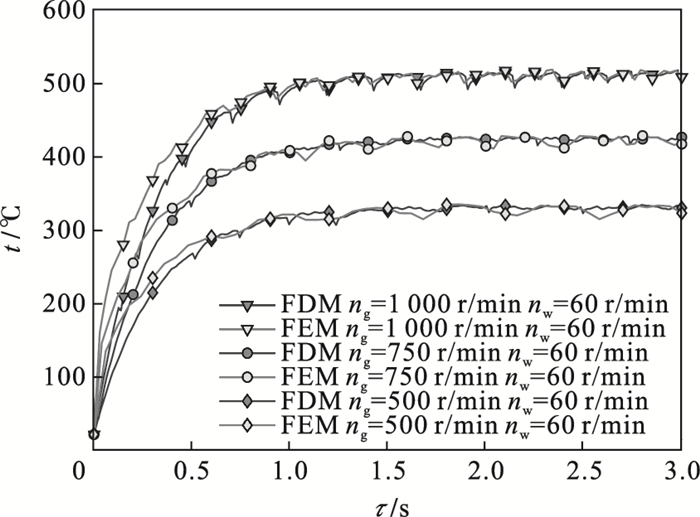 | 图 11 FDM模型与FEM模型温度计算结果对比Fig.11 Comparison of temperature calculation results between FDM model and FEM model |
3 实验研究本文对圆形片状工件进行端面磨削, 工件的径厚比(直径与厚度的比值)相对较大, 端面磨削加工接触区呈全覆盖状态, 加工过程不易直接观测, 因此, 可通过测量被加工工件表面高度进行间接分析.为验证上述端面磨削热力耦合效应的研究规律, 进行了具体的端面磨削实验.
图 12为采用DVM6超景深显微镜对工件表面观测的结果.选择两种观测位置, 中心区域和边缘区域.可以看出, 加工工件表面的轨迹分布差异性明显, 边缘区域轨迹分布比中心区域轨迹分布更均匀, 这是由于工件表面的动态热力耦合分布不均, 致使工件表面各区域的材料形变量不同, 进而使得磨削工件表面呈现不同的去除效果, 实验观测结果与模型分析结果一致.研究发现, 加工工件表面存在高度差.因此, 有必要对不同工况下的热力耦合效应引起的工件表面加工高度差进行分析.
图 12(Fig. 12)
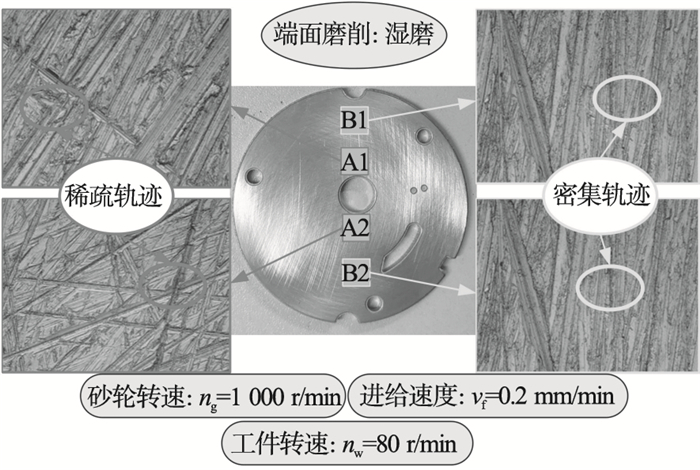 | 图 12 工件微观表面去除效果Fig.12 Removal effect of the workpiece micro surface |
以工件边缘所处水平面为零基准面, 用千分表沿工件半径方向求得加工工件表面高度差均值.实验结果如图 13所示, 可以发现, 工件中心区域与边缘区域存在高度差, 工件表面存在"中凸"状, 且中凸现象随砂轮转速的增加越加明显.上述现象与理论分析结果基本一致, 端面磨削工件表面材料去除效果主要受砂轮与工件相对运动影响, 而由于不同位置的磨粒与工件表面相对运动程度不同, 使加工工件表面动态热力耦合分布呈现一定的不均匀性, 这会引起加工表面材料去除的差异性, 结合本文的理论与实验分析, 在保证加工效率的前提下, 可适当降低砂轮速度来改善加工工件表面轮廓.
图 13(Fig. 13)
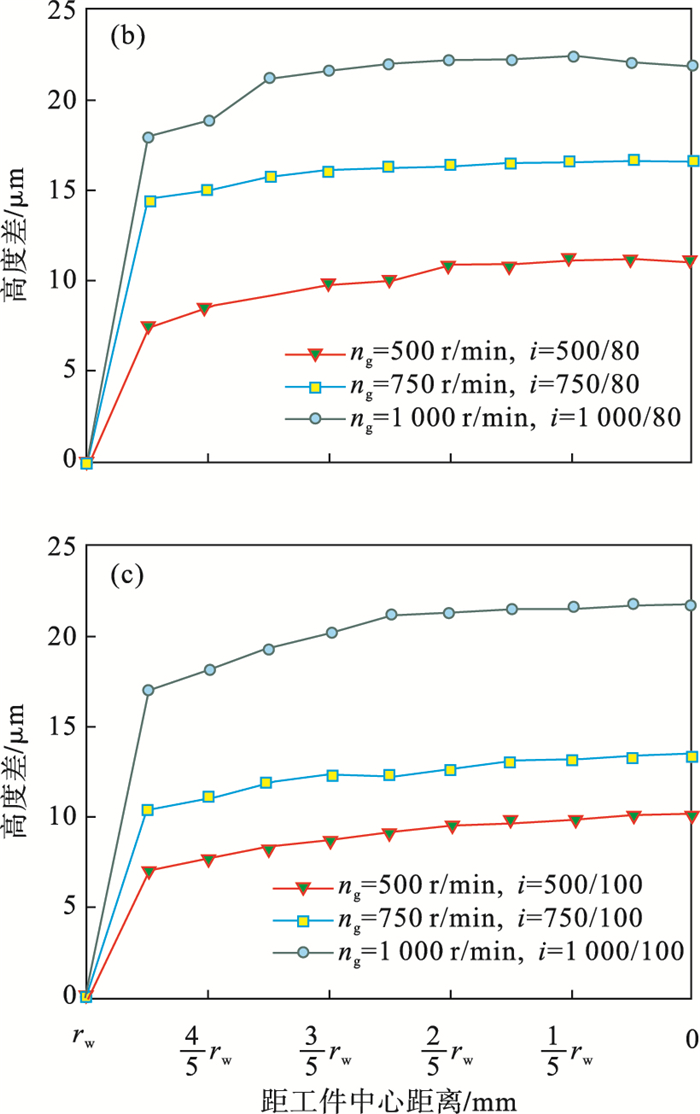 | 图 13 工件表面高度差测量结果Fig.13 Measured height difference of the workpiece surface (a)—nw=60 r/min; (b)—nw=80 r/min; (c)—nw=100 r/min. |
4 结论1) 工件表面所受动态磨削力呈带状分布, 距工件中心较远的区域磨削力较大.
2) 工件表面动态磨削温度先升高, 而后趋于稳定; 温度在工件表面的区域性分布明显, 工件边缘区域温度较高.
3) 工件表面动态热力耦合分布不均会导致其表面高度分布不均, 工件中心区域相对工件边缘的高度差较大; 此外, 在保证加工效率的前提下, 应适当降低砂轮转速以获得较好的加工表面轮廓精度.
参考文献
| [1] | 孙聪, 李清良, 修世超, 等. 端面磨削加工工件表面材料的去除机理[J]. 东北大学学报(自然科学版), 2020, 41(3): 393-398. (Sun Cong, Li Qing-liang, Xiu Shi-chao, et al. Workpieces' surface material removal mechanism of disc grinding[J]. Journal of Northeastern University (Natural Science), 2020, 41(3): 393-398.) |
| [2] | 陈鑫, 王栋, 刘昱范. 高速磨削对18CrNiMo7-6表面完整性的影响研究[J]. 表面技术, 2018, 47(9): 259-265. (Chen Xin, Wang Dong, Liu Yu-fan. Influence of high speed grinding on surface integrity of 18CrNiMo7-6[J]. Surface Technology, 2018, 47(9): 259-265.) |
| [3] | Wang L, Hu Z, Fang C, et al. Study on the double-sided grinding of sapphire substrates with the trajectory method[J]. Precision Engineering, 2017, 51: 308-318. |
| [4] | 杨金双, 朱祥龙. 行星式双面研磨轨迹均匀性研究[J]. 机械研究与应用, 2015, 28(6): 41-43. (Yang Jin-shuang, Zhu Xiang-long. Research on uniformity of trajectory in planetary double-side lapping process[J]. Mechanical Research and Application, 2015, 28(6): 41-43.) |
| [5] | Sun J, Qin F, Chen P, et al. A predictive model of grinding force in silicon wafer self-rotating grinding[J]. International Journal of Machine Tools and Manufacture, 2016, 109: 74-86. DOI:10.1016/j.ijmachtools.2016.07.009 |
| [6] | Koshy P, Iwasald A, Elbestawl M. Surface generation with engineered diamond grinding wheels: insights from simulation[J]. CIRP Annals, 2003, 52(1): 271-274. DOI:10.1016/S0007-8506(07)60582-4 |
| [7] | Sun C, Liu Z, Lan D, et al. Study on the influence of the grinding chatter on the workpiece's microstructure transformation[J]. The International Journal of Advanced Manufacturing Technology, 2018, 96(9/10/11/12): 3861-3879. DOI:10.1007/s00170-018-1794-3 |
| [8] | Malkin S, Guo C. Grinding technology: theory and applications of machining with abrasives[J]. International Journal of Machine Tools & Manufacture, 1991, 31(3): 435-436. |
| [9] | Zhang Z, Song Y, Xu C, et al. A novel model for undeformed nanometer chips of soft-brittle HgCdTe films induced by ultrafine diamond grits[J]. Scripta Materialia, 2012, 67(2): 197-200. DOI:10.1016/j.scriptamat.2012.04.017 |
| [10] | Sun C, Duan J, Lan D, et al. Prediction about ground hardening layers distribution on grinding chatter by contact stiffness[J]. Archives of Civil and Mechanical Engineering, 2018, 18(4): 1626-1642. DOI:10.1016/j.acme.2018.06.010 |
| [11] | 吴玉厚, 王浩, 李颂华, 等. 氮化硅陶瓷磨削热特性与表面成形机制[J]. 表面技术, 2019, 48(12): 360-368. (Wu Yu-hou, Wang Hao, Li Song-hua, et al. Grinding thermal characteristics and surface forming mechanism of silicon nitride ceramics[J]. Surface Technology, 2019, 48(12): 360-368.) |
