马辉, 于明月, 高昂, 赵晨光
东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2020-09-01
基金项目：国家自然科学基金资助项目(11972112)。
作者简介：马辉(1977-), 男, 河北衡水人, 东北大学教授, 博士生导师。

摘要：为仿真栓接结合部非线性动力学特性, 提出一种基于非线性横观各向同性虚拟材料的栓接结合部动力学建模方法.基于有限单元法, 利用8节点实体单元构建被连接件及用来等效栓接结合部的横观各向同性虚拟材料层, 虚拟材料层与被连接件固接.采用非线性虚拟材料等效栓接结合部, 以模拟含栓接结合部结构在不同幅值的外简谐激振下所体现出的非线性刚度特性.为提高非线性模型计算精度, 将非线性横观各向同性虚拟材料层进行分区处理, 每个区域虚拟材料参数分别由该区域虚拟材料的形变确定.最后, 对模型进行局部降维, 在时域下求解模型的幅频响应, 通过对比仿真计算结果和试验结果, 验证所提出建模方法的可行性与有效性.
关键词：栓接结合部虚拟材料有限元方法非线性刚度分区建模局部降维
Dynamic Modeling Method of Bolted Joint Interfaces Based on Nonlinear Transversely Isotropic Virtual Material
MA Hui, YU Ming-yue, GAO Ang, ZHAO Chen-guang
School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: MA Hui, E-mail: mahui_2007@163.com.

Abstract: To simulate the nonlinear dynamic characteristics of bolted joint, a dynamic modeling method of bolted joint based on nonlinear transversely isotropic virtual material is proposed. Based on the finite element method, 8-node solid elements are used to construct the connected parts and the bolted joint that is simulated by the transversely isotropic virtual material, and the virtual material is fixed to the connected parts. The nonlinear virtual material is used to simulate the nonlinear stiffness characteristics of the bolted joint under different external harmonic excitation forces. In order to make the calculation of the nonlinear model more accurate, the nonlinear transversely isotropic virtual material is partitioned, and the virtual material parameters of each region are determined by the deformation of the virtual material in the region. Finally, the dimension of the model is reduced partly and the amplitude frequency response of the model is solved in time domain. The feasibility and effectiveness of the as-proposed modeling method are verified by comparing the theoretical calculation results with that of the experiments.
Key words: bolted jointvirtual materialfinite element methodnonlinear stiffnesspartition modelinglocal dimensionality reduction
栓接结合部广泛存在于航空发动机转子系统中, 且栓接结合部的存在对转子系统的动力学响应有很大影响^[1-4], 因此, 在对含螺栓连接的转子系统进行动力学建模仿真时, 对栓接结合部的建模是不可省略的.建立栓接结合部的精细模型可以较精确地求解其动力学特性, 但对于发动机转子这类大型复杂构件, 精细模型会使整体模型的维度大幅增加而导致求解困难, 因此, 对含栓接结合部结构进行动力学建模时, 合理等效栓接结合部对后续的仿真分析至关重要.含栓接结合部结构在受外部简谐激振时会由于栓接结合部的存在体现出刚度非线性, 也称刚度渐软特性^[5].具体表现为当结构受外部简谐激励时, 结构共振频率相对结构固有频率减小, 且减小程度随简谐激振力幅值增大而增大.为仿真分析这一非线性刚度特性, 构建栓接结合部等效非线性模型是必要的.
虚拟材料法是比较常见的栓接结合部等效建模方法^[6-10].而采用虚拟材料法对含栓接结合部结构进行建模分析的文章大多将虚拟材料参数设为线性且各向同性的.通过观察栓接结合部的实际结构, 可以发现连接件对被连接件的作用力明显是各向异性的.考虑到这一实际情况, 将虚拟材料参数, 尤其是弹性模量, 设为各向异性更为合理.张晓霞等^[11]推导了完整的正交各向异性材料本构关系式.陈冲^[12]基于此理论研究了正交各向异性结合部建模方法.张学良等^[13]利用横观各向同性虚拟材料对栓接结合部进行等效, 并应用接触分形理论推导了虚拟材料各向材料参数表达式.这种横观各向同性材料是正交各向异性材料的一种特殊情况, 材料属性在相互正交的两个切向方向同性, 更适用于栓接结合部的等效; 但文献[13]所建模型为线性模型, 无法用于分析栓接结构非线性动力学特性.
许腾云^[14]利用分形理论和赫兹接触理论推导出用于等效机械结合部的虚拟材料的弹性模量与应力关系是非线性的, 并将虚拟材料层按接触面压力分布划分为多个区域, 每个区域根据该区域所受压力单独赋予弹性模量.这一分区建模方法更贴合实际.但文献[14]中只对螺栓连接结构进行了模态分析与静力分析, 未说明所提出建模方法是否可用于仿真螺栓连接结构在受外简谐激振时所体现出的刚度非线性, 且采用的虚拟材料为各向同性材料.
借鉴以上文章经验, 本文提出一种基于非线性横观各向同性虚拟材料构建考虑栓接结合部刚度非线性的动力学模型的分区建模方法.首先, 基于8节点实体单元用虚拟材料法对含栓接结合部结构进行有限元建模, 以各向同性单元构建被连接件, 以横观各向同性单元构建虚拟材料层.基于接触分形理论求出横观各向同性虚拟材料的各材料参数并以模态测试结果为目标对材料参数进行优化.对虚拟材料进行分区处理, 提出非线性材料属性与材料应变关系式; 以扫频试验所得幅频响应为目标, 利用二分法确定非线性材料属性公式中的待定参数, 得到非线性模型.最后, 将所提出理论用于实例计算, 以验证本文提出的建模方法的正确性和可行性.
1 基于横观各向同性虚拟材料的栓接结合部线性有限元模型构建1.1 有限元模型构建基于虚拟材料法构建栓接结合部线性有限元模型, 被连接结构和虚拟材料层均由8节点实体单元构成.其中, 构成被连接结构的单元材料属性各向同性, 构成虚拟材料的单元材料属性横观各向同性, 即虚拟材料在螺栓连接接触面法向与切向上材料属性相互独立, 在两正交切向上材料属性相同.所建线性模型如图 1所示.
图 1(Fig. 1)

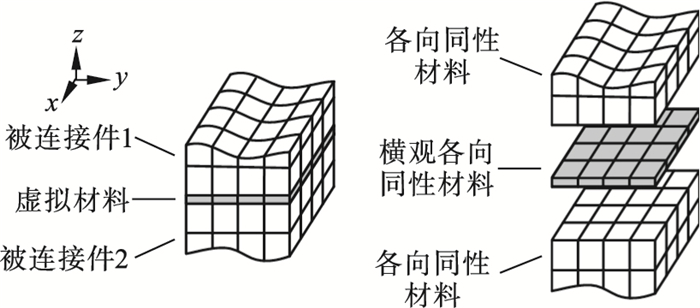图 1 基于虚拟材料法所建栓接结合部实体单元模型示意图Fig.1 Schematic diagram of bolted joint interface solid element model based on virtual material method

局部坐标系ξηζ下8节点实体单元如图 2所示.
图 2(Fig. 2)

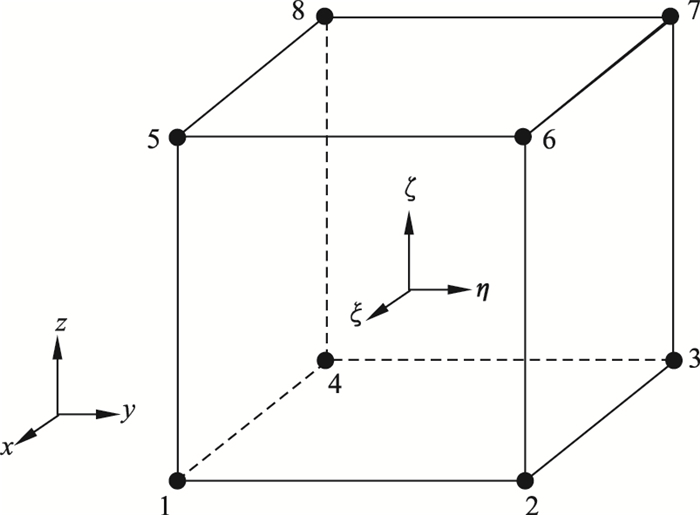图 2 实体单元示意图Fig.2 Schematic diagram of the solid element

在局部坐标系ξηζ中, 一个8节点实体单元的几何形状是正方体, 此正方体由ξ=－1，ξ=1，η=－1，η=1，ζ=－1和ζ=1六个平面围成, 如图 2所示, 每节点有三个自由度, 分别是沿x，y，z轴方向的平动.
实体单元各节点的形函数为

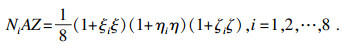(1)

形函数矩阵为

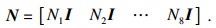(2)

其中, I为3×3阶单位矩阵.
对于各向同性材料, 弹性矩阵为

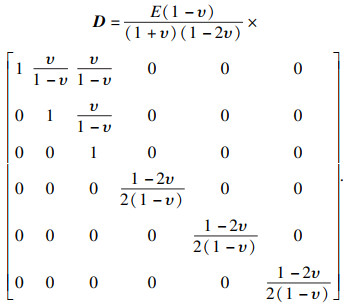(3)

式中: E为各向同性材料的弹性模量; υ为各向同性材料的泊松比.
对于正交各向异性材料, 弹性矩阵为

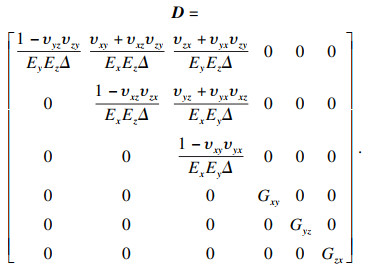(4)

其中,

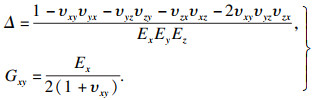(5)

式中: E_x, E_y和E_z分别为正交各向异性材料在x, y和z轴方向上的弹性模量; G_xy为材料在x-y平面内沿x轴方向剪切的切变模量; υ_xy为材料在x-y平面内沿x轴方向拉压的泊松比.其余符号含义依此类推, 且正交各向异性材料满足:

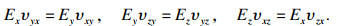(6)

将式(5)和式(6)代入式(4)可得, 正交各向异性材料的弹性矩阵中有9个相互独立的参数.设材料x轴方向和y轴方向属性各向同性, 即材料为横观各向同性材料, 其弹性矩阵中有5个相互独立的参数, 分别是E_x, E_z, υ_xy, υ_zx和G_zx.
8节点实体单元几何矩阵为

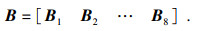(7)

其中,

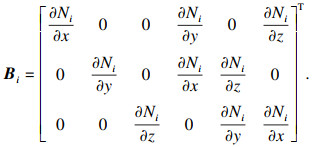(8)

8节点实体单元的单位刚度矩阵K_e和单位质量矩阵M_e分别为

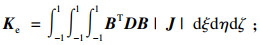(9)

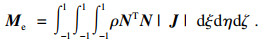(10)

其中: J为雅克比矩阵; ρ为单元密度.
利用上述8节点实体单元理论分别求得被连接件和虚拟材料的刚度矩阵和质量矩阵, 并进行总刚度矩阵和总质量矩阵组集, 即可得到基于等效横观各向同性虚拟材料的栓接结合部线性有限元模型.其中, 式(9)和式(10)可用两点高斯积分公式求解.
1.2 线性参数确定除结构尺寸参数外, 约束边界下的基于横观各向同性虚拟材料栓接结构的线性有限元模型中待定参数包括被连接件材料属性、虚拟材料层的材料属性和弹支边界处的弹支刚度.其中, 被连接件材料属性和弹支刚度可分别以自由边界下被连接试件模态测试结果和约束边界下螺栓连接试件模态测试结果为目标优化得到.优化算法不是本文重点, 不再展开叙述.
本文在确定横观各向同性虚拟材料属性时, 先由接触分形理论给定各待定材料属性初始参考值, 再以自由边界下螺栓连接试件模态测试结果为目标优化出虚拟材料各材料属性数值.
基于接触分形理论, 虚拟材料层沿x轴方向的弹性模量E_x可由式(11)确定^[13]:

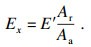(11)

其中,

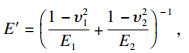(12)

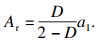E₁, E₂和υ₁, υ₂分别为两被连接件的弹性模量和泊松比; A_a为结合部名义接触面积; A_r为结合部实际接触面积, 可由式(13)求得

(13)

式中D为分形维度, 确定分形维度需要借助精密测量仪器并进行复杂的运算^[15].在本文后续计算中, 考虑到通用性, 直接利用已有资料, 结合接触表面粗糙度、加工工艺等对分形维度进行初步估算, 并基于试验结果对根据分形维度求出的材料参数进行修正.a_l为最大微接触点面积, 可参照文献[16], 根据结合面法向总载荷表达式反推出.
虚拟材料沿z轴方向的弹性模量E_z为

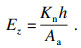(14)

式中: h为虚拟材料层厚度, 与两接触面微凸体高度有关; K_n为结合部法向等效刚度, 根据文献[16]中有关公式求出.虚拟材料的υ_xy和υ_zx约等于0^[13].
综上所述, 由接触分形理论可确定横观各向同性材料弹性矩阵中5个相互独立参数中的4个, 而G_zx需根据模态测试结果优化得到.虚拟材料的密度对仿真结果影响不大, 可设为0.由接触分形理论求得的虚拟材料各向材料参数数值可能由于加工误差或分形参数确定不合理等因素与实际值偏差较大, 应以接触分形理论公式求得的数值为参考, 以模态测试结果为目标, 适时调整, 以得出使仿真结果尽量贴近模态测试结果的有限元模型参数.
2 基于横观各向同性虚拟材料的栓接结合部非线性有限元模型构建含螺栓连接结构在其不同阶次固有频率附近所体现出的动力学特性非线性程度不同, 所以用于求解不同阶次固有频率附近的幅频响应的非线性模型对应的非线性参数也不同^[17-18].首先要明确所建非线性模型只用于反映含栓接结合部结构某一阶次的非线性动力学特性.确定仿真阶次后, 将对这一阶次固有频率影响最显著的材料属性设为非线性材料属性.
以图 3所示螺栓连接板结构为例, 工程中最关注的是其弯曲模态, 而虚拟材料垂直板面方向的弹性模量E_z对螺栓连接板结构弯曲模态影响最大.设E_z与虚拟材料层z轴方向形变呈非线性关系, 其余虚拟材料属性为固定值.
图 3(Fig. 3)

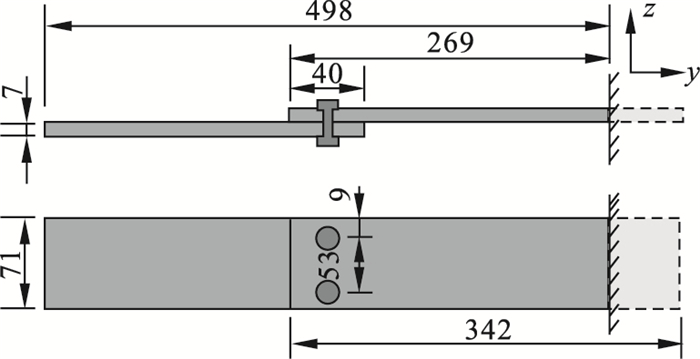图 3 螺栓连接板结构示意图(单位: mm)Fig.3 Structure of bolted connection plate(unit: mm)

本文将非线性弹性模量设为与虚拟材料形变有关的分段线性参数.考虑到螺栓连接处拉压非线性特性, 设虚拟材料压缩时E_z为定值.虚拟材料层垂直板面方向的非线性弹性模量E_z与虚拟材料层z轴方向变形量Δh关系式如下:

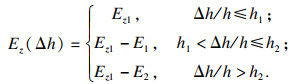(15)

式中: E_zl为线性模型中虚拟材料z轴方向线性弹性模量; h₁, h₂, E₁和E₂为待定参数, 依据扫频试验所得幅频响应结果由二分法求得; h为虚拟材料厚度.
以图 3所示螺栓连接板结构为例, 由虚拟材料法构建的螺栓连接板结构有限元模型处于弯曲模态时的虚拟材料层变形情况如图 4所示.
图 4(Fig. 4)

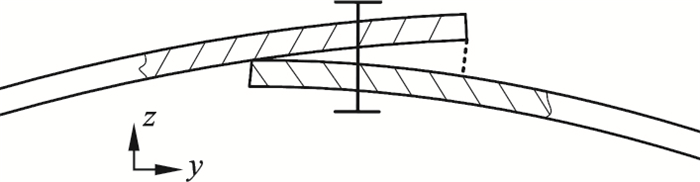图 4 螺栓连接板结构处于弯曲模态时螺栓结合部的变形Fig.4 Bolt joint deformation of bolt connection plate in bending mode

由图 4可见, 当模型处于弯曲模态时, 虚拟材料法向变形沿板长方向各处不同.此时, 由每个单元的应变确定对应单元的非线性材料属性数值需要大量计算时间; 而由一点处应变确定整个虚拟材料的非线性材料属性是不准确、不合理的.本文引入分区建模思想, 在构建如图 3所示螺栓连接板结构非线性有限元模型时, 将虚拟材料层沿板长方向等分成若干区域, 每一区域的虚拟材料非线性弹性模量E_z由该区域虚拟材料层上下面中心节点的z轴方向相对位移代入式(15)确定.由此建立的基于等效横观各向同性虚拟材料的栓接板结构非线性有限元分区模型示意图如图 5所示.
图 5(Fig. 5)

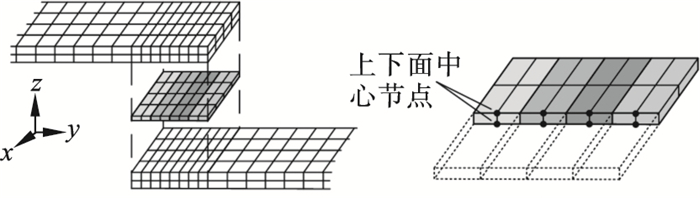图 5 虚拟材料层分区处理示意图Fig.5 Schematic diagram of virtual material layer partition processing

在时域下求解结构的幅频响应耗时较多, 为提高计算效率对模型进行降维.采用固定界面法^[19]将模型的线性部分进行降维, 保留非线性单元节点和幅频响应输出节点(拾取点)的各自由度.
对于无阻尼结构系统, 其自由振动方程为

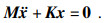(16)

式中: M为质量矩阵; K为刚度矩阵; x为位移向量; 为加速度向量.首先, 对整体结构进行划分.对于利用本文方法构建的含螺栓连接结构非线性有限元模型, 保留构成虚拟材料的实体单元节点对应的自由度和拾取点的各自由度, 其余自由度降维.
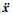
在固定界面法中, 保留自由度称为界面自由度, 降维自由度称为非界面自由度.将整体位移x分为非界面位移x_i和界面位移x_j, 重新排列后的位移向量为x=[x_i, x_j]^T.将式(16)中质量矩阵M和刚度矩阵K各维度进行重新排列, 使矩阵自由度与重新排列后的位移向量自由度相对应.划分后, 式(16)可写为

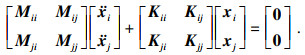(17)

将界面完全固定, 即x_j=0, 代入式(17), 得振动方程:

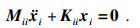(18)

由式(18)解出正则化模态集Ψ_n, Ψ_n=[Ψ_l, Ψ_h], 并保留低阶模态集Ψ_l, 低阶模态集的维度为模型非界面自由度数×降维维数.降维维数的选定要同时保证降维后模型的精度和计算效率.
由式(19)求解约束模态Ψ_J,

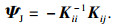(19)

Ritz基向量矩阵为

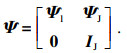(20)

式中I_J为单位矩阵.得到Ritz基向量矩阵后即可对动力学方程进行降维.降维前的含阻尼系统的受迫振动方程为

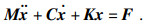(21)

式中: C为阻尼矩阵; 为速度向量; F为外力向量.
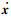
对方程中各矩阵维度进行重新排列, 排列方式与求取Ritz基向量矩阵时对质量和刚度矩阵维度重新排列顺序一致.维度重新排列后的振动方程为

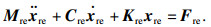(22)

对方程中各元素进行降维:

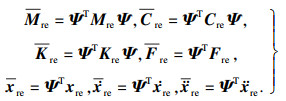(23)

得到模态坐标下的振动方程:

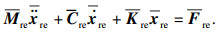(24)

基于所建非线性有限元模型, 求解含螺栓连接结构在受外部简谐激励时某一阶模态附近的幅频响应流程图如图 6所示.
图 6(Fig. 6)

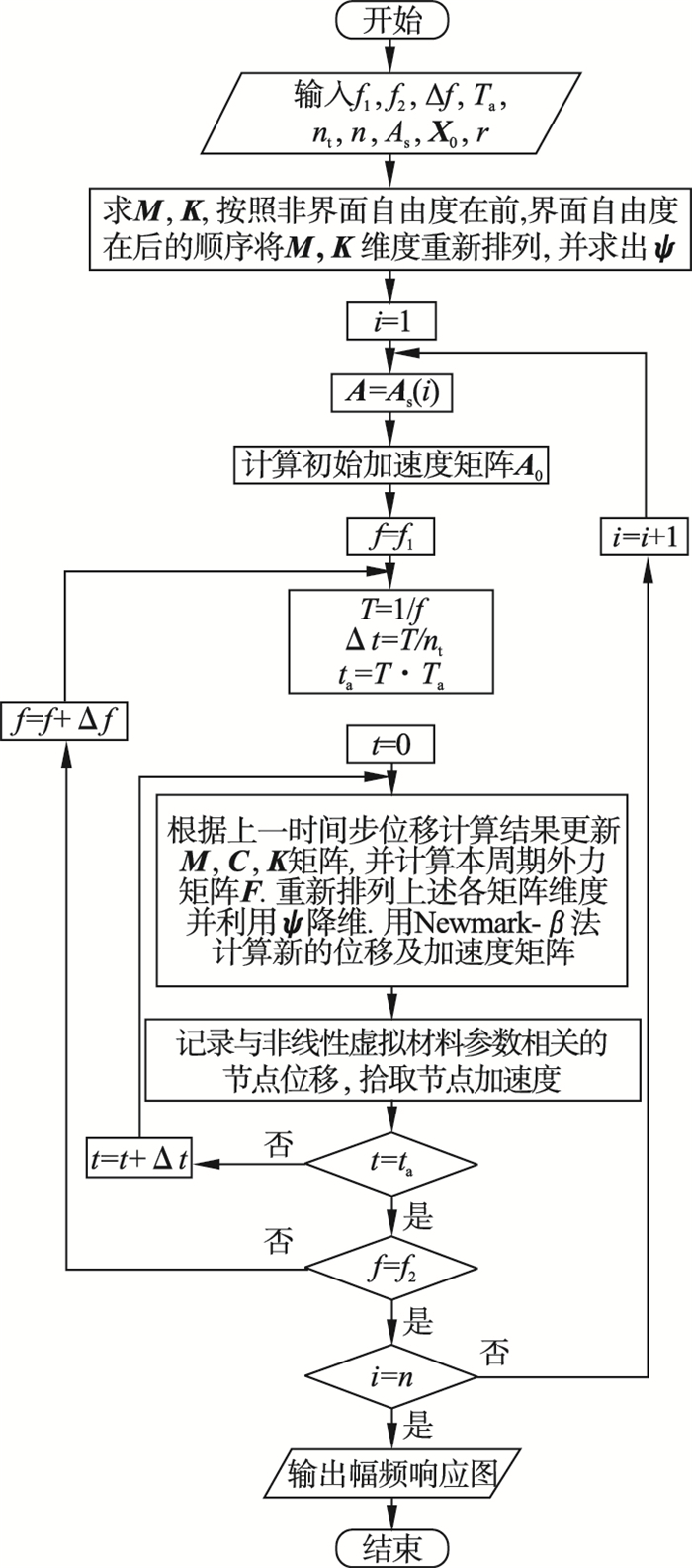图 6 基于非线性虚拟材料有限元模型求解系统幅频响应流程图Fig.6 Flow chart of the amplitude frequency response of the system with bolted joint based on the finite element model of the nonlinear virtual material

图 6中，f₁为扫频起始频率；f₂为扫频终止频率；Δf为仿真频率步长；n_t为每周期内时间步数；r为降维维度；T_a为每个频率下外简谐力施加周期数；n为不同激振加速度的对照组数；A_s=[A₁, A₂, …, A_n]为各组加速度激励值.
3 试验验证用于验证的螺栓连接板试件结构尺寸如图 3所示, 其中浅色部分为夹持部分.螺栓规格为M8, 螺栓拧紧力矩均为8 N·m.被连接板材料为45钢.对螺栓连接板试件在其第一阶弯曲固有频率附近进行正弦扫频激励, 激振加速度幅值分别为0.2 g, 1 g和2 g(g为重力加速度, m/s²).扫频试验所得幅频响应如图 7所示.
图 7(Fig. 7)

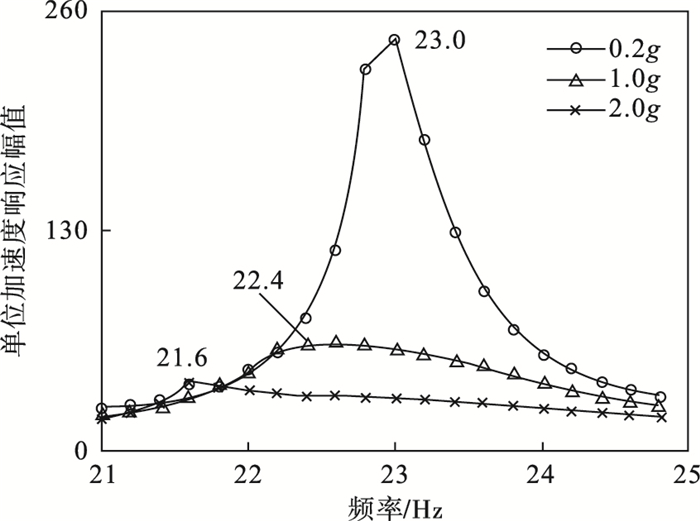图 7 螺栓连接板结构第一阶弯曲模态附近幅频响应Fig.7 Amplitude frequency response near the first bending mode of bolted plates structure

由图 7可见, 单位幅频响应曲线峰值对应的频率随激振加速度幅值增大而减小, 体现出刚度非线性特性.单位幅频响应曲线峰值随激振加速度的改变而变化, 体现出阻尼非线性特性^[20-21].
3.1 螺栓连接板结构线性有限元模型构建基于本文建模方法, 在Matlab中依次构建自由边界下单个被连接板和螺栓连接板有限元模型, 以及约束边界下螺栓连接板有限元模型，并在建模过程中依次以相应工况模态测试结果为目标, 对模型中待定参数进行优化，优化方法均采用粒子群遗传算法.线性模型建模流程如图 8所示.
图 8(Fig. 8)

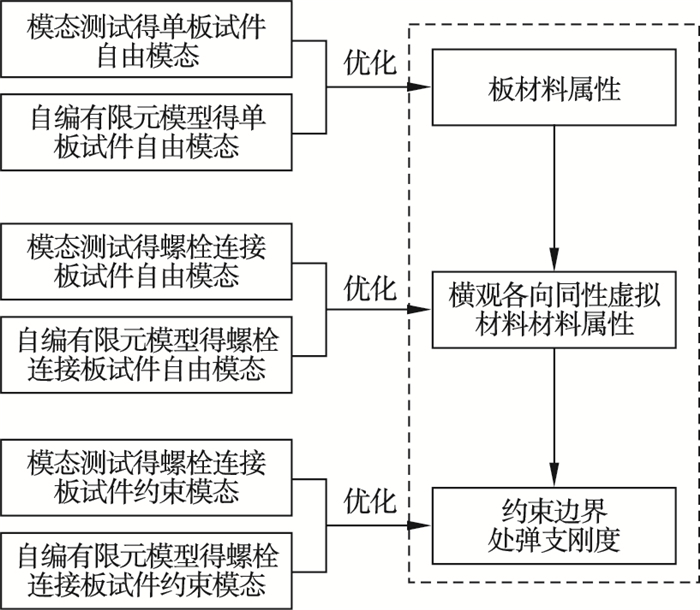图 8 基于等效横观各向同性虚拟材料的栓接板类结构线性有限元模型构建流程图Fig.8 Flow chart of constructing linear FEM of bolted plate structure based on equivalent transversely isotropic virtual material

优化目标函数为仿真所得固有频率结果与模态测试结果残差加权平方和最小, 即

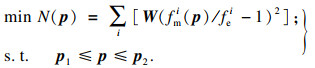(25)

式中: p为待优化参数向量; N(p)为目标函数; p₁和p₂分别为待优化参数的下界和上界; W为各阶模态相对权重的对角阵; f_eⁱ和f_mⁱ(p)分别为系统第i阶模态测试和仿真模态结果.
模态测试所用仪器: 东华信号采集系统DH5956;PCB力锤086C01, 灵敏度11.2 mV/N; 加速度传感器CA-YD-125, 灵敏度1.33 mV/(m·s^-2).
试验使用单向加速度传感器, 采用多点输入、单点输出的方法对试件进行模态测试, 通过配套的东华测试软件进行数据处理, 得到试件固有频率及振型.
基于实体单元理论构建自由边界下被连接板有限元模型, 设置被连接板材料属性优化初始值, 以自由边界下被连接板试件模态测试结果为目标对其材料属性数值进行优化, 优化结果如表 1所示.
表 1(Table 1)

表 1 被连接板材料属性优化前后数值Table 1 Material properties of connected plate before and after optimization 材料属性 优化前数值 优化后数值 弹性模量/ GPa 210 220 密度/(kg·m-3) 7 800.00 7 854.67 泊松比 0.300 0 0.305 3

表 1 被连接板材料属性优化前后数值 Table 1 Material properties of connected plate before and after optimization

优化后的仿真振型与被连接板自由模态测试所得振型一一对应, 试验与仿真所得被连接板试件前4阶固有频率对比见表 2.
表 2(Table 2)

表 2 自由边界下单个被连接板固有频率测试与仿真结果Table 2 Natural frequencies of single connected plate under free boundary obtained from modal test and simulation 阶次 模态测试结果/Hz 仿真分析结果/Hz 误差/% fn1 536.5 530.9 -1.04 fn2 1 193.0 1 184.7 -0.70 fn3 1 471.0 1 498.2 1.85 fn4 2 457.0 2 476.1 0.78

表 2 自由边界下单个被连接板固有频率测试与仿真结果 Table 2 Natural frequencies of single connected plate under free boundary obtained from modal test and simulation

表 2中, 仿真前4阶固有频率结果与试验对比误差在±2%以内, 说明优化得到的板材料参数合理, 后续建模中沿用此时的材料参数.
基于本文所述建模方法构建自由边界下螺栓连接板结构有限元模型, 利用式(11)~式(14)求得横观各向同性虚拟材料参数初始值.其中有关分形参数设置如下^{[13, 16]}: 材料表面分形维度D=1.424, 结合部名义接触面积A_a=0.002 84 m², 结合部实际接触面积A_r=3.921 65×10^-5 m², 栓接结合部等效法向刚度1.730 4×10¹⁰N/m, 虚拟材料层厚度h=1 mm.设x-z平面内沿x轴方向剪切的切变模量G_zx的优化初始数值与G_xy初始值相等.
将虚拟材料参数初始值代入有限元模型, 所得仿真振型结果与模态测试振型结果一一对应, 但此时试验与仿真各阶频率对比误差较大, 这可能是由加工误差或分形参数确定不合理等因素造成的.为减小误差累积, 以自由边界下螺栓连接板试件模态测试结果为目标优化横观各向同性虚拟材料5个相互独立的材料参数, 优化结果见表 3.
表 3(Table 3)

表 3 横观各向同性虚拟材料参数优化结果Table 3 Parameters optimization results of transversely isotropic virtual material 虚拟材料参数 优化初始值 优化结果 Ex(Ey)/Pa 1.675×109 1.951×107 Ez/Pa 6.513×109 6.265×107 Gzx(Gyz)/Pa 8.375×108 4.188×108 υxy 0 0 υzx 0 0

表 3 横观各向同性虚拟材料参数优化结果 Table 3 Parameters optimization results of transversely isotropic virtual material

虚拟材料参数优化后自由边界下螺栓连接板结构有限元仿真所得振型结果与模态测试振型结果一一对应, 优化前后仿真与试验所得前6阶固有频率对比情况见表 4.
表 4(Table 4)

表 4 自由边界下螺栓连接板固有频率测试与仿真结果Table 4 Natural frequencies of bolted plate under free boundary obtained from modal test and simulation 阶次 fn1 112.9 118.3 4.80 112.0 -0.80 fn2 319.8 324.2 1.38 319.3 -0.16 fn3 566.4 592.4 4.59 570.9 0.80 fn4 611.0 640.4 4.81 615.4 0.72 fn5 941.8 999.2 6.09 938.9 -0.31 fn6 1 017.0 1 076.2 5.82 1 030.1 1.29

表 4 自由边界下螺栓连接板固有频率测试与仿真结果 Table 4 Natural frequencies of bolted plate under free boundary obtained from modal test and simulation

在自由边界下螺栓连接板结构有限元模型的基础上构建约束边界下螺栓连接板结构有限元模型.以约束边界下螺栓连接板试件模态测试结果为目标优化模型弹支边界处各向弹支刚度数值, 结果见表 5.
表 5(Table 5)

表 5 弹支刚度优化结果Table 5 Optimization results of elastic support stiffness 弹支刚度方向 弹支刚度优化结果/(N·m-1) 垂直板面方向 2.735×108 沿板长方向 6.657×109 沿板宽方向 2.212×107

表 5 弹支刚度优化结果 Table 5 Optimization results of elastic support stiffness

弹支刚度优化后的约束边界下有限元模型振型仿真结果与模态测试振型结果一一对应, 试验与仿真前6阶固有频率对比情况见表 6.
表 6(Table 6)

表 6 约束边界下螺栓连接板固有频率测试与仿真结果Table 6 Natural frequencies of bolted plate under constrained boundary obtained from modal test and simulatio 阶次 fn1 fn2 fn3 fn4 fn5 fn6 模态测试结果/Hz 23.2 135.5 185.5 311.9 411.4 759.3 仿真分析结果/Hz 23.0 136.3 201.5 318.4 411.0 741.5 误差/% -0.95 0.62 8.63 2.08 -0.10 -2.34

表 6 约束边界下螺栓连接板固有频率测试与仿真结果 Table 6 Natural frequencies of bolted plate under constrained boundary obtained from modal test and simulatio

表 6中, 第一、二、五和六阶为弯曲模态, 第三阶为摆动模态, 第四阶为扭转模态.仿真结果与试验结果对比除第三阶误差较大, 其余阶次误差在±3%内.由于本文只关注弯曲模态, 不再继续优化.
仿真所得约束边界下螺栓连接板结构前4阶弯曲振型与试验振型对比如图 9所示.
图 9(Fig. 9)

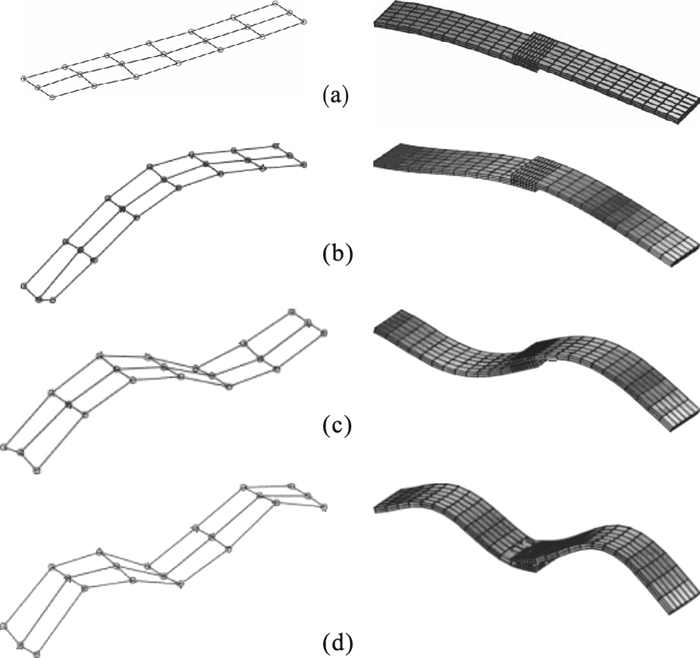图 9 弯曲振型的试验(左)与仿真(右)结果Fig.9 Test(left)and simulation(right)results of Bending mode (a)—第一阶; (b)—第二阶; (c)—第三阶; (d)—第四阶.

3.2 螺栓连接板结构非线性有限元模型构建设定仿真输出幅频响应在螺栓连接板结构第一阶弯曲模态附近.对模型进行敏感度分析, 确定对此结构第一阶弯曲固有频率影响最显著的虚拟材料属性.定义无量纲敏感度为

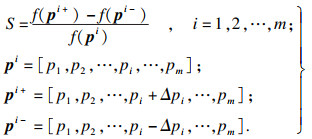(26)

式中: m为参与敏感度分析的虚拟材料参数个数, 考虑到泊松比对模态分析结果影响不大, 且其取值范围十分有限, 本文仅对表 3中除泊松比之外的其余3个横观各向同性虚拟材料独立参数进行敏感度分析, 即m=3, 其中p₁, p₂和p₃分别对应E_x, E_z和G_zx; f为仿真所得螺栓连接板结构第一阶弯曲固有频率; p为虚拟材料参数向量, Δp_i为第i个变量的摄动值, 此处, 统一取表 3中优化所得线性数值的10%.
求得各虚拟材料参数敏感度, 组成敏感度向量.将绝对值小于10^-4的元素视为0.处理后的敏感度向量如下:

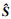
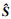
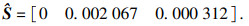(27)

由敏感度分析结果得, 此螺栓连接板结构第一阶弯曲模态对虚拟材料层的z轴方向弹性模量E_z最敏感, 与前文中假设一致.将虚拟材料层的z轴方向弹性模量设为非线性材料属性.将虚拟材料分区化, 如图 5所示, 建立非线性模型.各区域虚拟材料在z轴方向的弹性模量E_z与该区域薄层上下面中心点之间的材料形变关系见式(15).
以扫频试验所得加速度幅频响应为目标, 采用二分法计算式(15)中待定系数h₁, h₂, E₁和E₂的最优值, 求得h₁=5.448×10^-3, h₂=1.413×10^-2, E₁=3.455×10⁷和E₂=5.961×10⁷.在仿真求解螺栓连接板结构幅频响应时, 调整不同激振加速度下的系统阻尼, 使仿真所得幅频响应在幅值上与试验结果更加吻合.仿真所得幅频响应见图 10.
图 10(Fig. 10)

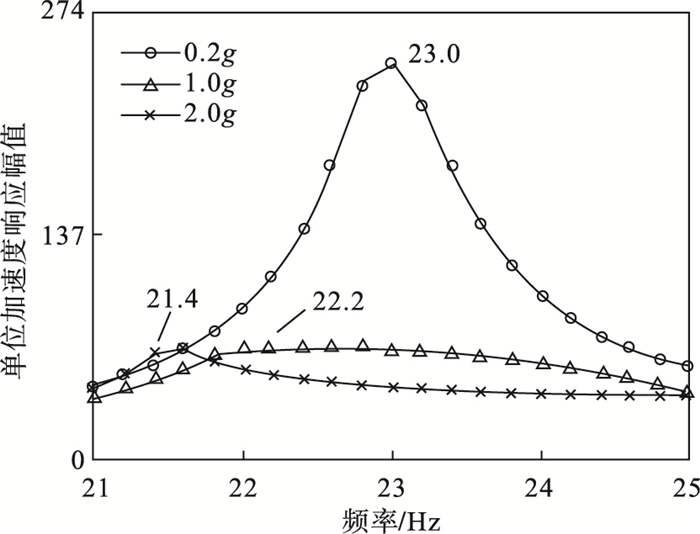图 10 仿真所得螺栓连接板结构第一阶弯曲模态附近幅频响应Fig.10 Amplitude frequency response near the first bending mode of bolted plate structure obtained by simulation

对比图 7和图 10可得, 基于本文方法所建的约束边界下螺栓连接板结构非线性有限元模型在结构第一阶弯曲固有频率附近的扫频仿真结果能够体现螺栓连接板结构在受外部简谐激振时所体现出的刚度非线性特性, 且在降维后, Matlab程序运行时间大大降低, 由大约50 000 s降到大约8 000 s.
4 结论1) 基于本文提出的方法对螺栓连接板试件进行动力学建模, 所得仿真分析结果与试件模态测试结果吻合较好, 验证了所建线性模型的正确性以及基于横观各向同性虚拟材料所建立的栓接结合部线性实体单元模型用于机械结构动力学求解的可行性.
2) 由接触分形理论确定横观各向同性虚拟材料线性参数时, 仿真结果可能由于加工误差或分形参数确定不合理等因素与试验结果偏差较大, 但可以将由分形理论求得的虚拟材料参数设为参考值或优化初始值, 以降低确定参数的工作量.
3) 通过对比仿真结果与扫频试验结果, 验证了基于非线性横观各向同性虚拟材料对栓接结合部进行动力学建模的可行性及本文方法的有效性.在构建栓接结合部非线性有限元模型时, 依据栓接结合部响应变形规律对虚拟材料进行分区处理, 即分区建模, 使所建模型更加合理, 为构建含栓接结合部结构的非线性动力学模型提供了一种新方法.
参考文献

[1]	Gaul L, Lenz J. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1/2/3/4): 169-181. DOI:10.1007/BF01177306
[2]	Abad J, Franco J M, Celorrio R, et al. Design of experiments and energy dissipation analysis for a contact mechanics 3D model of frictional bolted lap joints[J]. Advances in Engineering Software, 2011, 45(1): 42-53.
[3]	Law S S, Wu Z M, Chan S L. Vibration control study of a suspension footbridge using hybrid slotted bolted connection elements[J]. Engineering Structures, 2003, 26(1): 107-116.
[4]	de Benedetti M, Garofalo G, Zumpano M, et al. On the damping effect due to bolted junctions in space structures subjected to pyro-shock[J]. Acta Astronautica, 2007, 60(12): 947-956. DOI:10.1016/j.actaastro.2006.11.011
[5]	Worden K, Tomlinson G R. Nonlinearity in experimental modal analysis[J/OL]. Mathematical Physical and Engineering Sciences, 2001, 359(1778)[2020-10-12]. https://doi.org/10.1098/rsta.2000.0716.
[6]	姜东, 吴邵庆, 史勤丰, 等. 基于薄层单元的螺栓连接结构接触面不确定性参数识别[J]. 工程力学, 2015, 32(4): 220-227. (Jiang Dong, Wu Shao-qing, Shi Qin-feng, et al. Contact interface parameter identification of bolted joint structure with uncertainty using thin layer element method[J]. Engineering Mechanics, 2015, 32(4): 220-227.)
[7]	Zhai X, Zhai Q G, Wang J J. Dynamic model updating for bolted flange joints in the pipe structure[C]//Proceedings of 2014 International Conference on Simulation and Modeling Methodologies, Technologies and Applications. Sanya, China, 2014: 635-642.
[8]	Zhao G, Xiong Z L, Jin X, et al. Prediction of contact stiffness in bolted interface with natural frequency experiment and FE analysis[J]. Tribology International, 2018, 127: 57-164.
[9]	缪辉, 臧朝平, 罗欣洋, 等. 基于薄层单元的拉杆转子接触界面动力学建模及修正[J]. 航空动力学报, 2019, 34(9): 1927-1935. (Miao Hui, Zang Chao-ping, Luo Xin-yang, et al. Dynamic modeling and updating for contact interface of rod fastening rotor based on thin-layer element[J]. Journal of Aerospace Power, 2019, 34(9): 1927-1935.)
[10]	杨毅, 刘石, 高庆水, 等. 基于接触和虚拟材料的拉杆转子界面力学建模[J]. 广东电力, 2015, 28(7): 1-5. (Yang Yi, Liu Shi, Gao Qing-shui, et al. Mechanics modeling for rod fastening rotor interface based on contact and virtual materials[J]. Guangdong Electric Power, 2015, 28(7): 1-5. DOI:10.3969/j.issn.1007-290X.2015.07.001)
[11]	张晓霞, 周柏卓. 正交各向异性材料弹性本构关系分析[J]. 航空发动机, 1997(1): 20-25. (Zhang Xiao-xia, Zhou Bai-zhuo. Elastic constitutive analysis of orthotropic materials[J]. Aeroengine, 1997(1): 20-25.)
[12]	陈冲. 基于分形理论的正交各向异性结合部建模方法研究[D]. 西安: 西安理工大学, 2018. (Chen Chong. Research on modeling method of orthotropic joint based on fractal theory[D]. Xi'an: Xi'an University of Technology, 2018. )
[13]	张学良, 范世荣, 温淑花, 等. 基于等效横观各向同性虚拟材料的固定结合部建模方法[J]. 机械工程学报, 2017, 53(15): 141-147. (Zhang Xue-liang, Fan Shi-rong, Wen Shu-hua, et al. Modeling method of fixed joint interfaces based on equivalent transversely isotropic virtual material[J]. Journal of Mechanical Engineering, 2017, 53(15): 141-147.)
[14]	许腾云. 基于非线性虚拟材料的机械结合部建模及其应用[D]. 北京: 北京工业大学, 2014. (Xu Teng-yun. Modeling and application of mechanical joint based on nonlinear virtual materials[D]. Beijing: Beijing University of Technology, 2014. )
[15]	田红亮, 赵春华, 朱大林, 等. 弹塑性三维各向异性分形表面的接触分析[J]. 三峡大学学报(自然科学版), 2012, 34(1): 69-73. (Tian Hong-liang, Zhao Chun-hua, Zhu Da-lin, et al. Contact analysis of three dimensional anisotropic fractal surface of elastic-plastic[J]. Journal of Three Gorges University (Natural Science), 2012, 34(1): 69-73.)
[16]	张学良, 陈永会, 温淑花, 等. 考虑弹塑性变形机制的结合面法向接触刚度建模[J]. 振动工程学报, 2015, 28(1): 91-99. (Zhang Xue-liang, Chen Yong-hui, Wen Shu-hua, et al. The model of normal contact stiffness of joint interfaces incorporating elastoplastic deformation mechanism[J]. Journal of Vibration Engineering, 2015, 28(1): 91-99.)
[17]	Di Maio D, Schwingshackl C W, Sever I A. Development of a test planning methodology for performing experimental model validation of bolted flanges[J]. Nonlinear Dynamics, 2016, 83(1/2): 983-1002. DOI:10.1007/s11071-015-2382-9
[18]	Schwingshackl C W, Di Maio D, Sever I A, et al. Modeling and validation of the nonlinear dynamic behavior of bolted flange joints[J]. Journal of Engineering for Gas Turbines and Power, 2013, 135(12): 122504.
[19]	张锦, 刘晓平. 叶轮机振动模态分析理论及数值方法[M]. 北京: 国防工业出版社, 2001. (Zhang Jin, Liu Xiao-ping. Theory and numerical method of vibration modal analysis of turbomachinery[M]. Beijing: National Defense Industry Press, 2001.)
[20]	Ahmadian H, Jalali H. Generic element formulation for modelling bolted lap joints[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2318-2334.
[21]	Jalali H, Ahmadian H, Mottershead J E. Identification of nonlinear bolted lap-joint parameters by force-state mapping[J]. International Journal of Solids and Structures, 2007, 44(25/26): 8087-8105.