闫文凯#, 许明敏#, 张广乐, 乔宁, 徐炜娜, 陈园园, 张良云


南京农业大学理学院, 江苏 南京 210095
收稿日期:2016-10-14;修回日期:2016-11-24;网络出版日期:2017-02-20
基金项目:国家自然科学基金(11571173);江苏省自然科学基金(BK20141358)
*通信作者:张良云, Tel:+86-25-84396063;E-mail:zlyun@njau.edu.cn
#并列第一作者
摘要:[目的]识别原核生物全基因组中的16S rRNA基因。[方法]本文依据基因序列的GC碱基含量、碱基3-周期性和马尔可夫链3个方面的特性,构建了识别原核生物全基因组中16S rRNA基因的三层过滤模型。[结果]经检验,模型的特异性、敏感性和马修斯相关系数分别为99.58%、91.60%和91.49%。[结论]结果表明,本文所提出的方法可以高效、准确地识别出16S rRNA基因。
关键词: 16S rRNA基因 GC碱基含量 碱基3-周期性 马尔可夫链
Recognition of 16S rRNA genes in prokaryotic genomes
Yan Wenkai#, Xu Mingmin#, Zhang Guangle, Qiao Ning, Xu Weina, Chen Yuanyuan, Zhang Liangyun


College of Sciences, Nanjing Agricultural University, Nanjing 210095, Jiangsu Province, China
Received 14 October 2016; Revised 24 November 2016; Published online 20 February 2017
*Corresponding author: Zhang Liangyun, Tel:+86-25-84396063;E-mail:zlyun@njau.edu.cn
Supported by the National Natural Science Foundation of China (11571173) and by the Natural Science Foundation of Jiangsu Province (BK20141358)
#Those authors contributed equally to this work
Abstract: [Objective]We identified 16S rRNA genes in genomes of prokaryotes.[Methods]We constructed a 3-layer filtering model based on the three features of GC bases content of the gene sequences, 3-base periodicity and Markov chain to recognize the 16S rRNA genes from prokaryotic genomes.[Results]The specificity, sensitivity and Matthews correlation coefficients of the model were 99.58%, 91.60% and 91.49%, respectively.[Conclusion]The results showed that the 16S rRNA genes can be identified efficiently and accurately by using our model.
Key words: 16S rRNA gene GC base content 3-base periodicity Markov chain
细菌的系统分类学研究中最常用的分子标记是rRNA,它是核糖体的基本组成成分。rRNA的基因按5'-16S-23S-5S-3'方式排列,被2个非编码间隔区序列所分开,16S rDNA、23S和5S rDNA三部分组成一个操纵子,作为一个单位进行转录,转录后处理成为成熟的16S、23S、5S rRNA[1]。由于其种类少、含量大,并且存在于所有的生物中,既具有保守性又具有高变性,被广泛用于微生物分子差异与遗传特征的研究。16S rRNA基因约1.5 kb左右,大小合适,含有高度保守的片段,同时在不同的菌株间也含有变异的片段。既能体现相同菌种之间的相似性,又能体现不同菌种之间的差异性,因此是常用于细菌分类与鉴定的分子标记[2]。
基因预测是生物信息学领域的一个重要研究方向,是研究生物遗传、进化等工作的基础,其目的是对DNA序列中的功能性基因、调控元件等进行注释。许多统计概率方法及机器学习方法被用于此类研究工作中。如Zhao等[3]采用最大熵隐马尔可夫模型,基于TATA、CAAT框等启动子信号元件来识别启动子。Li等[4]利用序列的组分特征及位点关联特征,并结合支持向量机对基因剪接位点识别等。目前,针对16S rRNA基因进行预测的算法及软件,如RNAmmer[5]采用HMMer-2模型对原核生物的16S rRNA基因进行识别,该方法只适用于全基因组序列。Meta-RNA[6]是一个Python程序,可对宏基因组片段序列中16S rRNA序列进行筛选。rRNASelector[7]是以隐马尔可夫模型为基础,应用Java编写的rRNA基因预测软件。由于隐马尔可夫算法的初始参数是依据已知数据训练得出,因此rRNA Selector的预测结果受所选训练数据的影响较大。
为了快速、高效地对原核生物全基因组中的16S rRNA基因进行识别,本文提出一种集成算法。实验将真实的16S rRNA基因序列与对照序列(非16S rRNA基因序列)进行了GC碱基含量、序列碱基3-周期性和序列的马尔可夫链模型3个方面对比分析。通过分析,并针对每个方面的数据设定出了一个阈值对待选序列进行判别。经过3个方面分析、3种方法处理、3层过滤手段,构建出一种准确、高效的筛选16S rRNA基因序列模型。
1 材料和方法 1.1 材料 本实验选取的16S rRNA基因序列与细菌全基因组序列来自NCBI数据库(http://www.ncbi.nlm.nih.gov/)。其中,原核生物16S rRNA基因序列共41252条,实验从中随机选取序列碱基缺失个数小于50的基因序列,共9000条。非16S rRNA基因序列从50000个菌株的全基因组序列中随机选取,长度为1550 bp。训练集中,16S rRNA基因序列选用3000条作为正集,非16S rRNA基因序列选用3000条作为对照负集。测试集中,16S rRNA基因序列选用6000条作为正集,非16S rRNA基因序列选用6000条作为负集。
1.2 序列GC含量 GC含量是指所研究的DNA序列中鸟嘌呤与胞嘧啶两种碱基所占比例。在DNA双链结构中,G和C以3个氢键配对,与DNA链的稳定性密切相关。因此,GC含量是DNA序列碱基组成的重要特征,蕴含基因结构、功能和进化信息。对于功能性基因或特定的DNA、RNA序列,其GC碱基的含量有相对固定比例,利用这一特性可对其进行预测和识别。
1.3 序列碱基3-周期性 信号频谱分析通常利用离散傅里叶变换对信号进行离散处理,构建功率谱和信噪比,该方法在各领域取得了重要研究成果。Berryman等[8]在编码序列识别问题中引入了信号频谱分析的方法,基于离散傅里叶变换,给出了功率谱的定义。大量的研究发现,对DNA序列进行数值化映射和傅里叶变换后得到的功率谱,编码序列的功率谱在1/3处具有较大的峰值,而非编码序列却没有类似的峰值,故把这种统计现象叫做碱基的3-周期性[9]。3-周期性是生物长期演化后形成的本质属性,是DNA序列重要的生物特征。目前,已有较多关于基因3-周期性方法的创新与拓展。为使得到的数值序列具有更多的生物信息,许多****对数值化方法进行研究。如Voss映射[10-11]、Z-Curve映射[12]、复数法映射[13]、实数法[14]等。人们定义了信噪比R,用来衡量3-周期性的强弱,且大量研究表明特殊碱基序列的R通常大于或小于某个阈值R0。很多研究者给出了阈值R0的确定方法,并提出了基因识别的算法[15]。基因序列的数值化映射、功率谱和信噪比的详细定义如下。
对基因序列进行数值化映射(公式1),令I={A, T, G, C},现对任意确定的

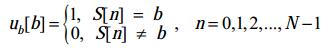 | 公式(1) |


 |
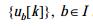
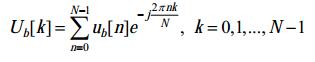 | 公式(2) |

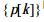
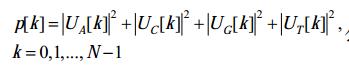 | 公式(3) |
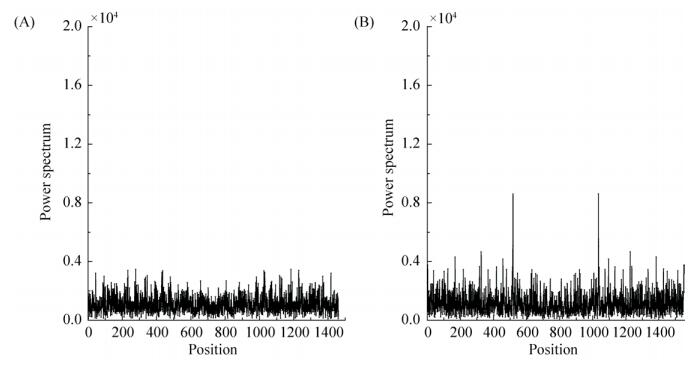 |
| 图 1 16S rRNA序列(A)与非16S rRNA序列(B)频谱图 Figure 1 Power spectrum curve of 16S rRNA sequence (A) and non-16S rRNA sequences (B). |
| 图选项 |
在图 1中,16S rRNA基因序列的频谱图在三分之一处无峰值出现,而非16S rRNA基因序列的功率谱在三分之一处有较大的峰值(公式4)。
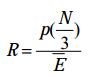 | 公式(4) |
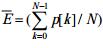
信噪比值的大小是给定DNA序列在N/3处的频谱峰值的大小的表征,即,16S rRNA基因序列或非16S rRNA基因序列的3-周期性的强弱,显然,16S rRNA基因序列的信噪比值较小,而非16S rRNA基因序列的信噪比较大。对于一段15 kb的DNA序列,选取一个最优的R0值,使尽可能多的非16S rRNA基因序列的信噪比大于R0,而16S rRNA基因序列的功率谱或信噪比小于R0。根据这个特征选定某个适当的阈值,通过信噪比和阈值的大小来判断待选序列是否为16S rRNA基因序列。若信噪比小于阈值,判断此序列为16S rRNA基因序列;若信噪比大于阈值,判断此序列为非16S rRNA基因序列。
1.4 马尔可夫模型 马尔可夫链是一种有效的概率模型。此模型已广泛应用于生物学领域,特别是在预测模型中有着深入的应用。如DNA序列的聚类研究中[19],遗传与进化分析[20],基于RNA-seq数据、甲基化数据以及拷贝数变异数据等构建遗传网络[21]等。马尔可夫过程[22–23]是一个无后效性的随机过程,即tm时刻所处状态的概率仅和tm–1时刻的状态有关,而与tm–1时刻之前的状态无关。马尔可夫过程中的时间和状态可以是连续的,也可以是离散的。其中,时间离散、状态离散的马尔可夫过程为马尔可夫链。
马尔可夫模型应用于16S rRNA基因序列分析需要建立能够体现核酸序列的模型,其中的主要工作是构建转移概率矩阵A。本文建立的概率模型由两条马尔可夫链组成,这两条马尔可夫链即为16S rRNA基因序列模型和非16S rRNA基因序列模型。通过计算待选序列在两个序列模型出现的概率来对其所属类别进行判定。出现的概率越大,说明序列内碱基状态转移模式最贴合相应的概率模型所生成的序列。即,待选序列在此概率模型出现的概率最大,则待选序列判定为此概率模型下的序列。转移概率按照公式(5) 计算。
 | 公式(5) |
对于本实验的马尔可夫模型,长度为L的待选序列
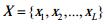
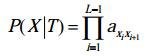 | 公式(6) |

设待选序列为
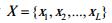
 | 公式(7) |
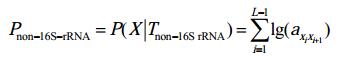 | 公式(8) |
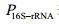
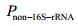
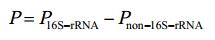 | 公式(9) |
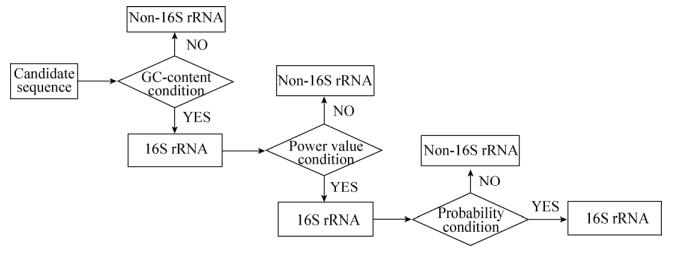 |
| 图 2 实验流程图 Figure 2 Flow chart. |
| 图选项 |
1.6 评价指标 本文通过敏感度(Sensitivity,Sn)、特异度(Specificity,Sp)、马修斯相关系数(MCC)来衡量模型的优劣,见公式(10)、(11)、(12)。
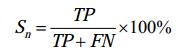 | 公式(10) |
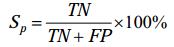 | 公式(11) |
 | 公式(12) |
2 结果和分析 本文运算环境为Matlab 2015b版本。获取实验原始数据、运算程序等资源,请访问:http://www.yucetianxia.com/ywk/。
2.1 序列GC含量的分析 对正负集样本序列的GC碱基含量进行统计。结果显示,3000条正样本的序列GC碱基含量百分比取值范围小,样本点聚集分布(图 3-A);3000条负样本的序列GC碱基含量百分比取值范围大,样本点离散分布(图 3-B)。正样本集中序列的GC含量在50%–60%之间的样本数高达92.63% (图 4),此区间之外的样本数为7.37%。而负样本集的统计结果与正样本集有较大差异,GC含量在50%–60%之间的样本数仅占21.87%,区间之外的样本数为78.13% (图 4)。
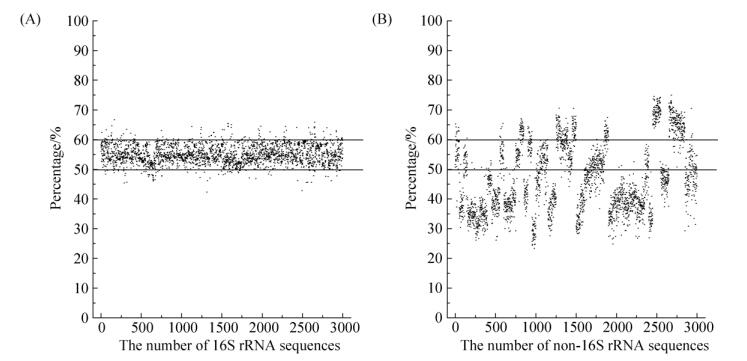 |
| 图 3 16S rRNA序列(A)和非16S rRNA序列(B) GC含量分布 Figure 3 The GC content distribution of 16S rRNA sequences (A) and non-16S rRNA sequences (B). Horizontal straight line is GC_content=50% and GC_content=60%. |
| 图选项 |
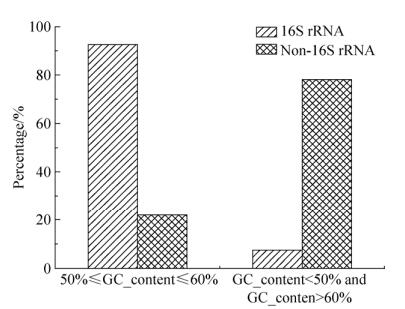 |
| 图 4 以阈值为基础,16S rRNA序列与非16S rRNA序列样本分布图 Figure 4 The distribution of 16S rRNA sequences and non-16S rRNA sequences based on the GC content threshold. The GC content threshold is 50%–60%. |
| 图选项 |
以碱基序列的GC碱基含量作为第1个筛选标准,根据以上统计结果,若待选序列的GC碱基含量在50%–60%区间内,则判定其为16S rRNA基因序列,在此区间之外,则判定为非16S rRNA基因序列。经此筛选后,正样本数量为2779,负样本数量为656。
2.2 序列碱基3-周期性分析 对正负集样本的序列信噪比进行统计。结果显示,2779条正样本与656条负样本的信噪比存在较大差异。正样本的信噪比值较小,呈规律性分布,一般在0–5区间内取值(图 5-A);负样本的信噪比值较大,分布离散,且大部分样本的信噪比大于5 (图 5-B)。正样本集中序列的信噪比在0–5区间的样本数高达99.60%,此区间之外的样本数仅占0.40% (图 6)。而负样本集的序列的信噪比在0–5区间的样本数仅占14.63%,区间之外的样本数为85.37% (图 6)。
 |
| 图 5 16S rRNA序列(A)和非16S rRNA序列(B)信噪比散点图 Figure 5 The SNR distribution of 16S rRNA sequences (A) and non-16S rRNA sequences (B). Horizontal straight line is R0=5. |
| 图选项 |
 |
| 图 6 以SNR阈值为基础的16S rRNA序列与非16S rRNA序列样本分布图 Figure 6 The distribution of 16S rRNA sequences and non-16S rRNA sequences based on the SNR threshold. The SNR threshold is 5.0; Sub-map is the ratio of 16S rRNA sequences that the SNR greater than 5.0. |
| 图选项 |
以碱基序列的信噪比作为第2个筛选标准,依据上述统计结果,若待选序列的信噪比小于5,则判定其为16S rRNA基因序列;若待选序列的信噪比大于等于5,则判定为非16S rRNA基因序列。经此进一步筛选后,正样本数量为2768,负样本数量为96。
2.3 基于马尔可夫模型对序列进行分析 以初始的正负样本为训练数据,得16S rRNA基因序列碱基转移概率矩阵和非16S rRNA基因序列碱基转移概率矩阵如表 1、表 2所示。
表 1. 16S rRNA基因序列碱基的转移概率矩阵 Table 1. The transition probability matrix of 16S rRNA gene sequence
| Transition probability | A | C | G | T |
| A | 0.280272 | 0.244106 | 0.296359 | 0.179264 |
| C | 0.236400 | 0.237846 | 0.309018 | 0.216737 |
| G | 0.234274 | 0.232156 | 0.321973 | 0.211597 |
| T | 0.238288 | 0.208642 | 0.356803 | 0.196267 |
表选项
表 2. 非16S rRNA基因序列碱基的转移概率矩阵 Table 2. The transition probability matrix of non-16S rRNA gene sequence
| Transition probability | A | C | G | T |
| A | 0.325077 | 0.1894242 | 0.205089 | 0.280393 |
| C | 0.279231 | 0.2339100 | 0.254084 | 0.232775 |
| G | 0.249651 | 0.3011530 | 0.233852 | 0.215343 |
| T | 0.211117 | 0.2183440 | 0.245791 | 0.324749 |
表选项
以16S rRNA基因序列和非16S rRNA基因序列碱基转移概率矩阵为基础,计算得出2768条正样本与96条负样本的P值。统计结果显示,P值大于20的正样本数较多(图 7-A),而负样本中P值小于20的样本点为多数(图 7-B)。正样本集中序列的P值大于20的样本数所占比例为96.48%,P值小于20的样本数仅占3.52% (图 8)。而负样本集中序列的P值小于20的样本数占85.42%,P值大于20的样本所占比例为14.58% (图 8)。
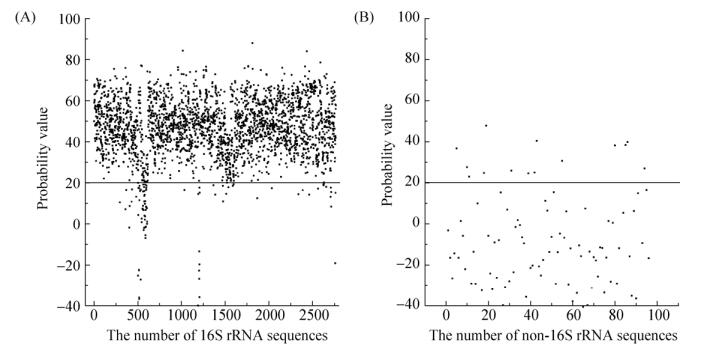 |
| 图 7 16S rRNA序列(A)和非16S rRNA序列(B) P值分布的散点图 Figure 7 The P value distribution of 16S rRNA sequences (A) and non-16S rRNA sequences (B). Horizontal straight line is P=20. |
| 图选项 |
 |
| 图 8 以P阈值为基础,16S rRNA序列与非16S rRNA序列样本分布图 Figure 8 The distribution of 16S rRNA sequences and non-16S rRNA sequences based on the P value threshold. The P value threshold is 20. |
| 图选项 |
以碱基序列的P值作为第3个筛选标准,依据上述统计结果,若待选序列的P值大于等于20,则判定其为16S rRNA基因序列;若待选序列的P值小于20,则判定为非16S rRNA基因序列。经此筛选后,正样本数量为2708,负样本数量为17。
2.4 基于测试数据对模型进行分析 本文通过对训练数据的碱基组分、碱基3-周期性以及序列马尔可夫性3方面的分析,得出GC碱基含量、信噪比和序列生成概率3个阈值,以此为条件构建出筛选模型。实验应用测试数据,通过3种评价指标对模型性能进行评价。
测试数据为6000条16S rRNA基因序列,6000条非16S rRNA基因序列。实验中测试数据分为3组,每组由2000条16S rRNA基因序列和2000条非16S rRNA基因序列组成。经过上述三级筛选过程,结合公式(10)、(11) 及(12) 可以计算出该模型的敏感性、特异性和马修斯系数,如表 3所示。
表 3. 模型的敏感性、特异性及马修斯相关系数 Table 3. The sensitivity, specificity and MCC of the model
| Test set | True positive | True negative | False positive | False negative | Sensitivity/% | Specificity/% | MCC/% |
| Data set 1 | 1876 | 1990 | 10 | 124 | 93.80 | 99.50 | 93.45 |
| Data set 2 | 1777 | 1994 | 6 | 223 | 88.85 | 99.70 | 89.06 |
| Data set 3 | 1843 | 1991 | 9 | 157 | 92.15 | 99.55 | 91.95 |
| Average value | – | – | – | – | 91.60 | 99.58 | 91.49 |
表选项
以表 3中3组平行实验的敏感性、特异性以及马修斯相关系数的平均值作为评价模型的指标,可得本实验所构建模型的敏感性、特异性以及马修斯相关系数分别为91.60%、99.58%和91.49%。通过数据表明,本文所提出的模型在筛选16S rRNA基因序列中是可行的,并且十分有效。
2.5 基于全基因组数据对模型进行分析 为进一步说明模型的有效性与实用性,本实验将在原核生物全基因组中用滑窗法检测模型对16S rRNA基因序列的识别能力,以起到对基因组进行注释的作用。本实验所用的滑窗法是指以DNA序列的第一个碱基为起始点,每隔一定数量的碱基取出一段连续的、固定长度的序列,带入本文所构建的模型进行预测,判断其是否为特征序列。此实验从NCBI数据库随机选取3株细菌,对其基因组序列进行实验,预测结果如表 4所示。
表 4. 模型的覆盖率和注释比例 Table 4. The coverage percentage and annotation ratio of the model
| Bacteria name | 16S rRNA | Predicted 16S rRNA | Coverage rate/% | Annotation rate | |||
| Start site | Termination site | Start site | Termination site | ||||
| Leuconostoc mesenteroides ID:116617174 | 22663 | 24222 | 22601 | 24151 | 95.45 | 2/4 | |
| 148398 | 149957 | 148401 | 149951 | 99.42 | |||
| Aeromonas hydrophila ID:117617447 | 85174 | 86723 | 84901 | 86451 | 82.44 | 6/10 | |
| 163372 | 164921 | 163051 | 164601 | 79.34 | |||
| 214907 | 216456 | 214601 | 220801 | 100 | |||
| 349946 | 351495 | 349701 | 351251 | 84.25 | |||
| 803843 | 805392 | 803601 | 805151 | 84.44 | |||
| 933020 | 934569 | 932801 | 934351 | 85.93 | |||
| Bacillus subtilis ID:740748848 | 20041 | 21595 | 19601 | 24251 | 100 | 7/8 | |
| 330891 | 332446 | 330551 | 335201 | 100 | |||
| 3563690 | 3565244 | 3563301 | 3567951 | 100 | |||
| 3584089 | 3586543 | 3585021 | 3588301 | 62.02 | |||
| 3644289 | 3645843 | 3644001 | 3648651 | 100 | |||
| 3650177 | 3651731 | 3649451 | 3654101 | 100 | |||
| 3715138 | 3716692 | 3714801 | 3719451 | 100 | |||
表选项
表 4中包括细菌名称,模型预测出的16S rRNA基因序列的起始和终止位置与真实的16S rRNA基因序列的起始和终止位置,覆盖率以及注释比例。覆盖率是指模型预测出的16S rRNA基因序列与真实的16S rRNA基因序列的重叠区域在真实的16S rRNA基因序列中所占比例。例如,模型预测肠膜明串珠菌的第一个16S rRNA基因序列的起始与终止碱基位置分别为22601和24151,而该16S rRNA基因序列真实的起始与终止碱基位置分别为22663和24222。重叠区域长度为1489,真实的16S rRNA基因序列长度1560,则覆盖率为95.45%。
注释比表示模型在某一细菌全基因组中识别出的16S rRNA基因的个数与该细菌全基因组中16S rRNA基因的总个数的比值。例如,模型预测出枯草芽孢杆菌全基因组中16S rRNA基因的个数为7,该细菌全基因组中16S rRNA基因的总个数为8,则注释比为7/8。
上述3组实验的平均覆盖率都在80%以上,因此,该模型可较为准确的定位16S rRNA序列所在位置。注释比结果中,以枯草芽孢杆菌的预测结果最为突出,全基因组中8个16S rRNA基因,通过本文所构建的模型可识别出7个。通过数据进一步表明,本文所提出的模型在筛选16S rRNA基因序列中是可行的,并且十分有效。
3 讨论 本文首次提出应用序列分析相关算法构建模型对16S rRNA基因进行识别。通过对序列GC碱基含量,序列碱基3-周期性以及马尔可夫链3种方法的有效结合,实现了对16S rRNA基因的识别。首先,对序列GC碱基含量进行统计,并设定初步筛选的阈值区间为50%–60%。其次,对GC碱基含量在50%–60%之间序列进行碱基3-周期性分析。由于16S rRNA基因序列属于非编码序列,因此,这类序列不具有3-周期性。依据统计训练数据的信噪比值,本文设定筛选阈值为5。最后,通过构建两种马尔可夫模型,对满足GC碱基含量在50%–60%之间,并且序列信噪比值小于5的序列进行P值求解。若待选序列P值大于20,则此序列被判定为16S rRNA基因序列;反之,则被判定为非16S rRNA基因序列。经过上述步骤对待选序列进行最终识别。
本文所构建的模型可对全基因组中的16S rRNA基因进行快速注释。与RNAmmer和Meta-RNA不同,本模型不仅可以识别原核生物全基因组中的16S rRNA基因,同样可以对片段型序列进行识别。相较于rRNASelector应用一种统计学算法对16S rRNA基因进行识别,本文集成了三种序列统计方法来构建基因识别模型, 因此,预测结果更具可靠性。但此方法同样存在不足之处,主要有以下三个方面:(1) 基因组中16S rRNA基因的数量较少且模型存在弃真行为,目标序列未能全部找出;(2) 5S rRNA和23S rRNA基因与16S rRNA基因序列性质相似,试验中未采取有效的剔除方法,筛选结果存在此类噪声;(3) 试验中选取的阈值组合有待进一步修正。如果上述问题能得到有效解决,模型识别的准确率将会进一步提高。
References
| [1] | Yu C, Guo HY, Wei JL, Qian AD. Application of 16S to 23S rRNA intergenic spacer region in identification of bacteria. China Animal Husbandry & Veterinary Medicine, 2012, 39(2): 57-60. (in Chinese) 于超, 郭海勇, 魏嘉良, 钱爱东. 16S-23S rRNA基因序列在细菌鉴定中的应用. 中国畜牧兽医, 2012, 39(2): 57-60. |
| [2] | Liu C, Li JB, Rui JP, An JX, Li XZ. The applications of the 16S rRNA gene in microbial ecology: current situation and problems. Acta Ecologica Sinica, 2015, 35(9): 2769-2788. (in Chinese) 刘驰, 李家宝, 芮俊鹏, 安家兴, 李香真. 16S rRNA基因在微生物生态学中的应用. 生态学报, 2015, 35(9): 2769-2788. |
| [3] | Zhao XY, Zhang J, Chen YY, Li Q, Yang T, Pian C, Zhang LY. Promoter recognition based on the maximum entropy hidden Markov model. Computers in Biology and Medicine, 2014, 51: 73-81. DOI:10.1016/j.compbiomed.2014.04.003 |
| [4] | Li JL, Wang LF, Wang HY, Bai LY, Yuan ZM. High-accuracy splice site prediction based on sequence component and position features. Genetics and Molecular Research, 2012, 11(3): 3432-3451. DOI:10.4238/2012.September.25.12 |
| [5] | Lagesen K, Hallin P, Rdland EA, Strfeldt HH, Rognes T, Ussery DW. RNAmmer: consistent and rapid annotation of ribosomal RNA genes. Nucleic Acids Research, 2007, 35(9): 3100-3108. DOI:10.1093/nar/gkm160 |
| [6] | Huang Y, Gilna P, Li WZ. Identification of ribosomal RNA genes in metagenomic fragments. Bioinformatics, 2009, 25(10): 1338-1340. DOI:10.1093/bioinformatics/btp161 |
| [7] | Lee JH, Yi H, Chun J. rRNASelector: a computer program for selecting ribosomal RNA encoding sequences from metagenomic and metatranscriptomic shotgun libraries. The Journal of Microbiology, 2011, 49(4): 689-691. DOI:10.1007/s12275-011-1213-z |
| [8] | Berryman MJ, Allison A. Review of signal processing in genetics. Fluctuation and Noise Letters, 2005, 5(4): R13-R15. DOI:10.1142/S021947750500294X |
| [9] | Yin CC, Yau SST. Prediction of protein coding regions by the 3-base periodicity analysis of a DNA sequence. Journal of Theoretical Biology, 2007, 247(4): 687-694. DOI:10.1016/j.jtbi.2007.03.038 |
| [10] | Voss RF. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Physical Review Letters, 1992, 68(25): 3805-3808. DOI:10.1103/PhysRevLett.68.3805 |
| [11] | Sharma SD, Shakya K, Sharma SN. Evaluation of DNA mapping schemes for exon detection//Proceedings of 2011 International Conference on Computer, Communication and Electrical Technology. Tamilnadu: IEEE, 2011: 71-74. |
| [12] | Zhang R, Zhang CT. Z curves, an intutive tool for visualizing and analyzing the DNA sequences. Journal of Biomolecular Structure and Dynamics, 1994, 11(4): 767-782. DOI:10.1080/07391102.1994.10508031 |
| [13] | Anastassiou D. Frequency-domain analysis of biomolecular sequences. Bioinformatics, 2000, 16(12): 1073-1081. DOI:10.1093/bioinformatics/16.12.1073 |
| [14] | Chakravarthy N, Spanias A, Iasemidis LD, Tsakalis K. Autoregressive modeling and feature analysis of DNA sequences. EURASIP Journal on Advances in Signal Processing, 2004, 2004(1): 952689. |
| [15] | Kwan HK, Kwan BYM, Kwan JYY. Novel methodologies for spectral classification of exon and intron sequences. EURASIP Journal on Advances in Signal Processing, 2012, 2012(1): 50. DOI:10.1186/1687-6180-2012-50 |
| [16] | Yan M, Lin ZS, Zhang CT. A new Fourier transform approach for protein coding measure based on the format of the Z curve. Bioinformatics, 1998, 14(8): 685-690. DOI:10.1093/bioinformatics/14.8.685 |
| [17] | Coward E. Equivalence of two Fourier methods for biological sequences. Journal of Mathematical Biology, 1997, 36(1): 64-70. DOI:10.1007/s002850050090 |
| [18] | Silverman BD, Linsker R. A measure of DNA periodicity. Journal of Theoretical Biology, 1986, 118(3): 295-300. DOI:10.1016/S0022-5193(86)80060-1 |
| [19] | J skinen V, Parkkinen V, Cheng L, Corander J. Bayesian clustering of DNA sequences using Markov chains and a stochastic partition model. Statistical Applications in Genetics and Molecular Biology, 2014, 13(1): 105-121. |
| [20] | Zhao L, Lascoux M, Waxman D. An informational transition in conditioned Markov chains: applied to genetics and evolution. Journal of Theoretical Biology, 2016, 402: 158-170. DOI:10.1016/j.jtbi.2016.04.021 |
| [21] | Wan YW, Allen GI, Baker Y, Yang E, Ravikumar P, Anderson M, Liu ZD. XMRF: an R package to fit Markov networks to high-throughput genetics data. BMC Systems Biology, 2016, 10(S3): 69. DOI:10.1186/s12918-016-0313-0 |
| [22] | Komorowski T, Peszat S, Szarek T. On ergodicity of some markov processes. The Annals of Probability, 2010, 38(4): 1401-1443. DOI:10.1214/09-AOP513 |
| [23] | Arns M, Buchholz P, Panchenko A. On the numerical analysis of inhomogeneous continuous-time Markov chains. Informs Journal on Computing, 2010, 22(3): 416-432. DOI:10.1287/ijoc.1090.0357 |
