 )
) 华南师范大学心理学院, 广州 510631
收稿日期:2019-08-09出版日期:2020-04-15发布日期:2020-02-24通讯作者:张敏强E-mail:2640726401@qq.com基金资助:义务教育质量关键影响因素监测框架构建项目(538-670329)What is the minimum number of effect sizes required in meta-regression? An estimation based on statistical power and estimation precision
FANG Junyan, ZHANG Minqiang( )
) School of psychology, South China Normal University, Guangzhou 510631, China
Received:2019-08-09Online:2020-04-15Published:2020-02-24Contact:ZHANG Minqiang E-mail:2640726401@qq.com摘要/Abstract
摘要: 元回归模型被广泛应用于调节变量的识别。从元分析技术的原理谈起, 介绍了元回归模型, 然后采用蒙特卡洛模拟, 基于统计功效和估计精度探究效应量个数对元回归模型参数估计的影响, 从而确立效应量的最小个数需求。主要研究结果为:(1) Wald-type z检验方法在元回归中易犯I类错误; (2)为达到参数估计要求, 元回归至少需要20个效应量; (3)纳入合适的调节变量能降低对效应量的个数需求。基于研究结果, 提出以下建议:(1)研究者应慎重使用Wald-type z检验方法和CMA软件; (2)研究者至少需要20个效应量, 且应当根据实际情况进一步增加效应量个数; (3)研究者应当积极探索合适的调节变量; (4)未来审稿人可参考最小效应量个数需求对元回归研究进行质量评估。
图/表 15
表1参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.08)
| 检验方法 | τ2 = 0.08 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0, 0) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| z-test | 23 | 25 | 23 | 25 | 23 | 25 | 25 |
表1参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.08)
| 检验方法 | τ2 = 0.08 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0, 0) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| z-test | 23 | 25 | 23 | 25 | 23 | 25 | 25 |
表2参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.32)
| 检验方法 | τ2=0.32 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0,0) | β = 0.2 | β = (0.2,0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 38 | 38 | 38 | 38 | 38 | 38 | 38 |
| z-test | 43 | 43 | 43 | 43 | 43 | 43 | 43 |
表2参数估计精度在不同情境下对最小效应量个数的需求(τ2 = 0.32)
| 检验方法 | τ2=0.32 | ||||||
|---|---|---|---|---|---|---|---|
| β为0 | β(均)较小 | β(均)较大 | β一个较大, 一个较小 | ||||
| β = 0 | β = (0,0) | β = 0.2 | β = (0.2,0.2) | β = 0.5 | β = (0.5,0.5) | β = (0.2,0.5) | |
| Knha-test | 38 | 38 | 38 | 38 | 38 | 38 | 38 |
| z-test | 43 | 43 | 43 | 43 | 43 | 43 | 43 |
表3统计功效在不同情境下对最小效应量个数的需求
| 检验 方法 | τ2 = 0.08 | τ2 = 0.32 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β(均)较小 | β(均)较大 | β一个较大 一个较小 | β(均)较小 | β(均)较大 | β一个较大 一个较小 | |||||
| β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| Knha-test | 30 | 30 | √ | √ | 20 | 70 | 70 | 20 | 20 | 50 |
| z-test | 38 | 38 | √ | √ | 30 | 80 | 80 | 20 | 20 | 52 |
表3统计功效在不同情境下对最小效应量个数的需求
| 检验 方法 | τ2 = 0.08 | τ2 = 0.32 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β(均)较小 | β(均)较大 | β一个较大 一个较小 | β(均)较小 | β(均)较大 | β一个较大 一个较小 | |||||
| β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | β = 0.2 | β = (0.2, 0.2) | β = 0.5 | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| Knha-test | 30 | 30 | √ | √ | 20 | 70 | 70 | 20 | 20 | 50 |
| z-test | 38 | 38 | √ | √ | 30 | 80 | 80 | 20 | 20 | 52 |
表4不同情境下模型对最小效应量个数的总体需求(Knapp and Hartung检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 20 | 20 | 38 | 38 |
| β(均)较小 | 30 | 30 | 70 | 70 |
| β(均)较大 | 20 | 20 | 38 | 38 |
| β1较小β2较大 | —— | 20 | —— | 50 |
表4不同情境下模型对最小效应量个数的总体需求(Knapp and Hartung检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 20 | 20 | 38 | 38 |
| β(均)较小 | 30 | 30 | 70 | 70 |
| β(均)较大 | 20 | 20 | 38 | 38 |
| β1较小β2较大 | —— | 20 | —— | 50 |
表5不同情境下模型对最小效应量个数的总体需求(Wald-type z检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 23 | 25 | 43 | 43 |
| β(均)较小 | 38 | 38 | 80 | 80 |
| β(均)较大 | 23 | 25 | 43 | 43 |
| β1较小β2较大 | —— | 30 | —— | 52 |
表5不同情境下模型对最小效应量个数的总体需求(Wald-type z检验方法)
| 回归系数取值 | 剩余异质性较小 | 剩余异质性较大 | ||
|---|---|---|---|---|
| 包含一个调节变量 | 包含两个调节变量 | 包含一个调节变量 | 包含两个调节变量 | |
| β(均)为0 | 23 | 25 | 43 | 43 |
| β(均)较小 | 38 | 38 | 80 | 80 |
| β(均)较大 | 23 | 25 | 43 | 43 |
| β1较小β2较大 | —— | 30 | —— | 52 |
附表1包含一个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | -0.0004 | -0.0001 | 0.0003 | -0.0012 | 0.0008 | 0.0056 |
| 40 | 0.0009 | 0.0004 | -0.0001 | -0.0031 | -0.0011 | -0.0009 |
| 60 | 0.0006 | 0.0000 | -0.0009 | 0.0010 | -0.0014 | -0.0009 |
| 80 | 0.0004 | -0.0003 | -0.0003 | 0.0000 | 0.0003 | -0.0005 |
| 100 | -0.0007 | 0.0000 | 0.0002 | -0.0006 | 0.0004 | 0.0000 |
| 120 | 0.0000 | 0.0000 | -0.0004 | 0.0003 | -0.0001 | 0.0002 |
附表1包含一个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | -0.0004 | -0.0001 | 0.0003 | -0.0012 | 0.0008 | 0.0056 |
| 40 | 0.0009 | 0.0004 | -0.0001 | -0.0031 | -0.0011 | -0.0009 |
| 60 | 0.0006 | 0.0000 | -0.0009 | 0.0010 | -0.0014 | -0.0009 |
| 80 | 0.0004 | -0.0003 | -0.0003 | 0.0000 | 0.0003 | -0.0005 |
| 100 | -0.0007 | 0.0000 | 0.0002 | -0.0006 | 0.0004 | 0.0000 |
| 120 | 0.0000 | 0.0000 | -0.0004 | 0.0003 | -0.0001 | 0.0002 |
附表2包含一个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | 0.0000 | 0.0000 | 0.0003 | 0.0026 | 0.0005 | -0.0009 |
| 40 | 0.0007 | 0.0004 | -0.0009 | 0.0000 | -0.0004 | 0.0003 |
| 60 | -0.0003 | 0.0007 | -0.0001 | -0.0005 | 0.0000 | 0.0003 |
| 80 | 0.0000 | 0.0001 | 0.0008 | 0.0001 | 0.0013 | 0.0017 |
| 100 | -0.0002 | 0.0001 | -0.0001 | 0.0005 | -0.0009 | -0.0014 |
| 120 | 0.0001 | 0.0003 | -0.0006 | 0.0007 | 0.0000 | 0.0002 |
附表2包含一个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||
|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0 | β = 0.2 | β = 0.5 | |
| 20 | 0.0000 | 0.0000 | 0.0003 | 0.0026 | 0.0005 | -0.0009 |
| 40 | 0.0007 | 0.0004 | -0.0009 | 0.0000 | -0.0004 | 0.0003 |
| 60 | -0.0003 | 0.0007 | -0.0001 | -0.0005 | 0.0000 | 0.0003 |
| 80 | 0.0000 | 0.0001 | 0.0008 | 0.0001 | 0.0013 | 0.0017 |
| 100 | -0.0002 | 0.0001 | -0.0001 | 0.0005 | -0.0009 | -0.0014 |
| 120 | 0.0001 | 0.0003 | -0.0006 | 0.0007 | 0.0000 | 0.0002 |
附表3包含两个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0008 | 0.0006 | -0.0007 | 0.0003 | 0.0001 | -0.0007 | 0.0003 | -0.0005 |
| 40 | 0.0003 | 0.0006 | -0.0001 | 0.0008 | -0.0008 | 0.0001 | -0.0017 | -0.0005 |
| 60 | 0.0000 | -0.0006 | -0.0003 | 0.0000 | 0.0004 | 0.0001 | 0.0003 | -0.0002 |
| 80 | 0.0001 | 0.0002 | -0.0004 | 0.0001 | 0.0005 | 0.0005 | 0.0006 | 0.0001 |
| 100 | -0.0002 | 0.0002 | -0.0003 | 0.0001 | 0.0004 | 0.0006 | -0.0003 | 0.0002 |
| 120 | 0.0000 | 0.0001 | 0.0001 | -0.0001 | -0.0003 | 0.0000 | 0.0002 | 0.0004 |
附表3包含两个调节变量时不同效应量个数下的参数估计偏差(knha-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0008 | 0.0006 | -0.0007 | 0.0003 | 0.0001 | -0.0007 | 0.0003 | -0.0005 |
| 40 | 0.0003 | 0.0006 | -0.0001 | 0.0008 | -0.0008 | 0.0001 | -0.0017 | -0.0005 |
| 60 | 0.0000 | -0.0006 | -0.0003 | 0.0000 | 0.0004 | 0.0001 | 0.0003 | -0.0002 |
| 80 | 0.0001 | 0.0002 | -0.0004 | 0.0001 | 0.0005 | 0.0005 | 0.0006 | 0.0001 |
| 100 | -0.0002 | 0.0002 | -0.0003 | 0.0001 | 0.0004 | 0.0006 | -0.0003 | 0.0002 |
| 120 | 0.0000 | 0.0001 | 0.0001 | -0.0001 | -0.0003 | 0.0000 | 0.0002 | 0.0004 |
附表4包含两个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0003 | -0.0002 | 0.0009 | 0.0006 | 0.0005 | -0.0002 | 0.0000 | 0.0000 |
| 40 | -0.0008 | -0.0001 | 0.0000 | -0.0002 | 0.0002 | -0.0002 | 0.0002 | 0.0010 |
| 60 | 0.0001 | -0.0002 | -0.0004 | -0.0001 | 0.0010 | 0.0002 | 0.0005 | 0.0001 |
| 80 | 0.0000 | -0.0003 | -0.0001 | 0.0002 | 0.0005 | -0.0002 | -0.0001 | 0.0001 |
| 100 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0006 | -0.0003 | 0.0000 | 0.0002 |
| 120 | 0.0001 | 0.0002 | 0.0005 | -0.0001 | 0.0005 | 0.0005 | 0.0000 | 0.0004 |
附表4包含两个调节变量时不同效应量个数下的参数估计偏差(z-test)
| k | τ2 = 0.08 | τ2 = 0.32 | ||||||
|---|---|---|---|---|---|---|---|---|
| β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | β = (0, 0) | β = (0.2, 0.2) | β = (0.5, 0.5) | β = (0.2, 0.5) | |
| 20 | -0.0003 | -0.0002 | 0.0009 | 0.0006 | 0.0005 | -0.0002 | 0.0000 | 0.0000 |
| 40 | -0.0008 | -0.0001 | 0.0000 | -0.0002 | 0.0002 | -0.0002 | 0.0002 | 0.0010 |
| 60 | 0.0001 | -0.0002 | -0.0004 | -0.0001 | 0.0010 | 0.0002 | 0.0005 | 0.0001 |
| 80 | 0.0000 | -0.0003 | -0.0001 | 0.0002 | 0.0005 | -0.0002 | -0.0001 | 0.0001 |
| 100 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0006 | -0.0003 | 0.0000 | 0.0002 |
| 120 | 0.0001 | 0.0002 | 0.0005 | -0.0001 | 0.0005 | 0.0005 | 0.0000 | 0.0004 |

附图1包含一个调节变量时不同效应量个数下的置信区间宽度
 附图1包含一个调节变量时不同效应量个数下的置信区间宽度
附图1包含一个调节变量时不同效应量个数下的置信区间宽度
附图2包含两个调节变量时不同效应量个数下的置信区间宽度
 附图2包含两个调节变量时不同效应量个数下的置信区间宽度
附图2包含两个调节变量时不同效应量个数下的置信区间宽度
附图3包含一个调节变量时不同效应量个数下的统计功效
 附图3包含一个调节变量时不同效应量个数下的统计功效
附图3包含一个调节变量时不同效应量个数下的统计功效
附图4包含两个调节变量时不同效应量个数下的统计功效
 附图4包含两个调节变量时不同效应量个数下的统计功效
附图4包含两个调节变量时不同效应量个数下的统计功效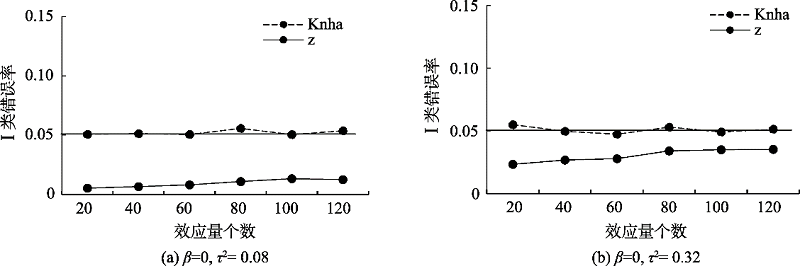
附图5包含一个调节变量时不同效应量个数下的I类错误率
 附图5包含一个调节变量时不同效应量个数下的I类错误率
附图5包含一个调节变量时不同效应量个数下的I类错误率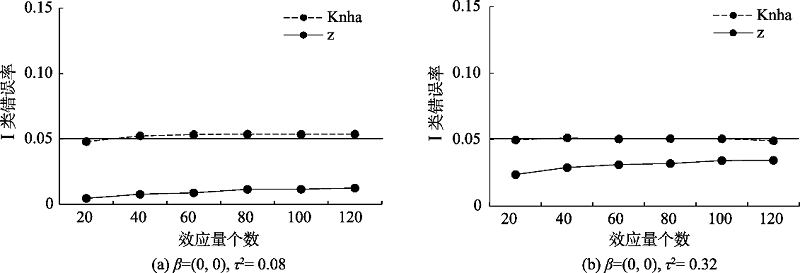
附图6包含两个调节变量时不同效应量个数下的I类错误率
 附图6包含两个调节变量时不同效应量个数下的I类错误率
附图6包含两个调节变量时不同效应量个数下的I类错误率参考文献 25
| 1 | 董圣杰, 曾宪涛, 郭毅 . ( 2012). R软件Metafor程序包在Meta分析中的应用. 中国循证医学杂志, 12( 9), 1141-1147. |
| 2 | 方杰, 张敏强 . ( 2012). 中介效应的点估计和区间估计:乘积分布法、非参数Bootstrap和MCMC法. 心理学报, 44( 10), 1408-1420. |
| 3 | 刘俊, 秦传燕 . ( 2018). 企业社会责任与员工绩效的关系:一项元分析. 心理科学进展, 26( 7), 1152-1164. |
| 4 | 王超, 袁蒙蒙, 姜媛, 方平 . ( 2019). 宜人性对企业家成就的影响:来自元分析的证据. 心理与行为研究, 17( 1), 126-133. |
| 5 | 张天嵩, 刘江波, 钟文昭 . ( 2009). Stata在探索异质性来源—Meta回归分析中的应用. 循证医学, 9( 1), 48-50. |
| 6 | 张云权, 马露, 冯仁杰, 朱耀辉, 李存禄 . ( 2015). 模型回归系数的合并分析在R软件metafor包中的实现. 中国循证医学杂志, 15( 3), 367-372. |
| 7 | Borenstein M., Hedges L. V., Higgins J. P. T., & Rothstein H. R . ( 2009). Introduction to meta-analysis. UK: John Wiley & Sons, Ltd., Publication. |
| 8 | Borenstein M., Hedges L. V., Higgins J. P.T., & Rothstein H. R . ( 2010). A basic introduction to fixed-effect and random-effects models for meta-analysis. Research Synthesis Methods, 1( 2), 97-111. |
| 9 | Cafri G., Kromrey J. D., & Brannick M. T . ( 2010). A meta-analysis: Empirical review of statistical power, type I error rates, effect sizes, and model selection of meta-analyses published in psychology. Multivariate Behavioral Research, 45( 2), 239-270. |
| 10 | Card N. A. (2012). Applied meta-analysis for social science research. New York: The Guilford Press. |
| 11 | Cheung, M. W. L., & Vijayakumar, R . ( 2016). A guide to conducting a meta-analysis. Neuropsychology Review, 26( 2), 121-128. |
| 12 | ?o?altay N., & Karada? E. . ( 2015). Introduction to meta-analysis. In E. Karada? (Eds.), Leadership and Organizational Outcomes (2nd ed, pp. 19-28). Switzerland: Springer International Publishing. |
| 13 | Cohn, L. D., & Becker, B. J . ( 2003). How meta-analysis increases statistical power. Psychological Methods, 8( 3), 243-253. |
| 14 | Field, A. P . ( 2001). Meta-analysis of correlation coefficients: A Monte Carlo comparison of fixed- and random-effects methods. Psychological Methods, 6( 2), 161-180. |
| 15 | Glass, G. V . ( 1976). Primary, secondary, and meta-analysis of research. Educational Researcher, 5( 10), 3-8. |
| 16 | Huizenga H. M., Visser I., & Dolan C. V . ( 2010). Testing overall and moderator effects in random effects meta-regression. British Journal of Mathematical and Statistical Psychology, 64, 1-19. |
| 17 | Knapp, G., & Hartung, G . ( 2003). Improved tests for a random effects meta-regression with a single covariate. Statistics in Medicine, 22, 2693-2710. |
| 18 | López-López J. A., Noortgate W. V. D., Tanner-Smith E. E., Wilson S. J., & Lipsey M. W . ( 2017). Assessing meta- regression methods for examining moderator relationships with dependent effect sizes: A Monte Carlo simulation. Research Synthesis Methods, 8( 4), 435-450. |
| 19 | Murphy, K. R . ( 2017). What inferences can and cannot be made on the basis of meta-analysis? Human Resource Management Review, 27( 1), 193-200. |
| 20 | Schmidt, F. L . ( 2017). Statistical and measurement pitfalls in the use of meta-regression in meta-analysis. Career Development International, 22( 5), 469-476. |
| 21 | Steel, P. D., & Kammeyer-Mueller, J. D . ( 2002). Comparing meta-analytic moderator estimation techniques under realistic conditions. Journal of Applied Psychology, 87( 1), 96-111. |
| 22 | Suchotzki K., Verschuere B., Bockstaele B. V., Ben-Shakhar G., & Crombez G . ( 2017). Lying takes time: A meta-analysis on reaction time measures of deception. Psychological Bulletin, 143( 4), 428-453. |
| 23 | Valentine J. C., Pigott T. D., & Rothstein H. R . ( 2010). How many studies do you need? A primer on statistical power for meta-analysis. Journal of Educational & Behavioral Statistics, 35( 2), 215-247. |
| 24 | Viechtbauer, W . ( 2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36, 1-48. |
| 25 | Viechtbauer W., López-López J. A., Sánchez-Meca J., & Marín-Martínez F . ( 2015). A comparison of procedures to test for moderators in mixed-effects meta-regression models. Psychological Methods, 20( 3), 360-374. |
相关文章 15
| [1] | 曾宪卿, 许冰, 孙博, 叶健彤, 傅世敏. EMMN受偏差-标准刺激对类型和情绪类型影响: 来自元分析的证据[J]. 心理科学进展, 2021, 29(7): 1163-1178. |
| [2] | 张雯, 胡娜, 丁雪辰, 李俊一. 拒绝敏感性与边缘型人格特征的关联:一项元分析[J]. 心理科学进展, 2021, 29(7): 1179-1194. |
| [3] | 叶静, 张戌凡. 老年人心理韧性与幸福感的关系:一项元分析[J]. 心理科学进展, 2021, 29(2): 202-217. |
| [4] | 陈钰, 莫李澄, 毕蓉, 张丹丹. 新生儿语音感知的神经基础:元分析[J]. 心理科学进展, 2020, 28(8): 1273-1281. |
| [5] | 黄崇蓉, 胡瑜. 组织内信任与创造力的关系:元分析的证据[J]. 心理科学进展, 2020, 28(7): 1118-1132. |
| [6] | 张建平, 秦传燕, 刘善仕. 寻求反馈能改善绩效吗?——反馈寻求行为与个体绩效关系的元分析[J]. 心理科学进展, 2020, 28(4): 549-565. |
| [7] | 张亚利, 李森, 俞国良. 孤独感和手机成瘾的关系:一项元分析[J]. 心理科学进展, 2020, 28(11): 1836-1852. |
| [8] | 胥彦, 李超平. 人口统计学特征对公共服务动机有什么影响?来自元分析的证据[J]. 心理科学进展, 2020, 28(10): 1631-1649. |
| [9] | 丁凤琴, 王冬霞. 道德概念具身隐喻及其影响因素:来自元分析的证据[J]. 心理科学进展, 2019, 27(9): 1540-1555. |
| [10] | 胥彦, 李超平. 领导风格与敬业度关系的元分析[J]. 心理科学进展, 2019, 27(8): 1363-1383. |
| [11] | 辛素飞, 姜文源, 辛自强. 1993至2016年医学生心理健康变迁的横断历史研究[J]. 心理科学进展, 2019, 27(7): 1183-1193. |
| [12] | 张亚利, 李森, 俞国良. 自尊与社交焦虑的关系:基于中国学生群体的元分析[J]. 心理科学进展, 2019, 27(6): 1005-1018. |
| [13] | 汤明, 李伟强, 刘福会, 袁博. 内疚与亲社会行为的关系:来自元分析的证据[J]. 心理科学进展, 2019, 27(5): 773-788. |
| [14] | 邵嵘, 滕召军, 刘衍玲. 暴力视频游戏对个体亲社会性的影响:一项元分析[J]. 心理科学进展, 2019, 27(3): 453-464. |
| [15] | 刘俊, 秦传燕. 企业社会责任与员工绩效的关系:一项元分析[J]. 心理科学进展, 2018, 26(7): 1152-1164. |
PDF全文下载地址:
http://journal.psych.ac.cn/xlkxjz/CN/article/downloadArticleFile.do?attachType=PDF&id=5024
