 ,School of Physical Science and Technology,
,School of Physical Science and Technology, Received:2020-11-11Revised:2020-12-7Accepted:2021-01-9Online:2021-02-08

Abstract
Keywords:
PDF (640KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Qing-Yuan Chen. First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb). Communications in Theoretical Physics, 2021, 73(3): 035703- doi:10.1088/1572-9494/abda1d
1. Introduction
The simple elemental metallic superconductors have been attracted many scientists’ attention over the past two decades [1–4]. As is known to all, the superconductors have no electrical resistivity when the temperature reaches an extremely low level, i.e. at or below the superconducting transition temperature (Tc). Nowadays, with the development of cryogenic science, many excellent low-temperature superconducting devices are tested in the lab and even used in practical productions. There are also more and more researchers exploring the physical and chemical properties of cryogenic superconducting materials, which has made it a focus in the field of the superconducting department, instead of just studying the improvement of the Tc. Notably, strain engineering is an effective tunable approach to alter the superconductive properties of materials. For instance, recent studies announced the enhancing superconductivity through strain for strained H3S, SrTiO3 films, and diamond [24–27]. Therefore, the study of the superconductive properties of materials tuned by strain is of great significance.Pb is always treated as an important material in the practical application of superconductors. As a superconductive element, it can remain a simple construction under the standard atmosphere, and also has a great superconductive property under high pressure, therefore, it has been used in Pb-based superconductors and Pb compounds. Therefore, the study of the superconductive properties of Pb plays a key role in all Pb-based superconductors research.
In this paper, we explored Pb’s crystal structure under high pressure and its superconducting properties by using ab initio studies. It is revealed that with the compressive strain increases from 0% to 10%, the Pb lattice structure is stable and its metallic properties remain unchanged, but at the same time, Tc shows a trend of decreasing. Therefore, the suitable Tc for the actual production could be achieved by exerting felicitous pressure. The electronic properties, such as the electronic DOS at the Fermi level explain the changes of the EPC lambda and the Tc. All of our calculations are greatly helpful to all Pb-based superconductors experiments and practical productions in the future.
2. Simulation details (method)
Calculations of geometrical optimization, electronic properties, electronic phonon coupling (EPC) parameter, and the superconductive properties were performed using the pseudopotential plane-wave method within the density functional theory [5] and linear response theory [6, 7] implemented in the QUANTUM-ESPRESSO package [8]. Pb showed a face-centered cubic structure (space group Fm3m) (figure 1) [9]. Convergence on total energy in the self-consistent field was ensured until 10−8 Ryd. For the exchange-correlation potential, we have used the Perdew–Burke–Ernzerhof exchange-correlation functional along with the Goedecker–Hartwigsen–Hutter–Teter wave potentials [10]. In order to generate the accuracy of pseudopotential and reduce negative error for Pb with an electronic configuration of 6s26p2, we used the norm-conserving scheme [11] for the high-pressure study in all of our calculations. Convergence tests gave a kinetic energy cutoff Ecutoff as 12 Ryd. We adopted Monkhorst–Pack k-point grid 16 × 16 × 16 for geometry optimization for the first BZ integrations. The technique for the calculation of EPC has been described in detail in the previous publication [12]. The applied compressive strain (or pressure) in our calculation is defined as ϵ% = ∣(a − a0)∣/a0. In this definition a is the lattice constant of the strained structure and a0 is the lattice constant of the free structure.Figure 1.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 1.Crystal structure of Pb.
In the calculation of the superconducting transition temperature (Tc) [13–15, 20–23], the strong-coupling theory was used based on Allen–Dynes [13] modified McMillan [14] equation by using the QUANTUM-ESPRESSO code
3. Results
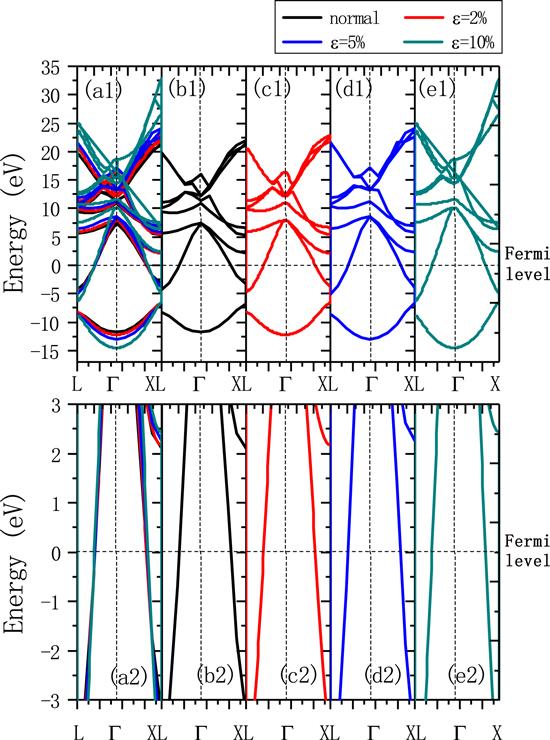
To probe the reason for Tc's changing under the different pressure, we calculated the electronic properties, dynamical properties, and EPC constant λ of Pb-based superconductors under the high pressure. In this paper, high pressure is achieved by altering the compressive strain from 0% to 10%, and the electronic properties have been studied first. The change of compressive strain from 0% to 10% leads to the changing of the lattice constant of Pb. Different band gaps and density of states (DOS) of Pb under different compressive strain are shown in figures 2 and 3.Figure 2.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 2.Band structures of Pb. (a1) Reveals all band structures under different compressive strain in one figure and (b1)–(e1) are band structures under different compressive strain in a separated way. (a2)–(e2) are the enlarged band structures correspond to (a1)–(e1) in the appropriate energy range around the Fermi level, respectively.
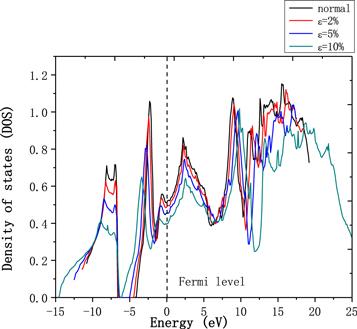
In our calculation, the Fermi levels of Pb under different compressive strains are set at the standard of zero for the more intuitive comparison. In the experiment and production, it is hard to make the compressive strain more than 10%. Therefore, we altered the compressive strain only from 0% to 10% in our study. According to the metal theory and our analysis of the DOS and the band structures, there is no band-gap of the Pb crystal. And at the same time, it is found that the energy bands have crossed the Fermi level, which indicated that the Pb compounds have remained metallic at all times. However, DOS at the Fermi level decreases when the compressive strain increases. It is obvious that changes in electronic properties mentioned above are based on the alterations of the compressive strain on Pb. Basically, the compressive strain leads to the following three changes: first, changes in the interaction between nuclei and electrons; second, changes in the interaction among different electrons; third, changes of the atomic bonds in Pb. The three changes are the fundamental reason for changes in the electronic properties of Pb. As shown in figures 2 and 3, the compressive strain has a relatively larger influence on the band that is far away from the Fermi level, but a much smaller impact on those close to the Fermi level. From 0% to 10%, the metallicity and the electronic structural properties of the Pb are stable, therefore, it is not necessary to redesign the structural framework of the Pb superconductor system within this range.
Figure 3.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 3.Electronic density of states of Pb under different compressive strain.
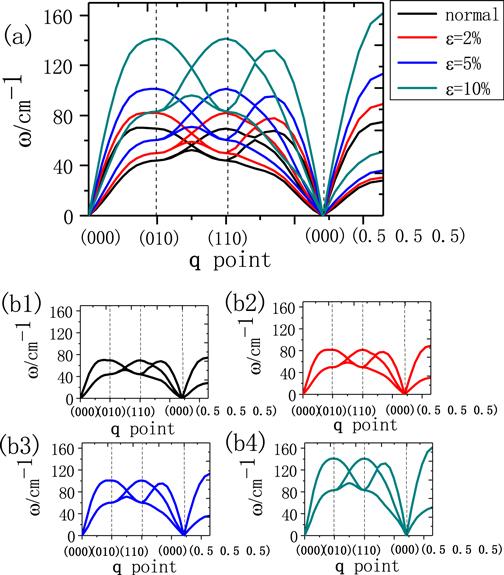
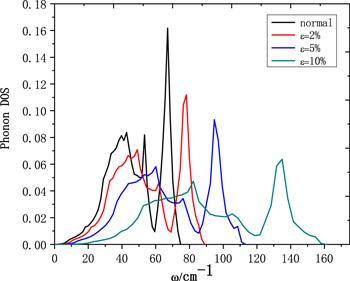
In this paragraph, the structural stability of Pb is analyzed based on the phonon dispersion curves in figure 4. From 0% to 10%, there are no imaginary phonon frequencies, suggesting that structures under different compressive strain within this range are all remaining dynamically stable [16]. Based on the fcc lattice structure and the metallicity of Pb, it only has the acoustic branch. In figure 4, there are some bent points in ω(q) curve around high symmetry q points, which is because of the strong coupling effect on the electron in Pb on the lattice waves of these q points. To compare the difference of phonon dispersion of Pb under different compressive strains, the same high-symmetry point and path of the Brillouin zone have chosen, as shown in figure 4. With different compressive strains, all of the curves show a similar shape, but the phonon frequencies and the bending degree of the ω(q) curve around high symmetry q points, and the phonon DOS of Pb are different as shown in figures 4 and 5. From 0% to 10%, the frequency ω(q) rising, due to the increased regular motion of all atoms in the Pb cell. Meanwhile, the coupling effect on the electron in Pb has enhanced with the increasing compressive strain, indicated by the larger curvature around the q points. As pressure increases, the value of the phonon DOS decreases while the frequency ω(q) increases, as shown in figure 5. When there is no pressure, the phonon DOS of the Pb mainly centers around the low-frequency range. When the compressive strain increases, the phonon DOS of Pb extends to a higher frequency. The difference of frequency between 0% and 10% is about 90 cm−1, which explains the stronger frequency ω(q) of the regular motion, and the coupling effect on the electron in Pb with the increasing compressive strain.
Figure 4.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 4.Calculated phonon spectrum of Pb. (a1) is all phonon spectrum under different compressive strain in one figure and (b1)–(b4) is phonon spectrum under different compressive strain in a separated way.
Figure 5.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 5.Phonon density of states of Pb under different compressive strain.
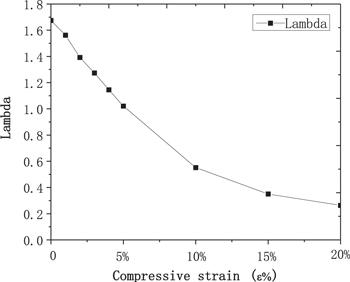
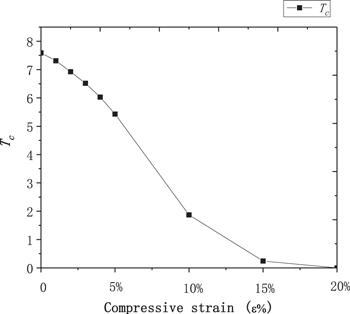
In order to obtain more physical insights into the characteristics of pressure dependence of the superconductive properties of Pb, we evaluated the EPC constant lambda (λ) and the superconducting transition temperature (Tc) in figures 6 and 7. When the compressive strain increases, the EPC constant lambda (λ) shows a decreasing trend, which further causes a decrease of the superconducting transition temperature (Tc). In our calculation, Tc is 7.5 K when there is no compressive strain, which is in good agreement with the data from the experiment (7.2 K) [17]. The decrease in λ is the result of phonon hardening and electronic DOS at the Fermi level decreasing. The electronic DOS at the Fermi level is always used to explain the change of the superconducting transition temperature (Tc) in the first-principles study. For example, the TaB2 is a kind of compound with high Tc, as its Fermi level is at the peak of electronic DOS of TaB2 theoretically [18]. In our calculation, Pb has low Tc under different compressive strain, and at the same time, the Fermi level in the electronic DOS figure is observed at the trough between two peaks. Therefore, our calculation is aligned with the theory to some extent. To be more specific, the electronic DOS at the Fermi level N(EF) shows a decreasing trend from 0% to 10%, and effective coupling weakened between electrons, which is because of the drop of Tc, according to the theory [19]. In all, with the increasing of the compressive strain from 0% to 10%, Tc decreases from 7.5 to 1.8 K while Pb remains structural stable.
Figure 6.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 6.The electronic phonon coupling (EPC) lambda (λ) under different compressive strain.
Figure 7.
 New window|Download| PPT slide
New window|Download| PPT slideFigure 7.The superconducting transition temperature (Tc) under different compressive strain.
4. Conclusion
In summary, we have presented a first-principles investigation of the pressure effects on the superconductivity of cryogenic superconductor lead (Pb). The crystal structures of Pb remained stable under different compressive strain. From 0% to 10%, the metallic properties of lead (Pb) remained the same, but the electronic DOS at the Fermi level changed and effective interaction between electrons decreased. The change of electronic DOS at the Fermi level leads to the decrease of the EPC constant lambda (λ). The decreasing of effective interaction between electrons, on the other hand, is the reason for Tc's decrease. Our study not only highlights the importance of atomic size and pressure that has put on Pb, but also provides great help to the experiments of all Pb-based superconductors, as well as the production of Pb-based superconductors application in the future.Acknowledgments
Computational resources were provided by the High Performance Computing Center of Yunnan University.Reference By original order
By published year
By cited within times
By Impact factor
DOI:10.1103/PhysRev.134.A511 [Cited within: 1]
DOI:10.1088/0953-2048/28/4/045011
DOI:10.1088/0953-2048/25/6/063001
DOI:10.1088/0953-2048/30/1/013002 [Cited within: 1]
DOI:10.1103/PhysRevB.43.7231 [Cited within: 1]
DOI:10.1007/978-1-4612-1264-5_33 [Cited within: 1]
DOI:10.1103/PhysRevLett.58.1861 [Cited within: 1]
[Cited within: 1]
DOI:10.1016/S0022-4596(03)00017-3 [Cited within: 1]
DOI:10.1103/PhysRevLett.77.3865 [Cited within: 1]
DOI:10.1103/PhysRevB.43.1993 [Cited within: 1]
DOI:10.1103/PhysRevLett.101.107002 [Cited within: 1]
DOI:10.1103/PhysRevB.12.905 [Cited within: 6]
DOI:10.1103/PhysRev.167.331 [Cited within: 2]
DOI:10.1103/PhysRevB.79.064518 [Cited within: 2]
DOI:10.1021/jp108136r [Cited within: 1]
DOI:10.1103/RevModPhys.26.277 [Cited within: 1]
DOI:10.1103/PhysRevB.53.1129 [Cited within: 1]
DOI:10.13380/j.cnki.chin.j.lowtemp.phys.2014.05.009 [Cited within: 1]
DOI:10.1103/PhysRev.125.1263 [Cited within: 2]
[Cited within: 1]
DOI:10.1103/PhysRev.106.162
DOI:10.1103/PhysRev.108.1175 [Cited within: 1]
DOI:10.1039/C8CP00205C [Cited within: 1]
DOI:10.1126/sciadv.aaw0120
DOI:10.1103/PhysRevLett.123.195504
DOI:10.1103/PhysRevLett.124.147001 [Cited within: 1]
