Yin Xia, Chuang Xue, Chen-Guang Li, Guang-Wei Meng, Ying-Kui Zhao, Jun Yan, Bai-Wen Li^,?Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

Corresponding authors: ? E-mail:li_baiwen@iapcm.ac.cn

Received:2019-09-6Online:2019-11-1

Fund supported:

*Supported by the National Key R&D Program of China under Grant.No. 2017YFA0403200 China Postdoctoral Science Foundation under Grant.No. 2018M630114

Abstract
With the actual mean free path for radiation in air and a simplified nuclear device, a one-dimension simulation research on fireball phenomenon in a sea level atmosphere is carried out based on the multi-group radiation hydrodynamic codes (RDMG). It is shown that our theoretical calculations can describe the whole process of the fireball evolution for strong explosions from the early X-ray expansion stage to the shock wave propagation stage. The radius of the shock wave and the brightness of the fireball are in good agreement with the experimental results. The whole thermal radiation power curve of the fireball evolution for strong atmospheric explosion at sea level is plotted for the first time. The impact of radiation opacity of the nuclear device material on the early fireball phenomenon is also studied. It is found that trajectories of the radiation fronts and case shocks change with the opacity of equivalent device material. From our simulations, we find that only the early fireball depends on the details of the nuclear device, and after the formation of main shock, the evolution is determined by the properties of hot air for strong atmospheric explosion.
Keywords： fireball phenomenon;radiation transfer equation;the shock wave;brightness


PDF (519KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Yin Xia, Chuang Xue, Chen-Guang Li, Guang-Wei Meng, Ying-Kui Zhao, Jun Yan, Bai-Wen Li. Numerical Study on the Whole Process of Fireball Evolution in Strong Explosion ^*. [J], 2019, 71(11): 1388-1392 doi:10.1088/0253-6102/71/11/1388

1 Introduction

The typical feature of strong explosions is that the nuclear device releases massive energy in an extremely short time with a small mass and volume. It causes a very strong luminance effect which can be observed at a far distance. And the high-energy-density plasma dominates the early stage of the fireball evolution. For atmospheric explosions, the radiation flux is the dominant mechanism of the energy flow in the early stage. Due to the short radiation mean free path (MFP) in air, the soft X-rays emitted by a device are immediately absorbed by the surrounding air. Then the surrounding air is heated to a high temperature (about $10^{7}$ K) layer-by-layer, forming a plasma of high pressure and high density. Driven by radiation transport and hydrodynamics, fireball expands with a fairly uniform temperature distribution.^[1-3]Studies of the fireball evolution in strong explosion are very important, since they can reveal the physical mechanism of fireball formation and evolution. It can also provide damage performance assessment for nuclear explosion, for example, the yield of a nuclear explosion can be obtained from the time evolution of radius and brightness of a fireball which can be measured in experiments. In addition, it can also be used as a reliable theoretical basis for scaled experiments of explosions in cavities by laser shooting in laboratory, which is designed to simulate the fireball formation and evolution in strong explosion.

Since the 1950s, a lot of theoretical works on fireball phenomenon in strong explosions^[1-7] have been carried out. The most systematic and comprehensive study was made by Brode,^[1-2]whose research covered almost the whole process of fireball with a two-stream assumption and a simple diffusion approximation. Horak^[6-7]developed a radiation-hydrodynamics code in spherical geometry that treats the evolution of fireballs. However, their treatment on the early stage of evolution turns out less satisfactory due to the transport approximation. Qiao et al.^[5,8-9]have also made a series of theoretical studies on fireball phenomenon with different radiation approximation models. Their studies mainly used X-ray fireball as the source of explosion rather than device. This approximation could lead to a loss of details of the early stage of evolution. X-ray fireball is a relatively small sphere of air with normal density, which contains a quite large amounts of energy at a high temperature created by X-ray emanations in atmospheric explosion.^[1,5]There are also some research that focused on early fireball stage. H. A. Sandmeir et al.^[10]introduced the S nuclear device which can be used to study the process of burning and energy releasing in the very early stage of explosions. G. C. Pomraning^[11]developed an early-stage model of air fireball to investigate the release of a large amount of X-ray energy in the atmosphere. A series of scaled experiments of explosions have also been carried out to study the fireball phenomenon.^[12-14]As far as we know, there is still not a suitable and accurate model for studying the whole process of fireball evolution. In this work, we adopt the segment number (S-N) discrete coordinate method^[15]to treat the radiation transfer process of the fireball evolution for the first time. The advantage is that it describes the radiation field in both optically thick and optically thin regions without the assumption that the resultant angular distributions of monochromatic intensities are approximately isotropic.^[16]Thus the energy radiation transfer during the whole process of fireball evolution can be better described. Radiation energy density, radiation pressures, and photon time-of-flight effects are all included in our study to improve the accuracy of radiation transport process, especially at the early stage of the fireball, while these terms were often omitted in previous studies for simplification.^[2,6-7]

Generally speaking, strong explosive fireball grows with five stages, namely X-ray deposition growth, radiative expansion growth, transition from radiative to shock growth, shock growth and fireball reburning growth respectively. And the radius of shock wave front as a function of time can be described by the self-similar solution of strong explosion in later stages, namely the radius $R$ is proportional to $({Et^{2}}/{\rho_{0}})^{1/5}$,^[4,17]where $E$ is the explosion energy and $\rho_{0}$ is the initial density of the surrounding air. The typical luminance characteristics of a fireball are the first maximum brightness, the minimum brightness and the second maximum brightness, which have also been observed in experiments.^[3-4]

In this paper, we will study the whole process of fireball phenomenon based on one-dimensional radiation hydrodynamic code RDMG with the actual mean free path for radiation in air and a simplified device structure. First, we will give a brief introduction to the radiation hydrodynamic codes and theoretical model. And some examples are given to test and verify the reliability and rationality of the numerical method. Then our accurate numerical model is used to describe the experimental results in strong explosions with the latest mean free path for radiation in air and a simplified nuclear device. At last, we will study the evolution of the temperature and density at the early fireball stage and how the material opacity of the simplified device impacts the early stage of fireball.

2 Simulation Model and Method

2.1 A Brief Introduction to RDMG Code

RDMG^[18-19]is a one-dimensional multi-group radiation hydrodynamic code, which mainly solves the two-temperature hydrodynamic equations and the multi-group radiation transfer equation. The hydrodynamic equations are

(1) $$ \frac{\partial \rho}{\partial t}+\nabla \cdot (\rho \vec{u}) =0\,, $$
(2) $$ \rho \frac{\partial \vec{u}}{\partial t}+ \nabla(P_{e}+P_{i}+P_{r}+q)=0\,, $$
(3) $$ C_{ve}\frac{\partial T_{e}}{\partial t}=W_{pe}+W_{fe}+W_{er}+W_{ei}\,, $$
(4) $$ C_{vi}\frac{\partial T_{i}}{\partial t}=W_{pi}+W_{fi}-W_{ei}\,. $$
where $P$, $q$, $C_{v}$ are the pressure, the artificial viscosity and the specific heat, respectively. The work terms $W_{p}$, $W_{f}$, $W_{ei}$, $W_{er}$ are done by pressures, the thermal conduction, the electron-ion energy exchange and the electron-radiation exchange, respectively. The subscripts $e$, $i$ and $r$ denote the electron, the ion and radiation, respectively. And other symbols have their usual meaning. The gravity effect is neglected in our simulations.

The radiation transfer equation describes radiation energy transport process in the most precise way. It is expressed as

(5) $$ \frac{1}{c}\frac{\partial I_{v}}{\partial t}+\vec{\Omega} \cdot \nabla I_{v} =J_{v}-\mu'_{v}I_{v}+S_{v}\,, $$
which can be solved with the S-N discrete coordinate scheme.^[19]Here, $I_{v}$ is the specific intensity of radiation at frequency $v$, traveling in direction $\vec{\Omega}$ at position $r$ and time $t$. And $J_{v}$, $\mu'_{v}$, $S_{v}$ are the radiation emission term, the effective absorption coefficient and the radiation source, respectively.

2.2 The Simplified Device

The radiation energy coming out from the explosive device is mainly determined by its structure. In our work, we use a device with a simplified structure (a uniform sphere of a single material is used to model the nuclear device) to explore the fireball phenomenon. The initial temperature, pressure and density of the device sphere are calculated by the equation of state according to the explosion yield and yield-to-mass ratio of explosion. This simplification allows the construction of a straightforward model to explore the effect of material properties on early fireball but ignore the process of burnout, which is only important when fireball has formed for less than a microsecond if the yield is not very large.^[10-11]X-ray fireball is used to approximate the early phases of fireball as completely independent of the details of the explosive device. Compared with X-ray fireball, our simplified nuclear device is more similar to the case of real nuclear explosion and it can provide more details of the early fireball stage. Our simulations below are all based on the simplified device unless specific statement is made.

It is well known that there exists an analytic solution to the evolution of blast wave in strong explosion. Thus, a one kiloton explosion yield with the ideal gas based on the X-ray fireball model is simulated to test the dependability and applicability of the fluid part of the program. The initial X-ray fireball is an ideal air sphere with the radius of $75$ cm, the initial density of $0.00129$ g/cm$^{3}$ and the temperature of $7.5$ MK. The radius of blast wave as a function of time given by the analytic solution can be expressed as

(6) $$ R_{s}=\epsilon_{0}\Big(\frac{Et^{2}}{\rho_{0}}\Big)^{1/5}\,, $$
where $E$ is the explosion energy, $\rho_{0}$ is the initial density of the surrounding ideal air, and constant $\epsilon_{0}$ is $1.033$ for the ideal air. The comparison result is shown in Fig. 1, and one can find that our simulation fits the analytic solution quite well.

Fig. 1

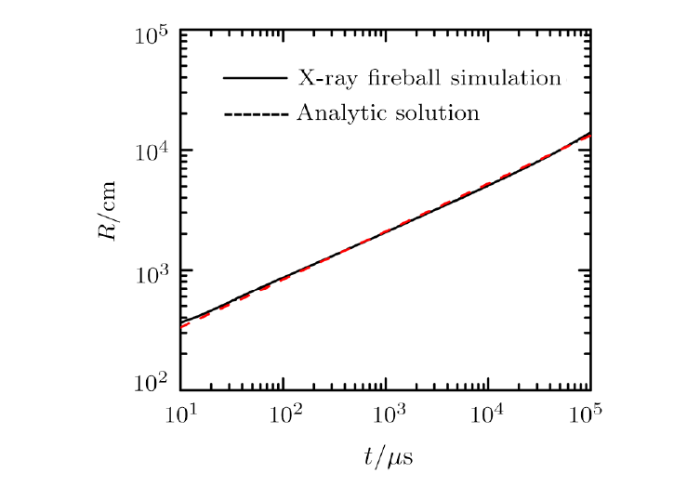New window|Download| PPT slide
Fig. 1The radius of blast wave as a function of time compared with the analytic solution for one kiloton explosion with the ideal gas. The black solid line is the simulation result, and the red dotted line is the analytic solution.



A one-kiloton explosion yield in a sea level atmosphere is also simulated to compare with Brode's result to verify the reliability of the model. The device is replaced by an iron sphere with the radius of $10$ cm, the initial density of $7.86$ g/cm$^{3}$ and the temperature of $16.5$ MK. The dependence of the various fronts on radius and time in early stage from radiative growth to shock growth on a logarithmic plot is illustrated in Fig. 2. Although our simulation is based on the simplified device, it shows that the result is in good agreement with Brode's result which was based on the nuclear device model.^[1-2]The radiation front expands to several meters at the earliest fractions of a microsecond, and then slows down remarkably as the energy from the nuclear device is depleted. At the same time, the nuclear device expands into the case shock. The case shock then catches up with the radiation front as the fireball itself also begins to shock up at its outer surface forming a strong shock.

Fig. 2

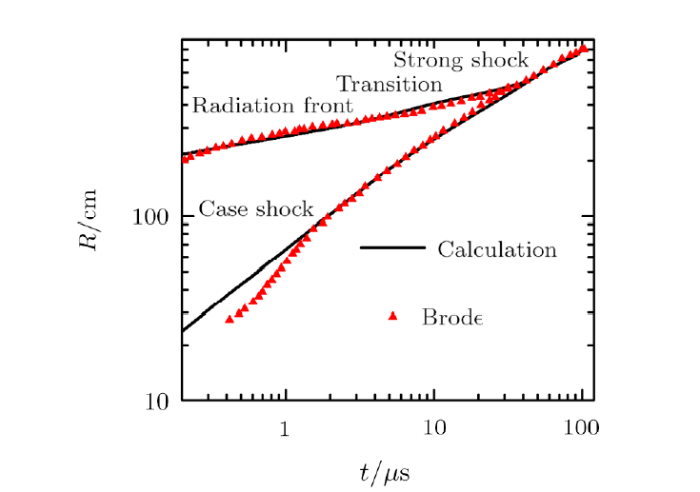New window|Download| PPT slide
Fig. 2The radius of the radiation fronts and case shocks vs. time compared with Brode's result for early fireball. At the beginning, the case shock is behind the radiation front, then it catches up with the radiation front forming a strong shock.The black solid line represents the simulation result of the simplified device. And the red upper triangle is Brode's result taken from Ref. ^[2].

3 Results and Discussion

3.1 Comparison with Experimental Results, Radius and Brightness

The radius and brightness of a fireball are important physical quantities which can be measured in experiments. We simulate a strong atmospheric explosion in similar explosion yield and altitude and compare it with the nuclear experiment in New Mexico in 1945^[3]to verify the reliability of our theoretical simulations. The nuclear device is replaced by an iron sphere with the radius of $22$ cm, the initial density of $7.86$ g/cm$^{3}$ and the temperature of $25$ MK. The results are shown in Figs. 3 and 4. Figure 3 illustrates that the radius of blast wave as a function of time predicted by our theoretical simulation is in agreement with the experimental results.^[17]Obviously, the evolution of the case shock at early stage may be lost if someone adopts the X-ray fireball model. The brightness of the fireball has also been studied, which can be considered as the ability of thermal radiation. The definition of the effective temperature $T_{eff}$ is expressed as

(7) $$ T_{eff}=\Big(\frac{F_{\rm flux}}{4\pi \times R_{f}^{2} \times \sigma}\Big)^{{1}/{4}}\,, $$

Fig. 3

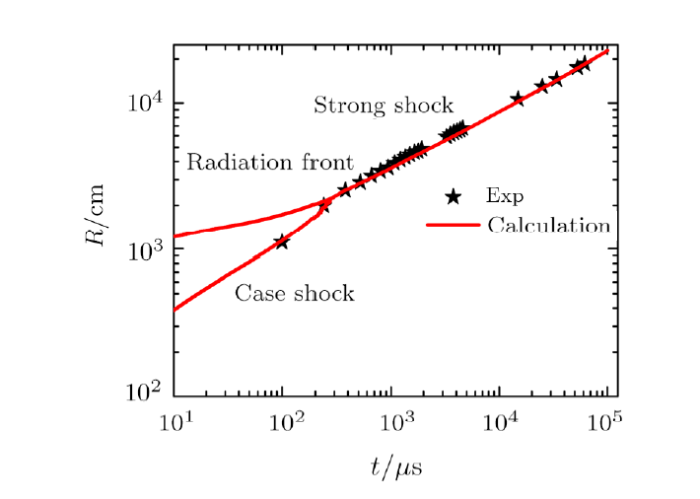New window|Download| PPT slide
Fig. 3Radius of blast wave vs. time compared with experimental data from $0.1$ ms to $62$ ms. At the beginning, the case shock is behind the radiation front, then it catches up with the radiation front forming a strong shock. The red solid line is the result of our simulation. And the pentagram is the experimental result taken from Ref. ^[17].

Fig. 4

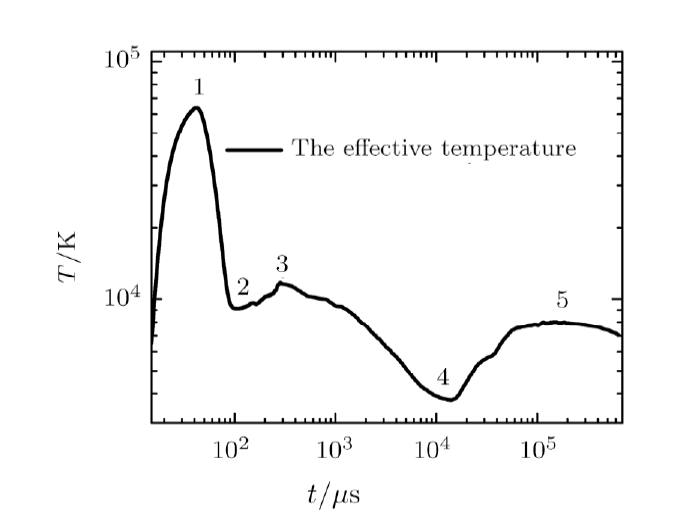New window|Download| PPT slide
Fig. 4The effective temperature curve observed for $20$ kiloton explosion at sea level. The five typical features are: (1) The maximum brightness of shock formation, (2) the minimum brightness of radiation shock wave, (3) the first maximum brightness, (4) the minimum brightness, (5) the second maximum brightness, respectively.



where $F_{\rm flux}$ is the power being radiated, $R_{f}$ is the radius of the fireball and $\sigma$ is the Stefan Constant. There are five brightness characteristic values during the whole process of the fireball evolution in Fig. 4, including three peaks and two troughs, i.e., the maximum brightness of shock formation, the minimum brightness of radiation shock wave, the first maximum brightness, the minimum brightness, the second maximum brightness, respectively. It is the first time to give out the whole thermal power radiated curve of the fireball evolution for strong atmospheric explosion at sea level. Only the last three characteristic values have been observed in experiments, while the first two can not be measured because of the insufficient time resolutions. The time of the last three characteristics are compared with the results observed in experiments, and the results of the comparison are shown in Table 1. It is seen that the theoretical results about the brightness of fireball are in good agreement with the experiments. It must be pointed out that how fireball evolves in the early stage is still not clear and it should be related to the detailed structure of nuclear device. And The first two extrema and their emerging time were seldom studied in previous research mainly due to the inaccurate of the radiation transport at early stage.^[2,5,7]


Table 1
Table 1The time of the first maximum brightness, the minimum brightness and the second maximum brightness compared with the results observed in experiments. The second row is the experimental results taken from Ref. ^[3], and the third row is the theoretical results.

New window|CSV

3.2 The Evolution of the Temperature and Density at the Early Fireball Stage

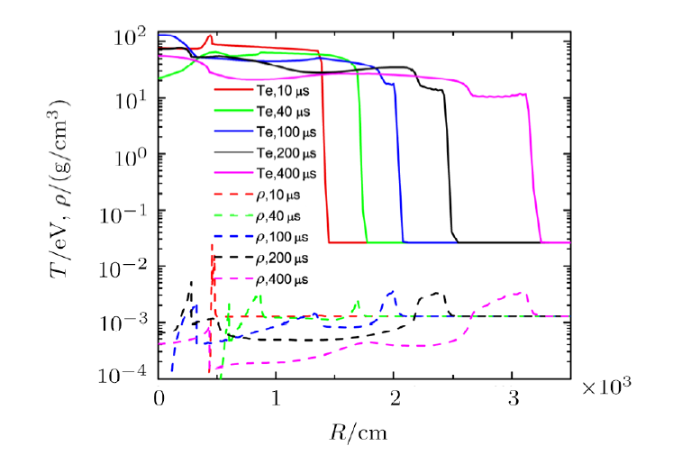
The typical evolution of the temperature and density during the early fireball stage is presented in Fig. 5. The nuclear device with the yield of $20$ kiloton is modeled as a uniform iron sphere with the radius of $22$ cm, the initial density of $7.86$ g/cm$^{3}$ and the temperature of $25$ MK. In the time scale shown in Fig. 5, the evolution of temperature and density experiences three distinct phases: radiative growth, transition from radiative to shock growth, and shock growth. At the time before $10$ $\mu$s, the fireball is in the radiative growth phase, with the existence of radiation front and nearly undisturbed density nearby. In the transition phase (between $40$ $\mu$s and $100$ $\mu$s), the density near the radiation front is disturbed and the case shock is chasing the radiation wave. At the moment when the case shock catches up with the radiation wave, the fireball enters the shock growth phase. Later on, the growth of the fireball is determined by the shock growth.

Fig. 5

New window|Download| PPT slide
Fig. 5The evolution of the profiles of the temperature and the density in the air for the $20$ kiloton explosion yield.

3.3 The Dependence of Early Fireball on the Opacity of the Simplified Device Material

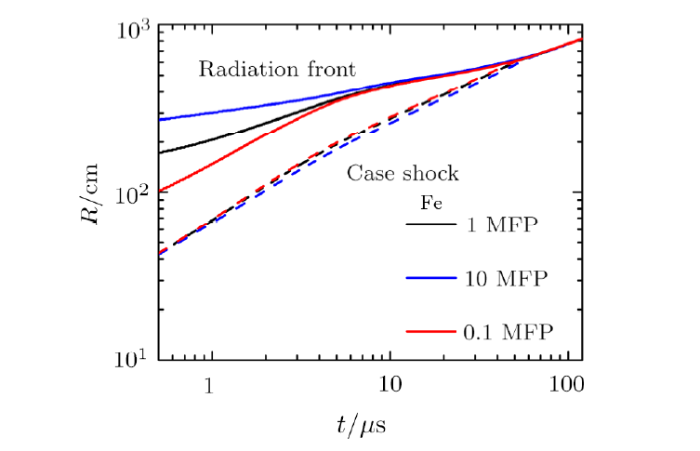
In order to explore the dependence of opacity of the nuclear device material on the early fireball phenomenon, a one kiloton explosion yield in a sea level atmosphere as above with different radiation MFPs of the nuclear device material is assumed. Different cases were investigated by changing the radiation MFPs to one time, ten times and one-tenth of Fe respectively. The result is shown in Fig. 6. It is seen that the radiation fronts and case shocks trajectories change with the opacity of equivalent device material. And the radiation front expands faster (slower) for larger (smaller) MFP, while the case shock expands slower (faster). This is due to fraction of the energy emitting out and remaining in the device. The radiation front with larger (smaller) MFP has a larger (smaller) radius because more energy is radiated out and deposit in the cold air in the early stage. Correspondingly, the radius of the case shock is smaller (larger) due to a smaller (larger) fraction of the energy remaining in the device. It is clear that the main shock after the shock transition and after the joining of the case shock with the fireball shock does almost not depend on the material properties of the nuclear device.

Fig. 6

New window|Download| PPT slide
Fig. 6The radius of the radiation fronts and case shocks vs. time for three different radiation mean free paths of device material. The solid lines are space-time plots of the radiation fronts. And the dash lines represent space-time plots of the case shocks. Color of line represents the magnitude of radiation mean free paths with black for one time, blue for ten times and red for one-tenth respectively.

4 Conclusions

In summary, the whole process of fireball phenomenon is studied by one-dimensional RDMG code with actual radiation opacity and EOS of air and equivalent device. It is the first time to study the all-stage evolution of fireball by solving the radiation transfer equation with the S-N discrete coordinate method. It is found that our method can improve the accuracy of radiation transport calculation, especially at the early stage of fireball. The radius of blast wave as a function of time is compared with the analytic solution for one kiloton explosion with the ideal gas. And the radius of the radiation fronts and case shocks trajectories of the early fireball are compared with Brode's results. All these comparisons demonstrate the reliability of our theoretical simulations. It is seen that our model fits the experimental results quite well. Moreover, the thermal power radiation curve that covers all the phases in the fireball evolution for strong atmospheric explosion at sea level is given for the first time, especially the maximum brightness of shock formation and the minimum brightness of radiation shock wave. The radiation energy delivered to air by a nuclear device is largely determined by the opacity of its material. And a larger (smaller) fraction of energy will be radiated out for the material with larger (smaller) MFP in the early stage. Thus, the radiation fronts and case shocks trajectories will change with the opacity of equivalent device material. After the joining of the case shock with the fireball shock, the main shock does almost not depend on the details of nuclear device which only influences the early fireball evolution. In the near future, the theoretical model can provide a reliable guidance for the following scaled experiments of explosions in cavities by laser shooting in laboratory.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] H. L. Brode , Fireball phenomenology,The RAND Corporation. AD612197 (1965).
[Cited within: 5]

[2] H. L. Brode, R. W. Hillendahl, R. K. Landshoff , Thermal radiation phenomena. Volume V: Radiation hydrodynamics of high temperature air, AD762837 (1967).
[Cited within: 5]

[3] S. Glasstone and P. J. Dolan, The effects of Nuclear Weapons, the United States Department of Defense and the Energy Research and Development Administration, Washington ( 1977).
[Cited within: 4]

[4] Y. B. Zel'dovich, and Y. P. Raizer. , Physics of Shock Waves and High-Temperature Hydrodynamic and Phenomena, Academic Press Inc, New York( 1966).
[Cited within: 2]

[5] D. J. Qiao , Introduction to the Physics of Nuclear Explosions, National Defense Industry Press, Beijing( 2003) (in Chinese).
[Cited within: 3]

[6] H. G. Horak and E. Jones , Two-Dimensional Radiation-Hydrodynamic Calculations for a Nominal 1-Mt Nuclear Explosion Near the Ground, Los Alamos National Laboratory report LA-9137 ( 1982).
[Cited within: 2]

[7] J. Zinn , J. Comput. Phys. 13 ( 1973) 569.
[Cited within: 4]

[8] J. H. Chen, X. Z. Wang, L. S. Xie , et al., Explosion and Shock Waves 2 ( 1981) 37 (in Chinese).
[Cited within: 1]

[9] Z. Tian, D. J. Qiao, Y. H. Guo , Chinese Journal of Computational Physics 27 ( 2010) 8 (in Chinese).
[Cited within: 1]

[10] H. A. Sandmeri, S. A. Dupree, G. E. Hansen , Nucl. Scie. And Engin 48 ( 1972) 343.
[Cited within: 2]

[11] G. C. Pomraning , Nucl. Scie. And Engin 53 ( 1974) 220.
[Cited within: 2]

[12] M. D. Denny and D. M. Goodman , J. Geophys. Res. 95 ( 1990) 19705.
[Cited within: 1]

[13] L. A. Glenn , Geophys. Res. Lett. 20 ( 1993) 919.


[14] J. Grun and G. A. Cranchet , et al., J. Appl. Phys. 119 ( 2016) 184903.
[Cited within: 1]

[15] B. G. Carlson , Solution of the Transport Equation by sn Approximations, Los Alamos Scientific Laboratory Report LA-1599 ( 1953).
[Cited within: 1]

[16] K. D. Lathrop and B. G. Carlson , J. Comp. Phys. 1 ( 1966) 173.
[Cited within: 1]

[17] T. Geoffrey, Proceedings of the Royal Society of Laondon. Series A, Mathematical and Physical 201 ( 1950) 175.
[Cited within: 3]

[18] T. Feng, D. Lai, Y. Xu , Chinese Journal of Computational Physics 16 ( 2005) 199 (in Chinese).
[Cited within: 1]

[19] G. W. Meng, J. Wang, X. Wang, J. Li, W. Zhang , Matter Radiat. Extremes 1 ( 2016) 249.
[Cited within: 2]