Nguyen Huy Bang¹, Le Nguyen Mai Anh^1,2, Nguyen Tien Dung¹, Le Van Doai^{,1,?? 1} Vinh University, 182 Le Duan Street, Vinh City, Vietnam
² Nong Lam University, Ho Chi Minh City, Vietnam

Corresponding authors: ? E-mail:doailv@vinhuni.edu.vn

Received:2019-03-21Online:2019-08-1

Fund supported:

*Supported by Vietnamese Ministry of Science and Technology under Grant .No. DTDLCN.17/17

Abstract
We present a comparative study of the control of-group velocity in three-level atomic systems including $\Lambda{}$-, Ladder-, and-V-types via spontaneously generated coherence (SGC) and relative phase of laser-fields. In the steady regime, expressions of group index are derived as an-analytical function of controllable parameters related to SGC and relative phase.-It is shown that the group velocity can be further slowed down or speeded up-under SGC in which modifications of group velocity due to the SGC in $\Lambda{}$--and V-systems are stronger than that in Ladder-system. In particular, when-interference strength of SGC p increases from 0.7 to 1.0, the light-propagation is switched from superluminal to subluminal modes (for $\Lambda{}$--and Ladder-systems) or from subluminal to superluminal modes (for V-system). In-the presence of relative phase, the group velocity changes between subluminal and-superluminal modes with a period of 2$\pi{}$. In resonant region, the largest-positive value of group index reaches at the relative phase $\varphi{}$ = $\pi{}$-while the largest negative value of group index reaches at $\varphi{}$ = 0 and-2$\pi{}$ for the $\Lambda{}$- and Ladder-systems, otherwise, for the V-system the-largest positive group index occurs at $\varphi{}$ = 0 and 2$\pi{}$, and the largest-negative group index occurs at $\varphi{}$ = $\pi{}$.
Keywords： electromagnetically induced transparency;spontaneously generated coherence;group velocity.


PDF (1756KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Nguyen Huy Bang, Le Nguyen Mai Anh, Nguyen Tien Dung, Le Van Doai. Comparative Study of Light Manipulation in Three-Level Systems Via Spontaneously Generated Coherence and Relative Phase of Laser Fields ^*. [J], 2019, 71(8): 947-954 doi:10.1088/0253-6102/71/8/947

1 Introduction

The manipulation of subluminal and superluminal light propagation in optical medium has attracted many attentions due to its potential applications during the last decades, such as controllable optical delay lines, optical switching, telecommunication, interferometry, optical data storage, and optical memories quantum information processing, and so on.^[1] The most important key to manipulate subluminal and superluminal light propagations lies in its ability to control the absorption and dispersion properties of a medium by a laser field. Slow light or subluminal propagation takes place in positive dispersion region, whereas negative dispersion region leads to fast light or superluminal propagation.

As we know that coherent interaction between atom and light field can lead to interesting quantum interference effects such as electromagnetically induced transparency (EIT)^[2] and spontaneously generated coherence (SGC).^[3] The EIT is a quantum interference effect between the probability amplitudes that leads to a reduction of resonant absorption for a weak probe light field propagating through a medium induced by a strong coupling light field.^[4] Basic configurations of the EIT effect are three-level atomic systems including the $\Lambda$-, Ladder-, and V-type configurations. In each configuration, the EIT efficiency is different, in which the $\Lambda$-type configuration is the best, whereas the V-type configuration is the worst,^[5] therefore, the manipulation of light in each configuration are also different. Whereas, the SGC effect can be created by the interference of spontaneously emission of either a single exited level to two closely lying atomic levels ($\Lambda$-type), two closely lying atomic levels to a common atomic level (V-type), or nearly equispaced atomic level case (Ladder-type). In 1996, Xia et al.^[6] carried out the first experimental investigation of spontaneously emission interference by using the sodium molecule.

Since the discovery of EIT, the control of optical properties of the medium becomes possible such as controlling group velocity,^[1,7] enhancement of Kerr nonlinearity,^[8] controlling optical bistability,^[9] controlling pulse propagation,^[10] and so on. Also, the effect of SGC on the optical properties in atomic systems was investigated for absorption and dispersion,^[11] group velocity,^[12] Kerr nonlinearity,^[13] optical bistability,^[14] and pulse propagation.^[15] It was shown that the atomic responses under SGC are sensitive to relative phase of the applied fields.^[15-17] Recently, several researchers have studied the possibility of switching light propagation from subluminal to superluminal modes in the EIT media by changing the interference strength of SGC effect or/and relative phase of applied fields.^[18-22] So far, the influence of SGC on the group velocity in three-level atomic systems investigated numerically,^[18-22] however, there is a lack of comparison of light manipulation between configurations. In this work, we develop an analytic model for a comparative study of influences of SGC and relative phase on group velocity in three-level systems including the $\Lambda$-, Ladder-, and V-type configurations. Such a comparison would be useful to choose an appropriate excitation configuration and parameters for experimental observations and related applications. Moreover, the analytical results have some advantages, such as it is easy to investigate the effect of controllable parameters on optical properties,^[23-24] to verify experimental observations^[25] and to study related applications, e.g., enhancement of Kerr nonlinearity,^[26] controlling optical bistability,^[27] controlling group velocity.^[28-29]

2 Theoretical Models

2.1 $\Lambda$-system

We first consider a $\Lambda$-type system as shown in Fig. 1(a). A coupling laser E$_{c}$ with frequency $\omega{}_{c}$ couples the transition $\vert3\rangle\leftrightarrow \vert2\rangle$ while a probe laser E$_{p}$ with frequency $\omega{}$$_{p}$ applies the transition $\vert{}$1$\rangle{}$ $\leftrightarrow{}$$\vert{}$2$\rangle{}$. We denote $\Gamma{}$$_{1}$ and $\Gamma{}$$_{2}$ are the spontaneous decay rates of the excited state $\vert{}$2$\rangle{}$ to the ground states $\vert{}$1$\rangle{}$ and $\vert{}$3$\rangle{}$, whereas $\Gamma{}$$_{0}$ is population relaxation between the hyperfine levels $\vert{}$1$\rangle{}$ and $\vert{}$3$\rangle{}$. When the two lower levels $\vert{}$1$\rangle{}$ and $\vert{}$3$\rangle{}$ are closely spaced such that the two transitions to the excited state interact with the same vacuum mode, spontaneously generated coherence can be present.

Fig. 1

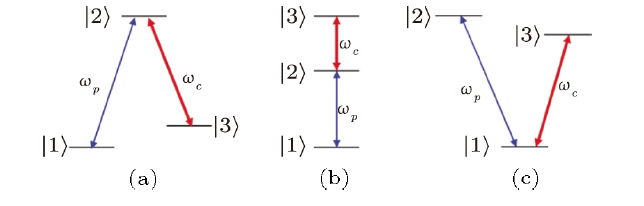New window|Download| PPT slide
Fig. 1(Color online) Three-level excitation schemes: (a) $\Lambda$, (b) Ladder, and (c) V.



The frequency detuning of the probe and coupling lasers from the relevant atomic transitions are respectively determined by:

(1) $$ \Delta{}_{p }= \omega{}_{p }- \omega{}_{21},\quad \Delta{}_{c} = \omega{}_{c} - \omega{}_{23}. $$
The Rabi frequencies of probe and coupling fields are given by:

(2)$$ {\Omega _p} = 2{\vec \mu _{21}} \cdot {\vec E_p}/\hbar, \quad {\Omega _c} = 2{\vec \mu _{23}} \cdot {\vec E_c}/\hbar, $$
with $\mu{}$$_{21}$ and $\mu{}$$_{23}$ being the electric dipole matrix elements. To ensure that one field acts on only one transition we chosen ${\vec E_c}$ $\bot$ ${\vec \mu _{21}}$ and ${\vec E_p}$ $\bot$ ${\vec \mu _{23}}$. We denote $\theta{}$ is the angle between the two dipole moments ${\vec\mu _{21}}$ and ${\vec \mu _{23}}$. We have:

(3)$$ p = \cos \theta = \frac{{{{\vec \mu }_{21}}\cdot{{\vec \mu }_{23}}}}{{\left| {{{\vec \mu }_{21}}} \right|\left| {{{\vec \mu }_{23}}} \right|}}, $$
is called as quantum interference parameter resulting from the cross coupling between spontaneous emission paths $\vert{}$2$\rangle{}$ $\rightarrow{}$ $\vert{}$1$\rangle{}$ and $\vert{}$2$\rangle{}$ $\rightarrow{}$ $\vert{}$3$\rangle{}$. If the two dipole moments are orthogonal to each other than p = 0, which clearly shows that there is no quantum interference due to spontaneous emission. When the two dipole moments are parallel to each other than the quantum interference is maximal and p = 1. So the quantum interference strength can be adjusted by control the alignments of two dipole moments.

Using a restriction that each of the linearly polarized field couples only one of the optical transitions, we can find that the Rabi frequencies are connected to the parameter p by the following relation:

(4)$$ {\Omega _p} = {G_{0p}}\sqrt {1 - {p^2}} = {G_{0p}}\sin \theta,\nonumber\\ {\Omega _c} = {G_{0c}}\sqrt {1 - {p^2}} = {G_{0c}}\sin \theta, $$
where G$_{0p}$ and G$_{0c}$ are the Rabi frequencies when ${p}$ = 0, namely ${\Omega_{0p}}=|{\vec \mu }_{21}|?|{{\vec E}_p}| /\hbar \ and \ {\Omega_{0p}}=2|{\vec \mu }_{23}|?|{{\vec E}_c}|/\hbar$. If we consider the phase of laser fields, so that the Rabi frequencies of the probe and coupling fields can respectively define as:

(5) $$ {\Omega _p} = {G_p}\exp \left( {{\rm i}{\varphi _p}} \right), \quad {\Omega _c} = {G_c}\exp \left( {{\rm i}{\varphi _c}} \right) $$
with, G$_{p}$ and G$_{c}$ are the real parameters, $\phi_{p}$ and $\phi_{c}$ are phase of the probe and coupling fields, respectively.

The evolution of the system, which is represented via the density operator $\rho$, is determined by the following Liouville equation:^[23]

(6)$$ \frac{{\partial \rho }}{{\partial t}} = - \frac{{\rm i}}{\hbar }\left[ {H,\rho } \right] + \Lambda \rho, $$
where H represents the total Hamiltonian and $\Lambda{}$$\rho{}$ represents the decay part, given by:^[30]

(7)$$ \Lambda \rho = - \sum\limits_{i,j = 1}^2 {{\Gamma _{{{ij}}}}} (S_i^ + S_j^ - \rho + \rho S_i^ + S_j^ - - 2S_j^ - \rho \,S_i^ + ), $$
where $S_i^ - = \left| i \right\rangle \left\langle 2 \right|$, $S_i^ + = \left| 2 \right\rangle \left\langle i \right|$, $S_j^ - = \left| 3 \right\rangle \left\langle j \right|$, and $S_j^ + = \left| j \right\rangle \left\langle 3 \right|$ represent respectively symmetric and antisymmetric superpositions of the dipole moments of the two bare systems; $\Gamma_{ij}$ describes cross-damping rates between the superpositions.

In the framework of the semiclassical theory, the density matrix equations involving the SGC and relative phase can be written as:

(8a) $$ \hspace{-24.5mm}{\dot \rho _{11}} = {\rm i}{G_p}({\rho _{21}} - {\rho _{12}}) + 2{\Gamma _1}{\rho _{22}} - {\Gamma _0}{\rho _{11}},$$
(8b)$${\dot \rho _{22}} = {\rm i}{G_p}({\rho _{12}} - {\rho _{21}}) + {\rm i}G_c({\rho _{32}} - {\rho _{23}}) -2(\Gamma_1+\Gamma_2)\rho_{22},$$
(8c) $$ \hspace{-24mm}{\dot \rho _{33}} = {\rm i}{G_c}\left( {{\rho _{23}} - {\rho _{32}}} \right) + 2{\Gamma _2}{\rho _{22}} - {\Gamma _0}{\rho _{33}},$$
(8d)$$ \hspace{-23.5mm}{\dot \rho _{21}} = {\gamma _{21}}{\rho _{21}} + {\rm i}{G_p}({\rho _{11}} - {\rho _{22}}) + {\rm i}{G_c}{\rho _{31}}, $$
(8e) $$\hspace{2mm}{\dot \rho _{31}} = {\gamma _{31}}{\rho _{31}} - {\rm i}{G_p}{\rho _{32}} + {\rm i}{G_c}{\rho _{21}} + 2{\eta _\varphi }p\sqrt {{\Gamma _1}{\Gamma _2}} {\rho _{22}}, $$
(8f)$$ \hspace{-23mm}{\dot \rho _{32}} = {\gamma _{32}}{\rho _{32}} - {\rm i}{G_p}{\rho _{31}} - {\rm i}{G_c}({{\rho_{33}}-{\rho_{22}}}). $$
The above equations are restricted by $\rho{}$$_{11}$ + $\rho{}$$_{22}$ + $\rho{}$$_{33}$ =1 and ${\rho _{ji}} = \rho _{ij}^ * $. Here, we are set ${\eta _\varphi } = \eta {{\rm e}^{{\rm i}\varphi }}$, ${\gamma _{31}} = - {\rm i}({\Delta _p} - {\Delta _c})$, ${\gamma _{21}} = - {\rm i}{\Delta _p} - ({\Gamma _1} + {\Gamma _2})$, ${\gamma _{23}} = - {\rm i}{\Delta _c} - {\Gamma _1} - {\Gamma _2}$, ${\gamma _{22}} = 2({\Gamma _1} + {\Gamma _2})$, and $\varphi{}$ = $\varphi{}$$_{p }-\varphi{}$$_{c}$ is the relative phase between the probe and the coupling fields. Term $\Gamma_{21}=p\sqrt{\Gamma_1\Gamma_2}$ represents the SGC effect that resulting from the cross coupling between the spontaneously emissions of the transitions $\vert{}$2$\rangle$$\leftrightarrow$$\vert{}$1$\rangle{}$ and $\vert{}$2$\rangle$$\leftrightarrow$$\vert{}$3$\rangle{}$. It depends on the nonorthogonality of the dipole moments ${\vec \mu _{21}}$ and ${\vec \mu _{23}}$, that is, depends on the interference parameter p.

Now, we analytically solve the density matrix equations under the steady-state condition by setting the time derivatives to zero. From Eqs. (8a), (8e), and (8f), we determine the terms $\rho{}$$_{31}$ as follows:

(9) $${\rho _{31}} = \frac{{{\rm i}{B_{20}}{\rho _{21}} + {\rm i}{B_{10}}{\rho _{12}} - {B_{11}}{\rho _{11}}}}{B},$$
where

(10) $$\hspace{-13mm}B = {A_{123}}{A_{321}^{\ast}} - {A_{31}}{A_{13}^{\ast}},$$
(11) $${B_{20}} = {A^*}{A_{123}} - {A_{21}^{\ast}}{A_{123}} + A{A_{13}^{\ast}},$$
(12) $$\hspace{-1mm}{B_{10}} = {A_{12}}{A_{13}^{\ast}} - {A^*}{A_{123}} - A{A_{13}^{\ast}},$$
(13) $$\hspace{-12mm}{B_{11}} = {A_{11}}{A_{13}^{\ast}} + {A_{11}^*}{A_{123}},$$
and (*) denotes the complex conjugation.

With

(14) $${A_{123}} = {\gamma _{13}}{\gamma _{23}}2{\Gamma _0}{\Gamma _1} - 2{\Gamma_1}G_c^2{\gamma _{13}} + 2G_p^2{\Gamma _0}{\Gamma _1},$$
(15) $${A_{12}} = 2G_c\Gamma_0\Gamma_1\gamma_{23},$$
(16) $${A_{31}} = 2G_c^2{\Gamma _1}{\gamma _{31}},$$
(17) $$A_{11} = G_cG_p\Gamma_0\Bigl[2\Gamma_2-\Gamma_0-\frac{2G_c\Gamma_{21}}{G_p} (\eta_{\varphi}+\eta_{\varphi}^*)\Bigr]\\ \quad\quad\quad+2\Gamma_0^2\Gamma_{21}\gamma_{23}\eta_{\varphi}^*,$$
(18) $$A = 2G_c^3{\Gamma _1} + G_p^2{G_c}\Bigl[2{\Gamma _2} - {\Gamma _0} -\frac{{2{G_c}{\Gamma _{21}}}}{{{G_p}}}(\eta _\varphi ^{} + \eta _\varphi ^*)\Bigr]\\ \quad\quad\quad+2{G_p}{\Gamma _0}{\Gamma _{21}}{\gamma _{23}}\eta _\varphi ^*.$$
By substituting Eq. (9) into Eq. (8d) and using the initial conditions: $\rho_{11}\approx 1$, $\rho_{22}\approx\rho_{33}\approx 0$, we find the solution $\rho_{21}$ for the probe transition as:

(19) $$\rho_{21}=\frac{i[(G_pB-G_cB_{11})(\gamma_{12}B^*)-G_cB_{10}(G_pB^*-G_cB_{11}^*)]}{G_c^2 B_{10}B_{10}^*-(\gamma_{12}B^*-G_cB_{20}^*)(\gamma_{21}B-G_cB_{20})}.$$

2.2 Ladder-System

The Ladder-type system is shown in Fig. 1(b). A coupling laser E$_{c}$ with frequency $\omega_{c}$ couples the transition $\vert{}$2$\rangle$$\leftrightarrow$$\vert{}$3$\rangle{}$ while a probe laser E$_{p}$ with frequency $\omega{}$$_{p}$ applies the transition $\vert{}$1$\rangle{}$$\leftrightarrow$$\vert{}$2$\rangle{}$. The frequency detuning of the probe and coupling lasers from the relevant atomic transitions are respectively determined as $\Delta{}$$_{p }$= $\omega{}$$_{p }- \omega{}$$_{21}$, $\Delta{}$$_{c}$ = $\omega{}$$_{c}-\omega{}$$_{32}$. The spontaneous decay rate from the higher excited state $\vert{}$3$\rangle{}$ to the lower excited state $\vert{}$2$\rangle{}$ is $\Gamma{}$$_{2}$ and the state $\vert{}$2$\rangle{}$ decays to the group state $\vert{}$1$\rangle{}$ with a rate $\Gamma{}$$_{1}$. When nearly equispaced levels than the effect of SGC can occur. The alignment of the two dipole moments ${\vec \mu _{21}}$ and ${\vec \mu _{32}}$ is determined by $p={\rm cos}\theta=\vec{\mu}_{21}\cdot\vec{\mu}_{32}/|\vec{\mu}_{21}||\vec{\mu}_{32}|$, with $\theta$ being the angle between the two dipole moments. Similarly, the density matrix equations of the Ladder-type system involving the SGC and relative phase are given by:

(20a) $$ 2 {\dot \rho _{11}} = 2{\Gamma _1}{\rho _{22}} + {\rm i}{G_p}({\rho _{21}} - {\rho_{12}}),$$
(20b)$$ {\dot \rho _{22}} = - 2{\Gamma _1}{\rho _{22}} + 2{\Gamma _2}{\rho _{33}} +{\rm i}{G_p}({\rho _{12}} - {\rho _{21}}) \\ \quad\quad+ {\rm i}{G_c}({\rho _{32}} - {\rho _{23}}),$$
(20c)$$ {\dot \rho _{33}} = - 2{\Gamma _2}{\rho _{33}} + {\rm i}{G_c}({\rho _{23}} - {\rho_{32}}),$$
(20d)$$ {\dot \rho _{21}} =\gamma_{21}\rho_{21}-{\rm i}G_p(\rho_{22}-\rho_{11})+{\rm i}G_c\rho_{31} \\ \quad\quad+2\eta_{\varphi}p\sqrt{\Gamma_1\Gamma_2}\rho_{32},$$
(20e)$$ \rho _{32}=\gamma_{32}\rho_{32}-{\rm i}G_p(\rho_{31}-{\rm i}G_c(\rho_{33}-\rho_{22}),$$
(20f)$$ {\dot \rho _{31}}=\gamma_{31}\rho_{31}-{\rm i}G_p(\rho_{32}+{\rm i}G_c\rho_{21},$$
where $\rho_{11} + \rho_{22} + \rho_{33} =1$ and $\rho_{ji}=\rho_{ij}^{\ast}$.

Here, we set ${\eta _\varphi } = \eta {e^{i\varphi }}, \gamma{}_{31} = i(\Delta{}_{p}+ \Delta{}_{c}) - \Gamma{}_{2}, \gamma{}_{21} = i\Delta{}_{p} - \Gamma{}_{1}, \gamma{}_{32} = i\Delta{}_{c} - \Gamma{}_{1} - \Gamma{}_{2}$

From Eqs. (20a), (20c), (20e), and (20f), we find the terms $\rho{}$$_{31}$ as follows:

(21) $$\rho_{31}=\frac{{\rm i}B_1\rho_{21}+{\rm i}B_2\rho_{12}}{B_3},$$
where

(22) $$B_1=AA_{321}^*+A_{13}A-A_{32}A_{321}^*,$$
(23) $$\hspace{-1.5mm}B_2=A_{13}A_{32}^*-A_{13}A-AA_{321}^*,$$
(24) $$\hspace{-10mm}B_3=A_{321}A_{321}^*-A_{13}^*A_{13},$$
and (*) denotes the complex conjugation.

With

(25)$$ 2{A_{321}} = 2{\Gamma _2}{\Gamma _1}{\gamma _{32}}{\gamma _{31}} + 2{\Gamma_2}{\Gamma _1}G_p^2 - {\Gamma _1}{\gamma _{31}}G_c^2,$$
(26) $${A_{32}} = 2{\Gamma _2}{\Gamma _1}{\gamma _{32}}{G_c},$$
(27) $${A_{13}} = \Gamma_1\gamma_{13}G_{c}^2,$$
(28) $$A = {G_c}[{\Gamma _1}G_c^2 + {\Gamma _2}G_p^2].$$
By substituting Eq. (21) into Eq. (20e), we find the terms $\rho_{32}$ as follows:

(29) $${\rho _{32}} = \frac{{(\gamma _{31}^{}B_1^{} + {G_c}B_3^{}){\rho _{21}} + \gamma _{31}^{}B_2^{}{\rho _{12}}}}{{{G_p}B_3}}.$$
Substituting Eqs. (21) and (29) into Eq. (20d) and using the initial conditions: $\rho_{11}\approx 1$, $\rho_{22}\approx\rho_{33}\approx 0$, we find the solution $\rho_{21}$ for the probe transition as:

(30) $${\rho _{21}} = \frac{{{\rm i}{G_p}({\gamma _{12}} + {F_1} + F_2^*)}}{{{F_1}F_1^* - ({\gamma _{21}} + {F_2})({\gamma _{12}} + F_2^*)}},$$
where

(31) $$\hspace{-14mm}{F_1} = \Big(\frac{{2{\Gamma _{12}}{\gamma _{31}}{{\rm e}^{{\rm i}\varphi }}}}{{{G_p}}} - {G_c}\Big)\frac{{{B_2}}}{{{B_3}}},$$
(32) $$F_2=2\Gamma_{12}{\rm e}^{{\rm i}\varphi}\Big(\frac{\gamma_{31}B_1}{G_pB_3}+\frac{G_c}{G_p}\Big)-G_c\frac{B_1}{B_3}.$$

2.3 V-type System

Atomic excitation for the three-level V-type configuration is shown in Fig. 1(c), where two closely spaced excited states $\vert{}$2$\rangle{}$ and $\vert{}$3$\rangle{}$ are coupled to the ground state $\vert{}$1$\rangle{}$. The transition $\vert{}$3$\rangle$$\leftrightarrow$$\vert{}$1$\rangle{}$ is excited by a coupling field of frequency $\omega{$$_{c}}$, whereas the transition $\vert{}$2$\rangle$$\leftrightarrow$$\vert{}$1$\rangle{}$ is excited by a probe field of frequency $\omega{$$_{p}}$. The frequency detuning of the probe and coupling lasers from the relevant atomic transitions are respectively determined by: $\Delta{}_{p }= \omega{}_{p }- \omega{}_{21}, \Delta{}_{c} = \omega{}_{c} - \omega{}_{31}$. We also denote $\Gamma_{1}$ and $\Gamma{}$$_{2}$ are spontaneous emission rates from $\vert{}$2$\rangle{}$ and $\vert{}$3$\rangle{}$ levels to $\vert{}$1$\rangle{}$, respectively. The alignment of the two dipole moments ${\vec \mu _{21}}$ and ${\vec \mu _{31}}$ is determined as, $p = \cos \theta = {{{{\vec\mu }_{21}}\cdot{{\vec \mu }_{31}}}}/{{\left| {{{\vec \mu }_{21}}} \right|\left| {{{\vec \mu }_{31}}} \right|}}$ with $\theta{}$ being the angle between the two dipole moments. Similarly, the evolution of the system in the presence of the SGC effect and relative phase can be represented by the following density matrix equations:

(33a) $$ {\dot \rho _{11}} = {\rm i}{G_p}({\rho _{21}} - {\rho _{12}}) + {\rm i}{G_c}({\rho _{31}} - {\rho _{13}}) + 2{\Gamma _1}{\rho _{22}} + 2{\Gamma _2}{\rho _{33}} + 2p\sqrt {{\Gamma _1}{\Gamma _2}} (\eta _\varphi ^*{\rho _{32}} + \eta _\varphi ^{}{\rho _{23}}), $$
(33b)$$ \hspace{-42.5mm}{\dot \rho _{22}} = {\rm i}{G_p}({\rho _{12}} - {\rho _{21}}) - 2{\Gamma _1}{\rho _{22}} - p\sqrt {{\Gamma _1}{\Gamma _2}} (\eta _\varphi ^*{\rho _{32}} + \eta _\varphi ^{}{\rho _{23}}), $$
(33c)$$ \hspace{-42.5mm}{\dot \rho _{33}} = {\rm i}{G_p}({\rho _{13}} - {\rho _{31}}) - 2{\Gamma _2}{\rho _{33}} - p\sqrt {{\Gamma _1}{\Gamma _2}} (\eta _\varphi ^*{\rho _{32}} + \eta _\varphi ^{}{\rho _{23}}), $$
(33d)$$ \hspace{-44mm}{\dot \rho _{21}} = {\gamma _{21}}{\rho _{21}} + {\rm i}{G_p}({\rho _{11}} - {\rho _{22}}) - {\rm i}{G_c}{\rho _{23}} - p\sqrt {{\Gamma _1}{\Gamma _2}} \eta _\varphi ^*{\rho _{31}},$$
(33e)$$ \hspace{-42.5mm}{\dot \rho _{31}} = {\gamma _{31}}{\rho _{31}} - {\rm i}{G_p}{\rho _{32}} + {\rm i}{G_c}({\rho _{11}}-\rho_{33}) - p\sqrt {{\Gamma _1}{\Gamma _2}} \eta _\varphi ^*{\rho _{21}},$$
(33f)$$ \hspace{-42.5mm}{\dot \rho _{32}} = {\gamma _{32}}{\rho _{32}} - {\rm i}{G_p}{\rho _{31}} + i{G_c}{\rho _{12}} - p\sqrt {{\Gamma _1}{\Gamma _2}} \eta _\varphi ^{}({\rho _{22}} + {\rho _{33}}),$$
where ${\gamma _{31}} = - {\rm i}{\Delta _c} - {\Gamma _2}$, $\gamma_{21}=-{\rm i}\Delta_p-\Gamma_1$, and ${\gamma_{32}} = {\rm i}({\Delta _p} - {\Delta _c}) - {\Gamma _1} - {\Gamma _2}$.

From Eqs. (33b), (33c), and (33f), we have

(34) $$\hspace{-53mm}{\rho _{31}} = \frac{{\! - {\rm i}A_3^*{\rho _{23}}\! -\! {\rm i}A_2^*{\rho _{32}}\! -\! {\rm i}A_x^*X + A_1^*{\rho _{21}} + A_{21}^*{\rho _{12}}}}{{{A^*}}},$$
(35) $$\hspace{-53mm}{\rho _{13}} = \frac{{{\rm i}{A_3}{\rho _{32}} + {\rm i}{A_2}{\rho _{23}} + {\rm i}{A_x}{X_{}} + {A_1}{\rho _{12}} + {A_{21}}{\rho _{21}}}}{A},$$
and (*) denotes the complex conjugation, where

(36) $${A_3} = - 2{\gamma _{32}}{\Gamma_{1}^{2}}{\Gamma_2}{\Gamma _{12}}{\rm e}^{ - {\rm i}\varphi{G_c}},$$
(37) $${A_2} = 2{\gamma _{23}}\Gamma _1^2{\Gamma _2}({\Gamma _{12}}{{\rm e}^{{\rm i}\varphi }}{G_c} - 2{G_p}{\Gamma _2}),$$
(38) $${A_x} = - \Gamma _{12}^3{\Gamma _1}{G_c}({\Gamma _1} + {\Gamma _2}) + {\Gamma _1}\Gamma _{12}^2{{\rm e}^{ - {\rm i}\varphi }}({\Gamma _1} + {\Gamma _2})({\Gamma _{12}}{{\rm e}^{{\rm i}\varphi }}{G_c} - 2{G_p}{\Gamma _2}),$$
(39) $${A_1} = {\Gamma _{12}}{\Gamma _1}{\Gamma _2}{{\rm e}^{ - {\rm i}\varphi }}[(2{G_c}{\Gamma _1} - {\Gamma _{12}}{{\rm e}^{{\rm i}\varphi }}{G_p}){G_c} + {G_p}({\Gamma _{12}}{{\rm e}^{{\rm i}\varphi }}{G_c} - 2{G_p}{\Gamma _2})],$$
(40) $${A_{21}} = {\Gamma _1}{\Gamma _2}[\Gamma _{21}^2{G_p}{G_c} + (2{G_c}{\Gamma _1} - {\Gamma _{12}}{{\rm e}^{ - {\rm i}\varphi }}{G_p})({\Gamma _{12}}{{\rm e}^{{\rm i}\varphi }}{G_c} - 2{G_p}{\Gamma _2})],$$
(41) $${A} = {\Gamma _{21}^2}{\Gamma _1^2}G_c^2-\Gamma_1^2(\Gamma_{12}{\rm e}^{-{\rm i}\varphi}G_c-2G_p\Gamma_2)(\Gamma_{12}{\rm e}^{{\rm i}\varphi}G_c-2G_p\Gamma_2),$$
(42) $$X = {\Gamma _{21}}({{\rm e}^{ - {\rm i}\varphi }}{\rho _{32}} + {{\rm e}^{{\rm i}\varphi }}{\rho _{23}}).$$
By substituting Eqs. (34) and (35) into Eq. (33e), we derive the terms $\rho_{32}$ as follows:

(43) $$\hspace{-72mm}{\rho _{32}} = \frac{{{C_{11}}{\rho _{11}} - {\rm i}{C_2}{\rho _{21}} - {\rm i}{C_1}{\rho _{12}}}}{C},$$
(44) $$\hspace{-72mm}{\rho _{23}} = \frac{{C_{11}^*{\rho _{11}} + {\rm i}C_2^*{\rho _{12}} + {\rm i}C_1^*{\rho _{21}}}}{{{C^*}}},$$
where

(45) $$\hspace{-47mm}{C_{11}} = {B_{}}(B_3^* + B_X^*{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }}) - B_{}^*({B_X}{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }} + {B_2}),$$
(46) $$\hspace{-46mm}{C_2} = B_1^*({B_X}{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }} + {B_2}) + {B_{21}}(B_3^* + B_X^*{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }}),$$
(47) $$\hspace{-46mm}{C_1} = B_{21}^*({B_X}{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }} + {B_2}) + {B_1}(B_3^* + B_X^*{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }}),$$
(48) $$C = (B_X^*{\Gamma _{21}}{{\rm e}^{ - {\rm i}\varphi }} + B_2^*)({B_X}{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }} + {B_2}) - (B_3^* + B_X^*{\Gamma _{21}}{{\rm e}^{{\rm i}\varphi }})({B_3} + {B_X}{\Gamma _{21}}{{\rm e}^{ - {\rm i}\varphi }}).$$
With

(49) $$\hspace{-44mm}{B_3} = G_c^2({A_3}{A^*} + A_2^*A) - 2{\gamma _{31}}{\Gamma _2}AA_2^* - 2{G_p}{\Gamma _2}A{A^*},$$
(50) $$\hspace{-62mm}{B_1} = G_c^2({A_1}{A^*} - A_{21}^*A) + 2{\gamma _{31}}{\Gamma _2}AA_{22}^*,$$
(51) $$\hspace{-33mm}{B_{21}} = G_c^2({A_{21}}{A^*} - A_1^*A) + 2{\gamma _{31}}{\Gamma _2}A_1^*A - 2{\Gamma _{21}}{\Gamma _2}{{\rm e}^{ - {\rm i}\varphi }}A{A^*},$$
(52) $$\hspace{-96mm}{B} = 2G_c\Gamma_2AA^*,$$
(53)$$\hspace{-62mm}{B_2} = G_c^2(A_2^{}{A^*} + A_3^*A) - 2{\gamma _{31}}{\Gamma _2}AA_3^*,$$
(54) $$\hspace{-42mm}{B_X} = G_c^2(A_X^*A + {A_X}{A^*}) + G_c^{}A{A^*} - 2{\gamma _{31}}{\Gamma _2}AA_X^*.$$
Substituting Eqs. (43) and (44) into Eq. (42), we have

(55) $$X=\frac{(C_{11}C^*E^{-{\rm i}\varphi}+C_{11}^*C{\rm e}^{{\rm i}\varphi})\Gamma_{21}\rho_{11}+{\rm i}(C_1^*C{\rm e}^{{\rm i}\varphi}-C_2C^*{\rm e}^{-{\rm i}\varphi})\Gamma_{21}\rho_{21}+{\rm i}(C_2^*C{\rm e}^{{\rm i}\varphi}-C_1C^*{\rm e}^{-{\rm i}\varphi})\Gamma_{21}\rho_{12}}{CC^*}.$$
Substituting Eqs. (43), (44), and (55) into Eq. (34), we have:

(56) $${\rho _{31}} = \frac{{{\rm i}{D_{11}}{\rho _{11}} + {D_{21}}{\rho _{21}} + {D_{12}}{\rho _{12}}}}{D},$$
where

(57) $${D_{12}} = A_{21}^*{(C{C^*})^2}^* + A_{3}^*{C^*}C_{2}^*{C^2} + (C_{2}^*C{{\rm e}^{{\rm i}\varphi }} - {C_1}{C^*}{{\rm e}^{ - {\rm i}\varphi }}){\Gamma _{21}}A_x^*C{C^*} - A_{2}^*C{C_{1}}{({C^*})^2},$$
(58) $${D_{21}} = A_{1}^*{(C{C^*})^2} + (C_{1}^*C{{\rm e}^{{\rm i}\varphi }} - {C_{2}}{C^*}{{\rm e}^{ - {\rm i}\varphi }}){\Gamma _{21}}A_x^*C{C^*} - A_{2}^*C{C_{2}}{({C^*})^2}+A_{3}^*C^*C_{1}^*C^2,$$
(59) $${D_{11}} = - A_{3}^*{C^*}C_{11}^*{C^2} - A_x^*[({C_{11}}{C^*}{{\rm e}^{ - {\rm i}\varphi }} + C_{11}^*C{{\rm e}^{{\rm i}\varphi }}){\Gamma _{21}}]C{C^*} - {\rm i}A_{2}^*C{C_{11}}{({C^*})^2},$$
(60) $$D=(CC^*)^2A^*.$$
Substituting Eqs. (44) and (56) into Eq. (33d) and using the initial conditions: $\rho{}_{11 }\approx1$, $\rho_{22}\approx\rho{}_{33 }\approx0$, we find the solution $\rho_{21}$ for the probe transition:

(61) $${\rho _{21}} = - {\rm i}\Big(\frac{{{F_{}}F_2^* + {F_1}F_{}^*}}{{{F_2}F_2^* - {F_1}F_1^*}}\Big),$$
where

(62) $$\hspace{-23mm}{F_1} = {G_c}C_2^*D - {\Gamma _{12}}{{\rm e}^{ - {\rm i}\varphi }}{D_{12}}{C^*},$$
(63) $${F_2} = {\gamma _{21}}{C^*}D - {\Gamma _{12}}{{\rm e}^{ - {\rm i}\varphi }}{D_{21}}{C^*} + {G_c}C_1^*D,$$
(64) $${F_{}} = {G_p}{C^*}D - {G_c}C_{11}^*D - {\Gamma _{12}}{{\rm e}^{ - {\rm i}\varphi }}{D_{11}}{C^*}.$$
In order to derive expressions for group velocity, we start from the susceptibility of atomic medium for the probe light that is determined by the following relation:

(65) $$\chi = \frac{{2N{{\left| {{{\vec \mu }_{21}}} \right|}^2}}}{{\hbar {\varepsilon _0}{G_p}}}{\rho _{21}}.$$
where N is the atomic density, c and $\epsilon{}$ $_{0}$ are the speed of light and permittivity of free space, respectively.

The linear dispersion coefficient $n$ for the probe light is written as

(66) $$n = 1 + \frac{{{\mathop{\rm Re}\nolimits} (\chi )}}{2}.$$
The group velocity is defined by

(67) $${v_g} = \frac{c}{{{n_g}}},$$
where $n_{g}$ is the group index which is related to the linear dispersion as:

(68) $$n_g=n+\omega_p\frac{\partial n}{\partial\omega_p}.$$

3 Light Manipulation Via SGC and Relative Phase

In order to illustrate the analytical results, we considered the case of $^{85}$Rb atomic medium at $D_{1}$ and $D_{2}$ transitions with the atomic parameters are chosen as:[31-32] $\mu_{21}$ = 2.53$\times{}$10$^{-29}$ Cm, $\omega{}$$_{p }$= 377$\times{}$10$^{12 }$ Hz, $\Gamma{}$$_{1}$ = $\Gamma{}$$_{2}$ = 5.7 MHz for the $\Lambda{}$- and V-systems, while $\Gamma{}$$_{1}$ = 5.7 MHz and $\Gamma{}$$_{2}$ = 0.97 MHz for the Ladder-system. For simplicity, all the parameters related to frequency are given in units of $\gamma{}$ = 1 MHz.

To start with, in order to see the change of the group index $n_{g}$ according to the interference parameter ${p}$ of the SGC effect, we keep the relative phase at $\phi{}$ = 0 and plot $n_{g}$ versus the probe detuning for different values of ${p}$, as shown in Fig. 2(a) for the $\Lambda{}$-type system, (b) for the Ladder-type system and (c) for the V-type system. Other parameters used in Fig. 2 are $\eta{}$ = 1, $\Delta{}$$_{c}$ = 0, G$_{p}$$_{ }$= 5$\gamma{}$, and G$_{c}$ = 10$\gamma{}$. From figure we can see that under SGC effect, the absolute value of $n_{g}$ is greatly enhanced (both positive and negative parts), therefore, the group velocity becomes slower or faster than those without SGC. In comparison between the three configurations, enhancement of group index due to the SGC in $\Lambda{}$- and V-systems are greater than that in the Ladder-system; variation of group index in V-system is opposite to the other two systems. In addition, spectral regions corresponding to slow light or fast light in the presence of SGC are narrower than those without SGC, so a frequency region of slow light in the case of the absence of SGC can switch into a region of fast light when the SGC presents, and vice versa. The physical reason for these phenomena arises from the influence of SGC on the absorption and dispersion that leads to the linewidth of absorption line deeper and narrower compared to in the case of SGC absents, therefore, the dispersion curve is also steeper as${ p}$ increases.^[11]

Fig. 2

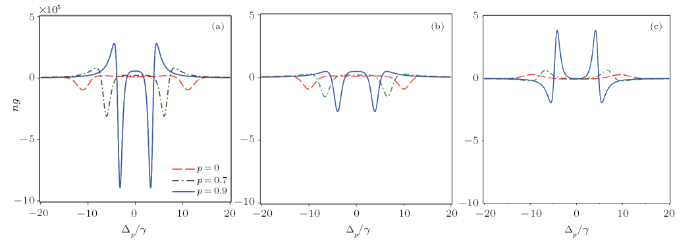New window|Download| PPT slide
Fig. 2(Color online) Variations of the group refractive index $n_{g}$ versus $\Delta{}$$_{p}$ for different values of p = 0 (dashed line), p = 0.7 (dot-dashed line), and p = 0.9 (solid line) when $\eta{}$ = 1, $\varphi{}$ = 0, $\Delta{}$$_{c}$ = 0, $G_{p}$$_{ }$= 5$\gamma{}$, $G_{c}$ = 10$\gamma{}$: (a) $\Lambda$-type system, (b) Ladder-type system, and (c) V-type system.



In order to see more clearly the ability to control group velocity according to parameter p, we plot $n_{g}$ versus p when fixing the parameters of the laser fields at $\varphi{}$ = 0, $\Delta{}$$_{c}$ = 0, $\Delta{}$$_{p}$ = 4$\gamma{}$, $G_{p}$$_{ }$= 5$\gamma{}$, and $G_{c}$ = 10$\gamma{}$. The results are described as in Fig. 3. It shows that the influence of SGC on group index or velocity becomes more obvious when p $>$ 0.7. In particular, when p increases from 0.7 to 1.0, $n_{g}$ also varies from negative to positive values (for $\Lambda{}$- and Ladded-systems) or from positive to negative values (for V-system). That is, the light propagation is switched from superluminal to subluminal modes (for $\Lambda{}$- and Ladded-systems) or from subluminal to superluminal modes (for V-system).

Fig. 3

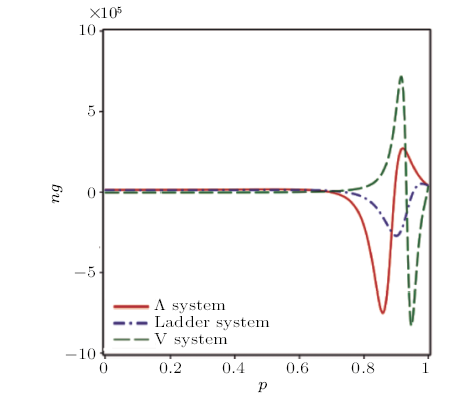New window|Download| PPT slide
Fig. 3(Color online) Variations of $n_{g}$ versus p in $\Lambda{}$-type system (solid line), Ladder-type system (dot-dashed line) and (c) V-type system (dashed line). The other parameters are chosen the same with those for Fig. 2, except $\Delta{}$$_{p}$ = 4$\gamma{}$.



Under the SGC effect, we can switch the propagation mode of light by changing the intensity (a) and the frequency (b) of the coupling laser as illustrated in Fig. 4 for the $\Lambda{}$-type system (solid line), for the Ladder-type system (dot-dashed line) and for the V-type system (dashed line). Other parameters used in Fig. 4 are $\eta{}$ = 1, p = 0.9, $\Delta{}$$_{p }$= 4$\gamma{}$, G$_{p}$$_{ }$= 5$\gamma{}$, $\Delta{}$$_{c }$= 0 (a) and $G_{c}$ = 10$\gamma{}$ (b). It is clear that the group index varies between negative and positive values with changing intensity and/or frequency of the coupling field. Similar to Figs. 2 and 3, variation of group index $n_{g}$ according to $G_{c}$ (a) and $\Delta{}$$_{c}$ (b) in V-system is opposite to the other two systems.

Fig. 4

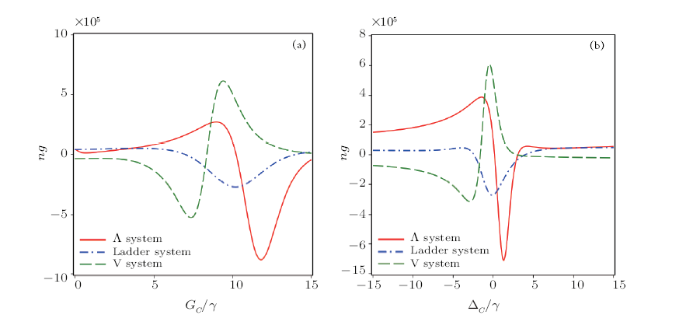New window|Download| PPT slide
Fig. 4(Color online) Variations of $n_{g}$ versus $G_{c}$(a) and $\Delta{}$$_{c}$ (b) in $\Lambda{}$-type (solid line),Ladder-system (dot-dashed line), V-system (dashed line). The employedparameters are $\varphi{}$ = 0, p = 0.9, $\Delta{}$$_{p }$=4$\gamma{}$, G$_{p}$$_{ }$= 5$\gamma{}$, $\Delta{}$$_{c }$= 0(a) and $G_{c}$ = 10$\gamma{}$ (b).



Now, we investigate the influence of relative phase on the groupvelocity by plotting $n_{g}$ versus $\Delta_{p}$ fordifferent values of relative phase $\phi{}$ in the presence of SGC withp = 0.9, as displayed in Fig. 5. Other parameters used in Fig. 5 are$\Delta{}$$_{p }$= 0, G$_{p}$$_{ }$= 5$\gamma{}$,$\Delta{}$$_{c }$= 0, and $G_{c}$ = 10$\gamma{}$. We foundthat, under the SGC condition, the group index is quite sensitive to variation inthe relative phase, namely, by changing the value of the relative phase, thevalue of the group index is greatly modified, in particular, at $\varphi{}$ =$\pi{}$/2 or 3$\pi{}$/2.

Fig. 5

New window|Download| PPT slide
Fig. 5(Color online) Variations of n$_{g}$versus$\Delta{}$$_{p}$ for different values of $\varphi{}$ = 0 (solid line),$\varphi{}$ = $\pi{}$/2 (dot-dashed line), $\varphi{}$ = $\pi{}$ (dashed line),and $\varphi{}$ = 3$\pi{}$/2 (dotted line) when $\eta{}$ = 1, p = 0.9,$\Delta_{c}$ = 0, $G_{p}$= 5$\gamma{}$,$G_{c}$ = 10$\gamma{}$: (a) $\Lambda{}$-type system, (b) Ladder-type system, and (c) V-type system.



In order to see more clearly this change, we plot $n_{g}$ according to $\varphi{}$ as shown in Fig. 6, here theparameters are similar to those in Fig. 5, except $\Delta_{p}$ = 0.It is shown that the group index varies periodically between a maximal positiveto a minimal negative values with a period of 2$\pi{}$. Correspondingly, thegroup velocity changes between subluminal and superluminal modes. Therefore, wecan also use the relative phase as a knob to switch the light propagation fromsubluminal to superluminal. In addition, we also find that in each period of2$\pi{}$, the largest positive value of group index reaches at the relative phase$\varphi{}$ = $\pi{}$, while the largest negative value of group index reaches at$\varphi{}$ = 0 and 2$\pi{}$ for the $\Lambda{}$- and Ladder-systems, otherwise, forthe V-system the largest positive group index occurs at $\varphi{}$ = 0 and2$\pi{}$, and the largest negative group index occurs at $\varphi{}$ =$\pi{}$.

Fig. 6

New window|Download| PPT slide
Fig. 6(Color online) Variations of the group index$n_{g}$ on relative phase $\varphi{}$ in $\Lambda{}$-type (solid line),Ladder-system (dot-dashed line), V-system (dashed line). The employedparameters are $\eta{}$ = 1, p = 0.9, $\Delta{}$$_{p }$= 0,$\Delta{}$$_{c }$= 0, G$_{p}$$_{ }$= 0.01$\gamma{}$, and$G_{c}$ = 5$\gamma{}$.

4 Conclusions

We have made a comparative study of light manipulation via the SGCand relative phase in three-level atomic systems including $\Lambda{}$-, Ladder-,and V-types under EIT condition. Under the SGC effect, the group velocity becomesslower or faster than those without SGC. The influence of SGC is significant whenthe interference strength of SGC p increases from 0.7 to 1.0, which leadsto the light propagation is switched from superluminal to subluminal modes. Inthe presence of relative phase, the group velocity changes between subluminal andsuperluminal modes with a period of 2$\pi{}$. Thus, we can use the SGC effect andthe relative phase as a knob to switch the light propagation from subluminal tosuperluminal modes. In comparison between the three configurations, modificationsof group index due to the SGC and relative phase in $\Lambda{}$- and V-systemsare greater than that in the Ladder-system; variation of group index according tothe SGC and relative phase in V-system is opposite to the other two systems. Wenote that unlike previous works, here we do not use incoherent pumping so the SGCeffect requires that the intensity of probe field must be greater that withincoherent pumping, therefore the found analytical solutions did not use the weakfield approximation. In addition, the analytical results are convenient todetermine controllable parameters for experimental observations and study otherrelated applications.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] R. W. Boyd, J. Mod. Opt. 56(2009) 1908
[Cited within: 2]

[2] K. J. Boller, A. Imamoglu, S. E. Harris, Phys. Rev. Lett. 66(1991) 2593
[Cited within: 1]

[3] J. Javanainen, Europhys. Lett. 17(1992) 407
[Cited within: 1]

[4] M. Fleischhauer, I. Mamoglu, J. P. Marangos, Rev. Mod. Phys. 77(2005) 633
[Cited within: 1]

[5] S. Sena, T. K. Dey, M. R. Nath, G. Gangopadhyay, J. Mod. Opt. 62(2014) 166
[Cited within: 1]

[6] H. R.Xia, C. Y. Ye, and S. Y. Zhu, Phys. Rev. Lett. 77(1996) 1032
[Cited within: 1]

[7] G. S. Agarwal, T. N. Dey, S. Menon, Phys. Rev. A 64 (2001) 053809
[Cited within: 1]

[8] L. V. Doai, D. X. Khoa, N. H. Bang, Phys. Scr. 90(2015) 045502
[Cited within: 1]

[9] A. Joshi, A. Brown, H. Wang, M. Xiao, Phys. Rev. A 67 (2003) 041801
[Cited within: 1]

[10] D. X. Khoa, H. M. Dong, L. V. Doai, N. H. Bang, Optik 131 (2017) 497
[Cited within: 1]

[11] H. M. Ma, S. Q. Gong, Z. R. Sun, et al., Chin. Phys. 11(2006) 2588
[Cited within: 2]

[12] Y. Bai, H. Guo, D. Han, H. Sun, Phys. Lett. A 340 (2005) 342
[Cited within: 1]

[13] Y. P. Niu and S. Q. Gong, Phys. Rev. A 73 (2006) 053811
[Cited within: 1]

[14] A. Joshi, W. Yang, M. Xiao, Phys. Lett. A 315 (2003) 203
[Cited within: 1]

[15] H. M. Dong, L. V. Doai, N. H. Bang, Opt. Commun. 426(2018) 553-557
[Cited within: 2]

[16] A. Li, H. Ma, X. Tan, et al. , Opt. Commun. 280(2007) 397


[17] X. J. Fan, A. Y. Li, F. G. Bu, et al., Optik 119 (2008) 540
[Cited within: 1]

[18] D. Bortman-Arbiv, A. D. Wilson-Gordon, H. Friedmann, Phys. Rev. A 63 (2001) 043818
[Cited within: 2]

[19] M. Mahmoudi, M. Sahrai, H. Tajalli, J. Phys. B 39 (2006) 1825


[20] F. Carre?o, O. G. Calderón, M. A. Antón, I. Gonzalo, Phys. Rev. A 71 (2005) 063805


[21] D. Han, Y. Zeng, W. Chen, H. Cao, H. Lu, J. Mod. Opt. 56(2009) 2357


[22] 22 Y. Bai, H. Guo, D. Han, H. Sun, Phys. Lett. A 340 (2005) 342
[Cited within: 2]

[23] L. V. Doai, P. V. Trong, D. X. Khoa, N. H. Bang, Optik 125 (2014) 3666
[Cited within: 2]

[24] D. X. Khoa, P. V. Trong, L. V. Doai, N. H. Bang, Phys. Scr. 91(2016) 035401
[Cited within: 1]

[ 25 D. X. Khoa, L. C. Trung, P. V. Thuan, et al., J. Opt. Soc. Am. B 34 (2017) 1255
[Cited within: 1]

[25][ 26 D. X. Khoa, L. V. Doai, D. H. Son, N. H. Bang, J. Opt. Soc. Am. B 31 (2014) 1330
[Cited within: 1]

[27] D. X. Khoa, L. V. Doai, L. N. M. Anh, et al., J. Opt. Soc. Am. B 33 (2016) 735
[Cited within: 1]

[28] N. T. Anh, L. V. Doai, N. H. B. Bang, J. Opt. Soc. Am. B 35 (2018) 1233
[Cited within: 1]

[ 29 N. T. Anh, L. V. Doai, D. H. Son, N. H. Bang, Optik 171 (2018) 721
[Cited within: 1]

[30] Z. Ficek and S. Swain, Quantum Interference in Atomic and Molecular Systems
Springer, New York, USA (2005)
[Cited within: 1]

[31] Daniel Adam Steck, $^{87}$Rb D Line Data:
URL [Cited within: 1]

[32] C. L. Wang, Z. H. Kang, S. C. Tian, et al., Phys. Rev. A 79 (2009) 043810.
[Cited within: 1]