Na Chen^,1,???, Wei Ye^,2,??? 1 School of Applied Mathematics, Nanjing University of Finance & Economics, Nanjing 210023, China;
2 Department of Physics, Southeast University, Nanjing 210096, China;

Corresponding authors: ? ? E-mail:chenna_njue@163.com? ? E-mail:yewei@seu.edu.cn

Received:2018-11-8Online:2019-06-1

Fund supported:

Supported by the National Nature Science Foundation of China under Grant.11575044 the Foundation of Nanjing University of Finance $\&$ Economics under Grant.JGY1859

PDF (396KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Na Chen, Wei Ye. Intermediate Energy Reactions Versus Heavy-Ion Fusion: Light Particle Emission and Post-Saddle Friction in the Presence of Deformation Effects ^*. [J], 2019, 71(6): 697-701 doi:10.1088/0253-6102/71/6/697

1 Introduction

Nuclear dissipation plays an important role in the large-scale collective motion, like fusion and quasi-fission.^[1-3] Its critical influence on the fission process of hot nuclei has recently attracted much attention.^[4] Dissipation hinders fission and hence increases pre-scission particle multiplicities with respect to the predictions by standard statistical models.^[5-6] It has been demonstrated that stochastic approaches based on Langevin models^[7-9] have been successfully applied to address dissipation effects in nuclear fission and provided a satisfactory description of different types of fission data.

When applying the Langevin model to handle fission, a key ingredient in it is the deformation dependence of nuclear friction.^[10] Currently, a number of works have been made to constrain pre-saddle friction by using evaporation residue cross sections,^[11] the first-chance fission probability,^[12-13] the widths of fission-fragment charge distributions,^[14] etc. As a result, the strength of pre-saddle friction is severely limited.^[15] However, these observables only depend on the pre-saddle friction and thereby they are not suited for exploring the post-saddle dissipation effects. Moreover, till now, less effort has been invested to constrain the post-saddle friction strength.^[7,16]

Different from previously mentioned observables, light particles are evaporated along the entire fission path. They are thus affected by post-saddle friction. Also, post-saddle multiplicities are an increasing function of size of the decaying system. So, the particle emission from heavy fissioning nuclei is usually used to obtain information of post-saddle dissipation properties.^[17-20] Further, when a fissioning nucleus evolves from ground state to the scission point, it experiences the change of deformations along the fission trajectory. This affects various particle emissions.^[21-23]

The nuclear systems formed in intermediate energy heavy-ion collisions and fusion reactions have different excitation energies and angular momenta. However, to date, few have studied the effect of deformation on the evolution of post-saddle neutrons and light charged particles (LCPs) with the post-saddle friction strength for heavy fissioning nuclei populated under these different initial conditions. The present work is devoted to this issue.

Our aim is to exploit the favorable experimental condition through which the post-saddle dissipation effects can be better revealed with the particle multiplicity; that is, which experimental approach is more optimal for probing post-saddle dissipation with light particle multiplicity in the presence of deformation effects. To this end, the Langevin model[7-9,22-25} is employed here and it is successfully used to reproduce a volume of fission data for many compound systems over a broad range of the excitation energy, angular momentum, and fissility.

2 Theoretical Framework

In the Langevin description of a fission process, the crucial quantity is free energy, which contains a thermodynamic correction.^[26] We use the following one-dimensional Langevin equation to perform the fully dynamical trajectory calculations:

(1) $\begin{matrix} && \frac{ d q}{ d t} = \frac{p}{m}\,, \nonumber \\ && \frac{ d p}{ d t} = \frac{p^2}{2m^2}\frac{ d m}{ d q}- \frac{\partial F}{\partial q}-\beta p + \sqrt{m\beta T}\Gamma(t). \end{matrix}$
Here $q$ is the dimensionless fission coordinate and is defined as half the distance between the center of mass of the future fission fragments divided by the radius of the compound nucleus, and $p$ is the conjugate momentum. $\beta$ and $T$ denote the dissipation strength and temperature, respectively. The inertia parameter $m$ is obtained under the Werner-Wheeler approximation of an incompressible irrotational flow.^[27] $\Gamma(t)$ is a fluctuating force satisfying $\langle \Gamma(t) \rangle = 0$ and $\langle \Gamma(t)\Gamma(t')\rangle = 2\delta(t-t')$.

The free energy is constructed from the Fermi gas expression of the level density parameter together with a finite-range liquid-drop potential $V(q)$^[28] that contains $q$-dependent surface, Coulomb, and rotation energy terms; that is,

(2) $\begin{equation} F(q; T) = V (q) - a(q)T^2. \end{equation}$
In Eq. (2), the coefficients proposed in Ref. ^[29] are used to calculate the deformation-dependent level density parameter, which reads as follows:

(3) $\begin{equation} a(q) = 0.073 A + 0.095 A^{2/3} B_s(q), \end{equation}$
where $A$ is the mass number of the compound nucleus and $B_s$ is the dimensionless surface area of the nucleus.^[30]

In our calculation, prescission particle evaporation along Langevin fission trajectories from their ground state to their scission point has been taken into account using a Monte Carlo simulation technique. The emission width of a particle of kind $\nu (= n, p, \alpha)$ is evaluated by Blann's parametrization^[31]

(4) $\begin{matrix} \Gamma_{\nu} &=& (2s_{\nu}+1)\frac{m_{\nu}}{\pi^2 \hbar^2 \rho_c(E^*)} \nonumber \\ && \times \int_{0}^{E^*-B_{\nu}} d\varepsilon_{\nu} \rho_R(E^*-B_{\nu}-\varepsilon_{\nu})\varepsilon_{\nu} \sigma_{\mathrm{inv}}(\varepsilon_{\nu}), \end{matrix}$
where $s_{\nu}$ is the spin of the emitted particle $\nu$, and $m_{\nu}$ its reduced mass with respect to the residual nucleus. The level densities of the compound and residual nuclei are denoted by $\rho_c(E^*)$ and $\rho_R(E^*-B_{\nu}-\varepsilon_{\nu})$. $B_{\nu}$ are the liquid-drop binding energies. $\varepsilon$ is the kinetic energy of the emitted particle. The inverse cross section is given by^[31]

(5) $\begin{equation} \sigma_\mathrm{inv}(\varepsilon_{\nu}) =\left\{\begin{array}{ll} \pi R_{\nu}^2(1-V_{\nu}/\varepsilon_{\nu}) & \;\mathrm{for} \ \varepsilon_{\nu} > V_{\nu}\,, \\ 0 & \;\mathrm{for} \ \varepsilon_{\nu} < V_{\nu}\,, \end{array} \right. \end{equation}$
with

(6) $\begin{equation} R_{\nu}=1.21[(A-A_{\nu})^{1/3}+A_{\nu}^{1/3}]+ \frac{3.4}{\varepsilon_{\nu}^{1/2}}\delta_{\nu,n}\,, \end{equation}$
where $A_\nu$ is the mass number of emitted particle $\nu = n,p,\alpha$.

The barriers for the charged particles are^[31]

(7) $\begin{equation} V_{\nu} =\frac{(Z- Z_{\nu})Z_{\nu} K_{\nu}}{R_{\nu} + 1.6}\,, \end{equation}$
with $K_{\nu} = 1.32$ for $\alpha$, and 1.15 for proton.

The mass formula^[32] contains the deformation-dependent surface and Coulomb energy terms. The particle binding energy $B_i$ $(i = n,p,\alpha)$ is thus a function of deformation[21-22} and it can be written as

(8) $\begin{equation} B_i(q) = M_p(q) - M_d(q) + M_i\,, \end{equation}$
where $M_i$ $(i=n,p,\alpha)$ is the mass of the emitted particles. $M_p(q)$ and $M_d(q)$ are the masses of the mother and daughter nuclei, respectively.

We use the formula suggested by Fr$\ddot{o}$brich and Gont-char^[7] to calculate the deformation-dependent charged-particle emission barriers:

(9) $\begin{equation} V_c(q) = V_{\nu} \times B_c(q)\,. \end{equation}$
Here the Coulomb energy $B_c(q)$ is evaluated using the method in Refs. ^{[30, 33]}.

When a dynamic trajectory reaches the scission point, it is counted as a fission event. Prescission particles are insensitive to the definition of the scission point (i.e., zero or a finite neck radius), as they can be emitted along the entire fission trajectory. In our calculation, multiple emissions of light particles and higher-chance fission are taken into account. Prescission particle multiplicities are calculated by counting the number of corresponding evaporated particle events. To accumulate sufficient statistics, 10$^7$ Langevin trajectories are simulated.

3 Results and Discussion

Due to the competition from quasi-fission channels, which become stronger with increasing bombarding energy, heavy compound nuclei (CNs) populated by fusion reaction channels generally have a low excitation energy ($<80$ MeV) and a high angular momentum (around 40$\hbar$). However, intermediate-energy (around Fermi energy domain) heavy-ion collisions can deposit more energy into the nuclear systems and yield a variety of fissioning nuclei with a different excitation energy and angular momentum. For example, in near-central collisions the generated nuclear systems have a high excitation energy ($\sim250$ MeV) and a low spin (near 10$\hbar$). However, in peripheral collisions, the produced fissioning systems have an excitation energy over 200 MeV and a large angular momentum ($\sim 40\hbar$).^[34-35]

In the present work, calculations under these three different initial conditions mentioned above for the produced heavy fissioning system are carried out and their sensitivities to nuclear friction are compared in the presence of deformation effects. Towards that goal, a heavy $^{240}$Am was chosen here to investigate post-saddle dissipation characteristics by using light particle multiplicity. To better reveal post-saddle dissipation effects, the pre-saddle friction strength is set to $4 \times 10^{21} s^{-1}$, in consistent with recent theoretical estimates and experimental analyses,^[8,14,36-37] and dynamical calculations of post-saddle emission are performed considering different values of the post-saddle friction strength ($\beta$).

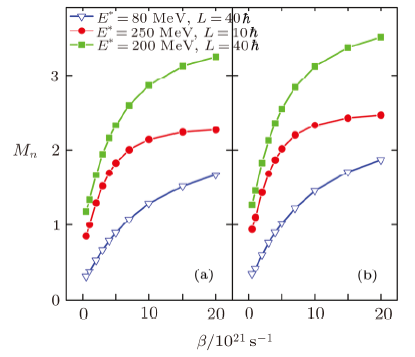
Shown in Fig.1 are the evolution of post-saddle neutrons with $\beta$ at three different initial conditions of excitation energy and angular momentum for the fissioning nucleus $^{240}$Am with and without deformation effects.

Fig.1

New window|Download| PPT slide
Fig.1(Color online) Post-saddle neutrons versus the post-saddle friction strength $\beta$ in the absence (a) and in the presence (b) of deformation effects for heavy system $^{240}$Am calculated for case (i) $E^* = 80$ MeV and $\ell = 40\hbar$, case (ii) $E^* = 250$ MeV and $\ell = 10\hbar$, and case (iii) $E^* = 200$ MeV and $\ell = 40\hbar$.



We first compare the results of case (i) and case (ii); that is, fusion reactions vs. intermediate-energy near-central collisions. Two typical features are observed. First, the calculated post-scission neutrons $M_n$ are larger in case (ii) than in case (i), indicating a stronger effect of dissipation on $M_n$ under the condition of case (ii).

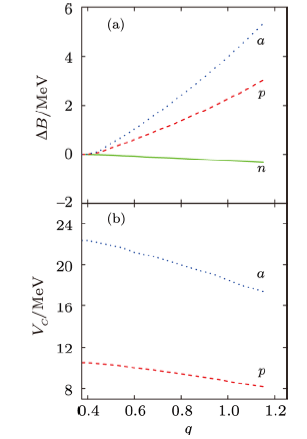
Another feature is that after incorporating deformation effects into the model calculations (Fig.1(b)), $M_n$ rises, exhibiting a larger influence of dissipation on post-saddle neutrons. A larger $M_n$ due to deformation is that neutron binding energies drop with increasing deformation (Fig.2(a)), enhancing the neutron emission.

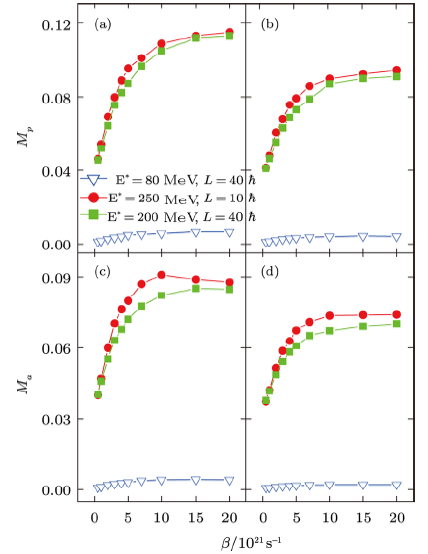
A comparison on charged-particle emission (i.e., protons and $\alpha$-particles) for case (i) and case (ii) is displayed in Fig.3. First, accounting for the deformation effects decreases $M_p$ and $M_{\alpha}$ in both cases. The reason is that though deformation lowers emission barriers of LCPs (Fig.2(b)), it increases their binding energies (Fig.2(a)), which is unfavorable for their emissions. As a result of the two opposite factors, the LCPs multiplicity decreases.

Fig.2

New window|Download| PPT slide
Fig.2(Color online) (a) A change in neutron, proton, and $\alpha$-particle binding energies of $^{240}$Am due to deformation with respect to their values at a spherical shape. (b) Emission barriers of protons and $\alpha$ particles of $^{240}$Am as a function of deformation coordinate $q$.



Secondly, when deformation effects are ignored (see triangles connected by blue lines in Figs. 3(a) and 3(c)), a variation in $M_p$ and $M_\alpha$ is still discernible as $\beta$ changes from $0.5 \times 10^{21}s^{-1}$ to $20 \times 10^{21}s^{-1}$, meaning a sensitivity of LCPs to $\beta$, though it is quite weak. However, in case (i), as a consequence of a reduced $M_p$ and $M_{\alpha}$ in the presence of the deformation effects (see triangles in Figs. 3(b) and 3(d)), LCPs almost do not vary with a change in $\beta$; that is, their sensitivity to friction disappears. In contrast, while deformation effects decrease $M_p$ and $M_{\alpha}$ in case (ii) (see circles connected by red lines in Figs. 3(b) and 3(d)), the LCPs multiplicity shows a significant sensitivity to the friction strength.

This comparison clearly shows the role of excitation energy in exploring the post-saddle dissipation properties after considering the deformation effects. Further, it suggests that when using LCPs to place a stricter constraint on the post-saddle friction strength, case (ii) is a more optimal experimental condition than case (i).

Unlike fusion reactions which form a CN, intermediate energy collisions generate a variety of excited nuclear systems having a different excitation energy and angular momentum, depending on the collision centralities. Further, fission events and the corresponding information on $A$, $Z$, $E^*$, etc. of fissioning sources coming from near-central or peripheral collisions can be identified and obtained experimentally.^{[34-35,38-39]} In these experiments, the folding angle technique was used to measure the correlation angle of the two fission fragments.

Fig.3

New window|Download| PPT slide
Fig.3(Color online) Post-saddle protons (top panel) and $\alpha$ particles (bottom panel) versus the post-saddle friction strength $\beta$ in the absence ((a) and (c)) and in the presence ((b) and (d)) of deformation effects for heavy system $^{240}$Am calculated for case (i) $E^* = 80$ MeV and $\ell = 40\hbar$, case (ii) $E^* = 250$ MeV and $\ell = 10\hbar$, and case (iii) $E^* = 200$ MeV and $\ell = 40\hbar$.



Previously, we compared the calculation concerning post-saddle particles as a function of $\beta$ for case (i) and case (ii), which represents the conditions provided via fusion and near-central collisions at intermediate energy, respectively. To better employ intermediate energy reactions as a way to probe the post-saddle friction strength, we make a further calculation at $E^* = 200$ MeV and $\ell = 40\hbar$ (case (iii)), which corresponds to conditions available in peripheral collisions which generate a fissioning nucleus with a lower $E^*$ and a higher $\ell$ than that generated in near-central collisions. The calculated results for case (iii) are also plotted in Figs. 1 and 3, which are shown by squares connected by green lines.

We note that in the presence of deformation effects, $M_n$ demonstrates an obvious quicker rise with increasing $\beta$ in case (iii) than in case (ii). This is because while case (iii) contains a lower $E^*$ than case (ii), a higher $\ell$ in case (iii) decreases the fission barrier, which shortens the transient time. Consequently, pre-saddle neutrons are decreased, and more energy is left for post-saddle evaporation, leading to a greater post-saddle multiplicity. This means that case (iii), i.e., peripheral collisions could provide a more favorable condition to probe $\beta$ using neutrons than near-central collisions. In addition, we also notice from Fig.1(b) that $M_n$ rises more rapidly with $\beta$ in case (iii) than in case (i), illustrating the effect of deformation on neutrons as an observable of the post-saddle friction strength.

However, a picture different from neutrons is seen for LCPs; that is, LCPs have a larger value in case (ii) than in case (iii), showing that dissipation has a larger effect on LCPs in case (ii). The reason is as follows. There exists a competition among different decaying channels. A strong neutron evaporation (compare squares and circles connected by the blue and red line in Fig.1(b), respectively) suppresses charged-particle evaporation. While a higher $\ell$ in case (iii) than in case (ii) raises the multiplicity of post-saddle particles including that of LCPs, the magnitude of excitation energy has a stronger effect than that of angular momentum. This further reveals the important role of $E^*$ in using light charged particles as a tool of the post-saddle friction strength. It implies that when one uses LCPs to better limit $\beta$, it is best to choose heavy fissioning nuclei populated in near-central collisions.

Putting together all the results calculated for the three cases, as shown in Figs. 1 and 3, one can find that intermediate energy reactions are a more preferable experimental approach than heavy-ion fusion, which is mostly adopted in the current experiments, to explore post-saddle dissipation properties with light particle emission, in particular in the presence of deformation effects.

4 Conclusions

In conclusion, we have studied the influence of deformation on probing the post-saddle friction strength ($\beta$) with light particle multiplicities of heavy $^{240}$Am under different excitation energies and angular momenta. It has been found that compared to the fusion approach, the high excitation energy condition provided in intermediate energy reactions apparently enhances the sensitivity of light particles (particularly for LCPs for the case with deformation effects) to $\beta$. Furthermore, it has been shown that when using neutrons to constrain $\beta$, fissioning systems generated in peripheral collisions at intermediate energies are more suitable than those generated in near-central collisions. For LCPs whose emission depends on excitation energy more strongly than on angular momentum, choosing those heavy fissioning nuclei from near-central collisions are favorable in experiments for more precisely determining the post-saddle friction strength.

The authors have declared that no competing interests exist.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] K. Wen, F. Sakata, Z. X. Li, X. Z. Wu, Y. X. Zhang, S. G. Zhou , Phys. Rev. Lett.. 111 ( 2013) 012501; Phys. Rev. C 90 (2014) 054613.
[Cited within: 1]

[2] M. V. Chushnyakova, R. Bhattacharya, I. I. Gontchar , Phys. Rev. C 90 ( 2014) 017603.


[3] J. Velkovska , et al., Phys. Rev. C 59 ( 1999) 1506.
[Cited within: 1]

[4] A. N. Andreyev, K. Nishio, K. H. Schmidt , Rep. Prog. Phys. 81(2018) 016301.
[Cited within: 1]

[5] H. Singh , et al., Phys. Rev. C 80 ( 2009) 064615.
[Cited within: 1]

[6] R. Mahajan , et al., Phys. Rev. C 98 ( 2018) 034601.
[Cited within: 1]

[7] P. Fr$\ddot{o}$brich and I.I. Gontchar , Phys. Rep. 292(1998) 131.
[Cited within: 3]

[8] A. V. Karpov , et al., Phys. Rev. C 63 ( 2002) 054610.
[Cited within: 1]

[9] M. T. S. Kannan , et al., Phys. Rev. C 98 ( 2018) 021601(R).
[Cited within: 1]

[10] H. J. Krappe and K. Pomorski , Theory of Nuclear Fission, Lecture Notes in Physics , Vol. 838, Springer, Berlin (2012).
[Cited within: 1]

[11] B. B. Back , et al., Phys. Rev. C 60 ( 1999) 044602.
[Cited within: 1]

[12] D. Peterson , et al., Phys. Rev. C 79 ( 2009) 044607.
[Cited within: 1]

[13] N. Wang and W. Ye , Phys. Rev. C 98 ( 2018) 034614.
[Cited within: 1]

[14] C. Schmitt , et al., Phys. Rev.Lett. 99(2007) 042701.
[Cited within: 2]

[15] D. Jacquet and M.Morjean, Prog. Part. Nucl. Phys. 63(2009) 155.
[Cited within: 1]

[16] W. Ye , Phys. Lett. B 681 ( 2009) 413.
[Cited within: 1]

[17] A. Chatterjee , et al., Phys. Rev. C 52 ( 1995) 3167.
[Cited within: 1]

[18] D. J. Hinde , et al., Phys. Rev. C 45 ( 1992) 1229.


[19] N. P. Shaw , et al., Phys. Rev. C 61 ( 2000) 044612.


[20] M. Thakur , et al., Phys. Rev. C 98 ( 2018) 014606.
[Cited within: 1]

[21] J. P. Lestone , Phys. Rev. Lett. 70(1993) 2245.
[Cited within: 1]

[22] K. Pomorski , et al., Nucl. Phys. A. 605 ( 1996) 87.


[23] N. Kumar , et al., Phys. Rev. C 96 ( 2017) 034614.
[Cited within: 1]

[24] H. Eslamizadeh , Eur. Phys. J. A 47 ( 2011) 134.


[25] K. Mazurek, at al ., Phys. Rev. C 94 ( 2016) 064602.


[26] S. G . McCalla and J. P.Lestone, Phys. Rev. Lett. 101(2008) 032702.
[Cited within: 1]

[27] K. T. R. Davies, A. J. Sierk, J. R. Nix , Phys. Rev. C 13 ( 1976) 2385.
[Cited within: 1]

[28] H. J. Krappe, J. R. Nix, A. J. Sierk , Phys. Rev. C 20 ( 1979) 992; A. J. Sierk, Phys. Rev. C 33 (1986) 2039.
[Cited within: 1]

[29] A. V. Ignatyuk , et al., Sov. J.Nucl. Phys. 21(1975) 612.
[Cited within: 1]

[30] I. I. Gontchar, P. Frobrich, N. I. Pischasov , Phys. Rev. C 47 ( 1993) 2228.
[Cited within: 2]

[31] M. Blann , Phys. Rev. C 21 ( 1980) 1770.
[Cited within: 3]

[32] P. M$\ddot{o}$ller , et al., At. Data & Nucl. Data Tables 39 ( 1988) 225.
[Cited within: 1]

[33] R. W. Hass and W. D. Myers , Geometrical Relationships of Macroscopic Nuclear Physics, Springer, New York ( 1988).
[Cited within: 1]

[34] E. M. Eckert , et al., Phys. Rev.Lett. 64(1990) 2483.
[Cited within: 2]

[35] R. S. Wang, Y. Zhang, Z. G. Xiao , et al., Phys. Rev. C 89 ( 2014) 064613.
[Cited within: 2]

[36] J. L. Rodriguez-S$\acute{a}$nchez , et al., Phys. Rev. C 94 ( 2016) 061601(R); Phys. Rev. C 90 (2014) 064606.
[Cited within: 1]

[37] J. Tian and W. Ye , Phys. Rev. C 94 ( 2016) 021601(R); W. Ye, et al., Phys. Rev. C 77 (2008) 011302(R).
[Cited within: 1]

[38] J. W. Zhen, E. J. Wu, C. Zhang , et al., High Enery Phys. Nucl.Phys. 23(1999) 946 (in Chinese).
[Cited within: 1]

[39] D. Hilscher , et al., Phys. Rev.Lett. 62(1989) 1099.
[Cited within: 1]