,1,2,*, Hassan Sabzyan,2,?Corresponding authors: * E-mail:R.Safari@qom.ac.ir;safari_physicalchemistry@yahoo.com? E-mail:sabzyan@sci.ui.ac.ir
Received:2018-06-3Online:2019-04-1
Abstract
Keywords：
PDF (12175KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Reza Safari, Hassan Sabzyan. Local Energy Dissipation/Transition in Field Effect Molecular Nanoelectronic Systems: a Quantum Mechanical Methodology. [J], 2019, 71(4): 441-454 doi:10.1088/0253-6102/71/4/441
1 Introduction
Various theoretical models and experimental methods have been used to describe field effects on molecular nanoelectronic devices.[1-3] Understanding intra-molecular energy dissipation, transition and conversion processes in field effect electrode-molecule-electrode (E-M-E) systems as molecular thermoelectric devices, has the central role in the development of molecular thermoelectric science, and is important for both prospective applications and fundamental research purposes.[4-15] In addition, considerable attention has been focused recently on the local heat (energy) and charge transfer in single molecule systems, which are the basic building blocks for molecular nanoelectronic systems.[16-22] Understanding of the fundamental mechanisms of heat/charge transport in single molecule nanoelectronic devices as well as the interpretation of the experimental observations requires the development of theoretical methods for the description of open quantum systems at the atomic/molecular scale. Furthermore, study of the local energy transfer in nanostructure semiconductors and organic molecular semiconductor-like systems is motivated industrially toward the miniaturization of thermoelectric devices.[23-25] Thermoelectric characteristics of thermoelectric-like devices vary with size (macro, meso, and nano/molecular), and thus interests for describing heat/electric transport characteristics of these devices have increased during recent years.[26-60] For example, in low temperature regimes, where electron-phonon interaction can be neglected, the thermoelectric figure of merit $(ZT)$, measuring efficiency of a thermoelectric devices, can be given by[15]where $G$ is the electrical conductance, $T$ is the operating/working temperature (the average temperature of the source and drain electrodes), $\kappa_{{\rm elec}}$ is the electronic thermal conductance, $\kappa_{\rm {vib(ph)}}$ is the thermal conductance due to the vibrational degrees of freedom (phonons), ${\bf {\pmb{\textit L}}}^{S}$ and ${\bf {\pmb{\textit L}}}^{P}$ are Seebeck and Peltier coefficients, respectively. The temperature-independence direct-tunneling electric conduction $(G)$ of a single molecule nanoelectronic system can be evaluated using the Landauer formula, i.e. $G\equiv 1/R=( {2e^{2}\tau_{{\rm elec}} (\varepsilon )})/h$, where $h/2e^{2}=12.91~{\rm k\Omega }$ and $\tau_{{\rm elec}} (\varepsilon )$ being the electronic transition function.[48-50] In most field-effect nanoelectronic molecular systems, transmission function $\tau_{{\rm elec}} (\varepsilon )$ represents the electric charge transport (electron transmission) through the molecular system induced by the applied external field.[50] This transmission function, which describes the probability of electron transfer from one contact point to another, can be calculated using Green's function (GF) method based on molecular density of states.\wen{2,23-25} Generally, in the real molecular nanoelectronic circuits, the $\tau_{{\rm elec}} (\varepsilon)$ value and thus molecular electronic conductance depend on the electrode-molecule-electrode coupling constant, $\Gamma$, which is determined by the external bias voltage regime, and molecular contact/junction properties.
During the past decade, different theoretical models have been presented for the calculation of $\tau_{{\rm elec}} (\varepsilon )$ and $G$.[51-57] For example, based on the transition voltage spectroscopy model, $\tau_{{\rm elec}} (\varepsilon)$ is given by
where $E_{F}$ is the Fermi energy which can be set to zero at low temperatures, ${E}'\approx E_{{\rm HOMO}},l^{M}$ is the potential barrier width, i.e. the effective (field-dependent) length of molecule, and $\beta$ is the tunneling decay length parameter. Also, the asymmetry factor $\eta =\Gamma _{{\rm elec, L(R)}} /\Gamma_{\rm {elec, tot}}~(\Gamma _{\rm {elec, tot}} =\Gamma_{{\rm elec, L}} +\Gamma_{{\rm elec, R}} )$ is a measure of the difference between the left (L) and right (R) electrode-molecule couplings $(\Gamma_{{\rm elec, L}}$ and $\Gamma _{{\rm elec, R}} )$.[51-54] For a symmetric junction, such as ${\rm Au}-{\rm S}-({\rm Ph)}_{\rm n} -{\rm S}-{\rm Au}$ for which $\Gamma _{{\rm elec}} \approx 0.5{\kern 1pt}{\kern 1pt}{\rm eV}$, we have $\eta \approx 1/2$.
Based on quantum coherent tunneling approach, in the low- and high-bias regimes ($\Phi^{\varepsilon } >1~{\rm eV}$ and $\Phi^{\varepsilon } <1~{\rm eV)}$, the tunneling decay length parameter $\beta $ is given respectively by:[55]
where $\hslash $ is $h/2\pi$, $\Phi^{\varepsilon }$ is the barrier height for tunneling through the LUMO level, $\Phi^{\varepsilon } \approx (E_{F} -E_{{\rm LUMO}} )$, or that of HOMO level, $\Phi^{\varepsilon }\approx (E_{{\rm HOMO}} -E_{F} )$. For most organic molecular nanoelectronic devices, $\Phi ^{\varepsilon }$ is nearly half of HOMO-LUMO gap $({\rm HLG}\equiv E_{{\rm HOMO}} -E_{{\rm LUMO}} )$, and $m_{e}^{\ast } $ is the electron effective mass (here $m_{e}^{\ast } = 0.16 m_{e}$ with $m_{e}$ being the free electron mass). Also, $\alpha \leq 1$ is a parameter that describes the asymmetry in the potential profile across the E-M-E junction; for symmetric cases $\alpha \approx 1$, also in very low temperature regimes, it has been established that non-resonant tunneling is the main conduction mechanism in single molecular devices. In this state, the tunneling probability and decay coefficients of the Landauer formula are given by $\tau_{{\rm elec}} (\varepsilon )\approx \exp (-\beta {\kern 1pt}{\kern 1pt}l^{M})$ and $\beta \approx \beta ^{\circ }$.[48-50]
In low temperature regime, the $\kappa_{{\rm elec}} (T)$ and $\kappa _{{\rm vib(ph)}} (T)$ heat conductions in Eq. (1) are given by
with $x_{k} =\hslash \nu_{k} /k_{B} T$ and $\nu_{D}$ being the Debye cut-off frequency of phonon reservoirs in the gold electrodes $(\nu_{D} \approx 2.16\times 10^{13}~{\rm S}^{-{\rm 1}})$.[58-61] Generally, at very low temperatures $(T\to 0)$, the electronic thermal conductance is approximated by $\kappa_{{\rm elec}} (T)\approx \left( {2\pi^{2}{\kern 1pt}{\kern 1pt}k_{B}^{2} {\kern 1pt}{\kern 1pt}T/3h} \right)\approx \kappa _{{\rm elec}}^{\circ }$ which can be regarded as an electronic quantum universal value of $\tau_{{\rm elec}} (\varepsilon )\approx 1$, approximately.
Also, $\tau_{{\rm vib(ph)}} (\nu )$ in Eq. (4) is the transmission function of the phonons ranging from zero to one at low temperatures. The values of $\tau _{{\rm vib(ph)}} (\nu )$ for the E-M-E devices can be obtained by $\tau_{{\rm vib(ph)}} (\nu )=\Gamma_{{\rm vib(ph)}}^{{\rm tot}} \delta (\nu -\nu_{i} )$ where $\Gamma _{{\rm vib(ph)}}^{{\rm tot}} =(\Gamma_{{\rm vib(ph)}}^{{\rm L}} \Gamma_{{\rm vib(ph)}}^{\rm R} )/(\Gamma_{{\rm vib(ph)}}^{\rm L} +\Gamma_{{\rm vib(ph)}}^{\rm R} )$ with $\Gamma _{{\rm vib(ph)}}$ being the phononic relaxation rate constant.[51] For weakly coupled molecular junctions and quantum dots, we can assume that $\Gamma_{{\rm vib(ph)}}^{\rm L}\approx \Gamma_{{\rm vib(ph)}}^{\rm R}$. In low temperature regimes, the heat current is carried at the molecular junctions mostly by low frequency phonons. In other words, contribution of the high frequency modes to the heat transfer is small because the Debye cut-off of the reservoir spectra is considerably below their frequencies. In addition, at very low temperatures, only the first energy phonon mode $(h\nu_{0})$ contributes significantly to $\tau_{{\rm vib(ph)}} (\nu )$, and thus $\kappa _{{\rm vib(ph)}} (\nu )$ can be simplified to $\kappa_{{\rm vib(ph)}} (T)\approx \left( {\pi^{2}{\kern 1pt}{\kern 1pt}k_{B}^{2} {\kern 1pt}{\kern 1pt}T/3h} \right)\approx \kappa_{{\rm vib(ph)}}^{\circ }$.[28] This quantum of phononic thermal conductance represents the maximum possible value of energy transported per phonon mode at these temperatures (or $\tau_{{\rm vib(ph)}} (\nu )\approx 1$).
In the present work, in continuation and development of our previous works, analogous to the known thermoelectric effects in molecular junction devices, low temperature coefficients of the intra-molecular energy dissipation (${\bf {\pmb{\textit{L}}}}^{{\rm JL}} $, as Joule-like coefficient), energy dissipation/transition ($\bf {\pmb{\textit{L}}}^{{\rm PL}} $, as Peltier-like coefficient), energy conversion ($\bf {\pmb{\textit{L}}}^{{\rm SL}} $, as Seebeck-like coefficient), and energy dissipation/transition/conversion ($\bf{\pmb{\textit{L}}}^{{\rm TL}} $, as Thomson-like coefficient) processes, and the intra-molecular figure of merit $(ZT_{\gamma }^{M})$, are introduced and computed for two candidate molecular nanoelectronic devices. The electronic and vibrational contributions to these intra-molecular thermoelectric-like coefficients (IMTLCs) describing these processes are computed using respectively quantum theory of atoms-in-molecule (QTAIM) and an energy partitioning scheme based on normal modes vibrational analysis.[62-63]
2 Extension of the Concept of Local Heat Distribution to Molecular Devices
In our previous reports,[52-53] we introduced intra-molecular thermoelectric-like effects, intra-molecular thermoelectric-like sections (IMTLS) and intra-molecular thermoelectric-like coefficients (IMTLC) for molecular nanoelectronic devices. In the present work, two intra-molecular partitioning schemes are used for the calculation of the local energy dissipation/transition and IMTLCs. The first includes four intra-molecular sections (IMS), denoted by $S_{\rm I} $, $S_{\rm II} $, $S_{\rm III} $ and $S_{\rm IV} $, as shown in Fig. 1(a), and is used for detailed intra-molecular energy/heat transfer analysis and the local temperature scaling. In the second partitioning scheme, as shown in parts (b), (c) and (d) of Fig. 1, the molecular system is divided into three sets of IMTLSs, either left (L) and right (R), up (U) and down (D), and, or diagonal-left (DL) and diagonal-right (DR) sections, denoted by $(S_{\rm L}$ and $S_{\rm R} )$, $(S_{\rm U} $ and $S_{\rm D} )$ and $(S_{\rm DL} $ and $S_{\rm DR} )$, which are used for the calculation of the local kinetic energy transfer and the corresponding parallel, perpendicular and diagonal intra-molecular thermoelectric-like coefficients (IMTLCs), respectively.Fig. 1
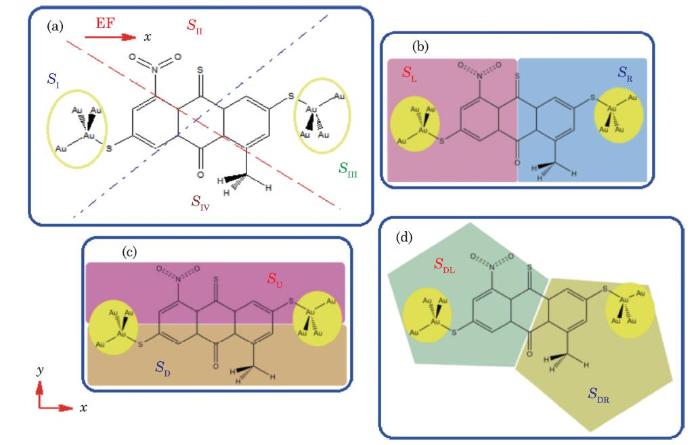New window|Download| PPT slideFig. 1(Color online) The molecular nanoelectronic device (E-M$_{1}$-E) studied in this work (a), and parallel (b), perpendicular (c), and diagonal (d) intra-molecular partitioning schemes adopted for the analysis of the thermoelectric performance of this system. The Au atoms represent the electrodes.
To study intra-molecular thermoelectric-like effects, details of the electronic and vibrational responses to the external EF, appearing as charge and energy transfer, should be known. For example, analysis of the EF effect on the local electron density, $\rho (r)$, of the proposed E-M$_{1}$-E molecular system (Fig. 1) is shown in Fig. 2. This E-M$_{1}$-E device can be grouped into $n$-type-like (electron density donor) and $p$-type-like (electron density acceptor) sections. Furthermore, the partitioning (decomposition) of the total molecular energy into a set of additive atomic contributions has been established by the quantum theory of atoms-in-molecules (QTAIM).[64-70] Based on the QTAIM, the atomic electronic energy, $E_{{\rm elec}} (\Omega )$, is given by
Fig. 2
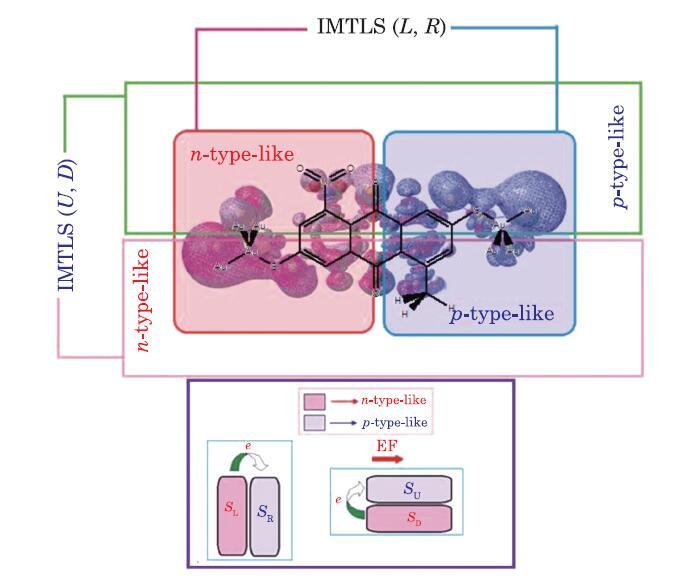New window|Download| PPT slideFig. 2(Color online) Local differential electron density map, $\Delta \rho (S_{i}, \varepsilon )=\sum\limits_{\Omega \in S_{i} }^{N_{S_{i} } } {\rho (\Omega ;\varepsilon )} -{\kern 1pt}\sum\limits_{\Omega \in S_{i} }^{N_{S_{i} } } {\rho (\Omega ;0)} $, obtained for the E-M$_{1}$-E system at EF of $\varepsilon =60\times 10^{-4}~{\rm au}$ strength, determining the donor ($n$-type-like) and acceptor ($p$-type-like) intra-molecular sections, highlighted in red and blue, respectively.
where $K_{{\rm elec}} (\Omega )$ and $V_{{\rm elec}} (\Omega )$ are total atomic kinetic and potential energies of the atomic basin $\Omega$, respectively. The atomic contributions to the vibrational energies can be expanded as $K_{\rm vib} (\Omega )=\sum\limits_k {K_{\rm vib}^{k} (\Omega )},V_{\rm vib} (\Omega )=\sum\limits_k {V_{\rm vib}^{k} (\Omega )} $ and $E_{\rm vib} (\Omega )=K_{\rm vib} (\Omega )+V_{\rm vib} (\Omega )=\sum\limits_k {E_{\rm vib}^{k} (\Omega )} $, with $K_{\rm vib}^{k} (\Omega ),V_{\rm vib}^{k} (\Omega )$ and $E_{\rm vib}^{k} (\Omega )$ being contributions of the atomic basin $\Omega $ to the kinetic potential and total energies of the $k$-th normal mode. In addition, based on harmonic oscillation (HO) approximation, we found that the potential energies of the $k$-th vibrational normal mode $_{,}V_{\rm vib}^{k} (\Omega )$, forms a portion of $V_{\rm vib}^{k} $ given by[62-63]
where $V_{\rm vib}^{k}$ is the potential energies of the vibrational mode $k$ and ${\bf {\pmb{\textit{Q}}}}_{k} =\sum\limits_i {l_{ki} {\bf {\pmb{\textit{q}}}}_{i} } $ is the normal coordinate corresponding to the $k$-th mode defined as linear combination of the 3$N$ mass-weighted nuclear Cartesian coordinates ${\bf {\pmb{\textit{q}}}}_{i} $, with $l_{ki}$ begin their weighting factors. The total energy of atomic basin $\Omega $ is thus obtained by summing its electronic and vibrational contributions as, $E(\Omega )=E_{{\rm elec}} (\Omega )+E_{\rm vib} (\Omega )$.
The intra-molecular inhomogeneous local energy dissipation in a field-effect molecular device due to thermoelectric-like processes arising from different responses of atomic basins of the molecular device to the applied electric field results in an electronic/vibrational temperature-like differences, which can then result in kinetic energy (heat-like) flows across the device. The extents of these heat flows depend on these temperature-like differences. In this scheme, an external EF of strength $\varepsilon $, for each IMTLS $S_{i} $ consisting of $N_{S_{i} } $ atoms induces a change in the local or sectional electronic/vibrational temperature-like difference, $\Delta T_{\gamma } (S_{i},\varepsilon )$, defined by:
where $\gamma =$ elec or vib and $c_{{\rm elec}} =2/3$ and $c_{\rm vib} =2$. In this definition, $\left\langle {K_{\gamma } } \right\rangle_{\Omega } (\varepsilon )$ is the electronic/vibrational kinetic energy expectation value of the atomic basin $\Omega $ belonging to the IMTLS $S_{i} $ in the EF strength of $\varepsilon $, and $T_{\gamma } (S_{i},\varepsilon )$ and $T_{\gamma } (S_{i},0)$ respectively denote its electronic/vibrational temperature-like in the presence and absence of EF. In other words, at a given EF strength of $\varepsilon $, the change in the kinetic energy of the IMTLS $S_{i} $ can be regarded as an index of its cooling or warming referenced to its state in the absence of EF $(\varepsilon =0)$. Thus, for each IMTLS $S_{i} $, the intra-molecular sectional heating/cooling due to the electronic/vibrational degrees of freedom $(\gamma )$ can be defined in terms of the variation in its total kinetic energy $K_{\gamma } (S_{i},\varepsilon )=\sum\limits_{\Omega \in {\kern 1pt}S_{i} }^{ N_{ S_{i} } } {\left\langle {K_{\gamma } } \right\rangle_{\Omega } (\varepsilon )}$ as
The $\Delta K_{\gamma } (S_{i},\varepsilon )$ value can be considered as the local heating at the $S_{i} $ IMTLS. Based on the values and signs of $\Delta K_{\gamma } (S_{i},\varepsilon )$ for all IMTLSs of the molecule, it can be determined which of them has become electronically and/or vibrationally warmer or colder, and also on a relative scale which of them has become colder or warmer than other IMTLSs at any given EF strength.
3 Phenomenological Analysis of the Intra-Molecular Thermoelectric-Like Effects
In the Onsager phenomenological approach to linear non equilibrium thermodynamics, the general flux of the quantity $\alpha (J_{\alpha } )$ induced by different forces $\beta (X_{\beta } )$ is given bywhere ${\bf {\pmb{\textit{L}}}}_{\alpha \beta } $ quantities are known as the phenomenological coefficients.[71-78] Starting from this linear relationship, the ${\bf {\pmb{\textit{J}}}}_{Q,\gamma } (S_{i},S_{j} )$ heat flux between the two $(S_{i},S_{j} )$ IMTLSs of a nanoelectronic E-M-E system via the $\gamma $ (electronic or vibrational) degree of freedom can be written in terms of the electric force represented by the electric current $I$, by defining the corresponding intra-molecular thermoelectric-like coefficients (IMTLC) ${\bf {\pmb{\textit{L}}}}_{\gamma } (S_{i},S_{j} )$ as
Based on the QTAIM analysis presented in the previous section, the ${\bf {\pmb{\textit{J}}}}_{Q,\gamma } (S_{i},S_{j} )$ heat flux can be defined as
where the flown heat $Q_{\gamma } (S_{i},S_{j} )$ is considered to be equal to the differential changes in the kinetic energies of the two $S_{i} $ and $S_{j} $ IMTLSs of the molecule via the $\gamma $ degree of freedom induced by the applied EF of $\varepsilon $ strength, i.e.
In other words, the differential changes in the kinetic energies of each IMTLS pair, induced by an EF, can be considered as the kinetic energy (heat-like) transfer between the corresponding pair of IMTLSs, as described pictorially in Fig. 3. This is one of the central ideas of this series of works on the thermoelectric-like effects in molecular nanoelectronic systems.[52] According to the partitioning schemes (Figs. 1 and 2) applicable for each E-M-E system, the $(S_{i},S_{j} )$ IMTLS pair can be $(S_{\text{L}},S_{\text{R}} ),(S_{\text{U}},S_{\text{D}} )$ and/or $(S_{\text{DL}},S_{\text{DR}} )$. The IMTLC ${\bf {\pmb{\textit{L}}}}_{\gamma } (S_{i},S_{j} )$ of each pair of IMTLS can thus be found be rearranging Eq. (10) as:
Fig. 3
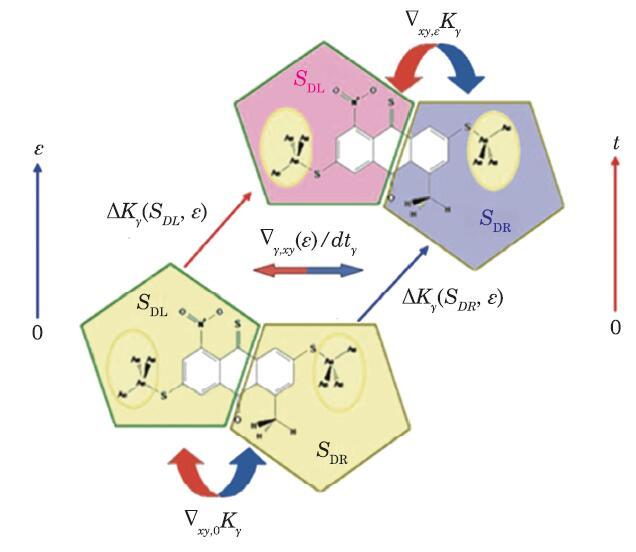New window|Download| PPT slideFig. 3(Color online) Pictorial presentation of the local kinetic energy transfer between different diagonal pairs of IMTLSs, Eq. (12). The intra-molecular/sectional kinetic energy transfer, $\Delta K_{\gamma } (S_{i},\varepsilon )$, and differential kinetic energy between the diagonal pair of sections,$\nabla_{xy, \varepsilon } K_{\gamma }$, and kinetic energy (heat-like) flux between the corresponding pair of IMTLSs, $\Delta_{\gamma } (\varepsilon )/dt_{\gamma } $, in the EF of $\varepsilon $strength, are also shown.
where $\gamma =$ elec or vib. For simplicity, notations of the intra-molecular thermoelectric-like heat flux ${\rm { J}}_{Q,\gamma } (S_{i},S_{j} )$ and phenomenological coefficient ${\bf {\pmb{\textit{L}}}}_{\gamma } (S_{i},S_{j} )$ will be abbreviated, where needed.
In the present work, based on the linear-response theory, the electronic and vibrational IMTLCs and thus $ZT_{\gamma }^{M}$ are computed based on the QTAIM and HO approximation in low temperature regime, where thermal energy $k_{B} T$ is much smaller than the molecular levels broadening originating from the coupling of the molecule to the leads of the circuit, it can be assumed that the molecular energy levels are time-independent when exposed to a static electric field. Different molecular time scale models have been used to describe electronic and vibrational energy fluxes in nanoelectronic systems. For example, the inverse of the Bohr frequency $(\nu_{B} )$, and the inverse of the Debye frequency $(\nu_{D} )$ are chosen as the electronic and vibrational time scales in E-M-E systems, respectively.[65-66] Therefore, for direct quantum methodology for the evaluation of electronic $({\bf {\pmb{\textit{L}}}}_{{\rm elec}} )$ and vibration $({\bf {\pmb{\textit{L}}}}_{\rm vib} )$ IMETCs, two field-dependent time scale models, attributed respectively to the electronic tunneling time scale $(t_{{\rm elec}})$, and vibration timescale $(t_{\rm vib})$, are used.
The tunneling traverse time $t_{{\rm elec}}$ which takes for the electron to pass across the molecular barrier width $d^{M}$ (which can be approximated by the length of the molecule, i.e. $d^{M}\approx l^{M}$) depends on the potential barrier width ($l^{M})$ and height $(\Phi^{\varepsilon })$ at EF strength of $\varepsilon$.[52,77-78] This traverse time can be defined as
in which $m_{e}$ is the mass of electron at rest. The field-induced change in the electronic tunneling time $\Delta t_{{\rm elec}} (\varepsilon )$ is defined as
with $t_{{\rm elec}} (0)$ and $t_{{\rm elec}} (\varepsilon )$ being tunneling times in the absence and presence of the EF of strength $\varepsilon $, respectively. The $t_{{\rm elec}} (0)$ tunneling time can arbitrary be set to zero. Also, the height of the barrier $\Phi^{\varepsilon }$ can be regarded as the energy spacing between the highest occupied molecular orbital (HOMO) and the Fermi level $E_{F}$, that is $\Phi^{\varepsilon }\approx E_{F} -E_{{\rm HOMO}}$. Furthermore, based on the Franck-Condon principle, electrons move much faster than nuclei, and compared to almost immediate electronic response, the nuclear motion has delayed response to external EF. Therefore, nuclear (vibrational) motion is described by a different time scale model. This vibrational time scale is usually chosen as the inverse of the characteristic frequency, $\nu_{C}$, of the E-M-E system (i.e. $t_{\rm vib} (\nu )\approx 1/\nu_{C} $) which depends on phononic characteristics of the E-M-E devices.[79-80] For the E-M-E systems, the Debye frequency ($\nu_{D} )$ of the gold electrodes $(\nu_{D} \approx (750$--$800)~{\rm cm}^{-{\rm 1}})$ is generally chosen as the upper limit of the characteristic frequency (i.e. $\nu_{C} \leq \nu_{D} $), since the $\nu_{D} $ vibrational mode plays dominant role in the electric-heat transfer in these systems at very low temperatures. The average vibrational time scale, $t_{\rm vib} (\nu,\varepsilon )$, and its change due to the application of electric field, $\left| {\Delta t_{\rm vib} (\nu,\varepsilon )} \right|$, are thus defined as
where $t_{\rm vib} (\nu,0)$ and $t_{\rm vib} (\nu,\varepsilon )$ are molecular vibrational time scales evaluated based on the vibrational frequencies of the system respectively in the absence and presence of the EF of $\varepsilon $ strength. Also, $N_{\nu_{D} } $ is the number of frequency modes below the Debye frequency.
4 Modeling Intra-Molecular Energy Dissipation/Transfer in Field-Effect Nanoelectronic Molecular Devices
At low temperatures and under external electric bias, the Joule and Peltier thermoelectric effects play dominant roles respectively in energy dissipation and energy dissipation/transfer processes in nanoelectronic devices. Since, Joule and Peltier heatings are respectively even (symmetrical) and odd (antisymmetric) functions of the external bias,[81-82] it is possible to decompose IMTLCs into two symmetrical and antisymmetrical components, which describe the intra-molecular Joule-like $({\bf {\pmb{\textit{L}}}}_{\gamma }^{\rm JL} )$ and Peltier-like $({\bf {\pmb{\textit{L}}}}_{\gamma }^{\rm PL} )$ coefficients. Thus, we assume thatin which ${\bf{\pmb{\textit{L}}}}_{\gamma, t, q}^{M,f} $ and ${\bf{\pmb{\textit{L}}}}_{\gamma, t, q}^{M,r} $ are the IMETCs for the forward $(f)$ and reverse $(r)$ biases, respectively. Based on the Thomson-Onsager relation $({\bf{\pmb{\textit{L}}}}^{\rm PL}=\bar{{T}}{\kern 1pt}{\kern 1pt}{\bf{\pmb{\textit{L}}}}^{\rm SL})$, the intra-molecular energy conversion coefficient which describes the intra-molecular Seebeck-like effect $({\pmb{\textit{L}}}_{\gamma }^{\rm SL} )$ can be defined as
in which intra-molecular temperature model defined in Eq. (7) is adopted for evaluation of the average temperature $\bar{{T}}_{_{\gamma,q} }^{\rm SL} $. In most thermoelectric systems, the Thomson coefficient $({\bf{\pmb{\textit{L}}}}^{T})$ is given by[83]
A new formulation and interpretation of the Thomson effect has recently been proposed by Logvinov et al. in which the Thomson heating/cooling coefficient is considered to be directly proportional to Seebeck coefficient even when $({\rm d}{\bf{\pmb{\textit{L}}}}^{S}/{\rm d}T=0)$.[83-84] Results of their study also show that contributions of Thomson effect to temperature changes $(\Delta T^{T})$ in an $n$/$p$-type semiconductor is related to thermal conductivity coefficients $(\kappa_{n},\kappa_{p})$, lengths of the $n$- and $p$-type semiconductors $(l_{n},l_{p} )$, electrode contact cross-sectional area $({A}')$, Seebeck coefficient $({\bf{\pmb{\textit{L}}}}_{n/p}^{S} )$, working temperature $(T_{w})$ and current density $(J=I/{A}')$ via
Analogously, contributions of intra-molecular Thomson-like effect to temperature changes $(\Delta T_{\gamma }^{\rm TL} )$ of each pair of IMTLS $S_{i}$ and $S_{j} $, as an $n/p$-type-like junction, can be approximated by
in which $l=l_{n} +l_{p},\kappa_{\gamma, S_{i} } \approx \kappa_{\gamma, S_{j} } \approx \kappa_{\gamma } /2$ at low temperatures. Other notations in this equation are defined in Eqs. (4), (18), and (20). According to this model, it is clear that ${\bf{\pmb{\textit{L}}}}_{\gamma }^{\rm TL} $ and thus $Q_{\gamma,q}^{\rm TL} $ are strongly length (size)-dependent. Using Eq. (20), and based on the linear flux-force response theory, ${\rm d}Q^{\rm TL}/t=\kappa \Delta T^{\rm TL}$, and Onsager phenomenological approach to Thomson effect, ${\rm d}Q^{\rm TL}/{\rm d}t\approx ({\bf{\pmb{\textit{L}}}}^{\rm TL} I)\Delta T\approx \kappa \Delta T^{\rm TL}$, for the current density $I$ as the flux and initial temperature gradient between the two IMTLSs $\Delta T$ as the force, the electronic and vibrational intra-molecular Thomson-like coefficient is also given by ${\rm d}Q^{\rm TL} /{\rm d}t=\kappa {\kern 1pt}{\kern 1pt}\Delta T^{\rm TL} \approx ({\bf{\pmb{\textit{L}}}}^{\rm TL} {\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}I{\kern 1pt}){\kern 1pt}{\kern 1pt}\Delta T$, and thus
Based on above discussion and using Eqs. (15)--(22), the electronic and vibrational intra-molecular Joule-like heating $Q_{\gamma, q}^{\rm JL} $, Peltier-like heating $Q_{\gamma, q}^{\rm PL}$, Thomson-like heating $Q_{\gamma, q}^{\rm TL} $ and their corresponding intra-molecular heat fluxes ${\rm { J}}_{\gamma, t, q}$ can be introduced as
In addition, based on Eq. (1), the electronic and vibrational intra-molecular thermoelectric-like figure of merit $ZT_{\gamma }^{M} (S_{i},S_{j} )$ at low temperatures, where the phonon-electron interaction can be neglected, is considered to be the sum of the two electronic and vibrational $(\gamma)$ components as
Finally, it is predicted that in real molecular thermoelectric devices, the $ZT$ increases when $ZT_{{\rm elec}}^{M}$ increases or $ZT_{\rm vib}^{M{\kern 1pt}}$ decreases implying that EF has induced nuclear motion. Therefore, the effective intra-molecular thermoelectric-like figure of merit $ZT_{q,{\rm eff}}^{M}$ in the field-effect molecular devices, can be defined as
5 Local Intra-Molecular Electronic Energy Dissipation
When external EF is applied on the molecular device, due the coupling between vibrational and electronic degrees of freedom, part of the energy acquired by the molecular device via its electronic degrees of freedom is converted (dissipated) into the nuclear motion, i.e. vibrational energy and thus can be regarded as the unrecoverable (wasted) electronic energy. This means that only the $\Delta E_{{\rm elec}}^{M}$ part of the total differential energy $(\Delta E_{\rm tot}^{M} =\Delta E_{{\rm elec}}^{M} +\Delta E_{\rm vib}^{M} )$ remains available to drive the nanoelectronic thermoelectric device. Thus, the local intra-molecularel ectronic energy dissipation coefficient, $\eta^{dis}(S_{i},\varepsilon )$, can be defined aswhere
$$ \Delta E_{\rm elec(vib)} (S_{i},\varepsilon )= \sum\limits_\Omega^{N_{S_{i} } } {E_{\rm elec(vib)} (\Omega,\varepsilon )} \\ \; -\sum\limits_\Omega^{N_{S_{i} } }{E_{\rm elec(vib)}(\Omega,0)}\,. $$
Using Eq. (25), the most and the least energy-dissipative sections (MEDS and LEDS) of the field-effect molecular nanoelectronic systems, having respectively the maximum $\eta _{\max }^{\rm dis} (S_{i},\varepsilon )$ and minimum $\eta_{\min }^{\rm dis} (S_{i} ,\varepsilon )$ values, can then be determined.
6 Computational Details
Geometry optimization and calculation of the structural and electronic properties of the E-M-E devices studied in this work have been carried out at B3LYP/6-31G* level of theory under different EF strengths applied along the $\pm x$ direction (Fig. 1), using G03 program.[85] For the gold atoms of the electrodes, the LANL2DZ pseudopotential is used. The EF effect on the intra-molecular vibrational energy transfer is worked out by following HO vibrational frequencies obtained for the optimized structures. Starting from the electronic wave functions obtained at each EF strength, the atomic basins are determined using density gradient method, and their electronic energies and their changes with EF strength are calculated. All QTAIM calculations are carried out using AIM2000 program package.[86]7 Results and Discussion
The change in the local charges and energies, induced by applied EF of $\varepsilon $ strength, can be considered respectively as electron density and as kinetic energy (heat) transfer between the atomic basins and IMTLSs. Both of these transport effects may thus contribute to a local temperature change, which is evaluated theoretically by intra-molecular temperature modeling, as defined in Eq. (7), the intra-molecular thermograph derived based on these local temperatures are shown in Fig. 4. In addition, using the QTAIM, the EF effects on the atomic energies and charges of the E-M$_{1}$-E device are studied, and samples of the results are demonstrated in Fig. 5(a).Fig. 4
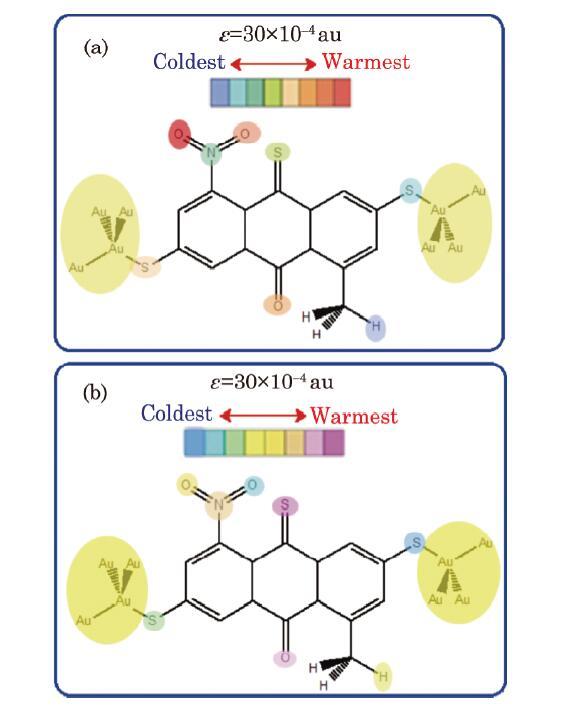New window|Download| PPT slideFig. 4(Color online) Intra-molecular atomic electronic (a) and vibrational (b) temperature changes calculated for some representative atoms of the E-M$_{1}$-E system at $\varepsilon =30\times 10^{-4}~{\rm au}$.
Fig. 5
New window|Download| PPT slideFig. 5(Color online) (a) Intra-molecular atomic electronic and vibrational temperature changes of the end gold-sulfur (-Au-S-) junctions (contact points) of the E-M$_{1}$-E system, as functions of the EF strength. (b) The current-voltage $(I$-$V)$ characteristic curve predicted for the E-M$_{1}$-E device.
Based on Eqs. (2) and (3), and using Ohm's law $(I=V/R)$, the $I$-$V$ characteristic curve of the E-M$_{1}$-E device is approximated at different EF strengths and is shown in Fig. 5(b). This figure shows that the current increases non-linearly with increasing the bias voltage.
Using Eqs. (12)--(21), values of the total local Joule-like $(Q_{{\rm elec},q}^{\rm JL} +Q_{{\rm vib},q}^{\rm JL} )$, Peltier-like $(Q_{{\rm elec},q}^{\rm PL} +Q_{{\rm vib},q}^{\rm PL} )$, and Thomson-like $(Q_{{\rm elec},q}^{\rm TL} +Q_{{\rm vib},q}^{\rm TL} )$ heatings of the E-M$_{1}$-E molecular system shown in Fig. 1, are calculated at different EF strengths and presented in Fig. 6(a). Analysis of these results show that generally $Q_{\rm tot}^{\rm JL} (S_{i},S_{j} )\gg Q_{\rm tot}^{\rm PL} (S_{i},S_{j} )$, and the Joule-Thomson-like heating $(Q_{\gamma,q}^{\rm JL} +Q_{\gamma,q}^{\rm TL})$ plays the dominant role in the local energy dissipation in single molecule nanoelectronic systems. In addition, the calculated values of the local Thomson-like heating, as demonstrated in Figs. 6(b) and 6(c), shows that for both vibrational and electronic degrees of freedom, the value of the diagonal-sectional Thomson-like heating $Q_{\gamma,q}^{\rm TL} (S_{\rm DL},S_{\rm DR} )$ is generally larger than the corresponding intra-molecular parallel $Q_{\gamma,q}^{\rm TL} (S_{\rm L},S_{\rm R} )$ and perpendicular $Q_{\gamma,q}^{\rm TL} (S_{\rm U},S_{\rm D} )$ values because the value and sign of $Q_{\gamma,q}^{\rm TL} (S_{\rm DL},S_{\rm DR} )$ have contributions from energy transfers along both $x$ and $y$ axes.
Fig. 6
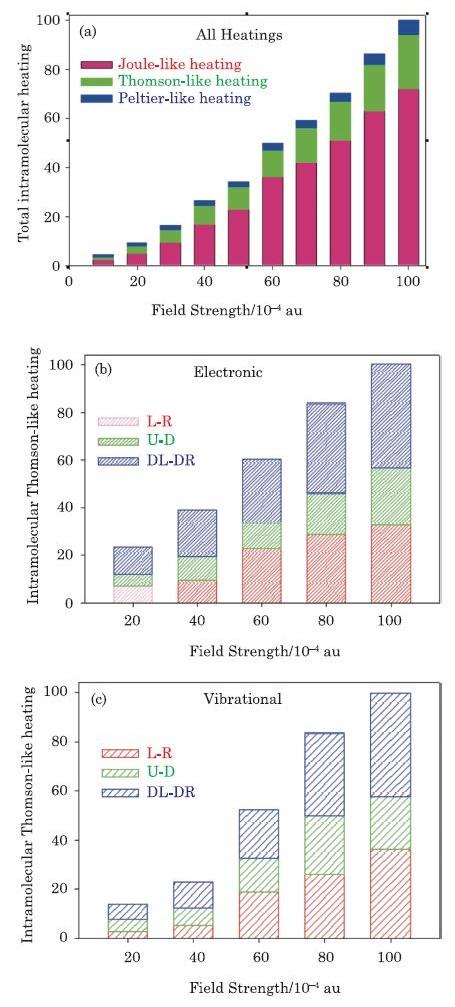New window|Download| PPT slideFig. 6(Color online) (a) The total intra-molecular Joule-like, Peltier-like and Thomson-like heat fluxes, ${\rm { J}}_{\rm tot} (S_{\rm DL}, S_{\rm DR} )={\rm { J}}_{{\rm elec}} (S_{\rm DL}, S_{\rm DR} )+{\rm { J}}_{\rm vib} (S_{\rm DL}, S_{\rm DR} )$, calculated at different EF strengths, for diagonal IMTLSs calculated for the E-M$_{1}$-E device. The electronic (b), $Q_{{\rm elec}}^{\rm TL} (S_{i},S_{j} )$, and vibrational (c), $Q_{\rm vib}^{\rm TL} (S_{i}, S_{j} )$, intra-molecular Thomson-like heatings of the parallel, L-R$(S_{\rm L},S_{\rm R} )$, perpendicular, U-D$(S_{\rm U},S_{\rm D} )$, and diagonal, DL-DR$(S_{\rm DL},S_{\rm DR} )$, IMTLSs of the E-M$_{1}$-E device (
As established and discussed in our previous reports,[62-63] based on the presented model, the IMTLCs can be calculated for any candidate E-M-E molecular device, to effectively design single molecule thermoelectric devices with controlled and known heat-electric interferences. As another example, a small molecular E-M$_{2}$-E device shown in Fig. 7(a) is also studied and its electronic and vibrational IMTLCs for Peltier effect are calculated and plotted respectively in parts (b) and (c) of Fig. 7. These results show that both electronic and vibrational parallel and perpendicular IMPLCs ${\bf {\pmb{\textit{L}}}}_{t,{\rm elec}}^{\rm PL} (S_{\rm L},S_{\rm R})$ and ${\bf{\pmb{\textit{L}}}}_{t,{\rm elec}}^{\rm PL} (S_{\rm U},S_{\rm D} )$, and oscillate with the EF strength. Furthermore, all vibrational IMTLCs, which are not reported here for brevity, such as ${\bf {\pmb{\textit{L}}}}_{t,{\rm vib}}^{\rm PL} (S_{\rm DL},S_{\rm DR} )$, oscillate with EF. Variations in the electric dipole moment $({\rm {\bf \mu }}_{q})$ with EF strength can be regarded as an alternative scalar index of the response of the electric charge distribution in the E-M$_{2}$-E molecular device to electric field.[87-88]
Fig. 7
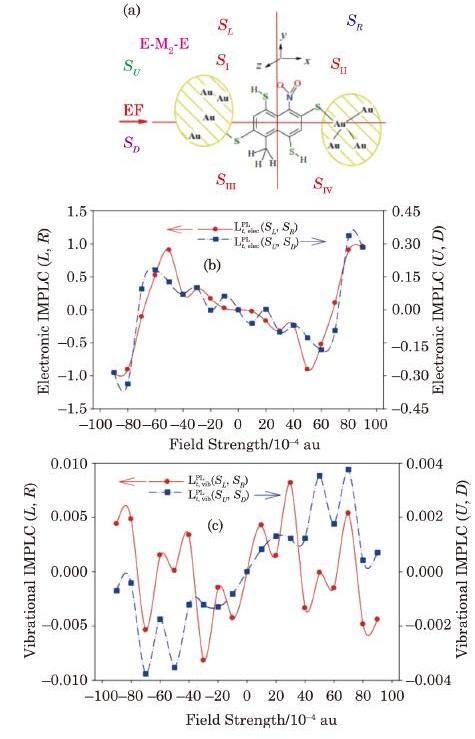New window|Download| PPT slideFig. 7(Color online) The E-M$_{2}$-E molecular device studied in this work (a), and its electronic (b) and vibrational (c) intra-molecular Peltier-like coefficients (IMPLC) calculated at different electric field strengths.
Therefore, size of the electric dipole moment vector and its components (in Debye) are calculated for the E-M$_{2}$-E molecular device at various EF strengths. Sample results are demonstrated in Fig. 8(a). Analysis of the calculated values of $\left| {{\rm {\bf \mu }}_{q} } \right|$ and its components shows that electric dipole moment components increases with EF strength almost linearly with low amplitude oscillations, and its variation is similar to that observed for the parallel electronic IMTLCs shown in Fig. 7. Moreover, analysis of the calculated values of the molecular orbital energies, demonstrated in Fig. 8(b), shows that with increasing the EF strength, the HOMO-LUMO gap, ${\rm HLG}(\equiv E_{{\rm HOMO}} -E_{{\rm LUMO}} )$, is decreased and therefore, it is expected that the parallel electronic IMTLCs, and thus parallel $ZT_{{\rm elec}}^{M{\kern 1pt}} (S_{\rm L},S_{\rm R} )$ to be generally increased. This is due to the fact that HLG is a measure of the electron transport barrier in molecular nanoelectronic systems. Smaller HLG value results in higher electric conductivity and less energy dissipation, and thus larger Seebeck IMTLC and figure of merit $ZT_{{\rm elec}}^{M{\kern 1pt}} (S_{\rm L},S_{\rm R} )$. Similar results have been observed for nano-size thermoelectric systems, for which the electronic Seebeck coefficient ${\bf {\pmb{\textit{L}}}}_{{\rm elec}}^{S} $ and electronic thermoelectric figure of merit $ZT_{{\rm elec}} $ are related to the Fermi energy (i.e. $E_{F} \approx (E_{{\rm HOMO}} +E_{{\rm LUMO}} )/2$).[23-25,40]
Fig. 8
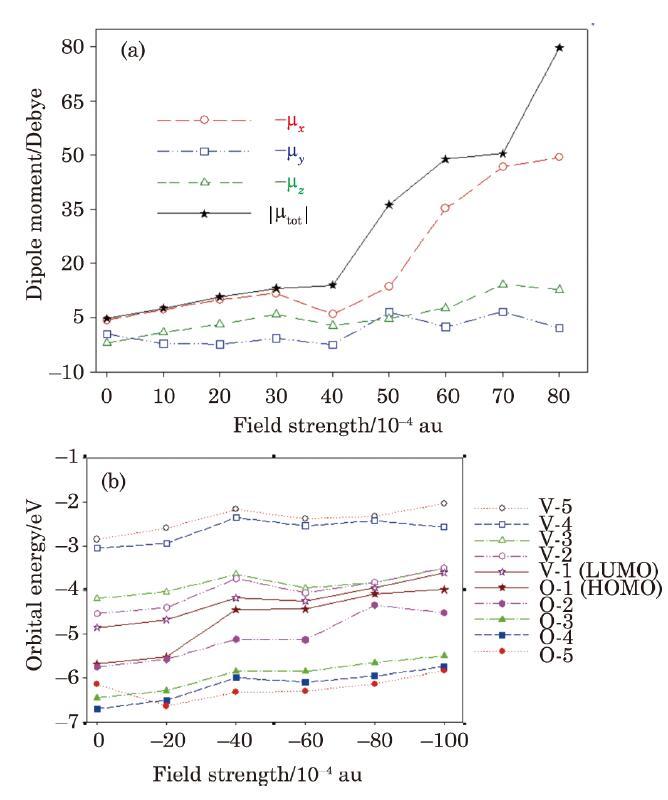New window|Download| PPT slideFig. 8(Color online) (a) Size of the electric dipole moment vector and its components (in Debye) at various EF strengths, and (b) electric field effects on the energies of the occupied (O) and virtual (V) molecular orbitals, calculated for the E-M$_{2}$-E molecular device at DFT-B3LYP/6-31G* level of theory using LANL2DZ basis set and pseudopotential for gold atoms.
It is possible to compare thermoelectric performances of two nanoelectronic systems E-M$_{1}$-E and E-M$_{2}$-E at a given EF strength based on their differential values of ${\kern 1pt}ZT_{q, {\rm eff}}^{M}$ defined in Eq. (23) using relative differential effective intra-molecular thermoelectric-like figure of merit $(\Delta {\kern 1pt}ZT_{q,{\rm eff}}^{M} )$ defined as
Using Eq. (26), the $\Delta {\kern 1pt}ZT_{q,{\rm eff}}^{M}$ values are calculated for the E-M$_{1}$-E (Fig. 1) and E-M$_{2}$-E (Fig. 7(a)) molecular devices and are plotted in Fig. 9 as functions of EF strength. These results shows that generally $ZT_{\rm eff}^{E-M_{1} -E} (S_{i},S_{j} )>ZT_{\rm eff}^{^{E-M_{2} -E}} (S_{i},S_{j} )$. Therefore, it can be predicted that the E-M$_{1}$-E device has a higher thermoelectric performance than the E-M$_{2}$-E device when applied in a real nanoelectronic circuit. This higher performance can be attributed to the more extended $\pi$-conjugated system of the E-M$_{1}$-E device compared to that of the E-M$_{2}$-E device. Analysis of the data demonstrated in Fig. 9 shows also that the effective intra-molecular figure of merit ${\kern 1pt}ZT_{q, {\rm eff}}^{M}$ increases non-linearly with EF strength which can be attributed to the non-linear variations of the molecular vibrational characteristics with EF strength.Oscillations in the IMTLCs (and thus thermoelectric performances)with the EF strengthobtained here are compatible with what already observed and reported for the electronic transport coefficients and performances of the ($n$/$p$)-type semiconductors and mesocopic conductors.\wen{23,89-100} By comparing the trends observed in Figs. 7 and 9, it can be said that oscillations of the $ZT^{M{\kern 1pt}}$ and $ZT_{\rm eff}^{M{\kern 1pt}}$ correspond predominantly to the oscillation of the ${\bf {\pmb{\textit{L}}}}_{\rm vib} $ and changes in the local charge distribution with increasing EF strength. Furthermore, it can be predicted that the overall performance $(ZT)$ of a real molecular thermoelectric device increases when $ZT_{{\rm elec}}^M$ increases or $ZT_{\rm vib}^{M}$ decreases.
Fig. 9
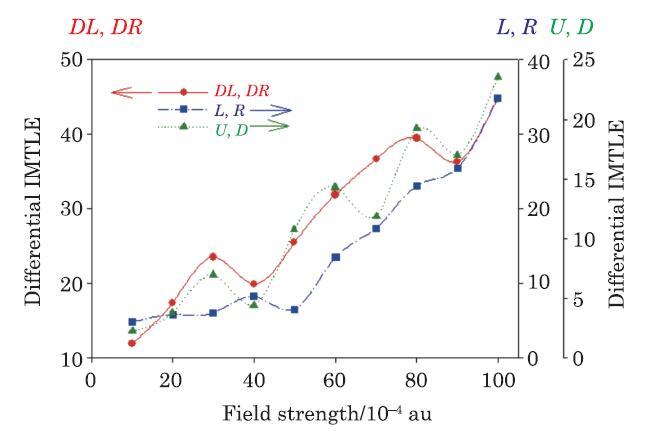New window|Download| PPT slideFig. 9(Color online) The relative differential intra-molecular thermoelectric-like figure of merit, $\% \Delta {\kern 1pt}ZT_{q,{\rm eff}}^{M} (S_{i},S_{j} )$, defined in Eq. (26), of the parallel, perpendicular, and diagonal IMTLSs of the E-M$_{1}$-E and E-M$_{2}$-E molecular devices, introduced in Figs. 1(a) and 7(a), respectively.
Generally, in low temperature regime, we have $\kappa_{{\rm vib(ph)}} \ll\kappa _{{\rm elec}}$. Interestingly, by increasing temperature, it is possible to have equal electronic and phononic heat conductances $\kappa_{{\rm elec}} (T^{\circ })\approx \kappa_{{\rm vib(ph)}} (T^{\circ })$ at a characteristic temperature $T^{\circ}$[87] and thus based on Eq. (23) we have ${\rm Z}T^{M^{\circ }} \approx 1/2( {{\bf{\pmb{\textit{L}}}}^{\rm SL} } )^{2}(l_{L} )^{-1}$, where ${\bf{\pmb{\textit{L}}}}^{\rm SL} \equiv {\bf{\pmb{\textit{L}}}}_{{\rm elec}}^{\rm SL} +{\bf{\pmb{\textit{L}}}}_{\rm vib}^{\rm SL}$ and $l_{L} \equiv \kappa_{{\rm elec}} /GT\approx (\pi^{2}/3)(k_{B} /e)^{2}$ is a Lorenz number (in the Wiedemann-Franz law). Recently, molecular Lorenz number $(l_{L}^{M} )$ of molecular junctions such as isoprene, 1, 3-benzenedithiol and annulene have been studied and it has been shown that the maximum value of $l_{L}^{M,{\rm peak}}$ is given by $L_{L}^{M,{\rm peak}} \approx 7\pi ^{2}/5\left( {k_{B} /e} \right)^{2}$.[88] It can thus be predicted that in an ideal (or good) molecular thermoelectric device, near a very low characteristic temperature $T^{\circ }\ll T_{{\rm room}}$, we have $\sqrt{2{\rm }l_{L}^{M,{\rm peak}} }\ll{\bf{\pmb{\textit{L}}}}_{{\rm elec}}^{\rm SL}$, and thus ${\rm Z}T^{M} \gg1$. Therefore, the factor $\eta \equiv [ {({\bf{\pmb{\textit{L}}}}_{{\rm elec}}^{\rm SL} )/\sqrt{2l_{L}^{M,{\rm peak}} }}]$ can be regarded as a measure of the efficiency of any multi-terminal molecular device at low temperatures. It can also be predicted that by increasing the working temperature $T$ above T$^{\circ}$ where $\kappa_{{\rm elec}} (T)\ll\kappa_{{\rm vib(ph)}} (T)$, the length-dependence of the $ZT^{M} $ is increased because $\kappa _{{\rm vib(ph)}} \propto l^{M}$ at $T^{\circ }\ll T$.[87]
The most and the least energy-dissipative sections, MEDS and LEDS, of the field-effect molecular devices E-M$_{1}$-E and E-M$_{2}$-E, at different EF strengths, are determined based in Eq. (25) and listed in Tables 1 and 2. This local/atomic energy dissipation scaling and its corresponding concepts presented in this work can be applied to extend the thermoelectric analysis down to molecular nanoelectronic systems.
Table 1
Table 1The most (least) energy-dissipative section MEDS (LES), $\eta_{\max }^{\rm dis} (S_{i},\varepsilon )(\eta_{\min }^{\rm dis} (S_{i}, \varepsilon ))$ of the proposed molecular nanoelectronic device E-M$_{1}$-E (
 |
New window|CSV
Table 2
Table 2The same as Table 1, but for the proposed molecular nanoelectronic device E-M$_{2}$-E (
 |
New window|CSV
Although the major focus of the present work has been on local energy dissipation/transfer in non-isolated molecular device (E-M-E) system, the methodology developed here can also be used to study local/atomic EF effect, and thus describe IMTLCs in the field effect isolated molecular systems (M). For example, sample results obtained for the isolated molecular system M$_{3}$ (Fig. 10(a)) are presented in Figs. 10 and 11. It should be mentioned here that QTAIM remains still valid for partitioning a molecular system with small violation of the virial theorem.[101-102] The validity of virial theorem for the M3 molecule (introduced in Fig. 10(a)) in the external EF is investigated by calculating the $-V_{{\rm elec}} /K_{{\rm elec}}$ factor. As can be seen from Fig. 10(b), virial theorem is well valid over the whole range of the EF strengths used in this work. This assures validity of the method proposed in this work for the QTAIM evaluation of the atomic responses (Fig. 10(c)) of an isolated molecular system to external EF.
Fig. 10
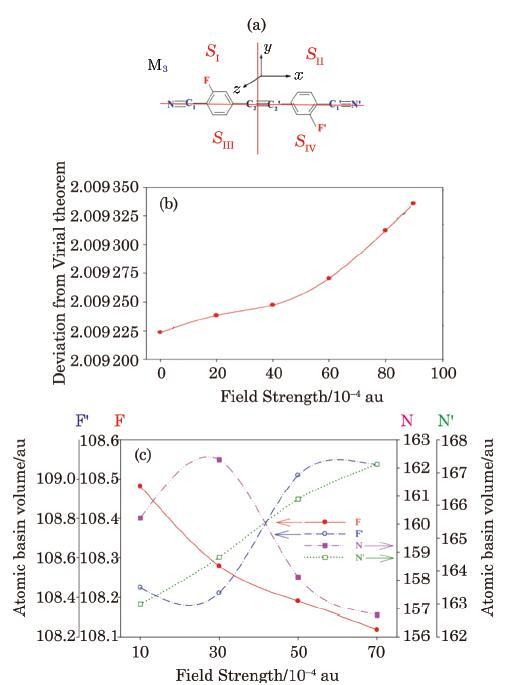New window|Download| PPT slideFig. 10(Color online) (a) The isolated molecular system M$_{3}$ studied in this work. (b) Examination of the validity of the virial theorem for the M$_{3}$ molecule at different EF strengths. (c) The QTAIM atomic basin volumes as an index of the response of the molecular system M$_{3}$. To external electric field.
The electronic and vibrational IMJLCs calculated for the M$_{3}$ molecule (Fig. 10(a)) plotted in Fig. 11 shows that the parallel IMJLCs are generally larger than the corresponding perpendicular IMJLCs. In addition, the parallel and perpendicular components of the electronic IMJLCs are larger than corresponding vibrational IMJLCs. The values of the diagonal IMTLCs are nearly similar to what obtained for parallel IMTLCs because of symmetric structure of M$_{3}$.
Fig. 11
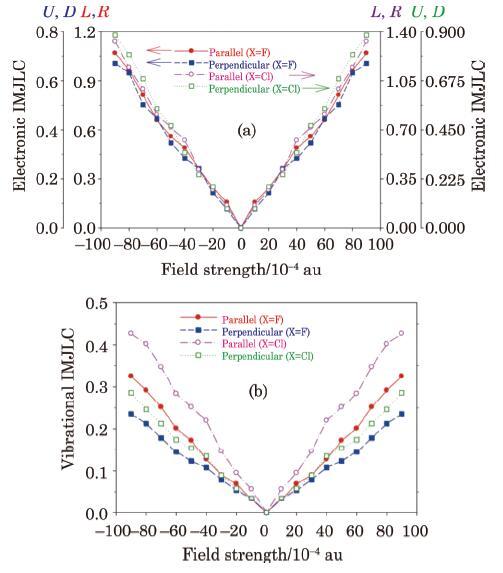New window|Download| PPT slideFig. 11(Color online) The electric field effect on the electronic (a) and vibrational (b) intra-molecular Joule-like coefficients (IMJLC) calculated for the molecular system M$_{3}$ (introduced in
Analysis of the results (not reported here for brevity)show that the intra-molecular Peltier-like coefficients (IMPLCs) calculated for the symmetrical molecular system M$_{3}$, are much smaller than the corresponding intra-molecular Joule-like coefficients (IMJLC), and thus for this molecular device, the value of the intra-molecular Peltier-like heating, $Q_{\gamma,q}^{\rm PL} (S_{i},S_{j})$, can be neglected as compared to the value of the intra-molecular Joule-like heating, $Q_{\gamma,q}^{\rm JL} (S_{i},S_{j})$.
Our complementary study showed that the intra-molecular Joule-like and Peltier-like effects occur in both non-symmetrical isolated (M) and non-isolate (E-M-E) molecular systems. Also, analysis of the electrode effects on the IMTLCs shows that numerical values of the electronic IMTLCs for the E-M-E system are generally larger than those of the isolated M system. In addition, based on the results obtained in this study, it is possible to determine which specific atom, group of atoms or sections of a single molecular system are the most appropriate points to be chosen for electrode junctions of interest. Consequently, it is possible to screen proposed E-M-E systems having thermoelectric function of interest with optimum thermoelectric figure of merit.
One advantage of our approach is that it enables us to study substitution (X) effect on the IMTLCs and thus thermoelectric performances. For example, Fig. 11 shows that by replacement of fluorine atoms (X$=$F) with chlorine atoms (X$=$Cl) in the molecular system M$_{3}$, values of the electronic and vibrational IMTLCs are gradually changed with the EF strength, since local/intra-molecular electro-thermal response features depend on the local electronic structures (density and its gradients and Laplacian), bonding and local vibrational characteristics of the molecule and their variation with the EF strength, which are obviously dependent on the type of substitution.
8 Conclusion
A straight forward quantum mechanical methodology is proposed to calculate electronic and vibrational intra-molecular thermoelectric-like coefficients (IMTLC) and intra-molecular thermoelectric-like figure of merits ($ZT_{\gamma }^{M{\kern 1pt}})$ in field-effect nanoelectronic molecular devices usingquantum theory of atoms-in-molecules (QTAIM) and harmonic oscillator (HO) approximation. Introduction of local $ZT_{\gamma }^{M{\kern 1pt}}$ in this work can open a whole new chart of researches to be carried out sequentially to analyze local thermoelectric performancesof any candidate or prospective molecular device prior to its synthesis and/or application in real nanoelectronic circuits. The performance of the real molecular thermoelectric devices $(ZT)$ is improved when $ZT_{{\rm elec}}^{M{\kern 1pt}}$ increases or $ZT_{\rm vib}^{M{\kern 1pt}}$ decreases. Furthermore, the atomic (sectional/local) electronic energy dissipation/transfer scaling presented in this work can be used to effectively design molecular nanoelectronic devices and select the best points for connection to the nanoelectronic circuit of interest by carrying out atomic/sectional response analysis on several proposed molecular nanoelectronic systems with different structures and functional groups acting as connection points or poles and different setups in the nanoelectronic circuit, and determining their efficiencies (local electronic energy transfers) and deficiencies (local energy dissipations).Although, the IMTLCs (and thus $ZT_{\gamma }^{M{\kern 1pt}}$) introduced in our work cannot reflect all physics of the thermoelectric effects of the working circuit, it can reveal, at least partly, the physical characteristics of the molecular and intra-molecular junctions which have not been accessible so far.
Finally, the model presented in this work may be verified by carrying out comparative theoretical and experimental studies on a couple of well-designed and workable molecular systems having distinctly different figures of merit (obtained from our model) for which actual performances can be measured experimentally by incorporating them in the well-established nano-circuits,[25,89-107] e.g. by probing the characteristics of the junctions and/or sections using AFM/MFM and STM techniques, in addition to the standard current and impedance measurements.
Acknowledgment
Financial supports from the Research and Technology offices of the University of Qom and the University of Isfahan are acknowledged.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 1]
[Cited within: 1]
DOI:10.1063/1.2977954URL [Cited within: 1]
DOI:10.1007/s12274-010-1019-zURL
Understanding energy dissipation and transport in nanoscale structures is of great importance for the design of energy-efficient circuits and energy-conversion systems. This is also a rich domain for...
DOI:10.1021/ja047432kURLPMID:15366922
Abstract Controlling the selectivity of a chemical reaction is a Holy Grail in chemistry. This paper reports theoretical results of unprecedented effects induced by moderately strong electric fields on the selectivity of two competing nonpolar bond activation processes, C-H hydroxylation vs C=C epoxidation, promoted by an active species that is common to heme-enzymes and to metallo-organic catalysts. The molecular system by itself shows no selectivity whatsoever. However, the presence of an electric field induces absolute selectivity that can be controlled at will. Thus, the choice of the orientation and direction of the field vis- -vis the molecular axes drives the reaction in the direction of complete C-H hydroxylation or complete C=C epoxidation.
DOI:10.1038/nchem.2651URLPMID:27874869
No longer a theoretical dream, this perspective describes effects of oriented external electric fields on rates and selectivity patterns of nonpolar reactions. Discussions of the Diels-Alder reaction, C-H and C=C bond activations, etc., underscore the potential usage of oriented electric fields as future smart catalysts, inhibitors and reagents in chemistry.
DOI:10.1039/c1cp20175aURLPMID:21720646
Molecules can be exposed to strong local electric fields of the order of 108–1010V m611in the biological milieu. The effects of such fields on the rate constant (k) of a model reaction, the double-proton transfer reaction in the formic acid dimer (FAD), are investigated. The barrier heights and shapes are calculated in the absence and presence of several static homogenous external fields ranging from 5.14 × 108to 5.14 × 109V m611using density functional theory (DFT/B3LYP) and second order M03ller–Plesset perturbation theory (MP2) in conjunction with the 6-311++G(d,p) Pople basis set. Conventional transition state theory (CTST) followed by Wigner tunneling correction is then applied to estimate the rate constants at 25 °C. It is found that electric fields parallel to the long axis of the dimer (the line joining the two carbon atoms) lower the uncorrected barrier height, and hence increase the rawk. These fields also flatten the potential energy surface near the transition state region and, hence, decrease the multiplicative tunneling correction factor. The net result of these two opposing effects is that fields increasek(corrected) by a factor ofca.3–4 (DFT–MP2, respectively) compared to the field-freek. Field strengths of 653 × 109V m611are found to be sufficient to double the tunneling-corrected double proton transfer rate constant at 25 °C. Field strengths of similar orders of magnitudes are encountered in the scanning tunneling microscope (STM), in the microenvironment of a DNA base-pair, in an enzyme active site, and in intense laser radiation fields. It is shown that the net (tunneling corrected) effect of the field onkcan be closely fitted to an exponential relationship of the formk=aexp(bE), whereaandbare constants andEthe electric field strength.
DOI:10.1103/PhysRevB.77.085320URL
DOI:10.1021/jz400354mURL
DOI:10.1021/jp5047535URLPMID:25054691
Reactivity and aromaticity of DNA and bases toward an external electric field are analyzed using density functional theory (DFT) and density functional reactivity theory (DFRT). Reactivity of the nucleobases is measured in terms of the DFT-based reactivity descriptor, such as energy of the HOMO, global hardness, electrophilicity, etc. and is observed to be sensitive toward the strength as well as direction of the applied external electric field. In addition, the reactivity pattern follows the maximum hardness and minimum electrophilicity principles. Further, aromaticity of the species is observed to be effected by the presence of an external electric field.
DOI:10.1063/1.4935176URLPMID:26567650
Recent advance in biophysics has made it possible to directly measure site-specific electric field atinternalsites of proteins using molecular probes with C = O or C groups in the context of vibrational Stark effect. These measurements directly probe changes of electric field at specific protein sites due to, e.g., mutation and are very useful in protein design. Computational simulation of the Stark effect based on force fields such as AMBER and OPLS, while providing good insight, shows large errors in comparison to experimental measurement due to inherent difficulties associated with point charge based representation of force fields. In this study, quantum mechanical calculation of protein internal electrostatic properties and vibrational Stark shifts was carried out by using electrostatically embedded generalized molecular fractionation with conjugate caps method. Quantum calculated change of mutation-induced electric field and vibrational Stark shift is reported at the internal probing site of enzyme human aldose reductase. The quantum result is in much better agreement with experimental data than those predicted by force fields, underscoring the deficiency of traditional point charge models describing intra-protein electrostatic properties.
DOI:10.1021/acsnano.7b04610URLPMID:29112378
Strong electric fields are known to influence the properties of molecules as well as materials. Here we show that by changing the orientation of an externally applied electric field, one can locally control the mixing behavior of two molecules physisorbed on a solid surface. Whether the starting two-component network evolves into an ordered two-dimensional (2D) cocrystal, yields an amorphous network where the two components phase separate, or shows preferential adsorption of only one component depends on the solution stoichiometry. The experiments are carried out by changing the orientation of the strong electric field that exists between the tip of a scanning tunneling microscope and a solid substrate. The structure of the two-component network typically changes from open porous at negative substrate bias to relatively compact when the polarity of the applied bias is reversed. The electric-field-induced mixing behavior is reversible, and the supramolecular system exhibits excellent stability and good response efficiency. When molecular guests are adsorbed in the porous networks, the field-induced switching behavior was found to be completely different. Plausible reasons behind the field-induced mixing behavior are discussed.
DOI:10.1002/anie.201702237URL [Cited within: 2]
[Cited within: 1]
DOI:10.1007/s00894-008-0345-5URLPMID:18648863
An organic molecule, designed in this study, is proposed as a candidate molecular switch and characterized using the B3LYP/6-31G* computational method. Structural and electronic properties of this molecular switch (M) and its singly charged (M + and M 61 ) species in their lowest and the first higher spin states are calculated and analyzed. Molecular volume and electronic spatial extent (ESE) of this nanoswitch undergo negligibly small changes (<2%) upon charging. Furthermore, the small difference between the calculated dipole moments of the M + and M 61 species shows that switching between negative and positive poles does not significantly affect the charge transfer performance of this molecular switch. Natural bond orbital (NBO) and spin density distributions are also calculated and analyzed. A preliminary study on the response of the proposed molecular switch to the external electric field approves its function as a multi-pole nanoswitch controlled by a bias voltage.
[Cited within: 1]
[Cited within: 2]
[Cited within: 3]
DOI:10.1007/s10825-008-0219-1URL [Cited within: 1]
First-principle calculations based on density functional and non-equilibrium Green’s functions are used to compute the power emitted in conducting molecular systems due to scattering with localized vibrations. The balance between the rate of phonons emitted and dissipated into the contacts allows the computation of the steady-state distribution of phonon quanta localized in the junction, from which we extract the local temperature reached by the molecule. The model includes two critical quantities; (i)02the rate of phonon emitted in the junction due to electron-phonon scattering and (ii)02a microscopic approach for the computation of the phonon decay rate, accounting for the dynamical coupling between the vibrational modes localized on the molecule and the contact phonons. The method is applied to the discussion of several limiting conditions and trends, depending on electron-phonon coupling, incoherent transmission and phonon dissipation rates, using both analytical results and numerical calculations.
DOI:10.1103/RevModPhys.83.131URL [Cited within: 1]
Advances in the fabrication and characterization of nanoscale systems now allow for a better understanding of one of the most basic issues in science and technology: the flow of heat at the microscopic level. In this Colloquium recent advances are surveyed and an understanding of physical mechanisms of energy transport in nanostructures is presented, focusing mainly on molecular junctions and atomic wires. Basic issues are examined such as thermal conductivity, thermoelectricity, local temperature and heating, and the relation between heat current density and temperature gradient—known as Fourier’s law. Both theoretical and experimental progress are critically reported in each of these issues and future research opportunities in the field are discussed.
DOI:10.1016/j.cplett.2010.03.028URL
Hybrid devices built from organic and inorganic moieties are being actively researched as replacements for inorganic electronics, thermoelectrics, and photovoltaics. However, energy transport and conversion, at the organic–inorganic interface is not well understood. One approach to study this interface is to look at the smallest hybrid building block – the heterojunction of a single organic molecule with inorganic contacts. We present a review of this work, focused on fundamental transport properties of metal–molecule–metal junctions that are related to thermoelectric energy conversion, i.e., electronic conductance, thermopower, and thermal conductance. We describe the motives, strategies, and future directions for considering heterojunctions as building blocks for thermoelectric materials.
DOI:10.1088/1742-6596/273/1/012155URL
DOI:10.1103/PhysRevB.81.235406URL
We propose a possible route to achieve high thermoelectric efficiency in molecular junctions by combining a local chemical tuning of the molecular electronic states with the use of semiconducting electrodes. The former allows to control the position of the highest-occupied molecular orbital (HOMO) transmission resonance with respect to the Fermi energy while the latter fulfills a twofold purpose: the suppression of electronlike contributions to the thermopower and the cutoff of the HOMO transmission tails into the semiconductor band gap. As a result a large thermopower can be obtained. Our results strongly suggest that large figures of merit in such molecular junctions can be achieved.
DOI:10.1103/PhysRevB.89.239907URL
Abstract: We derive formal expressions of time-dependent energy and heat currents through a nanoscopic device using the Keldysh nonequilibrium Green function technique. Numerical results are reported for a metal/dot/metal junction where the dot level energy is abruptly changed by a step-shaped voltage pulse. Analytical linear responses are obtained for the time-dependent thermoelectric coefficients. We show that the Seebeck coefficient can be enhanced in the transient regime up to an amount (here rising 40%) controlled by both the dot energy and the height of the voltage step.
DOI:10.1103/PhysRevB.79.174426URL
DOI:10.1146/annurev-matsci-062910-100445URL
Recent advances in semiconductor thermoelectric physics and materials are reviewed. A key requirement to improve the energy conversion efficiency is to increase the Seebeck coefficient (S) and the electrical conductivity (σ) while reducing the electronic and lattice contributions to thermal conductivity (κe + κL). Some new physical concepts and nanostructures make it possible to modify the trade-offs between the bulk material properties through changes in the density of states, scattering rates, and interface effects on electron and phonon transport. We review recent experimental and theoretical results on nanostructured materials of various dimensions: superlattices, nanowires, nanodots, and solid-state thermionic power generation devices. Most of the recent success has been in the reduction of lattice thermal conductivity with the concurrent maintenance of good electrical conductivity. Several theoretical and experimental results to improve the thermoelectric power factor (S2σ) and to reduce the Lorenz ...
DOI:10.1038/nnano.2011.39URLPMID:21460825
The performance and scaling of graphene-based electronics is limited by the quality of contacts between the graphene and metal electrodes. However, the nature of graphene-metal contacts remains incompletely understood. Here, we use atomic force microscopy to measure the temperature distributions at the contacts of working graphene transistors with a spatial resolution of ~ 10 nm (refs 5-8), allowing us to identify the presence of Joule heating, current crowding and thermoelectric heating and cooling. Comparison with simulation enables extraction of the contact resistivity (150-200 Ω 08m05) and transfer length (0.2-0.5 08m) in our devices; these generally limit performance and must be minimized. Our data indicate that thermoelectric effects account for up to one-third of the contact temperature changes, and that current crowding accounts for most of the remainder. Modelling predicts that the role of current crowding will diminish and the role of thermoelectric effects will increase as contacts improve.
DOI:10.1103/PhysRevB.75.035130URL
DOI:10.1080/00268970701837784URL
The influence of molecular vibration on the Seebeck coefficient is studied within a simple model. Results of a scattering theory approach are compared with those of a full self-consistent non-equilibrium Green's function scheme. We show, for a reasonable choice of parameters, that inelastic effects have a non-negligible influence on the resulting Seebeck coefficient for the junction. We note that the scattering theory approach may fail both quantitatively and qualitatively. The results of calculations with reasonable parameters are in good agreement with recent measurements [Science 315, 1568 (2007)].
DOI:10.1021/nl8031229URLPMID:19203208 [Cited within: 1]
Molecular nanojunctions may support efficient thermoelectric conversion through enhanced thermopower. Recently, this quantity has been measured for several conjugated molecular nanojunctions with gold electrodes. Considering the wide variety of possible metal/molecule systems-almost none of which have been studied-it seems highly desirable to be able to calculate the thermopower of junctions with reasonable accuracy and high efficiency. To address this task, we demonstrate an effective approach based on the single particle green function (SPGF) method combined with density functional theory (DFT) using B3LYP and PBE0 energy functionals. Systematic good agreement between theory and experiment is obtained; indeed, much better agreement is found here than for comparable calculations of the conductance.
DOI:10.1103/physrevb.84.041412URL
We propose thermoelectric devices where a single molecule is connected to two metallic zigzag graphene nanoribbons (ZGNRs) via highly transparent contacts that allow the injection of evanescent wave functions from ZGNRs. Their overlap generates a peak in the electronic transmission that is largely insensitive to the type of the short conjugated molecule, while ZGNRs additionally suppress hole-like contributions to the thermopower. Thus optimized thermopower, together with suppression of phonon transport through a ZGNR-molecule-ZGNR structure, yields the thermoelectric figure of merit ZT similar to 0.5 at room temperature and 0.5 < ZT < 2.5 below liquid nitrogen temperature. Using density functional theory combined with the nonequilibrium Green's function formalism for multiterminal devices, we show how the transmission resonance can be manipulated by the voltage applied to a third ZGNR top-gate electrode covering the molecule to further tune the value of ZT.
DOI:10.1016/j.cplett.2003.09.080URL
We report the observation of temperature dependent tunneling behavior of capillary tunnel junctions of octadecanol (C 18H 37OH) from room temperature to 130 °C. The molecular tunnel junction consists of octadecanol (C 18H 37OH) sandwiched between tin electrodes utilizing the naturally existing surface oxides. The resistance of the molecular junction was found to increase appreciably at temperatures around 80 °C . The transition of the junction resistance is suggested to be associated with the breaking of hydrogen bonding between molecular terminal groups with the electrode surface.
DOI:10.1021/nl801669eURL
DOI:10.1021/nl8025407URLPMID:19072125
Despite its intrinsic non-equilibrium origin, thermoelectricity in nanoscale systems is usually described within a static scattering approach which disregards the dynamical interaction with the thermal baths that maintain energy flow. Using the theory of open quantum systems we show instead that unexpected properties, such as a resonant structure and large sign sensitivity, emerge if the non-equilibrium nature of this problem is considered. Our approach also allows us to define and study a local temperature, which shows hot spots and oscillations along the system according to the coupling of the latter to the electrodes. This demonstrates that Fourier's law -- a paradigm of statistical mechanics -- is violated at the nanoscale.
DOI:10.1088/0953-8984/20/37/374102URLPMID:21694410
Heat production and dissipation induced by current flow in nanostructures is of primary importance to understand the stability of these systems. These effects have contributions from both electron-phonon and electron-electron interactions. Here, we consider the effect of the local electron and ionic heating on the conductance of nanoscale systems. Specifically we show that the non-linear dependence of the conductance on the external bias may be used to infer information about the local heating of both electrons and ions. We compare our results with available experimental data on transport in $\mathrm{D}_2$ and $\mathrm{H}_2$ molecules. The comparison between experiment and theory is reasonably good close to the lowest phonon mode of the molecule, especially for the $\mathrm{D}_2$ molecule. At higher biases we cannot rule out the presence of other effects like, e.g., current-induced forces that make the scenario more complex.
DOI:10.1103/PhysRevB.75.155312URL
DOI:10.1103/PhysRevB.73.205415URL
DOI:10.1002/adma.200306091URL [Cited within: 2]
Abstract We compile, compare, and discuss experimental results on low-bias, room-temperature currents through organic molecules obtained in different electrode–molecule–electrode test-beds. Currents are normalized to single-molecule values for comparison and are quoted at 0.2 and 0.565V junction bias. Emphasis is on currents through saturated alkane chains where many comparable measurements have been reported, but comparison to conjugated molecules is also made. We discuss factors that affect the magnitude of the measured current, such as tunneling attenuation factor, molecular energy gap and conformation, molecule/electrode contacts, and electrode material.
DOI:10.1016/j.ssc.2005.04.036URL
We have fabricated a variety of novel molecular tunnel junctions based on self-assembled-monolayers (SAM) of two-component solid-state mixtures of molecular wires (1,4-methane benzene-dithiol; Me-BDT with two thiol anchoring groups), and molecular insulator spacers (1-pentanethiol; PT with one thiol anchoring group) at different concentration ratios, r of wires/spacers, which were sandwiched between two metallic electrodes such as gold and cobalt. FTIR spectroscopy and surface titration were used, respectively, to verify the formation of covalent bonds with the electrodes, and obtain the number of active molecular wires in the device. The electrical transport properties of the SAM devices were studied as a function of (i) r-value, (ii) temperatures, and (iii) different electrodes, via the conductance and differential conductance spectra. The measurements were used to analyze the Me-BDT density of states near the electrode Fermi level, and the properties of the interface barriers. We measured the Me-BDT single molecule resistance at low bias and gold electrodes to be 6×10 9 Ω. We also determine the energy difference, Δ between the Me-BDT HOMO level and the gold Fermi level to be about 1.8 eV. In addition we also found that the temperature dependence of the SAM devices with r<10 614 is much weaker than that of the pure PT device (or r=0), showing a small interface barrier.
DOI:10.1007/s11224-010-9599-5URL [Cited within: 3]
In this study, an organic conjugated molecule, 4,4′-[ethane-1,2-diylidenedi(nitrilo)] dibenzenthiol designed and is proposed as a molecular wire. Structural and electronic responses of this aromatic molecular wire to the static electric field with intensities 611.602×0210 612 to +1.602×0210 612 a.u., are studied using the DFT-B3LYP/6-31G* level of theory. Natural bond orbital atomic charge analysis shows that the imposition of static external electric field induces polarization—localization of charge on the two ends of molecule, especially on considered terminal contact sulfur atoms. The frontier molecular orbitals (MOs) energy levels including the highest occupied MO (HOMO) and the lowest unoccupied MO (LUMO) and the HOMO–LUMO gap (HLG) values are modified by the static electric field as well. The electric dipole moment and polarizability of the proposed molecular wire under the studied electric field strengths are considerably increased. The current–voltage characteristic curve is estimated for the proposed molecular wire.
DOI:10.1103/PhysRevB.83.155407URL [Cited within: 3]
[Cited within: 3]
[Cited within: 1]
DOI:10.1088/0953-8984/23/1/013001URLPMID:21406815 [Cited within: 1]
In this review, possibilities to modify intentionally the electronic properties of metal/molecule/metal devices (MMM devices) are discussed. Here especially the influence of the metal work function, the metal-molecule interface, the molecule dipole and different tunneling mechanisms are considered. A route to evaluate the effective surface work function of metal-molecule systems is given and, based on experimental results, an exemplary estimation is performed. The across different metal-molecule interfaces is characterized by relating transmission coefficients extracted from experimentally derived molecular conductances, decay constants or tunneling barrier heights. Based on the reported results the tunneling decay constant can be assumed to be suitable to characterize intrinsic molecular properties, while the nature of the metal-molecule contacts is properly described by the transmission coefficient. A clear gradation of transmission efficiencies of metal-anchoring group combinations can be given.
DOI:10.1088/0034-4885/68/3/R01URL [Cited within: 1]
A review on the mechanisms and characterization methods of electronic transport through self-assembled monolayers (SAMs) is presented. Using SAMs of alkanethiols in a nanometre scale device structure, tunnelling is unambiguously demonstrated as the main intrinsic conduction mechanism for defect-free large bandgap SAMs, exhibiting well-known temperature and length dependences. Inelastic electron tunnelling spectroscopy exhibits clear vibrational modes of the molecules in the device, presenting direct evidence of the presence of molecules in the device.
DOI:10.1002/jcc.21749URLPMID:21370238
The electron transport mechanism changes from tunneling to hopping as molecular length increases. To validate the theoretical simulation after the transition point and clarify influence of electronic structures on the transition, we calculated the conductance of a series of conjugated molecules by density functional theory together with the nonequilibrium Green's function. We found that the highest occupied molecular orbital energy level, transmission spectrum, and the reorganization energy are good indicators for the transition of the electron transport mechanism. The calculated resistances of short junctions (<50 A, before the transition point) are consistent with the experimental result, following the tunneling mechanism. However, the theoretical predication failed for long molecules, indicating the limitation of the theoretical framework of elastic scattering when the electron transport mechanism changes to hopping. Copyright 2011 Wiley Periodicals, Inc.
[Cited within: 1]
DOI:10.1103/PhysRevLett.81.232URL [Cited within: 1]
DOI:10.1103/PhysRevLett.78.1114URL
DOI:10.1063/1.3457124URL [Cited within: 1]
We propose a high-efficiency molecular junction consisting of a double-coupled-quantum-dot molecule sandwiched between two metallic electrodes.ZTcan be enhanced in the Fano-line-shape regime, and it is sensitive to the magnetic flux threading through the double-coupled-quantum-dot molecular junction. This is mainly due to the local density of states in the Fano-line-shape regime may become narrower, and an abrupt changing in the conductance (transmission) spectrum is developed. We find the value ofZTcan exceed 1 at room temperature by controlling the chemical potential or magnetic flux. So our results indicate such a molecular junction may be used to the solid-state thermoelectric energy-conversion device at room temperature.
DOI:10.1103/PhysRevLett.94.034301URL [Cited within: 1]
DOI:10.1209/0295-5075/99/67005URL [Cited within: 3]
The response of a model molecular electronic device to external electric field is characterized in terms of an index named intramolecular thermoelectric-like coefficient (IMTLC). The electronic IMTLC is introduced and computed based on the density and energy transfers between different pairs of sections of the molecule using quantum theory of atoms-in-molecules. The contribution from nuclear motion to the energy transfer, quantified as vibrational IMTLC, is evaluated using an atomic partitioning scheme based on normal modes vibrational analysis. The dependencies of the electronic and vibrational IMTLCs on the electric-field intensity are studied. Symmetrical and asymmetrical contributions components of the IMTLCs, describing, respectively, the intramolecular Joule-like and Peltier-like effects, are also introduced. A simple semiclassical intramolecular temperature modeling is also introduced to describe intramolecular energy monitoring.
DOI:10.1007/s13738-014-0421-yURL [Cited within: 3]
The electronic and vibrational atomic responses to external electric field (EF) are computed to detail intramolecular energy transfer in a proposed molecular nanoelectronic field-effect system. The parallel and perpendicular electronic and vibrational contributions to intramolecular energy transfer are computed using, respectively, quantum theory of atoms-in-molecule and an energy partitioning scheme based on normal modes vibrational analysis. The symmetrical and asymmetrical intramolecular energy transfers are interpreted, respectively, as Peltier-like and Joule-like effects and quantified in terms of appropriate coefficients. Dependencies of these coefficients on EF are investigated. In addition, a semiclassical temperature model is introduced to describe symmetrical and asymmetrical temperature distributions which are attributed, respectively, to the Joule-like and Peltier-like heatings. This procedure can be used to map out intramolecular energy distribution in molecular nanoelectronic systems.
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
DOI:10.1063/1.457315URL
The theory of atoms in molecules is extended to the case where the molecule is in the presence of an electromagnetic field. This theory is based upon a generalization of quantum mechanics to an open system, as obtained through a corresponding extension of Schwinger principle of stationary action. The extension of this principle is possible only if the open system satisfies a particular boundary condition, one which is expressed as a constraint on the variation of the action integral. This is the condition that it be bounded by a surface of zero flux in the gradient vector field of the charge density, the definition of an atom in a molecule. It is shown that this boundary constraint again suffices to define an atom as a quantum subsystem when the molecule is in the presence of an electromagnetic field. The mechanics of an open system and its properties are determined by the fluxes in corresponding vector current densities through its surface. As in the fieldfree case, the obtainment of these currents from the variation of the action integral is a direct result of the variation of the atomic surface and of the imposition of the variational constraint on its boundary. The currents in this case consist of a paramagnetic and a diamagnetic contribution, currents whose presence are a necessary requirement for the description of the properties of a system in the presence of external fields. The variational statement of the Heisenberg equation of motion obtained from the principle of stationary action is used to derive the Ehrenfest force and virial theorems for an atom in a molecule in the presence of external electric and magnetic fields. In this case, there are forces acting on the interior of the atom which arise from the magnetic pressures acting on its surface. It is shown that the molecular electric polarizability and magnetic susceptibility, like other properties, are rigorously expressible as a sum of atomic contributions.
DOI:10.1063/1.3065972URLPMID:19191374 [Cited within: 1]
The effect of a homogeneous external electric field parallel to the hydrogen bond in theFH Hdimer has been studied by theoretical methods. The quantum theory of atoms in molecules methodology has been used for analyzing the electron distribution of the dimer, calculated with different hydrogen bond distances and external field magnitudes. It is shown that an electric field in the opposite direction to the dipole moment of the system strengthens the interaction due to a larger mutual polarization between both molecules and increases the covalent character of the hydrogen bond, while an external field in the opposite direction has the inverse effect. The properties of the complex at its equilibrium geometry with applied field have been calculated, showing that dependencies between hydrogen bond distance, dissociation energy, and properties derived from the topological analysis of the electron distribution are analogous to those observed in families ofXDH Ycomplexes. The application of an external field appears as a useful tool for studying the effect of the atomic environment on the hydrogen bond interaction. In the case ofFH H, both the kinetic energy density and the curvature of the electron density along the hydrogen bond at the bond critical point present a surprisingly good linear dependence on the dissociation energy. The interaction energy can be modeled by the sum of two exponential terms that depend on both the hydrogen bond distance and the applied electric field. Moreover, as indicated by the resulting interaction energy observed upon application of different external fields, the equilibrium distance varies linearly with the external field, and the dependence of the dissociation energy on either the hydrogen bond distance or the external electric field is demonstrated to be exponential.
[Cited within: 1]
DOI:10.1016/j.surfrep.2004.09.002URL
It is now generally recognized that the contact between a metal electrode and a single, a small group, or a thin film of molecules can play a critical, if not dominant, role in the performance of molecule-based electronics. The central issue is: how does an electron cross a metal–molecule interface? From a theoretical perspective, a quantitative answer to this question consists of three components: energetic alignment, electronic coupling, and dynamic localization due to polarization in nuclear coordinates. These three concepts are not unique to molecular electronics but have long been at the center of chemisorption studies. This account takes an experimentalist's view and discusses concepts of electron transfer/transport at metal–molecule interfaces and their intimate relationships to adsorption and non-adiabatic surface dynamics. Particular attention will be paid to photoemission measurements, including time-resolved two-photon photoemission, in probing energetic alignment, electronic coupling, and dynamic localization at molecule–metal interfaces.
DOI:10.1063/1.2938092URLPMID:18554046
We study the effect of non-Markovian reservoirs on the heat conduction properties of short to intermediate size molecular chains. Using classical molecular dynamics simulations, we show that the distance dependence of the heat current is determined not only by the molecular properties, rather it is also critically influenced by the spectral properties of the heat baths, for both harmonic and anharmonic molecular chains. For highly correlated reservoirs the current of an anharmonic chain may exceed the flux of the corresponding harmonic system. Our numerical results are accompanied by a simple single-mode heat conduction model that can capture the intricate distance dependence obtained numerically.
DOI:10.1021/nl9021094URLPMID:19685928 [Cited within: 1]
Abstract The promise of transition voltage spectroscopy (TVS) is that molecular level positions can be determined in molecular devices without applying extreme voltages. Here, we consider the physics behind TVS in more detail. Remarkably, we find that the Simmons model employed thus far is inconsistent with experimental data. However, a coherent molecular transport model does justify TVS as a spectroscopic tool. Moreover, TVS may become a critical test to distinguish molecular junctions from vacuum tunnel junctions.
DOI:10.1063/1.119871URL [Cited within: 2]
For molecular electronics, one needs the ability to electrically address a single conducting molecule. We report on the fabrication of stable Pt electrodes with a spacing down to 4 nm and demonstrate a new deposition technique, i.e., electrostatic trapping, which can be used to bridge the electrodes in acontrolledway with asingleconducting nanoparticle such as a conjugated or metal luster molecule. In electrostatic trapping, nanoparticles are polarized by an applied electric field and are attracted to the gap between the electrodes where the field is maximum. The feasibility of electrostatic trapping is demonstrated for Pd colloids. Transport measurements on a single Pd nanoparticle show single electron tunneling coexisting with tunnel-barrier suppression.
DOI:10.1103/PhysRevLett.94.206804URLPMID:16090269 [Cited within: 1]
We show that Franck-Condon physics leads to a significant current suppression at low bias voltages (termed Franck-Condon blockade) in transport through single molecules with strong coupling between electronic and vibrational degrees of freedom. We find that transport in this regime is characterized by remarkably large Fano factors ($10^2$--$10^3$), which arise due to avalanche-like transport of electrons. Avalanches occur in a self-similar manner over a wide range of time scales, as reflected in power-law dependences of the current noise on frequency and vibrational relaxation rate.
DOI:10.1007/s10909-009-9867-1URL [Cited within: 1]
We consider a molecular single electron transistor coupled to a vibrational mode. For some values of the bias and gate voltage the electronic transport is possible only by absorption of one or more phonons. The system acts then as a cooler for the mechanical mode at the condition that the electron temperature is lower than the phonon temperature. The final effective temperature of the vibrational mode depends strongly on the bias conditions and can be lower or higher than the reservoir in contact with the oscillator. We discuss the efficiency of this method, in particular we find that there is an optimal value for the electron honon coupling that maximizes cooling.
DOI:10.1063/1.3194156URL [Cited within: 1]
Lock-in thermography is applied to image Joule heating and Peltier-type heat transport separately. Images obtained for a multicrystalline silicon solar cell are quantitatively evaluated using an integration method. The results are interpreted in terms of diffusion and electron/hole drag contributions. The approach presented is especially interesting where the thermal contact resistance to the sample is a problem and where versatility with respect to sample geometry is needed. A further advantage of the method is that it does not need any separate power or temperature calibration.
[Cited within: 1]
[Cited within: 2]
DOI:10.1063/1.2345033URL [Cited within: 1]
A comprehensive study of the mechanisms of heating and cooling originated by an electrical current in semiconductor devices is reported. The authors studied the Peltier, Joule, and Thomson phenomena self-consistently and found that the magnitudes of all of them were commensurable. A new formulation and interpretation of the Thomson effect are offered. The main conclusion of the present work is that the thermal analysis of any semiconductor device under real working conditions demands the inclusion of all heating and cooling mechanisms simultaneously.
[Cited within: 1]
[Cited within: 1]
DOI:10.1016/j.carbon.2014.04.082URL [Cited within: 3]
The energy, dipole moment, and polarizability of a finite hydrogen terminated zigzag graphene flake (C46H20, in 2×7 rings) are calculated in the absence of and in the presence of external electric fields reaching 5×109Vm611 [=0.01atomic units (a.u.)]. The field intensities studied are typically found in nanoelectronics and in the tip-sample gap of a scanning tunneling microscope (STM). The change in the total energy ΔE(eV) can be closely fitted to a quadratic function of the field {1.549×104 [E (a.u.)]2} while the dipole moment μ(debye) to a linear function [2.7×E (a.u.)]. The results obtained with three different chemical models [MP2, density functional theory (B3LYP), and Hartree–Fock calculations, all with a 6-311G(2d,2p) basis set] are consistent in both trends and in absolute values. These results obtained from direct calculations are reproduced with a remarkable accuracy from a linear scaling fragmentation scheme called the kernel energy method (KEM). The KEM reproduces all studied field-free and response properties of this graphene flake model, in relative and absolute terms, independently of the underlying chemical model. An observation consistent with the known stiffness of graphene is that geometry optimization under a field as strong as 0.01a.u. insignificantly alters the total energy and the geometry of a (smaller) zigzag C28H14 flake, the difference in the field-induced stabilization energy (ΔΔE) being only 0.006eV (less than 1% of ΔE) and the average field-induced displacement of nuclear positions 650.004603 [B3LYP/6-31G(d,p)].
DOI:10.1063/1.4890345URLPMID:24116597 [Cited within: 2]
It is shown that the response of molecular properties of diatomics such as the total energy, the bond length, and the vibrational Stark shift to an external homogenous electric field (EF) can be predicted from field-free observable properties such as the equilibrium bond length, the bond dissociation energy, the polarizability and dipole moment functions, and the vibrational frequency. Delley [J. Mol. Struct.: THEOCHEM 434, 229 (1998)] suggested to approximate the potential energy surface under an EF by a Morse function augmented with a EF term proportional to the internuclear separation. In this work, this term is replaced by the expression of the field-induced energy change which yields a field-perturbed Morse potential that tends to a constant asymptotic limit when the EF term itself become proportional to the sum of the polarizabilities of the separated atoms. The model is validated by comparison with direct calculations on nine diatomics, five homo-nuclear (H, N, O, F, and Cl) and four hetero-nuclear (HF, HCl, CO, and NO), covering a range and combinations of dipole moments and polarizabilities. Calculations were conducted at the quadratic configuration interaction with single and double excitations (QCISD) and density functional theory (DFT)-B3LYP levels of theory using the 6-311++G(3df,2pd) basis set. All results agree closely at the two levels of theory except for the Stark effect of NO which is not correctly predicted by QCISD calculations as further calculations, including at the coupled cluster with single and double excitation (CCSD) level of theory, demonstrate.
DOI:10.1103/PhysRevB.65.245105URL [Cited within: 1]
DOI:10.1016/s0038-1098(99)80000-3URL
A theoretical analysis of the Peltier effect in two-dimensional quantum point contacts, in field-free conditions and under the influence of applied magnetic fields, is presented. It is shown that in the nonlinear regime (finite applied voltage) new peaks in the Peltier coefficient appear leading to violation of Onsager's relation. Oscillations of the Peltier coefficient in a magnetic field are demonstrated
DOI:10.1103/PhysRevLett.68.3765URLPMID:10045791
We report the observation of quantum size effects in the thermal conductance and Peltier coefficient of a quantum point contact. Our experimental method involves a novel usage of quantum point contacts as local electron gas thermometers.
DOI:10.1007/s11664-010-1470-3URL
We consider thermoelectric effects in a pseudo-one-dimensional electron gas (P1DEG) with a spin–orbit interaction (SOI). The SOI splits the dispersion relation of the P1DEG into subbands with an energy gap. We find quantum oscillations in transport coefficients, which coincide with the locations of the subband edges, as a function of the electrochemical potential.
DOI:10.1088/0268-1242/7/3B/052URL
I. Introduction II. Theoretical background (Landauer-Buttiker formalism of thermo-electricity, Quantum point contacts as ideal electron waveguides, Saddle-shaped potential) III. Experiments (Thermopower, Thermal conductance, Peltier effect) IV. Conclusions
DOI:10.1088/0256-307X/25/12/060URL
DOI:10.1103/PhysRevB.82.045412URL
DOI:10.1088/0953-8984/24/14/145301URLPMID:22410747
The thermoelectric effect in a quantum dot (QD) attached to two leads in the presence of microwave fields is studied by using the Keldysh nonequilibrium Green function technique. When the microwave is applied only on the QD and in the linear response regime, the main peaks in the thermoelectric figure of merit and the thermopower are found to decrease, with the emergence of a set of photon-induced peaks. Under this condition the microwave field cannot generate heat current or electrical bias voltage. Surprisingly, when the microwave field is applied only to one (bright) lead and not to the other (dark) lead or the QD, heat flows mostly from the dark to the bright lead, almost irrespective of the direction of the thermal gradient. We attribute this effect to microwave-induced opening of additional transport channels below the Fermi energy. The microwave field can change both the magnitude and the sign of the electrical bias voltage induced by the temperature gradient. (paper)
DOI:10.1103/PhysRevLett.99.136404URL
DOI:10.1103/PhysRevB.66.125316URL
The work described here is an investigation of thermoelectric phenomena in bipolar semiconductors and p-n junctions. In contrast to majority-carrier semiconductors in which a constant material-dependent Peltier coefficient is defined for a given temperature, bipolar devices can be modeled by introducing a bias-dependent Peltier coefficient at interfaces that takes into account the variation of the carriers' average transport energy. It is shown that this effective Peltier coefficient can vary by orders of magnitude as a function of applied bias, and can give rise to interfacial thermoelectric cooling or heating depending on device parameters. The bias-dependent bipolar Peltier coefficient is modeled analytically for short-length and long-length diodes, and the different regimes of bias for which cooling is achieved are described, as well as the effects of recombination, length, and doping. Analytical expressions to optimize the thermoelectric effect inside an idealized diode cooler are presented with numerical results for several common semiconductors, a figure of merit for internal diode cooling is introduced, and extensions of the model are given for applications such as the internal cooling of a semiconductor laser diode.
DOI:10.1021/nl901554sURLPMID:19610653
An exact expression for the heat current in an interacting is derived and used to calculate the thermoelectric response of three representative single-molecule junctions formed from , 1,3-benzenedithiol, and . Dramatic enhancements of the thermopower S and Lorenz number L are predicted when the junction is tuned across a node in the transmission function, with universal maximum values S(max) = (/3(1/2))(k(B)/e) and L(max) = (7pi(2)/5)(k(B)(2)/e(2)). The effect of a finite minimum transmission probability due, e.g., to incoherent processes or additional nonresonant channels, is also considered.
DOI:10.1016/j.ccr.2004.08.022URL [Cited within: 1]
The quantum theory of an atom in a molecule, QTAIM, provides chemists with a choice of how to interpret, understand and predict the observations of experimental chemistry. They may continue with the use of subjective orbital models and associated energy and charge partitioning schemes, or they may combine the classification and ordering of electronic states obtained from molecular orbital (MO) theory with QTAIM to obtain unique physical answers to chemical questions. MO theory provides a prediction and understanding of the electronic structure of atoms and molecules. The eminently useful models that spring from this theory, the ligand field description of the metal complexes for example, set the stage for the application of quantum mechanics to complete our understanding of the properties predicted by wave functions obtained from theory. The paper demonstrates the complementary nature of MO theory and QTAIM, together with the means of bridging the two approaches in a discussion of the bonding in the carbonyl complexes of Cr, Fe and Ni and the metallocene complexes of Fe, Al + and Ge. Particular emphasis is placed on the atomic expectation value of the exchange operator that determines the number of electron pairs exchanged between bonded atoms, obviating the need for the terms ‘covalency’ and ‘resonance’. One side of the dichotomy in approaches, one based on physics the other eschewing it, is illustrated by a quotation from the abstract of a talk presented by Roald Hoffmann at a symposium of the American Chemical Society on ‘Contemporary Aspects of Chemical Bonding’, Sept. 2003: “And yet the concept of a chem bond, so essential to chem., and with a venerable history, has a life, generating controversy and incredible interest. Even if we can’t reduce it to physics. … Push the concept to its limits, accept that a bond will be a bond by some criteria, maybe not by others, respect chem tradition, have fun with the richness of something that cannot be defined clearly, and spare us the hype”. The abstract laid the groundwork for the message that a chemical bond lies not only beyond the domain of physics but is incapable of precise physical understanding. Whether physics does or does not offer a definition of a chemical bond, it does set out the necessary and sufficient conditions for two atoms to be chemically bonded to one another, conditions summarised by Slater in terms of the two theorems that are pivotal to the physics of bonding: “… both the virial theorem and Feynman's theorem are exact consequences of wave mechanics. Both interpretations agree in pointing to the existence of the overlap charge density as the essential feature in the attraction between the atoms”. The attraction leads to a decrease in the potential energy and to the existence of a potential well which, if of a depth greater than that of the zero point energy, guarantees the system possesses an equilibrium structure wherein no Feynman forces act on the nuclei and wherein the bonding can be characterised by all of the criteria set forth by Hoffmann for the chemical bond; length, energy, force constant etc. So this article makes a modest proposal. Reserve the name and concept of a bond for use by those who believe that chemistry lies beyond the scope of physics (in spite of their reliance on molecular orbitals and valence bond structures), and reserve the concept of bonding for use by those intent on the pursuit and understanding of chemistry using the tools of quantum mechanics.
[Cited within: 1]
[Cited within: 1]
