,1,*, Amin Aminian3, Yousof Zangeneh1, Sirvan Naderi4Corresponding authors: * E-mail:arash_bch@yahoo.com;arash_bch@iauksh.ac.ir
Received:2018-07-8Online:2019-04-1
PDF (7586KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Maliheh Amiri, Hossein Akbari, Bashir Nedaee-shakarab, Arash Boochani, Amin Aminian, Yousof Zangeneh, Sirvan Naderi. Thermodynamic Stability, Half-Metallic and Optical Properties of Sc2CoSi [001] Film: a DFT Study. [J], 2019, 71(4): 455-462 doi:10.1088/0253-6102/71/4/455
1 Introduction
Due to the high potential in the spintronic industry, half-metallic compounds have been given a lot of attention[1-2] in the theoretical and experimental efforts. For the first time, de Groot et al. observed half-metallic behavior according to the quantum computations on the NiMnSb composition, which is metal in the majority spin and semiconductor in the minority one.[3-4] In recent years, various compositions have been reported to illustrate half-metallic properties, such as: Dilute provskites,[5-6] some oxides,[7-9] dilute magnetic semiconductors,[10-11] binary compounds[12-13] and Heusler compounds.[14-16] Heusler compounds are also classified into two categories of full- and half-Heuslers[17-19] so that their formalisms are $X_{2}$YZ and XYZ, respectively, in which the X and Y atoms belong to the transition metals in the periodic table, and the Z atom is an element of group III, IV, and V. The full-Heusler compounds are crystalized in two space groups; if the atomic number of X is greater than Y it would be Fm-3m, otherwise F-43m. Recently, extensive researches have been carried out on the mechanical, electronics, optical and thermoelectric behaviors of full-Heusler owing to the high potential of their application.[20-24] There is not much research but a few on the full-Heusler structure with the $Sc_{2}$Co base to study their electronic and half-metallic behaviors in the bulk mode. The DFT calculations showed that the $Sc_{2}$CoSi composition is a ferromagnetic half-metal with a magnetic moment of 0.999 $\mu_{B}$ and a lattice constant of 6.28?.[25] In this research, the half-metallic, optical and thermodynamic stability behaviors of bulk and thin films surfaces in [001] direction of $Sc_{2}$CoSi have been studied, which has not been done so far. The application of half-metals in the industry is often in the form of thin films, but one of the problems found in Heusler films is the reduction or elimination of spin polarization at their surfaces.[26-27] Hence, searching for thermodynamic Heusler films with high spin polarization has always been a matter of interest.2 Computational Methods
The physical studies of $Sc_{2}$CoSi bulk and its surfaces at the [001] direction including structural, half-metallic and optical properties and thermodynamic stability of the films have been employed based on density functional theory (DFT) and the full potential augmented plane waves (FP-LAPW) by Wien2K code.[28-29] The exchange correlation energy is approximated by GGA,[30] and the internal parameters, such as separation energy and RKmax, are set to $-6.0$ (Reyd) and 8.0 after optimization, respectively. The Kpoint for the bulk and film structures are considered 5000 and 300, respectively while the charge convergence and force minimization are set to 0.0001 and 1.0 (a.u./dyn).3 Results and Discussion
3.1 Structural Properties of Bulk and Films $Sc_{2}$CoSi
The $Sc_{2}$CoSi Heusler has the Fm$3^{-}$m space group[31-32] by 6.28? lattice constant,[22] and also the $Sc_{2}$CoSi films are grown in [001] direction including the 18 atomic layers by 20 {\AA} vacuum. The surfaces are terminated to four forms of Sc-Si, Sc-Co, Co-Si, and Sc-Sc atomic layers, which all surface structures are relaxed by miniposition command and their thermodynamic stability are discussed in the following. In the mentioned structures, Brich-Mournaghan equations are used to optimize the unit cell volumes to obtain the E-V curves which are shown in Fig. 1 and results are listed in Table 1.Table 1
Table 1The lattice parameters $(a)$, distance layers $(d)$, magnetic moments $(M)$, spin polarization at the Fermi level $(P)$ and band Gap energy (Gap) of the bulk Sc2CoSi, Sc-Si and Sc-Co terminations, which the magnetic moment and the Gap are compatible with the Ref. [22].
 |
New window|CSV
Fig. 1
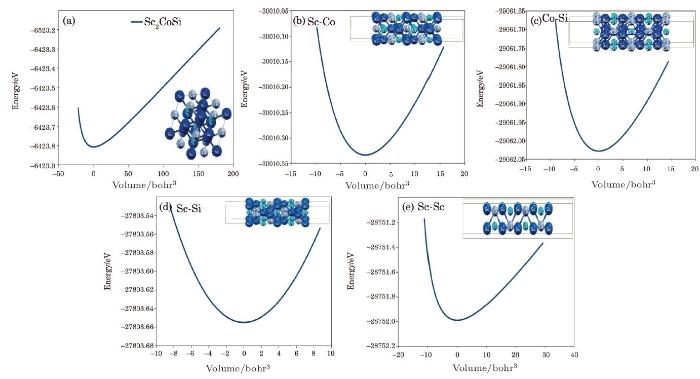New window|Download| PPT slideFig. 1(Color online) (a) and (b) Crystal structure of the full-Heusler alloy $Sc_{2}$CoSn. (c)--(j) Four different terminations Sc-Co, Co-Si, Sc-Sc, and Sc-Si of the $Sc_{2}$CoSn(100) films.
3.2 Electronic Properties
In Fig. 2(a), the band structure curves of the $Sc_{2}$CoSi bulk composition have been shown in both majority and minority spins because the band structure gives us very important information about the electronic structure of matter, such as metallic, semiconducting, magnetic and HM and etc. behaviors. As can be seen, $Sc_{2}$CoSi bulk is a semiconductor in spin up with a direct band gap 0.54 eV, and it has a metallic behavior in the spin down. In the spin up, the maximum valance level is located at the Γ symmetric point while the minimum conducting band is placed along Γ→X, so it implies the p-type semiconductor with an indirect band gap. Another point, the valance levels at the Γ point have a steeper slope than the conduction ones for both spins, so the holes mobility is far more than the electron mobility. In the following, band structure of the Sc-Si termination [001] is plotted in Fig. 2(b) for two spins of up and down which comparison between the two spin modes reveals the semiconductor conditions for down, and metallic behavior for up.Fig. 2
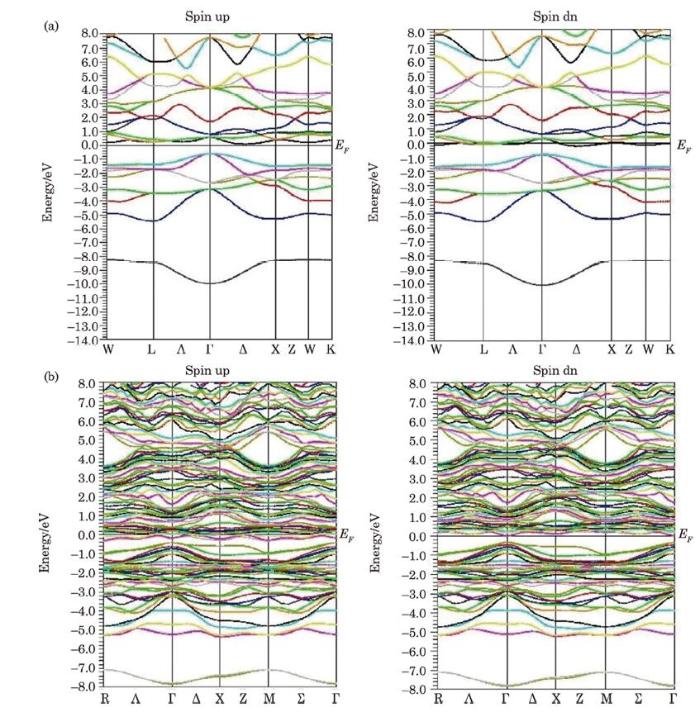New window|Download| PPT slideFig. 2(Color online) Calculated band structures of Sc$_{2}$CoSi alloy (a) and Sc-Si(001) (b).
It is important to note that the majority carriers for the bulk state belong to the spin down, but for Sc-Si [001], they are on the spin up. In addition, in the film phase, the band gap is converted into a direct gap for the spin down at the Γ point. It should also be mentioned that the curve slope of the energy levels in the region of maximum valence at the Γ point is declined regarding to its bulk state, and the flip spin gap is almost zero in the bulk and thin film [001].
Figure 3(a) shows the electron density of states (DOS) curves of the $Sc_{2}$CoSi bulk in two spins up and down. As it can be seen, this composition has a magnetic behavior with full spin polarization (100%) by zero spin flip gap implying to perfect HM behavior. In the following, by comparing the partial density of states of the atoms forming this composition, the highest contribution at Fermi level and the conduction region belongs to the half-filled d orbitals of Sc, and the biggest share below Fermi level and the valence region belongs to the cobalt atom states while the largest contribution of the magnetic anisotropy belongs to the d orbitals of Sc atom. In the following, the density of states curves of the $Sc_{2}$CoSi thin films at two Sc-Co and Sc-Si terminations [001] are shown in Figs. 3(b) and 3(c). Clearly, the Sc-Si termination has 100 % spin polarization at Fermi level while the spin polarization for the Sc-Co termination is about 40\%. Therefore, magnetic anisotropy is much less in the Sc-Co termination and shows metallic behavior, but one of the challenges related to the Heusler films is the absence of or decrease in the 100 % spin polarization at the Fermi level.[33-34]
Fig. 3
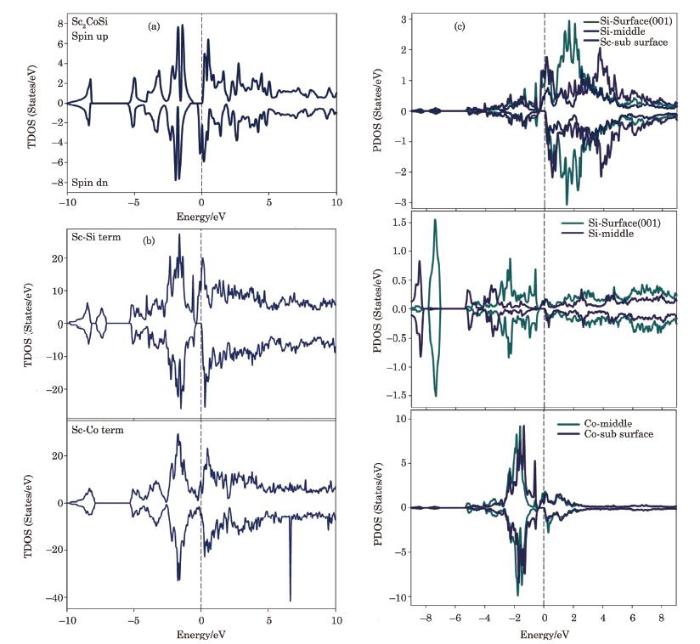New window|Download| PPT slideFig. 3(Color online) (a) Total density of states (DOS) of bulk $Sc{_2}CoSi$ alloy, (b) Sc-Si and Sc-Co terminations, (c) partial density of states (PDOS) of Sc-Si termination.
In Figs. 3(d), 3(e), 3(f), the partial densities of states for the Sc-Si termination are plotted for different layers so that the contributions of the Sc electron states in the surface and subsurface layers are much larger than those of the middle layers at Fermi level. Moreover, the surface effects of the Sc atoms lead to the magnetic anisotropy and splitting the states in the minority spin, although the contribution of magnetic anisotropy of Si atoms is very small. More interestingly, the electron states of valance band for the Si atoms of the middle and surface layers have almost isotropic behavior in the energy range of ($-$1 eV to $-$5 eV) and are completely non-magnetic. After that, the electron states of Co atoms for the middle and the subsurface layers are compared, and consequently, there is a little magnetic anisotropy in the valence region for middle Co atoms while the anisotropy of subsurface Co atoms is greater. In this case, the Co atoms of the mentioned layers have the magnetic asymmetry as the electron states of these layers demonstrate a polarization of 100%, but at higher energies and the conduction region, the anisotropy effects are greatly reduced.
In Table 1, the magnetic moments of the films are listed accompany with comparison to the bulk state. Significantly, the magnetic moment of Sc-Co [001] film is below 1 μB while the magnetic moment of the Sc-Si [001] film is the large number of 3 μB, where the magnetic moment of the bulk is $-$1 μB, the negative sign indicates the weak magnetic responsiveness of the bulk state, and the positive sign and the large number of 3 μB for the Sc-Si [001] film indicates high responsiveness and appropriate sensitivity to the external magnetic fields. As a result, this compound is a good candidate for GMR and TMR applications.
3.3 Optical Properties
The optical parameters give us very good information about the electronic structure and their optical properties, which are extractable by Kramers-Kronig equations. The matter response to the incident light in the real space is shown by the real part of the dielectric function, and for the energy space, it is the imaginary part of the dielectric function, which both can be extracted from the following equations:[35]The real part of the dielectric function is shown in Fig. 4(a) for the $Sc_{2}$CoSi bulk. The static value of Re ${\varepsilon }({\omega })$ has a very large amount indicating the strong metallic behavior at lower energies, but the sign of Re ${\varepsilon }({\omega })$ becomes negative in the regions of 0.35 eV to 0.65 eV (infrared region) and above 3.7 eV (UV region) meaning that the light does not pass through. Most significantly, due the peaks in the infrared and visible regions, this composition is a good candidate for optical applications in the optoelectronic industry and the optical electrodes of the solar cells.[36-37] After that, Re ${\varepsilon }({\omega })$ is zero at energies of 0.3 eV, 0.65 eV, 2.45 eV, 3.65 eV, and 16.3 eV, which can be a sign of Plasmon oscillations or the light refraction in matter, in the following, the Re ${\varepsilon }({\omega })$ curves have been illustrated for the [001] film with Sc-Si termination in two directions of $x$ and $z$. In general, except for differences in the static value of Re ${\varepsilon }({\omega })$ and in the shape of the Re ${\varepsilon }({\omega })$ curve in the visible region and the UV edge, the Re ${\varepsilon }({\omega })$ graphs are relatively similar in the two directions. In both directions, the static value of the Re ${\varepsilon }({\omega })$ is still a large number confirming the metallicity, but this metallic behavior at low energies along $x$ is larger than $z$ ones. Compared with the bulk Re ${\varepsilon }({\omega })$ curve, it is clear that the metallicity has decreased which, of course, was expected because the number of atoms in $z$ direction is reduced. Moreover, the film optical response rate is decreased with a steep slope so that it reaches a minimum value at about 0.3 eV. Importantly, the light responsiveness, Re ${\varepsilon }({\omega })$, has a positive value from zero energy to 3.4 eV for $x$ direction and 3.75 eV for $z$ one, which is in contrary to its bulk state that was negative in the infrared region. Therefore, this thin film has a high optical sensitivity in the infrared, visible and even UV edge regions, which may be due to the presence of bonding arms from Sc and Si atoms on the film surface. Another significant point is that the sign of the dielectric function is negative at other energies in the UV region up to 15 eV in both directions, so light does not pass through and the thin film is dark. The Re ${\varepsilon }({\omega })$ value is zero at energies of 3.3 eV and 13.3 eV for $x$ direction and 3.8 eV and 12.9 eV for $z$ direction, and this can also be another positive feature, which the light energy reduction is only occurred at the higher energies, not in the visible and infrared regions. The imaginary part of the dielectric function of the $Sc_{2}$CoSi structure is plotted in Fig. 4(b) for the bulk phase such that the peaks of the Im ${\varepsilon }({\omega })$ represent optical transitions from filled to empty levels. There is a very large peak in zero energy confirming again the metallic behavior, because with the minimum incident light, excited weak electrons transit from filled levels to empty ones. Furthermore, the Im ${\varepsilon }({\omega })$ curve experiences a significant decrease occurring at the energy of 0.88 eV corresponding to the zero value of Re ${\varepsilon }({\omega })$ because wherever there is Plasmon oscillations, there would be electron transitions and the matter response to the light vanishes completely. In addition, there is a large peak at 1.75 eV (in the visible area), however, the intensity of the peaks is reduced exponentially, so that the later peaks at the energies of 3.71 eV, 5.56 eV, and 7.8 eV are less and less.
Fig. 4
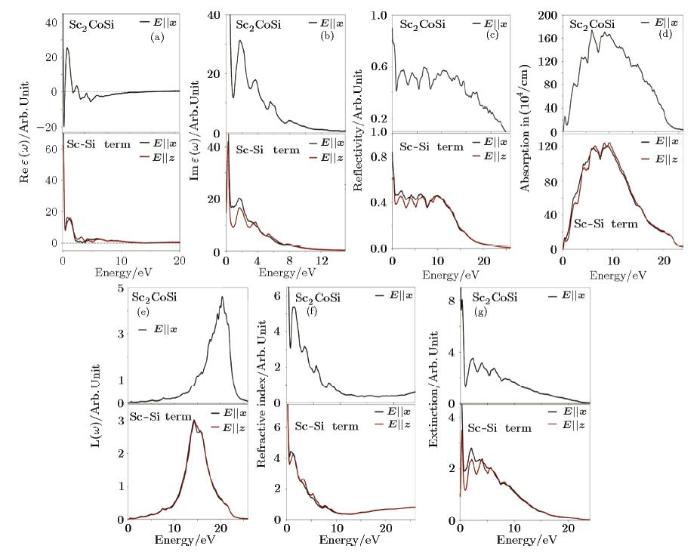New window|Download| PPT slideFig. 4(Color online) (a)--(g) Optical diagrams of Sc$_2$CoSi alloy and Sc-Si terminations.
In the following, the imaginary part of the dielectric function is plotted for the Sc-Si [001] termination for two mentioned directions. Although anisotropy is seen for optical behavior in the infrared area, the overall behavior is similar at higher energies. In this regard, the static value of Im ${\varepsilon }({\omega })$ in $x$ direction is a large number experiencing a sharp drop at about 0.7 eV while the static value of the dielectric function for $z$ direction is much smaller about 1/3 times of the value for $x$ one. Correspondingly, a sharp Dirac peak occurs at about 0.27 eV, and it then falls rapidly after 0.88 eV. In $x$ direction, there is a main peak in the visible range at the energy of 1.7 eV, but there are three other peaks in $z$ direction at 1.7 eV, 3.7 eV and 5.4 eV, which the peaks intensities constantly decrease. Comparing these two curves, if the light enters along $x$ direction, most of the light energy will be used for the electron transition, while in $z$ axis, a smaller portion of the light energy is spent on these transitions and a greater part of the light passes through. Due to the incident light and the electron excitation and transition, electrons lead to the optical conduction that have the chance of crossing Fermi level.
The optical conductivity of the $Sc_{2}$CoSi bulk phase has been depicted in Fig. 4(c), and as it appears, there is a large peak at lower energies indicating a drastic decline at about 0.8 eV. This peak is a strong verification of the metallic behavior, but significant conduction peaks are occurred in the visible and UV regions (energies of 2.2 eV, 3.7 eV, 5.5 eV and 8 eV). Afterward, a decrease in conductivity can be seen so that the conductivity becomes zero after 25 eV. The steep conduction valleys also occur at the same energies that Plasmon oscillations or refraction are observed. The optical conductivity of Sc-Si [001] film is shown for two directions of $x$ and $z$ in Fig. 4(c). In the $x$ direction, more metallic behavior can be detected especially in zero energy, and the optical conductivity is more uniform. Moreover, the reduction in the optical conductivity is much less than the bulk one and even along $z$ direction.
Figure 4(d) indicates the absorption graph of the bulk phase rising as a Gaussian curve so that in the visible region of 1.7 eV experiences a steep absorption slope. Additionally, high absorption is observed at the UV edge (3.6 eV) to reach the maximum light absorption in energy range between 6.2 eV and 10 eV, but the light absorption drops with a mild slope afterward to reach about zero at 25 eV. In the Sc-Si termination, similar to the bulk state, absorption experiences a pungent elevation in the visible and the UV edge region, and a small valley can be seen in the peak point at 7.5 eV for both directions owing to the refraction occurred in this energy area. The ELOSS curve in Fig. 4(e) shows the degree of light loss in the matter, and those peaks of the ELOSS spectrum that match the zero points of Re ${\varepsilon }({\omega })$ represent the Plasmon oscillations. As can be seen from the Re ${\varepsilon }({\omega })$ curve of the bulk phase, there is a sharp and large peak in the mentioned region, so the large Plasmon oscillations occur at these energies such that the energy of the plasma oscillations is 20.4 eV. Then, the ELOSS curve for the Sc-Si [001] film is plotted for two directions of $x$ and $z$. A point that should be considered is that the peaks of the mentioned curves show a red shift, and their main peak has shifted to about 14.5 eV. Accordingly, with respect to zero values of Re ${\varepsilon }({\omega })$ at this energy, the Plasmon oscillation has occurred in the thin film. One of the important optical coefficients derived from the dielectric function is the refractive index extracted from the following equation:[35]
The refractive index of the $Sc_{2}$CoSi in the bulk phase is shown in Fig. 4(f). Correspondingly, due to its metallic nature, the static refractive index is a large number and an intense decline can be seen, as a result, most of the incident light energy passes through or reflects. Furthermore, there is a peak in the visible region, so the light speed in matter is as high as possible. The refractive index decreases so that it exhibits semiconductor behavior in the range of 5 eV to 12 eV, since then, the refractive index is almost zero and becomes a transparent material. Along the $x$ axis of the [001] film, an exponential decrease can be detected after a sharp decline of the refractive index in the infrared region, and the refractive index peak also has a red shift. In the same way, along $z$ axis, a fading sawtooth exponential curve can be observed where the highest rate of the light refraction is again occurred in the visible area for both directions. Another important optical parameter in the field of the light transition through material is the imaginary part of the refractive index or the extinction coefficient, which by the definition, is the amount of loss occurring in the light intensity for penetration in matter. For the bulk state, the most loss has occurred at infrared energies, which it was also expected because it has a metallic nature. Even though there is a keen falloff in the extinction coefficient at about 0.8 eV, this is the area where the sign of Re ${\varepsilon }({\omega })$ was negative. Afterwards, there is a peak in the visible area and two other peaks in the UV region which, of course, this reduction rate is insignificant compared to the lower energies. In order that the reduction rate in the absorption amplitude is practically minimized at the higher energies, more light passes through the matter. Hereupon, the extinction coefficient of the mentioned film for two directions indicates that the extinction coefficient in the infrared area is more than the other energies as same as the bulk state; of course, it is still less than the bulk one. Comparing the two directions, the extinction coefficient value along the $z$ axis is approximately half of the one along the $x$ axis. Additionally, there are two peaks in the visible region with this difference that the reduction of the extinction coefficient is smooth in $x$ direction, but sawtooth in $z$ direction. In general, it is possible to say from the concepts of the optical section that the Sc-Si [001] thin films has a red shift and its optical sensitivity has been shifted to the visible area and the UV edge, which can have very useful applications in the optoelectronic devices.[36]
3.4 Thermodynamic Phase Diagram
In this section, the relative surface stabilities are studied from the thermodynamic point of view; including Sc-Si, Sc-Co, Co-Si, and Sc-Sc terminations. For this purpose, the surface free energies of these terminations are studied as a function of the atomic chemical potential in the framework of thermodynamic calculations. The surface free energy is calculated as following[37] in which $N{_{i}}$ and ${\mu }{_{i}}$ are the number and the chemical potentials of the $i$ atom, $G$ is Gibbs free energy for the surface, $2A$ is the total area of the supercell surface, and Γ is the surface free energy per unit area:In order to achieve the phase diagram, the various surface free energies are compared in a permissible chemical potential region to find a stable level with the lowest surface free energy. According to the fact that the created termination is considered in the thermodynamic equilibrium with the bulk core layers, the appropriate equilibrium conditions can be written as follow:
which $g{_{\rm bulk}}$ is the bulk Gibbs free energy. By considering the dynamic contribution of Gibbs free energy at lower temperatures, the total energy of the DFT calculations is only considered to obtain these energies.
By comparing the calculated values of Γ for different surfaces, the most stable surfaces can be obtained in different chemical potential values. By determining the most stable surface for each coordinate couple, ${\mu }{_{\rm Sc}}$ and ${\mu }{_{\rm Co}}$, the two-dimensional phase diagram is plotted on the coordinates of these two chemical potentials which the surface free energy is obtained by calculating ${\mu }{_{\rm Si}}$ from Eq. (2) in the terms of ${\mu }{_{\rm Sc}}$ and ${\mu }{_{\rm Co}}$. In this regard, the highest value of ${\mu }{_{\rm Sc}} ({\mu }{_{\rm Co}})$ is related to the structure of Sc (Co), hence, the permissible zone in the phase diagram is limited by the bulk Gibbs free energies of Sc and Co. The maximum values of ${\mu }{_{\rm Sc}} and {\mu }{_{\rm Co}}$ are obtained from the relationships of ${\mu }{_{\rm Sc}}$ $=$ $g{_{\rm Sc}}$ and ${\mu }{_{\rm Co}}$ $=$ $g{_{\rm Co}}$. Here, if the chemical potential of Sc and Co atoms is low, the escape probability of these atoms from the bulk structure increases; ergo, the permissible area will be limited to the minimum values of these two chemical potentials (according to the relationship ${\mu }{_{\rm Sc}}$ $=$ $g{_{\rm CoSi}}$ and {\mu }{_{\rm Co}} $=$ $g_{{\rm Sc}_2{\rm Si}})$. According to the obtained results, all for terminations of Sc-Si, Sc-Co, Co-Si, and Sc-Sc are accessible within the permissible area, and the location that these lines cross each other represents the stability zone for the bulk structure. The phase diagram is shown in Fig. 5, and the title of each region indicates the termination with the least surface energy; correspondingly the Sc-Co and Sc-Si terminations are more stable than the other surfaces by having the lowest $E{_{c}}$ value. Furthermore, it is observed that by increasing the chemical potential of cobalt and scandium, the concentration of these two increases in the surface. The major area within the permissible area is also appertained to the Sc-Sc and Sc-Co surfaces, and these two terminations are the most stable surfaces.
Fig. 5
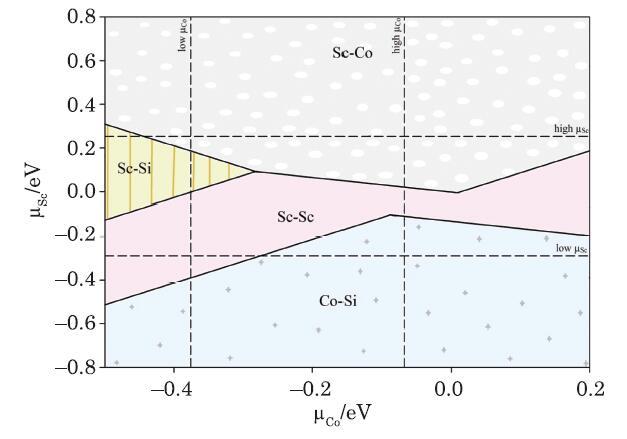New window|Download| PPT slideFig. 5(Color online) The thermodynamic phase diagram for Sc-Sc, Sc-Si, Sc-Co, and Co-Si terminations of Sc$_2$CoSi (001) film.
4 Conclusion
Thermodynamic stability, electronic, structural and optical properties of the $Sc_{2}$CoSi full-Heusler bulk and its four different terminations of the thin film [001] surface including Sc-Si, Sc-Co, Co-Si and Sc-Sc are investigated using the first principles calculations. The $Sc_{2}$CoSi compound is a ferromagnetic half-metal with a spin polarization of 100 % at Fermi level. Among the all mentioned terminations, the Sc-Si only has retained the half-metallic behavior. The study of optical parameters revealed that both the $Sc_{2}$CoSi bulk and the Sc-Si [001] films would be suitable candidates for using in the optoelectronic industry, solar cell electrodes, spintronics, and spin torque devices. Producing the thin film shifts the optical sensitivity of the Heusler compound into the visible and infrared regions. The study of the thermodynamic phase diagram indicates that the Sc-Si and Sc-Co surfaces are thermodynamically the most stable surfaces due to the lowest surface energy and the highest surface area under the phase diagram. In this regard, we hope that experimental studies will create these two terminations, if necessary and functionalize them.Reference By original order
By published year
By cited within times
By Impact factor
DOI:10.1016/j.commatsci.2015.03.010URL [Cited within: 1]
We investigate the electronic structure and magnetic properties of four quaternary Heusler alloys ZrMnVZ and ZrCoFeZ (Z=Si, Ge) by using first-principle calculations. It is shown that ZrMnVSi, ZrMnVGe and ZrCoFeSi are half-metallic ferromagnets with considerable half-metallic gaps of 0.14, 0.18 and 0.22eV, respectively. ZrCoFeGe is nearly half-metallic with a spin polarization of 98.99% at equilibrium lattice constant. Meanwhile, the changes of its properties under pressure are investigated.
DOI:10.1016/j.jmmm.2015.08.123URL [Cited within: 1]
We investigate the effect of eloping on FeCoZrGe. Electronic structure calculations reveal that doping of As or Nb into FeCoZrGe will transform it into half-metallic materials. They have half-metallic properties in a large range of proportion of As or Nb's doping. So by doping with different proportion of As or Nb, the controllable half-metallic gaps can be realized. In addition, this doped system can have higher Curie temperature. (C) 2015 Elsevier B.V. All rights reserved.
DOI:10.1103/PhysRevLett.50.2024URL [Cited within: 1]
The band structure of Mn-based Heusler alloys of the C1b crystal structure (MgAgAs type) has been calculated with the augmented-spherical-wave method. Some of these magnetic compounds show unusual electronic properties. The majority-spin electrons are metallic, whereas the minority-spin electrons are semiconducting.
[Cited within: 1]
DOI:10.1166/jnn.2017.14102URL [Cited within: 1]
We employed a sonochemical method to fabricate transition metal ion doped perovskite ZnTiO(M-ZnTiO) nanoparticles, including individual Co and Mn ions. The Zn:Ti was mixed in molar ratio of 1:1 to obtain starting precursor for ZnTiO. The different concentrations of Co (5–10 mol%) and Mn (3–7 mol%) were doped in ZnTiO, then the mixing solution were irradiated in high frequency ultrasound of a sonometer (20 kHz, 750 W) at room temperature to obtain the as-prepared samples. The final products were calcined at 800 °C for 3 h to improve the crystallinity. We confirmed formation structures of M-ZnTiOnanoparticles by X-ray diffraction (XRD), and used X-ray absorption near edge spectroscopy (XANES) and X-ray photoelectron spectroscopy (XPS) technique to investigate the crystal structure and valence states of the sample. Meanwhile, we studied their optical properties by diffuse reflectance spectroscopy, and evaluated magnetic properties of the samples at room temperature by vibrating sample magnetometer (VSM). Magnetization measurements revealed the paramagnetic behavior for Co–ZnTiOand weak ferromagnetic behavior for Mn–ZnTiO. We also investigated and discussed the effect of metal ion doping concentration on the structural, optical and magnetic properties.
[Cited within: 1]
[Cited within: 1]
DOI:10.1016/j.cplett.2009.10.024URL
The half metallic properties of the recent synthesized Sr 2CuOsO 6 were predicted by using the density functional theory. The effects of electron correlation and spin–orbit coupling (SOC) were studied. The calculations show that without considering SOC effect, Sr 2CuOsO 6 is half metallic and ferrimagnetic. By including both electron correlation and spin–orbit coupling, the total spin magnetic moment is 0.89 μ B, total orbital moment 0.43 μ B in opposite direction, making the net magnetic moment 0.46 μ B. SOC ruins the half metallic character.
[Cited within: 1]
DOI:10.1016/j.ssc.2007.12.022URL [Cited within: 1]
First-principles calculations based on spin density functional theory are employed to investigate the ferromagnetic and the spin-resolved electronic properties of Cr-doped AlP. The Cr impurities in AlP are found spin polarized and the calculated band structures suggest a 100% polarization of the conduction carriers. A net magnetic moment of about 3 μ B is found per Cr. At a Cr concentration of 12.5%, total energy calculations show that the ferromagnetic state is 108.802meV per Cr lower than the antiferromagnetic state and a Curie temperature higher than 65002K can be expected in Cr-doped AlP. Both double-exchange and p–d hybridization mechanism contribute to the ferromagnetic ground state of Cr-doped AlP, but the former is dominant. These results suggest that the Cr-doped AlP may be a promising dilute magnetic semiconductor for the applications in the field of spintronics.
[Cited within: 1]
[Cited within: 1]
DOI:10.1088/0253-6102/54/1/28URL [Cited within: 1]
The structural,electronic,and magnetic properties of VSb in zincblende,and NiAs phases,VSb (001)film surfaces and its interfaces with GaSb (001) have been investigated within the framework of the density functionaltheory using the FPLAPW+lo approach.The NiAs structure is more stable than the ZB phase,ZB VSb is found toa half-metallic ferromagnetic.The V-terminated surfaces retain the half-metallic character,while the half-metallicityis destroyed for Sb-terminated surfaces due to surface states,which originate from p electrons.The phase diagramobtained through the ab-initio atomistic thermodynamics shows that the formation energy of ZB VSb is about 0.1 Ryd.The half-metallicity character is also preserved at VSb/GaSb (001) interface.The conduction band minimum (CBM) ofVSb in the minority spin case lies about 0.47 eV above that of GaSb,suggesting that the majority spin can be injectedinto GaSb without being flipped to the conduction bands of the minority spin.
DOI:10.1016/j.jmmm.2010.05.006URL [Cited within: 1]
We have studied the electronic structure, magnetic and transport properties of some Co based full Heusler alloys, namely Co 2TiZ (Z = Si, Ge and Sn), in the frame work of first-principle calculations. The calculations show that Co 2TiZ (X = Si, Ge and Sn) are to be half-metallic compounds with a magnetic moment of 2 mu B, well consistent with the Slater-Pauling rule. The electronic structure results reveal that Co 2TiZ has the high density of states at the Fermi energy in the majority-spin state and show 100% spin polarization. Our results also suggest that both the electronic and magnetic properties in these compounds are intrinsically related to the appearance of the minority-spin gap. The origin of energy gap in the minority-spin states is discussed in terms of the electron splitting of Z (Z = Si, Ge and Sn) and 3d Co atoms and also the d-d hybridization between the Co and Ti atoms. The transport properties of these materials are discussed on the basis of Seebeck coefficients, electrical conductivity coefficients and thermal conductivity coefficients. [All rights reserved Elsevier].
DOI:10.1103/PhysRevApplied.8.034012URL
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
DOI:10.1016/j.commatsci.2015.03.010URL [Cited within: 1]
We investigate the electronic structure and magnetic properties of four quaternary Heusler alloys ZrMnVZ and ZrCoFeZ (Z=Si, Ge) by using first-principle calculations. It is shown that ZrMnVSi, ZrMnVGe and ZrCoFeSi are half-metallic ferromagnets with considerable half-metallic gaps of 0.14, 0.18 and 0.22eV, respectively. ZrCoFeGe is nearly half-metallic with a spin polarization of 98.99% at equilibrium lattice constant. Meanwhile, the changes of its properties under pressure are investigated.
DOI:10.1016/j.commatsci.2013.08.059URL [Cited within: 2]
The elastic stabilities, electronic, magnetic and thermodynamic properties of Ni2ZrX (X=Sn and Sb) alloy under pressure are extensively investigated by using the first-principle calculations and quasi-harmonic Debye model. Through a series of researches, for instance Gibbs free energy as a function of pressure, P–V equation of states and elastic stabilities, the optimized lattice constants, Bulk, Shear and Young’s moduli, Anisotropy, ductility, Density of State (DOS) and Poisson’s ratio of Ni2ZrX alloy are obtained. The effects of temperature (T) and pressure (P) on heat capacity are opposite, and the effect of T is larger than P, which are consistent with a compression rate of volume. The results of thermal expansion coefficient (α) show the effect of T and P on α is small. The magnetic studies indicate that Ni2ZrX has little magnetism due to different atomic position in the generalized Heusler alloy structure. The DOS of Sn p and Sb p electrons form double-peak.
[Cited within: 1]
DOI:10.1016/j.jallcom.2014.02.005URL [Cited within: 1]
First principles FPLAPW calculations were performed in the framework of Density Functional Theory (DFT), to study the electronic structures and magnetic properties for the new full-Heusler compounds: Sc2CoZ (Z=Si, Ge, Sn). The investigated materials are stable against decomposition, in ferromagnetic configuration and crystallize in the inverse Heusler structures. The half-metallic properties as function of the variation of unit cell volumes are analysed regarding the fourth main group constituent elements. The electronic structure calculations for Sc2CoSi and Sc2CoSn show half-metallic characters, with indirect band gaps of 0.544eV and 0.408eV at optimised lattice parameters of 6.2803 and 6.6203, respectively. For Sc2CoGe compound, the Fermi energy is not pinned inside the energy band gap from minority density of states, neither for unit cell contraction nor for enlargement. The calculated total magnetic moments are 1μB/f.u., for all compounds, in agreement with Slater–Pauling rule.
[Cited within: 1]
DOI:10.1063/1.4716183URL [Cited within: 1]
A recent experimental study indicates that full-Heusler alloy Co2VGa exhibits half-metallic ferromagnetism and the magnetic moment measured at 5 K is independent of high pressure up to 12.1 kbar [T. Kanomataet al.Phys. Rev. B82, 144415 (2010)]. Using the full potential linearized augmented plane-wave method, we here further investigate the structural, electronic, and magnetic properties of all possible (111) surfaces of Co2VGa. Both structural relaxation and calculated surface energy reveal that Ga-terminated surface is more stable than other terminations. From the analysis of the spin-polarized density of states, we find that the half-metallicity confirmed in bulk Co2VGa is lost at the Co-terminated surface but still maintained at the V- and Ga-terminated surfaces. Moreover, we also find that the atomic magnetic moments at the (111) surfaces are greatly different from the bulk values.
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
DOI:10.1016/j.jmmm.2015.03.090URL [Cited within: 1]
[Cited within: 2]
[Cited within: 2]
[Cited within: 2]
