 ,1,2,?, Li-Li Duan
,1,2,?, Li-Li Duan ,1,?
,1,? Corresponding authors: ?? E-mail:lihao@sdnu.edu.cn?? E-mail:duanll@sdnu.edu.cn
Received:2019-03-9Revised:2019-05-16Online:2019-09-1
| Fund supported: |

Abstract
Keywords:
PDF (4282KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Kai-Fang Huang, Shu-Heng Dong, Su-Su Zhong, Hao Li, Li-Li Duan. Study on the Amyloid A $\beta$42 with Accelerated Molecular Dynamics Simulations *. [J], 2019, 71(9): 1121-1126 doi:10.1088/0253-6102/71/9/1121
1 Introduction
Molecular dynamics (MD) simulation of biological macromolecules, beginning in 1977, have opened a new era "from structure to function" for the research of biophysics.[1] MD simulation can provide the kinetic and thermodynamics information of proteins at the atomic level and reveal the important roles that protein dynamics played in many physiological processes.[2]-[8] In addition, MD also makes up the shortcoming of the experiments and has becoming a significant complementary tool in explaining the experimental phenomenon and uncovering the experimental nature. Predicting and guiding the process of experiment in theory, importantly, MD simulation has been successfully applied to many fields due to its rapid development.[9]-[13] Among them, the milestone event is the study for protein folding. Duan and Kollman firstly performed a 1 $\mu$s folding simulation for Villin headpiece with 36 residues in explicit solvent using AMBER96 force field, and they obtained the middle state, which was similar with the native state.[14] The possible folding pathway of this protein is proposed in their study and from then that set off a folding simulation boom with MD. Shaw group has developed a specialized supercomputer to simulate the folding of some protein, which provides a new platform for solving a series of problems about protein folding using MD simulation technology.[15]-[16] However, due to the limited computational power of computer, MD simulation is often hindered by poor phase-space sampling efficiency on bumpy potential energy surfaces. It is difficult to traverse the thorough sampling of the entire phase space in the limited simulation time, which results into that the large-scale conformational changes usually are not observed.To solve this problem many accelerated dynamics algorithms have been proposed.[17]-[24] Among them, accelerated molecular dynamics (AMD) has become one of the popular approaches for the protein folding simulation.[25] The AMD method first proposed by Voter,[26]-[27] improved by the McCammon Group,[28] recently, which is an effective way to enhance the spatial sampling. This method reduces the energy barrier by increasing the nonnegative boost potential, expanding the probability of transition between different low-energy states with the potential energy landscape. But it still retains important details,[28]-[31] and the most significant advantage of AMD is that it does not need any predefined reaction coordinates. This method has been successfully applied to many studies of systems including bovine pancreatic trypsin inhibitor (BPT1),[32] alanine dipeptide,[33] fast-folding proteins,[34] a silk-like polypeptide,[35] insulin,[36] and some alpha helix folding.[37]
The accumulation of inside and outside the cell for protein can lead to a serious of diseases. Up to now, there are more than 20 kinds of human diseases, which are associated with the protein misfolding. Such as, the abnormal accumulation of amyloid-$\beta$ (A$\beta$) is linked to neurodegenerative Alzheimer's disease (AD). The length of A$\beta$ polypeptide ranges from 39 to 43 residues. Among them, A$\beta$40 with 40 residues and A$\beta$42 with 42 residues have been extensively studied. A$\beta$40 is a normal soluble product in the meninges and cerebrospinal fluid, and A$\beta$42 is the main component of senile plaques (SPs). Nelson et al. assumed that the structure of A$\beta$ in the case of aggregation is mainly the formation of $\beta$-sheet.[38] In contrast, A$\beta$ is mainly coil structure in non-aggregated aqueous solution, and $\alpha$-helical structure in biofilm or organic solvent. The misfolding of $\beta$-sheet promotes the aggregation of A$\beta$, which further forms the insoluble fibers. Therefore, this structure is not easily degraded by proteases, and finally results in the produce of the age spots. The conversion of A$\beta$ from a soluble state to an insoluble state is a key factor of forming AD.[39] This misfolding results in the aggregation, and then forms small and strong deleterious oligomers. So A$\beta$42 is considered to be an important reason of causing the AD disease.
Due to the property of poor solubility, difficulty in crystallization and easy in aggregation,the needed time for the conformational transformation of A$\beta$ is transient. The current experimental methods such as NMR and X-ray techniques can only provide the average structure, and they are hard to dynamically capture the misfolding process of A$\beta$. Therefore, it is impossible to explain the mechanism of aggregation from experiment at atomic level. With the rapid development of computer hardware and software technology in recent years, more and more research has focused on the conformational transformation of full sequence A$\beta$ in theory. Jiang group pointed out that the conformational transformation of A$\beta$40 from $\alpha$-helix to random coil undergoes the complex structure combined helix with $\beta$ sheet under normal temperature and pressure.[40] However, Kirkitadze et al. thought that the above mixed structure is most likely the intermediate state of the A$\beta$ oligomer.[41] Flock et al. performed an extensive MD simulation in various temperatures and pH conditions, which shows that helix 1 (residues 8 to 25) can convert into $\pi$-helix, and helix 2 (residues 28 to 39) can become random coils or $\beta$-sheet structures.[42] Olubiyi et al. used two different force fields (GROMOS96 43a2 and GROMOS96 53a6) to study the two systems of A$\beta$1-40 and A$\beta$1-42 under different pH conditions. Their study showed that the 10 residues in N-terminus are unordered, and the protonation of the three histidine accelerates the formation of the $\beta$-sheet structure via a reduction in electrostatic repulsion between the two terminal regions.[43]
Through these studies find that the N-terminal (residues 1 to 10) were mainly unordered structures, and the hydrophobic core region (residues 10 to 21) was mainly $\alpha$-helical structure, while the C-terminal (residues 30 to 42) are mainly $\beta$-sheet structures. Those residues 21 to 30 are the core parts of A$\beta$ aggregation. However, because the conformational conversion of A$\beta$ is relatively slow in traditional MD simulations, it is necessary to use the AMD method to speed up the A$\beta$ conformational transformation's process to obtain the detailed transient conformation. At the same time, we consider that it is usually difficult to obtain accurate canonical distribution at normal temperature, because those structures tend to tap in one of a large number of local minimum energy states. Importantly, it is still unclear that the effect of the different temperatures on the conformational change of A$\beta$42 and whether the temperature affects the aggregation of A$\beta$42. Therefore, AMD simulation at different temperatures is performed that allows the protein to pass through a higher energy barrier and obtains a wider sampling phase space than those conventional methods.
In this study, the AMD simulation is performed for 500 ns with explicit water at four different temperatures (300 K, 350 K, 400 K, and 450 K) to study the effect of temperature-induced conformation changes of A$\beta$42 protein during the unfolding process.
2 Methods
Before AMD simulation, traditional MD simulation is performed to obtain four parameters, which is used to run AMD simulation.The four parameters are $E_{D}$, $\alpha_{D}$, $E_{P}$, and $\alpha_{P}$ and they are used to define the AMD modification of potential by:While
Here, $V(r)$ is the actual potential, $\Delta V$ is the added potential energy and $V_{D}(r)$ is the actual dihedral torsion potential. $E_{P}$ and $E_{D}$ are threshold energies that we obtain from Eq. (3) and Eq. (5). $E_{P'}$ and $E_{D'}$ are the average potential energy and the dihedral potential energy, $N_{\rm res}$ and $N_{\rm atom}$ are the number of residues and the total number of atoms per protein, respectively. $a_{1}$ and $a_{2}$ are set 3.5 and 0.2 kcal/mol by AMBER reference manual, respectively. The final results of the $E_{D}$, $\alpha_{D}$, $E_{P}$, and $\alpha_{P}$ are shown in Table 1 under different temperatures.
Table 1
Table 1
 |
New window|CSV
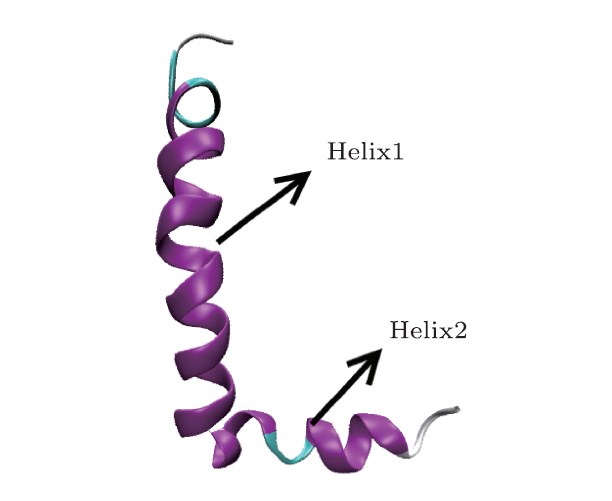
The initial structure of the A$\beta$42 is obtained from the Protein Data Bank (PDB entry: 1IYT). The structure consists of two helices in the residues 7-26 (named helix 1) and 27-40 (named helix 2), which are connected by the $\beta$-turn shown in Fig. 1. AMD simulation is performed using AMBER12 package, and the AMBER12SB force field is employed in all simulations. The system is immersed in a truncated periodic TIP3P water box with 10 ? buffer. In order to neutralize the charge of the system, counterions are placed around the protein. The system is relaxed in a two-step procedure. In the first step, only the protein is optimized using the steepest descent minimization followed by the conjugate gradient minimization with 500 kcal$\cdot$ mol$^{-1}\cdot $?$^{-2}$ harmonic constraint. In the second step, the system is optimized without any constraint until convergence is reached. After that, the system is heated from 0 to 300 K, 350 K, 400 K or 450 K over 300 ps with the weak restraint force constant of 10 kcal$\cdot$ mol$^{-1}\cdot $?$^{-2}$ harmonic constraint on all protein atoms, respectively. Langevin dynamics is used to regulate the temperature with a collision frequency of 1.0 ps$^{-1}$. In order to obtain the initial parameters for AMD simulation, traditional MD simulation is firstly performed, then the system is simulated for 500 ns using AMD method at each temperature until the energy, density and root mean square deviation (RMSD) all reach to equilibrate. The SHAKE algorithm is used to constrain all bonds involving hydrogen atoms.[1] The 12 ? cutoff is used for the van der Waals interaction and the particle mesh Ewald (PME) method is used to treat long range electrostatic interactions.[44] The time step is set for 2 fs.
Fig. 1
 New window|Download| PPT slide
New window|Download| PPT slideFig. 1The initial structure of A$\beta$42 (PDB entry:1IYT).
3 Results and Discussion
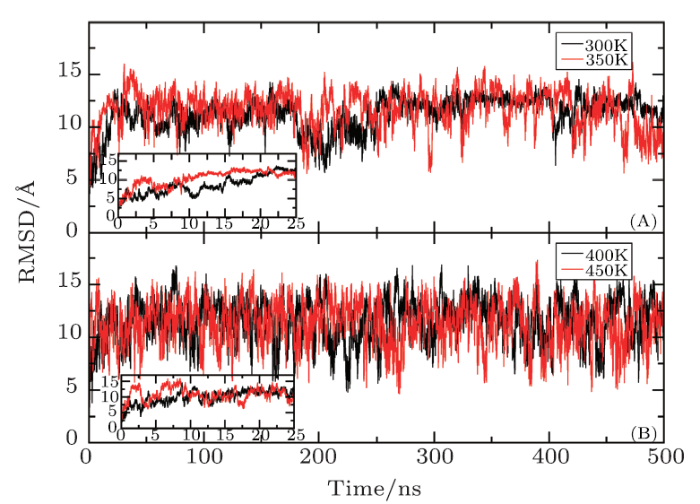
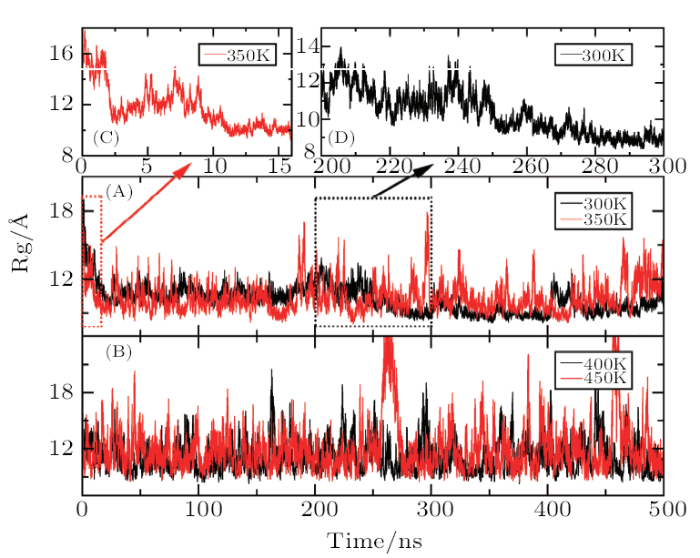
Firstly, the RMSD values of backbone atoms relative to the native structure are calculated at four different temperatures. As shown in Fig. 2, the RMSDs of the total system rapidly increase and finally fluctuate around 12 ? regardless of the temperature, suggesting the conformation of the protein undergoes very changes. The beginning time is 22 ns, 15 ns, 9 ns, and 1.5 ns when the RMSD reaches 12 ? at the temperature of 300 K, 350 K, 400 K, and 450 K, respectively. The result indicates that the effect of temperature on the protein structure is very significant, and the higher the temperature is, the faster the conformation changes. Since radius of gyration (Rg) of protein is usually used to describe the tightness of the protein system, Rg as the function of MD simulation time is furtherly calculated at different temperature. Figure 3 indicates that Rg rapidly decreases from the initial value of 16 ? illustrating that the volume of protein occurs significant reduction. By the analysis of the simulated structure finds that the L-shaped of the protein in the native state has disappeared completely and the spatial configuration has been changed. At the temperature of 300 K, while Rg fluctuates around 10 ? before the 250 ns, it rapidly drops in the next 250 ns and finally stabilized around 9 ?. This demonstrates that there are two conformational collapses occur in the protein structure. At the temperature of 350 K, Rg rapidly drops to 10 ? at about 10 ns and fluctuates around it during the subsequent simulation. At the high temperatures of 400 K or 450 K, Rg is about 12 ? with large fluctuation in the simulated process. The values of Rg is higher in the high temperature than that room temperature indicating that the protein becomes more stretch with the increasing of the temperature.Fig. 2
 New window|Download| PPT slide
New window|Download| PPT slideFig. 2Time-dependent RMSD of backbone atoms with respect to the native structure during the AMD simulation at four different temperatures.
Fig. 3
 New window|Download| PPT slide
New window|Download| PPT slideFig. 3Time-dependent Rg during the AMD simulation at four different temperatures.
By analyzing the RMSD and Rg, it can be found that the structure of the protein undergoes large changes after the long time AMD simulation at the four temperatures. At the room temperature of 300 K, the RMSD of A$\beta$42 compared to the native structure reaches 12 ? and Rg decreases by about 6 ?, which is in good consistent with the characteristic of the inherently disordered protein. That is to say, this structure is very unstable under physiological conditions.[45] The conformational collapse is very obvious at 350 K. When the temperature reaches to the 400 K or 450 K, this structure furtherly stretches after conformational collapse and those fluctuates of RMSD and Rg are very large. The above result indicates that the higher the temperature is, the faster the frequency of the conformational transition is.
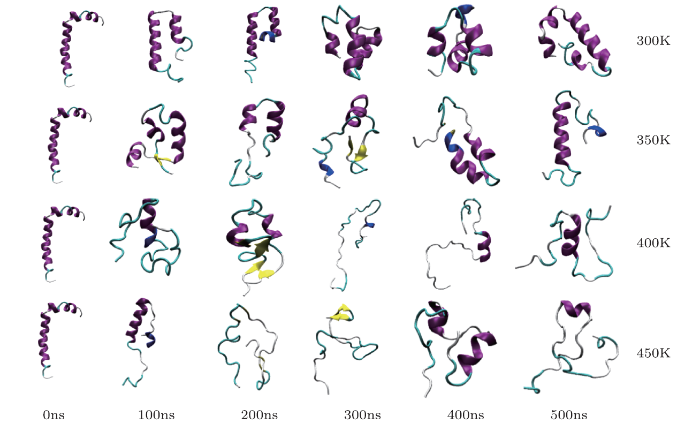
In order to investigate the conformational transition of A$\beta$42 in detail during the MD simulation, the instantaneous snapshots of A$\beta$42 at different temperatures as the function of time are shown in Fig. 4. Due to the large flexibility of $\beta$-turn, the structure is easy to change in MD simulation. The angle between helix 1 and helix 2 gradually decreases at 300 K, which transfers from vertical to parallel at about 100 ns. In 200 ns, the helix 1 and helix 2 begin to denature. With the increasing of simulated time, the topology structure of helix 1 has large change. At 500 ns, while helix 1 changes from one $\alpha$-helix to two helixes, structure of helix 2 almost completely extends. At the temperature of 350 K, the $\beta$-turn rapidly denatures and helix 1 changes two helix structure in which $\beta$-sheet structure is also formed by some residues. At the beginning of 200 ns, the helix structure of helix 1 is scarce and most of residues form irregular coiled structures followed by $\beta$-sheet structure. Until 500 ns, the helix 1 is partly unfolded, while helix 2 almost completely unfolded. At the high temperature of 400 K, the total protein is quickly denatured and only few residues form helix structure at 100 ns, while the $\beta$-sheet structure appears at about 200 ns. From this, the total conformation becomes irregular curl and $\beta$-turn structures. At 450 K, the $\beta$-sheet is again found and quickly is denatured due to the instability. The final structure simulated from 450 K is similar to that from 400 K, in which the total protein is composed of irregular curl and few helices. In summary, the conformation of A$\beta$42 has undergone large change during MD simulation, whether at the temperature of 300 K or a higher one. Although the topology of the protein has changed, the final helix content remains is very high at 300 K. However, the $\beta$-sheet structure appears following the less helix content at high temperature and the final structure is mainly irregular. In other word, under the high temperature, it can accelerate the process of unfolding for $\alpha$-helix.
Fig. 4
 New window|Download| PPT slide
New window|Download| PPT slideFig. 4Snapshots of the intermediate conformation of A$\beta$42 at four different temperatures.
As previously mentioned, the formation of $\beta$-sheet is critical for the aggregation of A$\beta$42. Through Fig. 4, we can clearly observe the rule of the formation for $\beta$-sheet structure. At room temperature, the $\beta$-sheet is not observed in the conformational transition of A$\beta$40 from $\alpha$-helix to random coil. But along the temperature increased, we observed the $\beta$-sheet, which has also described by other experimenter. What is more, when the temperature reaches 450 K, the $\beta$-sheet structure appears earlier (about 200 ns) than other high temperatures, and its conformation is more complicated. This indicates that with the temperature increases, the misfolding process of $\beta$-sheet also accelerates, and this can accelerate the rate of A$\beta$42 aggregation.
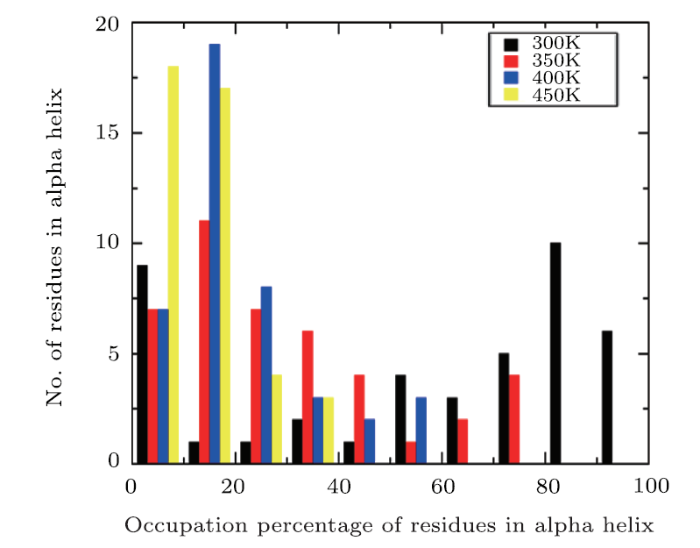
In order to furtherly investigate the structural change of $\alpha$-helix with the temperature, the occupancy of residues formed $\alpha$-helix are calculated under different temperature. And the defined secondary structure of proteins (DSSP) is used to identify the $\alpha$-helix structure motif.[46] If a particular residue belonged to $\alpha$-helix remains intact during 85% of the simulation time, its occupation percentage is 85%, and the numbers of residues formed $\alpha$-helix can be grouped within a certain occupation percentage range (0$-$10%, 10%$-$20%, …, 90%$-$100%). The fractions of these residues versus their occupancy are plotted using a histogram. Figure 5 suggests that the comparison of the residues formed $\alpha$-helix distributions obtained from MD simulation under four different temperatures, respectively. A significant difference is observed that the distribution of residues formed helix based on the simulation at room temperature is composed preferentially of high occupancy residues (80%$-$100%). However, the distribution is dominated by low occupancy residues (0$-$20%) with the increasing the temperature. In the four temperatures of 300 K, 350 K, 400 K, 450 K, the ratios of proportions for the number of residues formed $\alpha$-helix in high occupancy to the low occupancy are about 16/10, 0/18, 0/26, and 0/35, respectively, which indicates that the A$\beta$42 protein is mainly dominated by helical structure at room temperature and the protein becomes the unfolded state from the initial folded state at high temperature.
Fig. 5
 New window|Download| PPT slide
New window|Download| PPT slideFig. 5Comparison of occupation percentage of residues in $\alpha$ helix at four different temperatures.
4 Conclusions
Protein folding is a significant and challenging scientific problem in the 21st century. Many diseases, such as Alzheimer's disease, Parkinson's disease, and mad cow disease, have been found to be related to protein misfolding. Therefore, it is extra significant to understand the folding pathway and folding mechanism of protein. However, the potential energy barriers are always very high during traditional MD simulation, so the systems are usually trapped in one or another local minimum for long simulation time. Meanwhile, the rates of the systems moving from one potential energy basin to another are quite low. In order to improve the efficiency and achieve thorough sampling of the conformational space of protein, we study the folding process of A$\beta$42, which is closely related to Alzheimer's disease, by AMD simulation. In this paper, the AMD simulation is preformed up to 500 ns using AMBER12SB force field combined with the explicit water model under four different temperatures (300 K, 350 K, 400 K, and 450 K) to study the effect of the temperature on the conformational transfer of A$\beta$42. Our study asserts that the spatial configuration of protein undergoes very large change under four different temperatures, and there is no obvious stable structure obtained from the AMD simulation, indicating that the protein is inherently disordered protein. By the analysis of the structure and secondary structure occupancy in the process of MD simulation, it is found that although the initial topological structure disappears at room temperature, existing in the form of $\alpha$-helix. However, founded in the high temperature suggesting it may accelerate the formation of $\beta$-sheet in high temperature, the $\beta$-sheet structure is easier to aggregate than $\alpha$-helix structure. These results will be of great significance for understanding the pathogenesis of Alzheimer's disease to ultimately achieve its early prevention, diagnosis, and treatment.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
