Study of *(892) and (1020) meson production in proton-proton and Pb-Pb collisions at $\sqrt{{s}_{N

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

Y Ali^,¹, M Ahmed¹, A Arif¹, Q Ali¹, U Tabassam¹, U Rubab¹, M Suleymanov¹^,²¹Department of Physics, COMSATS University, Park Road, Islamabad, 44000, Pakistan
²Institute for Physical Problems, Baku State University, Baku, AZ 1000, Azerbaijan

Received:2020-09-11Revised:2020-12-03Accepted:2020-12-06Online:2021-01-28

Abstract
In this paper, we describe a study of charged particle yield as a function of p_T for K^*(892)⁰ and φ (1020) mesons in proton-proton (pp) and Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV in the central rapidity region of ∣y∣<0.5, in a p_T range of 0<p_T <15 GeV c⁻¹ in pp collisions and in a p_T range of 0<p_T<20 GeV c⁻¹ in Pb-Pb collisions. We also investigated a very important ratio, the nuclear modification factor, to study the effects of the medium in the most central region, i.e. 0%-5% centrality. For data simulation, we used the EPOS-LHC and EPOS-1.99 models. To check the validity of these models’ simulations, we compared the data obtained from these Monte Carlo simulation programs with ALICE experimental data for $\sqrt{{s}_{NN}}$=2.76 TeV. It was concluded that the models’ predictions for the φ-meson in pp and for the most central Pb-Pb collisions disagreed with the ALICE data, and that the difference increased with p_T. This may be connected with the essential role of collective parton behaviors which could not have been taken into account by the models. For K^*0 mesons, both programs gave almost the same predictions, and with p_T in the interval p_T>3 GeV c⁻¹, the predictions were very close to the experimental data. Both models gave higher predictions for the soft p_T interval and lower predictions for the hard interactions. The values of the R_AA distributions were lower than unity and both models were very close to the ALICE data. It is very interesting that the models were not able to describe the p_T distributions, but they gave good predictions for their ratios. This may possibly be due to parton collective behaviors. We observed some additional suppression of K^*0 at low values of p_T with respect to φ-mesons, which may be related to the role of the masses of the particles in soft interactions. The rising trend for R_AA in the region from p_T =10 GeV c⁻¹ to 20 GeV c⁻¹ observed by the ALICE experiment was absent for the φ-mesons.
Keywords： Quark Gluon Plasma;EPOS-LHC;nuclear modification factor

PDF (827KB)Metadata Metrics Related articlesExportEndNote|Ris|Bibtex Favorite
Cite this article
Y Ali, M Ahmed, A Arif, Q Ali, U Tabassam, U Rubab, M Suleymanov. Study of K*(892)⁰ and φ (1020) meson production in proton-proton and Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. Communications in Theoretical Physics, 2021, 73(2): 025202- doi:10.1088/1572-9494/abd0e7

Introduction

The measurement of φ-mesons and K^*0 provides us with an insight into Quark Gluon Plasma (QGP), which is a hot and dense state of matter produced right after the big bang. In the lab environment, QGP is created at Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) by heavy ion collisions at low baryonic densities and high relativistic energies ranging from 200 GeV to 14 TeV [1-3]. These systems produces evolution through different stages, which show a transition from the deconfined state of QGP to a confined hadron state. Quantum Chromodynamics (QCD), which is the theory of strong interactions, helps to predict the degrees of freedom of quarks and gluons. The properties of this dense medium can be characterized by the energy loss of quarks and gluons traveling through a color-charged medium [4]. At high transverse momenta, it manifests itself as hadron suppression. The study of high p_T differential yields is used to test perturbative QCD (pQCD).

In the lab environment, strange quarks are a key tool that provides insights when used to probe QGP [5], which is an interesting task in the study of what happened at the time of the big bang. In lab experiments where the enhanced production of strange quarks is predicted, it is thought to be one of the signatures of QGP. QGP cannot be directly detected, but we can get important information about QGP with the help of several signatures, such as strangeness enhancement, di-lepton production, electromagnetic radiation, jet quenching, elliptic flow, and J/$\Psi$ suppression [6]. The production of strange quarks is canonically suppressed in small collision systems such as pp, proton-nucleus (pA) and peripheral nucleus-nucleus (AA) collisions [7]. Light valence quarks exhibit the same suppression as heavy quarks at RHIC and LHC, since K^*0(d$\mathop{s}\limits^{^{\prime} }$) and φ (s$\mathop{s}\limits^{^{\prime} }$) mesons are used at these sites for the study of the particles depend upon the energy loss in the medium [8, 9]. The enhancement of strange quarks is a result of the restoration of chemical equilibrium between up, down and strange quarks with respect to electron-electron (ee) and pp collisions.

φ-mesons [10] do not rescatter significantly in the subsequent expanding hadronic phase. On the other hand, at hadronization, quarks always interact strongly with each other [11-14]. This shows that they have a long lifetime, (46.3±0.4) fm c⁻¹. The re-scattering effects of φ-mesons are negligible. On the other hand, the lifetime of K^*0 is very short at (4.16±0.05) fm c⁻¹ [15]. This means it decays and interacts with non-strange quarks. Its resonance can be used to probe QGP at different energies, and its yield can be measured through hadronic decays. K^*0 can be affected by hadronic re-scattering during the expansion that takes place during the hadronic phase [16]. The masses of the K^*0(892) and φ (1020) mesons are very close to that of the proton and are good probes for testing the production of hadrons.

In this paper, we study φ, K^*0 mesons in pp and Pb-Pb collisions at $\sqrt{{s}_{NN}}=2.76\,{\rm{TeV}}.$ We have plotted the distribution of differential yield as a function of p_T using the EPOS-LHC and EPOS-199 Monte Carlo simulation programs. For this purpose, the rapidity and transverse-momentum ranges are selected as ∣y∣<0.5, 2.5<∣y∣<4 with a p_T range of 0<p_T <20 GeV c⁻¹ at 2.76 TeV for φ in Pb-Pb collisions. For pp collisions, rapidity and transverse momentum ranges are ∣y∣< 0.5 and a p_T range of 0<p_T <20 GeV c⁻¹ at 2.76 TeV for φ and K^*0. These measurements are used in the calculation of ratios and for various pQCD tests. Although in this paper the K^*0 and φ results are averaged by the nuclear modification factor (R_AA) which is defined as the ratio of particles in Pb-Pb to pp collisions, it is scaled by the average nuclear overlap function.$\begin{eqnarray*}{R}_{{\rm{A}}{\rm{A}}}=\displaystyle \frac{\tfrac{\left({{\rm{d}}}^{2}{N}_{AA}\right)}{{\rm{d}}{y}{\rm{d}}{p}_{T}}}{\left\langle {T}_{{\rm{A}}{\rm{A}}}\right\rangle \tfrac{{{\rm{d}}}^{2}{\sigma }_{pp}^{{\rm{I}}{\rm{N}}{\rm{E}}{\rm{L}}}}{{\rm{d}}y{\rm{d}}{p}_{T}}},\end{eqnarray*}$where ⟨T_AA⟩ is the nuclear overlap function which can be calculated with the help of the Glauber model [17], and σ is the inelastic cross-section of proton-proton interactions [18]. We have a good understanding of the evolution of R_AA as a function of p_T for charged particles, which shows that in the range of p_T =5-10 GeV c⁻¹, the suppression is stronger than that observed previously at the RHIC. From p_T =10 GeV c⁻¹ up to 20 GeV c⁻¹, R_AA shows a rising trend, but the suppression effect is absent for φ mesons, which is the main motivation for seeking new information about the behavior of R_AA for the φ and K*⁰ mesons produced in pp and Pb-Pb collisions at LHC energies.

Method and models

For the Monte Carlo simulations, we used EPOS-1.99 [19] and EPOS-LHC [20] models to study the charged-particle yield as a function of p_T and R_AA for the K^*0(892) and φ (1020) mesons in pp and Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The EPOS model is based on a parton ladder as well as off-shell remnants and parton-ladder splitting. EPOS is a newly developed model [21], in which binary pp interactions create a parton ladder. In the cross-section and particle production calculations, energy conservation is taken into account in the EPOS model which, however, is not considered by other models [22]. EPOS is constructed on a completely theoretical basis and carefully tested using all the existing hadronic data, which fully validated all the results. EPOS is also used for air-shower simulations, which can better help us to understand the nature of cosmic rays. EPOS-LHC is one of the latest post-LHC high-energy hadronic interaction models, which has been tuned to reproduce several experimental data sets for hadronic interactions including the results of different LHC experiments up to √s=7 TeV. Like its predecessor (the EPOS-1.99 model), EPOS-LHC is based on Gribov-Regge theory of multiple scattering, perturbative QCD and string fragmentation. However, EPOS-LHC includes some changes regarding the flow parameterization of the high-density core of thermalized matter produced during pp or heavy-ion collisions, the decay of the core (which is now treated statistically) and baryon formation (with multi-strange production considered to be more important than string fragmentation). In the EPOS-1.99 model, we mostly deal with soft interactions. EPOS-LHC is the new updated version of EPOS-1.99 and has been developed for LHC energies. We have used EPOS models, because these are commonly used at LHC energies and because these models use the parton-based Gribov’s Reggeon theory. Parton-based theory is a theory dealing with hard interactions, where maximum momentum is transferred in the interaction and the particle exchanged for this interaction is a gluon, while Gribov’s Reggeon theory is based on soft interactions where a low momentum is transferred in the interaction and the exchanged particle for this interaction is called a pomeron. Therefore, these models can explain both regions i.e. the soft-interaction region (Low p_T) as well as the hard-interaction region (high p_T). There are also several other models available for similar study, such as QGSJETII-04, SIBYLL-2.3c etc., but these models are only based on Gribov’s Reggeon theory, meaning that these models can only explain the soft p_T regions. Therefore, we used EPOS models in our study to explain low values of p_T as well as high p_T regions.

Results and discussion

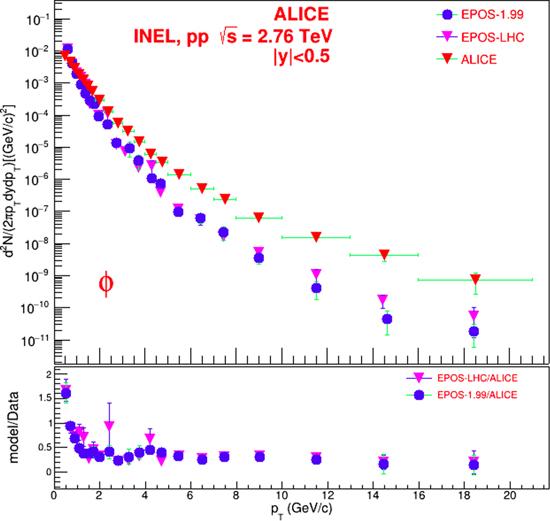
We studied the behavior of yields for the K^*0 (892) and φ (1020) mesons as a function of p_T in pp (figures 1 and 3) and Pb-Pb (figures 2 and 4) collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The central rapidity region, ∣y∣<0.5 was chosen for particle production. The transverse momentum of the particles was limited to values of 0<p_T <15 GeV c⁻¹ in the case of pp collisions and 0<p_T <20 GeV c⁻¹ in the case of Pb-Pb collisions for φ-mesons. We used two models to perform simulations, namely EPOS-1.99 and EPOS-LHC. The simulated data was compared to the experimental data from the ALICE experiment at the LHC, obtained from hepdata [4].

Figure 1.

New window|Download| PPT slide
Figure 1.Invariant yield of φ (1020) mesons in pp collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The statistical uncertainties and the systematic uncertainties are obvious for the simulated and experimental data respectively.

The behavior of R_AA was studied for the most central region, 0%-5% of the centrality class (figure 2 for φ-mesons and figure 4 for K^*0-mesons); figure 5. Shows the behavior of R_AA for K^*0-mesons and figure 6 does the same for φ-mesons.

One can see from figure 1 that the EPOS-LHC predictions are systematically higher than for EPOS-1.99, and are closer to the experimental data for φ-meson production in pp collisions. Moreover, at low values of p_T (p_T <1.0 GeV c⁻¹) they are overestimated, while at high values of p_T, we see an underestimate compared to the ALICE data. With increasing p_T , the difference between the model descriptions and the experimental data essentially increases.

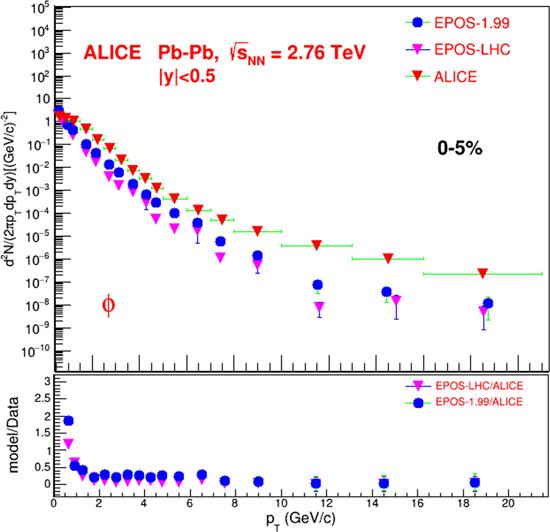
For the most central Pb-Pb collisions (see figure 2), the EPOS-1.99 predictions are again systematically higher than for EPOS-LHC and closer to the experimental data. Again, at p_T <1.0 GeV c⁻¹, the model predictions are higher than the experimental data; at p_T >1.0 GeV c⁻¹, one can see that the model’s predictions are lower, and with increasing p_T, the difference between the model predictions and the experimental data increases.

Figure 2.

New window|Download| PPT slide
Figure 2.Invariant yield of φ (1020) mesons in the most central class of 0%-5%, in Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The statistical uncertainties and the systematic uncertainties are obvious for the simulated and experimental data respectively.

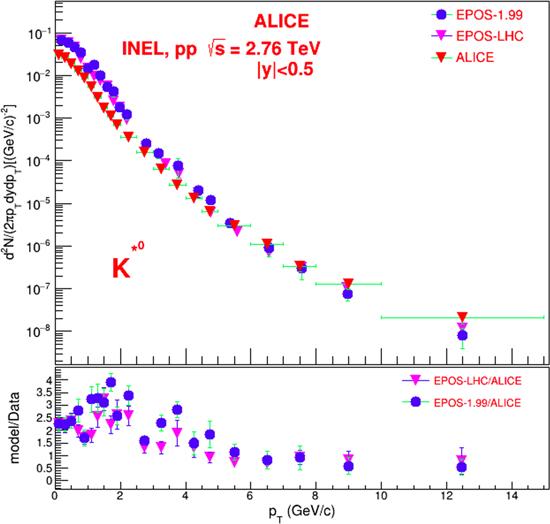
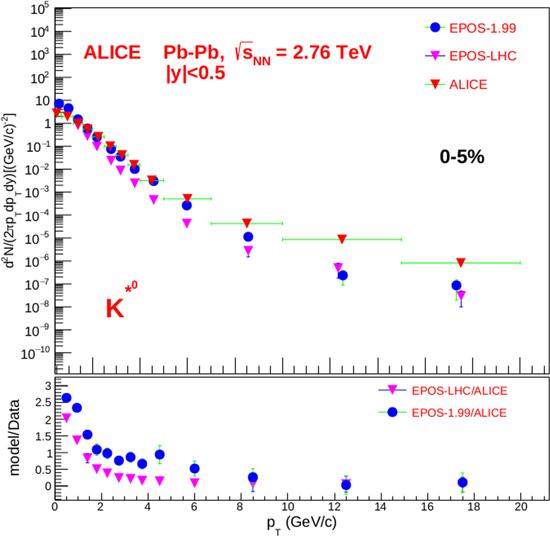
Overall, one can conclude that for soft interactions (at p_T <1.0 GeV c⁻¹), both models overestimate the φ-meson production, but for the high p_T region (for the hard interactions), they give low predictions. We think that this could be connected with the essential role of collective parton behaviors in the high p_T region which could not have been accounted for by the models, because for the production of massive particles such as φ-mesons, collective effects have to be essential. Figure 3 shows the yields of K^*0 from pp collisions as a function of p_T, obtained from the simulation models and the ALICE experiment. One can see that both programs give almost the same predictions and with values of p_T in the interval of p_T >3 GeV c⁻¹, the predictions become very close to the experimental results. Again, we can see that both models give the same predictions for the soft p_T interval (p_T <3 GeV c⁻¹), but for 0%-5% central Pb-Pb collisions (see figure 4), the situation changes.

Figure 3.

New window|Download| PPT slide
Figure 3.Invariant yield of K^*0 (892) in pp collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The statistical uncertainties and the systematic uncertainties are obvious for the simulated and experimental data, respectively.

Figure 4.

New window|Download| PPT slide
Figure 4.Invariant yield of K^*0 (892), mesons in the most central class of 0%-5%, in Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. The statistical uncertainties and the systematic uncertainties are obvious for the simulated and experimental data respectively.

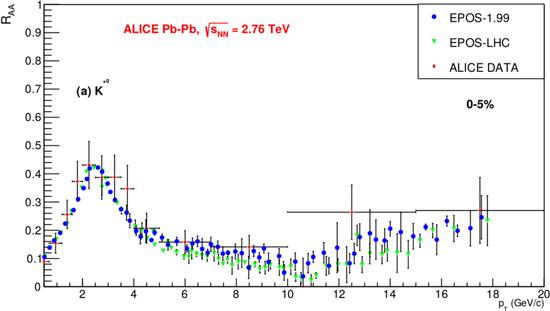
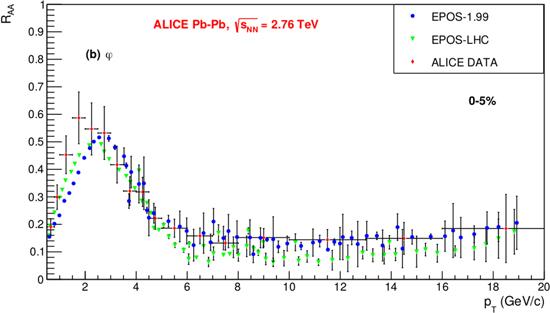
To get additional information to confirm the above results, we studied R_AA as a function of p_T. Figures 5 and 6 show the R_AA distributions for K^*0 and φ-mesons in the 0%-5% centrality class for Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV. These results for the R_AA of the K^*0 and φ-mesons obtained from EPOS-LHC and EPOS-1.99 are compared to the distribution of the ALICE experiment. It is necessary to note that the systematic and statistical errors of the experimental data are too high to do any quantitative comparisons with the simulation data. However, one can say that both R_AA distributions are lower than unity and both the EPOS-LHC and EPOS-1.99 models are very close to the ALICE data. It is very interesting that although the models were not able to describe the original p_T distributions, they gave good predictions for their ratios. The reason for that could be the existence of a dynamic in both the pp and Pb-Pb collisions which was not able to be described by the models; this dynamic could be the collective partonic behavior.

Figure 5.

New window|Download| PPT slide
Figure 5.Nuclear modification factor (R_AA) distributions for K^*0 (892), in the most central class, 0%-5%, at $\sqrt{{s}_{NN}}$=2.76 TeV.

Figure 6.

New window|Download| PPT slide
Figure 6.Nuclear modification factor (R_AA) distributions for φ(1020), in the most central class of 0%-5%, at $\sqrt{{s}_{NN}}$=2.76 TeV.

The distribution of R_AA could be considered as an additional confirmation that the role of the particle mass is essential at low p_T intervals, i.e. for soft interactions. The distribution of R_AA as a function of p_T in central Pb-Pb collisions is significantly suppressed, in comparison to pp collisions. In the range of p_T =5-10 GeV c⁻¹, the suppression is stronger than previously observed at the RHIC. From p_T =10 GeV c⁻¹ up to 20 GeV c⁻¹, R_AA shows a rising trend, as was shown by the data from the ALICE experiment. The Compact Muon Solenoid (CMS) measurement, with improved statistical precision, clearly shows that this rise continues at higher values of p_T, approaching a suppression factor for R_AA ≈0.5−0.6 in the range of 40-100 GeV c⁻¹. One can see that the last region is absent for φ-mesons. The T_AA value used for the calculation of R_AA was38.124 (1/26.23 mb).

Conclusions

We studied the production of K^*0 and φ-mesons in inelastic pp collisions and Pb-Pb collisions at $\sqrt{{s}_{NN}}$=2.76 TeV using the Monte Carlo simulation programs EPOS-LHC and EPOS-1.99. The simulated data was compared with the ALICE experimental data. The results obtained show that the model’s predictions at $\sqrt{{s}_{NN}}$=2.76 TeV for φ-meson production in pp collisions and in most of the central Pb-Pb collisions disagreed with the ALICE data. The differences between the model descriptions and experimental data essentially increased with p_T. For soft interactions (p_T <1.0 GeV c⁻¹), the models gave higher predictions, while for the hard interactions (high p_T), the models underestimated. This could be connected to the essential role of collective parton behaviors in the high p_T region, which was not accounted for by the models. For the production of massive particles such as φ-mesons, collective effects have to be essential. The conclusions seem to be confirmed by the data obtained for the behavior of the yields of K^*0 mesons. For these mesons, both programs gave almost the same predictions and for the p_T interval of p_T >3 GeV c⁻¹, the predictions became very close to the experimental results. Again, both models gave higher predictions for the soft p_T interval (p_T <3 GeV c⁻¹). The values of the R_AA distributions were lower than unity and both models were very close to the ALICE data. The distribution of R_AA for K^*0 was lower than than for the φ mesons. This additional suppression of K^*0 at low values of p_T with respect to the φ-mesons can be considered as an additional confirmation that the role of particle mass is essential at low p_T intervals, for soft interactions. The rising trend for R_AA in the region from p_T =10 GeV c⁻¹ to 20 GeV c⁻¹ which was observed by the ALICE experiment is absent for the φ-mesons.

Acknowledgments

We would like to acknowledge COMSATS University, Islamabad, Pakistan, which provided all possible facilities and a suitable platform to perform the simulations and analysis.