Effects of nuclear charge fluctuations on dilepton photoproduction

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

Guansong Li¹, Kai Zhou², Baoyi Chen^,¹^,³¹Department of Physics, Tianjin University, Tianjin 300350, China
²Frankfurt Institute for Advanced Studies, Ruth-Moufang-Straße 1, D-60438 Frankfurt am Main, Germany
³Institut für Theoretische Physik, Goethe-Universität Frankfurt, Max-von-Laue-Str. 1, D-60438 Frankfurt am Main, Germany

Received:2019-08-7Revised:2019-09-3Accepted:2019-10-31Online:2020-01-22

Abstract
Fluctuations of dilepton production from two photon interactions $\gamma \gamma \to {l}^{+}{l}^{-}$ are studied in semi-central and peripheral nuclear collisions. Based on the Weizsäcker–Williams approach, electromagnetic (EM) fields generated by moving nuclear charges are approximated as quasi-real photons. As fluctuating EM fields in each collision event are hard to be measured directly in experiments due to its short lifetime, we study the dilepton photoproduction with fluctuating EM fields, which are crucial for the EM fields induced chiral and charged particle evolutions, and calculate the relative standard deviation of the dilepton mass spectrum with the event-by-event fluctuating nuclear charge distributions. This fluctuation effect becomes smaller in more peripheral collisions where the shift of proton positions is implicit for EM fields outside the nucleus. The uncertainty of effective impact parameter Δb on the standard deviation is also studied, and its effect is around one-third of the effect of nuclear charge fluctuations when Δ b is taken as ∼1 fm.
Keywords： heavy ion collisions;photoproduction;quark gluon plasma

PDF (461KB)Metadata Metrics Related articlesExportEndNote|Ris|Bibtex Favorite
Cite this article
Guansong Li, Kai Zhou, Baoyi Chen. Effects of nuclear charge fluctuations on dilepton photoproduction. Communications in Theoretical Physics, 2020, 72(2): 025301- doi:10.1088/1572-9494/ab5cff

In relativistic heavy ion collisions, one of the main goals is to study the properties of the deconfined matter, called ‘Quark-Gluon Plasma’ (QGP) produced in the hadronic collisions of two nuclei [1–3]. In QGP, a huge number of light partons are excited and increase the energy density of hot medium in the colliding area. They expand outward violently due to the large spatial gradient of the pressure [4]. The evolutions of light partons with electric charge and chirality are believed to be controlled by the strong interactions. In another aspect, nuclei with electric charges Ze (e is the electron charge) are accelerated to near the speed of light, and generate extremely strong electromagnetic (EM) fields with a short lifetime ∼2R_A/γ_L [5–7], where R_A and γ_L are the nuclear radius and the Lorentz factor of fast moving nucleons. Besides nuclear hadronic collisions, these EM fields can also interact with the target nucleus (moving in the opposite direction) [8–11] or the other EM fields generated by the target nucleus [12–17]. These reactions have been extensively studied in the ultra-peripheral collisions (UPCs) absent of hadronic collisions [15, 18–22]. The EM fields can reach its maximum value at the order of ${eB}\sim 10{m}_{\pi }^{2}$ [6] in the semi-central and peripheral collisions with the impact parameter around b∼10 fm at the colliding energies of Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC).

In the semi-central collisions with the existence of both deconfined medium and strong EM fields, the EM fields can affect the evolutions of charged and chiral partons in the early stage of the hot medium expansion, such as chiral magnetic effect (CME) [23] and electric seperation effect (CSE) [24]. However, with the background of strong collective expansions driven by the pressure gradient, electric/magnetic field-induced parton evolutions are contaminated and difficult to be quantified with the final hadron spectra [25, 26]. Especially, nuclear proton fluctuating distributions generate non-zero fluctuating EM fields and affect the theoretical calculations of CME in comparison with experimental data. The quantitative signals of these effects in heavy ion collisions are still under debate. Whether these effects are observable or not depends sensitively on the magnitude and fluctuations of the initial electromagnetic fields. These electromagnetic fields can also produce vector mesons (J/$\Psi$, φ, et al) and dileptons (${e}^{+}{e}^{-}$, ${\mu }^{+}{\mu }^{-}$) [27], which have been widely studied in UPCs and is in good agreement with the lowest order quantum electrodynamics calculations. In semi-central nuclear collisions of RHIC and LHC energies, experiments have observed the significant yield enhancement of dileptons at the invariant mass of J/$\Psi$, with the feature only in extremely low transverse momentum p_T<0.3 GeV/c [10]. This enhancement is far above the hadronic contributions, and is attributed to the coherent photon-nuclear interactions: EM fields are approximated as quasi-real photons (the Weizsäcker–Williams method) [28, 29] which scatter with the target nucleus moving in the opposite direction and fluctuate into vector mesons [30, 31].

At the RHIC Au-Au and U-U collisions, experiments also observe a continuum enhancement of e⁺e⁻in the low invariant mass spectrum $0.4\ \mathrm{GeV}\lt {M}_{l\bar{l}}\lt 2.6\,\mathrm{GeV}$ with the limitation of p_T<0.15 GeV/c at the impact parameter b∼10 fm in their preliminary results [32]. The STAR continuum observables are compatible with the two-photon production contribution. This indicates that dilepton photoproduction dominates the yield in the low invariant mass region even with hadronic collisions [17]. In this work, we focus on the fluctuations of dilepton photoproduction with fluctuating EM fields, which is considered as an important input for the particle evolutions in QGP.

With large Lorentz factor ${\gamma }_{L}\sim \sqrt{{s}_{{NN}}}/(2{m}_{N})$ where m_N and $\sqrt{{s}_{{NN}}}$ are the nucleon mass and the colliding energy, the transverse electric fields of the fas-moving nucleus are enhanced by the Lorentz factor, ${E}_{T}^{i}={\gamma }_{L}{E}_{T}^{i-{RF}}$. And their magnitude is similar with the magnetic fields, $| {E}_{T}^{i}| \approx | {B}_{T}^{i}| $ (i = nucleus 1 or 2). Here ${E}_{T}^{i-{RF}}$ is the electric fields in the nuclear rest frame. Meanwhile, the longitudinal component is correspondingly suppressed and therefore negligible. These transverse electromagnetic fields can be approximated to be a swarm of quasi-real photons moving longitudinally [33]. The configuration of EM fields depends on the form factor, which is the Fourier transform of the nuclear charge density,(1)$\begin{eqnarray}F({\boldsymbol{q}})=\int {\rho }_{\mathrm{Au}}({\boldsymbol{r}})\exp ({\rm{i}}{\boldsymbol{q}}\cdot {\boldsymbol{r}}){\rm{d}}{\boldsymbol{r}}\end{eqnarray}$where ρ_Au(r) is the normalized nucleon distribution of Au, $\int {\rm{d}}{\boldsymbol{r}}{\rho }_{\mathrm{Au}}({\boldsymbol{r}})=1$. The photon spectrum is determined by the conservation of energy flux through the transverse plane, $\int {\rm{d}}{t}{\rm{d}}{{\boldsymbol{x}}}_{T}| {{\boldsymbol{E}}}_{T}\times {{\boldsymbol{B}}}_{T}| =\int {\rm{d}}{w}{\rm{d}}{{\boldsymbol{x}}}_{T}{wn}(w,{{\boldsymbol{x}}}_{T})$ with the definition $n(w,{{\boldsymbol{x}}}_{T})\equiv {{\rm{d}}{N}}_{\gamma }/({\rm{d}}{w}{\rm{d}}{{\boldsymbol{x}}}_{T})$. The photon density as a function of transverse coordinate x_T and photon energy w is written as(2)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{{{\rm{d}}}^{2}{{N}}_{\gamma }}{{\rm{d}}{w}{\rm{d}}{{\boldsymbol{x}}}_{T}}=\displaystyle \frac{{Z}^{2}\alpha }{4{\pi }^{3}w}\\ \ \ \times \,| {\int }_{0}^{\infty }{{\rm{d}}{k}}_{T}{k}_{T}^{2}\displaystyle \frac{F\left({{\boldsymbol{k}}}_{T}^{2}+{\left(\tfrac{w}{{\gamma }_{L}}\right)}^{2}\right)}{{{\boldsymbol{k}}}_{T}^{2}+{\left(\tfrac{w}{{\gamma }_{L}}\right)}^{2}}{J}_{1}({x}_{T}{k}_{T}){| }^{2}\end{array}\end{eqnarray}$with $\alpha ={e}^{2}/({\hslash }c)=(4\pi )/137$. w and k_T is the photon energy and transverse momentum respectively. J₁ is the first kind of Bessel function. In the collisions with b<2R_A, protons in the overlap area of two nuclei are partially decelerated after nuclear hadronic collisions, and the electric charge distributions in the overlap area also deviate from Woods–Saxon distributions. Meanwhile, the strong EM pulse from one nucleus can break the other target nucleus (called Coulomb dissociation [14]) and change its nuclear charge distribution. We neglect these effects on nuclear charge distributions and focus on the fluctuations of proton positions in the nucleus. The centers of protons satisfy the Woods–Saxon distribution,(3)$\begin{eqnarray}{\rho }_{\mathrm{Au}}({\boldsymbol{r}})=\displaystyle \frac{{\rho }_{0}}{1+\exp \Space{0ex}{1.9ex}{0ex}(\tfrac{r-{r}_{0}}{a}\Space{0ex}{1.9ex}{0ex})}\end{eqnarray}$with ${\rho }_{0}=\tfrac{0.169\,4}{{A}_{\mathrm{Au}}}$ ${\mathrm{fm}}^{-3}$, r₀=6.38 fm and a=0.535 fm. For the fluctuating distributions of electric charges (or protons) in the nucleus, we generate each proton position with equation (3) by Monte Carlo simulations in each colliding event [6]. The protons in the nucleus are not taken as point charge, instead, they are treated with a finite size to avoid the singularities in EM fields and the photon spatial densities. Lack of solid constraints on proton electric charge distribution, it can be treated as Gaussian [34] or even a disk-like distribution. Different smooth distributions for the proton does not contribute to the standard deviation of dilepton photoproduction, however, with Monte Carlo simulations, the fluctuations of dilepton photoproduction will be affected. Here for consistency we take equation (3) for charge distribution in the proton with different parameters, which makes proton shape a little ‘fatter’ than the situation of Gaussian function [34]. The proton electric charge distribution is(4)$\begin{eqnarray}{\rho }_{p}({\boldsymbol{r}})=\displaystyle \frac{{\rho }_{p0}}{1+\exp \left(\tfrac{r-{r}_{p0}}{{a}_{p}}\right)}\end{eqnarray}$where the origin of the coordinate is put at the center of the proton. r_p0=1.2 fm and a_p=a describe the mean radius and also shape of a proton. ρ_p0=0.045 8 ${\mathrm{fm}}^{-3}$ is fixed by the normalization of equation (4) to be a unit. With this method, the mean value of fluctuating nuclear charge distributions slightly deviate from the Woods–Saxon distribution. This difference is relatively small in the standard deviation of dilepton photoproduction.

After randomly generating proton positions with Monte Carlo method in the nucleus, the fluctuating charge densities in the nucleus can be written as(5)$\begin{eqnarray}{\rho }_{\mathrm{fluct}}({\boldsymbol{r}})=\displaystyle \sum _{i=1}^{Z}{\rho }_{p}({\boldsymbol{r}}-{{\boldsymbol{r}}}_{i})\end{eqnarray}$where r_i is the position of each proton relative to the nuclear center. The fluctuations of proton positions are in three dimensions, where electromagnetic fields generated by ρ_fluct(r) are not symmetric anymore and therefore are not suitable for the present Weizsäcker–Williams approach. Radial fluctuations of proton positions do not shift the center of all protons in the nucleus. Angular fluctuations will make the center of proton positions deviate from the center of the nucleus. Therefore, the distance between two centers of proton positions in two nuclei will be changed by angular fluctuations, which is like employing a different impact parameter b to calculate the electromagnetic fields in nucleus–nucleus collisions. Note that the angular fluctuations can shift the center of protons in a nucleus less than around 0.5 fm. In this work, we integrate ρ_fluct(r) over the angular variables and obtain the raidal fluctuating distributions in figure 1. The effects of angular fluctuations on the standard deviation of dilepton photoproduction are included by the fluctuations of impact parameter (see the figure below). In the following studies about standard deviation of dilepton photoproduction, we compare the situations of fluctuating distributions (dashed and dotted-dashed lines in figure 1) and the smooth distribution (solid line in figure 1).

Figure 1.

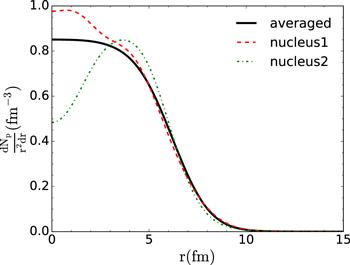New window|Download| PPT slide
Figure 1.Nuclear charge fluctuations in event-by-event MC simulations. The fluctuating electric charge densities (dashed and dotted-dashed lines) in nucleus 1 and nucleus 2 are independent from each other, and deviate from the averaged distribution (solid line).

With photon density n(w, x_T) ≡ d³N_γ/(dwdxdy) at the transverse coordinate x_T=r=(x, y), we can calculate the dilepton production from two-photon scatterings, $\gamma \gamma \to l\bar{l}$ (see figure 2). The EM fields from the nucleus spread over the entire transverse plane, which makes quasi-real photons also distribute over the entire transverse plane, including the area inside the nucleus and hadronic collision zone. Therefore, the spatial integration of $\gamma \gamma \to l\bar{l}$ is over the entire transverse plane, see equation (6). Now we write the dilepton photoproduction in Au-Au collisions with the impact parameter b<2R_A as below,(6)$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{{\rm{d}}{N}}{{{\rm{d}}{M}}_{l\bar{l}}} & = & {\displaystyle \int }_{-\infty }^{+\infty }{\rm{d}}{Y}{\displaystyle \int }_{0}^{2\pi }{\rm{d}}\theta {\displaystyle \int }_{0}^{+\infty }{r}{\rm{d}}{r}\\ & & {n}_{1}({w}_{1},{r}_{1}){n}_{2}({w}_{2},{r}_{2}){\sigma }_{\gamma \gamma \to l\bar{l}}\displaystyle \frac{{M}_{\gamma \gamma }}{2}\end{array}\end{eqnarray}$where $Y=1/2\mathrm{ln}({w}_{1}/{w}_{2})$ and ${M}_{l\bar{l}}=2\sqrt{{w}_{1}{w}_{2}}$ are determined by the energies of two scattering photons w₁ and w₂. The distance between the scattering position and two nuclear centers are ${r}_{1}=\sqrt{{b}^{2}/4+{r}^{2}-2{br}\cos \theta }$ and ${r}_{2}\,=\sqrt{{b}^{2}/4+{r}^{2}+2{br}\cos \theta }$ respectively, and r is the coordinate of the scattering in figure 2. The cross section of two-photon scattering is extracted by the Breit–Wheeler formula [35],(7)$\begin{eqnarray}\begin{array}{l}{\sigma }_{\gamma \gamma \to l\bar{l}}=\displaystyle \frac{4\pi {\alpha }^{2}}{{M}_{l\bar{l}}^{2}}\left[\left(2+\displaystyle \frac{8{m}^{2}}{{M}_{l\bar{l}}^{2}}-\displaystyle \frac{16{m}^{4}}{{M}_{l\bar{l}}^{4}}\right)\right.\\ \ \ \ \left.\times \ \mathrm{ln}\left(\displaystyle \frac{{M}_{l\bar{l}}+\sqrt{{M}_{l\bar{l}}^{2}-4{m}^{2}}}{2m}\right)-\sqrt{1-\displaystyle \frac{4{m}^{2}}{{M}_{l\bar{l}}^{2}}}\left(1+\displaystyle \frac{4{m}^{2}}{{M}_{l\bar{l}}^{2}}\right)\right]\end{array}\end{eqnarray}$where m is the lepton mass and ${M}_{l\bar{l}}$ is the invariant mass of the dilepton.

Figure 2.

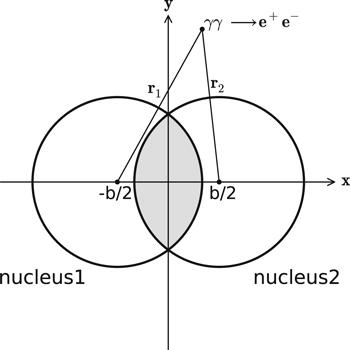New window|Download| PPT slide
Figure 2.Schematic diagram for two-photon scatterings $\gamma \gamma \to f\bar{f}$ (f is fermion) in the nuclear collisions. b is the impact parameter. The electric charges in the overlap area do not contribute to the two-photon scatterings. The origin of coordinates is set in the middle of two nuclear centers.

We take the radial fluctuating charge distribution ρ_fluct(r) to calculate the photon densities and the dilepton photoproduction in RHIC $\sqrt{{s}_{{NN}}}=200\,\mathrm{GeV}$ Au-Au collisions. In peripheral collisions without hadronic collisions, dilepton production come from the interactions of EM fields generated by two nuclei. In the semi-central collisions b∼10 fm, the dilepton final yields consist of photoproduction from two-photon scatterings and thermal emission from QGP. In the low invariant mass spectrum, dilepton production is dominated by the photoproduction in semi-central and peripheral collisions [36], and we neglect the contribution of QGP, which is the main source at the larger invariant mass region. The fluctuations of proton positions in the nucleus are random. With different charge distributions in each event of Au-Au collisions, the strength of EM fields is different. Considering that dilepton photoproduction is a scalar observable, the average of dilepton yields over many events will partially eliminate the effects of fluctuations. Therefore, we evaluate the relative standard deviation of dilepton production, $\tfrac{\sqrt{\langle {(X-\langle X\rangle )}^{2}\rangle }}{\langle X\rangle }$. Here $X\equiv {\rm{d}}{N}/{{\rm{d}}{M}}_{{e}^{+}{e}^{-}}$ is the dilepton production in one configuration of fluctuating EM fields, and $\langle X\rangle $ is the averaged yield over many events. This observable is weakly affected by the form of two-photon scattering cross sections ${\sigma }_{\gamma \gamma \to l\bar{l}}$ which appears in both the numerator and denominator, and is mainly attributed to the fluctuations of photon densities (or EM fields). The ratio is around (4∼6)% at b∼10 fm in the experimentally measurable region of invariant mass $0.4\lt {M}_{{e}^{+}{e}^{-}}\lt 2\,\mathrm{GeV}$, see figure 3. With a larger impact parameter, the effect of this fluctuation becomes smaller, as the two nuclei are far away from each other and fluctuations of proton positions become implicit for the EM fields outside the nucleus.

Figure 3.

New window|Download| PPT slide
Figure 3.Relative standard deviation $\tfrac{\sqrt{\langle {\left(X-\langle X\rangle \right)}^{2}\rangle }}{\langle X\rangle }$ for dilepton photoproduction with event-by-event fluctuating EM fields as a function of invariant mass at RHIC $\sqrt{{s}_{{NN}}}=200\,\mathrm{GeV}$ Au-Au collisions with impact parameter b=10, 12, 15 fm (solid, dashed, dotted-dashed lines). The rapidity cut of the dileptons is taken as $| {y}_{{e}^{+}{e}^{-}}| \lt 1$. And $X\equiv {\rm{d}}{N}/{{\rm{d}}{M}}_{{e}^{+}{e}^{-}}$ is the dilepton spectrum.

In realistic nuclear collisions, impact parameter b is almost unable to be determined with an exact value in experimental measurements. A certain range of b is often given for experimental data. We calculate the fluctuations of dilepton photoproductions in many events with different values of b. In figure 4, relative standard deviations of photoproduction is calculated with averaged charge distribution (solid line in figure 1) and random b at 10<b<11 fm. In this small range, the value of b can be treated as uniformly random at 10∼11 fm. The uncertainty of b contributes around (1∼2)% to the standard deviation. This magnitude is smaller that the effect of proton position fluctuations with b=10 fm (black solid line in figure 3). In the final complete analysis, both proton fluctuations and b uncertainty need to be considered, and the maximum value of standard deviation can be around (5∼7)% depending on the choice of b. However, if the experimental data can only measure a set of a few events without identifying each event, this partially averaged data will present a smaller fluctuation effect.

Figure 4.

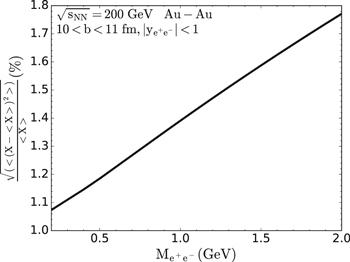New window|Download| PPT slide
Figure 4.Relative standard deviation $\tfrac{\sqrt{\langle {\left(X-\langle X\rangle \right)}^{2}\rangle }}{\langle X\rangle }$ for dilepton photoproduction due to the uncertainties of impact parameter as a function of invariant mass at RHIC $\sqrt{{s}_{{NN}}}=200\,\mathrm{GeV}$ Au-Au collisions. The impact parameter locates randomly at 10<b<11 fm. The rapidity cut of dileptons is $| {y}_{{e}^{+}{e}^{-}}| \lt 1$. The nuclear charge distribution is taken to be the smooth situation in figure 1. X $\,\equiv {\rm{d}}{N}/{{\rm{d}}{M}}_{{e}^{+}{e}^{-}}$ is the dilepton spectrum.

In summary, we calculate the fluctuations of dilepton photoproduction from event-by-event fluctuating electromagnetic fields in peripheral and semi-central collisions. In the low invariant mass region and close-to-peripheral collisions, the dilepton yields from hot medium radiation produced in the nuclear hadronic collisions are relatively small compared with the contribution of EM fields. We simulate the fluctuations of proton positions in the nucleus with the Monte Carlo method, which results in event-by-event fluctuating electromagnetic fields. We calculate the standard deviation of dilepton photoproduction $\tfrac{\sqrt{\langle {(X-\langle X\rangle )}^{2}\rangle }}{\langle X\rangle }$ of their yields with $X\equiv {\rm{d}}{N}/{{\rm{d}}{M}}_{l\bar{l}}$. Its value is mainly determined by the spatial configurations of quasi-real photons (or EM fields), which can help revealing the fluctuations of initial EM fields in the nuclear collisions. Also, we study the uncertainties of impact parameter on photoproduction. This effect is smaller than the effects of nuclear charge fluctuations. These theoretical results help to connect the configurations of initial EM fields in AA collisions with final experimental signals.

Acknowledgments

BC acknowledges helpful discussions with Enrico Speranza. This work is supported by NSFC Grant No. 11705125, 11547043 and the Sino-Germany (CSC-DAAD) Postdoc Scholarship. KZ kindly acknowledges support by the AI grant of SAMSON AG, Frankfurt.