Masood Khan¹, Aamir Hamid^,1,*, Hashim²1 Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
2 Department of Mathematics & Statistics, Riphah International University, Islamabad, Pakistan

Corresponding authors: *E-mail:aamirhameed@math.qau.edu.pk

Received:2019-07-22Online:2019-12-1


Abstract
The current investigation highlights the mixed convection slip flow and radiative heat transport of uniformly electrically conducting Williamson nanofluid yield by an inclined circular cylinder in the presence of Brownian motion and thermophoresis parameter. A Lorentzian magnetic body force model is employed and magnetic induction effects are neglected. The governing equations are reduced to a system of nonlinear ordinary differential equations with associated boundary conditions by applying scaling group transformations. The reduced nonlinear ordinary differential equations are then solved numerically by Runge-Kutta-Fehlberg fifth-order method with shooting technique. The effects of magnetic field, Prandtl number, mixed convection parameter, buoyancy ratio parameter, Brownian motion parameter, thermophoresis parameter, heat generation/absorption parameter, mass transfer parameter, radiation parameter and Schmidt number on the skin friction coefficient and local Nusselt are analyzed and discussed. It is found that the velocity of the fluid decreases with decrease in curvature parameter, whereas it increases with mixed convection parameter. Further, the local Nusselt number decreases with an increase in the radiation parameter. The numerical comparison is also presented with the existing published results and found that the present results are in excellent agreement which also confirms the validity of the present methodology.
Keywords： MHD;Williamson nanofluid;velocity and thermal slip;inclined stretching cylinder;heat generation/absorption


PDF (783KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Masood Khan, Aamir Hamid, Hashim. Effects of Thermal Radiation and Slip Mechanism on Mixed Convection Flow of Williamson Nanofluid Over an Inclined Stretching Cylinder. [J], 2019, 71(12): 1405-1415 doi:10.1088/0253-6102/71/12/1405

Nomenclature

1 Introduction

With the fast developing innovation, various high-tech industries, such as manufacturing, microelectronics and transportation are facing a problem of limiting cooling efficiency of heat transport liquids as water, glycol, lubrications and oil, etc. Then again, rapid cooling is additionally a basic need in nourishment science and technology. The thermal properties of conventional fluids can be enhanced by using dilute suspension on nanoparticles into base fluids. This suspension which is termed as "nanofluid" is a relatively new class of fluids which comprise of a base liquid with nano-sized particles (1-100 nm) suspended with them, which is firstly presented by Choi.^[1] Buongiorno^[2] displayed an extensive study for heat transfer by convective in nanofluids. In this examination, the author presented a logical explanation for abnormal rise in heat transfer coefficient for such fluid. He says that the nanofluids properties change essentially inside the boundary layer and this is because the impact of thermophoresis and temperature gradients. In this way, these impacts cause a reduction of viscosity within the boundary layer and consequently the heat transfer is improved. Kuznetsov and Nield^[3] used Buongiorno's model to investigate the heat transfer by convective boundary layer induced by a vertical plate via nanofluids. They demonstrated that rate of heat transfer is a diminishing function of buoyancy-ratio, Brownian motion and thermophoresis parameters. Further, Khan and Makinde^[4] discussed the nanofluid bioconvection having gyrotactic micro-organisms due to a convectively heated stretched surface. Sandeep et al.^[5] studied the convective heat transfer in non-Newtonian nanofluid flow over a permeable stretching surface. Their outcomes indicate that Biot number rises the rate of heat transfer at the surface.

Moreover, Mabood et al.^[6] investigated the boundary layer low and heat transfer of nanofluids generated by a nonlinear stretching surface.They showed that Brownian motion and thermophoresis parameters enhance the temperature as well as thermal boundary layer thickness. The analysis of rotating low of nanofluids induced by an exponentially stretching surface is presented by Mushtaq et al.^[7] Additionally, Pourmehran et al.^[8] obtained the numerical solution of convective nanofluid flow generated by a stretching surface in the presence of thermal radiation and buoyancy effects. Their results show that rate of heat transfer has a reverse relation with growing nanoparticle concentration. Furthermore, Ahmad et al.^[9] numerically investigated the features of heat transfer of nanofluid flow over an exponentially stretching sheet. They analyzed that rate of heat transfer becomes smaller when strong magnetic field is employed. Jahan et al.^[10] considered the revised model approach while discussing the stagnation-point low along a permeable stretching sheet in a nanofluid. Valipour et al.^[11] examined the effects of thermal radiation on CNT-water nanofluid flow induced by a stretching sheet. They reported that temperature of the fluid rises with the higher values of heat generation and radiation parameters. Eid and Mahny^[12] examined unsteady boundary layer flow of a nanofluid over a permeable stretching surface. They accomplished that the rate of mass transfer at the wall is a decreasing function of magnetic field parameter.

Recently, Gupta et al.^[13] explored the impact of thermal radiation and chemical reaction on non-Newtonian nanofluid past an inclined stretching sheet. They reported that concentration profile of nanoparticles is a decreasing function of Lewis and Prandtl number. Further investigations have considered about heat transfer and nanofluid flow.^[14-16]

Magnetohydrodynamics (MHD) is the investigation of the intricate collaboration between the magnetic field and electrically conducting fluids. The MHD of boundary-layer flow past a surface which stretches linearly or non-linearly has been broadly inspected as a result of its few modern applications in different mechanical and chemical industries. The combined effects of buoyancy force, Brownian motion, thermophoresis, magnetic field and convective heating on stagnation-point flow and heat transfer due to a nanofluid flow past a stretching or shrinking sheet are investigated by Makinde et al.^[17] Mukhopadhyay and Mandal^[18] discussed the effects of velocity and thermal slip on MHD mixed convection flow past a permeable sheet. They analyzed that increasing suction parameter declines the surface temperature. Fersadou et al.^[19] studied numerically the problem of MHD mixed convection around a porous channel in the presence of nanofluid. They found that heat transfer rate is increased with the higher nanoparticles volume fraction.Hayat et al.^[20] examined the characteristics of MHD mixed convection flow of Ag-water nanofluid past an inclined stretched cylinder in the presence of nonlinear thermal radiation. Later, Waqas et al.^[21] addressed the MHD flow of icropolar fluid over a nonlinear stretching sheet by considering viscous and Joule dissipation effects. Their study reveals that the temperature of the fluid and related boundary layer thickness increases with the enhancement in Prandtl number. In an another paper, Ibrahim et al.^[22] explored the magnetic field and mixed convection effects on Casson nanofluid over a nonlinear stretching sheet. They reported that the local skin friction coefficient decline with Casson parameter. Haq et al.^[23] explored the different aspects of MHD mixed convection flow along a vertical stretching sheet. They illustrated that velocity of the fluid increases with the rising values of power index. Further, Daniel et al.^[24] examined the MHD mixed convection unsteady flow induced due to nanofluid past a permeable stretching surface. Their investigation show that the buoyancy ratio parameter declined the thermal and concentration profiles. Very recently, Sharma et al.^[25] examined the MHD mixed convective low past a vertical stretched surface in the presence of heat generation/absorption effects. Their results indicated that rate of heat transfer increases due to rise in velocity ratio parameter.

Flow past a stretching cylinder was addressed by Wang.^[26] Latterly, Ishak et al.^[27] studied numerically the flow and heat transfer outside a permeable stretching cylinder by using Keller-box method. Their investigation show that water is a better cooling agent comparatively to air. Vajravelu et al.^[28] analyzed the effects of axisymmetric magneto-hydrodynamic flow and heat transfer induced by a non-isothermal stretching cylinder with internal heat source/sink effects. They revealed that heat generation/absorption parameter increases the temperature field in both the PST and the PHF cases. In another article, Butt and Ali^[29] presented the numerical solution of entropy generation and MHD flow and heat transfer past a stretching cylinder. They examined that the magnetic field increases the entropy production rate. Abbas et al.^[30] considered the laminar flow of a viscous fluid and heat transfer features due to a permeable stretching/shrinking cylinder. Their study explain that the magnitude of skin friction increases with higher velocity slip parameter. Hayat et al.^[31] carried out analysis of convective heat and mass transfer in the boundary layer flow due to an inclined stretching cylinder. They reported that the Eckert number increases the thermal and concentration boundary layer thicknesses. Khan and Malik^[32] have studied the heat transport characteristics of Sisko nanofluid over a stretching cylinder in the presence of variable thermal conductivity. They accomplished that thermophoresis parameter enhances the thermal and concentration boundary layer thickness. Recently, Pandey and Kumar^[33] have examined the effect of Cu-water nanofluid generated by a stretching cylinder. Their study indicate that the local Nusselt number is a decreasing function of porosity parameter. Merkin et al.^[34] have considered the stagnation-point flow and heat transfer past an exponentially stretching cylinder. Nourazar et al.^[35] employed the Optimal Collocation method to find the approximate solution for the thermal flow of a nanofluid past a cylinder under the magnetic field effect.

This research article is arranged in the following ways. Section 2 illustrates the problem description and its non-dimensionalization for a Williamson nanofluid flow past an inclined stretching cylinder. Next section deals with the grid generation and numerical method to solve the flow-field equations. In the results and discussion Sec. 4, the transient two-dimensional flow-field profiles, average wall, heat and mass transfer rates are analyzed. Also, the heat function has been derived and non-dimensionalized based on Nusselt number. Finally, in Sec. 5 the concluding remarks are made.

2 Problem Formulation

In this study, we have considered two-dimensional Williamson nanofluid flow past a permeable stretching cylinder that makes an angle of $\Phi $ with horizontal axis as signified in Fig. 1 with velocity ${W_w} = {{{{W_0}z}/ {1 - \varepsilon t}}}$. The thermal radiation and heat generation/absorption effects are examined. We also consider the velocity and thermal slips for velocity and temperature profiles. It is further assume that the surface temperature of the circular cylinder is ${T_{w}}$ and temperature far away from the cylindrical surface is ${T_{\infty }}$,where $( {{T_{w}} > {T_{\infty }}} )$. Nanofluid is electrically conducting such that uniform magnetic field ${B_0}$ acts in the radial direction. Magnetic Reynolds number is assumed very small so that the induced magnetic field is ignored. The buoyancy force is induced due to temperature difference between the cylindrical surfaces and surrounding under the gravitational force, this tends to accelerate the flow in upward direction. The concentration of nanoparticles at surface is controlled by the condition ${D_B}({{{\partial C}/ {\partial r}}}) + ({{{{D_T}} /{{T_\infty }}}})({{{\partial T} / {\partial r}}}) = 0$ and ambient concentration is assumed ${C_\infty }$.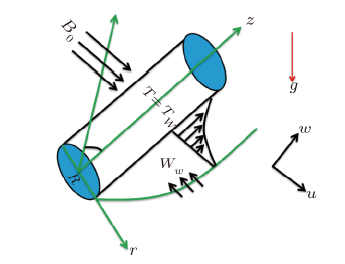

New window|Download| PPT slide
Fig. 1(Color online) Geometry of the model.



Invoking the above-mentioned frame of reference and assumptions, the governing flow equations included of mass, momentum and energy conservation can be written as

Continuity:

(1) $$ \frac{1}{r}\frac{{\partial ( {ru} )}}{{\partial r}} + \frac{{\partial w}}{{\partial z}} = 0\,, $$
Momentum equation:

(2) $$ \frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial r}} + w\frac{{\partial w}}{{\partial z}}\\\ \quad =\frac{\nu }{r}\frac{{\partial w}}{{\partial r}}\Big[ {{\beta ^ * }+ ( {1 - {\beta ^ * }} ){{\Big({1 - \Gamma \frac{{\partial w}}{{\partial r}}}\Big)}^{ - 1}}} \Big]\\\ \qquad + \nu \frac{{\partial ^{2}w}}{{\partial r^{2}}}\Big[ {{\beta ^ * } + ({1 - {\beta ^ * }} ){{\Big( {1 - \Gamma \frac{{\partial w}}{{\partial r}}}\Big)}^{ - 1}}} \Big]\\\ \qquad + \nu \Gamma \frac{{\partial w}}{{\partial r}}\frac{{\partial^{2}w}}{{\partial {r^2}}}\Big[ {( {1 - {\beta ^ * }} ){{\Big( {1 -\Gamma \frac{{\partial w}}{{\partial r}}} \Big)}^{ - 2}}} \Big]\\\ \qquad + \Big[ { - \frac{{( {{\rho _p} - \rho } )( {C - {C_\infty }} )}}{\rho } + ( {1 - {C_\infty }} )( {T - {T_\infty }})\lambda } \Big]\\\ \qquad - \frac{{\sigma {B_0^2}}}{\rho }w\,, $$
Energy equation:

(3) $ \frac{{\partial T}}{{\partial t}} + u\frac{{\partial T}}{{\partial r}} + w\frac{{\partial T}}{{\partial z}} = \frac{k}{{\rho {c_p}}}\Big({\frac{{{\partial ^2}T}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial T}}{{\partial r}}} \Big)\\\ \quad + \tau \Big[ {{D_B}\frac{{\partial C}}{{\partial r}}\frac{{\partial T}}{{\partial r}} + \frac{{{D_T}}}{{{T_\infty }}}{{\Big({\frac{{\partial T}}{{\partial r}}} \Big)}^2}} \Big] \\\ \quad + \frac{{16{\sigma ^ * }T_\infty ^3}}{{3{k^ * }{{(\rho {C_p})}_f}}}\frac{{{\partial ^2}T}}{{\partial {r^2}}} + \frac{{{Q_0}}}{{\rho{C_p}}}( {T - {T_\infty }} )\,,$
Concentration equation:

(4) $$ \frac{{\partial C}}{{\partial t}} + u\frac{{\partial C}}{{\partial r}} + w\frac{{\partial C}}{{\partial z}} = \frac{{{D_B}}}{r}\frac{\partial }{{\partial r}}\Big( {r\frac{{\partial C}}{{\partial r}}} \Big) + \frac{{{D_T}}}{{{T_\infty }}}\frac{1}{r}\frac{\partial }{{\partial r}}\Big({r\frac{{\partial T}}{{\partial r}}} \Big)\,. $$
along with the boundary conditions

(6) $$ w(z,r) = \chi {W_w} + L\frac{{\partial w}}{{\partial r}}\Big[ {{\beta ^*} +( {1 - {\beta ^*}} ){{\Big( {1 - \Gamma \frac{{\partial w}}{{\partial r}}} \Big)}^{ - 1}}} \Big]\,, {u_w} = {u_w}(z)\,,\quad T = {T_w} + N\frac{{\partial T}}{{\partial r}}\,, {D_B}\frac{{\partial C}}{{\partial r}} + \frac{{{D_T}}}{{{T_\infty }}}\frac{{\partial T}}{{\partial r}} = 0 \ \ {\rm at} \ \ r =R \,, w(z,r) \to 0\,,\quad T \to {T_\infty }\,, \ \ C \to {C_\infty }\,, \ \ r \to \infty\,. $$
Here, $\chi $ is the stretching/shrinking parameter, $L$ and $N$ are the velocity and thermal slip factors, respectively.

To convert the governing equations in non-dimensional form, let us consider the following dimensionless variables and parameters:

(7) $$ \eta = \frac{{{r^2} - {R^2}}}{{2R}}{\Big( {\frac{{{W_w}}}{{\nu z}}}\Big)^{1/2}}\,,\quad \psi = {( {{W_w}\nu z})^{1/2}}Rf( \eta )\,,\\\ \theta ( \eta )=\frac{{T - {T_\infty }}}{{{T_w}- {T_\infty }}}\,,\quad \phi ( \eta )=\frac{{C-{C_\infty }}}{{{C_\infty }}}\,. $$
The dimensionless form of the momentum, energy and concentration equations for boundary layer flow using the dimensionless variables and parameters, defined in Eq. (7), can be derived as:

(10) $$ ( {1+2\gamma \eta } )[ {{\beta ^ * } +( {1-{\beta ^ *}} ){{(1 - Wef^{\prime \prime })}^{-2}}}]f^{\prime \prime \prime }+ff^{\prime \prime } \quad +2\gamma f^{\prime \prime }\Big[ {{\beta ^*} +( {1-{\beta ^*}} )\Big(1-\frac {{Wef^{\prime \prime }}}{2}\Big){{(1-Wef^{\prime \prime })}^{-2}}} ] \quad -A(f^{\prime }+\frac{\eta }{2}f^{\prime \prime } +1)-{M^2}({f^{\prime }}-1) \quad +\lambda (\theta +{N_r}\phi )\cos \Phi=0\,,\Big( {1 + \frac{4}{3}{R_d}} \Big)[ {( {1 + 2\gamma \eta })\theta^{\prime \prime } + 2\gamma \theta^{\prime }} ] + Pr \beta \theta +Pr( {1 + 2\gamma \eta } )({N_b}\theta^{\prime }\phi^{\prime }+ {N_t}{\theta^{\prime 2}}) - Pr A\frac{\eta }{2}\theta^{\prime }=0\,,( {1 + 2\gamma \eta } )\phi^{\prime \prime } + 2\gamma \phi^{\prime } + Scf\phi^{\prime }\quad + \frac{{Nt}}{{Nb}}[( {1 + 2\gamma \eta } )\theta^{\prime \prime } + 2\gamma \theta^{\prime }]-ScA\frac {\eta }{2}\phi^{\prime }= 0\,. $$
The relevant boundary conditions (5)--(6) after employing Eq. (7) are given as:

(11)$$ f(0) = s\,, \ f^{\prime }(0) = \chi +\alpha [ {{\beta ^ * } + (1 - {\beta^*}){{( {1 - Wef^{\prime \prime }(0)} )}^{ - 1}}} ]\,,\theta (0) = 1 + \delta {\theta ^{\prime }}(0),\quad Nb{\phi^{\prime }}( 0 ) + Nt\theta ^{\prime }(0) = 0\,,f^{\prime }(\infty )\to 0\,,\quad \theta (\infty )\to 0\,,\quad \phi (\infty )\to 0\,, $$
where primes indicate differentiation with respect to $\eta $, $We = {[{{{{W_0^3{z^2}{r^2}{\Gamma ^2}}/{{{(1 - εt)}^3}{R^2}\nu }}}} ]^{1/2}}$ the local Weissenberg number, $\gamma={( {{{\nu / {{W_0}{R^2}}}}} )^{1/2}}$ the curvature parameter, $\lambda = {{{{\beta g( {1 - {C_\infty }} )( {T - {T_\infty }} )} / {zW_0^2}}}} $ the mixed convection parameter, ${N_r} = {{{{( {{\rho _p} - \rho} ){C_\infty }} / [{\beta \rho ( {1 - {C_\infty }} )( {T- {T_\infty }} )}}}}] $ the nanofluid buoyancy ratio parameter, $M= {( {{{{\sigma B_0^2} / {\rho {W_0}}}}} )^{1/2}}$ the magnetic parameter, $Nt = {{{{\tau {D_B}({T_w} - {T_\infty })} / {\nu {T_\infty }}}}} $ the thermophoresis parameter, $Nb = ( {{{{\tau {D_B}C_\infty })} / {\nu }}} $ the Brownian motion parameter, $Pr = {{{{\mu {C_p}} / k}}} $ the Prandtl number, ${R_d} = {{{{4T_\infty ^3\sigma } / {k{k^ * }}}}} $ the radiation parameter, $Sc ={{{\nu / {{D_B}}}}} $ the Schmidt number, $A = {{{\epsilon / {{W_0}}}}} $ the unsteadiness parameter, ${\beta ^ * } = {{{{{\mu _\infty }}/ {{\mu _0}}}}} $ the ratio of viscosities, $s = { -{{{r{W_w}} / ({R\sqrt {{W_0}\nu } })}}} $ the mass suction/injection parameter, $\alpha = {L({{r / R}})\sqrt {{{{{W_0}} / \nu }}} } $ velocity slip parameter, $\delta = {N({{r / R}})\sqrt {{{{{W_0}} / \nu }}} } $ thermal slip parameter and $\beta = {{{{{Q_0}}/({\rho {C_p}{W_0}})}}} $ the heat eneration/absorption parameter.

It should be noted that other important characteristics of the present investigation are the physical quantities of engineering interest, i.e., the local skin friction coefficient and the local Nusselt number which are defined as follows:

(13) $$ {C_f} = \frac{{{\tau _w}}}{{\rho W_w^2}},\quad N{u_z} =\frac{{z{q_w}}}{{k( {{T_w} - {T_\infty }} )}} + {q_r}\,, $$
where ${\tau _{rz}}$ and ${q_w}$ are written as:

(14) $$ {\tau _w} = {\mu _0}\frac{{\partial w}}{{\partial r}}\Big[ {{\beta ^ * } + (1 -{\beta ^ * }){{\Big( {1 - \Gamma \frac{{\partial w}}{{\partial r}}} \Big)}^{ -1}}} \Big]\,,\\\ {q_w} = - k{\Big( {\frac{{\partial T}}{{\partial r}}}\Big)_{r = {r_0}}}\,, $$
thus, we get

(15) $$ e^{1/2}C_{f}=f^{\prime \prime }(0)[ {{\beta^*} + (1 - {\beta^* }){{( {1-Wef^{\prime \prime }(0)} )}^{-1}}} ]\,, \\\ e^{-1/2}Nu_{z} = -\Big( {1 + \frac{4}{3}R_d} \Big)\theta^{\prime }(0)\,, $$
where $Re = zW_{w}/\nu $ defines the local Reynolds number based on the stretching velocity ${W_w}( {z,t} )$.

3 Numerical Simulation

3.1 Computational Procedure

Shooting algorithm with Runge-Kutta-Fehlberg me-thod is utilized to compute the non-linear ordinary differential equations (8) to (10) with the boundary conditions (11) and (12). For this we set the system of first order differential equations by defining:

(16) $$ =u_{1}\,,\quad f^{\prime }= {u_2}\,, \quad f^{\prime \prime }= u_{3}\,,\quad \theta = u_{4}\,,\\\ \theta^{\prime }= u_{5}, \quad \phi = u_{6},\quad \phi^{\prime } = u_{7}\,. $$
Therefore, the corresponding system of simultaneous first order ODEs are

(17) $$ u_{1}^{\prime }= u_{2}\,,\quad u_{2}^{\prime }= u_{3}\,, u_{3}^{\prime }\!=\!\frac{{ - {u_1}{u_3} \!- \!2\gamma {u_3}[ {{\beta ^ * }\! +\! (1 - {\beta ^ * })( {1- {{{We} \over 2}}{u_3}} ){{( {1 - We{u_3}} )}^{- 2}}} ] \!+\! A({u_2} \!+\! {{\eta \over 2}}{u_3} + 1)}+ \!{{M^2}({u_2} - 1)\! -\! \lambda ({u_4} \!+\! Nr{u_6})\cos \Phi }}{{( {1 + 2\gamma \eta } )[ {{\beta ^ * } + (1 - {\beta ^ * }){{( {1 - We{u_3}} )}^{ - 2}}} ]}}\,, $$
(18) $$ u_{4}^{\prime }= {u_5}\,,\quad u_{5}^{\prime } = \frac{{{ - Pr ( {1 + 2\gamma \eta } )( {Nb{u_5}{u_7} + Ntu_5^2}) + Pr A{{\eta \over 2}}{u_5})}}{ - \Pr A\beta {u_4} - 2[ {1 + {{4 \over 3}}{R_d}} ]\gamma{u_5}}}{{( {1 + 2\gamma \eta } )[ {1 + {{4 \over3}}{R_d}} ]}}\,, $$
(19) $$ u_6^{\prime } = {u_7}\,,\quad u_7^\prime = \frac{{ - 2\gamma {u_7} - {{{Nt}\over {Nb}}}[ {( {1 + 2\gamma \eta } )u_5^\prime + 2\gamma{u_3}} ] + ScA{{\eta \over 2}}{u_7} - Sc{u_1}{u_7}}}{{( {1+ 2\gamma \eta } )}} $$
along with the boundary conditions

(20) $$ u_{1}(0 ) = s\,,\quad u_{2}( 0 ) - \chi - \alpha [{{\beta ^ * } + (1 - {\beta ^ * }){{( {1 - We{u_3}(0)} )}^{ -1}}} ]\,,\\ u_{4}( 0 ) = 1 + \delta {u_5}( 0 )\,,\quad Nb{u_7}(0 ) + Nt{u_5}( 0 ) = 0\,, $$
(21)u_{2}( \infty ) = 1\,,\quad u_{4}( \infty ) =0\,,\quad u_{6}( \infty ) =0\,. $$
The solution of given initial value problem $( {IVPs} )$ is obtained by using RK-45 method. To find the better approximation for the solutions the values of initial guesses or missing conditions are adjusted. The fifth-order Runge-Kutta-Fehlberg method can be presented as:

(22) $$ {Z_{i + 1}} = {Z_i} + \Big( {\frac{{16}}{{135}}{K_{00}} + \frac{{6656}}{{12825}}{K_{22}} + \frac{{28561}}{{56430}}{K_{33}}-\frac{9}{{50}}{K_{44}} + \frac{2}{{55}}{K_{55}}} \Big)h\,, $$
where the coefficients ${K_{00}}$ to ${K_{55}}$ are, respectively defined as:

$ {K_{00}} = g( {{x_i},{y_i}} )\,, \quad {K_{11}} = g\Big( {{x_i} + \frac{1}{4}h,{y_i} + \frac{1}{4}h{K_{00}}} \Big)\,,\quad {K_{22}} = g\Big( {{x_i} + \frac{3}{8}h,{y_i} + \Big({\frac{3}{{32}}{K_{00}} + \frac{9}{{32}}{K_{11}}} \Big)h} \Big)\,,\\ {K_{33}} = g\Big( {{x_i} + \frac{{12}}{{13}}h,{y_i} + \Big({\frac{{1932}}{{2197}}{K_{00}} - \frac{{7200}}{{2197}}{K_{11}} +\frac{{7296}}{{2197}}{K_{22}}} \Big)h} \Big)\,,\\ {K_{44}} = g\Big( {{x_i} + h,{y_i} + \Big( {\frac{{439}}{{216}}{K_{00}} -8{K_{11}} + \frac{{3860}}{{513}}{K_{22}} - \frac{{845}}{{4104}}{K_{33}}}\Big)h} \Big)\,,\\ {K_{55}} = g\Big( {{x_i} + \frac{1}{2}h,{y_i} + \Big( { -\frac{8}{{27}}{K_{00}} + 2{K_{11}} - \frac{{3544}}{{2565}}{K_{22}} +\frac{{1859}}{{4104}}{K_{33}}-\frac{{11}}{{40}}{K_{44}}} \Big)h} \Big)\,.$

Finally, the maximum value of $\eta $ displaying the ambient conditions is taken to be ${\eta _\infty } = 25$ depending upon the physical parameters. The step size is used to be $h=0.001$ and the above proceeding is repeated until the converged results equivalent to the coveted level of precision ${10^{-6}}$.

3.2 Validation of Numerical Code

To make sense of the physical problem more clearly, the numerical technique is implemented to solve governing differential equations, since it gives opportunity to pick suitable values of involving flow parameters. The accuracy of the present computations is shown in Table 1 by comparing values of $-\theta^{\prime }(0)$ with previously published data for different values of $\Pr$ and neglecting the influences of all other parameters. It can be revealed from table that the result of present investigations are same with previous result calculated by Khan and Pop,^[36] Wang,^[37] Gorla and Sidwai,^[38] and Dhanai et al.^[39]


Table 1
Table 1Comparison of present numerical results for $ - \theta^{\prime }(0)$ with already published results in literature for flat stretching sheet $( {\gamma = 0, \chi = 1} )$ with no slip condition when $M = 0 = \lambda = \alpha = \delta = {R_d} = Nb = Nt = s = A $.

New window|CSV

4 Results and Discussions

The prime objective of the present analysis is to investigate the physical characteristic MHD mixed convective flow past an inclined stretching cylinder in the presence of velocity and thermal slip effects. Effects of dimensionless parameters, such as local Weissenberg number $( {We} )$, curvature parameter $( \gamma )$ , unsteadiness parameter $( A )$, magnetic parameter $(M)$, mixed convection parameter $(\lambda )$, buoyancy force parameter $( {Nr})$, heat source/sink parameter $( \beta )$, viscosity ratio parameter $( {{\beta^*}} )$ radiation parameter $( {{R_d}} )$, suction/injection parameter $( s )$, Prandtl number $( {Pr} )$, Schmidt number $( {Sc} )$, stretching parameter $( \chi )$, velocity slip parameter $( {\alpha } )$, thermal slip parameter $( {\delta } )$, Brownian motion parameter $( {Nb} )$ and thermophoresis parameter $({Nt} )$ are mainly interested of this study. Flow, temperature and concentration fields of the stagnation flow have been examined by employed the boundary layer concept to obtain a set of coupled momentum equations, energy equations and concentration equations. A suitable transformation has then utilized to alter the nonlinear, coupled partial differential equations to a set of nonlinear, coupled ordinary differential equations with the aid of RKF scheme via shooting procedure. The computation has been investigated for fix value of various physically parameter on use momentum, thermal and concentration fields such as $We = 1.0$, $\gamma = 0.1$, $M = 0.2$, $\lambda = 0.1$, $\alpha = 0.1$, $\beta = 0.1$, ${\beta ^ * } = 0.1$, $\delta = 0.1$, $\chi = 0.1$, $\Pr = 2.0$, $Sc = 5.0$, $Nb = 0.1$, $Nt = 0.1$, ${R_d} = 0.1$, $Nr = 0.5$ and $\Phi= \pi /4$, otherwise mentioned.

4.1 Behavior of Velocity Profiles

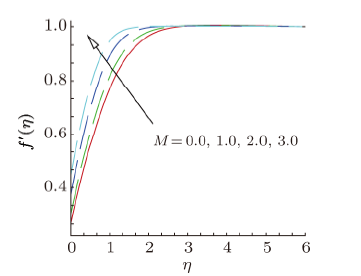
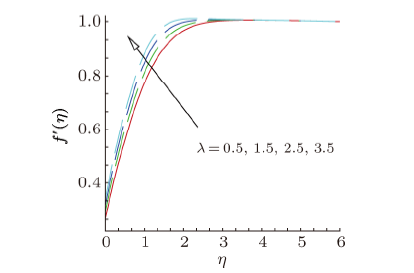
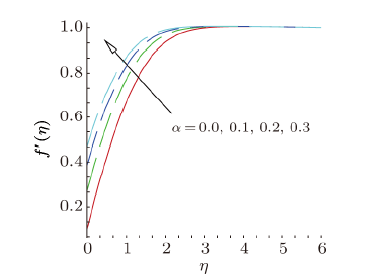
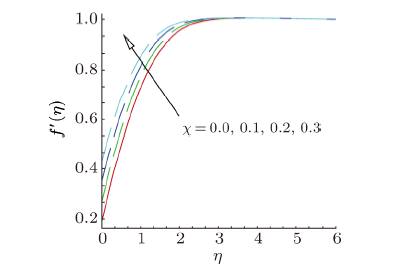
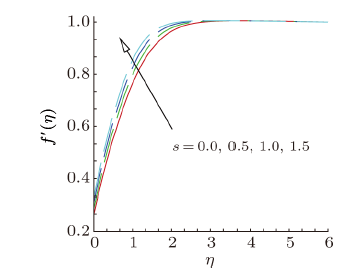
parameter $\gamma $ on velocity profiles $f^{\prime }(\eta )$. From this plot, we observe that velocity of the fluid decreases as the curvature parameter $\gamma $ rises for vertical $( {\phi = 0} )$, inclined $( {\phi = \pi /4})$ and horizontal $( {\phi = \pi /4} )$ cylinder. This is due to the fact that as the angle of inclination grows the effect of the buoyancy force due to thermal diffusion declines by a factor of cos${\phi }$. Consequently, the driving force to the fluid diminishes as a result there is decline in the velocity profile. It is also observed that as curvature parameter $\gamma $ the velocity field initially decreases and then it decreases after a distance $\eta $ from the surface. Physically, it is noteworthy to mention that as $\gamma $ increases, the radius of the curvature decreases, thus the contact area between the cylinder and fluid decreases which creates less resistance to fluid flow. Figure 3 depicts the variation in velocity profil $f^{\prime }(\eta )$ due to the variation in magnetic field parameter $M$. Velocity field illustrates the increasing behavior as up surging magnetic parameter. The parameter $M$ is the ratio of electromagnetic force to the viscous force and magnetic field is applied in the opposite direction of the fluid, therefore as enhancing magnetic field causes reduction in the boundary layer thickness. Variation in velocity field for distinct estimations of mixed convection parameter $\lambda $ is established in Fig. 4. This figure explains that as enhances the mixed convection parameter the velocity profile increases. Physically, rise in thermal buoyancy force that leads to enhance the velocity of the fluid within the boundary layer. Figure 5 is plotted to examine the variation in velocity profile against the velocity slip parameter $\alpha $. It is cleared from this figure that on rising the values of velocity slip parameter $\alpha $, the velocity of nanofluid continuously increases in the range of $0\leq \eta <3$, and for this reason layer width diminishes. The effect of stretching parameter $\chi $ the velocity field is depicted in Fig. 6. As we increasing the stretching parameter $\chi $ the velocity of nanofluid increases and associated boundary layer thickness decreases. Figure 7 shows the velocity profile for suction/injection parameter $s$. It can be seen that velocity increases gradually with increasing suction/injection parameter $s$.

4.2 Behavior of Temperature Profiles

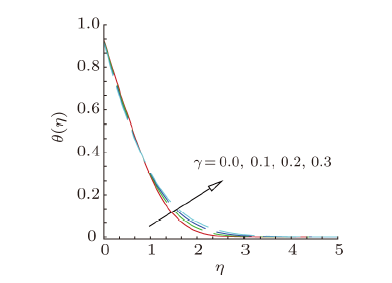
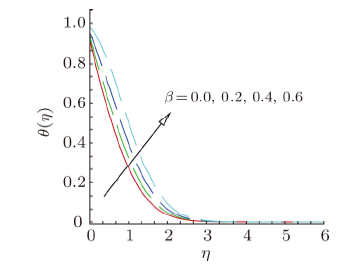
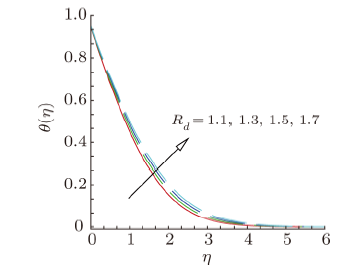
Effects of curvature parameter $\gamma $, heat generation/absorption parameter, radiation parameter, thermophoresis parameter and thermal slip parameter on the temperature profile $\theta ( \eta )$ are shown in Figs. 8--12. Figure 8 indicates that impact of curvature parameter $\gamma $ on the temperature field. It is noted from this plot, the temperature of the nanofluid initially decreasing slightly and then it increases. Higher values of curvature parameter $\gamma $ decline the rate of heat transfer, therefore temperature of fluid and related boundary layer thickness increases. The influence of heat generation/absorption parameter $\beta $ on the temperature profile $\theta ( \eta )$ is illustrated in Fig. 9. This graph shows that temperature of nanofluid and thermal boundary layer thickness intensifies together with heat generation/absorption parameter $\beta $. Impact of radiation parameter ${R_d}$ on $\theta ( \eta )$ is captured in Fig. 10. Increase in radiation parameter corresponds to increase in temperature and thermal boundary layer thickness. Thus, radiative heat transport rate upgrades and consequently temperature of the liquid rises.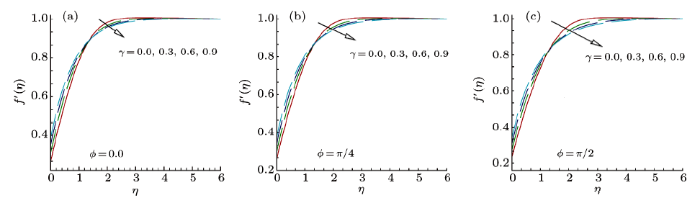

New window|Download| PPT slide
Fig. 2(Color online) Velocity profile, for different values of curvature parameter $\gamma $.

New window|Download| PPT slide
Fig. 3(Color online) Velocity profile, for different values of magnetic parameter $M$.

New window|Download| PPT slide
Fig. 4(Color online) Velocity profile, for different values of mixed convection parameter $\lambda $.

New window|Download| PPT slide
Fig. 5(Color online) Velocity profile, for different values of velocity slip parameter $\alpha $.

New window|Download| PPT slide
Fig. 6(Color online) Velocity profile, for different values of stretching parameter $\chi $.

New window|Download| PPT slide
Fig. 7(Color online) Velocity profile, for different values of suction parameter $s$.

New window|Download| PPT slide
Fig. 8(Color online) Temperature profile, for different values of curvature parameter $\gamma $.

New window|Download| PPT slide
Fig. 9(Color online) Temperature profile, for different values of heat generation/absorption parameter $\beta$

New window|Download| PPT slide
Fig. 10(Color online) Temperature profile, for different values of heat radiation parameter ${R_d}$.



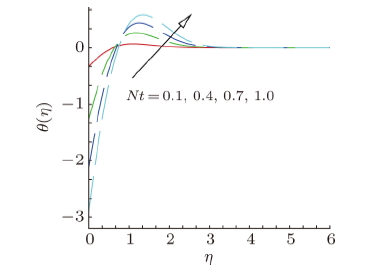
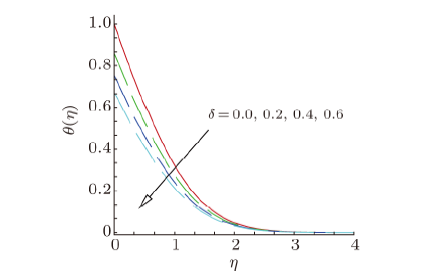
Effects of thermophoresis parameter $Nt$ on temperature profile $\theta ( \eta)$ is demonstrated in Fig. 11. It is observed that temperature of nanofluid boosts with the higher values of thermophoresis parameter $Nt$.Behavior of temperature profile $\theta ( \eta )$ for varying values of thermal slip parameter $\delta $ is displayed in Fig. 12. According to Fig. 12, on uplifting the values of thermal slip parameter $\delta $,temperature profile $\theta ( \eta )$ of nanofluid decreases along with thermal boundary layer thickness.

New window|Download| PPT slide
Fig. 11(Color online) Temperature profile, for different values of thermophoresis parameter $Nt$.

New window|Download| PPT slide
Fig. 12(Color online) Temperature profile, for different values of thermal slip parameter $\delta $.

4.3 Behavior of Concentration Profiles

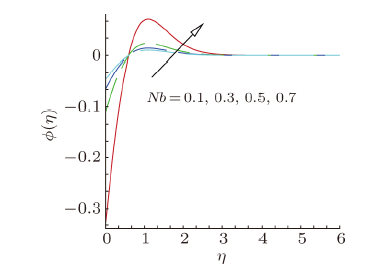
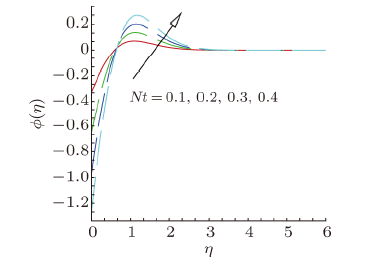
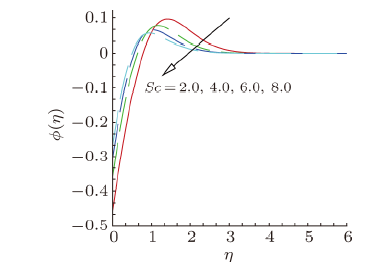
The variation in concentration profile $\phi ( \eta )$ of nanofluid with $\eta $, in domain $[1,6)$, of distinct values of curvature parameter $\gamma $, Brownian motion parameter $Nb$, thermophoresis parameter $Nt$ and Schmidt number $Sc$ are portrayed in Figs. 13$-$16. The variation in concentration profile $\phi ( \eta )$ with respect to variable $\eta $, is presented in Fig. 13, for some values of curvature parameter $\gamma $. It is clear from this figure that the concentration profile $\phi ( \eta )$ increases with the larger values of curvature parameter $\gamma $. Variation in concentration profile $\phi ( \eta )$ due to the variation in Brownian motion and thermophoresis parameters is displayed in Figs. 14 and 15. It is observed that concentration profiles $\phi ( \eta )$ show the decreasing behavior against Brownian motion parameter $Nb$ and increasing behavior against thermophoresis parameter $Nt$. Effect of Schmidt number $Sc$ on the dimensionless concentration profile is shown in Fig. 16. From this figure, we can noticed that concentration of nanoparticles and concentration boundary layer thickness diminishes with the growth of Schmidt number $Sc$.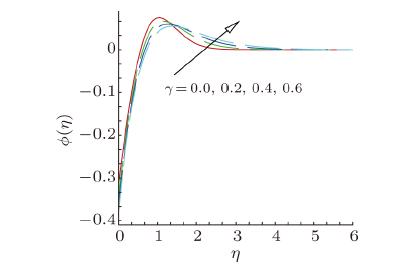

New window|Download| PPT slide
Fig. 13(Color online) Concentration profile, for different values of curvature parameter $\gamma $.

New window|Download| PPT slide
Fig. 14(Color online) Concentration profile, for different values of Brownian motion parameter $Nb$.

New window|Download| PPT slide
Fig. 15(Color online) Concentration profile, for varying thermophoresis parameter $Nt$.

New window|Download| PPT slide
Fig. 16(Color online) Concentration profile, for different values of Schmidt number $Sc$.

4.4 Behavior of Skin Friction and Nusselt Number

Figure 17 is illustrated to analyze the effects of several parameters on the physical quantities.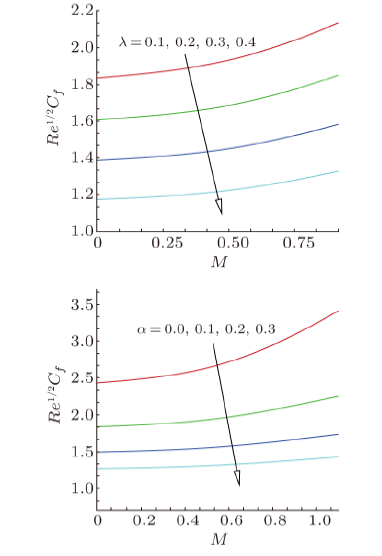

New window|Download| PPT slide
Fig. 17(Color online) Effect of $\lambda $ and $\alpha $ on dimensionless skin friction coefficient $R{e^{1/2}}{C_f}$.

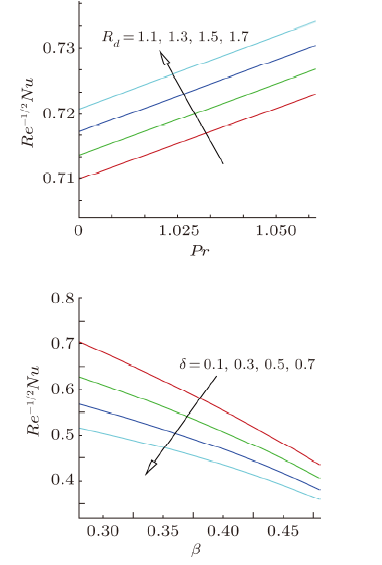New window|Download| PPT slide
Fig. 18(Color online) Effect of ${R_d}$ and $\delta $ on dimensionless heat transfer rate $R{e^{- 1/2}}Nu$.



Behavior of skin friction coefficient $Re^{1/2}C_{f}$ under the effects of magnetic field parameter $M$, mixed convection parameter $\lambda $ and velocity slip parameter $\alpha $ is presented in Fig. 17. From this figure we observe that the local skin-friction coefficient $Re^{1/2}C_{f}$ decreases for both mixed convection parameter $\lambda $ and velocity slip parameter $\alpha $ increases against the magnetic parameter $M$.

Figure 18 is portrayed to show the influences of radiation parameter $R_{d}$ and thermal slip parameter $\delta $ on local Nusselt number $Re^{-1/2}Nu$ against the magnetic field parameter against Prandtl number $Pr$ and heat generation/absorption $\beta $. It is observed that rate of heat transfer increases with an increment in radiation parameter $R_{d}$ while an opposite behavior is observed for higher thermal slip parameter $\delta $.

5 Concluding Remarks

In this article, we have consider the MHD flow through an inclined stretched cylinder in the presence of slip effects. The mixed convection, thermal radiation and heat generation/absorption effects with new mass flux condition and suction parameter are also incorporated in this investigation. Buongiorno's model is adapted to discuss the effects of Brownian motion and thermophoresis. The governing PDEs are reduced into nonlinear ODEs and solved numerically using RK 45 method. The variations of skin friction, Nusselt number, velocity,temperature as well as concentration have been discussed in this study for some values of flow parameters, like, magnetic field parameter $M$, mixed convection parameter $\lambda $, mass transfer parameter $s$, velocity slip parameter $\alpha $, thermal slip parameter $\delta $, radiation parameter $R_{d}$,curvature parameter $\gamma $, Prandtl number $Pr$, Schmidt number $Sc$, Brownian motion $Nb$ and thermophoresis parameter $Nt$. The following conclusions are drawn from the analysis.

(i) The curvature parameter increases the temperature and concentration profiles.

(ii) Velocity field increases with an increase in magnetic field parameter and suction parameter.

(iii) The thickness of the thermal boundary layer increases with an increase in thermal radiation parameter, heat generation/absorption parameter and thermophoresis parameter.

(iv) The results of this article indicate that the skin friction reduces for larger mixed convection and velocity slip parameters.

(v) Nusselt number shows the increasing behavior as increasing radiation parameter and decreasing behavior as increasing thermal slip parameter.

(vi) The nanoparticles volume fraction is upgrades by higher Brownian motion and thermophoresis parameter.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] S. U. S. Choi , ASME-Publications-Fed 231 ( 1995) 99.
[Cited within: 1]

[2] J. Buongiorno, J. Heat Transf . 128(2006) 240.
[Cited within: 1]

[3] A. Kuznetsov and D. Nield, Int. J. Heat Mass Transf. 65(2013) 682.
DOI:10.1016/j.ijheatmasstransfer.2013.06.054URL [Cited within: 1]

[4] W.A Khan . and O. D. Makinde, Int. J. Thermal Sci. 81(2014) 118.
DOI:10.1016/j.ijthermalsci.2014.03.009URL [Cited within: 1]

[5] N. Sandeep, B. R. Kumar, M. S. J . Kumar, J. Mol. Liq. 212(2015) 585.
[Cited within: 1]

[6] F. Mabood, W. A. Khan, A. I. M . Ismail, J. Magn. Magn. Mat. 374(2015) 569.
[Cited within: 1]

[7] A. Mushtaq, M. Mustafa, T. Hayat, A. Alsaedi , Advan. Powd. Tech. 27(2016) 2223.
[Cited within: 1]

[8] O. Pourmehran, M. R. Gorji, D. D. Ganji, J. Taiwan Inst . Chem. Eng. 65(2016) 162.
[Cited within: 1]

[9] R. Ahmad, M. Mustafa, T. Hayat, A. Alsaedi, J. Magn.Magn.Mat. 407(2016) 69.
[Cited within: 1]

[10] S. Jahan, H. Sakidin, R. Nazar, I. Pop, J. Mol. Liq . 233(2017) 211.
[Cited within: 1]

[11] P. Valipour, R. Moradi, F. S. Aski, J. Mol. Liq . 237(2017) 242.
[Cited within: 1]

[12] M.R Eid .and K. L. Mahny, Advan. Powd. Tech. 28(2017) 3063.
[Cited within: 1]

[13] S. Gupta, D. Kumar, J. Singh , Int. J. Heat Mass Transf. 118(2018) 378.
DOI:10.1016/j.ijheatmasstransfer.2017.11.007URL [Cited within: 1]

[14] M. Sheikholeslami, T. Hayat, T. Muhammad, A. Alsaedi , Int. J. Mech. Sci. 135(2018) 532.
DOI:10.1016/j.ijmecsci.2017.12.005URL [Cited within: 1]

[15] T. Muhammad, A. Alsaedi, S. A. Shehzad, T. Hayat , Chinese J. Phys. 55(2017) 963.
DOI:10.1016/j.cjph.2017.03.006URL

[16] T. Hayat, T. Muhammad, M. Mustafa, A. Alsaedi , J. Mol.Liq .229(2017) 541.
[Cited within: 1]

[17] O. D. Makinde , Curr. Nanosci. 9(2013) 673.
URL [Cited within: 1]
The thermal boundary layer of nanofluids over an unsteady stretching sheet with a convective surface boundary condition is investigated. Two types of water based Newtonian nanofluids containing metallic or nonmetallic nanoparticles such as Copper (Cu) and Alumina (Al2O3) are considered from a theoretical viewpoint and for a range of nanoparticle volume fractions. Using a similarity transformation the governing time dependent nonlinear boundary layer equations for momentum and thermal energy are reduced to a set of nonlinear ordinary differential equations. The resulting four-parameter problem is solved numerically using fourth order Runge-Kutta integration scheme with shooting technique for some representative values of the unsteadiness parameter (A), the Prandtl number (Pr), local Biot number (Bi) and solid volume fraction parameter (phi). It is shown the both the shear stress and heat transfer rate at the sheet surface are higher for Cu-water as compared to Al2O3-water. Besides, it is found that the heat transfer rate at the surface decreases with increasing flow unsteadiness (A) and increases with increasing with increasing Bi and phi. A comparison with a previous study available in the literature has been done and we found an excellent agreement with them.

[18] S. Mukhopadhyay and I.C. Mandal , Eng. Sci. Tech. Int. J. 18(2015) 98.
[Cited within: 1]

[19] I. Fersadou, H. Kahalerras, M. E. Ganaoui , Computer Fluids 121 ( 2015) 164.
[Cited within: 1]

[20] T. Hayat, S. Qayyum, M. Imtiaz, A. Alsaedi , Int. J. Heat Mass Transf. 102(2016) 723.
DOI:10.1016/j.ijheatmasstransfer.2016.06.059URL [Cited within: 1]

[21] M. Waqas, M. Farooq, M. Khan , et al., Int. J.Heat Mass Transf. 102(2016) 766.
[Cited within: 1]

[22] S. M. Ibrahim, G. Lorenzini, P. Vijaya Kumar, C. S.K Raju . Int. J. Heat Mass Transf. 111(2017) 346.
DOI:10.1016/j.ijheatmasstransfer.2017.03.097URL [Cited within: 1]

[23] R. U. Haq, Z. Hamouch, S. T. Hussain , T. Mekkaoui, 42(2017) 15925.
[Cited within: 1]

[24] Y. S. Daniel, Z. A. Aziz, Z. Ismail, F. Salah, J. Appl.Res.Tech. 15(2017) 464.
[Cited within: 1]

[25] P. R. Sharma, S. Sinha, R. S. Yadav, A. N. Filippov , Int. J. Heat Mass Transf. 117(2018) 780.
DOI:10.1016/j.ijheatmasstransfer.2017.10.026URL [Cited within: 1]

[26] C. Y. Wang , Phys. Fluids 31 ( 1988) 466.
[Cited within: 1]

[27] A. Ishak , R. Nazar and Ioan Pop, Appl.Math. Model. 32(2008) 2059.
[Cited within: 1]

[28] K. Vajravelu, K. V. Prasad, S. R. Santhi , Appl. Math. Comp. 219(2012) 3993.
DOI:10.1016/j.amc.2012.10.034URL [Cited within: 1]

[29] A.S Butt . and A. Ali, J.Taiwan Inst. Chem. Eng. 45(2014) 780.
[Cited within: 1]

[30] Z. Abbas, S. Rasool, M. M. Rashidi , Ain Shams Engin. J. 69(2015) 939.
[Cited within: 1]

[31] T. Hayat, Y. Saeed, S. Asad, A. Alsaedi, J. Mol.Liq . 220(2016) 573.
[Cited within: 1]

[32] M. Khan and R. Malik, J. Mol. Liq. 218(2016) 1.
DOI:10.1016/j.molliq.2016.02.024URL [Cited within: 1]

[33] A.K Pandey .and M. Kumar, Alex.Eng. J. 56(2017) 671.
[Cited within: 1]

[34] J. H. Merkin, N. Najib, N. Bachok , et al., Inst. Chem.Eng. 74(2017) 65.
[Cited within: 1]

[35] S. S. Nourazar, M. Hatami, D. D. Ganji, M. Khazayinejad , Powd. Tech. 317(2017) 310.
DOI:10.1016/j.powtec.2017.05.010URL [Cited within: 1]

[36] W.A Khan . and I. Pop, Int.J. Heat Mass Transf. 53(2010) 2477.
[Cited within: 1]

[37] C. Y. Wang , J. Appl. Math. Mech. 69 ( 1989) 418
[Cited within: 1]

[38] R. S. R. Gorla and I. Sidawi , Appl. Sci. Res. 52(1994) 247.
DOI:10.1007/BF00853952URL [Cited within: 1]

[39] R. Dhanai, P. Rana, L. Kumar , Powd. Tech., 288(2016) 140.
DOI:10.1016/j.powtec.2015.11.004URL [Cited within: 1]