删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Mapping Between Charge-Dyon and Position-Dependent Mass Systems

本站小编 Free考研考试/2022-01-02
Anderson L. de Jesus, Alexandre G. M. Schmidt,?Departamento de Física de Volta Redonda, Instituto de Ciências Exatas — Universidade Federal Fluminense, R. Des.Ellis Hermydio Figueira, 783, Bloco C, Volta Redonda RJ, CEP 27213-145, Brazil

Corresponding authors: E-mail:agmschmidt@gmail.com

First author contact:
Received:2019-01-22Online:2019-10-9


Abstract
The primary purpose of this work is to reproduce the scenario composed of a charge-dyon system utilizing position-dependent effective mass (PDM) background in the non-relativistic and in the relativistic regimes. In the non-relativistic case we substitute the exact charge-dyon eigenfunction into PDM Schr?dinger equation, in the Zhu-Kroemer parametrization, and then solve it for the mass distribution considering $M=M(r)$. Analogously, in the relativistic case we study the Klein-Gordon equation for a position-dependent mass, and in this case, we are able to analytically solve the equation for $M=M(r,\theta)$.
Keywords： position-dependent mass;Schr?dinger equation;Klein-Gordon equation;dyon


PDF (709KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Anderson L. de Jesus, Alexandre G. M. Schmidt. Mapping Between Charge-Dyon and Position-Dependent Mass Systems. [J], 2019, 71(10): 1261-1266 doi:10.1088/0253-6102/71/10/1261

1 Introduction

Dyon is a hypothetical particle having electric and magnetic charges proposed by Schwinger in 1969 as a phenomenological alternative to quark model.[1] In his article, Schwinger speculates that hadrons are composed of these dual charged particles, having fractional electric and magnetic charges and following the idea of electroweak interaction with its vectorial bosons exchanging electric charge, he postulated the existence of a vectorial boson $S$ (strong) of unit magnetic charge intermediating charge-exchange process for the dyon. The study of dyons and isolated magnetic monopoles has received attention over the latest years, in part by the possible explanation of the electric charge quantization by Dirac.[2] In the experimental aspect there is also plenty of research and the physics of magnetic monopoles was reproduced in spin ice system,[3-5] as well as, more recently, in quantum fields,[6] synthetic magnetic fields,[7] creation of a Dirac monopole-antimonopole pair in a spin-1 Bose-Einstein condensate[8] and by the use of metamaterials.[9]

On the other hand, quantum systems with position-dependent effective mass (PDM) have been studied and used in a great number of works and a considerable interest in this subject has grown up over the latest years. The quantum systems with position-dependent effective mass arose initially in the study of transport phenomena in semiconductors of variable, position-dependent chemical composition and the ordering problem was studied by von Roos.[10]PDM systems can also be used to model scattering in abrupt heterostructures,[11] quantum dots[12] and, surprisingly, Dirac magnetic monopoles. The investigation about mapping charge-monopole into PDM systems was initially carried out by the authors in Ref. [13] where an exact mapping was constructed between these systems. In the present work, our goal is to make a similar map between charge-dyon and a PDM system, in other words, we study the possibility of having a PDM charge with the same eigenfunctions and energy eigenvalues of the constant mass charge-dyon system. Thus, we look for a PDM system which could, in principle, be realized in the laboratory and that can simulate another one --- the charge dyon system --- that in the present day cannot be studied experimentally. The idea of simulating a difficult or even unrealizable[14] quantum system using a controllable condensed matter system is explored in several ways.[15-17]

To determine the mass distribution --- which on its turn can also be interpreted as an effective potential --- which exactly reproduces the eigenfunctions and energy eigenvalues of the target charge-dyon system we proceed as in Ref. [13]. We substitute both the exact eigenfunctions and energy eigenvalues of the charge-dyon system into the Schr?dinger equation and solve it not for $\psi$ but the mass $M$. In the non-relativistic case, the Hamiltonian bears the so-called ordering problem, and we use the Zhu-Kroemer parametrization[18] which is one of the two parametrizations physically admissible.[19] The differential equation for the mass $M$ becomes non-linear, and we look for simple solutions studying a two-point boundary value problem numerically. Still, in the relativistic problem, using the PDM Klein-Gordon equation, we manage to obtain an exact solution for the mass distribution as a function of spherical coordinates $(r,\theta)$.

The outline for our paper is the following: In Sec. 2 we derive the mapping equation satisfied by the mass distribution in the non-relativistic case. In Sec. 3 we turn to the relativistic case, utilizing the PDM Klein-Gordon equation, and obtain an exact solution for $m=m(r,\theta)$. Finally, in Sec. 4 we conclude the work.

2 Mapping a Non-Relativistic Dyon-Charge System into Position-Dependent Effective Mass Background

In this section we introduce the study of the quantum system composed of a non-relativistic charged point particle in the presence of a dyon, using a position-dependent effective mass background. The physical model can be obtained from an eigenvalue problem,

$$ H_0 \psi(r, \theta)=E\psi(r,\theta)\,, $$
where the Hamiltonian when the mass is position-dependent reads,

$$ H_0=-\frac{1}{M}\nabla^2+\frac{1}{M^2}\vec{\nabla}M\cdot\vec{\nabla}+U_{eff}\,, $$
where the effective potential $U_{eff}$ has the form,

$$U_{eff}=\frac{(\beta+1)}{2}\frac{\nabla^2 M}{M^2}-[\alpha(\alpha+\beta+1)+\beta+1] \times\frac{(\vec{\nabla}M)^2}{M^3}+V_{\rm ext}\,,$$
in some cases the external potential $V_{\rm ext}$ may be zero. The parameters $\alpha$, $\beta$, and $\gamma$ obey the constrain $\alpha+\beta+\gamma=-1$.

In our developments we will use spherical coordinates and in the non-relativistic problem we will use natural units --- namely $\hbar = m_e =c= 1 $ and $ e = \sqrt{2} $, where $\alpha$ the so-called fine-structure constant, namely $\alpha\approx1/137$. To determine the effective potential $U_{eff}$ for a particular system, we need to know the mass function $M$ and also to select a given ordering, that must obey certain physical considerations proposed by Dutra and Almeida.[19] In this work we will use a parametrization of von Roos Hamiltonian which fulfills the test, that is, the Zhu-Kroemer (ZK) ordering where $\alpha=\gamma = -1/2$, and $\beta=0$. This choice produces an effective potential $U_{eff}$ given by,

$$ U_{eff}=\frac{1}{2}\frac{\nabla^2 M}{M^2}-\frac{3}{4}\frac{(\vec{\nabla}M)^2}{M^3}\,.$$
The main idea is to construct a map between a system composed of a quantum scalar charged particle of mass $m_0=1$ interacting with a dyon located at the origin into a charged particle interacting with a position-dependent effective mass background. In order to obtain such a mapping we substitute the exact wavefunction of the charge-dyon system into the PDM Schr?dinger equation and solve it for the mass. The target system --- a charged particle with position-dependent mass, or in other words, a charged particle interacting with the effective potential (4) --- reproduces exactly the behavior of the original charge-dyon system.

The eigenfunctions for the charged particle interacting with a dyon are

$$ \psi_{\rm dyon}(r,\theta,\phi) = F_{Nl}(r)Y_{\mu l m}(\theta,\phi)\,,$$
where the angular part is known as generalized spherical harmonics,[20]

$$ Y_{\mu lm}(\theta,\phi)= 2^m\sqrt{\frac{(2l+1)(l-m)!(l+m)!}{4\pi (l-\mu)!(l+\mu)!}} \hphantom{Y_{\mu lm}(\theta,\phi) =} \\ \times\frac{P_{l+m}^{(-\mu-m,-\mu+m)}(\cos\theta)\exp[{i(m+\mu)\phi}]}{(1-\cos\theta)^{(\mu+m)/2} (1+\cos\theta)^{(\mu-m)/2}}\,,$$
where $P_n^{(a,b)}(\cos\theta)$ are the Jacobi polynomials, $\mu=eg$ is the product of electric and magnetic charges --- and it must be such that Dirac quantization condition holds,[2] i.e., $\mu=n/2$, where $n$ is an integer number, we consider here $Q=-\sqrt{\alpha}/\alpha$, where $Q$ is the electric charge of dyon. The quantum numbers are such that $l=\mu, \mu+1, \ldots$ and $-l\leq m\leq l$. The normalized radial functions reads,

$$ F_{N\ell}(r) =\frac{2^{\ell+1}[\Gamma(N+2\ell+2)]^{1/2}}{(N!)^{1/2}(N+\ell+1)\Gamma(2\ell+2)} (kr)^{\ell} \times e^{-kr} {_1F}_1(-N;2\ell+2;2kr)\,,$$
where $k^2= - 2m_0E > 0$, the function $_1F_1$ is the confluent hypergeometric function, $N$ is a radial quantum number $N=0,1,2,\ldots$ and $\ell$ is related to the angular quantum number $l$ via

$$ \ell=\sqrt{\Big(l+\frac{1}{2}\Big)^2-\mu^2}-\frac{1}{2}\,. $$

2.1 Non-Linear Differential Equation for the Mass Distribution

Substituting the eigenfunction $\psi_{\rm dyon}$ into the PDM Schr?dinger equation with Hamiltonian (2), using the effective potential (4), we obtain

$$ -\Big\{ \frac{1}{r^2}\frac{\partial }{\partial r}\Big(r^2\frac{\partial \psi_{\rm dyon}}{\partial r}\Big) +\frac{1}{r^2\sin\theta} \frac{\partial }{\partial \theta} \Big(\sin\theta \frac{\partial \psi_{\rm dyon}}{\partial \theta}\Big) + \frac{1}{r^2\sin^2\theta} \frac{\partial^2 \psi_{\rm dyon}}{\partial^2 \phi}\Big\} + \frac{1}{M} \vec{\nabla}M\cdot \vec{\nabla} \psi_{\rm dyon} \quad + \Big(M V_{\rm ext} + \frac{1}{2M}\nabla^2M - \frac{3}{4M^2} \vec{\nabla}M\cdot\vec{\nabla}M\Big) \psi_{\rm dyon} = ME_{N\ell}\psi_{\rm dyon}\,, $$
where we used ZK-parametrization. So as to search a differential equation for the mass distribution $M(r,\theta,\phi)$, let us use the following property of the $Y_{\mu lm}$ functions,

$$ -\Big\{\frac{1}{\sin\theta} \frac{\partial }{\partial \theta} \Big(\sin\theta \frac{\partial }{\partial \theta}\Big) + \frac{1}{\sin^2\theta} \frac{\partial^2}{\partial^2 \phi}\Big\}Y_{\mu lm} = \Big[ l(l+1)-\mu^2 - \frac{2 i\mu (1-\cos\theta)}{\sin^2\theta}\frac{\partial }{\partial \phi}- \frac{\mu^2(1-\cos\theta)^2}{\sin^2\theta}\Big] Y_{\mu lm}\,,$$
substituting the above result into Eq. (9) we obtain,

$$ - Y_{\mu lm}\Big(\frac{d^2}{d r^2} + \frac{2}{r}\frac{d}{d r}\Big)F_{N\ell}+ \frac{F_{N\ell}}{r^2} \Big[ l(l+1)-\mu^2 - \frac{2i\mu (1-\cos\theta)}{\sin^2\theta}\frac{\partial }{\partial \phi} -\frac{\mu^2(1-\cos\theta)^2}{\sin^2\theta}\Big] Y_{\mu lm} \quad + \Big(\frac{1}{M} \vec{\nabla}M\cdot \vec{\nabla} + M V_{\rm ext} + \frac{1}{2M}\nabla^2M - \frac{3}{4M^2} \vec{\nabla}M\cdot\vec{\nabla}M\Big) F_{N\ell} Y_{\mu lm} = ME_{N\ell}F_{N\ell} Y_{\mu lm}\,, $$
using the confluent differential equation the first four terms yields,

$$ - Y_{\mu lm}\Big(\frac{d^2}{d r^2} + \frac{2}{r}\frac{d}{d r}\Big)F_{N\ell}+\frac{l(l+1)F_{N\ell} Y_{\mu lm}}{r^2}- \frac{\mu^2F_{N\ell} Y_{\mu lm}}{r^2} = \frac{2 F_{N\ell} Y_{\mu lm}}{r} + E_{N\ell}F_{N\ell} Y_{\mu lm}\,, $$
and recalling that the generalized spherical harmonics are eigenfunctions of $L_z$, we write

$$ -i\frac{\partial Y_{\mu lm}}{\partial \phi} =(m+\mu)Y_{\mu lm}\,.$$
We intend to investigate if there exists a solution, so let us simplify the equation taking $m+\mu=0$. This constrain gives an azimuthal symmetry to the system and Eq. (9) becomes,

$$ \nabla^2 M - \frac{3}{2}\frac{(\vec{\nabla}M)^2}{M}+\frac{4M}{r} + \frac{2}{\psi_{\rm dyon}}\vec{\nabla}M \cdot \vec{\nabla}\psi_{\rm dyon}-\frac{2\mu^2(1-\cos\theta)^2M}{r^2{\sin}^2\theta}= 2M(M-1)E_{N\ell}\,,$$
which is a quite difficult equation. Let us tackle this equation considering a special where the mass depends only on the radial coordinate, consequently $\partial M/\partial\theta=0$, using the gradient and Laplacian in spherical coordinates, we obtain a non-linear ODE for the mass distribution function $M(r)$. This differential equation reads,

$$ \frac{d^2 M}{d r^2}+\frac{2}{r}\frac{d M}{d r}-\frac{3}{2M}\Big(\frac{d M}{d r}\Big)^2+\frac{4M}{r}+\frac{2}{F_{N\ell}}\frac{d F_{N\ell}}{d r}\frac{d M}{d r}-\frac{2\mu^2(1-\cos\theta)^2M}{r^2{\sin}^2\theta}=2M(M-1)E_{N\ell}\,,$$
where the term $4M/r$ involves the product $eQ$, remembering that we are considering $eQ=-1$. In the system composed of a charged particle and a dyon the energy spectrum is discrete, because of the electric charge $Q$ of dyon, so the energy eigenvalues are

$$ E_{N\ell}=\frac{-1}{(N+\ell+1)^2}\,, $$
namely these are the allowed bound states of the charged particle interacting with a static dyon field.

2.2 Numerical Solutions

Considering that the mass depends only on the radial coordinate, namely $M=M(r)$, we need to take a particular value of $\theta$, say $\theta_0$, in order to solve Eq. (15) numerically. Let us choose the initial conditions $ M(r_i) = M(r_f) = 1/2 $ for $r_i=0.22$, and $r_f=1$, and let $\theta_0 = \pi/4$. We also search for solutions where $m+\mu=0$ so let us take $\mu=l=-m=1$. Equation (15) will be numerically solved by the {\it Mathematica} software --- this is an example of the so-called two-point boundary value problem --- only for certain values of energy, given by the expression (16).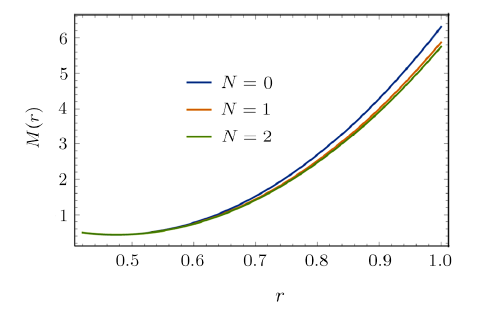

New window|Download| PPT slide
Fig. 1(Color online) Plot of numerical solutions of Eq. (15) for $\mu=1$ and $l=1$. Boundary conditions are $M(r)$ using $M(r_i) = M(r_f) = 1/2$ for $r_i=0.22$ and $r_f=1$, here we fix $\theta_0 = \pi/4$. As close as one approaches the origin, where the dyon is located, the solution diverges.



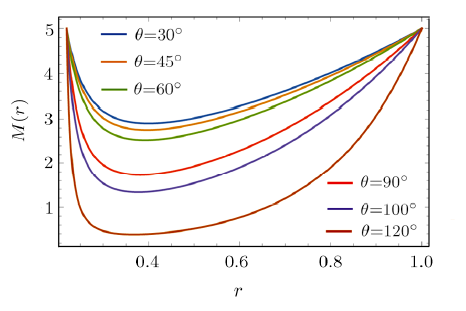
New window|Download| PPT slide
Fig. 2(Color online) Plot of numerical solutions of Eq. (15) for some values of $\theta$. In these solutions we consider $\mu=1$, $l=1$, and $N=0$. Boundary conditions are $M(r)$ using $M(r_i) = M(r_f) = 1/2$ for $r_i=0.22$ and $r_f=1$, for $\theta$ between $10^\circ$, and $140^\circ$ approximately, there is a continuum of radial solutions.



New window|Download| PPT slide
Fig. 3(Color online) Effective potentials calculated using solutions of Eq. (15) with $M(r_i) = M(r_f) = 1/2$ for $\theta_0 = \pi/4$, $r_i=0.22$, and $r_f=1$. The three curves for $N=0,1,2$ (blue, yellow and green) are overlapped. Parameters are $\mu=l=1$.



The solutions for three values of quantum number $N$ are presented in Fig. 1. The solutions tend to infinity near $r_i$ and possess local maximum. The effective potential corresponding to each solution is given by Eq. (3) and the curves for each radial solution are plotted in Fig. 2 and for this case it has no local minimum. The radial solutions also depend on $\theta$, this dependence is presented in Fig. 3, where we enumerate some values of $\theta$ and their respective radial solutions.

3 Mapping a Relativistic Dyon-Charge Sys-tem into Position-Dependent Effective Mass Background - The Klein-Gordon Equation

In the present section we accomplish the mapping between a relativistic charge-dyon system and position-dependent mass system. This mapping is carried out using the Klein-Gordon equation introducing a position-dependent mass. The Klein-Gordon equation for constant mass reads,

$$ (\square^2 + m^2)\psi=0\,, $$
in the relativistic treatment we are going to use natural units where $\hbar = m_e =c = 1$ and $e=\sqrt{\alpha}$, the d'Alembertian operator reads,

$$ \square^2 = \frac{\partial^2}{\partial t^2} -\nabla^2\, $$
and let us assume the mass to be dependent on spherical coordinates $(r,\theta,\phi)$, that is, $m=m(r,\theta,\phi)$. Taking the Laplacian in spherical coordinates we obtain the following expression to the PDM Klein-Gordon equation,

$$ \Big[\frac{\partial^2}{\partial t^2}- \frac{1}{r^2}\frac{\partial}{\partial r}\Big(r^2\frac{\partial}{\partial r}\Big)-\frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\Big(\sin\theta \frac{\partial}{\partial \theta}\Big)-\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial \phi^2}+ m^2(r,\theta,\phi)\Big]\psi=0\,, $$
following the same methodology of the previous sections we need to substitute the exact solution for the relativistic charge-dyon system into PDM Klein-Gordon equation. This solution is well-known, see for instance,[20] and it reads,

$$ \psi=\psi(r,\theta,\phi,t)=F_{N\ell}(r)Y_{\mu lm}(\theta,\phi) e^{-i\omega t}\,, $$
where $\omega$ is the eigenvalue of energy (in present section we use the discrete part of the spectrum), $F_{N\ell}(r)$ is given in Eq. (7) and $Y_{\mu lm}(\theta,\phi)$ are the generalized spherical harmonics. Replacing the above exact solution into Eq. (19) and solving for the mass yields,

$$ m^2(r,\theta,\phi) = \frac{1}{F_{N\ell}}\frac{d^2 F_{N\ell} }{d r^2}+ \frac{2}{r F_{N\ell}}\frac{d F_{N\ell}}{d r}+ \frac{1}{Y_{\mu lm}}\Big[\frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\Big(\sin\theta \frac{\partial Y_{\mu lm}}{\partial \theta}\Big)-\frac{1}{r^2\sin^2\theta}\frac{\partial^2Y_{\mu lm}}{\partial \phi^2}\Big]+\omega^2\,, $$
utilizing Eq. (10) and considering the azimuthal symmetry, $m+\mu = 0$, we can set up the following expression,

$$ m^2(r,\theta)=\omega^2+\frac{1}{F_{N\ell}}\frac{d^2 F_{N\ell} }{d r^2}+ \frac{2}{r F_{N\ell}}\frac{d F_{N\ell}}{d r}+ \frac{[\mu^2-l(l+1)]}{r^2}+\frac{\mu^2(1-\cos \theta)^2}{r^2 \sin^2 \theta}\,. $$
The second step is to deal with the radial part. The radial equation for the relativistic charge-dyon system via Klein-Gordon equation is the confluent differential equation,

$$ \Big(\frac{d^2 }{d r^2}+ \frac{2}{r}\frac{d}{d r}-k^2 +2\omega\frac{1}{r}-\frac{[1+l(l+1)-\mu^2]}{r^2}\Big)F_{N\ell}(r)=0\,,$$
using this equation to eliminate the terms involving the derivatives of $F_{N\ell}(r)$ and using also the relativistic relation $k^2=\omega^2 - m_0^2$ we can obtain the exact mass distribution for the mapping between a charge-dyon system and PDM system in the relativistic regime. So our exact mass distribution reads,

$$ m(r,\theta)=\sqrt{2\omega^2-m_0^2-2\omega\frac{1}{r}+\frac{1}{r^2}+\frac{\mu^2(1-\cos\theta)^2}{r^2\sin^2\theta}}\,, $$
where $m_0$ is scalar particle mass interacting relativistically with the dyon located at the origin. So what we intend to do is to reproduce this scenario in a PDM background, keeping in mind there is no real dyon, but instead a relativistic scalar charged particle having a position-dependent mass, which can also be interpreted as a constant mass particle interacting with an effective potential $U_{eff}$. The discrete energy spectrum for this bound system has the following form,

$$ \omega=m_0\sqrt{1-\frac{1}{1+(N+\ell+1)^2}}\,, $$
where $N=0,1,2,\ldots$ is the quantum number for energy discrete levels. The relation between the angular quantum numbers $\ell$ and $l$ is,

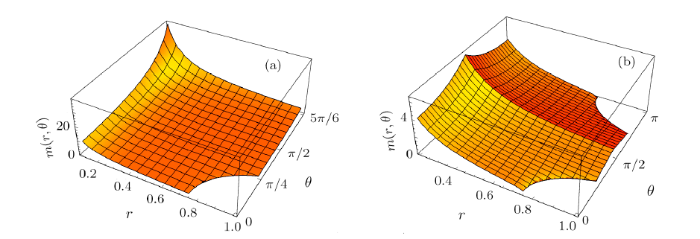
$$ \ell=\sqrt{\Big(l+\frac{1}{2}\Big)^2 -\mu^2+1}-\frac{1}{2}\,. $$
It is important to remember that the dyon shares the same problem the Dirac magnetic monopole has: the vector potential has a singularity which gives rise to the well-known Dirac string.[2] It is either located at $\theta=0$ or at $\theta=\pi$ since the vector potential has a pole at one of these points. Wu and Yang[21] correctly interpreted the problem and presented a solution introducing two vector potentials related by a gauge transformation and thus eliminated the string. In Fig. 4(a) we plot the mass distribution which would produce the charge-dyon system with the Dirac string located at $\theta=\pi$. Note that the mass increases as $\theta$ approaches the string. In fact it diverges for $\theta\rightarrow\pi$. In Fig. 4(b) we plot the mass distribution following the Wu-Yang construction, namely, we introduce a vector potential valid for $0\leq \theta\leq \pi/2 +\alpha$ that has a singularity at $\theta=\pi$, and another vector potential valid for $\pi/2-\alpha\leq\theta\leq \pi$ and singular at $\theta=0$. Both of them are related by a gauge transformation. The first one produces a mass distribution (24) and the second an analogous function where instead of $(1-\cos\theta)^2$ we have $(1+\cos\theta)^2$. So, a position-dependent electric charge such that $m=m(r,\theta)$ behaves as it would be interacting with a dyon located at the origin.

New window|Download| PPT slide
Fig. 4(Color online) Plot of analytical solution of Eq. (19) given by Eq. (24). In Fig. 4(a) we plot the mass distribution which would produce the pure Dirac magnetic monopole. Observe that the mass increases as one approaches the Dirac string which is located at $\theta=\pi$.In Fig. 4(b) we plot the mass distribution which would produce the Dirac magnetic monopole without the string using the well-known Wu-Yang construction.[21] The above position-dependent mass reproduces exactly the eigenfunction of a relativistic charge-dyon system with $\mu=1$, $l=0$, $N=1$, and $eQ=-1$.



4 Conclusion

We introduced a mapping between a charge-dyon and a PDM system in non-relativistic and relativistic regimes, in the former we replaced the exact solution (7) into PDM Schr?dinger equation to obtain the non-linear partial differential equation (14) for the mass distribution, so considering a radial dependence only, we solved this equation numerically and plotted the results. The treatment for the relativistic case is quite similar: instead of using PDM Schr?dinger equation we tackled the PDM Klein-Gordon equation (19). The ordering problem does not occur because of the absence of product between the mass and momentum operators, the last case is then more straightforward and gives us an analytical expression for the mass distribution $m(r,\theta)$, the plot of this solution is shown in Fig. 4. In Table 1, we present a summary of our results. This approach could lead to an experimental model, using a condensed matter system, which could simulate a charge-dyon system.


Table 1
Table 1Summary of the mapping between charge-dyon and PDM systems in the non-relativistic and relativistic regimes, respectively.

New window|CSV


Reference By original order
By published year
By cited within times
By Impact factor

J. Schwinger , Science 165(1969) 3895.
[Cited within: 1]

P. A. M. Dirac , Proc. R. Soc. A 133(1931) 60.
[Cited within: 3]

C. Castelnovo, R. Moessner, S. L. Sondhi , Nature (London) 451(2008) 42.
[Cited within: 1]

D. J. P. Morris, D. A. Tennant, S. A. Grigera , et al., Science 326 ( 2009) 411.


H. M. Revell, L. R. Yaraskavitch, J. D. Mason , et al., Nat. Phys. 9(2013) 34.
[Cited within: 1]

M. W. Ray, E. Ruokokoski, K. Tiurev , et al., Science 348 ( 2015) 544.
[Cited within: 1]

M. W. Ray, E. Ruokokoski, S. Kandel , et al., Nature (London) 505(2014) 657.
[Cited within: 1]

K. Tiurev, P. Kuopanportti, M. M?tt?nen , Phys. Rev. A 99(2019) 023621.
[Cited within: 1]

J. Wang, S. Qu, Z. Xu , et al., Photonics Nanostruct. 12(2014) 429.
[Cited within: 1]

O. von Roos , Phys. Rev. B 27(1983) 7547.
[Cited within: 1]

R. Koξ, M. Koξa, G. Sahinoglu , Eur. Phys. J. B 48(2005) 583.
[Cited within: 1]

A. Keshavarz and N. Zamani, Superlattices Microstruct. 58(2013) 191.
[Cited within: 1]

A. G. M Schmidt .and A. L. Jesus, J. Math. Phys. 59(2018) 102101.
[Cited within: 2]

J. Casanova, C. Sabín, J. León , et al., Phys. Rev. X 1 ( 2011) 021018.
[Cited within: 1]

O. Boada, A. Celi, J. I. Latorre, M. Lewenstein , New J. Phys. 13(2011) 035002.
[Cited within: 1]

H. Kim, G. Zhu, J. V. Porto, M. Hafezi , Phys. Rev. Lett. 121(2018) 133002.


O. Boada, A. Celi, J. R. Laguna , et al., New J. Phys. 17(2015) 045007.
[Cited within: 1]

Q. G. Zhu and H. Kroemer , Phys. Rev. B 27(1983) 3519.
[Cited within: 1]

A. S. Dutra and C. A. S. Almeida , Phys. Lett. A 275(2000) 25.
[Cited within: 2]

Ya. M. Shnir, Magnetic Monopoles , Springer-Verlag,Berlin, Heideberg ( 2005).
[Cited within: 2]

T. T. Wu and C. N. Yang , Nucl. Phys. B 107(1976) 365.
[Cited within: 2]

相关话题/Mapping Between Charge

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.